|
|
|
Menu 1 .55 Time :28
|
Menu 2 1.74 Time 1:27
|
| Total: 425,792 1,704 23:40 |
| Menu-Body 30%, 4% 1/3, 1/980 |
| Chapters 96 |
| Pages per chapter 17.75 14:48 |
Views
 |
Visitors
 |
|
1 Eratosthenes wrong 4 137 1:50
| 1. The science of Geography, which I now propose to investigate, is, I think, quite as much as any other science, a concern of the philosopher. In the first place, those who in earliest times ventured to treat the subject were philosophers — Homer, Anaximander of Miletus, and Hecataeus. Philosophers were also Democritus, Eudoxus, Dicaearchus, Ephorus, with several others of their times, and further, their successors — Eratosthenes, Polybius, and Poseidonius. Wide learning makes it possible to undertake geography, possessed solely by the man who has investigated things both human and divine. The utility of geography is manifold, concerning the activities of statesmen and commanders, knowledge of the heavens, and things on land and sea, animals, plants, fruits, and everything else seen in various regions. It presupposes in the geographer the philosopher, who busies himself with investigating the art of life, that is, of happiness. I must go back and consider each point in greater detail. First, Homer is the founder of the science of geography. He declared that the inhabited world is washed on all sides by Oceanus and mentioned some countries by name, leaving others to be inferred. Homer describes Ethiopia and Libya and the people living in the far east and west. He places the Elysian Plain in the west, where Menelaus will be sent by the gods, and describes the Islands of the Blest to the west of Maurusia. Homer also indicates that Oceanus surrounds the earth, describing the Ethiopians living at the ends of the earth and on the banks of Oceanus. |
|
| 2. In undertaking to write on a subject previously addressed by others, I should not be blamed unless my treatment is entirely repetitive. Despite excellent contributions by past geographers, much remains to be explored. If I can add even a little to their work, it justifies my efforts. The Roman and Parthian empires have expanded our geographic knowledge, much like Alexander's conquests did in earlier times, as noted by Eratosthenes. Alexander's campaigns opened up much of Asia and northern Europe to us, while the Romans have detailed western Europe and beyond the Ister River to the Tyras River. Mithridates and his generals extended our knowledge to regions near Lake Maeotis and Colchis, and the Parthians have illuminated Hyrcania, Bactriana, and the northern Scythians. Hence, I might have new insights to offer. My criticisms will mainly target successors of Eratosthenes, though contradicting such authoritative figures is challenging. If I criticize respected geographers like Eratosthenes, Hipparchus, Poseidonius, and Polybius, it’s with respect for their generally accurate work. Addressing Eratosthenes specifically, I will also consider objections raised by Hipparchus against him. While Eratosthenes, who studied under many eminent figures, might not be as unreliable as some suggest, his judgment in selecting philosophers to follow shows inconsistency. He studied under Zeno of Citium but ignored Zeno’s successors, favoring those who opposed Zeno and failed to establish lasting schools. This vacillation reflects his reluctance to fully commit to philosophy, evident in his various works. Nonetheless, I aim to correct his geographic errors wherever possible. |
|
| 3. Eratosthenes is wrong in giving undue attention to unreliable sources, like Damastes, despite occasionally acknowledging their inaccuracies. Even if parts of their accounts hold truth, they shouldn't be considered authoritative. Instead, credible figures, known for their accuracy and integrity, should be cited. Eratosthenes himself recounts a tale from Damastes, who claimed the Arabian Gulf was a lake and that Diotimus sailed an improbable route to Susa. Eratosthenes' critique of such stories is undermined by his own acceptance of dubious claims, like his assertion that the Gulf of Issus is the easternmost point of the Mediterranean, which contradicts his own measurements. Furthermore, Eratosthenes' approach is inconsistent. While he recognizes the limitations of ancient geographical knowledge, he still perpetuates certain myths. For example, he asserts that early Greeks only coasted for trade or piracy but later contradicts himself by claiming ancient mariners lacked the courage to venture into the Euxine Sea. Historical figures like Jason and Odysseus, however, are evidence of extensive ancient voyages. Eratosthenes also mishandles geographical phenomena, like the presence of shells far from the sea. He praises Strato's and Xanthus's theories about changing sea levels and continental shifts but offers no substantial critique. While Strato suggests varying sea depths cause these changes, the actual reasons involve geological activities like earthquakes and volcanic eruptions. Eratosthenes also fails to grasp the concept of a continuous sea level, misunderstanding the work of mathematicians like Archimedes. Ultimately, Eratosthenes' reliance on questionable sources and his inconsistent reasoning weaken his credibility. His acceptance of unfounded tales and misunderstanding of scientific principles demonstrate significant flaws in his geographical methodology. |
|
| 4. In his Second Book, Eratosthenes revises geographical principles, introducing mathematics and physics, and asserting the earth's spherical shape. While some assumptions are commendable, his earth measurement is disputed by later scholars. Hipparchus, although critical, uses Eratosthenes’ meridian measurements. Eratosthenes measures the inhabited world's breadth from Meroë to Thule, totaling 38,000 stadia. However, the distance from Borysthenes to Thule is questionable. Pytheas, who claims Thule is north of Britain, is considered unreliable. The true length of Britain contradicts Pytheas' exaggerated figures. Hipparchus notes that the parallel through Britain and Byzantium align, but Eratosthenes' distance estimation from Thule lacks basis. Eratosthenes' errors extend to the world's length. He asserts that the inhabited world's length from India to Iberia is more than double its breadth, but his calculations are flawed. He incorrectly estimates various distances, including from India to the Pillars of Heracles, adding unnecessary stadia. He also claims the inhabited world extends east to west along a parallel, dismissing the potential for multiple inhabited zones within the temperate region. His adherence to the earth's spheroidal shape leads to unnecessary disputes with Homer. Eratosthenes discusses continents' boundaries, criticizing the division by rivers and isthmuses as impractical. He argues that practical boundary separation, like that of districts, is necessary but underestimates its importance in larger geopolitical contexts. His closing remarks propose evaluating people based on qualities rather than Greek and Barbarian distinctions, praising Alexander's inclusive approach. However, he overlooks that such distinctions reflect societal traits, not individual merits, aligning with Alexander's strategic inclusiveness. |
|
|
|
2 Eratosthenes wrong, Hipparchus' worse 5 143 2 Hrs.
|
| 2. In his treatise on Oceanus, Poseidonius addresses geography from both geographical and mathematical perspectives. He starts with the hypothesis that the earth is sphere-shaped, a view aligned with understanding the universe. This leads to the conclusion that the earth has five zones. Poseidonius credits Parmenides with the division into five zones but criticizes his description of the torrid zone. Parmenides overstates its breadth, extending it beyond the tropics into the temperate zones. Aristotle's division is also flawed, according to Poseidonius, because the "torrid" should only refer to the uninhabitable regions due to heat. He argues that more than half of the zone between the tropics is uninhabitable, as evidenced by the Ethiopians south of Egypt. Poseidonius' calculations refine these boundaries. From Syene to Meroë is 5,000 stadia, and from Meroë to the Cinnamon-producing Country is 3,000 stadia, totaling 8,000 stadia. Adding Eratosthenes' calculation of 8,800 stadia to the equator, Poseidonius finds that the torrid zone's breadth is about half the distance between the tropics. His measurements, which estimate the earth's circumference at 180,000 stadia, further support this. Poseidonius also criticizes using the "arctic circles" to define temperate zones, as they vary in visibility and aren't consistent everywhere. He proposes five zones based on celestial phenomena: two periscian (beneath the poles), two heteroscian (next to the tropics), and one amphiscian (between the tropics). For human purposes, he adds two narrow zones beneath the tropics, characterized by extreme heat and sparse vegetation, producing unique human and animal adaptations. Overall, Poseidonius' work emphasizes the need for accurate geographical and mathematical measurements in understanding the earth's zones. |
|
| 3. Polybius divides the Earth into six zones: two beneath the arctic circles, two between the arctic circles and the tropics, and two between the tropics and the equator. However, a five-zone division aligns better with physics and geography. This division accounts for celestial phenomena and atmospheric temperature, which are crucial for understanding the organization of plants, animals, and semi-organic matter. The five zones consist of two frigid zones (lacking heat), two temperate zones (moderate heat), and one torrid zone (excess heat). This division is harmonious with geography as it defines the habitable earth by the temperate zone. Boundaries on the west and east are set by the sea, while the south and north are defined by the nature of the air, making the central area well-suited for life due to moderate temperatures. Poseidonius criticizes the division into five zones, proposing seven, adding two narrow zones beneath the tropics that experience extreme heat, making them arid and barren, with unique fauna adapted to harsh conditions. He asserts that these areas differ significantly from regions further south, which are more temperate and fertile. Polybius's method of defining zones using the arctic circles is flawed because non-variable points should not be defined by variable points. Despite this, dividing the torrid zone into two parts is practical, as it aligns with the division of the earth into northern and southern hemispheres, each comprising three zones. Poseidonius also challenges Polybius's claim that the region under the equator is the highest point on Earth. He argues that a spherical surface cannot have a high point and that the equatorial region is not mountainous but rather level with the sea. Despite inconsistencies, Poseidonius suspects mountains beneath the equator influence rainfall patterns. Finally, Poseidonius dismisses the idea of a continuous ocean around the Earth, and critiques various claims of circumnavigation of Libya, deeming them unsupported by evidence. His skepticism extends to the credibility of explorers’ accounts, favoring empirical verification over anecdotal stories. |
|
| 4. Polybius critiques ancient geographers, particularly Dicaearchus, Eratosthenes, and Pytheas. Pytheas claimed to have explored Britain and the mysterious Thule, describing bizarre phenomena. Polybius doubts a poor man's ability to travel extensively, criticizing Eratosthenes for partially believing Pytheas, and suggesting Euhemerus, who only claimed one journey, is more credible. Poseidonius questions the reliability of Eratosthenes and Dicaearchus. He highlights errors in their distance measurements, particularly from the Peloponnesus to the Pillars and the Adriatic. Polybius corrects some errors but makes others, such as exaggerating distances in Iberia. He questions Polybius's method of comparing the lengths of continents by segments of the northern semicircle and insists on using fixed measures parallel to the equator. Polybius's division of Europe into promontories is seen as inadequate. He acknowledges Europe extends into several promontories but disputes Polybius's subdivisions. Polybius identifies three primary promontories but proposes five: Iberia, Italy, Greece, Thrace, and the region of the Cimmerian Bosporus. Poseidonius finds this division problematic due to the complex nature of these regions and the need for further subdivisions. Finally, Poseidonius points out Polybius's errors regarding Europe and Libya, stressing the need for corrections and additions. This critique justifies Poseidonius's endeavor to treat these subjects, emphasizing the necessity for accurate geographical understanding and the correction of past mistakes. |
|
| 5. Polybius critiques ancient geographers Dicaearchus, Eratosthenes, and Pytheas. He challenges Pytheas' claims of exploring Britain and Thule, which featured strange phenomena. Polybius doubts a poor man's ability to travel extensively and criticizes Eratosthenes for believing Pytheas' accounts of Britain, Iberia, and Gades. Polybius prefers Euhemerus' single journey claim over Pytheas' extensive exploration assertion, which he finds unbelievable. Poseidonius further critiques Eratosthenes and Dicaearchus, highlighting their errors in distance measurements, especially between Peloponnesus and the Pillars. Polybius corrects some mistakes but makes others, exaggerating distances in Iberia. He questions Polybius' method of comparing continent lengths using segments of the northern semicircle, advocating fixed measures parallel to the equator instead. Polybius' division of Europe into promontories is deemed inadequate. While acknowledging Europe's several promontories, Poseidonius disputes Polybius' subdivisions. Polybius identifies three primary promontories but proposes five: Iberia, Italy, Greece, Thrace, and the Cimmerian Bosporus region. Poseidonius finds this division problematic due to the complex nature of these regions, necessitating further subdivisions. Poseidonius also points out Polybius' errors regarding Europe and Libya, stressing the need for corrections and additions. This critique justifies Poseidonius' efforts to address these subjects accurately, emphasizing the necessity for precise geographical understanding and rectifying past mistakes. |
|
|
3 Iberia 5 115 1:38
| 1. I have outlined geography generally, and now discuss parts of the inhabited world, starting with Europe and specifically Iberia. Iberia's larger part offers poor living conditions due to its mountainous and thinly-soiled regions, especially in the north, which is cold, rugged, and isolated by the ocean. Southern Iberia, particularly outside the Pillars, is fertile. Iberia resembles an ox-hide, stretching 6000 stadia in length from west to east and 5000 stadia in width from north to south. The Pyrenees form its eastern boundary, separating it from Celtica, which also varies in breadth. Iberia's most westerly point is the Sacred Cape, projecting 1500 stadia beyond Libya's headlands. Artemidorus likens the cape to a ship due to its shape and surrounding islands, but refutes Ephorus's claim of a temple of Heracles there, mentioning only stones turned by visitors. He also dismisses myths of the sun setting noisily and immediately bringing night in these regions. From the Sacred Cape, the western Iberian coast runs to the Tagus River's mouth, and the southern coast to the Anas River. Inland, the region houses Celtic peoples and some transplanted Lusitanians. The fertile Baetica region, named after the Baetis River, includes the ancient and wise Turdetanians, known for their historical records and alphabet. The Atlantic Ocean breaks in at the Pillars, forming a strait linking the interior and exterior seas. Near the strait, Mount Calpe rises steeply, resembling an island. Cities like Calpe, Menlaria, and Belon dot the coast, with Gades, renowned for its prosperity, located offshore. Iberia's coast also features the Port of Menestheus, estuaries, and the Baetis and Anas Rivers, leading to the Sacred Cape. |
|
| 2. Turdetania lies above the coast near the Anas River, through which the Baetis River flows. It is bounded by the Anas River to the west and north, Carpetania and Oretania to the east, and the Bastetanians to the south. The region includes over two hundred cities, with Corduba and Gades being the most prominent. Corduba, founded by Marcellus, is noted for its fertile soil and extensive territory, while Gades is famous for maritime commerce and its alliance with Rome. Other notable cities include Hispalis, Italica, and Ilipa, all situated along the Baetis River, which is navigable up to Corduba. Turdetania's rich soil and access to rivers facilitate extensive agricultural production and trade. The Baetis and Anas Rivers, along with numerous estuaries, support navigation and commerce. Turdetania is renowned for its exports, including grain, wine, olive oil, wax, honey, pitch, and wool. The region also boasts a significant fish-salting industry and abundant natural resources, including timber and salt quarries. The land is rich in metals, particularly silver, copper, and gold, with numerous mines scattered throughout. Turdetania's mineral wealth is so vast that it has been described as an "everlasting storehouse of nature." Mining techniques include washing gold-bearing sands and refining ores. Turdetania’s mines produce high-quality metals, and the region’s wealth has been known since ancient times, with historical references to its opulence. The Turdetanians have largely adopted Roman customs, with many cities now Latinized and integrated into Roman society. The Celtiberians, once considered brutish, have also embraced Roman culture, becoming part of the civilized world. |
|
| 3. Polybius defines six zones: two beneath the arctic circles, two between the arctic circles and the tropics, and two between the tropics and geography. This division relates to celestial phenomena and atmospheric temperature. The periscian, heteroscian, and amphiscian regions help determine constellations' appearances, while atmospheric temperature variations—excess heat, lack of heat, and moderate heat—affect plants and animals. The earth's division into five zones accounts for these temperature differences: two frigid zones with no heat, two temperate zones with moderate heat, and one torrid zone with excess heat. Polybius's use of the arctic circles to define zones is criticized for using variable points. He divides the torrid zone into two parts, aligning with the division of the earth into northern and southern hemispheres. This approach results in six zones, unlike other methods, which yield five. Eratosthenes suggested a third temperate zone at the equator due to its temperate climate, but Poseidonius criticized Polybius’s idea of the inhabited region under the equator being the highest, arguing that a spherical surface has no high point. Poseidonius recounts Eudoxus of Cyzicus’s voyage, claiming he found proof of circumnavigation around Libya. Eudoxus's journey included finding a ship’s prow from Gades, leading him to believe in the possibility of circumnavigation. Poseidonius supports the idea of a circumnavigable ocean, but his acceptance of Eudoxus's story is questionable. Poseidonius also discusses earth's changes due to natural phenomena and suggests that the Atlantis story might be based on fact. He speculates on migration due to sudden sea inundations and criticizes the traditional division of the world into continents, proposing a division based on zones and climates instead. However, he eventually agrees with the prevailing continental division. |
|
| 4. Polybius, in discussing Europe's geography, critiques previous geographers like Dicaearchus, Eratosthenes, and Pytheas. Pytheas claimed extensive travels in Britain and beyond, describing fantastical regions and coastlines. Polybius doubts the credibility of such claims, questioning how a private, impoverished individual could travel so extensively. He criticizes Eratosthenes for accepting Pytheas' accounts of Britain and Iberia but not those of Euhemerus, who only claimed to visit Panchaea. Polybius also disagrees with Eratosthenes' estimates of distances, particularly the 7,000 stadia from the Strait of Sicily to the Pillars of Hercules. Instead, he suggests it is much greater. Polybius believes errors exist in distance estimates, such as from Ithaca to Corcyra and from Epidamnus to Thessalonica, arguing they are longer than Eratosthenes claims. However, when estimating distances from Massilia to the Pillars and from the Pyrenees, he overestimates compared to Eratosthenes. He also finds fault with Eratosthenes' lack of knowledge about Iberia, noting inconsistencies in his descriptions of the Gauls and Iberians. Additionally, Polybius challenges the conventional understanding of Europe's length relative to Libya and Asia, arguing against the use of celestial positions for measurement. He critiques those who suggest the Tanaïs (Don) River flows from the summer sunrise or through the Caucasus. Polybius concludes that the geographical errors and misconceptions necessitate significant corrections and additions to the existing knowledge, underscoring the need for a more accurate and comprehensive understanding of the world's geography. |
|
| 5. Polybius critiques the geography of Europe by evaluating ancient geographers like Dicaearchus, Eratosthenes, and Pytheas. Pytheas claimed extensive travels and described fantastical regions and coastlines, which Polybius doubted. He questioned the credibility of such claims, considering Pytheas a poor individual, making such extensive travels improbable. Polybius also criticized Eratosthenes for accepting Pytheas' accounts of Britain and Iberia but rejecting Euhemerus' account of Panchaea. Polybius found errors in Eratosthenes' distance estimates, such as the 7,000 stadia from the Strait of Sicily to the Pillars of Hercules, suggesting it is much greater. He also pointed out inconsistencies in Eratosthenes' descriptions of the Gauls and Iberians, doubting his knowledge of Iberia. Additionally, Polybius challenged the understanding of Europe’s length relative to Libya and Asia, arguing against using celestial positions for measurements. He critiqued the suggestions that the Tanaïs (Don) River flows from the summer sunrise or through the Caucasus. In summary, Polybius emphasized the need for a more accurate and comprehensive understanding of the world’s geography, highlighting the significant errors and misconceptions in previous accounts and the importance of correct geographical measurements and descriptions. |
|
|
4 Transalpine Gaul 6 71 1 Hr
| 1. Transalpine Celtica is divided into three parts: Aquitani, Belgae, and Celtae. The Aquitani, distinct in language and physique, resemble the Iberians more than the Galatae. The Celtae and Belgae vary slightly in language and government. The region is bordered by the Pyrenees, the River Rhenus, the Alps, and the sea near Massilia and Narbo. Augustus Caesar divided Transalpine Celtica into four parts: the province of Narbonitis, Aquitani, and two parts under the boundaries of Lugdunum and Belgae. The country is watered by rivers flowing from the Alps, Cemmenus, and Pyrenees, supporting agriculture and transport. The Rhodanus River, with its many tributaries, is significant for navigation and connects with the Mediterranean Sea. Narbonitis resembles a parallelogram, bordered by the Pyrenees, Cemmenus, Alps, and the sea. Massilia, a Phocaean-founded city, lies on a rocky promontory with a well-fortified harbor. The city's government is aristocratic, with an Assembly of six hundred men. The region's economy is based on seafaring and trade, supplemented by agriculture in surrounding plains. Narbonitis' seaboard is notable for its natural features, such as the "Stony Plain" and the unique "dug mullets" found in its marshes. The region's rivers facilitate trade and transport, linking the interior to both the Mediterranean and the Atlantic. The country is fertile, producing various crops and livestock. The inhabitants, known for their fighting spirit, have adapted to farming under Roman rule. Narbonitis, rich in history and culture, continues to thrive with its strategic location and natural resources. |
|
| 2. The Aquitani, distinct from the Galatic tribes in physique and language, resemble the Iberians. Their territory spans from the Garumna River to the Pyrenees and includes fourteen Galatic tribes between the Garumna and Liger Rivers. These rivers are parallel to the Pyrenees, forming parallelograms bounded by the ocean and the Cemmenus Mountains. The Aquitani live mostly along the ocean, with some tribes reaching the Cemmenus Mountains. The Garumna discharges between the Bituriges Vivisci and the Santoni, while the Liger flows between the Pictones and the Namnitae. The Aquitani's ocean-coast is sandy, growing millet but few other crops. The Tarbelli in the region hold significant gold mines, with gold found in large slabs and nuggets. The interior regions, like those of the Convenae and Auscii, have better soil and notable features such as hot springs and good agricultural land. Tribes between the Garumna and Liger include the Elui, Vellavii, Arverni, Lemovices, Petrocorii, Nitiobriges, Cadurci, Bituriges Cubi, Santoni, Pictones, Ruteni, and Gabales. These regions have iron works, linen factories, and silver mines. The Romans have granted "Latin right" to some Aquitani tribes, enhancing their status. The Arverni, situated on the Liger, have a history of resisting Roman conquest with large armies, including notable battles against Caesar, Maximus Aemilianus, and Dometius Ahenobarbus. They once controlled extensive territories from Narbo to the Pyrenees, the ocean, and the Rhenus. Their wealth and power are exemplified by the extravagance of their leaders, such as Luerius. |
|
| 3. The Aquitanian division and Narbonitis extend to the Rhenus, starting from the Liger and the Rhodanus near Lugdunum. This region is divided: the upper parts near the river sources belong to Lugdunum, while the rest, including coastal areas, are under the Belgae. Lugdunum, a city at the confluence of the Arar and the Rhodanus, is a Roman stronghold and a populous emporium where Roman governors mint coins. A temple dedicated to Caesar Augustus by all the Galatae is nearby, featuring an altar with inscriptions of sixty tribes and their images. The Segusiavi tribe lives between the Rhodanus and the Dubis. Other tribes stretch towards the Rhenus, bounded by the Dubis and Arar rivers. The Sequana River, also originating in the Alps, flows to the ocean and is known for its fine salted hog-meat. The Aedui tribe, with their city Cabyllinum on the Arar, were the first to ally with the Romans. The Sequani, often in conflict with the Aedui and Romans, demonstrated significant power by aligning with the Germans. The Elvetii, near the Rhenus's sources on Mount Adula, have been reduced in number but were once powerful. The Rhenus flows through marshes and a large lake, contrary to claims of its exaggerated length. Beyond the Elvetii and Sequani, the Aedui, Lingones, Mediomatrici, and Tribocchi tribes dwell. The Treveri, who constructed a bridge for the Germanic war, live along the Rhenus. The Nervii, Menapii, and other tribes extend to the river's mouth, living in forests like Arduenna, which served as defensive refuges. All these tribes are now at peace and under Roman control. |
|
| 4. After the aforementioned tribes, the remaining Belgae tribes live on the ocean coast. The Veneti, who fought a naval battle against Caesar, were prepared to hinder his voyage to Britain, using their emporium there. Caesar defeated them by hauling down their sails with pole-hooks. The Veneti built their ships with broad bottoms, high sterns, and high prows using oak and seaweed to prevent drying. The Osismii, who live on a promontory projecting into the ocean, are also notable among the Belgae. The whole Gallic race is warlike, high-spirited, and quick to battle, though otherwise simple and not ill-mannered. They gather quickly for battle, making them easy to defeat with stratagems. They are physically large and numerous, easily provoked to defend their neighbors. Currently, they live in peace under Roman command, but historically they were more autonomous. The Belgae, divided into fifteen tribes, are the bravest, particularly the Bellovaci and the Suessiones. The Belgae could resist the Germanic Cimbri and Teutones. Their population was large, with about 300,000 able to bear arms. They wore the "sagus," had long hair, and wore tight breeches. Their armor included long sabres and oblong shields. They had large flocks and herds, supplying Rome with "sagi" and salted meat. Their governments were mostly aristocratic, with one leader annually chosen for war. Three classes of men held in high honor among the Gauls: the Bards (singers and poets), the Vates (diviners and natural philosophers), and the Druids (moral philosophers). The Druids were trusted to decide private and public disputes and believed men's souls and the universe were indestructible. The Gallic people are also known for their witlessness, boastfulness, and fondness for ornaments. They wore golden chains and bracelets, and their dignitaries wore garments sprinkled with gold. Their customs included hanging enemy heads from their horses and homes. The Romans stopped such customs and human sacrifices. |
|
| 5. Britain is triangular, with its longest side parallel to Celtica, both about 4,300 stadia long. The Celtic length extends from the Rhenus to the northern Pyrenees, while Britain's extends from Cantium to the western end opposite the Aquitanian Pyrenees. The shortest distance between the Pyrenees and Rhenus is around 5,000 stadia. There are four main passages from the mainland to the island, starting from the rivers Rhenus, Sequana, Liger, and Garumna. Voyages from near the Rhenus often start from the Morini coast. Caesar used Itium as a naval station for his voyage to Britain. Most of Britain is flat and forested, with some hilly regions. It produces grain, cattle, gold, silver, and iron, along with hides, slaves, and hunting dogs. The Britons are taller than the Celti but less muscular. They are somewhat primitive in agricultural practices and use chariots in war, similar to some Celti. Their cities are forest enclosures for temporary habitation. The climate is rainy, with frequent fogs. Caesar crossed to Britain twice but did not venture far due to local conflicts and ship losses. He won victories and returned with hostages, slaves, and booty. Some British chieftains sought Augustus's friendship, dedicating offerings in the Capitol and making the island virtually Roman property. They easily submit to duties on imports and exports, making garrisoning unnecessary. Besides smaller islands, there is a large island, Ierne, north of Britain, with more savage inhabitants who are rumored to practice cannibalism and incest. Information about Thule is uncertain, with much of Pytheas's accounts considered fabricated. However, some details align with what might be expected near the frozen zone, like scarce animal life and reliance on
herbs, roots, and stored grain. |
|
|
5 North Italy 4 89 1:15
| 1. After the foothills of the Alps comes the beginning of what is now Italy. Initially, only Oenotria was called Italy, extending from the Strait of Sicily to the Gulfs of Tarentum and Poseidonia. The name Italy later expanded to include areas up to the Alps and parts of Ligustica and Istria. The name spread due to the prosperity of the original Italians, who extended it to neighboring peoples until the Roman conquest. The Romans later included the Cisalpine Galatae and the Heneti, calling all Italiotes and Romans, and established many colonies. Italy is roughly triangular, with its vertex at the Strait of Sicily and its base at the Alps. The Alps form a curved base, with a central gulf near the Salassi and extending to the Adriatic and Ligurian seaboards. A large plain lies at the base of the Alps, divided by the Padus River into Cispadana and Transpadana. Cispadana lies next to the Apennine Mountains and Liguria, while Transpadana is inhabited by Ligurian and Celtic tribes. The Celts are related to the Transalpine Celts, while the Heneti are believed to be descendants of the Paphlagonian Heneti. The country is rich in rivers and marshes, particularly the Heneti's part, which experiences ocean-like tides. This area, intersected by channels and dikes, has cities surrounded by water and fertile plains drained for agriculture. Notable cities include Patavium, Ravenna, and Altinum, which are connected by inland waterways. Patavium is particularly prosperous, known for its manufacturing and large army. Ravenna is built on wood and surrounded by rivers, making it healthful despite being in a marsh. |
|
| 2. Liguria and Tyrrhenia: The Second Portion is Liguria, in the Apennines, between Celtica and Tyrrhenia. Its inhabitants live in villages, quarrying stones and farming rough land. The Third Portion is Tyrrhenia, extending to the River Tiber and bounded by the Tyrrhenian and Sardinian Seas. The Tiber flows from the Apennines, traversing Tyrrhenia and separating it from Ombrica, the Sabini, and part of Latium, which stretches to the coastline near Rome. The Latini's country extends from Ostia to Sinuessa, reaching Campania and the Samnite mountains. The Sabini lie between the Latini and Ombrici, extending to the Samnite mountains and Apennines. The Ombrici extend over the mountains to Ariminum and Ravenna. Tyrrheni: The Tyrrheni, called "Etrusci" and "Tusci" by Romans, were named after Tyrrhenus, who led Lydian colonists. Initially united and powerful, they later fragmented into separate cities due to neighboring pressures. Post-Rome's founding, Demaratus brought Corinthians to Tarquinii, influencing Rome’s early culture. The Tyrrheni thrived and were known for their contributions to Roman customs, such as the fasces and sacrificial rites. Notable achievements include the Caeretani defeating the Galatae and saving Rome's sacred fire and Vestal priestesses during a Gallic invasion. Geography and Cities: Tyrrhenia's coast from Luna to Ostia is about 2,500 stadia long. Key cities include Luna, with its significant harbor and marble quarries, and Pisa, founded by Greek settlers from the Peloponnesus. Volaterrae is situated in a ravine, known for its resistance against Sulla’s forces. Poplonium, located on a promontory, has an ancient harbor and historical mines. Ravenna, built on wood and surrounded by rivers, was a healthful city used for training gladiators. The Tyrrheni also inhabited areas rich in lakes, hot springs, and agricultural lands. |
|
| 3. The Sabini live in a narrow region stretching about a thousand stadia from the Tiber and Nomentum to the Vestini. Their few cities include Amiternum, Reate (near the cold springs of Cotiliae), and Foruli, a rocky elevation more suited for revolt than habitation. Cures, once significant, is now a small village but notable as the home of two Roman kings, Tatius and Numa Pompilius. The Sabini region is fertile, producing olives, vines, acorns, and renowned for Reate-breed mules. The Sabini are ancient, indigenous people, with the Picentini, Samnitae, Leucani, and Brettii as their descendants. They were known for their bravery and have endured through time. The Latin region, including Rome, originally comprised several tribes like the Aeci, Volsci, Hernici, Rutuli, and aborigines. Aeneas, after landing at Laurentum, allied with Latinus against the Rutuli of Ardea, leading to the founding of Lavinium and Alba. The Romans, Latini, and Albani jointly offered sacrifices to Zeus on Mount Albanus. The region expanded under Roman rule, eventually including Campania, the Samnitae, and the Peligni. Latium is fertile but some coastal and marshy areas are less so. Cities like Ostia, Antium, and Circaeum were important, with Ostia founded by Ancus Marcius and Antium being a resort for Roman rulers. Inland, Rome, founded out of necessity rather than choice, expanded through fortifications by successive rulers. Augustus improved city safety, reduced building heights, and organized fire protection. Rome's natural blessings include abundant materials, and the foresight in constructing roads, aqueducts, and sewers has added to its prosperity. Notable infrastructure improvements and public works were carried out by Agrippa, Caesar, and other leaders, making Rome a city of remarkable structures and resources. |
|
| 4. The country of the Sabini extends lengthwise up to a thousand stadia from the Tiber and Nomentum to the Vestini. Their few cities, including Amiternum and Reate, have suffered due to constant wars. Notably, Cures, once significant, is now a small village. The Sabini region is fertile, producing olives, vines, and renowned Reate-breed mules. The Sabini are an ancient, indigenous people, with the Picentini, Samnitae, Leucani, and Brettii as their descendants. They are known for their bravery and have endured through time. The Latin region, including Rome, initially comprised several tribes such as the Aeci, Volsci, Hernici, and Rutuli. Aeneas, after landing at Laurentum, allied with Latinus against the Rutuli of Ardea, leading to the founding of Lavinium and Alba. The Romans, Latini, and Albani jointly offered sacrifices to Zeus on Mount Albanus. Under Roman rule, the region expanded to include Campania, the Samnitae, and the Peligni. Latium is fertile, but some coastal and marshy areas are less so. Cities like Ostia, Antium, and Circaeum were important, with Ostia founded by Ancus Marcius and Antium becoming a resort for Roman rulers. Rome, founded out of necessity, expanded through fortifications by successive rulers. Augustus improved city safety, reduced building heights, and organized fire protection. Rome's natural blessings include abundant materials, and foresight in constructing roads, aqueducts, and sewers has added to its prosperity. Notable infrastructure improvements and public works were carried out by Agrippa, Caesar, and other leaders, making Rome a city of remarkable structures and resources. |
|
| 5. After the Sabini, the Latini, including Rome, extended their power over surrounding tribes. The Latini originally comprised several tribes such as the Aeci, Volsci, Hernici, and Rutuli. Aeneas, after landing at Laurentum, allied with Latinus against the Rutuli of Ardea, leading to the founding of Lavinium and Alba. The Romans, Latini, and Albani jointly offered sacrifices to Zeus on Mount Albanus. Under Roman rule, the region expanded to include Campania, the Samnitae, and the Peligni. Latium is fertile but some coastal and marshy areas are less so. Cities like Ostia, Antium, and Circaeum were important, with Ostia founded by Ancus Marcius and Antium becoming a resort for Roman rulers. Inland, Rome, founded out of necessity rather than choice, expanded through fortifications by successive rulers. Augustus improved city safety, reduced building heights, and organized fire protection. Rome's natural blessings include abundant materials, and foresight in constructing roads, aqueducts, and sewers has added to its prosperity. Notable infrastructure improvements and public works were carried out by Agrippa, Caesar, and other leaders, making Rome a city of remarkable structures and resources. |
|
|
6 South Italy. 4 74 1:02
| 1. After the mouth of the Silaris River lies Leucania, featuring the temple of the Argoan Hera, built by Jason. Close by is Poseidonia. Sailing past the gulf, one reaches Leucosia, an island named after a Siren from myth. Near this island is a promontory forming the Poseidonian Gulf. Beyond this is the city of Elea, founded by Phocaeans and home to philosophers Parmenides and Zeno. Despite its poor soil, Elea thrived due to its governance and salt fish industry.
Next comes the promontory of Palinurus, followed by Pyxus, and then Laüs, a city founded by Sybaritae. The entire Leucanian coast stretches 650 stadia. The Leucani occupied these lands after displacing the Chones and Oenotri, but were later overshadowed by Greek colonies and the Carthaginians. As a result, much of Magna Graecia, once dominated by Greeks, fell into barbarism, with regions now controlled by Romans, Leucani, Brettii, and Campani.
The interior settlements, like Petelia founded by Philoctetes, remain significant. The Leucani, originally Samnite, governed democratically except during wars. The Brettii, revolting from the Leucani, established themselves during Dio's expedition. Temesa, initially an Ausonian settlement, and other cities like Terina and Consentia, faced Hannibal’s destruction or Roman conquest. Near Consentia is Pandosia, where Alexander the Molossian met his end, deceived by an oracle. Hipponium, renamed Vibo Valentia by the Romans, and other cities like Medma and Metaurus hold historical significance, showcasing the region’s rich yet turbulent history. |
|
| 2. Sicily, triangular in shape, was once called "Trinacria" and later "Thrinacis." Its three capes are Pelorias, Pachynus, and Lilybaeum, facing different directions: Pelorias towards the strait, Pachynus towards the east, and Lilybaeum towards Libya. The longest side, from Lilybaeum to Pelorias, is about 1,720 stadia. The entire coastline, as Poseidonius states, is about 4,000 stadia.
The main cities along the strait side are Messene, Tauromenium, Catana, and Syracuse. Ancient cities like Naxus and Megara have disappeared. Messene, founded by Peloponnesian Messenians, is now predominantly known for its wine, which rivals Italy's best. Catana, more populous, was originally founded by Naxians. Hiero, tyrant of Syracuse, once repopulated it, calling it Aetna. The city of Aetna, situated near the mountain, often suffers from volcanic activities.
Syracuse, founded by Archias from Corinth, became immensely wealthy. The city, originally sprawling over five towns, was partly restored by Augustus Caesar. Ortygia, connected to the mainland, hosts the famous fountain of Arethusa.
Sicily's interior features Enna, known for its temple of Demeter, and the lofty Eryx, home to a revered temple of Aphrodite. Many ancient cities, like Himera, Gela, and Selinus, have been deserted and turned into pastures. The region's fertility, particularly in grain, honey, and saffron, makes it a vital supplier to Rome.
Near Centoripa, the town of Aetna serves as a base for ascents up Mount Etna. The mountain's summit features shifting volcanic activity, including ash eruptions and lava flows. The Nebrodes Mountains, lower yet broader, rise opposite Etna. The entire island is rich with hot springs and underground rivers, showcasing its volcanic nature. |
|
| 3. Now that I have traversed the regions of Old Italy as far as Metapontium, I must speak of those that border on them. Iapygia, also called Messapia by the Greeks, borders them. The natives call one part (near the Iapygian Cape) Salentini, and the other Calabri. North of these are the Peucetii and Daunii. The whole country after Calabri is called Apulia. Messapia forms a peninsula enclosed by the isthmus from Brentesium to Taras, three hundred and ten stadia. The distance from Metapontium to Taras is about two hundred and twenty stadia.
Taras has a large, beautiful harbor, enclosed by a bridge and one hundred stadia in circumference. The city, partly forsaken, still has a noteworthy part near the acropolis, featuring a gymnasium and a large marketplace with a bronze colossus of Zeus. The acropolis, though looted by Carthaginians and Romans, still holds significant remnants.
Antiochus recounts Taras' founding: During the Messenian war, Spartans who did not participate were enslaved and their children, born during the expedition, called Partheniae, deprived of citizenship. They plotted against the free citizens, but their plot was discovered. The Partheniae, under Phalanthus, were sent to found a colony. They settled in Taras, welcomed by the natives and some Cretans. The city was named after a hero.
At one time, Taras was powerful, with a strong democratic government, a large fleet, and significant military force. However, luxury led to poor governance. They hired foreign generals, including Alexander the Molossian, Archidamus, Cleonymus, Agathocles, and Pyrrhus, but could not maintain stability. Eventually, they were deprived of their freedom during the wars with Hannibal, received a Roman colony, and now live more peacefully. |
|
| 4. Italy, resembling an island, is securely guarded by seas and mountains, making it well-protected. Most of its coast is harbourless, aiding in defense, while its few harbors are excellent for trade and counter-attacks. Its diverse climates support a variety of life, contributing to its strength. The Apennine Mountains run its length, providing both fertile plains and hills. Italy's many rivers, lakes, and springs, along with abundant resources, enhance its livability. Centrally located between major regions, it is well-suited for leadership and can easily interact with surrounding areas.
The Romans, after founding Rome, wisely continued under kings until ejecting the last Tarquin and establishing a government mixing monarchy and aristocracy. They expanded by dealing with neighboring peoples, eventually making all of Latium their subjects and stopping the Tyrrheni and Celts. They subdued the Samnites, Tarentines, Pyrrhus, and others in Italy before moving on to Sicily and Carthage. They fought three wars against Carthage, ultimately destroying it and expanding into Libya and Iberia. Conquests extended to Greece, Macedonia, and Asia, subduing kings like Antiochus, Philip, and Perseus. They also subdued Illyrians, Thracians, Iberians, and Celts, with significant campaigns led by Julius Caesar and Augustus.
Augustus Caesar brought peace and prosperity, continued by his successor Tiberius and his sons Germanicus and Drusus. Under their rule, Italy thrived, despite internal factions, due to their effective governance. |
|
|
|
7 Central Europe. 8 114 1:35
| 1. Italy is uniquely positioned and well-guarded by seas and mountains, making it nearly impenetrable. It has a mix of climates, fostering a variety of life, and boasts numerous rivers, lakes, and mineral springs. Italy's geography, extending north to south, includes the Apennine Mountains, which offer both fertile plains and hill regions. Its natural resources, including mines and fertile lands, contribute to its abundance. Centrally located between major regions, it benefits from its proximity to both large races and Greece, facilitating hegemony.
After Rome's founding, the Romans wisely maintained a monarchy, later shifting to a mixed government after expelling the last Tarquin king. They expanded their territory by incorporating neighboring regions, defeating the Latins, Tyrrhenians, Celts, Samnites, and others. They moved beyond Italy, conquering Sicily and fighting Carthage in three wars, ultimately destroying it and expanding into Libya and Iberia. Their conquests included Greece, Macedonia, and parts of Asia, defeating notable kings like Antiochus, Philip, and Perseus.
The Romans continued expanding into Illyria, Thrace, Iberia, and Celtica, with significant campaigns led by Julius Caesar and Augustus. Augustus Caesar brought unprecedented peace and prosperity, which continued under his successor Tiberius and his sons, Germanicus and Drusus. Despite internal factions, their effective governance ensured the stability and success of the Roman Empire. |
|
| 2. The accounts of the Cimbri contain inaccuracies and improbabilities. It is unlikely that they became nomadic due to a great flood-tide, as they still occupy their original lands. They even sent a sacred kettle to Augustus, seeking friendship and amnesty for past offenses. The notion that they left their homes because of natural, daily occurring tides is absurd. Assertions of a catastrophic flood are fabrications; ocean tides are regular and periodic. The idea that the Cimbri fought the tides or that Celts trained to face tidal destruction is also unfounded. Regular tidal patterns would have made such misunderstandings improbable.
Poseidonius criticizes these tales, suggesting the Cimbri were a piratical people who ventured as far as Lake Maeotis and that the "Cimmerian" Bosporus was named after them, equating "Cimmerii" with "Cimbri." He notes that the Cimbri, repulsed by the Boii in the Hercynian Forest, moved to the Ister, encountering various Galatae tribes. They allied with the Helvetii, whose wealth prompted them to join the Cimbri. All these groups were eventually subdued by the Romans.
The Cimbri had a custom involving their priestesses, who, clad in white with bronze girdles, performed ritual sacrifices of prisoners. These priestesses would prophesy from the blood and entrails of the victims, and during battles, they would create unearthly noises by beating on hide-covered wagons.
The Germans, extending from the Rhenus to the Albis, include the Sugambri and Cimbri, but the regions beyond the Albis remain largely unknown to the Romans. The extent and nature of the lands beyond Germany and their inhabitants are still a mystery. |
|
| 3. The Cimbri, a Germanic tribe, are often misunderstood in historical accounts. Contrary to some stories, they did not become nomadic due to flood-tides; they still inhabit their ancestral lands. They even sought friendship with Augustus, sending him a sacred kettle. The idea that they fled due to natural tidal patterns is absurd, given the regularity of such tides. Poseidonius, a historian, criticizes these tales and suggests the Cimbri were a piratical people who traveled far, even to Lake Maeotis. He theorizes that the "Cimmerian" Bosporus was named after the Cimbri, known as "Cimmerii" by the Greeks. The Cimbri, after being repulsed by the Boii in the Hercynian Forest, moved towards the Ister and allied with the Helvetii. Both were eventually subdued by the Romans.
The Cimbri had unique customs, involving priestesses who performed sacrificial rituals. These priestesses, dressed in white with bronze girdles, would prophesy from the blood and entrails of prisoners. The Germans, extending from the Rhenus to the Albis, include tribes like the Sugambri and the Cimbri. However, regions beyond the Albis remain largely unknown to the Romans.
The Getae, another significant group, lived on both sides of the Ister River and were sometimes considered Thracians. Poseidonius notes that some Mysians, known for their peaceful, religious life, abstained from eating living things and lived on honey, milk, and cheese. This peacefulness earned them the titles "god-fearing" and "capnobatae." The region also hosted various tribes, including the Bastarnians and Roxolani, who lived nomadic lifestyles.
Despite historical inaccuracies, it is clear that the Cimbri, Getae, and related tribes had complex societies with unique customs and interactions with neighboring cultures and the Romans. |
|
| 4. The isthmus separating Lake Sapra from the sea, forming the Tauric Chersonese, is forty stadia wide. Lake Sapra, part of Lake Maeotis, is very marshy, making it difficult to navigate with larger boats. The gulf contains islands, shoals, and reefs. Sailing out of the gulf, one encounters a small city and harbor belonging to the Chersonesites. Nearby is a cape housing the city of the Heracleotae, known as Chersonesus. This city features the temple of the Parthenos and three harbors. The Old Chersonesus, now in ruins, once served as a pirate haven. The harbor Symbolon Limen and Ctenus Limen form a narrow isthmus enclosing the Little Chersonesus.
This city became subject to Mithridates Eupator after being sacked by barbarians. Mithridates also established control over the Bosporus region. The city of the Chersonesites remains under the control of the Bosporus rulers. The coast from Symbolon Limen to Theodosia, about a thousand stadia, is rugged and stormy, with a promontory called Criumetopon opposite the Paphlagonian promontory Carambis, dividing the Euxine Pontus into two seas.
The city Theodosia, in a fertile plain, features a large harbor. The fertile region extends to Panticapaeum, the Bosporian metropolis. Panticapaeum, a Miletian colony, lies on a hill with a harbor and docks. It was ruled by the dynasty of Leuco, Satyrus, and Parisades until the last Parisades surrendered to Mithridates due to pressure from barbarians. The Bosporian kingdom has since been subject to the Romans, spanning both Europe and Asia.
The mouth of Lake Maeotis, the Cimmerian Bosporus, is about seventy stadia wide, with crossings from Panticapaeum to Phanagoria. The Tanaïs River, opposite the Bosporus, flows into the lake, forming part of the boundary between Asia and Europe. |
|
| 5. The remainder of Europe lies between the Ister and the encircling sea, starting at the recess of the Adriatic and extending to the Sacred Mouth of the Ister. This region includes Greece, Macedonian, and Epeirote tribes, extending to the Ister and seas on either side. To the north are parts between the Ister and the mountains, while to the south are Greece and adjoining barbarian lands. The Haemus Mountain, near the Pontus, is the largest and highest in this region, dividing Thrace. Polybius incorrectly claimed that both seas are visible from Haemus, as the distance to the Adriatic is too great.
The country also includes Illyrian, Paeonian, and Thracian mountains, which are parallel to the Ister. This division separates the northern parts from those towards Greece and barbarian lands extending to the mountains. The Illyrian regions connect with Italy, the Alps, and territories of the Germans, Dacians, and Getans. The Dacians devastated part of this country, subduing the Celtic tribes Boii and Taurisci. The Pannonii occupy the remaining land, reaching Segestica and the Ister, with territories extending further.
Segestica, a Pannonian city, lies at the confluence of navigable rivers and is a strategic base for wars against the Dacians. Rivers flow from Mount Ocra, carrying merchandise to Segestica from Italy. Pannonian tribes include the Breuci, Andizetii, Ditiones, Peirustae, Mazaei, and Daesitiatae, extending as far south as Dalmatia and Ardiaei land. The mountainous country stretching from the Adriatic recess to the Rhizonic Gulf and Ardiaei land is Illyrian, positioned between the sea and P
annonian tribes. |
|
| 6. The remaining part of Europe between the Ister and the mountains includes the Pontic seaboard from the Sacred Mouth of the Ister to the mouth at Byzantium. Starting at the Sacred Mouth of the Ister and keeping the coast on the right, one reaches Ister, a small town founded by the Milesians, after 500 stadia, then Tomis after 250 stadia, followed by Callatis, a colony of the Heracleotae, after 280 stadia, and Apollonia, a Milesian colony, after 1,300 stadia. Between Callatis and Apollonia are Bizone, Cruni, Odessus (a Milesian colony), and Naulochus (a small town of the Mesembriani).
The Haemus Mountain, reaching the sea near Mesembria (a Megarian colony), divides the coast. Apollonia is also home to Cape Tirizis, used as a treasury by Lysimachus. From Apollonia to the Cyaneae, the distance is about 1,500 stadia, passing Thynias, Anchiale, Phinopolis, and Andriaca. Salmydessus, a desert, stony beach, extends to the Cyaneae over 700 stadia. The Cyaneae are two islets near the mouth of the Pontus, separated by 20 stadia, and 20 stadia from the temples of Byzantines and Chalcedonians.
The narrowest part of the mouth of the Euxine is five stadia wide, leading to the Propontis. From this narrow point to the harbor "Under the Fig-tree" is 35 stadia, and five stadia further to the Horn of the Byzantines, a gulf resembling a stag's horn, extending 60 stadia. Pelamydes fish, hatched in Lake Maeotis, rush to these gulfs, where they are easily caught. This abundance benefits Byzantium, providing significant revenue, while Chalcedonians, on the opposite shore, miss out on this wealth. |
|
| 7. The remaining part of Europe between the Ister and the mountains includes the Pontic seaboard from the Sacred Mouth of the Ister to the mouth at Byzantium. Starting at the Sacred Mouth of the Ister and keeping the coast on the right, one reaches Ister, a small town founded by the Milesians, after 500 stadia, then Tomis after 250 stadia, followed by Callatis, a colony of the Heracleotae, after 280 stadia, and Apollonia, a Milesian colony, after 1,300 stadia. Between Callatis and Apollonia are Bizone, Cruni, Odessus (a Milesian colony), and Naulochus (a small town of the Mesembriani).
The Haemus Mountain, reaching the sea near Mesembria (a Megarian colony), divides the coast. Apollonia is also home to Cape Tirizis, used as a treasury by Lysimachus. From Apollonia to the Cyaneae, the distance is about 1,500 stadia, passing Thynias, Anchiale, Phinopolis, and Andriaca. Salmydessus, a desert, stony beach, extends to the Cyaneae over 700 stadia. The Cyaneae are two islets near the mouth of the Pontus, separated by 20 stadia, and 20 stadia from the temples of Byzantines and Chalcedonians.
The narrowest part of the mouth of the Euxine is five stadia wide, leading to the Propontis. From this narrow point to the harbor "Under the Fig-tree" is 35 stadia, and five stadia further to the Horn of the Byzantines, a gulf resembling a stag's horn, extending 60 stadia. Pelamydes fish, hatched in Lake Maeotis, rush to these gulfs, where they are easily caught. This abundance benefits Byzantium, providing significant revenue, while Chalcedonians, on the opposite shore, miss out on this wealth. |
|
| 8. In earlier times, an oracle existed near Scotussa, a city of Pelasgiotis in Thessaly, and was transferred to Epirus after a fire, following an oracle given by Apollo at Dodona. The oracle used symbols rather than words, similar to Zeus Ammon in Libya. Observations and prophecies were made from the flight of three pigeons. Among the Molossians and Thesprotians, old women were called "peliai" and old men "pelioi," suggesting the Peleiades were not birds but old women associated with the temple.
The sacred oak tree in Dodona was revered as the earliest plant and first to supply food. Doves, observed for augury, were also significant in the temple rituals. The term "tomouroi" likely evolved from "tomarouroi," indicating temple guardians. The oracle, initially under the Thesprotians, later came under the Molossians, and the interpreters of Zeus were called "tomouroi."
A proverbial phrase, "the copper vessel in Dodona," originated from a copper vessel and a copper scourge dedicated by the Corcyraeans. The scourge's bones struck the vessel continuously when swung by the wind, producing prolonged tones, leading to the term "the scourge of the Corcyraeans."
Paeonia lies east of these tribes and west of the Thracian mountains, north of Macedonia, and south of the Autariatae, Dardanii, and Ardiaei. It stretches as far as the Strymon River. The Haliacmon River flows into the Thermaean Gulf. Orestis is a large mountainous area extending to Mount Corax in Aetolia and Mount Parnassus, inhabited by various tribes, including the Orestae and Tymphaei. |
|
|
|
|
8 Peloponnesus. 8 112 1:35
| 1. I began my description of Europe with its western parts between the inner and outer sea, covering all the barbarian tribes up to the Tanaïs and part of Greece, including Macedonia. Now, I will describe the remainder of Greece. This topic was first treated by Homer and subsequently by others in treatises like "Harbours," "Coasting Voyages," and "General Descriptions of the Earth." Notable historians such as Ephorus and Polybius, as well as physicists and mathematicians like Poseidonius and Hipparchus, have also addressed it. Homer's work requires critical inquiry since it is poetic and reflects ancient times, not the present.
I will begin with the Greek peoples following the Epeirotes and Illyrians, covering the Acarnanians, Aetolians, and Ozolian Locrians, then the Phocians and Boeotians. Opposite these regions across the sea is the Peloponnesus, shaping and being shaped by the Corinthian Gulf. After Macedonia, I will cover Thessaly and the countries outside and inside the Isthmus.
Greece once had many tribes, corresponding to its four dialects: Ionic, Doric, Aeolic, and Attic. Over time, these dialects evolved due to geographic and social factors. The Ionians and Aeolians predominated in different regions, with Dorians later mixing with other tribes.
Ephorus begins his description with Acarnania, as it borders the Epeirotes. Using the sea as a guide, I will describe Greece starting from the Sicilian Sea, extending to the Corinthian Gulf and the Peloponnesus. Greece is divided into two main parts: inside and outside the Isthmus. The Peloponnesus, resembling an acropolis, is noted for its topography, power, and historical significance. This region features several significant peninsulas, starting with the Peloponnesus itself. The sequence of peninsulas provides a natural order for describing the geography of Greece, beginning with the smallest but most famous. |
|
| 2. The Peloponnesus resembles a plane tree leaf, with its length and breadth both about 1400 stadia. It spans from Chelonatas in the west, through Olympia and Megalopolis, to the Isthmus in the east. The width, from Maleae in the south through Arcadia to Aegium in the north, is similar. According to Polybius, the perimeter, without following the gulf sinuosities, is 4000 stadia; Artemidorus adds 400 more. Following the sinuosities, it's over 5600 stadia. The Isthmus, where ships are hauled from one sea to the other, is 40 stadia wide.
The western part is occupied by the Eleians and Messenians, washed by the Sicilian Sea. The Eleian country curves north to the Corinthian Gulf as far as Cape Araxus, facing Acarnania and its coastal islands—Zacynthos, Cephallenia, Ithaca, and the Echinades, including Dulichium. The Messenian country extends south to the Libyan Sea, near Taenarum. Next is Achaea, facing north along the Corinthian Gulf to Sicyonia, followed by Sicyon and Corinth, the latter extending to the Isthmus. Then come Laconia and Argolis, also reaching the Isthmus. The gulfs here are the Messenian, Laconian, Argolic, Hermionic, and Saronic. The first two are filled by the Libyan Sea, the others by the Cretan and Myrtoan Seas. The Saronic Gulf is also called "Strait" or "Sea." Arcadia, in the peninsula's interior, borders all these regions.
The Corinthian Gulf starts at the Evenus or Acheloüs River and Araxus, where the shores draw closer, meeting at Rhium and Antirrhium, separated by a five-stadia strait. Rhium, in Achaea, has a Poseidon temple. Antirrhium is on the Aetolia-Locris boundary. The shoreline widens again into the Crisaean Gulf, ending at Boeotia and Megaris. The Corinthian Gulf's perimeter from the Evenus to Araxus is 2230 stadia, or slightly more from the Acheloüs. The coast from the Acheloüs to the Evenus is Acarnanian, then Aetolian to Antirrhium, and Phocian, Boeotian, and Megarian to the Isthmus. The sea from Antirrhium to the Isthmus is the Alcyonian part of the Crisaean Gulf. The distance from the Isthmus to Araxus is 1030 stadia. This outlines the Peloponnesus and the land across the gulf. Now, I will detail the Eleian country. |
|
| 3. The Eleian country currently includes the seaboard between the Achaeans and Messenians, extending inland to Arcadian districts such as Pholoë, Azanes, and Parrhasians. Historically, it was divided into domains ruled by the Epeians and Nestor, as described by Homer. The city of Elis did not exist in Homer's time; the inhabitants lived in villages, and the area was called Coelê Elis. After the Persian wars, many communities formed the city of Elis.
Elis borders the Achaeans to the north, ending at Sicyonia, and the Messenians to the south, near Taenarum. Notable geographical features include the Corinthian Gulf, Rhium and Antirrhium capes, and the Alpheius River, which flows through Pylian territory, not the city of Pylus.
Arcadia, located in the peninsula's interior, neighbors all these regions. Homer’s descriptions align with current conditions, emphasizing the poet's historical significance.
The Corinthian Gulf begins at Evenus River, stretching to Araxus. Its perimeter is 2,230 stadia from Evenus to Araxus, increasing if measured from the Acheloüs River. The coast is occupied by Acarnanians, Aetolians, and Phocians up to the Isthmus, known as the Alcyonian Sea.
Eleia's significant points include Cape Araxus, naval station Cyllenê, the promontory Chelonatas, and the Peneius River. Cyllenê is a small village with an Asclepius statue by Colotes. The Eleians’ gymnasium was built long after acquiring Nestor's districts, including Pisatis, Triphylia, and Cauconian territories. The name "Triphylia" comes from the three tribes: Epeians, Minyans, and Eleians.
These historical and geographical details form the backdrop of Eleia's development and its connection to the rest of Greece. |
|
| 4. Messenia borders Eleia and extends south towards the Libyan Sea. During the Trojan War, Messenia was part of Laconia and under Menelaüs's rule. The city now called Messenê, with its acropolis Ithomê, was not yet founded. After Menelaüs's death, the Neleidae ruled Messenia. Upon the return of the Heracleidae, Melanthus became king of the now autonomous Messenians. Agamemnon's promise to Achilles of seven cities, including those on the Messenian Gulf, indicates that these regions were under his control.
Messenê is bordered by Triphylia, with Cyparissia and Coryphasium located nearby. Above Coryphasium lies Mount Aegaleum. The ancient city of Messenian Pylus was situated at the foot of Aegaleum. The Athenians later rebuilt this city as a fortress against the Lacedaemonians. Nearby are the islands of Protê and Sphagia, the latter also known as Sphacteria, where the Lacedaemonians suffered a significant defeat by the Athenians.
Methonê, believed to be the Pedasus mentioned by Homer, is where Agrippa executed Bogus during the Actium War. Adjacent to Methonê is Acritas, marking the beginning of the Messenian Gulf. The Asinaean Gulf starts at Asinê and ends at Thyrides, with notable places such as Oetylus, Leuctrum, Cardamylê, Pherae, and Gerena along the way.
Significant rivers include the Pamisus, which flows through the Messenian plain, and another smaller Pamisus near Laconian Leuctrum. Messenia's landscape features cities such as Pylus, Cyparissia, and Erana. Historically, Cresphontes divided Messenia into five cities, later consolidating power in Stenyclarus. The city's strategic importance is highlighted by its acropolis, Ithomê, similar to Corinth's Acrocorinthus. |
|
| 5. After the Messenian Gulf comes the Lacon
ian Gulf, which lies between Taenarum and Maleae, curving from the south towards the east. Thyrides, a steep rock, is located in the Messenian Gulf, about 130 stadia from Taenarum. Above Thyrides lies Mount Taygetus, a lofty and steep mountain close to the sea, connecting with the Arcadian foothills. Sparta, Amyclae, and Pharis lie below Taygetus. The site of Sparta is in a hollow district, yet not marshy. Near the coast, Taenarum features a headland and a temple of Poseidon, and the mythological cavern where Heracles brought up Cerberus from Hades.
The distance across the sea from Taenarum to Phycus in Cyrenaea is 3,000 stadia, to Pachynus in Sicily is 4,000 to 4,600 stadia, and to Maleae is 670 stadia. Cythera, an island with a good harbor and city, lies 40 stadia off Onugnathus, a low-lying peninsula near Maleae.
After Taenarum, one encounters Psamathus, Asine, and Gythium, the seaport of Sparta, situated 240 stadia from the city. The Eurotas River flows between Gythium and Acraea. Helus, once a city founded by Helius, son of Perseus, is now a village in a marshy district. Following the coast, one reaches the plain called Leuce, then Cyparissia, Onugnathus, Boea, and finally Maleae. The distance from Onugnathus to Maleae is 150 stadia.
According to Ephorus, Eurysthenes and Procles, the Heracleidae, divided Laconia into six parts, founding cities, and used Las as a naval station. The surrounding peoples, initially equals, became known as Helots after being subdued by Agis, son of Eurysthenes, and forced into servitude, shaping the Spartan system of Helot-slavery. |
|
| 6. After Maleae follows the Argolic Gulf, and then the Hermionic Gulf; the former stretches to Scyllaeum, facing east and towards the Cyclades, while the latter extends to Aegina and Epidauria. The first places on the Argolic Gulf are occupied by Laconians, and the rest by the Argives. Among the Laconian places is Delium, sacred to Apollo, Minoa, a stronghold, and Epidaurus Limera, which has a good harbour. Immediately after sailing from Maleae, the Laconian coast is rugged but provides anchoring places and harbours.
The Argives have Prasiae, Temenium, where Temenus was buried, and the district through which flows the river Lerna, sharing its name with the marsh where the Hydra myth unfolds. Temenium lies twenty-six stadia from Argos; from Argos to Heraeum is forty stadia, and then to Mycenae is ten. After Temenium comes Nauplia, the Argives' naval station. Next are the caverns and labyrinths called Cyclopeian.
The Hermionic Gulf begins at the town of Asine. Then come Hermione and Troezen, and the island of Calauria, which has a circuit of 130 stadia, separated from the mainland by a strait four stadia wide. Then comes the Saronic Gulf, called a sea or strait, stretching from the Hermionic Sea and the Isthmus' sea, connecting with the Myrtoan and Cretan Seas. The Saronic Gulf includes Epidaurus and the island of Aegina off Epidaurus; then Cenchreae, the eastern naval station of the Corinthians; and Schoenus, a harbour forty-five stadia away. The distance from Maleae to Schoenus is about 1800 stadia. Near Schoenus is the "Diolcus," the narrowest part of the Isthmus, where the temple of Isthmian Poseidon is located. |
|
| 7. In antiquity, this region was under the Ionians, who were from the Athenians. Originally called Aegialeia, its people were known as Aegialeians. Later, it was called Ionia after the Ionians, similar to how Attica was named after Ion, the son of Xuthus. Hellen, the son of Deucalion, ruled between the Peneius and Asopus rivers in Phthia, passing his rule to his eldest son, while the rest sought settlements elsewhere. Dorus united the Dorians around Parnassus, and Xuthus, who married Erechtheus' daughter, founded the Tetrapolis of Attica. Achaeus fled to Lacedaemon, naming its people Achaeans, and Ion gained such repute from defeating the Thracians that the Athenians gave him governance.
Ion organized the people into four tribes and four occupational groups: farmers, artisans, sacred officers, and guards. Due to overpopulation, Athenians sent Ionians to colonize the Peloponnesus, naming it Ionia. They established twelve cities, but were later driven out by the Achaeans and returned to Athens. From there, they colonized Asia Minor, founding twelve cities in Caria and Lydia. The Achaeans, originally from Phthia but living in Lacedaemon, attacked the Ionians and took over their land.
The Achaeans, under democratic governance, became renowned for their constitutions, influencing Italiote cities after the Pythagorean uprising. After Leuctra, the Thebans used them to arbitrate city disputes. Despite Macedonian interference, the Achaeans reformed their league, starting with four cities including Patrae and Dyme, growing powerful and eventually forming a notable league. This league persisted until Philopoemen's generalship, despite Roman dominance over Greece. |
|
| 8. Arcadia, centrally located in the Peloponnesus, is predominantly mountainous. Cyllene is its highest peak, reaching a perpendicular height of fifteen to twenty stadia. Arcadia's tribes, like the Azanes and Parrhasians, are considered some of the oldest Greek tribes. Continuous wars have devastated the region, leading to the disappearance of famous cities and their tillers. Despite this, Arcadia offers excellent pastures for horses and asses.
Mantineia gained fame through Epameinondas, who defeated the Lacedaemonians there, losing his life. Today, Mantineia and other cities like Orchomenus, Heraea, and Cleitor are either non-existent or barely traceable. However, Tegea remains relatively intact, housing the temple of the Alean Athena and the temple of Zeus Lycaeus near Mount Lycaeum.
Arcadia boasts several notable mountains besides Cyllene, such as Pholoe, Lycaeum, Maenalus, and Parthenium, which extends into the Argive territory. The Alpheius, Eurotas, and Erasinus rivers exhibit unique behaviors. The Erasinus, for example, flows underground from the Stymphalian Lake to the Argive region, though it previously had no outlet due to blocked passages. Similarly, the Ladon's flow was once halted due to an earthquake-induced blockage near Pheneus.
Polybius noted that the distance from Maleae to the Ister was about ten thousand stadia. However, Artemidorus corrected this to six thousand five hundred and forty stadia, considering the specific route taken by one general. Ephorus mentions several colonizers who settled the Peloponnesus post-Heracleidae, including Aletes in Corinth, Phalces in Sicyon, Tisamenus in Achaea, Oxylus in Elis, Cresphontes in Messenê, Eurysthenes and Procles in Lacedaemon, and Temenus and Cissus in Argos. |
|
|
|
|
9 Greece. 5 103 1:25
| 1 Now that I have completed my circuit of the Peloponnesus, the next step is to traverse the peninsulas connected to it. The second peninsula includes Megaris, making Crommyon part of the Megarians, not the Corinthians. The third peninsula adds Attica, Boeotia, and parts of Phocis and the Epicnemidian Locrians to the second. According to Eudoxus, a line from the Ceraunian Mountains to Sunium divides the Peloponnesus from the continuous coastline to Megaris and Attica. He suggests that the coastline from Sunium to the Isthmus would not appear as concave if not for the districts forming the Hermionic Gulf and Actê. Similarly, the coast from the Ceraunian Mountains to the Corinthian Gulf would not appear so concave without Rhium and Antirrhium.
Peiraeus, the seaport of Athens, is located centrally on the line from Sunium to the Isthmus, about three hundred and fifty stadia from Schoenus and three hundred and thirty from Sunium. The area from Sunium northwards, bending westwards, and Actê’s eastern side towards Oropus in Boeotia is described as a peninsula with Attica and Boeotia forming an isthmus of the third peninsula.
After Crommyon, above Attica, are the Sceironian Rocks. The road from the Isthmus to Megara and Attica passes closely by these rocks, with the myth of Sceiron and Pityocamptes linked to this region. Following the Sceironian Rocks is Cape Minoa, forming the harbor at Nisaea, the naval station of the Megarians. This historical description includes the founding of Megara by the Heracleidae, displacing the Ionians. |
|
| 2 Next is Boeotia, and for clarity, I must recall my earlier remarks. The seaboard from Sunium to Thessaloniceia inclines slightly westward, with the sea on the east, and the land above it extending in ribbon-like stretches parallel to each other. The first stretch is Attica and Megaris, bordered by the seaboard from Sunium to Oropus and Boeotia on the east, the Isthmus and Alcyonian Sea on the west, and the seaboard from Sunium to the Isthmus and the mountainous country separating Attica from Boeotia. The second stretch is Boeotia, extending from the Euboean Sea to the Crisaean Gulf.
Ephorus declares Boeotia superior to neighboring countries due to its fertile soil and access to three seas with good harbors, facilitating trade with Italy, Sicily, Libya, Egypt, Cyprus, Macedonia, and the Propontis. Despite its natural advantages, Boeotian leaders historically neglected education and training, focusing solely on military virtues, which limited their success. Boeotia was once inhabited by Aones, Temmices, Leleges, Hyantes, and Phoenicians led by Cadmus, who founded Thebes. The Phoenicians' dominance continued until displaced by the Epigoni and later the Thracians and Pelasgians.
The Boeotians allied with Penthilus for the Aeolian colony, sent most of their population, and called it a Boeotian colony. Their land was ravaged by the Persian War near Plataeae but later recovered, with the Thebans defeating the Lacedaemonians and briefly dominating Greece until Epameinondas's death. Subsequent wars and Macedonian attacks led to Boeotian decline, leaving Thebes and other cities in ruins, except for Tanagra and Thespiae, which fared better. |
|
| 3 After Boeotia and Orchomenus, one comes to Phocis, which stretches north alongside Boeotia, nearly from sea to sea. Historically, Daphnus belonged to Phocis, splitting Locris into two parts. However, Phocis now no longer extends to the Euboean Sea but borders the Crisaean Gulf. Key places in Phocis include Crisa, Cirrha, Anticyra, Delphi, Cirphis, and Daulis. Parnassus, also part of Phocis, forms its western boundary.
Locris, divided by Parnassus, lies alongside Phocis. The western part, occupied by the Ozolian Locrians, extends to the Crisaean Gulf, while the eastern part ends at the Euboean Sea. The Ozolian Locrians have Hesperus engraved on their public seal. Phocis, bordered by Parnassus and inhabited by Locrians and Dorians, also lies near Aetolia and Thessaly.
Parnassus, esteemed as sacred, contains notable caves, including Corycium. Its western side is occupied by the Ozolian Locrians and some Dorians, while Phocians and most Dorians occupy the eastern side.
Delphi and Elateia are the most famous cities in Phocis. Delphi is renowned for the temple of Apollo and its oracle. Elateia, the largest city, controls passes into Phocis and Boeotia. Delphi, situated on Parnassus's western boundary, has a rocky, theatre-like setting. Cirrha, an ancient city by the sea, lies below Cirphis mountain.
Anticyra, known for its medicinal hellebore, endures, while Cirrha and Crisa were destroyed. The temple at Delphi, once exceedingly honored, now shows neglect. Historically, the seat of the oracle was a cave inspiring divine frenzy, with oracles delivered by the Pythian priestess. |
|
| 4 Locris is divided into two parts: one inhabited by the Locrians facing Euboea, split into two parts by Daphnus, with the Opuntians named after their metropolis and the Epicnemidians after Mount Cnemis. The other part is inhabited by the Ozolian Locrians, separated from the Opuntians and Epicnemidians by Parnassus and the Dorian Tetrapolis.
After Halae, the Boeotian coast facing Euboea, lies the Opuntian Gulf. Opus is the metropolis, about fifteen stadia from the sea, and Cynus is its seaport, opposite Aedepsus in Euboea. Deucalion is said to have lived in Cynus. Between Opus and Cynus lies a fertile plain. The island Atalanta is situated opposite Opus.
After Cynus, one comes to Alopê and Daphnus, now in ruins, followed by Cnemides, a stronghold. Opposite Cnemides, in Euboea, lies Cenaeum, separated by a strait about twenty stadia wide. This marks the territory of the Epicnemidian Locrians. The Boagrius River flows past Thronium into the sea. Next is Scarpheia, then Nicaea, and finally Thermopylae.
Homer mentions the Western Locrians indirectly. Their cities included Amphissa and Naupactus; Naupactus survives near Antirrhium. The Opuntians and Epicnemidians also had territories in Phocis. The Aetolians border the Western Locrians, and the Aenianians inhabit Mount Oeta.
Mount Oeta extends from Thermopylae to the Ambracian Gulf. Near Thermopylae are forts such as Nicaea and Heracleia. The Spercheius River flows past Anticyra. The Asopus River empties into the sea outside Pylae.
These regions once held strategic importance. At Thermopylae, Leonidas and his men resisted the Persians. Today, their polyandrium and pillars remain. There is also a large harbor and a temple of Demeter, where the Amphictyons performed sacrificial rites. |
|
| 5 Thessaly comprises the coastal region from Thermopylae to the Peneius River, facing Euboea and the east. The eastern side is held by the Malians, Achaean Phthiotae, and Magnetans. The northern side borders Macedonia, while the southern side borders the Oetaean and Aetolian mountains, Dorians, and Parnassus. The western side is surrounded by Aetolians, Acarnanians, Amphilochians, and Epeirotes. Thessaly is mostly a plain, except for Pelion and Ossa mountains.
Thessaly was divided into four parts: Phthiotis, Hestiaeotis, Thessaliotis, and Pelasgiotis. Phthiotis occupies the southern part, Hestiaeotis the western, Pelasgiotis the eastern, and Thessaliotis the central plains. Famous cities include Larisa, which retains its ancient dignity.
Homer's Catalogue lists the people under Achilles, who occupied the southern side, including Phthia and Hellas. Phoenix also shared the expedition. Homer describes Phthia and Hellas as distinct, with some later authorities placing Hellas between Palaepharsalus and Phthiotic Thebes. The Phthiotic
domain included cities such as Phthiotic Thebes, Echinus, Lamia, Narthacium, Erineus, and Melitaea.
The Dolopians, under Peleus, occupied the farthermost parts of Phthia. Thessalian plains were subject to inundations by the Peneius River, forming a lake until the cleft at Tempe drained it. Remaining lakes include Nessonis and Boebeïs. Pindus Mountain borders Thessaly to the north, with the Talares, a Molossian tribe, and Aethices. The Pindus area was historically significant.
The coastline was subject to Achilles, and the region from Thermopylae to Cenaeum included strategic locations like Thermopylae and Heracleian Trachin. Homolium, near Tempê, was a key site, and Cape Sepias, celebrated in literature, marks the eastern edge. The whole Thessalian and Magnetan plain was inhabited by Pelasgians, later displaced by Lapiths. |
|
|
10 Greek Islands. 5 86 1:12
| Euboea lies parallel to the coast from Sunium to Thessaly, excluding the ends on either side. The island is about 1200 stadia in length and roughly 150 stadia in breadth. Cenaeum lies opposite Thermopylae, while Geraestus and Petalia lie towards Sunium. Euboea approaches closest to the mainland at Chalcis, forming the Euripus.
The island was called Macris, Abantis, and Ellopia, among other names. Aristotle states that Thracians from Phocian Aba recolonized the island, renaming its inhabitants "Abantes." Ellopians, named after Ellops the son of Ion, migrated to Histiaea, enlarging the city. Philistides, the tyrant set up by Philip, named the city Oreus.
Oreus, situated at the foot of Mount Telethrius, lies on the River Callas. Carystus, near Mount Oche, is noted for producing a unique stone used for weaving. Geraestus, although not mentioned in the Catalogue of Ships, is noted for its temple of Poseidon.
Eretria, a significant city in Euboea, was originally colonized by Athenians. The Lelantine Plain near Chalcis was known for its hot springs. Chalcis, considered the metropolis of Euboea, and Eretria were founded by Aïclus and Cothus, respectively. The cities sent notable colonies into Macedonia, Italy, and Sicily.
Euboea experienced frequent earthquakes, particularly near the Euripus. Ancient philosophers like Menedemus established schools in Eretria. The Euboeans excelled in close combat, using outstretched spears. There are two notable rivers in Euboea, Cereus and Neleus, which influence the color of sheep that drink from them. The island has historical connections to various regions, including Macedonia, Sicily, and Lemnos. |
|
| The Aetolians and Acarnanians border each other, separated by the Acheloüs River. This river flows from Pindus southward through the Agraeans' and Amphilochians' lands, with the Acarnanians on the western side and the Aetolians on the eastern side. The Acheloüs was once called Thoas. In the south, both regions are washed by the sea, forming the Corinthian Gulf.
Acarnanian cities include Anactorium, Stratus, Oeneiadae, Palaerus, Alyzia, Leucas, Argos Amphilochicum, and Ambracia. Most have become dependencies of Nicopolis. Stratus lies midway between Alyzia and Anactorium.
Aetolian cities like Calydon and Pleuron were once significant. Aetolia is divided into Old Aetolia, a fertile coastal region from the Acheloüs to Calydon, and Aetolia Epictetus, a rugged area bordering the Locrians. Aetolia features the large mountain Corax, and the inland mountain Aracynthus, near which New Pleuron was founded.
The Evenus River begins in the Bomians' territory and flows past Chalcis and Calydon. Olenus and Pylenê are Aetolian cities, with Olenus destroyed by the Aeolians and Pylenê renamed Proschium.
Near the Acarnanian coast lies Actium, with the temple of Actian Apollo. Leucas, now an island, was a Corinthian colony.
Cephallenia, a Tetrapolis, is notable for its cities, including Samê or Samos, now extinct. It lies opposite Acarnania. Ithaca and its surrounding islands were part of Odysseus' domain. The Echinades islands are nearby, with Dulichium now called Dolicha.
Both regions were historically significant but weakened by continuous wars. The Acarnanians once joined the Trojan War, while the Aetolians fought for autonomy against various powers. |
|
| The Curetes are attributed to both Acarnanians and Aetolians, with origins linked to Crete or Euboea. Homer's account suggests they were Aetolians since the sons of Porthaon lived in Pleuron and Calydon, Aetolian cities. Opponents of this view are misled by Homer's expression "the Curetes were fighting, and the Aetolians steadfast in battle, about the city of Calydon." This phraseology is typically Homeric and used by other poets as well.
Ephorus claims that Aetolians were never subjugated due to their rugged terrain and warlike nature. He states that the Curetes initially inhabited the region but were driven to Acarnania by Aetolus, son of Endymion, who then founded the earliest Aetolian cities. Ephorus supports this with inscriptions: one in Aetolia honoring Aetolus, and another in Elis honoring Oxylus, who founded the city after ten generations.
These inscriptions highlight the kinship between Eleians and Aetolians, as both peoples were founders of each other. However, Ephorus inconsistently states that Aetolia remained undevastated despite the Curetes being overpowered and driven out by Aetolus. This contradicts his claim of Aetolia's uninterrupted sovereignty.
Further accounts suggest the Curetes migrated to Aetolia and clashed with Aeolians for control. They settled in Chalcis but moved due to constant war over the Lelantine Plain. In Pleuronia, they were known as Acarnanians for keeping their hair unshorn, unlike the shorn Curetes.
These historical narratives intertwine with mythological and cultural elements, reflecting the complex heritage and identity of the Curetes. |
|
| Since I have already described the Peloponnesian islands in detail, I will now discuss Crete, which is part of the Peloponnesus, and the surrounding islands, including the Cyclades and the Sporades. Let me first discuss Crete. Eudoxus mistakenly says it is in the Aegaean Sea; it lies between Cyrenea and Greece, parallel to these regions from west to east, and is bordered by the Aegaean and Cretan Seas to the north and the Libyan Sea to the south. Its western end near Phalasarna is divided into promontories: Criumetopon to the south and Cimarus to the north. The eastern extremity is Samonium, near Sunium.
According to Sosicrates, Crete is over 2,300 stadia long, and its circumference is more than 5,000 stadia, though Artemidorus claims it is 4,100 stadia. Hieronymus describes it as about 2,000 stadia long with an irregular breadth. The island is broadest near the middle, with Mount Ida as its tallest mountain, circular in shape, with a circuit of 600 stadia. The Leuca mountains in the west rival Taÿgetus in height.
Crete's journey from Cyrenea to Criumetopon takes two days and nights, and from Cimarus to Taenarum is 700 stadia. The voyage from Samonium to Egypt takes four days and nights, covering about 5,000 stadia. Crete hosts various people: Achaeans, Eteo-Cretans, Cydonians, Dorians, and Pelasgians. Staphylus says Dorians live in the east, Cydonians in the west, and Eteo-Cretans in the south, with the powerful plains inhabited by others. The island's significant cities include Cnossus, Gortyna, and Cydonia, with Cnossus famed for its association with Minos and its historical significance.
Crete has a rich history of laws and governance, influencing other Greek states, particularly Sparta. However, over time, it declined due to piracy and other conflicts. The Romans eventually subdued piracy and established their rule, with Cnossus now housing a Roman colony. |
|
| The islands near Crete include Thera, the metropolis of the Cyrenaeans, a colony of the Lacedaemonians, and Anaphê, where the temple of Aegletan Apollo is located. Thera, a long island with a perimeter of 200 stadia, lies opposite Dia, near the Cnossian Heracleium, 700 stadia from Crete. Nearby are Anaphê and Therasia, with the small island Ios, reputedly the burial place of Homer, located 100 stadia from Therasia. West of Ios are Sicinos, Lagusa, Pholegandros, Cimolos, and Siphnos. Melos, notable and located 700 stadia from both the Hermionic promontory and the Dictynnaeum, was once attacked by the Athenians, resulting in a massacre of its inhabitants.
Delos, renowned for its association with Apollo and Artemis, features a city, the temple of Apollo, the Letöum, and the mountain Cynthus. The river Inopus flows through Delos, a small island revered since ancient times. The Cyclades, once twelve islands, now number fifteen, including Ceos, Cyth
nos, Seriphos, Melos, Siphnos, Cimolos, Prepesinthos, Oliaros, Paros, Naxos, Syros, Myconos, Tenos, Andros, and Gyaros. Gyaros, a small fishing village, is noted for its poverty.
Delos's fame increased after the Romans destroyed Corinth, attracting importers to its temple and harbour. When Mithridates's generals attacked, Delos was ruined and remains impoverished under Athenian control. Rheneia, a desert isle near Delos, serves as a burial place since burials are forbidden in Delos itself.
Ceos, once a Tetrapolis, now has Iulis and Carthaea. Notable natives include poets Simonides and Bacchylides. The island had a law requiring those over sixty to drink hemlock. After Ceos, notable islands include Naxos, Andros, Paros, Syros, and Myconos, with Seriphos linked to the myth of Perseus. Tenos features a significant temple of Poseidon. |
|
|
11 West Asia 1 14 83 1:10
| 1 Asia borders Europe along the Tanaïs River. The Taurus mountains divide Asia into two parts: Cis-Tauran (north) and Trans-Tauran (south). The Taurus stretches about 45,000 stadia from Rhodes to eastern India and Scythia, with a width of up to 3,000 stadia. Significant tribes such as the Parthians, Medes, Armenians, Cappadocians, Cilicians, and Pisidians are distributed across its width, with the northern parts generally colder and the southern parts hotter. Most rivers originating from the Taurus flow either north or south, aiding in the continent's division. The first portion of northern Asia includes the region around the Tanaïs River and Lake Maeotis, extending to the Caspian Sea, and bordered on the south by Albania and Armenia. This region is akin to a peninsula. Poseidonius claims the isthmus between Lake Maeotis and the Ocean is about 1,500 stadia wide, comparable to the isthmus from Pelusium to the Red Sea. However, this measurement is debated. The second portion of northern Asia lies beyond the Caspian Sea, extending to the Scythians near India. The third portion includes areas adjacent to the previously mentioned isthmus, such as Media, Armenia, and Cappadocia. The fourth portion comprises the land inside the Halys River and the Taurus region, within the peninsula formed by the isthmus separating the Pontic and Cilician Seas. The Trans-Tauran region includes not only India but also Ariana, extending to the Persian Sea, the Arabian Gulf, the Nile, and the Egyptian and Issic Seas. |
|
| 2 The first portion of Asia is inhabited by Scythian nomads and waggon-dwellers near the north and the Ocean, followed by Sarmatians, Aorsi, and Siraci, extending to the Caucasian Mountains. Near Lake Maeotis live the Maeotae, and along the sea, the Asiatic side of the Bosporus. Nearby are the Achaei, Zygi, Heniochi, Cercetae, and Macropogones. Above these tribes lie the passes of the Phtheirophagi and the Colchian country at the Caucasian Mountains' foot. The Tanaïs River flows from the north, more to the east than the Nile, with unknown sources. Its outlets are in Lake Maeotis's northern region. The river and lake bear the city Tanaïs, founded by Greeks from the Bosporus, which King Polemon sacked. Tanaïs was a trading hub for nomads and navigators, exchanging slaves, hides, wine, and other goods. From Tanaïs, one travels 800 stadia to the Greater Rhombites River, known for fish suitable for salting, and another 800 stadia to the Lesser Rhombites River. Maeotae live along this coast, being farmers and warriors. The Maeotae near Tanaïs are fierce, while those by the Bosporus are more tractable. The Cimmerian Bosporus, once powerful, was overtaken by Greeks who founded cities like Panticapaeum. The narrowest part of the Maeotis, about 20 stadia, lies between Achilleium and Myrmecium. The Caucasus Mountains form a boundary between Albania, Iberia, and the Sarmatae plains. The Caucasus is rich in timber and marks the boundary of various tribes. The region around Dioscurias is a significant trading center, connecting seventy tribes with diverse languages and cultures. |
|
| 3 Iberia is well-developed, with cities and farmsteads boasting tiled roofs and architecturally skilled public buildings. The country is bordered by the Caucasian Mountains, which are fertile and encompass all of Iberia, adjoining Armenia and Colchis. The central plain is intersected by rivers, the largest being the Cyrus, which originates in Armenia, flows through the plain, and empties into the Caspian Sea. This river, formerly known as Corus, receives several tributaries, including the Aragus, Alazonius, Sandobanes, Rhoetaces, and Chanes. The Iberian plain is inhabited by peaceful farmers, who dress in Armenian and Median fashion. The warlike inhabitants occupy the mountainous areas, living similarly to the Scythians and Sarmatians. They engage in farming and can assemble large numbers for defense. Four passes lead into Iberia: one through Sarapana, a Colchian stronghold with the Phasis River flowing through ravines; another from the northern nomads' territory via a difficult ascent and a narrow valley along the Aragus River; a third from Albania through a rocky pass and marsh; and the fourth from Armenia via the defiles on the Cyrus and Aragus Rivers, each guarded by fortified cities on rocks. Iberians have four castes: the ruling caste, from which kings are appointed based on kinship and age; the priests, who handle disputes with neighboring peoples; the soldiers and farmers; and the common people, who are slaves of the king and manage all livelihood services. Possessions are held communally by families, with the eldest as ruler and steward. |
|
| 4 The Albanians, more inclined to a shepherd's life than the Iberians and akin to nomadic people, are moderately warlike. Their country lies between the Iberians and the Caspian Sea, bordered on the north by the Caucasian Mountains and on the south by Armenia. The fertile Caucasian Mountains encompass all of Iberia, and the central plain is intersected by the Cyrus River and its tributaries, including the Aragus, Alazonius, Sandobanes, Rhoetaces, and Chanes, which empty into the Caspian Sea. The Iberian plain is inhabited by peaceful farmers who dress in Armenian and Median fashion. The warlike inhabitants occupy mountainous areas, living similarly to the Scythians and Sarmatians. Four passes lead into Iberia: through Sarapana, a Colchian stronghold; from the northern nomads' territory via a difficult ascent and narrow valley along the Aragus River; from Albania through a rocky pass and marsh; and from Armenia via the defiles on the Cyrus and Aragus Rivers, each guarded by fortified cities on rocks. Iberians have four castes: the ruling caste, from which kings are appointed based on kinship and age; the priests, who handle disputes with neighboring peoples; the soldiers and farmers; and the common people, who are slaves of the king and manage all livelihood services. Possessions are held communally by families, with the eldest as ruler and steward. Albanians use javelins and bows, wear breastplates, oblong shields, and animal-skin helmets. Their kings are respected, and twenty-six languages are spoken due to their isolated tribes. They honor Helius, Zeus, and Selenê, with special reverence for Selenê, conducting sacrificial rituals with religious fervor. |
|
| The Amazons are said to inhabit the mountains above Albania. The Gelae and Legae, Scythian peoples, live between the Amazons and the Albanians, with the Mermadalis River flowing midway between them and the Amazons. According to Metrodorus of Scepsis and Hypsicrates, the Amazons live near the Gargarians, in the northern foothills of the Ceraunian Mountains of the Caucasus. They engage in tasks like ploughing, planting, and horse training, with the bravest among them focused on hunting and war exercises. Infants' right breasts are seared so they can use their right arms effectively, wielding javelins, bows, and shields made of wild animal skins. Twice a year, they gather with the Gargarians in the nearby mountains for rituals and clandestine mating, where Gargarian men impregnate them, and female offspring remain Amazons while males are raised by the Gargarians. The Mermodas River descends from the mountains, passing through Amazon territory and Siracene and emptying into Lake Maeotis. The Gargarians initially joined the Amazons from Themiscyra but later revolted, establishing a pact where they only interact through childbearing, living independently otherwise. Accounts of the Amazons blend myth with history, attributing city foundations like Ephesus and Smyrna to them, alongside tombs and monuments. They were said to have been ousted from territories like Themiscyra and the Thermodon plains. While some historians speculate on their current whereabouts, details lack substantiation. Stories of the Amazons, though mythical, persist across ages, suggesting their influence spanned regions from Ionia to Attica. Their legends, despite incredulity, continue to captivate, influencing ancient and modern narratives alike. |
|
| The second portion begins at the Caspian Sea, also known as the Hyrcanian Sea. This gulf stretches southwards from the ocean, narrowing at its entrance and widening inland to approximately 5000 stadia at its recess. The voyage from entrance to recess spans slightly more than this due to its location on the edge of the inhabited world. Eratosthenes notes the Greek understanding of its circumference: 5400 stadia along the Albanian and Cadusian
coasts, 4800 stadia along the Anariaci, Mardi, and Hyrcani to the Oxus River mouth, and 2400 stadia to the Iaxartes. These measurements, while general, give insight into distant regions and their distances. To the right, as one sails into the Caspian Sea, live the Scythians or Sarmatians, nomads extending from the Tanais River to Europe's edge. To the left are eastern Scythians, nomads reaching the Eastern Sea and India. Ancient Greek historians grouped northern peoples under "Scythians" or "Celtoscythians," with earlier distinctions like "Hyperboreans," "Sauromatians," and "Arimaspians" for those above the Euxine, Ister, and Adriatic. Peoples across the Caspian were termed "Sacians" and "Massagetans," involved in historical events like Cyrus' war, though details are often mythologized. Historians like Ctesias and Herodotus, blending myth and history, sought to entertain rather than strictly document. Alexander's conquests, reaching Asia's ends, inspired embellished histories difficult to verify. Roman and Parthian records provide more credible insights into distant regions and tribes than earlier traditions, reflecting greater scrutiny and knowledge accumulation. These accounts, blending historical fact with mythological allure, shaped perceptions of distant peoples and their lands, leaving a legacy of fascination and occasional skepticism in ancient historiography. |
|
| Those nomads along the left coast of the Caspian Sea today are called Däae, specifically the Aparni. Beyond them lies a desert region, followed by Hyrcania, where the Caspian resembles an open sea near the Median and Armenian mountains. These crescent-shaped mountains extend to the sea, inhabited by Gelae, Cadusii, Amardi, Vitii, and Anariacae. Some Parrhasii settled with the Anariacae, now known as Parsii, and Aenianes founded Aeniana in Vitian territory, famed for Greek artifacts and an oracle for dreamers. Cadusii dominate the rugged coastline for nearly 5000 stadia, with barren soils prevailing. Hyrcania contrasts with its fertility and level terrain, boasting cities like Talabrocê, Samarianê, Carta, and the royal capital, Tapê, situated slightly inland. The region is known for its abundant vineyards and fig trees, where grapes yield one metretes of wine and fig trees produce sixty medimni of fruit. Hyrcania and its eponymous sea, however, received little maritime attention due to the region's brigands, nomads, and remote locations under Persian, Median, and Parthian rule, with brief Macedonian oversight. Hyrcania is crisscrossed by the Ochus and Oxus rivers, the latter being the largest in Asia after Indian rivers, navigable for trade in Indian goods to Albania via the Caspian Sea and Cyrus River. The Ochus, lesser known in antiquity, flows near Parthian territory according to Apollodorus. Historical accounts, often embellished due to Alexander's fame, linked Lake Maeotis and the Caspian Sea, claiming a subterranean connection and mistakenly classifying them both as lakes. The region also boasts remarkable natural formations, such as cliffs with caverns and powerful rivers that discharge into the sea without wetting the shore, a site frequented by locals for feasts and rituals amidst lush, flower-filled meadows. |
|
| As one travels eastward from the Hyrcanian Sea, the mountains known as the Taurus by the Greeks stretch to the right, starting from Pamphylia and Cilicia, and continuing in a continuous line. These mountains bear different names along their length, housing various tribes. To the north dwell the Gelae, Cadusii, Amardi, and some Hyrcanians, followed by the Parthians, Margianians, and Arians. Beyond them lies a desert, separated from Hyrcania by the Sarnius River, extending towards the Ochus River. This mountain range, from Armenia to this point, is called Parachoathras, spanning about six thousand stadia to reach the Arians. Beyond them lie Bactriana, Sogdiana, and eventually the Scythian nomads. To the left, opposite these lands, lie the Scythian tribes, covering the northern expanse. Starting from the Caspian Sea, these Scythians are known as Däae, further east as Massagetae and Sacae, collectively termed Scythians. Notable among them are the Asii, Pasiani, Tochari, and Sacarauli, who migrated from across the Iaxartes River, adjoining the Sogdiani and Sacae lands. The Däae, known also as Aparni, Xanthii, and Pissuri, inhabit lands adjacent to Hyrcania, extending to areas parallel to Aria. Between these nomads and Hyrcania, Parthia, and up to Aria, lies a vast waterless desert. These nomadic peoples frequently raid their neighbors, establishing agreements that include tribute payments and occasional conflicts when terms are breached. The Sacae, notably, raided regions from Bactriana to Armenia, where their influence persisted, leading to conflicts and historical events memorialized in local customs and festivals. |
|
| The Parthian territory, historically small and impoverished, once shared its tributary status with Hyrcania under Persian and Macedonian rule. It includes regions like Comisenê, Chorenê, and stretches to the Caspian Gates, Rhagae, and Tapyri, formerly part of Media. Rhagae, marked by earthquakes, is situated 500 stadia from the Caspian Gates and 1,260 stadia from Hecatompylus, the Parthian royal seat. The Tapyri, residing between Derbices and Hyrcanians, had customs such as remarriage of wives after bearing children, akin to ancient Roman practices. Outside the Taurus Mountains, revolutions arose as Syria and Media's kings were occupied elsewhere. Bactriana rebelled under Euthydemus, followed by Arsaces, a Scythian, and his Aparnian Däae followers, who conquered Parthia. Initially weak, Arsaces and his successors expanded aggressively, eventually dominating lands up to the Euphrates, including parts of Bactriana, challenging Roman hegemony due to their Scythian-influenced lifestyle and successful military strategies. Regarding Arsaces' origins, debates suggest Scythian or Bactrian ancestry, with conflicting views on his flight from Diodotus' growing influence in Bactriana leading to the Parthian revolt. Poseidonius describes the Parthian Council, comprising kin and wise men including Magi, responsible for appointing kings. |
|
| Aria and Margiana, prominent districts in Asia, are distinguished by their geography and productivity. Aria, enclosed partly by mountains and partly by plains, is irrigated by rivers like the Arius and Margus. It borders Margiana and Bactria, located approximately 6,000 stadia from Hyrcania. Drangiana, linked in tribute with Aria and extending from Carmania to the northern reaches opposite Aria, lies predominantly south of the mountains. Arachosia, also nearby, stretches southward to the Indus River, forming part of Ariana. Aria spans about 2,000 stadia in length and 300 stadia in breadth, featuring cities like Artacaëna, Alexandreia, and Achaïa, known for their wine production, which ages well for generations in non-pitched vessels. Margiana, similar to Aria, is distinguished by its fertile plain surrounded by deserts. Antiochus Soter recognized its agricultural potential, enclosing a 1,500 stadia circuit with walls and establishing Antiocheia. The region's soil is particularly suited for vines, with reports of exceptionally large grapevines and clusters reaching two cubits in length. |
|
| Bactria, positioned north and east of Aria, is renowned for its fertility except in oil production. Greek influence here grew powerful after causing Bactria to revolt, extending their dominion over Ariana and India. Menander, notably, surpassed even Alexander in conquests, reaching Patalena and the coasts of Saraostus and Sigerdis. Bactriana, according to Apollodorus, adorned Ariana, expanding as far as the Seres and Phryni. Cities like Bactra (Zariaspa), through which flows the river Bactrus (Oxus), and Darapsa thrived. Eucratidia, named after its ruler, was divided into satrapies, some later taken by Parthians. The Greeks also held Sogdiana, between the Oxus and Iaxartes rivers. These regions, once similar to nomadic lifestyles, slightly more civilized in Bactria, reflected customs that Alexander's campaigns altered. Alexander founded cities like Maracanda and Cyra, the latter razed due to recurrent revolts despite its significance under Cyrus. Notably, Alexander married Rhoxana at the fortress of Sisimithres, where hospitality was lavish. Near Sogdiana, Alexander also subdued the Branchidae for their betrayal of Didyma
's treasures, reflecting his intolerance of sacrilege. Sogdiana's river Polytimetus, according to Aristobulus, waters fertile lands before dissipating into deserts. The Ochus River, debated in relation to the Oxus, flows through Bactriana and possibly converges later. The Iaxartes, distinct from the Oxus, marks the boundary into nomadic territories. The Taurus mountains, extending to the Indian Sea and tapering towards Asia's east, frame this segment from the Hyrcanian to Caspian seas, spanning around thirty thousand stadia in length and less than ten thousand in width. Tribes across Hyrcania to Sogdiana were noted for diverse customs, reflecting a mosaic of cultures from Persians to Scythians. These lands, steeped in history and customs, define a region where Alexander's conquests left lasting legacies amid varied tribal practices and geographical features. |
|
| The northern regions of Asia, known as Cis-Tauran Asia, are my focus here due to their intricate geography and varied inhabitants. These areas are primarily mountainous, extending eastward from the Caspian Gates, characterized by rugged terrain and wild populations. Media, positioned west of the Caspian Gates, was historically a powerful and expansive territory nestled amidst the Taurus Mountains. This region, fragmented into numerous valleys, shares similarities with neighboring Armenia. The Taurus Mountain range, originating in Caria and Lycia, starts modestly but gains height and breadth as it progresses eastward, enclosing vast valleys in Cilicia. It bifurcates into the Amanus and Antitaurus Mountains, with the latter hosting Comana in Upper Cappadocia. Amanus extends further east, reaching the Euphrates River near Melitenê, bordering Commagenê and Cappadocia. Beyond the Euphrates, the mountains continue, splitting but maintaining their continuity across the river. Here, the Taurus proper delineates the southernmost edge, separating Armenia from Mesopotamia. From the Taurus Mountains originate two significant rivers, the Euphrates and the Tigris, which define Mesopotamia as they meander toward the Persian Sea. The Euphrates, larger and more winding, originates northward in the Taurus, traversing Greater Armenia westward to Lesser Armenia and Cappadocia before bending southward through Syria into Babylonia. Conversely, the Tigris flows south from the southern Taurus, running parallel to the Euphrates until they converge near Seleuceia, forming the Mesopotamian basin before emptying into the Persian Gulf. Their sources, about 2,500 stadia apart, mark significant geographical features of the region. The Taurus Mountains, extending northward, branch into the Antitaurus and other ranges, encompassing Armenia, Iberia, and Albania. Eastward, towards the Caspian Sea and Media, they continue as the Parachoathras Mountains, known for their rugged terrain and diverse tribal populations engaging in mountain life and occasional banditry. Thus, within the Taurus lies the complex geography and varied territories of Media and Armenia, central to the ancient understanding of northern Asia. |
|
| Media is divided into two main regions: Greater Media and Atropatian Media. Greater Media, centered around Ecbatana, houses the royal residence of the Median empire, a city also used by the Parthian kings for its cool climate, with Seleuceia serving as their winter retreat near Babylon. Atropatian Media, named after the commander Atropates, initially part of Greater Media, became an independent state under his rule. His descendants continued to govern independently, forging alliances through royal marriages with Armenians, Syrians, and later with Parthians. Geographically, Atropatian Media lies east of Armenia and Matianê, west of Greater Media, and north of these regions, bordering the Hyrcanian Sea and Matianê to the south. It boasts significant military strength, capable of fielding ten thousand horsemen and forty thousand foot soldiers. The region features Capauta, a harbor known for efflorescing salts that, while painful, are mitigated by olive oil. Atropatian Media, despite being frequently plundered by neighbors like Armenians and Parthians, has historically regained lost territories like Symbacê from the Armenians, benefiting from strategic alliances, including with Roman leaders. The region's administrative centers include Gazaca for summer and Vera fortress for winter, the latter besieged by Antony during his Parthian campaign. The northern mountainous terrain, inhabited by tribes like the Cadusii and Amardi, contrasts with fertile southern lowlands conducive to horse breeding and agriculture. Media's cultural influence on neighboring lands, particularly Persia and Armenia, is evident in shared customs and royal practices rooted in its ancient history and strategic geographical position. |
|
| Armenia is situated in a geographically diverse region, surrounded by significant natural features that define its borders and landscapes. To the south, it faces the Taurus Mountains, separating it from Mesopotamia. Eastward, it borders Greater Armenia and Atropatenê, while to the north lie the Parachoathras Mountains near the Caspian Sea, and neighboring regions like Albania, Iberia, and the Caucasus. Westward, Armenia shares borders with Cappadocia and Commagenê, marked by the Paryadres and Scydises Mountains, extending into Lesser Armenia and the Euphrates River basin. The Euphrates River originates north of the Taurus Mountains, flows west through Armenia, bends southwards cutting through the Taurus into Syria, and eventually reaches Babylon, forming Mesopotamia with the Tigris River. Both rivers ultimately empty into the Persian Gulf. Armenia's terrain is predominantly mountainous and rugged, interspersed with valleys of varying fertility. Notable plains include the fertile Araxene Plain, traversed by the Araxes River, which extends into Albania and empties into the Caspian Sea. Armenia is renowned for its agricultural richness, boasting orchards, vineyards, and even olive groves. Regions like Phauenê, Comisenê, and Orchistenê are agriculturally productive, with Orchistenê particularly noted for its strong cavalry tradition. Northern regions like Chorzenê and Cambysenê, bordering the Caucasus, are characterized by severe winters and heavy snowfalls, affecting travel routes through mountain passes. Historically, Armenia's territory expanded under Artaxias and Zariadris, former generals turned kings who enlarged their domains through strategic alliances and conquests. The country's strategic location and natural resources have influenced its complex history, from Persian and Macedonian rule to autonomous periods under local kings recognized by the Romans. Today, Armenia remains a land rich in cultural heritage and historical significance, shaped by its unique geographical position and natural resources. |
|
|
|
12 West Asia 2 8 92 1:17
| 1 Cappadocia, a region with diverse boundaries and linguistic groups, is delineated by the Cilician Taurus to the south, Armenia and Colchis to the east, and the Euxine (Black Sea) to the north up to the Halys River outlets. To the west, it borders the Paphlagonians and Galatae extending into Phrygia and Lycaonia, alongside the Cilicians of Cilicia Tracheia. Historically, the Cataonians were distinct from the Cappadocians, despite speaking the same language. Cataonia was recognized separately and included Melitenê up to the Euphrates, forming a tenth part of Cappadocia. Over time, these distinctions blurred, with Ariarathes, the first Cappadocian king, integrating Cataonia into the kingdom. Geographically, Cappadocia forms an isthmus of sorts between the Issian Gulf towards Cilicia Tracheia and the Euxine Sea extending to Sinopê and the Tibareni coast. It occupies the western portion of the peninsula described by Herodotus as the land this side of the Halys River. During Persian rule, Cappadocia was divided into two satrapies, later transforming into kingdoms under Macedonian influence: "Cappadocia Proper" near Taurus and "Pontus" (Cappadocia Pontica). Roman rule further subdivided Greater Cappadocia into prefectures, including Melitenê, Cataonia, Cilicia, Tyanitis, and Garsauritis near Taurus, and Laviansenê, Sargarausenê, Saravenê, Chamanenê, and Morimenê elsewhere. In summary, Cappadocia's historical evolution reflects its strategic location and political changes under Persian, Macedonian, and Roman administrations, shaping its linguistic, geographical, and administrative landscape over time. |
|
| 2 Melitene resembles Commagene in its abundant fruit-tree plantations, unique in all of Cappadocia. It produces olives and Monarite wine, renowned like Greek wines. Situated opposite Sophene, the Euphrates River divides it from Commagene. Across the river lies Tomisa, a notable Cappadocian fortress sold to Sophene's ruler for a hundred talents, later gifted by Lucullus to Cappadocia's king for valor in the war against Mithridates. Cataonia, a vast hollow plain, cultivates all crops but evergreens. Bordered by southern mountains including Amanus and Antitaurus, Amanus stretches to Cilicia and the Syrian Sea, encircling the Gulf of Issus and Cilician plains. Antitaurus veers north-east, hosting deep valleys housing Comana and the Enyo temple, revered locally as "Ma." Comana, a significant city, thrives with divinely inspired residents and temple servants, numbering over six thousand. The Pyramus River, navigable from Cataonia, features a remarkable abyss where water flows underground, rising later. Its narrow passage through Taurus mountains roars like thunder, carrying silt to the sea, reminiscent of the Nile enriching Egypt. In the Taurus gorges, Enyo's temple oversees a saltwater reservoir, enclosed by steep hillsides, accessed by ladder-like steps. Melitene and Cataonia lack cities but boast strongholds like Azamora and Dastarcum, each guarding rivers and temples crucial to Cappadocia's landscape. Mazaca, the Cappadocian capital, sits in a challenging environment devoid of natural defenses or water, relying on nearby strongholds for security and timber from nearby forests. The kingdom, governed under Charondas' laws, endured challenges from Armenian invasions, its people displaced temporarily into Mesopotamia. Cappadocia, spanning 1800 stadia from Pontus to Taurus and 3000 stadia from Lycaonia to the Euphrates, thrives agriculturally, though colder than Pontus. Its diverse geography, from volcanic plains to mountainous borders, shapes its strategic and economic importance in the region. |
|
| 3 Mithridates Eupator established his kingdom in Pontus, extending from the Halys River to Armenia and controlling the coastline from Heracleia to Colchis and Lesser Armenia. Pompey reorganized the region, distributing parts to allies and forming a new province with Bithynia. The Romans continued to manage the area, making various administrative changes. Sailing into the Euxine Sea from the Propontis, one encounters Thracians, Bithynians, Mariandyni, Paphlagonians, and Pontic Cappadocians. The Bithynians, originally Mysians, were renamed after Thracian tribes. Heracleia, a significant city with good harbors, had a history of autonomy, tyrants, and Roman control. Between Chalcedon and Heracleia, notable rivers include Psillis, Calpas, and Sangarius. Sinopê, founded by the Milesians, was captured by the Romans. Paphlagonia, bounded by the Halys River, Phrygians, Galatians, Bithynians, and the Euxine Sea, was divided into coastal and inland areas, with Mithridates controlling parts. Amastris, founded by Dionysius' wife, was known for its excellent box-wood. Themiscyra, associated with the Amazons, was a fertile plain supporting herds and agriculture. The Eneti, notable Paphlagonians mentioned by Homer, migrated westward. The region was rich in resources, including mines and fertile land, with key locations like Cabeira and Nicopolis built by Pompey. Lesser Armenia and regions like Tibareni and Chaldaei were integrated into Mithridates' kingdom and later governed by Romans and local rulers. Pontus, with its rich resources and strategic importance, was significantly shaped by Roman reorganization and administration. |
|
| 4 Bithynia is bounded by the Paphlagonians, Mariandyni, and some of the Epicteti to the east; the Pontic Sea to the north; the Propontis to the west; and Mysia and Phrygia "Epictetus" to the south. Chalcedon, founded by the Megarians, and Chrysopolis, a village, lie at the mouth of the Pontus. The Astacene Gulf, part of the Propontis, is followed by Nicomedeia, named after a Bithynian king. Prusias, formerly Cius, was rebuilt by Prusias, who welcomed Hannibal. Above Prusias is the Arganthonium mountain, linked to the myth of Hylas. Prusa, founded by Prusias, is a well-governed city near Mysian Olympus. The boundaries between the Bithynians, Phrygians, and Mysians are difficult to define due to historical migrations and conquests. Mysia lies between Bithynia and the Aesepus River, extending to Olympus. Epictetus lies inland, around Mysia. The poet Homer references Mysia and Phrygia in relation to the Ascanian Lake. Various rulers, including Phrygians, Mysians, Lydians, Aeolians, Ionians, Persians, Macedonians, and Romans, have influenced the region, often changing its political and cultural landscape. In the interior of Bithynia are Bithynium and Nicaea, the latter founded by Antigonus and renamed by Lysimachus. Nicaea is a metropolis by the Ascanian Lake. Bithynia has produced notable scholars like Xenocrates, Dionysius, and Hippocrates. To the south of Bithynia are the Mysians, Hellespontian Phrygia, and Galatae, with Greater Phrygia and Lycaonia extending further south. |
|
| 5 The Galatians, south of the Paphlagonians, comprise three tribes: the Trocmi, Tolistobogii, and Tectosages. Named after their leaders or a Celtic tribe, they settled in Galatia after wandering and occupying territories. Led by Leonnorius, they spoke the same language and had a tetrarchy system with twelve tetrarchs forming a council. Over time, power shifted to one ruler, Deiotarus, then Amyntas, and now the Romans control the region. The Trocmi, near Pontus and Cappadocia, are the most powerful. Their garrisons include Tavium, Mithridatium, and Danala. The Tectosages are near Greater Phrygia, Pessinus, and Orcaorci, with the fortress Ancyra. The Tolistobogii border the Bithynians and Phrygia "Epictetus," with fortresses Blucium and Peium. Pessinus, a major emporium, hosts the revered temple of the Mother of the gods, Agdistis. Once controlled by powerful priests, its significance was enhanced by the Romans who brought the goddess's statue to Rome. The nearby Dindymum mountain and Sangarius River mark ancient Phrygian settlements, including Gordium. South of Galatia lies Lake Tatta, near Greater Cappadocia, known for its natural salt properties, where submerged objects become encrusted with salt. The surrounding region extends to the Taurus Mountains and was mostly held by Amyntas.
Lake Tatta is a natural salt-pan, easily solidifying around immersed objects and even trapping birds touching its water. |
|
| 6 Tatta is a region characterized by cold plateaus, scarce water, and wild asses grazing. Despite the arid conditions, it produces coarse wool, which has made some inhabitants wealthy. Amyntas had over three hundred flocks here. The area includes lakes Coralis and Trogitis and the town of Iconium, which has a more prosperous territory. The Taurus mountains separate Cappadocia and Lycaonia from Cilicia Tracheia. Isauricê, near Taurus, includes the two villages named Isaura, known for their robbers. These villages caused trouble for the Romans, notably Publius Servilius, who subdued them. Derbê, near Cappadocia, was the seat of tyrant Antipater Derbetes and later held by Amyntas, who killed Derbetes. Amyntas also captured Old Isaura and began building a new wall there before being killed by Cilicians during an invasion. Amyntas controlled territories including Antiocheia near Pisidia, Apollonias near Apameia Cibotus, and parts of Lycaonia. He sought to exterminate the Cilicians and Pisidians, capturing many previously impregnable places like Cremna. Cremna is now occupied by Roman colonists. Amyntas was eventually betrayed and killed by the wife of the Homonadeis' tyrant, leading to his downfall. Cyrinius later subdued the Homonadeis, capturing four thousand men and resettling them, leaving their country desolate. The Taurus heights contain a fertile plain divided into valleys, where the inhabitants lived on mountain brows or in caves, often raiding neighboring areas. |
|
| 7 The Pisidians, particularly the Selgeis, are notable inhabitants of the Taurus mountains. Some live above Sidê and Aspendus, while others occupy hilly, olive-planted areas. The region also includes the Catenneis and the Sagalasseis, with the latter facing Milyas. Artemidorus lists several Pisidian cities: Selgê, Sagalassus, Petnelissus, Adada, Tymbriada, Cremna, Pityassus, Amblada, Anabura, Sinda, Aarassus, Tarbassus, and Termessus. These cities range from mountainous to foothill areas, bordering peaceful tribes like the Phrygians, Lydians, and Carians. However, Pamphylians, influenced by Cilician piracy, often disturb neighboring regions. The Pisidians are divided into tribes governed by tyrants and engage in piracy. Ancient Leleges intermixed with them due to similar characteristics. Selgê, originally founded by Lacedaemonians and Calchas, became a powerful, independent city with a peak population of twenty thousand. The fertile region supports extensive olive groves, vineyards, and pastures, surrounded by timber forests. The styrax-tree, used for making javelins, is abundant. Selgeis extract a fragrant gum from these trees, used as incense. The Selgic iris and its ointment are also praised. The mountainous and ravine-filled territory, including the Eurymedon and Cestrus rivers, provides natural fortifications. Selgê's strategic location and fortifications have kept it independent until becoming part of Roman territory, formerly ruled by Amyntas. The Selgeis maintained autonomy by engaging in specific agreements with the Romans. |
|
| 8 Bordering the Bithynians to the south are the Mysians and Phrygians around the Mysian Olympus. These tribes are divided into two parts: Greater Phrygia, where Midas reigned, partially occupied by the Galatians, and Lesser Phrygia, or Phrygia Epictetus, near the Hellespont. Mysia is similarly divided into Olympenê, near Bithynia and Phrygia Epictetus, and the area around the Caïcus River extending to Teuthrania. The boundaries between these regions are confusing, particularly around Mt. Sipylus, which the ancients called Phrygia. This area includes Pergamenê, Elaïtis, and Teuthrania, lying between the Hellespont and regions around Sipylus and Magnesia. The Lydians and Maeonians, whom Homer called Meïones, are also entangled with these groups, with debates over their distinctions. The confusion extends to the myths and migrations involving these tribes, compounded by the fertility of the region, making it a target for invasions. The Pelasgians, Cauconians, and Leleges, among others, wandered through Europe, becoming allies of the Trojans. The existence of dual groups of Lycians and Cilicians suggests shared origins, though evidence is sparse. The region's rich history includes the Selgeis and Pisidians in the Taurus, famed for olive groves and vineyards, and known for piracy. The region's fertility and strategic importance made it a prize for various conquerors, including Greeks, Trerans, Cimmerians, Lydians, Persians, Macedonians, and finally the Romans, who established their influence over these fragmented territories. |
|
|
|
|
13 West Asia 3 4 71 1 Hr
| 1 Bordering the Bithynians to the south are the Mysians and Phrygians around the Mysian Olympus. These tribes are divided into Greater Phrygia, where Midas reigned, and Lesser Phrygia, or Phrygia Epictetus, near the Hellespont. Mysia is similarly divided into Olympenê and the area around the Caïcus River extending to Teuthrania. The boundaries between these regions are confusing, particularly around Mt. Sipylus. This area includes Pergamenê, Elaïtis, and Teuthrania, lying between the Hellespont and regions around Sipylus and Magnesia. The Lydians and Maeonians, whom Homer called Meïones, are also entangled with these groups, with debates over their distinctions. The region's rich history includes the Selgeis and Pisidians in the Taurus, famed for olive groves and vineyards, and known for piracy. The area's fertility and strategic importance made it a prize for various conquerors, including Greeks, Trerans, Cimmerians, Lydians, Persians, Macedonians, and finally the Romans, who established their influence over these fragmented territories. This region was subject to various rulers and tribes, each leaving their mark and contributing to its complex history. Despite the confusion in boundaries and names, the area's strategic and fertile lands made it a significant and contested region throughout ancient history. The influence of different cultures and rulers, from the Phrygians to the Romans, shaped the region into a diverse and historically rich area. |
|
| 2 Since Lesbos, an island worthy of a full account, lies alongside and opposite the coast extending from Lectum to Canae, and also has small islands around it, it is time to describe these. Lesbos is the metropolis of the Aeolian cities. Starting from Lectum to Assus, the Lesbian country begins at Sigrium, its northern promontory. Nearby is Methymna, a city of the Lesbians, sixty stadia from the coast stretching from Polymedium to Assus. The island's perimeter is eleven hundred stadia, with distances from Methymna to Malia (southernmost promontory) being three hundred and forty stadia, from Malia to Sigrium five hundred and sixty, and from Sigrium to Methymna two hundred and ten. Mitylene, the largest city, lies between Methymna and Malia, seventy stadia from Malia, one hundred and twenty from Canae, and the same distance from the Arginussae islands. Mitylene has two harbors, one southern that holds fifty triremes and can be closed, and a larger, deeper northern harbor sheltered by a mole. Off both harbors lies a small island, part of the city. Mitylene produced notable figures: Pittacus, one of the Seven Wise Men; poet Alcaeus; his brother Antimenidas; and the poetess Sappho. The city was once ruled by several tyrants due to internal dissensions, which are the subject of Alcaeus' poems. Theophanes the historian and statesman, a friend of Pompey the Great, also hailed from Mitylene. Pyrrha has been destroyed, but its suburb is inhabited and has a harbor, with an eighty-stadia passage over hills to Mitylene. After Pyrrha, one comes to Eressus on a hill, then to Sigrium, twenty-eight stadia from Eressus. Antissa, with a harbor, follows Sigrium, and then Methymna, home of Arion the cithara player, and Terpander, who introduced the seven-stringed lyre. |
|
| 3 Since the Leleges and Cilicians were closely related to the Trojans, people question why they aren't included with the Trojans in the Catalogue. It is reasonable to assume that due to the loss of their leaders and the sacking of their cities, the few remaining Cilicians were placed under Hector's command. Both Eëtion and his sons were said to have been slain before the Catalogue: "My father was slain by goodly Achilles, who sacked the city of Cilicians, Thebê of the lofty gates." Similarly, those under Mynes lost their leaders and city: "He laid low Mynes and Epistrophus, and sacked the city of godlike Mynes." However, the Leleges are mentioned in the battles: "Towards the sea are situated the Carians, Paeonians, Leleges, and Caucones." The poet omitted them from the Catalogue, possibly because their organization was insufficient, or included them under Hector due to their close relation; for instance, Lycaon, Hector's brother, says, "My mother, daughter of old man Altes, bore me — Altes, lord over the war-loving Leleges." These are the probable explanations. Reasoning from probabilities, one might inquire about the exact bounds of the Cilicians, Pelasgians, and Ceteians under Eurypylus, who lived between the Cilicians and Pelasgians. Homer indicates that the number of Pelasgians was considerable: "Hippothoüs led the tribes of the Pelasgians that rage with the spear, dwelling in fertile Larisa." The best assumption is that this refers to the Larisa near Cymê, not the one near Hamaxitus or the one in the Caÿster Plain near Ephesus. The Aeolians found the Pelasgians in Larisa when they arrived from Phricium, built Neon Teichos, and later founded Cymê. This indicates the presence of Pelasgians in the area. The Pelasgians were significant historically, inhabiting the Ionian coast and nearby islands. The Lesbians claim Pylaeus, a Pelasgian ruler, founded their mountain, while the Chians say Thessalian Pelasgians founded their city. The Pelasgians, quick to migrate, rapidly increased and disappeared, especially during the Aeolian and Ionian migrations to Asia. |
|
| 4 Pergamum, a famous city, prospered under the Attalic kings. It began as the treasure-hold of Lysimachus, one of Alexander's successors, and was situated on a cone-like mountain peak. The fortress and treasure, amounting to nine thousand talents, were entrusted to Philetaerus of Tieium, a eunuch who later rebelled against Lysimachus due to conflicts with his wife, Arsinoë. Philetaerus then governed Pergamum, leveraging the region's instability after Lysimachus' fall and Seleucus Nicator's invasion. Philetaerus maintained control for twenty years, navigating political turmoil through diplomacy. Philetaerus was succeeded by his nephew Eumenes, who expanded Pergamum's influence by defeating Antiochus, the son of Seleucus. Eumenes' successor, Attalus, became the first to be proclaimed king after defeating the Galatians. Attalus formed alliances with the Romans, supporting them against Philip and dying after a forty-three-year reign. His sons included Eumenes, who enhanced the city's infrastructure, and Attalus, who served as his brother's guardian and later fought successfully against various adversaries. The territory of Pergamum, initially limited, expanded significantly after Eumenes allied with the Romans against Antiochus the Great. Pergamum grew into a cultural and intellectual hub, with significant contributions to architecture and libraries. Eumenes' son, Attalus Philometor, ruled briefly before the Romans declared the region a province named Asia. Prominent Pergamenians included Mithridates, a friend of Caesar, and Apollodorus the rhetorician. The region around Pergamum featured cities like Apollonia and Thyateira, highlighting its strategic and cultural significance in ancient Asia Minor. |
|
|
|
14 Islands. 6 101 1:23
| 1 The Ionians, Carians, Lycians, Pamphylians, and Cilicians occupy the seaboard outside the Taurus, forming the peninsula's coast from the Pontic to the Issic Sea. The Ionian coast spans 3,430 stadia, winding through gulfs and peninsulas. The straight-line distance between Ephesus and Smyrna is 320 stadia, contrasting with the nearly 2,200 stadia coasting voyage. The Ionian coast extends from the Poseidium of the Milesians to Phocaea and the Hermus River.
Miletus, Myus, and areas around Mycalê and Ephesus were once Carian, while the region from Phocaea and Chios to Samos was occupied by Leleges. Androclus, son of Codrus, led the Ionian colonization, founding Ephesus, the royal seat of the Ionians. Miletus was established by Neleus, a Pylian, with settlers claiming kinship with the Messenians.
The twelve Ionian cities included Miletus, Myus, Lebedus, Colophon, Prienê, Teos, Erythrae, Phocaea, Clazomenae, Chios, Samos, and later Smyrna, incorporated into the Ionian League by the Ephesians. The cities have rich histories and connections to notable figures like Bias of Prienê, Thales of Miletus, and Heracleitus of Ephesus.
After Miletus is the Latmian Gulf and Heracleia below Latmus, a small town. The region includes the oracle of Apollo Didymeus, the sacred precinct of Branchus, and the temple set ablaze by Xerxes. Miletus itself has four harbors, notable colonizations, and connections to figures like Anaximenes and Hecataeus. The Ephesians, driven out by Androclus, later flourished under Croesus, Lysimachus, and Alexander, who contributed to the development and expansion of the city. |
|
| 2 The region beyond the Maeander River is predominantly Carian, with Milesians and Myesians occupying a portion of the seaboard. The coast starts from the Peraea of the Rhodians and ends at the Poseidium of the Milesians, with the interior extending to the Taurus Mountains near the Maeander. The Taurus range begins near the Chelidonian Islands off Pamphylia and Lycia and continues through the country, including the Cibyrans' land and the Rhodian Peraea.
The coast from the Peraea of the Rhodians to the Propontis measures about 4,900 stadia, including a 1,500-stadia segment around the Rhodian Peraea. This area features notable locations like Daedala, Mount Phoenix, the island of Elaeussa, and the Gulf of Glaucus. Key cities include Caunus, with its deep river Calbis, and Physcus, which has a harbor and a sacred precinct dedicated to Leto. The city of Rhodes, situated on the eastern promontory of its island, is renowned for its harbors, walls, and administration, which have made it a significant maritime power and ally to the Romans.
Prominent Carians, such as the Heracleidae, founded several cities, including Mylasa, known for its fertile plain and marble quarry, and Stratoniceia, notable for its temples of Hecate and Zeus Chrysaoreus. Alabanda, situated at the foot of hills, is known for its luxurious lifestyle and prominent orators. The Carians' military prowess is evidenced by their distinct shield emblems and crests, with historical records noting their involvement in various Greek campaigns.
In summary, the Carian region, enriched with historical cities and significant mythological associations, played a vital role in the ancient geopolitical landscape. |
|
| 3 After the Peraea of the Rhodians, starting from Daedala, one encounters Lycia, extending to Pamphylia, then to the Tracheian Cilicians, and finally to the Cilicians around the Gulf of Issus. The isthmus stretches from Issus to Amisus or Sinopê, lying outside the Taurus on the narrow coast from Lycia to Soli, now Pompeïopolis. The coast then spreads into plains starting from Soli and Tarsus.
After Daedala, one reaches the mountain Daedala in Lycia, beginning a 1,720-stadia Lycian coastline, rugged but rich in harbors and inhabited by decent people. Unlike the Pamphylians and Cilicians, who engaged in piracy, the Lycians maintained a civil and orderly society, forming the Lycian League with 23 cities. The largest cities had three votes each, medium-sized ones two, and the rest one. They contributed to a general congress, elected a "Lyciarch," officials, and designated courts. Their good governance kept them free under Roman rule, while pirates were eradicated by Servilius Isauricus and Pompey the Great.
Next, one comes to Telmessus, an ancient Lycian town, and then to Anticragus and Cragus mountains. At the foot of Cragus lies Pinara, one of the largest Lycian cities. Further along, the Xanthus River leads to Xanthus, Lycia’s largest city, and then to Patara, with its temple of Apollo. Other notable locations include Myra, Limyrus River, and the islands Megistê and Cisthenê.
The Lycian coast ends at Hiera promontory and the Chelidoniae islands. The Taurus mountains are said to begin here, extending from the Rhodian Peraea to Pisidia. This mountainous tract connects to Pisidia, with significant locations like Phaselis, Solyma, and Termessus. |
|
| 4 After Phaselis, one reaches Olbia, a large fortress marking the start of Pamphylia. Next is the Cataractes River, which cascades from a high rock with such force that its sound is heard from afar. Then comes Attaleia, named after its founder Attalus Philadelphus, who also established a colony at Corycus, a nearby town. According to Callisthenes, the Trojan Cilicians, driven from the plain of Thebê, settled between Phaselis and Attaleia.
Next, one encounters the Cestrus River. Sailing sixty stadia up this river leads to Pergê, a city with the temple of Artemis Pergaea, which hosts an annual festival. About forty stadia from the sea is Syllium, a visible lofty city from Pergê. Further along is the large lake Capria, then the Eurymedon River. Sailing sixty stadia up this river leads to Aspendus, a thriving city founded by the Argives. Above Aspendus is Petnelissus.
Continuing, one finds another river and numerous isles. Then Sidê, a Cymaean colony with a temple of Athena, near the coast of the Lesser Cibyratae. Following are the Melas River, a mooring place, and the city of Ptolemaïs. The boundaries of Pamphylia end at Coracesium, the start of Cilicia Tracheia. The entire Pamphylian coast voyage covers six hundred and forty stadia.
Herodotus states that the Pamphylians descend from peoples led by Amphilochus and Calchas from Troy, with some settling in Pamphylia and others spreading across various regions. Callinus adds that while Calchas died in Clarus, Mopsus's followers crossed the Taurus, settling in Pamphylia, Cilicia, Syria, and even Phoenicia. |
|
| 5 Cilicia, outside the Taurus, is divided into Tracheia and Pedias. Tracheia, narrow and rugged, lies at the Taurus's foot, providing a poor livelihood up to the regions of Isaura and Pisidia. Tracheiotis and its people, the Tracheiotae, occupy this area. Cilicia Pedias extends from Soli and Tarsus to Issus, featuring plains and fertile land, bordering the Cappadocians north of the Taurus. Having described the areas within the Taurus, the focus now shifts to those outside, beginning with the Tracheiotae.
Coracesium, the first Cilician stronghold on an abrupt rock, served as Tryphon's base when he revolted against Syrian kings. Tryphon's actions, combined with ineffective rulers, spurred piracy, exacerbated by the lucrative slave trade to places like Delos, where up to 10,000 slaves could be sold in a single day. The increasing demand for slaves, spurred by Roman wealth from the destruction of Carthage and Corinth, fueled piracy. The kings of Cyprus and Egypt, as well as the Rhodians, didn't assist the Syrians, allowing piracy to flourish until the Romans intervened with force.
Following Coracesium are Arsinoë, Hamaxia, Laertes, Selinus, and Cragus. Notable locations include Anemurium, closest to Cyprus
, and the beginning of Cilicia Pedias at Nagidus. Important cities like Mallus, founded by Amphilochus and Mopsus, and Tarsus, an educational hub surpassing even Athens and Alexandria, highlight Cilicia's significance. Tarsus is known for its devotion to education and has produced numerous philosophers and scholars.
The coastline from Pamphylia to Anemurium spans 820 stadia, with an additional 500 stadia to Soli. Near Soli is Celenderis, and from there, the journey continues inland to notable cities and rivers, including the Cestrus and Eurymedon Rivers. |
|
| 6 Cyprus, an island in the eastern Mediterranean, is bordered by the Aegyptian, Pamphylian, and Issic seas. The northern part of Cyprus is closest to Cilicia Tracheia, with the eastern side bordering the Issic Gulf, the western side facing the Pamphylian Sea, and the southern side by the Aegyptian Sea.
The island's circumference is 3,420 stadia, with its length from Cleides to Acamas being 1,400 stadia. Cleides comprises two islands off the eastern coast, 700 stadia from the Pyramus River. Acamas, a promontory in the west, extends northward and is closest to Selinus in Cilicia Tracheia. The distance to Sidê in Pamphylia is 1,600 stadia and to the Chelidonian islands is 1,900 stadia.
Starting from Anemurium, the journey to Cleides passes several cities: Lapathus with mooring places and dockyards, Aphrodisium, and Carpasia with a harbour. The island narrows near Salamis. Notable locations include Olympus, with its temple of Aphrodite Acraea, and the Carpasian Islands. Salamis is followed by Arsinoë, Leucolla, and Pedalium. Citium, the birthplace of Zeno, founder of the Stoic school, and Apollonius, lies further along. Other important cities are Amathus, Palaea, Curium, and Paphus with its temple of Paphian Aphrodite.
The island is rich in resources, producing wine, oil, and grain. It also has abundant copper mines. Once ruled by tyrants, Cyprus became part of the Ptolemaic kingdom and later a Roman province, following the deposition of the last Ptolemaic king due to Publius Claudius Pulcher's influence. Cyprus briefly came under Cleopatra's rule before reverting to a Roman province. |
|
|
|
|
|
|
15 East Asia. 3 90 1:19
| 1 Cyprus is an island in the eastern Mediterranean bordered by the Aegyptian, Pamphylian, and Issic seas. Its northern part is closest to Cilicia Tracheia, the east borders the Issic Gulf, the west faces the Pamphylian Sea, and the south is by the Aegyptian Sea.
The island's circumference is 3,420 stadia, with a length of 1,400 stadia from Cleides to Acamas. Cleides comprises two islands off the eastern coast, 700 stadia from the Pyramus River. Acamas, a promontory in the west, extends northward and is closest to Selinus in Cilicia Tracheia. The passage to Sidê in Pamphylia is 1,600 stadia, and to the Chelidonian islands is 1,900 stadia.
Starting from Anemurium, the journey to Cleides passes cities like Lapathus with mooring places and dockyards, Aphrodisium, and Carpasia with a harbour. The island narrows near Salamis. Notable locations include Olympus, with its temple of Aphrodite Acraea, and the Carpasian Islands. Salamis is followed by Arsinoë, Leucolla, and Pedalium. Citium, the birthplace of Zeno, founder of the Stoic school, and Apollonius, lies further along. Other important cities are Amathus, Palaea, Curium, and Paphus with its temple of Paphian Aphrodite.
Cyprus is rich in resources, producing wine, oil, and grain. It also has abundant copper mines. Once ruled by tyrants, Cyprus became part of the Ptolemaic kingdom and later a Roman province, following the deposition of the last Ptolemaic king due to Publius Claudius Pulcher's influence. Cyprus briefly came under Cleopatra's rule before reverting to a Roman province. |
|
| 2 Ariana is the first Persian-controlled region after India, bounded by the Indus River and the Taurus mountains. Its southern side starts at the Indus outlets and ends at Carmania and the Persian Gulf. The coastline is 12,900 stadia long, inhabited by various tribes like the Arbies, Oreitae, and Ichthyophagi, who mainly live off fish, using whale bones for building.
Gedrosia, north of the Ichthyophagi, is less torrid than India but still harsh, producing spices like nard and myrrh. Alexander's army used these for tent coverings. Gedrosia experiences rains in summer, filling its rivers and wells, aiding Alexander's march. He divided his forces, with one division led by Craterus through the interior and a fleet led by Nearchus.
Nearchus started his autumn voyage, facing hostile barbarians. Alexander faced significant hardships, with his army suffering from hunger and thirst, surviving on date palms. The journey was grueling, with long marches and extreme heat causing many deaths. Eventually, they reached Carmania, reuniting with Craterus.
The Carmanians use whale bones for construction and have silver and copper mines. They primarily use asses for transport and war due to the scarcity of horses. They worship Ares, sacrificing asses, and value enemy heads as war trophies. Their customs and language are similar to the Medes and Persians.
Nearchus also reported large, harmless whales spouting water, initially frightening the sailors but eventually driven away by loud noises. The fleet’s hardships highlight the challenging conditions of Alexander's conquests. |
|
| 3 After Carmania, one enters Persis, a region with a significant coastline along the Persian Gulf and a larger interior extending north towards Media. Persis has three distinct climates: a hot, sandy coast with limited fruit production; a fertile, river-rich central plain excellent for cattle; and a wintry, mountainous northern area inhabited by camel-breeders. Eratosthenes notes its length towards the Caspian Gates as about 8,000 stadia. The inhabitants include the Pateischoreis, Achaemenidae, and Magi, who live austere lives, unlike the brigand Cyrtii and Mardi.
Susis, bordering Persis and Babylonia, houses the notable city of Susa, established as a royal seat by Cyrus for its strategic location and high standing. The city's layout includes a royal palace built with materials similar to Babylon's. Alexander preferred Babylon over Susa for its size and other qualities. Susis is fertile but extremely hot, producing abundant grain and barley.
Persis has several palaces, including those at Persepolis and Pasargadae, where Cyrus is buried. Alexander, after significant conquests and hardships, amassed treasures in Susa and Persis, valued at up to 50,000 talents, preferring Babylon as his royal seat. The Persians, who worship natural elements like fire and water, follow rigorous sacrificial rituals. They are trained in archery, horsemanship, and truth-speaking from ages five to twenty-four, with an emphasis on endurance and practical skills.
Alexander's conquests disrupted Persian power, which was later diminished by the Macedonians and Parthians. The Persian hegemony over Asia lasted about 250 years before being divided among Alexander’s successors. Today, Persians are under Parthian rule. |
|
|
|
|
16 Syria. 4 114 1:35
| 1 The Assyrians' country borders Persis and Susiana. This region includes Babylonia and Aturia, encompassing Ninus, Apolloniatis, Elymaei, Paraetacae, and the Chalonitis near Mt. Zagrus. It stretches from the plains around Ninus to Dolomenê, Calachenê, Chazenê, and Adiabenê, extending to the Euphrates and inhabited by various tribes, including those now called Syrians, who extend to Cilicians, Phoenicians, Judaeans, and the Gulf of Issus. The name Syrians historically extended from Babylonia to the Gulf of Issus, including the Cappadocians known as "White Syrians." Historians recount that the Medes overthrew the Syrians, who built Babylon and Ninus. Ninus founded the city of the same name in Aturia, and his wife, Semiramis, succeeded him, founding Babylon and undertaking vast infrastructure projects across Asia. Their empire lasted until the Medes took over. Ninus was destroyed after the Syrian Empire's fall, larger than Babylon, located in Aturia near the Lycus River. Arbela, across from Babylonia, is famous for the battle where Dareius lost his empire. The Macedonians, finding Arbela more significant, credited it for the victory over Dareius, though the battle occurred near Gaugamela, meaning "Camel's House," named for Dareius’s camel. Babylon, lying in a plain, had a wall circumference of 385 stadia, with significant height and width, featuring one of the Seven Wonders: the Hanging Gardens. The Euphrates runs through the city, providing water for the gardens. Babylon was later overshadowed by Seleuceia, founded by Seleucus Nicator, becoming a greater city as Babylon fell into ruin. |
|
| 2 Syria is bounded on the north by Cilicia and Mt. Amanus, and on the east by the Euphrates and Arabian Scenitae. On the south, it borders Arabia Felix and Egypt, and on the west, it meets the Egyptian and Syrian Seas. The distance from the Gulf of Issus to the Euphrates bridge is about fourteen hundred stadia. Syria includes Commagenê, the Seleucis of Syria, Coelê-Syria, Phoenicia, and Judaea. Commagenê is a small country with Samosata as its main city. Seleucis is known for its four major cities: Antiocheia, Seleuceia in Pieria, Apameia, and Laodiceia, all founded by Seleucus Nicator. Antiocheia, the metropolis of Syria, was significant in power and size. The Orontes River flows near the city, with the settlement of Daphnê located forty stadia away, featuring a temple of Apollo and Artemis. Phoenicia, a narrow coastal region, extends from Orthosia to Pelusium. Tyre and Sidon are its prominent cities. Tyre, an island city connected to the mainland by Alexander’s mole, has two harbors and is known for its superior purple dye. Sidon is celebrated for its arts, philosophy, and crafts. Judaea extends from Casius to Jerusalem, with its people known for their unique religious practices and historical connection to Egypt. Moses, an Egyptian priest, led his followers to Jerusalem, establishing a new form of worship. Jerusalem, a well-watered but rocky city, was fortified with towers and trenches. Pompey conquered it during a period of internal strife among its leaders. These regions showcase Syria’s diversity, from fertile plains and bustling cities to rugged, mountainous territories and historically rich sites. |
|
| 3 Above Judaea and Coelê-Syria lies Arabia, extending southward to Babylonia and the Euphrates. While Mesopotamia is home to various tribes, the Arabian Scenitae inhabit the land near the Euphrates and further south in barren areas due to water scarcity. These tribes are mostly nomadic, herding camels, and farming minimally. South of them is Arabia Felix, bordered by the desert to the north, the Persian Gulf to the east, the Arabian Gulf to the west, and the Erythraean Sea to the south. The Persian Gulf, also known as the Persian Sea, is described by Eratosthenes as having a narrow mouth, with the coasts of Carmania and Arabia visible from each other. The gulf stretches about ten thousand stadia, with Carmanians, Persians, Susians, and Babylonians inhabiting the surrounding areas. Further sailing brings one to Gerrha, a city on a deep gulf inhabited by Chaldaeans, exiles from Babylon, living in salt houses. Gerrhaeans engage in trade, particularly in Arabian merchandise and aromatics. Nearby islands, Tyre and Aradus, claim Phoenician origins and feature temples similar to those in Phoenicia. Nearchus and Orthagoras mention the island Ogyris in the high sea, with the grave of Erythras, after whom the sea is named. Mithropastes, an exiled Persian noble, guided the Macedonians in their voyage in the Persian Gulf. Eratosthenes also notes unique trees growing in the Red Sea, visible during low tides but submerged during high tides. Nearchus adds that these islands are rich in pearls and aromatic trees, and that large sea creatures, like crabs and whales, inhabit the region. |
|
| 4 Arabia begins near Babylonia with Maecenê, bordered by the desert of the Arabians, Chaldaean marshes from the Euphrates, and the Persian Sea. It has foul air, mist, rain, scorching heat, but excellent products. Vines grow in marshes on reed hurdles. Eratosthenes describes northern Arabia, between Arabia Felix, Coelê-Syria, and Judaea, reaching the Arabian Gulf near the Nile, spanning 5,600 stadia to Babylon, through Nabataeans, Chaulotaeans, and Agraeans. Arabia Felix extends 12,000 stadia south to the Atlantic Sea. Initially, farmers inhabit it, then sandy, barren soil with some palms, thorny trees, tamarisk, and water by digging, occupied by nomads and camel herders. The southernmost areas, opposite Aethiopia, have summer rains, double sowing seasons, and fertile lands with abundant honey-making places. The region, rich in domesticated animals except for horses, mules, and hogs, and all birds except geese and chickens, is home to four large tribes: Minaeans by the Red Sea, with Carna as their main city; Sabaeans, with Mariaba as their capital; Cattabanians, extending to the Arabian Gulf straits with Tamna as their royal seat; and the Chatramotitae, with Sabata as their city. These cities, ruled by monarchs, are prosperous with temples and royal palaces. Succession isn't hereditary but determined by the firstborn son of a notable man after the king’s appointment, raised royally as the future successor. Cattabania produces frankincense, Chatramotitis myrrh, traded by merchants from Aelana to Gerrha in seventy to forty days. The Arabian Gulf along Arabia, beginning at Aelana, spans fourteen thousand stadia, according to Alexander’s associates and Anaxicrates. |
|
|
|
17 Africa. 3 110 1:32
| 1 Since I included the gulfs making Arabia a peninsula, such as the Persian and Arabian Gulfs, and parts of Aegypt and Aethiopia, up to the Cinnamon-bearing country, I must describe remaining parts near the Nile and Libya. According to Eratosthenes, the Nile is 900 or 1000 stadia west of the Arabian Gulf, shaped like a reversed N. It flows from Meroê northwards for 2700 stadia, then south and west for 3700 stadia, nearly reaching Meroê's parallel, before turning north 5300 stadia to the great cataract, 1200 stadia to Syenê's smaller cataract, then 5300 more to the sea. Two rivers from eastern lakes, enclosing Meroê, join it: Astaboras and Astapus. Meroê, a city 700 stadia from the Astaboras-Nile confluence, has another island above it held by Aegyptian fugitives from Psammitichus' time, called "Sembritae," ruled by a queen under Meroê's kings. Lower parts along the Nile towards the Red Sea are inhabited by Megabari and Blemmyes under Aethiopians and bordering Aegyptians. Troglodytes live across from Meroê, a 10-12 day journey from the Nile. Left of the Nile in Libya are the independent Nubae tribes extending from Meroê to the river bends. The extent of Aegypt along the sea from Pelusiac to Canobic mouth is 1300 stadia. |
|
| 2 In the earlier parts of my work, I have described many Aethiopian tribes alongside Aegypt. Generally, the extremities of the inhabited world are inferior due to extreme heat or cold, evident in the harsh lives of the inhabitants. They live almost naked, are nomadic, and have small domestic animals. They mainly consume millet and barley, use butter and tallow instead of olive oil, and eat meat, blood, milk, and cheese. They regard their kings as gods, who usually stay secluded. The greatest royal seat is Meroê, a city on an island said to be like an oblong shield, containing numerous mountains, thickets, and mines of copper, iron, gold, and precious stones. Meroê is bounded by sand-dunes on the Libyan side and precipices on the Arabian side, with three rivers—Astaboras, Astapus, and Astasobas—converging on the south and the Nile on the north. Their dwellings are made of palm-wood or brick, and they quarry salt like the Arabians. The island is inhabited by nomads, hunters, and farmers and has abundant plants, elephants, lions, and leopards. Above Meroê lies Lake Psebo, which contains a well-settled island. The Aethiopians also use long wooden bows and arm their women. They appoint kings based on beauty, cattle-breeding, courage, or wealth. Previously, priests held the highest rank and could order kings to die, but one king ended this custom by attacking the temple and killing the priests. Some Aethiopians worship Heracles, Pan, and Isis and have various burial customs. |
|
| 3 Libya remains to be described to complete my Geography. Earlier, I mentioned that the world was divided into three parts, but Libya, combined with Europe, still falls short of Asia's size. Much of its interior and coastline is desert, with scattered, small, and mostly nomadic settlements. It overlaps the torrid zone, making parts uninhabitable due to wild beasts. The coast from the Nile to the Pillars, especially the area once under Carthaginian control, is settled and prosperous but has arid regions. Libya resembles a right-angled triangle, with the Nile and Egypt as the base, extending to the ocean, and the coastline between the Aethiopians and Maurusians as the hypotenuse. The region near the torrid zone is conjectured to be inaccessible. From Alexandria to Meroê, it's about ten thousand stadia, and another three thousand to the torrid zone boundary. Libya's maximum breadth is about thirteen or fourteen thousand stadia, with a length nearly double that. The western part of Libya is inhabited by the Maurusians, called Mauri by Romans and natives. The strait at the Pillars of Heracles lies here, leading to Atlas Mountain. This region contains the Emporicus Gulf, Phoenician merchant settlements, and other coastal indentations. Inland, the Maurusians inhabit mountains, alongside the large Gaetulian tribe. Historians like Ophelas have added many fabrications about Libya's coast. For instance, the Emporicus Gulf is said to have a cave admitting the sea, and nearby, an altar of Heracles supposedly remains dry at high tide—claims I consider exaggerated. Despite these tales, Maurusia is fertile, with lakes, rivers, and large trees, producing significant resources for the Romans. |
|
|
|
|
1 Eratosthenes wrong. 4 137 1:50
|
1 - 1 Preface, on the scope and usefulness of geography 
The science of Geography, which I now propose to investigate, is, I think, quite as much as any other science, a concern of the philosopher; and the correctness of my view is clear for many reasons. In the first place, those who in earliest times ventured to treat the subject were, in their way, philosophers — Homer, Anaximander of Miletus, and Anaximander's fellow-citizen Hecataeus — just as Eratosthenes has already said; philosophers, too, were Democritus, Eudoxus, Dicaearchus, Ephorus, with several others of their times; and further, their successors — Eratosthenes, Polybius, and Poseidonius — were philosophers. In the second place, wide learning, which alone makes it possible to undertake a work on geography, is possessed solely by the man who has investigated things both human and divine — knowledge of which, they say, constitutes philosophy. And so, too, the utility of geography — and its utility is manifold, not only as regards the activities of statesmen and commanders but also as regards knowledge both of the heavens and of things on land and sea, animals, plants, fruits, and everything else to be seen in various regions — the utility of geography, I say, presupposes in the geographer the same philosopher, the man who busies himself with the investigation of the art of life, that is, of happiness.
2 But I must go back and consider each one of these points in greater detail; and, first, I say that both I and my predecessors, one of whom was Hipparchus himself, are right in regarding Homer as the founder of the science of geography; for Homer has surpassed all men, both of ancient and modern times, not only in the excellence of his poetry, but also, I might say, in his acquaintance with all that pertains to public life. And this acquaintance made him busy himself not only about public activities, to the end that he might learn of as many of them as possible and also give an account of them to posterity, but also about the geography both of the individual countries and of the inhabited world at large, both land and sea; for otherwise he would not have gone to the uttermost bounds of the inhabited world, encompassing the whole of it in his description.
3 In the first place, Homer declares that the inhabited world is washed on all sides by Oceanus, and this is true; and then he mentions some of the countries by name, while he leaves us to infer the other countries from hints; for instance, he expressly mentions Libya,1 Ethiopia, Sidonians, and Erembians — by Erembians he probably means Arabian Troglodytes2 — whereas he only indicates in general terms the people who live in the far east and the far west by saying that their countries are washed by Oceanus. For he makes the sun to p7rise out of Oceanus and to set in Oceanus; and he refers in the same way to the constellations: "Now the sun was just beating on the fields as he climbed heaven from the deep stream of gently-flowing Oceanus." "And the sun's bright light dropped into Oceanus drawing black night across the earth." And he declares that the stars also rise from Oceanus "after having bathed in Oceanus."
4 As for the people of the west, Homer makes plain that they were prosperous and that they lived in a temperate climate — doubtless having heard of the wealth of Iberia,3 and how, in quest of that wealth, Heracles invaded the country, and after him the Phoenicians also, the people who in earliest times became masters of most of the country (it was at a later date that the Romans occupied it). For in the west the breezes of Zephyrus blow; 3and there it is that Homer places the Elysian Plain itself, to which he declares Menelaus will be sent by the gods: "But the deathless gods will convey thee to the Elysian Plain and the ends of the earth, where is Rhadamanthys of the fair hair, where life is easiest. No snow is there, nor yet great storm; but always Oceanus sendeth forth the breezes of the clear-blowing4 Zephyrus."
5 And, too, the Islands of the Blest5 lie to the westward of most western Maurusia,6 that is, west p9of the region where the end of Maurusia runs close to that of Iberia. And their name shows that because those islands were near to blessed countries they too were thought to be blessed abodes.
6 Furthermore, Homer assuredly makes it plain that the Ethiopians live at the ends of the earth, on the banks of Oceanus: that they live at the end of the earth, when he speaks of "the Ethiopians that are sundered in twain, the farthermost of men" (and indeed the words "are sundered in twain" are not carelessly used, as will be shown later on); and that they live on the banks of Oceanus, when he says "for Zeus went yesterday to Oceanus, unto the noble Ethiopians for a feast." And he has left us to infer that the farthest land in the north is also bounded by Oceanus when he says of the Bear that "She alone hath no part in the baths of Oceanus." That is, by the terms "Bear" and "Wain" he means the "arctic circle";7 for otherwise he would not have said of the Bear that "She alone hath no part in the baths of Oceanus," since so many stars complete their diurnal revolutions in that same quarter of the heavens which was always visible to him. So it is not well for us to accuse him of ignorance on the ground that he knew of but one Bear instead of two; for it is likely that in the time of Homer the other Bear had not yet been marked out as a constellation, and that the star-group did not become known as such to the Greeks until the Phoenicians so designated it and used it for purposes of navigation; the same is true of Berenice's Hair and of Canopus, for we know that these two constellations have received p11their names quite recently, and that there are many constellations still unnamed, just as Aratus says. Therefore Crates is not correct, either, when in seeking to avoid what needs no avoidance, he alters the text of Homer so as to make it read, "And the arctic circle8 alone hath no part in the baths of Oceanus." Better and more Homeric is Heracleitus, who likewise employs "the Bear" for "the arctic circle": "The Bear forms limits of morning and evening, and over against the Bear fair breezes blow from fair skies";9 for the arctic circle, and not the Bear, forms a boundary beyond which the stars neither rise nor set. 4Accordingly, by "the Bear," which he also calls "the Wain" and describes as keeping watch upon Orion, Homer means the "arctic circle," and by Oceanus he means the horizon into which he makes the stars to set and from which he makes them to rise. And when he says that the Bear makes its revolution in that region without having a part in Oceanus, he knows that the arctic circle touches the most northerly point of the horizon. If we construe the poet's verse in this way, then we should interpret the terrestrial horizon as closely corresponding to Oceanus, and the arctic circle as touching the earth — if we may believe the evidence of our sense — at its most northerly inhabited point. And so, in the opinion of Homer, this part of the earth also is p13washed by Oceanus. Furthermore, Homer knows of the men who live farthest north; and while he does not mention them by name — and even to the present day there is no common term that will embrace them all — he characterises them by their mode of life, describing them as "nomads," and as "proud mare-milkers, curd-eaters, and a resourceless folk."
7 In other ways, too, Homer indicates that Oceanus surrounds the earth, as when Hera says as follows: "For I am going to visit the limits of the bountiful earth, and Oceanus, father of the gods." By these words he means that Oceanus touches all the extremities of the earth; and these extremities form a circle round the earth. Again, in the story of the making of the arms of Achilles, Homer places Oceanus in a circle round the outer edge of the shield of Achilles. It is another proof of the same eagerness for knowledge that Homer was not ignorant about the ebb and flow of the tide of Oceanus; for he speaks of "Oceanus that floweth ever back upon himself," and also says: "For thrice a day shespouts it forth, and thrice a day she sucks it down." For even if it be "twice" and not "thrice" — it may be that Homer really strayed from the fact on this point, or else that there is a corruption in the text— the principle of his assertion remains the same. And even the phrase "gently-flowing" contains a reference to the flood-tide, which comes with a gentle p15swell, and not with a violent current. Poseidonius conjectures both from Homer's reference to the headlands as sometimes covered with the waves and sometimes bare, and from his calling Oceanus a river, that by the current of Oceanus Homer is indicating the flow of the tides. The first conjecture of Poseidonius is correct, but the second is unreasonable. For the swell of the tide is not like a stream of a river, and still less so is the ebb. The explanation given by Crates is more plausible. Homer speaks of the whole of Oceanus as "deep-flowing" and "back-flowing," and, likewise, as being a river; 5he also speaks of a part of Oceanus as a river, or as a "river-stream"; and he is speaking of a part of Oceanus, and not of the whole, when he says: "Now after the ship had left the river-stream of Oceanus, and was come to the wave of the wide sea." Not the whole, I say, but the stream of the river, which stream is in Oceanus, being therefore a part of it and this stream, Crates says, is a sort of estuary or gulf, which stretches from the winter tropicin the direction of the south pole. Indeed, one might leave this estuary and still be in Oceanus; but it is not possible for a man to leave the whole and still be in the whole. At any rate Homer says: "The ship had left the river-stream, and was come to the wave of the sea," where "the sea" is surely nothing other than Oceanus; if you interpret it otherwise, the assertion becomes: "After Odysseus had gone out of Oceanus, he came into Oceanus." But that is a matter to be discussed at greater length.
p1We may learn both from the evidence of our senses and from experience that the inhabited world is an island; for wherever it has been possible for man to reach the limits of the earth, sea has been found, and this sea we call "Oceanus." And wherever we have not been able to learn by the evidence of our sense, there reason points the way. For example, as to the eastern (Indian) side of the inhabited earth, and the western (Iberian and Maurusian) side, one may sail wholly around them and continue the voyage for a considerable distance along the northern and southern regions; and as for the rest of the distance around the inhabited earth which has not been visited by us up to the present time (because of the fact that the navigators who sailed in opposite directions towards each other never met), it is not of very great extent, if we reckon from the parallel distances that have been traversed by us. It is unlikely that the Atlantic Ocean is divided into two seas, thus being separated by isthmuses so narrow and that prevent the circumnavigation; it is more likely that it is one confluent and continuous sea. For those who undertook circumnavigation, and turned back without having achieved their purpose, say that they were made to turn back, not because of any continent that stood in their way and hindered their further advance, inasmuch as the sea still continued open as before, but because of their destitution and loneliness. This theory accords better, too, with the behaviour of the ocean, that, in respect of the ebb and flow of the tides; everywhere, at all events, the same principle, or else one that does not vary much, accounts for the changes both of high tide and low p19tide,as would be the case if their movements were produced by one sea and were the result of one cause.
9 Hipparchus is not convincing when he contradicts this view on the ground, first, that the ocean does not behave uniformly throughout, and, secondly, that, even if this be granted, it does not follow that the Atlantic Ocean runs round the earth in one unbroken circle. In support of his opinion that the ocean does not behave uniformly he appeals to the authority of Seleucus of Babylon. But for a further discussion of the ocean and its tides I refer the reader to Poseidonius and Athenodorus, who have examined the argument on this subject with thoroughness. For my present purpose I merely add that it is better to accept this view of the uniform behaviour of the ocean; and that the farther the mass of water may extend around the earth, the better the heavenly bodies will be held together by the vapours that arise therefrom.
Homer, then, knows and clearly describes the remote ends of the inhabited earth and what surrounds it; and he is just as familiar with the regions of the Mediterranean Sea. For if you begin at the Pillars of Heracles, you will find that the Mediterranean Sea is bounded by Libya, Egypt, and Phoenicia, and further on by the part of the continent lying over against Cyprus; then by the territory of the Solymi, by Lycia, and by Caria, and next by the seaboard between Mycale and the Troad, together with the islands adjacent thereto; and all these lands are p21mentioned by Homer, as well as those farther on, about the Propontis and the Euxine Sea as far as Colchis and the limits of Jason's expedition; more than that, he knows the Cimmerian Bosporus, because he knows the Cimmerians — for surely, if he knows the name of the Cimmerians, he is not ignorant of the people themselves — the Cimmerians who, in Homer's own time or shortly before his time, overran the whole country from the Bosporus to Ionia. At least he intimates that the very climate of their country is gloomy, and the Cimmerians, as he says, are "shrouded in mist and in cloud, and never does the shining sun look upon them, but deadly night is spread o'er them." Homer also knows of the River Ister,since he mentions Mysians, a Thracian tribe that lives on the Ister. More than that, he knows the sea-board next to the Ister, on the Thracian side, as far as the PeneusRiver; for he speaks of Paeonians, of Athos and Axius, and of their neighbouring islands. And next comes the sea-board of Greece, as far as Thesprotia, which he mentions in its entirety. And yet more, he knows the promontories of Italy also, for he speaks of Temesa and of Sicily; he also knows about the headland capes of Iberia, and of the wealth of Iberia, as I have stated above. If between these countries there are some countries which he leaves out, one might pardon him; for the professed geographer himself omits many details. And we might pardon the poet even if he has inserted things p23of a mythical nature in his historical and didactic narrative. That deserves no censure; for Eratosthenes is wrong in his contention that the aim of every poet is to entertain, not to instruct; indeed the wisest of the writers on poetry say, on the contrary, that poetry is a kind of elementary philosophy.But later on I shall refute Eratosthenes at greater length, when I come to speak of Homer again.
For the moment what I have already said is sufficient, I hope, to show that Homer was the first geographer. And, as every one knows, the successors of Homer in geography were also notable men and familiar with philosophy. Eratosthenes declares that the first two successors of Homer were Anaximander, a pupil and fellow-citizen of Thales, and Hecataeus of Miletus; that Anaximander was the first to publish a geographical map, and that Hecataeus left behind him a work on geography, a work believed to be his by reason of its similarity to his other writings.
Assuredly, however, there is need of encyclopaedic learning for the study of geography, as many men have already stated; and Hipparchus, too, in his treatise Against Eratosthenes, correctly shows that it is impossible for any man, whether layman or scholar, to attain to the requisite knowledge of geography without the determination of the heavenly bodies and of the eclipses which have been observed; for instance, it is impossible to determine whether Alexandria in Egypt is north or south of Babylon, or how much north or south of Babylon it is, without investigation through the means of the "climata." In like manner, we cannot accurately fix points that lie at varying distances from us, whether to the east or the west, except by a comparison of the eclipses of the sun and the moon. That, then, is what Hipparchus says on the subject.
All those who undertake to describe the distinguishing features of countries devote special attention to astronomy and geometry, in explaining matters of shape, of size, of distances between points, and of "climata," as well as matters of heat and cold, and, in general, the peculiarities of the atmosphere. Indeed, an architect in constructing a house, or an engineer in founding a city, would make provision for all these conditions; and all the more would they be considered by the man whose purview embraced the whole inhabited world; for they concern him more than anyone else. Within the area of small countries it involves no very great discrepancy if a given place be situated more towards the north, or more towards the south; but when the area is that of the whole round of the inhabited world, the north extends to the remote confines of Scythia and Celtica, and the south to the remote confines of Ethiopia, and the difference between these two extremes is very great. The same thing holds true also as regards a man's living in India or Iberia; the one country is in the far east, and the other is in the far west; indeed, they are, in a sense, the antipodes of each other, as we know.
Everything of this kind, since it is caused by the movement of the sun and the other stars as well as by their tendency towards the centre, compels us to look to the vault of heaven, and to observe the phenomena of the heavenly bodies peculiar to our individual positions; and in these phenomena we see very great variations in the positions of inhabited place. So, if one is about to treat of the differences between countries, how can he discuss his subject correctly and adequately if he has paid no attention, even superficially, to any of these matters? For even if it be impossible in a treatise of this nature, because of its having a greater bearing on affairs of state, to make everything scientifically accurate, it will naturally be appropriate to do so, at least in so far as the man in public life is able to follow the thought.
Moreover, the man who has once thus lifted his thoughts to the heavens will surely not hold aloof from the earth as a whole; for it is obviously absurd, if a man who desired to give a clear exposition of the inhabited world had ventured to lay hold of the celestial bodies and to use them for the purposes of instruction, and yet had paid no attention to the earth as a whole, of which the inhabited world is just a part — neither as to its size, nor its character, nor its position in the universe, nor even whether the world is inhabited only in the one part in which we live, or in a number of parts, and if so, how many such parts there are; and likewise how large the uninhabited part is, what its nature is, and why it is uninhabited. It seems, then, that the special branch of geography represents a union of meteorology and geometry, since it unites terrestrial and celestial phenomena as being very closely related, and in no sense separated from each other "as heaven is high above the earth."
Well, then, to this encyclopaedic knowledge let us add terrestrial history — that is, the history of animals and plants and everything useful or harmful that is produced by land or sea (this definition will, I think, make clear what I mean by "terrestrial history"). In fact all such studies are important as preliminary helps toward complete understanding. And to this knowledge of the nature of the land, and of the species of animals and plants, we must add a knowledge of all that pertain to the sea; for in a sense we are amphibious, and belong no more to the land than to the sea. That the benefit is great to anyone who has become possessed of information of this character, is evident both from ancient traditions and from reason. At any rate, the poets declare that the wisest heroes were those who visited many places and roamed over the world; for the poets regard it as a great achievement to have "seen the cities and known the minds of many men." Nestor boasts of having lived among the Lapithae, to whom he had gone as an invited guest, "from a distant land afar — for of themselves they summoned me." Menelaus, too, makes a similar boast, when he says: "I roamed over Cyprus and Phoenicia and Egypt, and came to Ethiopians and Sidonians and Erembians and Libya" and at this point he added the distinctive peculiarity of the country — "where lambs are horned from the birth; for there the ewes yean thrice within the full circle of the year." 9And in speaking of Thebes in Egypt, he says that Egypt is the country "where earth the grain-giver yields herbs in plenty"; and again he says: "Thebes of the hundred gates, whence sally forth two hundred warriors though each, with horses and chariots." And doubtless it was because of Heracles' wide experience and information that Homer speaks of him as the man who "had knowledge of great adventures." And my contention, made at the outset, is supported by reason as well as by ancient tradition. And that other argument, it seems to me, is adduced with especial force in reference to present-day conditions, namely, that the greater part of geography subserves the needs of states; for the scene of the activities of states is land and sea, the dwelling-place of man. The scene is small when the activities are of small importance, and large when they are of large importance; and the largest is the scene that embraces all the rest (which we call by the special name of "the inhabited world") and this, therefore, would be the scene of activities of the largest importance. Moreover, the greatest generals are without exception men who are able to hold sway over land and sea, and to unite nations and cities under one government and political administration. It is therefore plain that geography as a whole has a direct bearing upon the activities of commanders; for it describes continents and seas — not only the sea inside the limits of the whole inhabited world, but also those outside these limits. And the description which geography gives is of importance to these men who are concerned as to whether this or that is so or otherwise, and whether known or unknown. For thus they can manage their various affairs in a more satisfactory manner, if they know how large a country is, how it lies, and what are its peculiarities either of sky or soil. But because different kings rule in different quarters of the world, and carry on their activities from different centres and starting-points, and keep extending the borders of their empires, it is impossible either for them or for geographers to be equally familiar with all parts of the world; nay, the phrase "more or less" is a fault much in evidence in kings and geographers. For even if the whole inhabited world formed one empire or state, it would hardly follow that all parts of that empire would be equally well known; nay, it would not be true even in that case, but the nearer regions would be better known. And it would be quite proper to describe these regions in greater detail, in order to make them known, for they are also nearer to the needs of the state. Therefore it would not be remarkable even if one person were a proper chorographer for the Indians, another for the Ethiopians, and still another for the Greeks and Romans. 10For example, wherein would it be proper for the Indian geographer to add details about Boeotia such as Homer gives: "These were they that dwelt in Hyria and rocky Aulis and Schoenus and Scolus"? For me these details are proper; but when I come to treat India it is no longer proper to add such details; and, in fact, utility does p35not urge it — and utility above all things is our standard in empirical matters of this kind.
The utility of geography in matters of small concern, also, is quite evident; for instance, in hunting. A hunter will be more successful in the chase if he knows the character and extent of the forest; and after, only one who knows a region can advantageously pitch camp there, or set an ambush, or direct a march. The utility of geography is more conspicuous, however, in great undertakings, in proportion as the prizes of knowledge and the disasters that result from ignorance are greater. Thus Agamemnon and his fleet ravaged Mysia in the belief that it was Troy-land, and came back home in disgrace. And, too, the Persians and the Libyans, surmising that the straits were blind alleys, not only came near great perils, but they left behind them memorials of their folly, for the Persians raised the tomb on the Euripus near Chalcis in honour of Salganeus, whom they executed in the belief that he had treacherously conducted their fleet from the Gulf of Malis to the Euripus, and the Libyans erected the monument in honour of Pelorus, whom they put to death for a similar reason; and Greece was covered with wrecks of vessels on the occasion of the expedition of Xerxes; and again, the colonies sent out by the Aetolians and by the Ionians have furnished many examples of similar blunders. There have also been cases of success, in which success was due to acquaintance with the regions involved; for instance, at the pass of Thermopylae it is said that Ephialtes, by showing the Persians the pathway across the mountains, put Leonidas and his troops at their mercy, and brought the Persians south of Thermopylae. But leaving antiquity, I believe that modern campaign of the Romans against the Parthians is a sufficient proof of what I say, and likewise that against the Germans and the Celts, for in the latter case the barbarians carried on a guerilla warfare in swamps, in pathless forests, and in deserts; and they made the ignorant Romans believe to be far away with was really near at hand, and kept them in ignorance of the roads and of the facilities for procuring provisions and other necessities.
Now just as the greater part of geography, as I have said, has a bearing on the life and the needs of rulers, so also does the greater part of the theory of ethics and the theory of politics have a bearing on the life of rulers. And the proof of this is the fact that we distinguish the differences between the constitutions of states by the sovereignties in those states, in that we call one sovereignty the monarchy or kingship, another the aristocracy, and still another the democracy. And we have a corresponding number of constitutions of states, which we designate by the names of the sovereignties, because it is from these that they derive the fundamental principle of their specific nature; for in one country the will of the king is law, in another the will of those of highest rank, and in another the will of the people. It is the law that gives the type and the form of the constitution. And for that reason some have defined "justice" as "the interest of the more powerful." If, then, political philosophy deals chiefly with the rulers, and if geography supplies the needs of those rulers, then geography would seem to have some advantage over political science. This advantage, however, has to do with practice.
And yet, a work of geography also involves theory of no mean value, the theory of the arts, of mathematics, and of natural science, as well as the theory which lies in the fields of history and myths — though myths have nothing to do with practice; for instance, if a man should tell the story of the wanderings of Odysseus or Menelaus or Jason, it would not be thought that he was making any contribution to the practical wisdom of his hearers — and that is what the man of affairs demands — unless he should insert the useful lessons to be drawn from the hardships those heroes underwent; still, he would be providing no mean entertainment for the hearer who takes an interest in the regions which furnished the scenes of the myths. Men of affairs are fond of just such entertainment, because the localities are famous and the myths are charming; but they care for no great amount of it, since they are more interested in what is useful, and it is quite natural that they should be. For that reason the geographer, also, should direct his attention to the useful rather than to what is famous and charming. The same principle holds good in regard to history and the mathematical sciences; for in these branches, also, that which is useful and more trustworthy should always be given precedence.
Most of all, it seems to me, we need, as I have said, geometry and astronomy for a subject like geography; and the need of them is real indeed; for without such methods as they offer it is not possible accurately to determine our geometrical figures, "climata," dimensions, and the other cognate things; but just as these sciences prove for us in other treatises all that has to do with the measurement of the earth as a whole and as I must in this treatise take for granted that the universe is sphere-shaped, and also that the earth's surface is sphere-shaped, and, what is more, I must take for granted the law that is prior to these two principles, namely that the bodies tend toward the centre; and I need only indicate, in a brief and summary way, whether a proposition comes — if it really does — within the range of sense-perception or of intuitive knowledge. Take, for example, the proposition that the earth is sphere-shaped: whereas the suggestion of this proposition comes to us mediately from the law that bodies tend toward the centre and that each body inclines toward its own centre of gravity, the suggestion comes immediately from the phenomena observed at sea and in the heavens; 12for our sense-perception and also our intuition can bear testimony in the latter case. For instance, it is obviously the curvature of the sea that prevents sailors from seeing distant lights at an elevation equal to that of the eye; however, if they are at a higher elevation than that of the eye, they become visible, even though they be at a greater distance from the eyes; and similarly if the eyes themselves are elevated, they see what was before invisible. This fact is noted by Homer, also, for such is the meaning of the words: "With a quick glance ahead, being upborne on a great wave, he saw the land very near." So, also, when sailors are approaching land, the different parts of the shore become revealed progressively, more and more, and what at first appeared to be low-lying land grows gradually higher and higher. Again, the revolution of the heavenly bodies is evident on many grounds, but it is particularly evident from the phenomena of the sun-dial; and from these phenomena our intuitive judgment itself suggests that no such revolution could take place if the earth were rooted to an infinite depth. As regards the "climata," they are treated in our discussion of the Inhabited Districts.
But at this point we must assume off-hand a knowledge of some matters, and particularly of all that is useful for the statesman and the general to know. For one should not, on the one hand, be so ignorant of the heavens and the position of the earth as to be alarmed when he comes to countries in which some of the celestial phenomena that are familiar to everybody have changed, and to exclaim: "My friends, lo, now we know not where is the place of darkness, nor of dawning, nor where the sun, that gives light to men, goes beneath the earth, nor where he rises"; nor, on the other hand, need one have such scientifically accurate knowledge as to know what constellations rise and set and pass the p45meridian at the same time everywhere; or as to know the elevations of the poles, the constellations that are in the zenith, and all other such changing phenomena as meet one according as he changes his horizons and arctic circles, whether those changes be merely visual, or actual as well. Nay, he should pay no attention at all to some of these things, unless it be in order to view them as a philosopher. But he should take some other things on faith, even if he does not see a reason for them; for the question of causes belongs to the student of philosophy alone, whereas the statesman does not have adequate leisure for research, or at least not always. However, the reader of this book should not be so simple-minded or indifferent as not to have observed a globe, 13or the circles drawn upon it, some of which are parallel, others drawn at right angles to the parallels, and still others oblique to them; or, again, so simple as not to have observed the position of tropics, equator, and zodiac — the region through which the sun is borne in his course and by his turning determines the different zones and winds. For if one have learned, even in a superficial way, about these matters, and about the horizons and the arctic circles and all the other matters taught in the elementary courses of mathematics, he will be able to follow what is said in this book. If, however, a man does not know even what a straight line is, or a curve, or a circle, nor the difference between a spherical and a plane surface, and if, in the heavens, he have not learned even the seven stars of the Great Bear, or anything else of that kind, either he will have no use for this book, or else not at present — in fact, not until he has studied those topics without which he cannot be familiar with geography. And so those who have written the treatises entitled Harbours and Coasting Voyages leave their investigations incomplete, if they have failed to add all at mathematical and astronomical information which properly belonged in their books.
In short, this book of mine should be generally useful — useful alike to the statesman and to the public at large — as was my work on History. In this work, as in that, I mean by "statesman," not the man who is wholly uneducated, but the man who has taken the round of courses usual in the case of freemen or of students of philosophy. For the man who has given no thought to virtue and to practical wisdom, and to what has been written about them, would not be able even to form a valid opinion either in censure or in praise; nor yet to pass judgment upon the matters of historical fact that are worthy of being recorded in this treatise.
And so, after I had written my Historical Sketches, which have been useful, I suppose, for moral and political philosophy, I determined to write the present treatise also; for this work itself is based on the same plan, and is addressed to the same class of readers, and particularly to men of exalted stations in life. Furthermore, just as in my Historical Sketches only the incidents in the lives of distinguished men are recorded, while deeds that are petty and ignoble are omitted, so in this work also I must leave untouched what is petty and inconspicuous, and devote my attention to what is noble and great, and to what contains the practically useful, or memorable, or entertaining. Now just as in judging of the merits of colossal statues we do not examine each individual part with minute care, but rather consider the general effect and endeavour to see if the statue as a whole is pleasing, so should this book of mine be judged. For it, too, is a colossal work, in that it deals with the facts about large things only, and wholes, except as some petty thing may stir the interest of the studious or the practical man. I have said thus much to show that the present work is a serious one, and one worthy of a philosopher. |
|
|
|

|
1 - 2 Introduction 
1 Beginning If I, too, undertake to write upon a subject that has been treated by many others before me, I should not be blamed therefor, unless I prove to have discussed the subject in every respect as have my predecessors. Although various predecessors have done excellent work in various fields of geography, yet I assume that a large portion of the work still remains to be done; and if I shall be able to make even small additions to what they have said, that must be regarded as a sufficient excuse for my undertaking. Indeed, the spread of the empires of the Romans and of the Parthians has presented to geographers of to‑day a considerable addition to our empirical knowledge of geography, just as did the campaign of Alexander to geographers of earlier times, as Eratosthenes points out. For Alexander opened up for us geographers a great part of Asia and all the northern part of Europe as far as the Ister River; the Romans have made known all the western part of Europe as far as the River Albis (which divides Germany into two parts), and that regions beyond the Ister as far as the Tyras River; and Mithridates, surnamed Eupator, and his generals have made known the regions beyond the Tyras as far as Lake Maeotis and the line of coast that ends at Colchis; and, again, the Parthians have increased our knowledge in regard to Hyrcania and Bactriana, and in regard to the Scythians who live north of Hyrcania and Bactriana, all of which countries were but imperfectly known to the earlier geographers. I therefore may have something more to say than my predecessors. This will become particularly apparent in what I shall have to say in criticism of my predecessors, but my criticism has less to do with the earliest geographers than with the successors of Eratosthenes and Eratosthenes himself. For it stands to reason that because Eratosthenes and his successors have had wider knowledge than most geographers, it will be correspondingly more difficult for a later geographer to expose their errors if they say anything amiss. And if I shall, on occasion, be compelled to contradict the very men whom in all other respects I follow most closely, I beg to be pardoned; for it is not my purpose to contradict every individual geographer, but rather to leave the most of them out of consideration — men whose arguments it is unseemly even to follow — and to pass upon the opinion of those men whom we recognize to have been correct in most cases. Indeed, to engage in philosophical discussion with everybody is unseemly, but it is honourable to do so with Eratosthenes, Hipparchus, Poseidonius, Polybius, and others of their type.
2 First, I must consider Eratosthenes, at the same time setting forth the objections which Hipparchus urges against the statements of Eratosthenes. Now Eratosthenes is not so open to attack as to warrant my saying that he never saw even Athens, as Polemon undertakes to prove; nor, on the other hand, is he so trustworthy as some have been taught to believe that he is — notwithstanding the fact that he had been associated with many eminent men, as he himself tells us. "For," says he, "philosophers gathered together at this particular time, as never before within one wall or one city; I refer to those who flourished in the time of Ariston and Arcesilaus." But I do not think that sufficient; what we need is a clear-cut judgment as to what teachers we should choose to follow. But he places Arcesilaus and Ariston at the head of the scholars who flourished in his day and generation; and Apelles is much in evidence with him, and so is Bion, of whom he says: "Bion was the first to drape philosophy in embroidered finery"; and yet he states that people frequently applied to Bion the words: "Such a thigh as Bion shews from out his rags."Indeed, in these very statements Eratosthenes reveals a serious infirmity in his own judgment; and because of this infirmity, although he himself studied in Athens under Zeno of Citium, he makes p55no mention of any of Zeno's successors, but speaks of those men who dissented from the teachings of Zeno and who failed to establish a school that lived after them as "flourishing" at that particular time. His treatise entitled On the Good, also, and his Studies in Declamation, and whatever else he wrote of this nature, go to show his tendency, namely, that of the man who is constantly vacillating between his desire to be a philosopher and his reluctance to devote himself entirely to this profession, and who therefore succeeds in advancing only far enough to have the appearance of being a philosopher; or of the man who has provided himself with this as a diversion from his regular work, either for his pastime or even amusement; and in a sense Eratosthenes displays this tendency in his other writings, too. But let this pass; for my present purpose I must correct Eratosthenes' geography as far as possible; and first, on the point which I deferred a while ago.
3 As I was saying, Eratosthenes contends that the aim of every poet is to entertain, not to instruct. The ancients assert, on the contrary, that poetry is a kind of elementary philosophy, which, taking us in our very boyhood, introduces us to the art of life and instructs us, with pleasure to ourselves, in character, emotions, and actions. And our School goes still further and contends that the wise man alone is a poet. That is the reason why in Greece the various states educate the young, at the very beginning of their education, by means of poetry; not for the mere sake of entertainment, of course, but for the sake of moral discipline. Why, even the musicians, when they give instruction in singing, in lyre-playing, origin flute-playing, lay claim to this virtue, for they maintain that these studies tend to discipline and correct the character. You may hear this contention made not merely by the Pythagoreans, but Aristoxenus also declares the same thing. And Homer, too, has spoken of the bards as disciplinarians in morality, as when he says of the guard of Clytaemnestra: "Whom the son of Atreus as he went to Troy strictly charged to keep watch over his wife"; and he adds that Aegisthus was unable to prevail over Clytaemnestra until "he carried the bard to a lonely isle and left him there — while as for her, he led her to his house, a willing lady with a willing lover." But, even apart from this, Eratosthenes contradicts himself; for shortly before the pronouncement above-mentioned, and at the very beginning of his treatise on geography, he says that from the earliest times all the poets have been eager to display their knowledge of geography; that Homer, for instance, made a place in his poems for everything that he had learned about the Ethiopians and the inhabitants of Egypt and Libya, and that he has gone into superfluous detail in regard to Greece and the neighbouring countries, speaking of Thisbe as the "haunt of doves," Haliartus as "grassy," Anthedon as "on the uttermost borders," Lilaea as "by the springs of Cephisus"; and he adds that Homer never lets fall an inappropriate epithet. Well then, I ask, is the poet who makes use of these epithets like a person engaged in entertaining, or in instructing? "The latter, of course," you reply; "but while these epithets have been used by him for purposes of instruction, everything beyond the range of observation has been filled, not only by Homer but by others also, with mythical marvels." Eratosthenes, then, should have said that "every poet writes partly for purposes of mere entertainment and partly for instruction"; but his words were "mere entertainment and not instruction." And Eratosthenes gives himself quite unnecessary pains when he asks how it contributes to the excellence of the poet for him to be an expert in geography, or in generalship, or in agriculture, or in rhetoric, or in any kind of special knowledge with which some people have wished to "invest" him. Now the desire to "invest" Homer with all knowledge might be regarded as characteristic of a man whose zeal exceeds the proper limit, just as would be the case if a man — to use a comparison of Hipparchus — should hang apples and pears, or anything else that it cannot bear, on an Attic "eiresione"; so absurd it would be to "invest" Homer with all knowledge and with every art. You may be right, Eratosthenes, on that point, but you are wrong when you deny to Homer the possession of vast learning, and go on to declare that poetry is a fable-prating old wife, who has been permitted to "invent" (as you call it) whatever she deems suitable for purposes of entertainment. What, then? Is no contribution made, either, to the excellence of him who hears the poets recited? I again refer to the poet's being an expert in geography, or generalship, or agriculture, or rhetoric, the subjects in which the poet naturally "invests" the hearer with special knowledge.
Assuredly Homer has attributed all knowledge of this kind, at least, to Odysseus, whom he adorns beyond his fellows with every kind of excellence; for his Odysseus "of many men the towns did see and minds did learn," and he is the man who "is skilled in all the ways of wile and cunning device." Odysseus is continually spoken of as "the sacker of cities" and as the capturer of Troy "by means of his counsels and his persuasiveness and his deceitful arts"; and Diomedes says of him: "But while he cometh with me, even out of burning fire might we both return." More than that, Odysseus prides himself on being a farmer. For instance, with round to reaping he says: "In the deep grass might the match be, and might I have a crooked scythe, and thou another like it"; and with regard to ploughing: "Then shouldst thou see me, whether or no I would cut a clean furrow unbroken before me." And not only does Homer thus possess wisdom about these matters, but all enlightened men cite the poet as a witness whose words are true, to prove that practical experience of this kind contributes in the highest degree to wisdom.
5 Rhetoric is, to be sure, wisdom applied to discourse; and Odysseus displays this gift throughout the entire Iliad, in the Trial, in the Prayers, and in the Embassy, where Homer says: "But when p63he uttered his great voice from his chest, and words like unto the snowflakes of winter, then could no mortal man contend with Odysseus." Who, then, can assume that the poet who is capable of introducing other men in the rôle of orators, or of generals, or in other rôles that exhibit the accomplishments of excellence, is himself but one of the buffoons or jugglers, capable only of bewitching and flattering his hearer but not of helping him? Nor can we assume that any excellence of a poet whatever is superior to that which enables him to imitate life through the means of speech. How, then, can a man imitate life if he has no experience of life and is a dolt? Of course we do not speak of the excellence of a poet in the same sense as we speak of that of a carpenter or a blacksmith; for their excellence depends upon no inherent nobility and dignity, whereas the excellence of a poet is inseparably associated with the excellence of the man himself, and it is impossible for one to become a good poet unless he has previously become a good man.
6 So, then, to deny the art of rhetoric to Homer is to disregard my position entirely. For what is so much a part of rhetoric as style? And what is so much a part of poetry? And who has surpassed Homer in style? "Assuredly," you answer, "but the style of poetry is different from that of rhetoric." In species, yes; just as in poetry itself the style of tragedy differs from that of comedy, and in prose the style of history differs from that of forensic speech. Well then, would you assert that discourse is not a generic term, either, whose species are metrical discourse and prose discourse? Or, rather, is discourse, in its broadest sense, generic, while rhetorical discourse is not generic, and style andº excellence of discourse are not? — But prose and discourse — I mean artistic prose — is, I may say, an imitation of poetic discourse; for poetry, as an art, first came upon the scene and was first to win approval. Then came Cadmus, Pherecydes, Hecataeus, and their followers, with prose writings in which they imitated the poetic art, abandoning the use of metre but in other respects passing the qualities of poetry. Then subsequent writers took away, each in his turn, something of these qualities, and brought prose down to its present form, as from a sublime height. In the same way one might say that comedy took its structure from tragedy, but that it also has been degraded — from the sublime height of tragedy to its present "prose-like" style, as it is called. And further, the fact that the ancients used the verb "sing" instead of the verb "tell" bears witness to this very thing, namely, that poetry was the source and origin of style, I mean ornate, or rhetorical, style. For when poetry was recited, it employed the assistance of song; this combination formed melodic discourse, or "ode"; and from "ode" they began to use the terms rhapsody, tragedy, and comedy. Therefore, since "tell" was first used in reference to poetic "style" and since among the ancients this poetic style was accompanied by song, the term "sing" was to them equivalent to the term "tell"; and then after they had misused the former of these two terms by applying it to prose p67discourse, the misuse passed over to the latter term also. And, furthermore, the very fact that non-metrical discourse was termed "pedestrian" indicates its descent from a height, or from a chariot, to the ground.
7 Nor, indeed, is the statement of Eratosthenes true that Homer speaks only of places that are near by and in Greece; on the contrary, he speaks also of many places that are distant; and when Homer indulges in myths he is at least more accurate than the later writers, since he does not deal wholly in marvels, but for our instruction he also uses allegory, or revises myths, or curries popular favour, and particularly in his story of the wanderings of Odysseus; and Eratosthenes makes many mistakes when he speaks of these wanderings and declares that not only the commentators on Homer but also Homer himself are dealers in nonsense. But it is worth my while to examine these points more in detail.
8 In the first place, I remark that the poets were not alone in sanctioning myths, for long before the poets the states and the lawgivers had sanctioned them as a useful expedient, since they had an insight into the natural affections of the reasoning animal; for man is eager to learn, and his fondness for tales is a prelude to this quality. It is fondness for tales, then, that induces children to give their attention to narratives and more and more to take part in them. The reason for this is that myth is a new language to them — a language that tells them, not of things as they are, but of a different set of things. And what is new is pleasing, and so is what one did not know before; and it is just this that makes men eager to p69learn. But if you add thereto the marvellous and the portentous, you thereby increase the pleasure, and pleasure acts as a charm to incite to learning. At the beginning we must needs make use of such bait for children, but as the child advances in years we must guide him to the knowledge of facts, when once his intelligence has become strong and no longer needs to be coaxed. Now every illiterate and uneducated man is, in a sense, a child, and, like a child, he is fond of stories; and for that matter, so is the half-educated man, for his reasoning faculty has not been fully developed, and, besides, the mental habits of his childhood persist in him. Now since the portentous is not only pleasing, but fear-inspiring as well, we can employ both kinds of myth for children, and for grown-up people too. In the case of children we employ the pleasing myths to spur them on, and the fear-inspiring myths to deter them; for instance, Lamia is a myth, and so are the Gorgon, and Ephialtes, and Mormolyce. Most of those who live in the cities are incited to emulation by the myths that are pleasing, when they hear the poets narrate mythical deeds of heroism, such as the Labours of Heracles of Theseus, or hear of honours bestowed by gods, or, indeed, when they see paintings or primitive images or works of sculpture which suggest any similar happy issue of fortune in mythology; but they are deterred from evil courses when, either through descriptions or through typical representations of objects unseen, they learn of divine punishments, terrors, and threats — or even when they merely believe that men have met with such experiences. For in dealing with a crowd of women, at least, or with any promiscuous mob, a philosopher cannot influence them by reason or exhort them to reverence, piety and faith; nay, there is need of religious fear also, and this cannot be aroused without myths and marvels. For thunderbolt, aegis, trident, torches, snakes, thyrsus-lances, — arms of the gods — are myths, and so is the entire ancient theology. But the founders of states gave their sanction to these things as bugbears wherewith to scare the simple-minded. Now since this is the nature of mythology, and since it has come to have its place in the social and civil scheme of life as well as in the history of actual facts, the ancients clung to their system of education for children and applied it up to the age of maturity; and by means of poetry they believed that they could satisfactorily discipline every period of life. But now, after a long time, the writing of history and the present-day philosophy have come to the front. Philosophy, however, is for the few, whereas poetry is more useful to the people at large and can draw full houses — and this is exceptionally true of the poetry of Homer. And the early historians and physicists were also writers of myths.
9 Now inasmuch as Homer referred his myths to the province of education, he was wont to pay considerable attention to the truth. "And he mingled therein" a false element also, giving his sanction to the truth, but using the false to win the favour of the populace and to out-general the masses. "And as when some skilful man overlays gold upon silver," just so was Homer wont to add a mythical element to actual occurrences, thus giving flavour and adornment to his style; but he has the same end in view as the historian or the person who narrates facts. So, for instance, he took the Trojan war, an historical fact, and decked it out with his myths; and he did the same in the case of the wanderings of Odysseus; but to hang an empty story of marvels on something wholly untrue is not Homer's way of doing things. For it occurs to us at once, doubtless, that a man will lie more plausibly if he will mix in some actual truth, just as Polybius says, when he is discussing the wanderings of Odysseus. This is what Homer himself means when he says of Odysseus: "So he told many lies in the likeness of truth;" for Homer does not say "all" but "many" lies; since otherwise they would not have been "in the likeness of truth." Accordingly, he took the foundations of his stories from history. For instance, history says that Aeolus was once king over the islands about Lipara, and that the Cyclopes and the Laestrygonians, inhospitable peoples, were lords over the region about Aetna and Leontine; and that for this reason the region about the Strait might not be visited by men of that time, and that Charybdis and the Rock of Scylla were infested by brigands. And from history we learn that the rest of the peoples mentioned by Homer lived in other parts of the world. And, too, it was on the basis of Homer's actual knowledge that the Cimmerians lived p75about the Cimmerian Bosporus, a gloomy country in the north, that he transferred them, quite appropriately, to a certain gloomy region in the neighbourhood of Hades — a region that suited the purpose of his mythology in telling of the wanderings of Odysseus. The writers of chronicles make it plain that Homer knew the Cimmerians, in that they fix the date of the invasion of the Cimmerians either a short time before Homer, or else in Homer's own time.
And likewise it was on the basis of Homer's actual knowledge of the Colchians, of Jason's expedition to Aea, and of the stories of fact and fiction told about Circe and Medea regarding their use of magic potions and their general similarity of character, that he invented a blood-relationship between the two, although they lived so very far apart, the one in the remote recess of the Pontus, and the other in Italy, and also invented a residence for both of them out by Oceanus, though it may be that Jason wandered as far as Italy; for there are some indications that point to the wanderings of the Argonauts in the region of the Ceraunian Mountains, about the Adriatic Sea, in the Gulf of Poseidonia, and in the islands that lie off Tyrrhenia. And the Cyaneae also, which some call the Symplegades, furnished the poet an additional matter of fact, in that they made the passage through the mouth of the strait at Byzantium very difficult; so that when we compare the Aeaea of Circe with the Aea of Medea, and Homer's Planctae with the Symplegades, Jason's voyage through the Planctae was clearly plausible also; and so was Odysseus' passage between the Rocks, when we think of Scylla and Charybdis. Again, the men of Homer's day, in general, regarded the Pontic Sea as a kind of second Oceanus, and they thought that those who voyaged thither got beyond the limits of the inhabited world just as much as those who voyaged far beyond the pillars of Heracles; the Pontic Sea was thought to be the largest of the seas in our part of the world, and for that reason they applied to this particular sea the term "The Pontus," just as they spoke of Homer as "The Poet." Perhaps it was for that very reason that Homer transferred to Oceanus things that were true of the Pontus, in the belief that such a change would prove acceptable because of the prevailing notions in regard to the Pontus. And I think that since the Solymi occupied the loftiest peaks of the Taurus Range, I mean the peaks about Lycia as far as Pisidia, and since their country presented to people who lived north of the Taurus Range, and particularly to those who lived about the Pontus, the most conspicuous altitudes on the south — for this reason, on the strength of a certain similarity of position, these people too were transferred to the position out by Oceanus; for in speaking of Odysseus sailing on his raft he says: "Now the lord, the shaker of the earth, on his way from the Ethiopians espied Odysseus from afar, from the mountains of the Solymi." Perhaps Homer also borrowed his idea of the one-eyed Cyclopes from the history of Scythia; for it is reported that the Arimaspians are a one-eyed people — a people whom Aristeas of Proconnesus has made known in his Arimaspian Epic.
Having made these preliminary remarks, I must ask what people mean when they affirm that Homer places the wanderings of Odysseus in the region of Sicily and Italy? It is possible to accept this view in two senses, one better and the other worse. The better is to assume that Homer was convinced that those regions were the scene of the wanderings of Odysseus, and that, taking his hypothesis as fact, he elaborated the story in poetic fashion. So much may be said with propriety about Homer; at any rate one may find traces of the wanderings of Odysseus, and of several others, not only in the region of Italy, but also as far as the extreme frontiers of Iberia. But the worse is to accept Homer's elaboration of the story as history also, because the poet is obviously indulging in marvels when he tells of Oceanus, Hades, cattle of Helius, entertainment by goddesses, metamorphoses, huge Cyclopes and huge Laestrygonians, Scylla's shape, distances traversed on the voyage, and many other things of a similar nature. But, on the one hand, it is not worth while to refute one who so obviously misinterprets the poet — any more than it would be if one should contend that the return of Odysseus to Ithaca, the massacre of the suitors, and the fight which took place out in the country between the Ithacans and Odysseus, all happened precisely as described by the poet; nor, on the other hand, is it right to quarrel with the man who interprets Homer in a proper fashion.
Eratosthenes, however, has taken issue with both these answers to my question, and in so doing he is wrong; he is wrong as regards the second answer, in that he attempts to misrepresent things that are obviously fictitious and that do not deserve protracted discussion; and he is wrong as regards the first, because he declares that all poets are dealers in absurdities and thinks their knowledge either of places or of arts does not conduce to virtue. Again, because Homer lays the scenes of his myths not only in non-fictitious places, such as Ilion, Mt. Ida, and Mt. Pelion, but also in fictitious places, such as those in which the Gorgons and Geryon dwell, Eratosthenes says that the places mentioned in the story of the wanderings of Odysseus, also, belong to the category of fiction, and that the persons who contend that they are not fictitious but have a foundation in fact, stand convicted of error by the very fact that they do not agree among themselves; at any rate, that some of them put the Sirens on Cape Pelorias, while others put them more than two thousand stadia distant on the Sirenussae, which is the name given to a three-peaked rock that separates the Gulf of Cumae from the Gulf of Poseidonia. But neither does this rock have three peaks, nor does it run up into a peak at all; instead it is a sort of elbow that juts out, long and narrow, from the territory of Surrentum to the Strait of Capreae, with the sanctuary of the Sirens on one side of the hilly headland, while on the other side, looking towards the Gulf of Poseidonia, lie three uninhabited rocky little islands, called the Sirens, and on the Strait of Capreae itself is situated the sanctuary of Athene, from which the elbow takes its name.
However, even if those who hand down to us our knowledge of the regions under consideration do not agree among themselves, we should not on that account set aside the entire body of that knowledge; indeed there are times when the account as a whole is all the more to be accepted for this reason. For example, suppose the question is raised whether the wanderings took place in the regions of Sicily and Italy, and whether the Siren Rocks are anywhere thereabouts: the man who places the Siren Rocks on Cape Pelorias is in disagreement with the man who places them on the Sirenussae, but neither disagrees with the man who says that the Siren Rocks are placed in the neighbourhood of Sicily and Italy; nay, they even add to the credibility of the third witness, because, though they do not name the self-same spot for the Rocks, yet, at all events, they have not gone beyond the regions of Italy and Sicily for them. Then, if some one adds that a monument of Parthenope, one of the Sirens, is shown in Neapolis, we have still further proof, although a third site has been introduced into the discussion. Furthermore, the fact that Neapolis also lies on this gulf (called by Eratosthenes the gulf of Cumae), which is formed by the Sirenussae, induces us to believe all the more firmly that the Sirens were in the neighbourhood of these places; for we do not demand of the poet that he should have inquired accurately into every detail, nor do we in our School demand scientific accuracy in his statements; yet, even so, we surely are not entitled to assume that Homer composed the story of the wanderings without any inquiry at all, either as to where or as to how they occurred.
But Eratosthenes conjectures that Hesiod learned by inquiry that the scene of the wanderings of Odysseus lay in the region of Sicily and Italy, and, adopting this belief, mentioned not only the places spoken of by Homer, but also Aetna, Ortygia (the little island next to Syracuse), and Tyrrhenia; and yet he contends that Homer knew nothing about these places and had no intention of placing the wanderings in any known regions. Now were Aetna and Tyrrhenia well-known places, but Scyllaeum, Charybdis, Circaeum, and the Sirenussae wholly unknown? Or was it the proper thing for Hesiod not to talk nonsense and to follow prevailing opinions, but the proper thing for Homer to "give utterance to every thought that comes to his inopportune tongue"? For apart from what I have said concerning the type of myth which it was proper for Homer to employ, most of the writers who discuss the same topics that Homer discusses, and also most of the various local traditions, can teach us that these matters are not fictions of poets nor yet of prose writers, but are traces of real persons and events.
Polybius also entertains correct views in regard to the wanderings of Odysseus, for he says that Aeolus, the man who taught navigators how to steer a course in the regions of the Strait of Messina, whose waters are subject to a constant ebb and flow and are difficult to navigate on account of the reverse currents, has been called lord of the winds and regarded as their king; and just as Danaüs, because he discovered the subterranean reservoirs of water in Argos, and Atreus, because he discovered that the sun revolves in a direction opposite to the movement of the heavens, were appointed kings; 24and just as the priests of the Egyptians, the Chaldaeans, and the Magi, because they excelled their fellows in knowledge of some kind or other, attained to leadership and honour among the peoples before our times; so, says Polybius, each one of the gods came to honour because he discovered something useful to man. Having said this much by way of preamble, Polybius insists that we shall not interpret Aeolus as a myth, nor yet the wanderings of Odysseus, as a whole; but that insignificant elements of myth have been added by the poet, just as had already been done in the case of the Trojan War, and that the scene of the whole story has been laid in the neighbourhood of Sicily by Homer as well as all the other writers who deal with local matters pertaining to Italy and Sicily. Neither does Polybius approve of this sort of declaration from Eratosthenes: "You will find the scene of the wanderings of Odysseus when you find the cobbler who sewed up the bag of the winds." And the description of Scylla by the poet, says Polybius, is in agreement with what takes place off the Scyllaean Rock and in the hunting of the "galeotae": "And there she fishes, swooping round the rock, for dolphins or for dog-fish, or whatso greater beast she may anywhere take." For when the tunny-fish, Polybius goes on to say, as they swim along in schools by the coast of Italy, meet with the current from the strait and are prevented from reaching Sicily, they fall a prey to the larger sea-animals, such as dolphins, dog-fish and cetaceans in general; and the "galeotae" (which are called both sword-fish and dog-fish) grow fat from the chase of the tunny-fish. Indeed, the same thing occurs here, and at the rise of the Nile and other rivers, as happens when there is a conflagration or a forest fire, namely, the assembled animals attempt to escape the fire or the flood and become prey of animals more powerful than themselves.
After making this statement Polybius goes on to describe the hunting of the "galeotae," which takes place off the Scyllaean Rock: one man on the look-out acts for all the fishermen, who lie in wait in many two-oared skiffs, two men in each skiff, one rowing and the other standing in the bow with his spear poised in hand. And when the man on the look-out signals the appearance of the "galeotes" (the creature swims along with a third of its body out of the water), and when the skiff draws near it, the man in the bow strikes the fish at close range, and then withdraws the spear-shaft, leaving the spear-head in the body of the fish; for the spear-head is barbed and loosely attached to the spear-shaft on purpose, and has a long line fastened to it. They pay out this line to the wounded fish until he becomes tired out by his struggles and his attempts at escape; then they tow him to the shore, or take him aboard the skiff — unless he be of enormous size. If the spear-shaft fall into the water, it is not lost; for it is made of both oak and pine wood, so that although the oaken end sinks because of its weight, the rest stays afloat and is easily recovered. It sometimes happens, says Polybius, that the man who rows the skiff is wounded through the bottom of the boat because of the great size of the sword of the "galeotae" and because the edge of the sword is sharp and biting like the wild boar's tusk. So, from such facts as these, Polybius concludes, one may conjecture that the wanderings of Odysseus took place in the neighbourhood of Sicily according to Homer, inasmuch as Homer attributed to Scylla that sort of fish-hunting which is most characteristic of Scyllaeum; and also from Homer's statements in regard to Charybdis, which correspond to the behaviour of the waters of the Strait. But the use of the word "thrice" instead of "twice" in the statement "for thrice a day she spouts it forth" is either an error of a copyist or an error of fact.
Furthermore, the facts about Meninx, continues Polybius, agree with what Homer says about the Lotus-Eaters. But if there be some discrepancy we must ascribe it to the changes wrought by time, or to ignorance, or to poetic license — which is compounded of history, rhetorical composition, and myth. Now the aim of history is truth, as when in the Catalogue of Ships the poet mentions the topographical peculiarities of each place, saying of one city that it is "rocky," of another that it is "on the uttermost border," of another that it is the "haunt of doves," and of still another that it is "by the sea"; the aim of most rhetorical composition is vividness, as when Homer introduces men fighting; the aim of myth is to please and to excite amazement. But to invent a story outright is neither plausible nor like Homer; for everybody agrees that the poetry of Homer is a philosophic production — contrary to the opinion of Eratosthenes, who bids us not to judge the poems with reference to their thought, nor yet to seek history in them. And Polybius says it is more plausible to interpret the poet's words, "Thence for nine days was I borne by baneful winds," as applying to a restricted area (for baneful winds do not maintain a straight course), than to place the incident out on Oceanus, as though the phrase had been "fair winds continually blowing." Now, if we reckon the distance from Cape Malea to the Pillars of Heracles at twenty-two thousand five hundred stadia, and if, says Polybius, we suppose that this distance was traversed at an even speed for those nine days, the distance covered each day would be two thousand five hundred stadia. But where do we find it recorded that anyone ever arrived at Alexandria from Lycia or Rhodes on the second day, though the distance is only four thousand stadia? And to those who ask the further question how it came about, if Odysseus touched Sicily three times, that he never once sailed through the Strait, Polybius replies that it was for the same reason that all later navigators have avoided that passage.
Such are the words of Polybius, and what he says is in the main correct. But when he demolishes the argument that places the wanderings of Odysseus on Oceanus, and when he reduces the nine days' voyage and the distances covered thereon to exact measurements, he reaches the height of inconsistency. For at one moment he quotes the words of the poet: "Thence for nine whole days was I borne by baneful winds"; and at another moment he suppresses statements. For Homer says also: "Now after the ship had left the river-stream of Oceanus"; and "In the island of Ogygia, where is the navel of the sea," going on to say that the daughter of Atlas lives there; and again, regarding the Phaeacians, "Far apart we live in the wash of the waves, the farthermost of men, and no other mortals are conversant with us." Now all these incidents are clearly indicated as being placed in fancy in the Atlantic Ocean; but Polybius by suppressing them destroys what the poet states in express terms. In so doing he is wrong; but he is right in placing the wanderings in the neighbourhood of Sicily and Italy; and the words of the poet are confirmed by the geographical terms of those regions. For what poet or prose writer ever persuaded the Neapolitans to name a monument after Parthenope the Siren, or the people of Cumae, of Dicaearchia, and of Vesuvius, to perpetuate the names of Pyriphlegethon, of the Acherusian Marsh, of the oracle of the dead at Lake Avernus, and of Baius and Misenus, two of the companions of Odysseus? The same question may be asked regarding Homer's stories of the Sirenussae, the Strait, Scylla, Charybdis, and Aeolus — stories which we should neither scrutinize rigorously, nor set aside as baseless and as without logical setting, having no claim to truthfulness or to utility as history.
Eratosthenes himself had a suspicion of this, for he says one may suppose that the poet wished to place the wanderings of Odysseus in the far west, but abandoned his purpose, partly because of his lack of accurate information, and partly because he had even preferred not to be accurate but rather to develop each incident in the direction of the more awe-inspiring and the more marvellous. Now Eratosthenes interprets rightly what Homer actually did, but wrongly his motive for doing it; for Homer's object was not to indulge in empty talk, but to do useful service. It is therefore right that Eratosthenes should submit to examination both on this point and on his assertion that far distant places are made the scenes of Homer's marvellous stories because of the fact that it is safer to fabricate about them. For his stories of marvels whose scenes are laid in distant places are very few in number in comparison with those laid in Greece or in countries near Greece; as such I may mention the stories about the labours of Heracles and Theseus, and the myths whose scenes are laid in Crete and Sicily and in the other islands, and on Cithaeron, Helicon, Parnassus, Pelion, and in various places in Attica or in the Peloponnesus. No one accuses the myth-makers of ignorance because of the myths they create; furthermore, since the poets, and Homer in particular, do not narrate pure myths simply but more often use mythical elements as additions to fact, the man who investigates what mythical additions the ancients make does not seek to discover whether the additions were once true or are true to‑day, but rather seeks to discover the truth in regard to the places to which, or the persons to whom, these mythical elements are added; for instance, in regard to the wanderings of Odysseus, whether they took place and, if so, where.
Generally speaking, it is wrong to place the poetry of Homer on the same level with that of other poets, and to decline to rank him above them in any respect, and particularly in the subject that now occupies our attention, namely, geography. For if you did no more than go over the Triptolemus of Sophocles or the prologue to the Bacchae of Euripides, and then compare Homer's care with respect to geographical matters, it would be easy for you to perceive this difference, which lies on the surface. Indeed, wherever there is need of an orderly sequence in the places he mentions, Homer is careful to preserve that order, not only in regard to places in Greece, but equally in regard to those beyond the limits of Greece: "They strove to pile Ossa on Olympus, and on Ossa Pelion with the trembling forest leaves"; "And Hera, rushing down, left the peak of Olympus, and touched on Pieria and pleasant Emathia, and sped over the snowy hills of the Thracian horsemen; and she went from Athos across the sea." In the Catalogue of Ships he does not, indeed, mention the cities in their order, for that was not necessary, but he does mention the peoples in their order. And so in case of the peoples remote from Greece: "I roamed over Cyprus and Phoenicia and Egypt, and reached the Ethiopians and Sidonians and Erembians and Libya"; Hipparchus also noted this fact. But Sophocles and Euripides, even where there is need of orderly sequence — the latter when he describes the visits of Dionysus to the various peoples, and the former when he tells Triptolemus visiting the earth that is being sown with seed — both poets, I say, bring near together regions that are very widely separated, and separate those that are contiguous: "I have left behind me," says Dionysus, "the gold-bearing glades of Lydia and of Phrygia, and I have visited the sun-stricken plains of Persia, the walled towns of Bactria, the wintry lands of the Medes, and Arabia the Blest." And Triptolemus does the same sort of thing. Again, in the case of the "climata"and of the winds, Homer displays the breadth of his geographical knowledge; for in marking the sites of places he often touches upon both these points too: "Now Ithaca lies low, uppermost on the sea-line towards the darkness, but those others face the dawning and the sun"; "Two gates there are, the one set toward the north wind, but the other toward the south"; "Whether they fare to the right, to the dawn and to the sun, or to the left, to darkness." In point of fact, Homer p103regards ignorance of these matters as tantamount to utter confusion in all particulars: "My friends, lo, we know not where is the place of darkness or of dawning, nor where the sun." In still another passage Homer is accurate when he speaks of "the north wind and the west wind that blow from Thrace" but Eratosthenes puts a false interpretation upon these words and falsely accuses the poet, as though he were making the universal statement that the west wind blows from Thrace; whereas Homer is not speaking in a universal sense, but refers to the time when these two winds meet in the Gulf of Melas upon the Thracian Sea, which is a part of the Aegean itself. For Thrace, running out into a promontory at the point where Thrace borders on Macedonia, takes a turn towards the west, and, thus projecting into the sea, gives the impression to the people in Thasos, Lemnos, Imbros, Samothrace, and on the sea that lies round about those islands, that the west winds actually blow from Thrace; precisely as, for Attica, they seem to come from the Scironian Rocks; and it is from these that the west winds, and particularly the north-west winds, get their name "Scirones." But Eratosthenes did not perceive this, though he suspected it; at any rate he himself describes the turn of the coast which I have mentioned. In any case, he interprets Homer's verse as a universal statement, and then charges the poet with ignorance, on the ground that, while the west wind blows from the west and from Iberia, Thrace does not extend so far west. Now is Homer really unaware that the west wind blows from the west? But Homer keeps it in its own proper place when he says: "The east wind and the south wind clashed, and the stormy west and the north." Or is he unaware that Thrace does not extend westward beyond the mountains of Paeonia and Thessaly? But he knows and correctly names the Thracian country as well as the country contiguous to it, both the sea-coast and the interior; and while he lists Magnesians, Malians, and the Hellenes next after them as far as the Thesprotians, and likewise the Dolopians and Sellans about Dodona, next neighbours to the Paeonians, as far as Acheloüs, yet he mentions no Thracians further west. And besides, Homer has a special fondness for the sea that lies nearest his home and is best-known to him, as is shown when he says: "And the assembly swayed like high waves of the Icarian deep."
There are some writers who say that there are only two principal winds, Boreas and Notus; and that the rest of the winds differ from these only by a slight variation of direction — Eurus blowing from the direction of summer sunrise, Apeliotes from the direction of winter sunrise, Zephyrus from the direction of summer sunset, Argestes from the direction of winter sunset. And to prove that there are only two winds they adduce the testimony of Thrasyalces and of Homer himself, on the ground that Homer assigns Argestes to Notus in the phrase "of Argestes Notus," and Zephyrus to p107Boreas in the verse: "Boreas and Zephyrus that blow from Thrace." But Poseidonius says that none of the recognised authorities on these matters, such as Aristotle, Timosthenes, and Bion the astrologer, have taught any such doctrine about the winds; rather do they maintain that Caecias is the name of the wind that blows from the direction of summer sunrise, while Lips is the name of the wind that blows diametrically opposite to Caecias from the direction of winter sunset; and again, that Eurus is the name of the wind that blows from the direction of winter sunrise, while Argestes is its opposite; and that the winds that lie between these are Apeliotes and Zephyrus. He says further that when Homer speaks of "the boisterous Zephyrus" he means what we call Argestes; that Homer's "clear-blowing Zephyrus" is what we call Zephyrus, and that Homer's "Argestes Notus" is our Leuconotus; for Leuconotus causes very few clouds, while Notus proper is somewhat cloudy: "Even as when Zephyrus divideth the clouds of Argestes Notus, smiting with deep storm." Homer here means "the boisterous Zephyrus," which usually scatters the thin clouds assembled by Leuconotus; for in this passage "Argestes" is applied to "Notus" as an epithet. Such, then, are the corrections that must be made to the remarks of Eratosthenes at the beginning of the first chapter of his Geography.
But, persisting in his false assumptions, Eratosthenes says that Homer does not even know that there are several mouths of the Nile, nor yet does he know the real name of the river, though Hesiod knows, for he mentions it. Now, as to the name, it is likely that in Homer's time it was not yet in use; but as to the mouths, if the fact that there were several, and not one only, was unnoticed or known to only a few, one might grant that Homer had not heard of it. But if the river was then, as it still is, the best-known and most marvellous thing in Egypt and decidedly the most worthy of mention and of historical record — and the same applies to its inundations and its mouths — who could ever assume either that those who brought to Homer the story of the River "Aegyptus" and the country "Aegyptus," 30and Egyptian Thebes, and Pharos, did not know about these mouths, or that if they knew, did not tell about them — except for the reason that they were already well known? But it is more incredible still that he mentioned Ethiopia, Sidonians, Erembians, the sea beyond, and the fact that the Ethiopians are "sundered in twain," and yet did not know about what was near at hand and well known. The fact that he did not mention them is no sign that he did not know about them — he does not mention his own native country, either, nor many other things — but rather would one say that Homer thought the best-known facts were not worth mentioning to those who already knew them.
Equally unjust is the reproach they cast upon Homer in the matter of the island of Pharos, because he says that it is "in the open sea" — as though he said this in ignorance. On the contrary, one might use that statement as bearing witness to the fact that not one of the things which we have just been talking about regarding Egypt was unknown to the poet. You might convince yourself of it in the following way: Everybody who tells the story of his own travels is a braggart; to this class belonged Menelaus, who had ascended the Nile as far as Ethiopia, and had heard about the inundations of the Nile and the quantity of alluvial soil which the river deposits upon the country, and about the large extent of territory off its mouths which the river had already added to the continent by silting — so that Herodotus was quite right in saying that the whole of Egypt is "a gift of the River Nile"; and even if this is not true of the whole of Egypt, it certainly is true of the part embraced by the Delta, which is called Lower Egypt; and Menelaus was told that the island of Pharos had been "in the open sea" in ancient times; so he falsely added that it was still "in the open sea," although it was no longer "in the open sea." However, it was the poet who elaborated this story, and therefore from it we may conjecture that Homer knew about the inundations of the Nile and about its mouths as well.
(30) The same mistake is made by those who say that Homer is not acquainted with the isthmus that lies between the Egyptian Sea and the Arabian Gulf, and that he is in error when he speaks of "the Ethiopians that are sundered in twain, the farthermost of men." Men of later times are wrong when they censure Homer for saying that, for it is correct. Indeed, the reproach that Homer is ignorant of this isthmus is so far from being true, that I affirm not only that he knows about it, but that he describes it in express terms, and that the grammarians beginning with Aristarchus and Crates, the leading lights in the science of criticism, even though Homer speaks of it, do not perceive that he does. The poet says: "the Ethiopians that are sundered in twain, the farthermost of men." About the next verse there is a difference of opinion, Aristarchus writing: "Abiding some where Hyperion sets, and some where he rises"; but Crates: "abiding both where Hyperion sets and where he rises." Yet so far as the question at issue is concerned, it makes no difference whether you write the verse one way or the other. For Crates, following the mere form of mathematical demonstration, says that the torrid zone is "occupied" by Oceanus and that on both sides of this zone are the temperate zones, the one being on our side, while the other is on the other side of it. Now, just as these Ethiopians on our side of Oceanus, who face the south throughout the whole length of the inhabited land, are called the most remote of the one group of peoples, since they dwell on the shores of Oceanus, so too, Crates thinks, we must conceive that on the other side of Oceanus also there are certain Ethiopians, the most remote of the other group of peoples in the temperate zone, since they dwell on the shores of this same Oceanus; and that they are in two groups and are "sundered in twain" by Oceanus. Homer adds the words, "abiding both where Hyperion sets and where he rises," because, inasmuch as the celestial zodiac always lies in the zenith above its corresponding terrestrial zodiac and inasmuch as the latter does not by reason of its obliquity extend outside the territory of the two Ethiopias, we must conceive that the entire revolution of the sun takes place within the width of this celestial zone, and that his risings and his settings take place herein, appearing differently to different peoples, and now in this sign and now in that. Such, then, is the explanation of Crates, who conceives of the matter rather as an astronomer; but he might have put it more simply — still saving his point that this was the sense in which the Ethiopians are "sundered in twain," as Homer has stated — namely, by declaring that the Ethiopians stretch along both shores of Oceanus from the rising to the setting of the sun. What difference, I say, does it make with respect to this thought whether we read the verse as Crates writes it, or as Aristarchus does — "abiding some where Hyperion sets and some where he rises"? For this, too, means that Ethiopians live on both sides of Oceanus, both towards the west and towards the east. But Aristarchus rejects this hypothesis of Crates, and thinks that the people referred to as divided "in twain" are the Ethiopians in our part of the world, namely, those that to the Greeks are most remote on the south; but he thinks these are not so divided "in twain" that there are two Ethiopias, the one lying towards the east and the other towards the west, but that there is just one, the one that lies south of the Greeks and is situated along Egypt; and he thinks that the poet, ignorant of this fact, just as he was ignorant of those other matters which Apollodorus has mentioned in the second book of his work entitled "On the Catalogue of Ships," told what was not true about the regions in question.
To reply to Crates would require a long discourse, which would perhaps be irrelevant to my present purpose. As for Aristarchus, I approve of him in this, that he rejects the hypothesis of Crates, which is open to many objections, and inclines to the view that the words of Homer have reference to our Ethiopia. But let us examine Aristarchus on the other points; and, in the first place, take the fact that he too indulges in a petty and fruitless discussion of the text. For if the verse be written in either of the two ways, it can fit his thought on the subject. For what difference does it make whether we say: "On our side of Oceanus there are two groups of Ethiopians, some in the east and some in the west," or, "both in the east and in the west"? In the second place, take the fact that Aristarchus champions a false doctrine. Well, let us suppose that the poet is ignorant of the existence of the isthmus, but is referring to Ethiopia on the confines of Egypt when he speaks of "Ethiopians that are sundered in twain." What then? Are they not thus "sundered in twain"? And does the poet make that statement in ignorance? Is not Egypt also, are not the Egyptians also, from the Delta up to Syene, "sundered in twain" by the Nile, "some where Hyperion sets and some where he rises"? What is Egypt but a river valley, which the water floods? And this valley lies on both sides of the river, toward the east and toward the west. But Ethiopia lies directly beyond Egypt and it is analogous to Egypt in its relation both to the Nile and the other physical characteristics of the regions in question. For it, too, is narrow, long, and subject to inundations; and its parts that lie beyond the territory subject to inundations are desert, without water, and habitable only in spots, both on the east and on the west. Of course, then, Ethiopia also is "sundered in twain." Or, again, did the Nile seem important enough for those who were drawing a boundary-line between Asia and Libya to serve as that boundary-line (since in length it stretches toward the south for more than ten thousand stadia, and is of such width that it contains islands with many thousands of inhabitants, the largest of which is Meroë, the residence of the King and the metropolis of the Ethiopians) and yet was not important enough to "sunder" Ethiopia itself "in twain"? And furthermore, the critics of the men who make the River Nile the boundary-line between the continents bring this against them as their most serious charge, that they dismember Egypt and Ethiopia, and that they reckon one part of each country to Libya and one part to Asia; or that, if they do not wish such dismemberment, then either they do not divide the continents at all, or else do not make the river the boundary-line.
But Ethiopia may be divided in still another way, quite apart from this. For all those who have made coasting-voyages on the ocean along the shores of Libya, whether they started from the Red Sea or from the Pillars of Heracles, always turned back, after they had advanced a certain distance, because they were hindered by many perplexing circumstances, and consequently they left in the minds of most people the conviction that the intervening space was blocked by an isthmus; and yet the whole Atlantic Ocean is one unbroken body of water, and this is particularly true of the Southern Atlantic. All those voyagers have spoken of the last districts to which they came in their voyagings as Ethiopic territory and have so reported them. Wherein, then, lies the absurdity, if Homer, too, was misled by a report of this character and divided the Ethiopians into two groups, placing the one group in the east and the other in the west, since it was not known whether the intervening people really existed or not? Furthermore, Ephorus mentions still another ancient tradition, and it is not unreasonable to believe that Homer also had heard it. Ephorus says the Tartessians report that Ethiopians overran Libya as far as Dyris, and that some of them stayed in Dyris, while others occupied a great part of the sea-board; and he conjectures it was from this circumstance that Homer spoke as he did: "Ethiopians that are sundered in twain, the farthermost of men."
These arguments one might urge in reply to Aristarchus and his followers, and also others still more convincing, and thus set the poet free from the charge of gross ignorance. I maintain, for example, that in accordance with the opinion of the ancient Greeks — just as they embraced the inhabitants of the known countries of the north under the single designation "Scythians" ("or "Nomads," to use Homer's term) and just as later, when the inhabitants of the west also were discovered, they were called "Celts" and "Iberians," or by the compound words "Celtiberians" and "Celtiscythians," the several peoples being classed under one name through ignorance of the facts — I maintain, I say, that just so, in accordance with the opinion of the ancient Greeks, all the countries in the south which lie on Oceanus were called "Ethiopia." And there is the following testimony to this statement. Aeschylus, in his Prometheus Unbound, speaks thus: "The sacred flood of the Red Sea with its bed of scarlet sands, and the mere on the shore of Oceanus that dazzles with its gleam of brass and furnishes all nourishment to Ethiopians, where the Sun, who sees all things, gives rest to his tired steeds and refreshes his immortal body in warm outpourings of soft water." For since Oceanus renders this service and maintains this relation to the sun along the whole southern belt, Aeschylus obviously places the Ethiopians also along this whole belt. And Euripides, in his Phaëthon, says that Clymene was given "to Merops, the king of this country which is the first country that the Sun, as he rises in his chariot and four, strikes with his golden flame. And the swarthy men who dwell upon the confines of that country call it the bright stables of Dawn and Sun." In this passage Euripides assigns the stables jointly to Dawn and Sun, but in what immediately follows he says that these stables are near to the dwelling of Merops, and indeed this is woven into the whole structure of the play, not, I am sure, because it is a peculiarity of the Ethiopia which lies next to Egypt, but rather because it is a peculiarity of the sea-board that stretches along the entire southern belt.
Ephorus, too, discloses the ancient belief in regard to Ethiopia, for in his treatise On Europe he says that if we divide the regions of the heavens and of the earth into four parts, the Indians will occupy that part from which Apeliotes blows, the Ethiopians the part from which Notus blows, the Celts the part on the west, and the Scythians the part from which the north wind blows.And he adds that Ethiopia and Scythia are the larger regions; for it is thought, he says, that the nation of the Ethiopians stretches from the winter sunrise to sunset, and that Scythia lies directly opposite in the north. That Homer is in agreement with this view is also clear from his assertion that Ithaca lies "toward the darkness" — that is, of course, toward the north — "but those others face the dawning and the sun"; by which he means the whole country on the southern side. And again this is clear when he says: "Whether they fare to the right, to the dawn and to the sun, or to the left, to mist and darkness"; and from this passage too: "My friends, lo, now we know not where is the place of darkness or of dawning, nor where the sun that gives light to men goes beneath the earth, nor where he rises." But about all these passages I shall speak more fully in my account of Ithaca. And so, when Homer says, "For Zeus went yesterday to Oceanus, unto the noble Ethiopians," we must understand both words in a more general sense, "Oceanus" meaning the body of water that extends along the entire southern belt, and the "Ethiopians" meaning the people along this same extent; for upon whatever point of this belt you fix your attention, you will be both on Oceanus and in Ethiopia. And this is the meaning also of the words: "On his way from the Ethiopians he espied Odysseus from afar, from the mountains of the Solymi" — which is equivalent to saying "from the regions of the south"; for he does not mean the Solymi in Pisidia, but, as I said before, he invents a people of the same name whom he depicts as occupying the same position relatively to the sailor on his raft and the people to the south of him (who would be the Ethiopians) as the Pisidians occupy relatively to the Pontus and to the Ethiopians that lie beyond Egypt. And in like manner Homer puts his assertion about the cranes in general terms: "When they flee from the coming of winter and sudden rain, and fly with clamour toward the streams of Oceanus, bearing slaughter and doom to the Pygmy men." For it is not the case that the crane is seen migrating toward the south only in Greek lands, and never in Italy or Iberia, or in the regions of the Caspian Sea and Bactriana. Since, then, Oceanus stretches along the entire southern sea-board, and since the cranes migrate in winter to this entire sea-board, we must admit that the Pygmies also are placed by mythology along the entire extent of that sea-board. And if men of later generations restricted the story about the Pygmies to the Ethiopians next to Egypt alone, that would have no bearing on the facts in ancient times. For nowadays we do not use the terms "Achaeans" and "Argives" of all who took part in the expedition against Troy, though Homer so uses them. Now what I contend in the case of the Ethiopians that are "sundered in twain" is similar to this, namely, that we must interpret "Ethiopians" as meaning that the Ethiopians extend along the whole sea-board of Oceanus from the rising to the setting sun. For the Ethiopians that are spoken of in this sense are "sundered in twain" naturally by the Arabian Gulf (and this would constitute a considerable part of a meridian circle) as by a river, being in length almost fifteen thousand stadia, and in width not much more than one thousand stadia, I mean at its greatest width; and to the length we must add the distance by which the head of this gulf is separated from the sea at Pelusium, a journey of three or four days — the space occupied by the isthmus. Now, just as the abler of the geographers who separate Asia from Libya regard this gulf as a more natural boundary-line between the two continents than the Nile (for he says the gulf lacks but very little of stretching from sea to sea, whereas the Nile is separated from Oceanus by many times that distance, so that it does not separate Asia as a whole from Libya), in the same way I also assume that the poet considered that the southern regions as a whole throughout the inhabited world were "sundered in twain" by this gulf. How, then, can the poet have been ignorant of the isthmus which the gulf forms with the Egyptian Sea?
And indeed it is in the highest degree unreasonable that the poet had accurate knowledge about Thebes in Egypt, which is distant from the Mediterranean Sea but a trifle less than four thousand stadia, and yet had no knowledge about the head of the Arabian Gulf, or about the adjoining isthmus, whose width is not more than one thousand stadia; but it would seem to be much more unreasonable that he knew the Nile bore the same name as the vast country Aegyptus and yet did not see the reason therefor; for the thought which has been expressed by Herodotus would occur to one at once, namely, that the country was "a gift of the river" and laid claim for this reason to the same name as the river. Moreover, those peculiarities of each several country which are in some way marvellous are most widely known, and manifest to everybody; such is the case with the rising of the Nile as also the silting up of the sea. And just as those who visit Egypt learn no fact concerning the country before they learn the nature of the Nile, because the natives cannot tell foreigners anything more novel or more remarkable about their country than these particulars (for the nature of the entire country becomes quite clear to one who has learned about the river), so also those who hear about the country at a distance learn this fact before anything else. To all this we must add the poet's fondness for knowledge and for travel, to which all who have written on his life bear witness; and one may find many illustrations of such a predilection in the poems themselves. And so it is proved, on many grounds, that Homer both knows and expressly says what is to be said, and that he keeps silent about what is too obvious to mention, or else alludes to it by an epithet.
But I must express my amazement at the Egyptians and Syrians, against whom I am directing this argument, that they do not understand Homer even when he tells them about matters in their own countries, and yet actually accuse him of ignorance — a charge to which my argument shows that they themselves are subject. In general, silence is no sign of ignorance; for neither does Homer mention the refluent currents of the Euripus, nor Thermopylae, nor yet other things in Greece that are well-known, though assuredly he was not ignorant of them. However, Homer also speaks of things well-known, though those who are wilfully deaf do not think so; and therefore the fault of ignorance is theirs. Now the poet calls the rivers "heaven-fed" — not merely the winter torrents, but all rivers alike — because they are all replenished by the rains. But the general epithet becomes particular when applied to things in relation to their pre-eminence. For one would interpret "heaven-fed" in one way of the winter torrent and in quite another way of the ever-flowing stream; and in the latter case the pre-eminence is, one may say, twofold. And just as there are cases of hyperbole on hyperbole — for example, "lighter than the shadow of a cork," "more timid than a Phrygian hare," "to own a farm smaller than a Laconian letter" — just so there is a parallel case of pre-eminence on pre-eminence when the Nile is spoken of as being "heaven-fed." For while the winter torrent surpasses the other rivers in respect of being "heaven-fed," the Nile, when at its flood, surpasses even the winter torrents to just that extent, not only in the amount of its flood but also in the duration thereof. And so, since the behaviour of the river was known to the poet, as I have urged in my argument, and since he has applied this epithet to it, we cannot interpret it in any other way than that which I have pointed out. But the fact that the Nile empties its waters through several mouths is a peculiarity it shares with several other rivers, and therefore Homer did not think it worthy of mention, particularly in addressing people who knew the fact; just as Alcaeus does not mention those mouths, either, although he affirms that he too visited Egypt. But the matter of the silting may be inferred not only from the risings of the river but also from what Homer says about Pharos. For the man who told Homer about Pharos — or rather, I should say, the common report that it was so and so far from the mainland — this report, I say, would not have got abroad falsified to such an extent as the distance which Homer gives, namely, a day's run for a ship; but as for the rising and silting, it is reasonable to suppose that the poet learned as a matter of common knowledge that they were such and such; and concluding from these facts that at the time of the visit of Menelaus the island was more distant from the mainland than it was in his own times, he added a distance many times as great on his own responsibility for the sake of the fabulous element. Moreover, the fabulous creations are not, I take it, a sign of ignorance — not even those stories about Proteus and the Pygmies, nor the potent effects of magic potions, nor any other such inventions of the poets; for these stories are told, not in ignorance of geography, but in order to give pleasure and enjoyment. How does it come, then, that Homer says that Pharos has water, when it is without water: "And therein is a good haven, whence men launch the well-proportioned ships into the deep when they have drawn a store of black water"? Now, in the first place, it is not impossible that the source of the water has dried up; and, in the second place, Homer does not say that the water came from the island, but merely that the launching of the ships took place thence — on account of the excellence of the harbour; but the water itself may have been drawn from the opposite mainland, since, in a way, the poet by implication confesses that, when he applied the term "in the open sea" to Pharos, he did not use it in a literal sense, but as an hyperbolical or mythical statement.
Now, since it is thought that Homer's account of the wanderings of Menelaus, also, argues for ignorance of those countries on his part, it is perhaps better to make a preliminary statement of the questions called forth by those poems, and then at once to separate these questions and thus speak more clearly in defence of the poet. Menelaus says, then, to Telemachus, who has marvelled at the decorations of the palace: "Yea, after many a woe and wanderings manifold, I brought my wealth home in ships, and in the eighth year came hither. I roamed over Cyprus and Phoenicia and Egypt, and came to Ethiopians, Sidonians, Erembians, and to Libya." Now they ask to what Ethiopians he came in thus sailing from Egypt (for no Ethiopians live in the Mediterranean Sea, nor was it possible for ships to pass the cataracts of the Nile); and who the Sidonians are (for they are certainly not those that live in Phoenicia, since he would not have put the genus first and then brought in the species); and who the Erembians are (for that is a new name). Now Aristonicus, the grammarian of our own generation, in his book On the Wanderings of Menelaus, has recorded opinions of many men on each one of the points set forth; but for me it will be sufficient to speak briefly on these questions. Of those who say that Menelaus "sailed" to Ethiopia, some propose a coasting-voyage by Gades as far as India, making his wanderings correspond exactly to the time which Homer gives: "In the eighth year I came back"; but others propose that he sailed across the isthmus that lies at the head of the Arabian Gulf, while still others propose that he sailed through one of the canals of the Nile. But, in the first place, Crates' theory of a coasting-voyage is unnecessary — not that such a voyage would be impossible (for the wanderings of Odysseus would have been impossible), but because it serves no purpose either as regards Crates' mathematical hypotheses or as regards the time consumed in the wanderings. For Menelaus was detained against his will because of the difficulties of sailing (he himself says that out of sixty ships only five were left to him), he also made intentional stops for the sake of trafficking. For Nestor says: "Thus Menelaus, gathering much substance and gold, was wandering there with his ships"; to which Menelaus adds: "having roamed over Cyprus and Phoenicia and Egypt." Again, the voyage through the isthmus or one of the canals would, if Homer mentioned such a city, be interpreted as a kind of fiction; but since he does not mention such a voyage it would be gratuitous and absurd for one to propose it. It would be absurd, I repeat, since before the Trojan War there was no canal; and the person who undertook to build one — I mean Sesostris— is said to have abandoned the undertaking because he supposed the level of the Mediterranean Sea was too high. Furthermore, the isthmus was not navigable either, and Eratosthenes' conjecture is wrong. For he thinks that the breaking of the channel at the Pillars of Heracles had not yet taken place and that in consequence the Mediterranean Sea, since it was of a higher level, joined the exterior sea at the isthmus and covered it, but after the breaking of the channel took place at the Pillars, the Mediterranean Sea was lowered and thus exposed the land about Casium and Pelusium, as far as the Red Sea. Now what historical information have we regarding this break at the Pillars to the effect that it did not yet exist before the Trojan War? But perhaps — you will say — the poet has represented Odysseus as sailing through the strait at the Pillars into the ocean (as though a channel were already in existence) at the same time that he conveys Menelaus by ship from Egypt into the Red Sea (as though a channel were not yet in existence)! Furthermore, Homer brings in Proteus as saying to Menelaus: "Nay, the deathless gods will convey thee to the Elysian Plain and to the end of the earth." What end of the earth, pray? Why, the citing of "Zephyrus" shows that he means by this remote region a place somewhere in the west: "But always Oceanus sendeth forth the breezes of the clear-blowing Zephyrus." Really, these matters are full of puzzling questions.
If, however, the poet had heard that this isthmus was once submerged, should we not have all the greater reason for believing that the Ethiopians, since they were separated by so great a strait, were really "sundered in twain"? And how could Menelaus have gotten treasures from the remote Ethiopians who lived along Oceanus? For at the moment when they marvelled at the ornaments themselves in the palace of Menelaus, Telemachus and his companions marvelled at the great quantity of them — "of gold and of amber and of silver and of ivory"; but with the exception of ivory, there is no great store of any of these things among those people, most of whom are the poorest of all peoples and are wandering shepherds. "Very true," you say; "but Arabia and the regions as far as India belonged to them; and though Arabia alone of all these countries has the name 'Blest,' India is supposed and reported to be in the highest degree 'blest,' even though people do not so call it by name." Now as to India, Homer did not know of it (for had he known of it, he would have mentioned it); but he did know the Arabia which is to‑day called "Blest." In his time, however, it was not rich, and not only was the country itself without resources but most of it was occupied by dwellers in tents. The part of Arabia that produces the spices is small; and it is from this small territory that the country got the name of "Blest," because such merchandise is rare in our part of the world and costly. To‑day, to be sure, the Arabs are well to do and even rich, because their trade is extensive and abundant, but it is not likely to have been so in Homer's time. So far as the mere spices are concerned, a merchant or camel-driver might attain to some sort of wealth by trafficking in them, whereas Menelaus needed booty or presents from kings or dynasts who had not only the means to give, but also the good-will to make him presents because of his distinction and fame. The Egyptians, however, and the neighbouring Ethiopians and Arabs, were not wholly destitute of the means of livelihood, as were the other Ethiopians, nor wholly ignorant of the fame of the sons of Atreus, particularly in view of the successful issue of the Trojan War, and hence Menelaus might hope for profit from them. Compare what Homer says of the breastplate of Agamemnon: "The breastplate that in time past Cinyrasa gave him for a guest-gift; for afar in Cyprus did Cinyras hear the mighty tale." Furthermore, we must assert that Menelaus' time in his wanderings was spent mostly in the regions about Phoenicia, Syria, Egypt, and Libya, and in the countries round Cyprus, and, generally speaking, along the Mediterranean sea-board and among the islands. For Menelaus might procure guest-gifts among these peoples and also enrich himself from them by violence and robbery, and more particularly from those who had been allies of the Trojans. But the barbarians that lived outside these regions or at a distance could prompt in him no such expectations. Now Homer says that Menelaus "came to" Ethiopia, not meaning that he really came into Ethiopia, but that he reached its frontier next to Egypt. For perhaps at that time the frontier was still nearer Thebes (though to‑day it is quite near) — I mean the frontier that runs by Syene and Philae. Of these towns the former belongs to Egypt, but Philae is inhabited alike by Ethiopians and Egyptians. Accordingly, when Menelaus came to Thebes, it need not cause surprise if he also came as far as the frontier of the Ethiopians or even farther, especially since he was enjoying the hospitality of the king of Thebes. And it is in the same sense that Odysseus says he "came to" the country of the Cyclopes, although he did not get any further away from the sea than the cavalry; for he says that the cavalry lay "on the edge" of the country, I believe; and again, in referring to the country of Aeolus, to the Laestrygonians and the rest — wherever, I say, he so much as came to anchor, he says he "came to" the country. It is in this sense, therefore, that Menelaus "came to" Ethiopia and in this sense to Libya, too, namely, that he "touched at" certain points; and it is from his having touched there that the harbour at Ardanis above Paraetonium is called "Menelaus."
Now if Homer, in speaking of the Phoenicians, mentions Sidonians also, who occupy the Phoenician metropolis, he is but employing a familiar figure of speech, as when he says: "Now Zeus, when he had brought the Trojans and Hector to the ships"; and, "For the sons of great-hearted Oeneus were no more, neither did he still live, and the golden-haired Meleager was dead"; and, "So fared he to Ida" and "to Gargaros"; and, "But they possessed Euboea" and "Chalcis and Eretria"; and likewise Sappho, in the verse: "Either Cyprus or Paphos of the spacious harbour holds thee." And yet there was another reason which induced Homer, although he had already mentioned Phoenicia, to repeat Phoenicia in a special way — that is, to add Sidon to the list. For merely to list the peoples in their proper order it was quite enough to say: "I roamed over Cyprus and Phoenicia and Egypt, and came to Ethiopia." But in order to suggest also the sojourn of Menelaus among the Sidonians, it was proper for Homer to repeat as he did, or even add still more than that; and he suggests that this sojourn was of long duration by his praise of their skill in the arts and of the hospitality formerly extended to Helen and Paris by these same people. That is why he speaks of many Sidonian works of art stored up in the house of Paris — "where were her embroidered robes, the work of Sidonian women, whom godlike Alexandros himself brought from Sidon, that journey wherein he brought back Helen to his home"; and in the house of Menelaus too, for Menelaus says to Telemachus: "I will give thee a mixing-bowl beautifully wrought; it is all of silver, and the lips thereof are finished with gold, the work of Hephaestus; and the hero Phaedimus, the king of the Sidonians, gave it me, when his house sheltered me on my coming thither." But the expedition "the work of Hephaestus" must be regarded as a case of hyperbole, just as beautiful things are spoken of as "works of Athene," or of the Graces, or of the Muses. For Homer makes it clear that the Sidonians were makers of beautiful works of art, by the praise he bestows on the bowl which Euneos gave as a ransom for Lycaon; his words are: "In beauty it was far the best in all the earth, for artificers of Sidon wrought it cunningly, and men of the Phoenicians brought it."
Much has been said about the Erembians; but those men are most likely to be correct who believe that Homer meant the Arabians. Our Zeno even writes the text accordingly: "And I came to the Ethiopians and Sidonians and Arabians." However, it is not necessary to change the reading, for it is old. It is better to lay the confusion to the change of their name, for such change is frequent and noticeable among all nations, than to change the reading — as in fact some do when they emend by changing certain letters. But it would seem that the view of Poseidonius is best, for here he derives an etymology of the words from the kinship of the peoples and their common characteristics. For the nation of the Armenians and that of the Syrians and Arabians betray a close affinity, not only in their language, but in their mode of life and in their bodily build, and particularly wherever they live as close neighbours. Mesopotamia, which is inhabited by these three nations, gives proof of this, for in the case of these nations the similarity is particularly noticeable. And if, comparing the differences of latitude, there does exist a greater difference between the northern and the southern people of Mesopotamia than between these two peoples and the Syrians in the centre, still the common characteristics prevail. And, too, the Assyrians, the Arians, and the Aramaeans display a certain likeness both to those just mentioned and to each other. Indeed, Poseidonius conjectures that the names of these nations also are akin; for, says he, the people whom we call Syrians are by the Syrians themselves called Arimaeans and Arammaeans; and there is a resemblance between this name and those of the Armenians, the Arabians and the Erembians, since perhaps the ancient Greeks gave the name of Erembians to the Arabians, and since the very etymology of the word "Erembian" contributes to this result. Most scholars, indeed, derive the name "Erembian" from eran embainein, a name which later peoples changed to "Troglodytes" for the sake of greater clearness. Now these Troglodytes are that tribe of Arabians who live on the side of the Arabian Gulf next to Egypt and Ethiopia. It was natural for the poet to mention these Erembians and to say that Menelaus "came to" them, in the same sense in which he says that Menelaus "came to" the Ethiopians (for they too are near the territory of Thebes); however, they were mentioned not on account of their handicraft nor yet on account of the profit Menelaus made among them (for that could not amount to much), but on account of the length of his sojourn among them and the fame of having visited them; for it was a famous thing to have travelled so far abroad. This is the meaning of: "Many were the men whose towns he saw whose mind he learnt"; and of: "Yea, and after many woes and wanderings manifold, I brought my wealth home in ships." Hesiod in his Catalogus speaks of "the daughter of Arabus, the son of guileless Hermaon and of Thronia the daughter of king Belus." And Stesichorus says the same thing. Therefore, we may conjecture that at the time of Hesiod and Stesichorus the country was already called Arabia from this "Arabus," although it may be that it was not yet so called in the times of the heroes.
Those scholars who invent the explanation that the Erembians are some particular Ethiopian tribe, or, again, a tribe of Cephenians, or thirdly, a tribe of Pygmies — or a host of other tribes — are less deserving of credence, since in addition to the incredibility of their theories they betray a tendency to confound myth and history. Like them are the writers who tell of Sidonians on the Persian Gulf, or somewhere else on Oceanus, and who place the wanderings of Menelaus, and likewise place the Phoenicians, out in Oceanus. And not the least reason for not believing them is the fact that they contradict one another. For some of them say that even the Sidonians who are our neighbours are colonists from the Sidonians on Oceanus, and they actually add the reason why our Sidonians are called Phoenicians,namely, because the colour of the Persian Gulf is "red"; and the others hold that the Sidonians on Oceanus are colonists from our Phoenicia. And there are some who transfer Ethiopia also to our Phoenicia, and who say that the adventure of Andromeda took place in Joppa, though the story is surely not told in ignorance of its local setting but rather in the guise of myth; and the same is true of the stories that Apollodorus cites from Hesiod and the other poets without even realising in what way he is comparing them with the stories in Homer. For he compares what Homer says about the Pontus and Egypt and charges him with ignorance, on the ground that, though he wanted to tell the truth, he did not do so, but in his ignorance stated as true what was not true. Yet no one could charge Hesiod with ignorance when he speaks of "men who are half-dog," of "long-headed men" and of "Pygmies"; no more should one charge Homer with ignorance when he tells these mythical stories of his, one of which is that of these very Pygmies; nor Alcman when he tells about "web-footed men"; nor Aeschylus when he speaks of "dog-headed men," or of "men with eyes in their breasts," or of "one-eyed men"; since, at all events, we do not pay much attention to prose writers, either, when they compose stories on many subjects in the guise of history, even if they do not expressly acknowledge that they are dealing in myths. For it is self-evident that they are weaving in myths intentionally, not through ignorance of the facts, but through an intentional invention of the impossible, to gratify the taste for the marvellous and the entertaining. But they give the impression of doing this through ignorance, because by preference and with an air of plausibility they tell such tales about the unfamiliar and the unknown. Theopompus expressly acknowledges the practice when he says that he intends to narrate myths too in his History — a better way than that of Herodotus, Ctesias, Hellanicus, and the authors of the Histories of India.
What Homer says about the behaviour of Oceanus is set forth in the guise of a myth (this too is a thing the poet must aim at); for he borrowed the myth of Charybdis from the ebb and flow of the tides; though even Charybdis herself is not wholly an invention of Homer, for she was dressed up by him in accordance with what had been told him about the Strait of Sicily. And suppose that by the words, "For thrice a day she spouts it forth, and thrice a day she sucks it down," Homer does affirm that the refluent tide comes in three times within the course of each day and night (although it comes in but twice), he might be permitted to express it in this way; for we must not suppose that he used these words in ignorance of the facts, but for the sake of the tragic effect and of the emotion of fear upon which Circe plays largely in what she says to Odysseus in order to terrify him; and for that reason she mingled the false with the true. At any rate, in these very lines Circe has said: "For thrice a day she spouts it forth and thrice a day she sucks it down — a terrible sight! Never mayest thou be there when she sucks the water, for none might save thee from thy bane, not even the Earth-Shaker." Yet Odysseus later on was present when she "sucked it down," and he did not perish; as he himself says: "Now she had sucked down the salt sea-water, but I was swung up on high to a tall fig-tree, whereto I clung like a bat." Then waiting for the pieces of wreckage and laying hold of them again, he saved himself on them; and so Circe lied. And as she lied in this statement, so she lied in that other statement, "for thrice a day she spouts it forth," instead of "twice a day," although it is true, at the same time, that this kind of hyperbole is familiar to everybody — as, for instance, when we say "thrice-blessed" and "thrice-wretched." The poet himself says: "Thrice-blessed those Danaäns"; and again: "Welcome, thrice-prayed for"; and yet again: "Into three, yea, into four pieces." Perhaps one might infer also from the time involved that Homer is, in a way, hinting at the truth; for the fact that the pieces of wreckage remained so long engulfed and were only tardily cast up for Odysseus, who was longing for them and constantly clinging to the limbs of the tree, better suits the assumption that the refluent tide came in twice, rather than thrice, during the twofold period, consisting of a day and a night: "Steadfastly I clung," he says, "till she should vomit forth mast and keel again; and late they came to my desire. At the hour when a man rises up from the assembly and goes to supper, p163the arbiter of many quarrels of the young men that plead their cases, at that hour the timbers came forth to view from out Charybdis." All this gives the impression of a considerable lapse of time, and particularly the fact that the poet prolongs time to the evening, for he does not merely say in general terms, "at the hour when the judge rises up," but he adds "arbiter of many quarrels"; hence he had been detained somewhat longer than usual. And another consideration: the means of escape which the poet offers the shipwrecked Odysseus would not be plausible, if each time, before he was carried far away by the tide, he was immediately thrown back by the refluent tide.
Apollodorus, agreeing with Eratosthenes and his school, censures Callimachus, because, though a scholar, Callimachus names Gaudos and Corcyra as scenes of the wanderings of Odysseus, in defiance of Homer's fundamental plan, which is to transfer to Oceanus the regions in which he describes the wanderings as taking place. But if the wanderings never took place anywhere, and if this is wholly a fiction of Homer's, then Apollodorus' censure is just. Or if the wanderings did take place, but in other regions, then Apollodorus should have said so at the outset and should have told in what regions they took place, thus at once correcting the ignorant view of Callimachus. But since the story cannot with plausibility be called wholly a fiction, as I have shown above, and since no other places are pointed out that have a greater claim to our credence, Callimachus might be absolved from censure.
Nor is Demetrius of Scepsis right; on the contrary, he is the cause of some of the mistakes of Apollodorus. For in his excessive eagerness to refute the statement of Neanthes of Cyzicus that the Argonauts erected the sanctuary of the Idaean Mother1in the neighbourhood of Cyzicus when they were sailing to Phasis1on the voyage which is admitted by Homer and other writers, Demetrius says that Homer knew absolutely nothing about the voyage of Jason to Phasis. Now this is opposed not only to Homer's statements but to the statements made by Demetrius himself. For Demetrius says that Achilles sacked Lesbos and other places, but spared Lemnos and the islands adjacent thereto on account of his kinship with Jason and with Jason's son Euneos who at that time possessed the island of Lemnos. Now how comes it that the poet knew this, namely, that Achilles and Jason were kinsmen or fellow-countrymen, or neighbours, or friends in some way or other (a relationship that could not be due to any other fact than that both men were Thessalians, and that one was born in Iolcus and the other in Achaean Phthiotis), and yet did not know what had put it into the head of Jason, a Thessalian and an Iolcan, to leave no successor on the throne of his native country, but to establish his son as lord of Lemnos? And did he know about Pelias and the daughters of Pelias, and about Alcestis, the noblest of them, and about her son "Eumelus, whom Alcestis, fair among women, bare to Admetus, Alcestis that was most beauteous to look upon of the daughters of Pelias," and yet, as regards the adventures of Jason and the Argo and the Argonauts, had never heard of the things that are agreed upon by everybody, but invented the voyage away from Aeëtes' country and placed it on Oceanus, without any foundation for his story in history?
For, as all admit, the original voyage to Phasis ordered by Pelias, the return voyage, and the occupation, however considerable, of islands on the coasting-voyage thither, contain an element of plausibility, as do also, I am sure, the wanderings which carried Jason still further — just as there is an element of plausibility in the wanderings of both Odysseus and Menelaus — as evidenced by things still to this day pointed out and believed in, and by the words of Homer as well. For example, the city of Aea is still shown on the Phasis, and Aeëtes is believed to have ruled over Colchis, and the name Aeëtes is still locally current among the people of that region. Again, Medea the sorceress is a historical person; and the wealth of the regions about Colchis, which is derived from the mines of gold, silver, iron, and copper, suggests a reasonable motive for the expedition, a motive which induced Phrixus also to undertake this voyage at an earlier date. Moreover, memorials of both expeditions still exist: the sanctuary of Phrixus, situated on the confines of Colchis and Iberia, and the sanctuaries of Jason, which are pointed out in many places in Armenia and Media and in the countries adjacent thereto. More than that, it is said that there are many evidences of the expeditions of Jason and of Phrixus in the neighbourhood of Sinope and the adjacent sea-board and also about the Propontis and the Hellespont as far as the regions about Lemnos. And there are traces of the expedition of Jason, and of the Colchians who pursued him, as far as Crete and Italy and the Adriatic Sea, woman of which Callimachus notes when he says, "Aegletes and Anaphe hard by Laconian Thera," in an elegy whose opening words are, "At the outset I shall sing how the heroes sailed back from the kingdom of Aeëtes of Cytaea to ancient Haemonia." In another place Callimachus speaks about the Colchians, who "stayed their oars in the Sea of Illyria beside the tomb-stone of blonde Harmonia, and there built a little city, which a Greek would call 'the city of the exiles,' but which their language has named Polae." Some say that Jason and his companions even sailed up the Ister a considerable distance, while others say that he ascended as far as the Adriatic Sea; the former make their statement in ignorance of these regions, whereas the latter make the assertion that a river Ister branches off from the great Ister and empties into the Adriatic Sea; but apart from this, what they say is neither improbable nor incredible.
Accordingly, it is by availing himself of some such basis of fact that Homer tells his story, agreeing in some respects with matters of history, but adding to them an element of myth, thus adhering to a custom that is not only his own but one common to poets. He agrees with history when he uses the name of "Aeëtes," when he tells of Jason and the Argo, when, with "Aea" in mind, he invents "Aeaea," when he established Euneos in Lemnos, when he makes the island of Lemnos beloved of Achilles, and when, with Medea in mind, he makes the sorceress Circe "own sister to the baleful Aeëtes." But he adds an element of myth when he transfers to Oceanus the wanderings that follow the voyage to Aeëtes' country. For if the facts above-mentioned be assumed, then the words, "the Argo that is in all men's minds," are also properly used, inasmuch as the expedition is supposed to have taken place in well-known and populous regions. But if the facts were as Demetrius of Scepsis maintains, on the authority of Mimnermus (Mimnermus places the home of Aeëtes in Oceanus, outside the inhabited world in the east, and affirms that Jason was sent thither by Pelias and brought back the fleece), then, in the first place, the expedition thither in quest of the fleece would not sound plausible (since it was directed to unknown and obscure countries), and in the second place, the voyage through regions desolate and uninhabited and so out‑of-the‑way from our part of the world would be neither famous nor "in all men's minds." Mimnermus says: "Never would Jason himself have brought back the great fleece from Aea, accomplishing his mind-racking journey and fulfilling the difficult task for insolent Pelias, nor would they have come even to the fair stream of Oceanus"; and further on he says: "To the city of Aeëtes, where the rays of the swift Sun lie in a chamber of gold beside the lips of Oceanus, whither glorious Jason went." |
|
|
|
|
1 - 3 Eratosthenes is wrong 
1 Eratosthenes is wrong on this point too, that he makes mention at too great length of men who do not deserve mention, censuring them in some things, while in other things he believes them and uses them as authorities — for instance, Damastes and others of his type. For even if there is an element of truth in what they say, we should not on that account use them as authorities, or believe them, either; on the contrary, we should use in such a way only men of repute — men who have been right on many points, and who, though they have omitted many things, or treated them inadequately, have said nothing with false intent. But to use Damastes as an authority is no whit better than to cite as authorities the "Bergaean" — or rather the Messenian — Euhemerus and the other writers whom Eratosthenes himself cites, in order to ridicule their absurdities. Eratosthenes himself tells us one of the absurd stories of Damastes, who assumes that the Arabian Gulf is a lake, and that Diotimus, the son of Strombichus, sailed, at the head of an embassy of the Athenians, from Cilicia up the Cydnus River to the Choaspes River, which flows by Susa, and reached Susa on the fortieth day; and Eratosthenes says that Damastes was told all this by Diotimus himself. And then, Eratosthenes adds, Damastes wonders whether it was really possible for the Cydnus River to cut across the Euphrates and the Tigris and to empty into the Choaspes.
2 Not only might one disapprove of Eratosthenes for telling such a story, but also for this reason: after admitting that the exact details about the seas were not yet known even in his own time, and although he bids us not to be too ready to accept the authority of people at haphazard, and although he gives at length the reasons why we should believe no one who writes mythical tales about the regions along the Euxine and the Adriatic, yet he himself accepted the authority of people at haphazard. So, for example, he believed that the Gulf of Issus is the most easterly point of the Mediterranean; whereas the point at Dioscurias in the extreme corner of the Euxine Sea is farther east by almost three thousand stadia, even according to Eratosthenes himself, if we follow the reckoning by stadia which he gives. And when he describes the northernmost and extreme parts of the Adriatic Sea there is nothing fabulous about them from which he holds aloof. And he has also given credence to many fables about the regions beyond the Pillars of Heracles, mentioning an island named Cerne and other countries which are nowhere pointed out to‑day — matters about which I shall speak later on. And although Eratosthenes has said that the earliest Greeks made voyages for the sake of piracy or of commerce, not, indeed, in the open sea, but along the coast — as did Jason, who actually abandoned his ships and, starting from the Colchians, penetrated as far as Armenia and Media — he says later on that in ancient times no one had the courage to sail on the Euxine Sea, or along Libya, Syria, or Cilicia. Now if by "the ancients" he means those who lived in the times of which we of to‑day have no records, then I am in no wise concerned to speak about them, as to whether they made voyages or not. But if he means men who are mentioned in history, then one would not hesitate to affirm that the ancients will be shown to have made longer journeys, both by land and by sea, than have men of a later time, if we are to heed what tradition tells us: for instance, Dionysus, and Heracles, and Jason himself; and, again, Odysseus and Menelaus, whose stories are narrated by the poet. And again, it is doubtless because Theseus and Pirithous had the hardihood to make such long journeys as they made that they left behind them the reputation of having gone down to Hades, and that the Dioscuri were called "guardians of the sea" and "saviours of sailors." Again, the maritime supremacy of Minos is far-famed, and so are the voyages of the Phoenicians, who, a short time after the Trojan War, explored the regions beyond the Pillars of Heracles and founded cities both there and in the central parts of the Libyan sea-board. As to Aeneas, Antenor, and the Enetians, and, in a word, p179the survivors of the Trojan War that wandered forth into the whole inhabited world — is it proper not to reckon them among the men of ancient times? For it came about that, on account of the length of the campaign, the Greeks of that time, and the barbarians as well, lost both what they had at home and what they had acquired by the campaign; and so, after the destruction of Troy, not only did the victors turn to piracy because of their poverty, the still more the vanquished who survived the war. And, indeed, it is said that a great many cities were founded by them along the whole sea-coast outside of Greece, and in some places in the interior too.
3 Now after Eratosthenes has himself told what great advances in the knowledge of the inhabited world had been made not only by those who came after Alexander but by those of Alexander's own times, he passes to his discussion of the shape of the world, not indeed of the inhabited world — which would have been more appropriate to his discussion of that subject — but of the earth as a whole; of course, one must discuss that point too, but not out of its proper place. And so, after he has stated that the earth as a whole is spheroidal — not spheroidal indeed as though turned by a sphere-lathe, but that it has certain irregularities of surface — he proceeds to enumerate the large number of its successive changes in shape — changes which take place as the result of the action of water, fire, earthquakes, volcanic eruptions, and other similar agencies; and here too he does not preserve the proper order. For the spheroidal shape that characterises the earth as a whole results from the constitution of the universe, but such changes as Eratosthenes mentions do not in any particular alter the earth as a whole (changes so insignificant are lost in great bodies), though they do produce conditions in the inhabited world that are different at one time from what they are at another, and the immediate causes which produce them are different at different times.
4 Eratosthenes says further that this question in particular has presented a problem: how does it come about that large quantities of mussel-shells, oyster-shells, scallop-shells and also salt-marshes are found in many places in the interior at a distance of two thousand or three thousand stadia from the sea — for instance (to quote Eratosthenes) in the neighbourhood of the temple of Ammon and along the road, three thousand stadia in length, that leads to it? At that place, he says, there is a large deposit of oyster-shells, and many beds of salt are still to be found there, and jets of salt-water rise to some height; besides that, they show pieces of wreckage from seafaring ships which the natives said had been cast up through a certain chasm, and on small columns dolphins are dedicated that bear the inscription: "Of Sacred Ambassadors of Cyrene." Then he goes on to praise the opinion of Strato, the physicist, and also that of Xanthus of Lydia. In the first place he praises the opinion of Xanthus, who says that in the reign of Artaxerxes there was so great a drought that the rivers, lakes, and wells dried up; that far from the sea, in Armenia, Matiene, and Lower Phrygia, he himself had often seen, in many places, stones in the shape of a bivalve, shells of the pecten order, impressions of scallop-shells, and a salt-marsh, and therefore was persuaded that these plains were once sea. Then Eratosthenes praises the opinion of Strato, who goes still further into the question of causes, because Strato says he believes the Euxine Sea formerly did not have its outlet at Byzantium, but the rivers which empty into the Euxine forced and opened a passage, and then the water was discharged into the Propontis and the Hellespont. The same thing, Strato says, happened in the Mediterranean basin also; for in this case the passage at the Pillars was broken through when the sea had been filled by the rivers, and at the time of the outrush of the water the places that had hitherto been covered with shoal-waters were left dry. Strato proposes as a cause of this, first, that the beds of the Atlantic and the Mediterranean are on different levels, and, secondly, that at the Pillars even at the present day a submarine ridge stretches across from Europe to Libya, indicating that the Mediterranean and the Atlantic could not have been one and the same formerly. The seas of the Pontus region, Strato continues, are very shallow, whereas the Cretan, the Sicilian, and the Sardinian Seas are very deep; for since the rivers that flow from the north and east are very numerous and very large, the seas there are being filled with mud, while the others remain deep; and herein also is the reason why the Pontus is sweetest, and why its outflow takes place in the direction of the inclination of its bed. Strato further says it is his point that the whole Euxine Sea will be silted up at some future period, if such inpourings continue; for even now the regions on the left side of the Pontus are already covered with shoal waters; for instance, Salmydessus, and the land at the mouth of the Ister, which sailors call "the Breasts," and the desert of Scythia; perhaps too the temple of Ammon was formerly on the sea, but is now situated in the interior because there has been an outpouring of the sea. Strato conjectures that the oracle of Ammon with good reason became so distinguished and so well-known as it is if it was situated on the sea, and that its present position so very far from the sea gives no reasonable explanation of its present distinction and fame; and that in ancient times Egypt was covered by the sea as far as the bogs about Pelusium, Mt. Casius, and Lake Sirbonis; at all events, even to‑day, when the salt-lands in Egypt are dug up, the excavations are found to contain sand and fossil-shells, as though the country had been submerged beneath the sea and the whole region round Mt. Casius and the so‑called Gerrha had once been covered with shoal water so that it connected with the Gulf of the Red Sea; and when the sea retired, these regions were left bare, except that the Lake Sirbonis remained; then the lake also broke through to the sea, and thus became a bog. In the same way, Strato adds, the beaches of the so‑called Lake Moeris more nearly resemble sea-beaches than river-banks. Now one may admit that a great part of the continents was once covered by water for certain periods and was then left bare again; and in the same way one may admit also that the whole surface of the earth now submerged is uneven, at the bottom of the sea, just as we might admit, of course, that the part of the earth above water, on which we live, is subject to all the changes mentioned by Eratosthenes himself; and therefore, so far as the argument of Xanthes is concerned, one cannot bring against it any charge of absurdity.
5 Against Strato, however, one might urge that, although there are many real causes of these changes, he overlooks them and suggests causes that do not exist; for he says their primary cause is that the beds of the Mediterranean Sea and of the Atlantic Ocean are not on the same level, and that their depth is not the same. But I reply that the cause of the rising and the falling of the sea, of its inundation of certain tracts of country, and of its subsequent retirement from them, is not to be sought for in the varying levels of the beds of the sea, in that some are lower and others higher, but in the fact that the beds of the sea themselves sometimes rise, and, on the other hand, sometimes sink, and in the fact that the sea rises or recedes along with its beds; for when the sea is lifted up, it will overflow, and when it is lowered, it will subside to its former level. Indeed, if what Strato says is true, then the overflow will necessarily follow every sudden increase in the volume of the sea; for instance, at every high tide of the sea or whenever the rivers are at their flood — in the one case the water having been brought in from other parts of the sea, in the other case the volume of water having been increased. But neither do the increases from the rivers thus cause a swelling of the sea, nor do the tides persist long enough to do so (they are not irregular, either), nor do they cause inundations either on the Mediterranean Sea or anywhere else. Therefore, it remains for us to find the cause in the floor of the sea, either that which underlies the sea or that which is temporarily flooded, but preferably the submarine floor. For the floor that is saturated with water is far more easily moved and is liable to undergo more sudden changes; for the air-element, which is the ultimate cause of all such occurrences, is greater there. But, as I have said, the immediate cause of such occurrences is that the beds of the sea themselves are sometimes elevated and sometimes undergo a settling process, and not that some of the beds are high, while others are less so. Strato, however, assumes this, believing that what happens in the case of rivers occurs also in the case of the sea, namely, that the flow is away from the high places; otherwise, he would not have suggested that the bed is the cause of the current at Byzantium, saying that the bed of the Euxine is higher than that of the Propontis and the sea next after the Propontis, and at the same time adding the reason, namely, that the deeps of the Euxine are being filled up by the mud which is carried down from the rivers, and are becoming shallow, and that, on this account, the current is outward. He applies the same reasoning to the Mediterranean Sea as a whole compared with the Atlantic Ocean, since, in his opinion, the Mediterranean Sea is making its bed higher than that which lies beneath the Atlantic Ocean; for the Mediterranean Sea, too, is being filled up with silt from many rivers, and is receiving a deposit of mud similar to that of the Euxine Sea. It should also be true, then, that the inflow at the Pillars and Calpe is similar to the inflow at Byzantium. But I pass this point by, for people will say that the same thing does occur here, but that the inflow is lost in the ebb and flow of the tides and thus escapes observation.
6 But what I wish to learn is this: supposing the bed of the Euxine Sea was lower than that of the Propontis and of the sea next after the Propontis before the opening of the outlet at Byzantium, what was there to prevent the Euxine from being filled up by the rivers, whether it was previously a sea or merely a lake greater than Lake Maeotis? If this point be conceded, then I shall go on to ask this question too: Is it not true that the water-levels of the Euxine and the Propontis were such that, so long as they remained the same, there could be no straining for an outflow, for the reason that resistance and pressure were equal, but that, as soon as the inner sea reached a higher level, it set up a strain and discharged its excess water? And is not this the reason why the outer sea became confluent with the inner sea and why it assumed the same level as the inner sea — regardless of whether the latter was originally a sea or once a lake and later a sea — simply because of its mingling with the inner sea and prevailing over it? For if this point be granted as well as the first, the outflow that now takes place would go on just the same, but it would not be away from a higher sea-bed, or from a sloping one, as Strato contended.
7 Now we must apply these principles to the whole of the Mediterranean Sea and to the Atlantic Ocean, finding the cause of the outflow not in their beds, nor in the sloping of their beds, but in the rivers. For according to Strato and Eratosthenes, it is not improbable that our whole Mediterranean Sea (even granting that in former times it was a lake) became flooded by the rivers, overflowed, and poured its waters out through the narrows at the Pillars as over a waterfall; and that the Atlantic Ocean, swollen ever more and more, was finally made confluent by it, and united with it on one sea-level; and that thus the Mediterranean basin was turned into a sea because the Atlantic prevailed over it. It is wholly contrary to physical science, however, to liken the sea to rivers; for the rivers are carried down a sloping course, whereas the sea has no slope. But the current through the straits is accounted for by another principle, and is not due to the fact that the mud carried down by the rivers silts up the deeps of the sea. For this silting up occurs only at the very mouths of the rivers, as for example the so‑called "Breasts" at the mouth of the Ister, the Scythian desert, and Salmydessus — where other violent streams also contribute to the result; and, at the mouths of the Phasis, the Colchian seaboard, which is sandy, low-lying and soft; and, at the mouths of the Thermodon and the Iris, the whole of Themiscyra, that plain of the Amazons, and the most of Sidene. The same is true of the other rivers also; for they all imitate the Nile in that they keep converting the channel just in front of them into land, some to a greater and others to a less extent; to a less extent those that do not bring down much mud, but to a greater extent those that flow for a great distance through a country with a soft soil and have many torrents as tributaries. To the latter class belongs the Pyramus, which has added much land to Cilicia, and it is to this fact that the following oracle refers: "Men that are yet to be will experience this at the time when the Pyramus of the silvery eddies shall silt up its sacred sea-beach and come to Cyprus." The Pyramus, making its course as a navigable stream from the midst of the plains of Cataonia, and then breaking a passage for itself into Cilicia through the gorges of the Taurus Mountains, empties into the strait that lies between Cilicia and Cyprus.
8 Now the reason why the alluvium brought down by the rivers does not reach the open sea in its forward course is that the sea, which is naturally refluent, drives it back again; for the sea is like animated beings, and, just as they inhale and exhale their breath unremittingly, so in like manner the sea too is subject to a certain recurrent motion that proceeds from itself and returns to itself unremittingly. This is apparent to any one who stands on the beach at the time when the waves break; for no sooner are one's feet washed than they are left bare by the waves, and then again they are washed, and this goes on unremittingly. And close upon the wash comes a wave also, which, however gentle it may be, possesses a certain increase of power as it rushes in, and casts all foreign matter out upon the land — "and casteth much tangle out along the sea." Now while this takes place to a greater extent when there is wind, yet it occurs both when there is a calm and when the winds blow from the land; for the wave is carried to the land none the less even against the wind, as though it were subject, along with the sea itself, to the sea's own motion. This is what Homer means when he says: "And goeth with arching crest about the promontories, and speweth the foaming brine afar," and "The shores cry aloud as the salt sea belches forth."
9 Accordingly, the onset of the wave has a power sufficient to expel foreign matter. They call this, in fact, a "purging" of the sea — a process by which dead bodies and bits of wreckage are cast out upon the land by the waves. But the ebb has not power sufficient to draw back into the deep sea a corpse, or a stick of wood, or even that lightest of substances, a cork (when once they have been cast by the wave upon the land) from the places on the shore that are near the sea, where they have been stranded by the waves. And so it comes about that both the silt and the water fouled by it are cast out by the waves, the weight of the silt coöperating with the wave, so that the silt is precipitated to the bottom near the land before it can be carried forward into the deep sea; in fact, even the force of the river ceases just a short distance beyond the mouth. So, then, it is possible for the sea, beginning at its beaches, to be entirely silted up, if it receives the inflow from the rivers uninterruptedly. And this would be the result even if we assume that the Euxine Sea is deeper than the Sea of Sardinia, which is said to be the deepest of all the seas that have been sounded — about one thousand fathoms, as Poseidonius states.
However, one might be rather disinclined to accept such an explanation, and so it is necessary for me to bring my discussion into closer connection with things that are more apparent to the senses and that, so to speak, are seen every day. Now deluges as we have seen, are caused by upheavals of the bed of the sea; and earthquakes, volcanic eruptions, and upheavals of the submarine ground raise the sea, whereas the settling of the bed of the sea lowers the sea. For it cannot be that burning masses may be raised aloft, and small islands, but not large islands; nor yet that islands may thus appear, but not continents. And in a similar way settlings in the bed of the sea, both great ones and small, may also occur, if it be true, as people say, that yawning abysses and engulfments of districts and villages have been caused by earthquakes — as happened in the case of Bura and Bizone and several other places; and as for Sicily, one might conjecture that it is not so much a piece broken away from Italy as that it was cast up from the deeps by the fire of Aetna and remained there; and the same is true both of the Lipari Islands and the Pithecussae.
But Eratosthenes is so simple that, although he is a mathematician, he will not even confirm the doctrine of Archimedes, who, in his treatise On Floating Bodies says that the surface of every liquid body at rest and in equilibrium is spherical, the sphere having the same centre as the earth — a doctrine that is accepted by every one who has studied mathematics at all. And so, although Eratosthenes himself admits that the Mediterranean Sea is one continuous sea, yet he does not believe that it has been brought under a law of one continuous surface, even in places that lie close together. And as authorities for such an ignorant opinion as this he summons engineers, although the mathematicians have declared that engineering is a branch of mathematics. For he says that Demetrius, too, attempted to cut through the Isthmus of Corinth in order to provide a passage for his fleets, but was prevented by the engineers, after they had taken measurements and reported to him that the sea in the Corinthian Gulf was higher than at Cenchreae, so that, if he should cut through the intervening land, the whole strait about Aegina, Aegina itself, and the neighbouring islands would be submerged, and the canal would not be useful, either. And Eratosthenes says that this is the reason why the narrow straits have strong currents, and in particular the strait of Sicily, which, he declares, behaves in a manner similar to the flow and the ebb of the ocean; for the current changes twice within the course of every day and night, and like the ocean, it floods twice a day and falls twice a day. Now corresponding to the flood-tide, he continues, is the current that runs down from the Tyrrhenian Sea to the Sicilian Sea as though from a higher water-level — and indeed this is called the "descending" current — and this current corresponds to the flood-tides in that it begins at the time of the rising and the setting of the moon, and it stops when the moon attains either meridian, namely, the meridian above the earth or that below the earth; on the other hand, corresponding to the ebb-tide is the return-current — and this is called the "ascending" current — which begins when the moon attains either meridian, just as the ebbs do, and stops when the moon attains the points of her rising and setting.
Now Poseidonius and Athenodorus have satisfactorily treated the question of the flow and ebb of the tides; but concerning the refluent currents of straits, which also involve a discussion that goes deeper into natural science than comports with the purpose of the present work, it is sufficient to say that neither does one principle account for the straits' having currents, the principle by which they are classified as straits (for if that were the case, the Strait of Sicily would not be changing its current twice a day, as Eratosthenes says it does, but the strait of Chalcis seven times a day, while the strait at Byzantium makes no change at all but continues to have its outflow only from the Pontus into the Propontis, and, as Hipparchus reports, even stands still sometimes), nor, if one principle should account for the currents, would the cause be what Eratosthenes alleges it to be, namely, that the two seas on the sides of a strait have different levels. Indeed this would not be the case with the rivers either, except when they have cataracts; but since they have cataracts, they are not refluent, but run continuously toward the lower level. And this, too, results on account of the fact that the stream and its surface are inclined. But who would say that a sea-surface is inclined? And particularly in view of the hypotheses by which the four bodies (which, of course, we also call "elements") are made spheres. And so not only is a strait not refluent, but it is also not subject to standing still without any current at all, since, although there is confluence therein of two seas, yet there is not merely one level, but two of them, one higher, the other lower. The case of the water, indeed, is not the same as that of the earth, which, being solid in character, has than shape accordingly; and therefore it has hollows that keep their shape, and elevations as well; but the water, through the mere p207influence of gravity, rides upon the earth and assumes the sort of surface which Archimedes says it does.
Eratosthenes adds to what he has said about Ammon and Egypt his opinion that Mt. Casius was once washed by the sea, and also that all the region where the so‑called Gerrha now is, was in every part covered with shoal-water since it was connected with the gulf of the Red Sea, and that it became uncovered when the seas came together. Now it is ambiguous to say that the region mentioned was covered with shoal-water since it was connected with gulf of the Red Sea, for "to be connected with" means either "to come near to" or "to touch"; so that, if we were referring to bodies of water, that phrase would mean, in the latter sense, that one body of water is confluent with another. My interpretation, however, is that the shoal-waters "came near to" the Red Sea as long as the narrows at the Pillars of Heracles were still closed, and that after the narrows had been broken through, the retirement of the shoal-water took place because the level of the Mediterranean Sea had been lowered by the outflow at the Pillars. But Hipparchus, interpreting the phrase "to be connected with" to be the same thing as "to be confluent with," that is, that our Mediterranean Sea "became confluent with" the Red Sea because of its being filled up with water, finds fault by asking why in the world it is that, at the time when our Mediterranean Sea, because of the outflow of its waters at the Pillars, underwent its change in that direction, it did not also cause the Red Sea, which had become confluent with it, to make the same change, and why in the world the Red Sea continued at the same level into being lowered with the Mediterranean? For, says he, even according to Eratosthenes himself the whole exterior sea is confluent, and consequently the western sea and the Red Sea form one sea. After saying this, Hipparchus adds his corollary: that the Sea outside the Pillars, the Red Sea, and the Mediterranean Sea, too, which has become confluent with the Red Sea, all have the same level.
But Eratosthenes replies to this that he has not said that the confluence with the Red Sea took place at the time the Mediterranean Sea had become filled, but merely that the Mediterranean Sea had come near to it; and, besides, that it does not follow from the notion of one continuous sea that it has the same height and the same level — just as the Mediterranean has not, and as most assuredly its waters at Lechaeum and those about Cenchreae have not. This very point Hipparchus himself makes in his book against Eratosthenes; since, then, he knows that such is the opinion of Eratosthenes, let him give some argument of his own against Eratosthenes, and let him not assume off-hand that, forsooth, if a man says the exterior sea is one, he at the same time affirms also that its level is everywhere the same.
Again, when Hipparchus says that the inscription on the dolphins, made by sacred ambassadors of Cyrene, is false, he gives an unconvincing reason when he says that although the founding of Cyrene falls within historical times, yet no historian has recorded that the oracle was ever situated on a sea. Well, what if no historian does record the fact, and yet, according to the evidence on which we base the conjecture that the region was once coast-land, the dolphins were in fact dedicated and the inscription was engraved by sacred ambassadors of Cyrene? Again, although Hipparchus has admitted that, along with the elevation of the bed of the sea, the sea itself was elevated, and that it inundated the country as far as the oracle, a distance of somewhat more than three thousand stadia from the sea, he does not admit the elevation of the sea to such a point that both the whole island of Pharos and the greater part of Egypt were covered — just as though so high an elevation of the sea were not sufficient to inundate these districts too! And again, after saying that if, he says the outbreak of the waters at the Pillars took place, the Mediterranean Sea was really filled to such an extent as Eratosthenes has stated, the whole of Libya and the greater part of Europe and Asia must first have been covered, he adds thereto that the Pontus would then have been confluent with the Adriatic in some places, for the reason that the Ister, as he supposes, branches off from the Pontus regions and thus flows into both seas, on account of the lie of the land. But neither does the Ister rise in the Pontus regions (on the contrary, it rises in the mountains above the Adriatic), nor does it flow into both seas, but into the Pontus alone, and it branches off near its mouths only. However, this mistake of Hipparchus is shared with him by some of his predecessors, who supposed that there was a river of the same name as the Ister, which branched off from it and emptied into the Adriatic, and that the tribe of Istrians, through whose territory this Ister flows, got their appellation from it, and that it was by this route that Jason made his return voyage from the land of the Colchians.
Now, in order to promote the virtue of not marvelling at such changes as I have declared to be responsible for deluges and for such operations of nature as I have spoken of in the case of Sicily, the islands of Aeolus, and the Pithecussae, it is worth while to set forth still other instances of things similar thereto that exist, or else have taken place, in other regions. For if a large number of such instances are placed in view, they will put a stop to one's amazement. But, as it is, the unfamiliar thing disturbs the senses and shews one's ignorance of natural occurrences and of the conditions of life generally; for instance, suppose one should tell the story of Thera and Therasia (islands situated in the roadstead between Crete and Cyrenaea, the first of which, Thera, is the mother-city of Cyrene), and of Egypt, and of many such places in Greece. For midway between Thera and Therasia fires broke forth from the sea and continued for four days, so that the whole sea boiled and blazed, and the fires cast up an island which was gradually elevated as though by levers and consisted of burning masses — an island with a stretch of twelve stadia in circumference. After the cessation of the eruption, the Rhodians, at the time of their maritime supremacy, were first to venture upon the scene and to erect on the island a temple in honour of Poseidon Asphalios. And in Phoenicia, says Poseidonius, on the occasion of an earthquake, a city situated above Sidon was swallowed up, and nearly two-thirds of Sidon itself was engulfed too, but not all at once, so that no considerable destruction of human life took place. The same operation of nature extended also over the whole of Syria, but with rather moderate force; and it also passed over to certain islands, both the Cyclades and Euboea, with the result that the fountains of Arethusa (a spring in Chalcis) were stopped up, though after many days they gushed up at another mouth, and the island did not cease from being shaken in some part or other until a chasm in the earth opened in the Lelantine Plain and vomited forth a river of fiery lava.
Though many writers have made collections of such instances, those collected by Demetrius of Scepsis will suffice since they are appropriately cited. For example, he mentions these verses of Homer: "And they came to the two fair-flowing springs, where two fountains rise of deep-eddying Scamander; the one floweth with warm water, while the other in summer floweth forth like hail"; and then he does not allow us to marvel if at the present time the spring of cold water is still there, whereas the one of hot water is no longer visible.a For, says he, we must lay the cause to the shutting off of the hot water. And he recalls on this point the words of Democles, who records certain great earthquakes, some of which long ago took place about Lydia and Ionia as far north as the Troad, and by their action not only were villages swallowed up, but Mt. Sipylus was shattered — in the reign of Tantalus. And lakes arose from swamps, and a tidal wave submerged the Troad. Again, the Egyptian Pharos was once an island of the sea, but now it has become, in a sense, a peninsula; and the same is true of Tyre and Clazomenae. And when I was residing in Alexandria, in Egypt, the sea about Pelusium and Mt. Casius rose and flooded the country and made an island of the mountain, so that the road by Mt. Casius into Phoenicia became navigable. Hence it is nothing to marvel at even if, at some time, the isthmus should be parted asunder or else undergo a settling process — I mean the isthmus that separates the Egyptian Sea from the Red Sea — and thus disclose a strait and make the outer sea confluent with the inner, just as happened in the case of the strait at the Pillars of Heracles. I have already said something about such things at the beginning of this treatise; and all these instances must needs contribute to one result, namely, to fix strong our belief in the works of nature and also in the changes that are being brought to pass by other agencies.
And as for the Peiraeus, it was because the Peiraeus was formerly an island and lay "over against" the mainland, they say,b that it got the name it has; but contrariwise Leucas, since the Corinthians cut a canal through the isthmus, has become an island, although it was formerly a headland. Indeed, it is with reference to Leucas, they say, that Laertes remarks: "As I was when I took Nericus, the well-built castle on the headland of the continent." Here, then, a partition cut by hand has been made; in other places man has built moles or bridges — just as, in the case of the island next to Syracuse, there is at the present time a bridge which connects it with the mainland, whereas formerly there was a mole, as Ibycus says, built of selected stones, which he calls stones "picked out." Then there are Bura and Helice; Bura disappeared in a chasm of the earth, and Helice was wiped out by a wave from the sea. And about Methone in the Hermionic Gulf a mountain seven stadia in height was cast up in consequence of a fiery eruption, and this mountain was unapproachable by day on account of the heat and the smell of sulphur, while at night it shone to a great distance and was so hot that the sea boiled for five stadia and was turbid even for twenty stadia, and was heaped up with massive broken-off rocks no smaller than towers. And again, by Lake Copaïs both Arne and Mideia were swallowed up, places which have been named by Homer in the Catalogue of Ships: "And they that possess Arne rich in vineyards, and they that possess Mideia." And by Lake Bistonis and by the lake which they now call Aphnitis certain cities of Thracians appear to have been overwhelmed; and some say cities of Trerans also, thinking they were neighbours of the Thracians. And, too, one of the Echinades Islands, which used to be called Artemita, has become part of the continent; and they say that still others of the little islands about the mouth of the Acheloüs have suffered the same change from the silting up of the sea by the river; and the rest of them too, as Herodotus says, are in process of fusion with the continent. Again, there are certain Aetolian promontories which were formerly islands; and Asteria has been changed, which the poet calls Asteris: "Now there is a rocky isle in the mid-sea, Asteris, a little isle; and there is a harbour therein with a double entrance, where ships may lie at anchor." But at the present time it has not even a good anchorage. Further, in Ithaca there is no cave, neither grotto of the Nymphs, such as Homer describes; but it is better to ascribe the cause to physical change rather than to Homer's ignorance or to a false account of the places to suit the fabulous element in his poetry. Since this matter, however, is uncertain, I leave it to the public to investigate.
Antissa was formerly an island, as Myrsilus says; and since Lesbos was formerly called Issa, it came about that this island was called Antissa; but now Antissa is a city of Lesbos. And some believe that Lesbos itself is a fragment broken off from Mt. Ida, just as Prochyta and Pithecussa from Misenum, Capri from the Promontory of Athene, Sicily from the district of Rhegium, and Ossa from Olympus. And it is a fact that changes of this sort have also occurred in the neighbourhood of these places. And, again, the River Ladon in Arcadia once ceased to flow. Duris says that Rhagae in Media has received its name because the earth about the Caspian Gates had been "rent" by earthquakes to such an extent that numerous cities and villages were destroyed, and the rivers underwent changes of various kinds. Ion says of Euboea in his satyr-drama Omphale: "The slender wave of Euripus hath separated the land of Euboea from Boeotia, in that by means of a strait it hath cut a projecting headland away."
Demetrius of Calatis, in his account of all the earthquakes that have ever occurred throughout all Greece, says that the greater part of the Lichades Islands and of Cenaeum was engulfed; the hot springs at Aedepsus and Thermopylae, after having ceased to flow for three days, began to flow afresh, and those at Aedepsus broke forth also at another source; at Oreus the wall next to the sea and about seven hundred of the houses collapsed; and as for Echinus and Phalara and Heracleia in Trachis, not only was a considerable portion of them thrown down, but the settlement of Phalara was overturned, ground and all. And, says he, something quite similar happened to the people of Lamia and of Larissa; and Scarphia, also, was flung up, foundations and all, and no fewer than seventeen hundred human beings were engulfed, and over half as many Thronians; again, a triple-headed wave rose up, one part of which was carried in the direction of Tarphe and Thronium, another part to Thermopylae, and the rest into the plain as far as Daphnus in Phocis; fountains of rivers were dried up for a number of days, and the Spercheiusº changed its course and made the roadways navigable, and the Boagrius was carried down a different ravine, and also many sections of Alope, Cynus, and Opus were seriously damaged, and Oeum, the castle above Opus, was laid in utter ruin, and a part of the wall of Elateia was broken down, and at Alponus, during the celebration of the Thesmophoria, twenty-five girls ran up into one of the towers at the harbour to get a view, the tower fell, and they themselves fell with it into the sea. And they say, also, of the Atalanta near Euboea that its middle portions, because they had been rent asunder, got a ship-canal through the rent, and that some of the plains were overflowed even as far as twenty stadia, and that a trireme was lifted out of the docks and cast over the wall.
Writers also add the changes resulting from the migrations of peoples, wishing to develop in us, to a still greater extent, that virtue of not marvelling at things (a virtue which is lauded by Democritus and all the other philosophers; for they put it in a class with freedom from dread and from perturbability and from terror). For instance: the migration of Western Iberians1to the regions beyond the Pontus and Colchis (regions which are separated from Armenia by the Araxes according to Apollodorus, but rather by the River Cyrus and the Moschican Mountains); and the migration of Egyptians to Ethiopia and Colchis; and that of Enetians from Paphlagonia to the Adriatic. This is what took place in the case of the Greek tribes also — Ionians, Dorians, Achaeans, and Aeolians; and the Aenianians that are now neighbours of the Aetolians used to live about Dotium and Mt. Ossa among the Perrhaebians; and, too, the Perrhaebians themselves are emigrants. And the present treatise is full of such instances. A number of them, to be sure, are matters even of ready knowledge to most people, but the emigrations of the Carians, Trerans, Teucrians, and Galatians, and likewise also the expeditions of the princes to lands far remote (I refer to Madys the Scythian, Tearko the Ethiopian, Cobus the Treran, Sesostris and Psammitichus the Egyptians, and to Persians from Cyrus to Xerxes) are not likewise matters of off-hand knowledge to everybody. And those Cimmerians whom they also call Trerans (or some tribe or other of the Cimmerians) often overran the countries on the right of the Pontus and those adjacent to them, at one time having invaded Paphlagonia, and at another time Phrygia even, at which time Midas drank bull's blood, they say, and thus went to his doom. Lygdamis, however, at the head of his own soldiers, marched as far as Lydia and Ionia and captured Sardes, but lost his life in Cilicia. Oftentimes both Cimmerians and Trerans made such invasions as these; but they say that the Trerans and Cobus were finally driven out by Madys, the king of the Scythians. Let these illustrations be given here, inasmuch as they involve matters of fact which have a bearing upon the entire compass of the world in general.
I now return to the points next in order, whence I digressed. First, as for the statement of Herodotus that there are no Hyperboreans because there are also no Hypernotians. Eratosthenes says the argument presented is absurd and like the following quibble: suppose some one should say "There are none who rejoice over the ills of others because there are also none who rejoice over the blessings of others." And, adds Eratosthenes, it so happens that there are also Hypernotians — at all events, Notus does not blow in Ethiopia, but farther north. But it is a marvellous thing if, although winds blow in every latitude, and although the wind that blows from the south is everywhere called Notus, there is any inhabited place where this is not the case. For, on the contrary, not only might Ethiopia have the same Notus as we have, but even the whole country further south as far as the equator might have it. However that may be, this charge should be laid against Herodotus, that he assumed that by "Hyperboreans" those peoples were meant in whose countries Boreas does not blow. For even if the poets do speak thus, rather mythically, those, at least, who expound the poets should give ear to sound doctrine, namely, that by "Hyperboreans" were meant merely the most northerly peoples. And as for limits, that of the northerly peoples is the north pole, while that of the southerly peoples is the equator; and the winds too have the same limits.
Next in order, Eratosthenes proceeds to reply to those whose stories are plainly fictitious and impossible, some of which are in the form of myths, and others in the form of history — persons whom it is not worth while to mention; neither should he, when treating a subject of this kind, have paid heed to persons who talk nonsense. Such, then, is Eratosthenes' course of argument in the First Book of his Commentaries. |
|
|
|
|
1 - 4 Eratosthenes is wrong P2 
(6 In his Second Book Eratosthenes undertakes a revision of the principles of geography; and he declares his own assumptions, to which, in turn, if there is any further revision to be made, I must undertake to supply it. Now his introduction of the principles of mathematics and physics into the subject is a commendable thing; also his remark that if the earth is sphere-shaped, just as the universe is, it is inhabited all the way round; and his other remarks of this nature. But as to the question whether the earth is as large as he has said, later writers do not agree with him; neither do they approve his measurement of the earth. Still, when Hipparchus plots the celestial phenomena for the several inhabited places, he uses, in addition, those intervals measured by Eratosthenes on the meridian through Meroë and Alexandria and the Borysthenes, after saying that they deviate but slightly from the truth. And, too, in Eratosthenes' subsequent discussion about the shape of the earth, when he demonstrates at greater length that not only the earth with its liquid constituent is sphere-shaped but the heavens also, he would seem to be talking about things that are foreign to his subject; for a brief statement is sufficient.
2 Next, in determining the breadth of the inhabited world, Eratosthenes says that, beginning at Meroë and measuring on the meridian that runs through Meroë, it is ten thousand stadia to Alexandria; and thence to the Hellespont about eight thousand one hundred; then to the Borysthenes five thousand; then to the parallel circle that runs through Thule (which Pytheas says is a six days' sail north of Britain, and is near the frozen sea) about eleven thousand five hundred more. Accordingly, if we add three thousand four hundred stadia more to the south of Meroë, in order to embrace the Island of the Egyptians, the Cinnamon-producing country, and Taprobane, we shall have thirty-eight thousand stadia.
3 However, with one exception, let all the distances of Eratosthenes be granted him — for they are sufficiently agreed upon; but what man of sense could grant his distance from the Borysthenes to the parallel of Thule? For not only has the man who tells about Thule, Pytheas, been found, upon scrutiny, to be an arch-falsifier, but the men who have seen Britain and Ierne do not mention Thule, though they speak of other islands, small ones, about Britain; and Britain itself stretches alongside of Celtica with a length about equal thereto, being not greater in length than five thousand stadia, and its limits are defined by the extremities of Celtica which lie opposite its own. For the eastern extremity of the one country lies opposite the eastern extremity of the other, and the western extremity of the one opposite the western of the other; and their eastern extremities, at all events, are near enough to each other for a person to see across from one to the other — I mean Cantium1and the mouths of the Rhine. But Pytheas declares that the length of Britain is more than twenty thousand stadia, and that Cantium is several days' sail from Celtica; and in his account both of the Ostimians and of what is beyond the Rhine as far as Scythia he has in every case falsified the regions. However, any man who has told such great falsehoods about the known regions would hardly, I imagine, be able to tell the truth about places that are not known to anybody.
4 The parallel through the mouth of the Borysthenes is conjectured by Hipparchus and others to be the same as that through Britain, from the fact that the parallel through Byzantium is the same as that through Massilia; for as to the relation of the dial-index to the shadow, which Pytheas has given for Massilia, this same relation Hipparchus says he observed at Byzantium, at the same time of the year as that mentioned by Pytheas. But it is not more than five thousand stadia from Massilia to the centre of Britain. Furthermore, if you were to proceed not more than four thousand stadia north from the centre of Britain you would find a region that is inhabitable only after a fashion (which region would be in the neighbourhood of Ierne); and so, as for the regions farther on, far out where Eratosthenes places Thule, you would find places no longer habitable. But by what guesswork Eratosthenes could say that the distance from the parallel through Thule to that through the mouth of the Borysthenes is eleven thousand five hundred stadia, I do not see.a
5 And since he entirely missed the breadth of the inhabited world, he has necessarily failed to guess its length also. For, in the first place, that the known length is more than double the known breadth is agreed to by the later writers as well as by the most accomplished of the early writers (I mean the distance from the extremities of India to the extremities of Iberia, double that from Ethiopia up to the parallel that runs by Ierne). Again, after Eratosthenes has determined the said breadth, namely, that from extreme Ethiopia up to the parallel of Thule, he extends the length beyond the due measure, in order to make the length more than double the aforesaid breadth. At all events he says that the narrowest part of India up to the river Indus measures sixteen thousand stadia (for the part of India that extends to its capes will increase this length by three thousand stadia); and the distance hence to the Caspian Gates, fourteen thousand; then, to the Euphrates, ten thousand, and from the Euphrates to the Nile five thousand, and on to its Canobic mouth thirteen hundred more; then, to Carthage, thirteen thousand five hundred; then, to the Pillars, at least eight thousand; there is, accordingly, he says, an excess of eight hundred stadia over seventy thousand stadia. We must still add, he says, the bulge of Europe outside the Pillars, which lies over against Iberia and leans westward, reaching not less than three thousand stadia; we must also add all the capes, but in particular that of the Ostimians, called Cabaeum, and the islands about it — the outermost of which, Uxisame,1Pytheas says, is a three days' sail distant. And after mentioning these last places, though all of them in their stretch add nothing to the length of the inhabited world, he has added the regions in the neighbourhood of the capes, of the Ostimians, of Uxisame, and of all the islands he names. (In fact, these places all lie towards the north and belong to Celtica, not to Iberia — or rather they are inventions of Pytheas.) And he adds to the aforesaid length-distances still other stadia, namely, two thousand on the west, and two thousand on the east, in order to keep the breadth from being more than half the length.
6 Again, attempting still further to appease us by saying that it is "in accordance with nature" to call the distance from east to west greater, he says it is "in accordance with nature" that from the east to the west the inhabited world is longer, and, "just as I have already stated in the manner of the mathematicians," he says, "it forms a complete circle, itself meeting itself; so that, if the immensity of the Atlantic Sea did not prevent, we could sail from Iberia to India along one and the same parallel over the remainder of the circle, that is, the remainder when you have subtracted the aforesaid distance, which is more than a third of the whole circle — if it be true that the circle that runs through Athens, along which I have made the said reckoning of stadia from India to Iberia, is less than two hundred thousand stadia in circuit." However, Eratosthenes is not happy in this statement, either; for although this argument might be used in the treatment of the temperate zone (that is, our zone) from the point of view of mathematics (since the inhabited world is a fraction of the temperate zone) yet in the treatment of the inhabited world — why we call "inhabited" the world which we inhabit and know; though it may be that in this same temperate zone there are actually two inhabited worlds, or even more, and particularly in the proximity of the parallel through Athens that is drawn across the Atlantic Sea. And again, by dwelling on his demonstration of the spheroidal shape of the earth he might meet with the same criticism as before. And in the same way also he does not cease to quarrel with Homer about the very same things.
7 Next, after saying that there has been much discussion about the continents, and that some divide them by the rivers (the Nile and the Tanaïs), declaring them to be islands, while others divide them by the isthmuses (the isthmus between the Caspian and the Pontic Seas, and the isthmus between the Red Sea and the Ecregma), and that the latter call the continents peninsulas, Eratosthenes then says that he does not see how this investigation can end in any practical result, but that it belongs only to persons who choose to live on a diet of disputation, after the manner of Democritus; for if there be no accurate boundaries — take the case of Colyttus and Melite — of stone posts, for example, or enclosures, we can say only this, "This is Colyttus," and "That is Melite," but we should not be able to point out the boundaries; and this is the reason also why disputes often arise concerning districts, such as the dispute between the Argives and the Lacedaemonians about Thyrea, and between the Athenians and the Boeotians about Oropus; and the Greeks named the three continents wrongly, because they did not look out upon the whole inhabited world, but merely upon their own country and that which lay directly opposite, namely, Caria, where Ionians and their immediate neighbours now live; but in time, ever advancing still further and becoming acquainted with more and more countries, they have finally brought their division of the continents to what it now is. The question, then, is whether the "first men" who divided the three continents by boundaries (to begin with Eratosthenes' last points, dieting upon disputation, not after the manner of Democritus, but after that of Eratosthenes) were those "first men" who sought to divide by boundaries their own country from that of the Carians, which lay opposite; or, did the latter have a notion merely of Greece, and of Caria and a bit of territory that is contiguous thereto, without having, in like manner, a notion of Europe or Asia, or of Libya, whereas the men of subsequent times, travelling over what was enough of the earth to suggest the notion of the inhabited world — are these the men, I say, who made the division into three parts? How, pray, could they have failed to make a division? And who, when speaking of three parts and calling each of the parts a continent, does not at the same time have a notion of the integer of which he makes his division into parts? But suppose he does not have a notion of the inhabited world, but should make his division of some part of it — of what part of the inhabited world, I ask, would anyone have said Asia was a part, or Europe, or a continent in general? Indeed these points of his have been crudely stated.
8 Still cruder is it, after he has said that he does not see what practical result there can be of the investigation of the boundaries, to cite Colyttus and Melite, and then turn round to the opposite side of the question. For if the wars about Thyrea and Oropus resulted through ignorance of the boundaries, then the separation of countries by boundaries is a thing that results in something practical. Or does Eratosthenes mean this, that in the case of the districts and, of course, of the several nations it is practical at once divide them by accurate boundaries, whereas in case of the continents it is superfluous? And yet, I answer, not even here is it any the less practical; for there might arise also in case of the continents a controversy between great rulers, for example, one ruler who held Asia and another who held Libya, as to which one of them really owned Egypt, that is to say, the so‑called "Lower" country of Egypt. Moreover, if anyone dismisses this example on account of its rarity, at all events it must be said that the continents are divided according to a process of grand division which also has relation to the whole inhabited world. In following that principle of division we must not worry about this point, either, namely, that those who have made the rivers the dividing lines leave certain districts without dividing lines, because the rivers do not reach all the way to the ocean and so do not really leave the continents as islands.
9 Now, towards the end of his treatise — after withholding praise from those who divide the whole multitude of mankind into two groups, namely, Greeks and Barbarians, and also from those who advised Alexander to treat the Greeks as friends but the Barbarians as enemies — Eratosthenes goes on to say that it would be better to make such divisions according to good qualities and bad qualities; for not only are many of the Greeks bad, but many of the Barbarians are refined — Indians and Arians, for example, and, further, Romans and Carthaginians, who carry on their governments so admirably. And this, he says, is the reason why Alexander, disregarding his advisers, welcomed as many as he could of the men of fair repute and did them favours — just as if those who have made such a division, placing some people in the category of censure, others in that of praise, did so for any other reason than that in some people there prevail the law-abiding and the political instinct, and the qualities associated with education and powers of speech, whereas in other people the opposite characteristics prevail! And so Alexander, not disregarding his advisers, but rather accepting their opinion, did what was consistent with, not contrary to, their advice; for he had regard to the real intent of those who gave him counsel. |
|
|
|
|
2 Countries of Earth. 5 143 1:50 
|
2 - 1 Eratosthenes is often wrong P3 
(6In the Third Book of his Geography Eratosthenes, in establishing the map of the inhabited world, divides it into two parts by a line drawn from west to east, parallel to the equatorial line; and as ends of this line he takes, on the west, the Pillars of Heracles, on the east, the capes and most remote peaks of the mountain-chain that forms the northern boundary of India. He draws the line from the Pillars through the Strait of Sicily and also through the southern capes both of the Peloponnesus and of Attica, and as far as Rhodes and the Gulf of Issus. Up to this point, then, he says, the said line runs through the sea and the adjacent continents (and indeed our whole Mediterranean Sea itself extends, lengthwise, along this line as far as Cilicia); then the line is produced in an approximately straight course along the whole Taurus Range as far as India, for the Taurus stretches in a straight course with the sea that begins at the Pillars, and divides all Asia lengthwise into two parts, thus making one part of it northern, the other southern; so that in like manner both the Taurus and the Sea from the Pillars up to the Taurus lie on the parallel of Athens.
After Eratosthenes has said that, he thinks he must needs make a complete revision of the early geographical map; for, according to it, he says, the eastern portions of the mountains deviate considerably towards the north, and India itself is drawn up along with it, and comes to occupy a more northerly position than it should. As proof of this he offers, first, an argument to this effect: the most southerly capes of India rise opposite to1 the regions about Meroë, as many writers agree, who judge both from the climatic conditions and from the celestial phenomena; and from the capes on to the most northerly regions of India at the Caucasus Mountains, Patrocles (the man who has particular right to our confidence, both on account of his worthiness of character and on account of his being no layman in geographical matters) says the distance is fifteen thousand stadia; but, to be sure, the distance from Meroë to the parallel of Athens is about that distance; and therefore the northerly parts of India, since they join the Caucasus Mountains, come to an end in this parallel.
3 Another proof which he offers is to this effect: the distance from the Gulf of Issus to the Pontic Sea is about three thousand stadia, if you go towards the north and the regions round about Amisus and Sinope, a distance as great as that which is also assigned to the breadth of the mountains; and from Amisus, if you bear towards the equinoctial sunrise, you come first to Colchis; and then you come to the passage which takes you over to the Hyrcanian Sea, and to the road next in order that leads to Bactra and to the Scythians on beyond, keeping the mountains on your right; and this line, if produced through Amisus westwards, runs through the Propontis and the Hellespont; and from Meroë to the Hellespont is not more than eighteen thousand stadia, a distance as great as that from the southern side of India to the parts round about the Bactrians, if we added three thousand stadia to the fifteen thousand, some of which belonged to the breadth of the mountains, the others to that of India.
4 As for this declaration of Eratosthenes, Hipparchus contradicts it by throwing discredit on the proofs. In the first place, says he, Patrocles is not trustworthy, since two men bear testimony against him, both Deïmachus and Megasthenes, who say that in some places the distance from the southern sea is twenty thousand stadia and in other places even thirty thousand; so these two men, at least, make such a statement, and the early maps agree with them. It is an incredible thing, of course, he thinks, that we have to trust Patrocles alone, in disregard of those whose testimony is so strong against him, and to correct the early maps throughout as regards the very point at issue, instead of leaving them as they are until we have more trustworthy information about them.
5 Now I think this reasoning of Hipparchus is open to censure on many grounds. In the first place, although Eratosthenes used many testimonies, he says that Eratosthenes uses only one — that of Patrocles. Who, pray, were the men that affirmed that the southern capes of India rose opposite to the regions of Meroë? And who the men that said the distance from Meroë up to the parallel of Athens was such a distance? And who, again, the men that gave the breadth of the Taurus Mountains, of the men that called the distance from Cilicia to the Amisus the same as that of this breadth? And who said as regards the distance from Amisus, through Colchis and Hyrcania up to Bactria and through the regions beyond Bactria which reach down to the eastern sea, that it was in a straight line and toward the equinoctial east and that it was alongside the mountains which you keep on your right hand? Or, again, as regards the distance towards the west in a straight course with this line, that it was towards the Propontis and the Hellespont? Why, Eratosthenes takes all these as matters actually established by the testimony of the men who had been in the regions, for he has read many historical treatises — with which he was well supplied if he had a library as large as Hipparchus says it was.
6 Further, the trustworthiness of Patrocles, itself, rests upon many testimonies; I refer to the Kings who had entrusted to him such an important office; to the men who followed him, to the men who oppose him, whom Hipparchus himself names; for the tests to which those men are subjected are but proofs of the statements of Patrocles. Neither does this statement of Patrocles lack plausibility, namely, that those who made the expedition with Alexander acquired only cursory information about everything, but Alexander himself made accurate investigations, since the men best acquainted with the country had described the whole of it for him; and this description was later presented to p261Patrocles (so Patrocles says) by Xenocles, Alexander's treasurer.
7 Hipparchus further says, in his Second Book, that Eratosthenes himself throws discredit on the trustworthiness of Patrocles, in consequence of Patrocles' disagreement with Megasthenes about the length of India on its northern side, which Megasthenes calls sixteen thousand stadia, whereas Patrocles affirms that it is a thousand short of that; for, having started from a certain "Itinerary" as basis, Eratosthenes distrusts both of them on account of their disagreement and holds to the "Itinerary." If, then, says Hipparchus, Patrocles is untrustworthy on account of the disagreement at that point, although the discrepancy is only a matter of a thousand stadia, how much more should we distrust him where the discrepancy is a matter of eight thousand stadia, as against two men, and that, too, men who agree with one another; for both of them call the breadth of India twenty thousand stadia, whereas Patrocles calls it twelve thousand?
8 My answer will be that it was not the bare disagreement with Megasthenes that Eratosthenes found fault with, but he found fault when he compared their disagreement with the harmony and trustworthiness of the "Itinerary." Yet we should not be surprised if one thing proves to be more trustworthy than another trustworthy thing, and if we trust the same man in some things, but distrust him in others, whenever greater certainty has been established from some other source. Again, it is ridiculous to think that the amount by which the authorities disagree makes the parties to the disagreement less trustworthy. Why, on the contrary, this is more likely to be the case where the matter of disagreement is slight; for if the matter of disagreement is but slight, error is more likely to result, not merely among ordinary writers, but even among writers who are somewhat superior to the other class; but where the matters of disagreement are considerable, though the ordinary man would go astray, the more scientific man would be less likely to do so, and for that reason he is more quickly trusted.
9 However, all who have written about India have proved themselves, for the most part, fabricators, but preëminently so Deïmachus; the next in order is Megasthenes; and then, Onesicritus, and Nearchus, and other such writers, who begin to speak the truth, though with faltering voice. I, too, had the privilege of noting this fact extensively when I was writing the "Deeds of Alexander." But especially do Deïmachus and Megasthenes deserve to be distrusted. For they are the persons who tell us about the "men that sleep in their ears," and the "men without mouths," and "men without noses"; and about "men with one eye," "men with long legs," "men with fingers turned backward"; and they revived, also, the Homeric story of the battle between the cranes and the "pygmies," who, they say, were three spans tall. These men also tell about the ants that mine gold and Pans with wedge-shaped heads; and about snakes that swallow oxen and stags, horns and all; and in these matters the one refutes the other, as is stated by Eratosthenes also. For although they were sent on an ambassadorial mission to Palimbothra (Megasthenes to Sandrocottus, Deïmachus to Allitrochades the son of Sandrocottus), still, as memoirs of their stay abroad, they have left behind such writings as these, being prompted to do so by — I know not what cause! Patrocles, however, is by no means that sort of man. And also the other witnesses whom Eratosthenes has used are not lacking in credibility.
For instance, if the meridian through Rhodes and Byzantium has been correctly drawn, then that through Cilicia and Amisus will have been correctly drawn too; for from many observations the parallel relation of lines is obvious whenever it is proved by test that there is no meeting in either direction.
Again, that the voyage from Amisus to Colchis lies in the direction of the equinoctial east is proved by the winds, by the seasons, by the crops, and by the risings of the sun themselves; and thus, in the same way, both the pass that leads over to the Caspian Sea and the road from there on to Bactra. For in many cases the way things appear to the sight and the agreement of all the testimony are more trustworthy than an instrument. Indeed, even the same Hipparchus, in taking the line from the Pillars on to Cilicia to be in a straight course and to be in the direction of the equinoctial east, did not depend wholly on instruments and geometrical calculations, but for the whole line from the Pillars on to the Strait he trusted the sailors. So that this statement of his is not good, either, where he says: "Since we cannot tell either the relation of the longest to the shortest, or of gnomon to shadow, along the mountain-side that runs from Cilicia on to India, neither can we say whether the slant of the mountains lies in a parallel line, but we must leave the line uncorrected, keep it aslant as the early maps give it." For, in the first place, "cannot tell" is the same thing as to withhold opinion, and the man who withholds opinion also inclines to neither side; but when Hipparchus bids us leave the line as the ancients give it, he inclines to that side. Rather would he be "keeping" the consistent course, if he also advised us not to treat geography at all; for we "cannot tell" in that way the positions of the other mountains, either — for instance, the Alps, the Pyrenees, and the Thracian, the Illyrian, and the German Mountains. But who would think the early geographers more trustworthy than those of later times, since in their map-drawing the ancients made all those blunders that Eratosthenes has rightly accused them of and not one of these blunders has been objected to by Hipparchus?
Again, the next remarks of Hipparchus are full of great difficulties. For example, see how many absurdities would arise if one should not disallow the statement that the southern capes of India rise opposite to the regions of Meroë, or the statement that the distance from Meroë to the mouth of the strait at Byzantium is about eighteen thousand stadia, but yet should make the distance from Southern India of the mountains thirty thousand stadia. Why, in the first place, if it be true that the parallel which runs through Byzantium is the same as that which runs through Massilia (as Hipparchus has stated, on the authority of Pytheas), and that the meridian which runs through Byzantium is the same as that through the Borysthenes (which very thing, also, Hipparchus approves), and if he also approves the statement that the distance from Byzantium to the Borysthenes is three thousand seven hundred stadia, then this last number would be the number of stadia from Massilia to the parallel that runs through the Borysthenes; which parallel, of course, would run through the sea-coast of Celtica, for on going about this number of stadia through Celtica you reach the ocean.
Again, since the Cinnamon-producing Country is the most remote inhabited country towards the south, as we know, and since, according to Hipparchus himself, the parallel that runs through it is the beginning of the temperate zone and of the inhabited world, and is distant from the equator about eight thousand eight hundred stadia; and further, since, as Hipparchus says, the parallel through the Borysthenes is thirty-four thousand stadia distant from the equator, there would remain twenty-five thousand two hundred stadia for the distance from the parallel that divides the torrid from the temperate zone to the parallel that runs through the Borysthenes and the sea-coast of Celtica. And yet the voyage from Celtica to the north is nowadays called the remotest voyage to the north; I mean the voyage to Ierne, which island not only lies beyond Britain but is such a wretched place to live in on account of the cold that the regions on beyond are regarded as uninhabitable. And Ierne is not farther from Celtica, he says, than five thousand stadia; so that about thirty thousand stadia all told, or perhaps a few more, would represent the breadth of the inhabited world.
Well, then, let us pass on to the country that rises opposite to the Cinnamon-producing Country and lies toward the East on the same parallel. This is the region about Taprobane.We have strong assurance that Taprobane is a large island in the open, which lies off India to the south. It stretches lengthwise in the direction of Ethiopia for more than five thousand stadia, as they say; and from it, they say, much ivory is brought to the markets of India, and also tortoise-shell and other merchandise. Now if we assign to this island a breadth that is proportional to its length, and if we add thereto the expanse of the sea between it and India, the sum would be a distance of not less than three thousand stadia — as much as the distance from the border of the inhabited world to Meroë — that is, if the capes of India are to rise opposite to Meroë; but it is more plausible to set down still more than three thousand stadia. So if you should add these three thousand stadia to the thirty thousand stadia which Deïmachus gives as the distance to the pass that leads over Bactriana and Sogdiana, then all these people would fall outside the inhabited world and the temperate zone. Who, pray, would venture to maintain this, when he hears of men of both ancient and modern times telling about the mild climate and the fertility, first of Northern India, and then of Hyrcania and Aria, and, next in order, of Margiana and Bactriana? For, although all these countries lies next to the northern side of the Taurus Range, and although Bactriana, at least, lies close to the pass that leads over to India, still they enjoy such a happy lot that they must be a very long way off from the uninhabitable part of the earth. In Hyrcania, at any rate, they say that the vine produces one metretes of wine, the fig-tree sixty medimni of figs, the wheat grows again from the waste seed of the stubble-field, bees have their hives in the trees, and honey drips from the leaves; and this is also true of Matiana, a province of Media, and of Sacasene and of Araxene, districts of Armenia. But in the case of the latter districts this is not equally amazing, if it be true that they lie further south than Hyrcania, and are superior to the rest of the country in mildness of climate; but in the case of Hyrcania it is more amazing. And in Margiana, they say, it is oftentimes found that the trunk of the grape-vine can be encircled only by the outstretched arms of two men, and that the cluster of grapes is two cubits long.a And they say that Aria also is similar, but that it even excels in good vintage, since there, at all events, the wine actually keeps for three generations in unpitched casks; and that Bactriana, too, which lies on the border of Aria, produces everything except olive-oil.
But if all the parts of these regions that are high and mountainous are also cold, we should not be amazed; for even in the southern latitudes the mountains are cold, and in general all high-lying lands, even if they be plateaux, are cold. At any rate, in Cappadocia the regions next to the Euxine are much farther north than those next to the Taurus; but Bagadaonia, an enormous plain which falls between the Argaeus Mountain and the Taurus Range, only scantily (if anywhere) produces fruit-trees, although it is three thousand stadia farther south than the Pontic Sea, whereas the suburbs of Sinope and Amisus and the greater part of Phanaroea are planted with olive-trees. And further, the River Oxus, which divides Bactriana from Sogdiana, is so easily navigable, they say, that the Indian merchandise packed over the mountains to it is easily brought down to the Hyrcanian Sea, and thence, on the rivers, to the successive regions beyond as far as the Pontus.
Now what comparable blessings of nature can you find round about the Borysthenes or in the part of Celtica that lies on the ocean, where the grape either does not grow at all, or else does not bear fruit? In the more southern districts of these countries, both on the Mediterranean Sea and in the regions about the Bosporus, the vine does bear fruit, but the grapes are small, and the vines are buried during the winter. The frosts are so severe at the mouth of Lake Maeotis that, at a certain spot where, in winter time, Mithridates' general conquered the barbarians in a cavalry engagement fought on the ice, he afterwards, in summer time, when the ice had melted, defeated the same barbarians in a naval engagement. And Eratosthenes brings forward, also, the following epigram from the temple of Asclepius at Panticapaeum, which was inscribed on the bronze water-jar that had been burst by freezing: "If any man is incredulous in regard to what happens in our country, let him look at this water-jar and know the truth; which, not as a fair offering unto God but as an illustration of our severe winters, has been dedicated by Stratius the priest." Since, therefore, the climatic conditions in the Asiatic regions that I have enumerated are not to be compared even with those at the Bosporus, nay, not even with those at Amisus and Sinope (which places one would call milder in climate than the regions at the Bosporus), those Asiatic regions could hardly be thrown on the same parallel with those about Borysthenes and with the country of the northernmost Celts. In fact, the Asiatic regions could hardly be in the same latitude as the regions about Amisus, Sinope, Byzantium, and Massilia, which are conceded to be thirty-seven hundred stadia farther south than the Borysthenes and the Celts.
Now if Deïmachus and his followers add to the thirty thousand stadia the distance to Taprobane and to the boundary of the torrid zone, which must be put at not less than four thousand stadia, they will thus be placing both Bactra and Aria outside the inhabited world in the regions that are thirty-four thousand stadia from the torrid zone — the number of stadia Hipparchus gives as the distance from the equator to the Borysthenes. And so Bactria and Aria will be thrown outside into the regions that are eight thousand eight hundred stadia farther north than the Borysthenes and Celtica — the number of stadia by which the equator is south of the circle that divides the torrid zone from the temperate; and this circle we say is drawn, in a general way, through the Cinnamon-producing Country. Now I myself was pointing out that the regions beyond Celtica as far as Ierne were scarcely habitable, and that this distance is not more than five thousand stadia; but this argument of Deïmachus declares that there is a habitable parallel of latitude three thousand eight hundred stadia still farther north than Ierne! Thus Bactra will be a very considerable distance farther north than even the mouth of the Caspian (or Hyrcanian) Sea; and this mouth is about six thousand stadia distant from the inmost part of the Caspian Sea and from the Armenian and Median mountains (and it seems to be a more northerly point than the coast-line itself that runs thence to India; and to offer a practicable route of circumnavigation from India, according to Patrocles, who was once governor of these regions). Accordingly, Bactriana stretches out still farther for a thousand stadia toward the north. But the Scythian tribes inhabit a much larger country than Bactriana, on beyond it, and they end at the northern sea; who, though it be as nomads, still manage to live. How, then, if even Bactra itself is thrown outside of the inhabited world, could this distance from the Caucasus up to the northern sea, measured on the meridian line through Bactra, be slightly more than four thousand stadia? If these stadia, then, be added to the stadia-reckoning from Ierne to the northern regions, they make the total distance through the uninhabitable region, on the stadia-reckoning made through Ierne, seven thousand eight hundred stadia. But if one should leave out the four thousand stadia, at least the very parts of Bactriana that are next to the Caucasus will be farther north than Ierne by three thousand eight hundred stadia, and farther north than Celtica and the Borysthenes by eight thousand eight hundred stadia.
Hipparchus says, at all events, that at the Borysthenes and Celtica, throughout the nights in summer-time, the light of the sun shines dimly, moving round from the west to the east, and at the winter solstice the sun ascends at most only nine cubits; but that among the people who are six thousand three hundred stadia distant from Massilia (people who live two thousand five hundred stadia north of Celtica, whom Hipparchus assumes still to be Celts, though I think they are Britons) this phenomenon is much more marked; and on the winter days there the sun ascends only six cubits, and only four cubits among the people who are distant from Massilia nine thousand one hundred stadia; and less than three cubits among the people who live on beyond (who, according to my argument, would be much farther north than Ierne). But Hipparchus, trusting Pytheas, puts this inhabited country in the regions that are farther south than Britain, and says that the longest day there has nineteen equinoctial hours, but that the longest day has eighteen hours where the sun ascends only four cubits; and these people, he says, are distant from Massilia nine thousand and one hundred stadia; and hence the most southerly of the Britons are more northerly than these people. Accordingly, they are either on the same parallel as the Bactrians that live near the Caucasus or on some parallel close to it; for, as I have stated, according to Deïmachus and his followers our result will be that the Bactrians that live near the Caucasus are more northerly than Ierne by three thousand eight hundred stadia; and if these stadia be added to those from Massilia to Ierne, we get twelve thousand five hundred stadia. Now who has ever reported in these regions (I mean the regions about Bactra) such a length of the longest days, or such a meridian height of the sun at the winter solstice? Why, all such phenomena are obvious to the eye even of a layman and do not require mathematical notation; so that many men, both of the early writers of Persian history and of their successors down to our own times, could have compiled them. Again, how could the above-mentioned happy lot of these regions be conceded to those regions that have such celestial phenomena? And so from what I have said it is clear how very cleverly Hipparchus contradicts the demonstration of Eratosthenes on the ground that the latter (although their objects of inquiry are in effect equivalent) were taking the object of inquiry for granted as an aid to his demonstration thereof!
And so, again, where Eratosthenes wishes to show that Deïmachus is a layman and inexperienced in such matters. For he says Deïmachus thinks that India lies between the autumnal equinox and the winter tropic, and contradicts the statement of Megasthenes that, in the southern parts of India, the Bears set and the shadows fall in the opposite directions, asserting that neither phenomenon takes place anywhere in India; and so, says Eratosthenes, when Deïmachus asserts this, he speaks ignorantly, since it is mere ignorance to think that the autumnal equinox differs from the vernal equinox in distance from the tropic, because both the circle and the rising of the sun are the same at the equinoxes; and, since the distance between the terrestrial tropic and the equator, between which Deïmachus places India, has been shown in the measurement of the earth to be much less than twenty thousand stadia, the result would be, even according to Deïmachus himself, precisely what Eratosthenes thinks, and not what Deïmachus thinks; for if India be twenty, or as much as thirty, thousand stadia in breadth it could not even fall within such a space. But if India has the breadth which Eratosthenes himself has given it, then it would fall therein; and that it is also a mark of the same ignorance for Deïmachus to assert that in no part of India do the Bears set or the shadows fall in the opposite directions, since, at any rate, if you proceed only five thousand stadia south from Alexandria the phenomena begin at once to take place. So Hipparchus is again not right in correcting Eratosthenes on that statement, because, in the first place, he interprets Deïmachus as saying "the summer tropic" instead of "the winter tropic," and because, in the second place, he thinks we should not use as a source of evidence on mathematics a man who is unversed in astronomy — just as if Eratosthenes were reckoning in the evidence of Deïmachus above that of other men and not merely following a common custom used in replying to men that talk foolishness. For one way of refuting men who contradict foolishly is to shew that the very declaration they make, whatever it may be, pleads our case.
Up to this point, then, having taken as hypothesis that the most southerly regions of India rise opposite the regions about Meroë — which many have stated and believed — I have pointed out the absurdities that result from this hypothesis. But since Hipparchus up to this point offers no objection to this hypothesis, and yet later on, in his Second Book, will not concede it, I must consider his argument on this matter, too. Well, then, he says: If only the regions that lie on the same parallel rise opposite each other, then, whenever the intervening distance is great, we cannot know this very thing, namely, that the regions in question are on the same parallel, without the comparison of the "climata" as observed at the other of the two places; now as for the "clima" at Meroë Philo, who wrote an account of his voyage to Ethiopia, reports that the sun is in the zenith forty-five days before the summer solstice and tells also the relations of the gnomon to the shadows both in the solstices and the equinoxes, and Eratosthenes agrees very closely with Philo; whereas nobody reports the "clima" in India, not even Eratosthenes himself; however, if it is really true that in India the Bears set (both of them, as they think, relying on Nearchus and his followers), then it is impossible that Meroë and the capes of India lie on the same parallel. Now if Eratosthenes joins those who have already so stated in reporting that both Bears do set, how can it be that nobody reports about the "clima" in India, not even Eratosthenes himself? For this statement concerns the "clima." But if Eratosthenes does not join them in the report, let him be free from the accusation. No, he does not join them in the report; nay, because Deïmachus said that the Bears do not set and the shadows do not fall in the opposite direction anywhere in India (as Megasthenes assumed), Eratosthenes convicts him of inexperience, regarding as falsehood the combined statement, wherein by the acknowledgement of Hipparchus himself the false statement that the shadows do not fall in the opposite direction is combined with that about the Bears. For even if the southern capes of India do not rise opposite to Meroë, Hipparchus clearly concedes that they are at least farther south than Syene.
In what follows, also, Hipparchus, in attempting proofs on the same questions, either states again the same things that I have already disproved, or employs additional false assumptions, or appends conclusions that do not follow. In the first place, take the statement p293of Eratosthenes that the distance from Babylon to Thapsacus is four thousand eight hundred stadia, and thence northwards to the Armenian Mountains two thousand one hundred: it does not follow from this that the distance from Babylon measured on the meridian through it to the northern mountains is more than six thousand stadia. Secondly, Eratosthenes does not say that the distance from Thapsacus to the mountains is two thousand one hundred stadia, 78but that there is a remainder of that distance which has not been measured; and hence the ensuing attack, made from an assumption not granted, could not result in a valid conclusion. And, thirdly, Eratosthenes has nowhere declared that Thapsacus lies north of Babylon more than four thousand five hundred stadia.
Next, still pleading for the early maps, Hipparchus does not produce the words of Eratosthenes in regard to the Third Section, but for his own gratification invented his statement, making it easy to overthrow. For Eratosthenes, pursuing his aforementioned thesis about the Taurus and the Mediterranean Sea, beginning at the Pillars, divides the inhabited world by means of this line into two divisions, and calls them respectively the Northern Division and the Southern Division, and then attempts to cut each of these divisions again into such sections as are possible; and he calls these sections "Sphragides." And so, after calling India Section First of the Southern Division, and Ariana Section Second, since they had contours easy to sketch, he was able to represent not only length and breadth of both sections, but, after a fashion, shape also, as would a geometrician. In the first place, India, he says, is rhomboidal, because, of its four sides, two are washed by seas (the southern and the eastern seas) which form shores without very deep gulfs; and because the remaining sides are marked, one by the mountain and the other by the river, and because on these two sides, also, the rectilinear figure is fairly well preserved. Secondly, Ariana. Although he sees that it has at least three sides well-suited to the formation of the figure of a parallelogram, and although he cannot mark off the western side by mathematical points, on account of the fact that the tribes there alternate with one another, yet he represents that side by a sort of line that begins at the Caspian Gates and ends at the capes of Carmania that are next to the Persian Gulf. Accordingly, he calls this side "western" and the side along the Indus "eastern," but he does not call them parallel; neither does he call the other two sides parallel, namely, the one marked by the mountain, and the one marked by the sea, but he merely calls them "the northern" and "the southern" sides.
And so, though he represents the Second Section merely by a rough outline, he represents the Third Section much more roughly than the Second — and for several reasons. First is the reason already mentioned, namely, because the side beginning at the Caspian Gates and running to Carmania (the side common to the Second and Third Sections) has not been determined distinctly; secondly, because the Persian Gulf breaks into the southern side, as Eratosthenes himself says, and therefore he has been forced to take the line beginning at Babylon as though it were a straight line running through Susa and Persepolis to the frontiers of Carmania and Persis, on which he was able to find a measured highway, which was slightly more than nine thousand stadia, all told. This side Eratosthenes calls "southern," but he does not call it parallel to the northern side. Again, it is clear that the Euphrates, by which he marks off the western side, is nowhere near a straight line; but after flowing from the mountains towards the south, it then turns eastward, and then southward again to the point where it empties into the sea. And Eratosthenes makes clear the river's lack of straightness when he indicates the shape of Mesopotamia, which results from the confluence of the Tigris and the Euphrates — "like a galley" as he says. And besides, as regards the stretch from Thapsacus to Armenia — Eratosthenes does not even know, as a distance that has been wholly measured, the western side that is marked off by the Euphrates; nay, he says he does not know how great is the stretch next to Armenia and the northern mountains, from the fact that it is unmeasured. For all these reasons, therefore, he says he represents the Third Section only in rough outline; indeed, he says that he collected even the distances from many writers who had worked out the itineraries — some of which he speaks of as actually without titles. So, then, Hipparchus would seem to be acting unfairly when he contradicts with geometrical accuracy a mere rough outline of this nature, instead of being grateful, as we should be, to all those who have reported to us in any way at all the physiography of the regions. But when Hipparchus does not even take his geometrical hypotheses from what Eratosthenes says, but fabricates on his own account, he betrays his spirit of jealousy still more obviously.
Now Eratosthenes says that it is only thus, "in a rough-outline way," that he has represented the Third Section, with its length of ten thousand stadia from the Caspian Gates to the Euphrates. And then, in making subdivisions of this length, he sets down the measurements just as he found them already assigned by others, after beginning in the inverse order at the Euphrates and its passage at Thapsacus. Accordingly, for the distance from the Euphrates to the Tigris, at the point where Alexander crossed it, he lays off two thousand four hundred stadia; thence to the several places in succession, through Gaugamela, the Lycus, Arbela, and Ecbatana (the route by which Darius fled from Gaugamela to the Caspian Gates) he fills out the ten thousand stadia, and has a surplus of only three hundred stadia. This, then, is the way he measures the northern side, not having first put it parallel with the mountains, or with the line that runs through the Pillars, Athens, and Rhodes. For Thapsacus lies at a considerable distance from the mountains, and the mountain-range and the highway from Thapsacus meet at the Caspian Gates. — And these are the northern portions of the boundary of the Third Section.
After having thus represented the northern side, Eratosthenes says it is not possible to take the southern side as along the sea, because the Persian Gulf breaks into it; but, says he, from Babylon to Susa and Persepolis to the frontiers of Persis and Carmania, it is nine thousand two hundred stadia — and this he calls "southern side," but he does not call the southern side parallel to the northern. As to the difference in the lengths of the estimated northern and southern sides, he says it results from the fact that the Euphrates, after having flowed southwards to a certain point, makes a considerable bend towards the east.
Of the two transverse sides Eratosthenes speaks of the western first; and what the nature of this side is, whether it is one line or two, is a matter open to consideration. For from the passage at Thapsacus, he says, along the Euphrates to Babylon, it is four thousand eight hundred stadia, and thence to the outlet of the Euphrates and the city of Teredon, three thousand; but as regards the distances from Thapsacus northward, the stadia have been measured up to the Armenian Gates and amount to about one thousand one hundred; whereas the stadia through Gordyene and Armenia are still unmeasured, and so for this reason he leaves them out of consideration. But of the side on the east, that part which runs through Persis lengthwise from the Red Sea, approximately toward Media and the north, is, he thinks, no less than eight thousand stadia (though, if reckoned from certain promontories, even above nine thousand stadia); and the remaining part, through Paraetaceneand Media to the Caspian p305Gates, about three thousand stadia. The Tigris and the Euphrates, he says, flow from Armenia southwards; and then, as soon as they pass the mountains of Gordyene, they describe a great circle and enclose a considerable territory, Mesopotamia; and then they turn toward the winter rising of the sunand the south, but more so the Euphrates; and the Euphrates, after becoming ever nearer to the Tigris in the neighbourhood of the Wall of Semiramis and a village called Opis (from which village the Euphrates was distant only about two hundred stadia), and, after flowing through Babylon, empties into the Persian Gulf. "So it comes to pass," he says, "that the shape of Mesopotamia and Babylonia is like that of a galley." Such, then, are the statements which Eratosthenes has made.
Now, as regards the Third Section, although there are certain other errors which Eratosthenes makes — and I shall discuss these — still he does not err at all in the matters for which Hipparchus reproaches him. Let us see what Hipparchus says. In his desire to establish his initial statement, namely, that we must not shift India farther to the south, as Eratosthenes requires, he says it will be particularly obvious from Eratosthenes' own utterances that we must not do so; for after first saying that the Third Section is marked off on its northern side by the line drawn from the Caspian Gates to the Euphrates, a distance of ten thousand stadia, Eratosthenes adds, later on, that the southern side, which runs from Babylon to the frontiers of Carmania, is slightly more than nine thousand stadia in length, and the side on the west from Thapsacus along the Euphrates to Babylon is four thousand eight hundred stadia, and, next, from Babylon to the outlet of the Euphrates is three thousand stadia, and as for the distances north of Thapsacus, one of them has been measured off as far as one thousand one hundred stadia, while the remainder is still unmeasured. Then, says Hipparchus, since the northern side of the Third Section is about ten thousand stadia, and since the line parallel thereto, straight from Babylon to the eastern side, was reckoned by Eratosthenes at slightly more than nine thousand stadia, it is clear that Babylon is not much more than a thousand stadia farther east than the passage at Thapsacus.
My reply will be: If, with geometrical precision, we took the Caspian Gates and the frontiers of Carmania and Persis as upon the same straight meridian, and if we drew the line to Thapsacus and the line to Babylon at right angles with the said straight meridian, then that conclusion of Hipparchus would be valid. Indeed, the line through Babylon, if further produced as far as the straight meridian through Thapsacus, would, to the eye, be equal — or at all events approximately equal — to the line from the Caspian Gates to Thapsacus; and hence Babylon would come to be farther east than Thapsacus by as much as the line from the Caspian Gates to Thapsacus exceeds the line from the Carmanian frontiers to Babylon! But, in the first place, Eratosthenes has not spoken of the line that bounds a western side of Ariana as lying on a meridian; nor yet of the line from the Caspian Gates to Thapsacus as at right angles with the meridian line through the Caspian Gates, but rather of the line marked by the mountain-range, with which line the line to Thapsacus forms an acute angle, since the latter has been drawn down from the same point as that from which the mountain-line has been drawn. In the second place, Eratosthenes has not called the line drawn to Babylon from Carmania parallel to the line drawn to Thapsacus; and even if it were parallel, but not at right angles with the meridian line through the Caspian Gates, no advantage would accrue to the argument of Hipparchus.
But after making these assumptions off-hand, and after showing, as he thinks, that Babylon, according to Eratosthenes, is farther east than Thapsacus by slightly more than a thousand stadia, Hipparchus again idly fabricates an assumption for use in his subsequent argument; and, he says, if we conceive a straight line drawn from Thapsacus towards the south and a line perpendicular to it from Babylon, we will have a right-angled triangle, composed of the side that extends from Thapsacus to Babylon, of the perpendicular drawn from Babylon to the meridian line through Thapsacus, and of the meridian itself through Thapsacus. Of this triangle he makes the line from Thapsacus to Babylon the hypotenuse, which he says is four thousand eight hundred stadia; and the perpendicular from Babylon to the meridian line through Thapsacus, slightly more than a thousand stadia — the amount by which the line to Thapsacus exceeded the line up to Babylon;and then from these sums he figures the other of the two lines which form the right angle to be many times longer than the said perpendicular. And he adds to that line the line produced northwards from Thapsacus up to the Armenian mountains, one part of which Eratosthenes said had been measured and was one thousand one hundred stadia, but the other part he leaves out of consideration as unmeasured. Hipparchus assumes for the latter part a thousand stadia at the least, so that the sum of the two parts amounts to two thousand one hundred stadia; and adding this sum to his straight-line side of the triangle, which is drawn to meet its perpendicular from Babylon, Hipparchus computes a distance of several thousand stadia, namely, that from the Armenian Mountains, or the parallel that runs through Athens, to the perpendicular from Babylon — which perpendicular he lays on the parallel that runs through Babylon. At any rate, he points out that the distance from the parallel through Athens to that through Babylon is not more than two thousand four hundred stadia, if it be assumed that the whole meridian is the number of stadia in length that Eratosthenes says; and if this is so, then the mountains of Armenia and those of the Taurus could not lie on the parallel that runs through Athens, as Eratosthenes says they do, but many thousand stadia farther north, according to Eratosthenes' own statements. At this point, then, in addition to making further use of his now demolished assumptions for the construction of his right-angled triangle, he also assumes this point that is not granted, namely, that the hypotenuse — the straight line from Thapsacus to Babylon — is within four thousand eight hundred stadia. For Eratosthenes not only says that this route is along the Euphrates, but when he tells us that Mesopotamia, including Babylonia, is circumscribed by a great circle, by the Euphrates and the Tigris, he asserts that the greater part of the circumference is described by the Euphrates: consequently, the straight line from Thapsacus to Babylon 83could neither follow the course of the Euphrates, nor be, even approximately, so many stadia in length. So his argument is overthrown. And besides, I have already stated that, if we grant that two lines are drawn from the Caspian Gates, one to Thapsacus, the other to that part of the Armenian Mountains that corresponds in position to Thapsacus (which, according to Hipparchus himself, is distant from Thapsacus at the least two thousand one hundred stadia), it is impossible for both these lines to be parallel either to each other or to the line through Babylon, which Eratosthenes called "southern side." Now because Eratosthenes could not speak of the route along the mountain-range as measured, he spoke of only the route from Thapsacus to the Caspian Gates as measured, and he added the words "roughly speaking"; moreover, since he only wished to tell the length of the country between Ariana and the Euphrates, it did not make much difference whether he measured one route or the other. But Hipparchus, when he tacitly assumes that the lines are spoken of by Eratosthenes as parallel, would seem to charge the man with utterly childish ignorance. Therefore, I must dismiss these arguments of his as childish.
But the charges which one might bring against Eratosthenes are such as follow. Just as, in surgery, amputation at the joints differs from unnatural piecemeal amputation (because the former takes off only the parts that have a natural configuration, following some articulation of joints or a significant outline — the meaning in which Homer says, "and having cut him up limb by limb" — whereas the latter follows no such course), and just as it is proper for us to use each kind of operation if we have regard to the proper time and the proper use of each, just so, in the case of geography, we must indeed make sections of the parts when we go over them in detail, but we must imitate the limb-by‑limb amputations rather than the haphazard amputations. For only thus it is possible to take off the member that is significant and well-defined, the only kind of member that the geographer has any use for. Now a country is well-defined when it is possible to define it by rivers or mountains or sea; and also by a tribe or tribes, by a size of such and such proportions, and by shape where this is possible. But in every case, in lieu of a geometrical definition, a simple and roughly outlined definition is sufficient. So, as regards a country's size, it is sufficient if you state its greatest length and breadth (of the inhabited world, for example, a length of perhaps seventy thousand stadia, a breadth slightly less than half the length); and as regards shape, if you liken a country to one of the geometrical figures (Sicily, for example, to a triangle), or to one of the other well-known figures (for instance, Iberia to an oxhide, the Peloponnesus to a leaf of a plane-tree). And the greater the territory you cut into sections, the more rough may be the sections you make.
Now the inhabited world has been happily divided by Eratosthenes into two parts by means of the Taurus Range and the sea that stretched to the Pillars. And in the Southern Division: India, indeed, has been well-defined in many ways, by a mountain, a river, a sea, and by a single term, as of a single ethnical group — so that Eratosthenes rightly calls it four-sided and rhomboidal. Ariana, however, has a contour that is less easy to trace because its western side is confused, but still it is defined by the three sides, which are approximately straight lines, and also by the term Ariana, as of a single ethnical group. But the Third Section is wholly untraceable, at all events as defined by Eratosthenes. For, in the first place, the side common to it and Ariana is confused, as I have previously stated. And the southern side has been taken very inaccurately; for neither does it trace a boundary of this section, since it runs through its very centre and leaves out many districts in the south, nor does it represent the section's greatest length (for the northern side is longer), nor does the Euphrates form its western side (it would not do so even if its course lay in a straight line), since its extremities do not lie on the same meridian. In fact, how can this side be called western rather than southern? And, quite apart from these objections, since the distance that remains between this line and the Cilician and Syrian Sea is slight, there is no convincing reason why the section should not be extended thereto, both because Semiramis and Ninus are called Syrians (Babylon was founded and made the royal residence by Semiramis, and Nineveh by Ninus, this showing that Nineveh was the capital of Syria) and because up to the present moment even the language of the people on both sides of the Euphrates is the same. However, to rend asunder so famous a nation by such a line of cleavage in this region, and to join the parts thus dissevered to the parts that belong to other tribes, would be wholly improper. Neither, indeed, could Eratosthenes allege that he was forced to do this by considerations of size; for the addition of the territory that extends up to the sea would still not make the size of the section equal to that of India, nor, for that matter, to that of Ariana, not even if it were increased by the territory that extends up to the confines of Arabia Felix and Egypt. Therefore it would have been much better to extend the Third Section to these limits, and thus, by adding so small a territory that extends to the Syrian Sea, to define the southern side of the Third Section as running, not as Eratosthenes defined it, nor yet as in a straight line, but as following the coast-line that is on your right hand as you sail from Carmania into and along the Persian Gulf up to the mouth of the Euphrates, and then as following the frontiers of Mesene and Babylonia, which form the beginning of the Isthmus that separates Arabia Felix from the rest of the continent; then, next, as crossing this Isthmus itself, and as reaching to the recess of the Arabian Gulf and to Pelusium and even beyond to the Canobic mouth of the Nile. So much for the southern side; the remaining, or western, side would be the coast-line from the Canobic mouth of the Nile up to Cilicia.
The Fourth Section would be the one composed of Arabia Felix, the Arabian Gulf, all Egypt, and Ethiopia. Of this section, the length will be the space bounded by two meridian lines, of which lines the one is drawn through the most western point on the section and the other through the most eastern point. Its breadth will be the space between two parallels of latitude, of which the one is drawn through the most northern point, and the other through the most southern point; for in the case of irregular figures whose length and breadth it is impossible to determine by sides, we must in this way determine their size. And, in general, we must assume that "length" and "breadth" are not employed in the same sense of a whole as of a part. On the contrary, in case of a whole the greater distance is called "length," and the lesser, "breadth" but, in case of a part, we call "length" any section of a part that is parallel to the length of the whole — no matter which of the two dimensions is the greater, and no matter if the distance taken in the breadth be greater than the distance taken in the length. Therefore, since the inhabited world stretches lengthwise from east to west and breadthwise from north to south, and since its length is drawn on a line parallel to the equator and its breadth on a meridian line, we must also, in case of the parts, take as "lengths" all the sections that are parallel to the length of the inhabited world, and as "breadths" all the sections that are parallel to its breadth. For by this method we can better indicate, firstly, the size of the inhabited world as a whole, and, secondly, the position and the shape of its parts; because, by such comparison, it will be clear in what respects the parts are deficient and in what respects they are excessive in size.
Now Eratosthenes takes the length of the inhabited world on the line that runs through the Pillars, the Caspian Gates, and the Caucasus, as though on a straight line; and the length of his Third Section on the line that runs through the Caspian Gates and Thapsacus; and the length of his Fourth Section on the line that runs through Thapsacus and Heroönpolis to the region between the mouths of the Nile — a line which must needs come to an end in the regions near Canobus and Alexandria; for the last mouth of the Nile, called the Canobic or Heracleotic mouth, is situated at that point. Now whether he places these two lengths on a straight line with each other, or as though they formed an angle at Thapsacus, it is at any rate clear from his own words that he does not make either line parallel to the length of the inhabited world. For he draws the length of the inhabited world through the Taurus Range and the Mediterranean Sea straight to the Pillars on a line that passes through the Caucasus, Rhodes, and Athens; and he says that the distance from Rhodes to Alexandria on the meridian that passes through those places is not much less than four thousand stadia; so that also the parallels of latitude of Rhodes and Alexandria would be just this distance apart. But the parallel of latitude of Heroönpolis is approximately the same as that of Alexandria, or, at any rate, more to the south than the latter; and hence the line that intersects both the parallel of latitude of Heroönpolis and that of Rhodes and the Caspian Gates, whether it be a straight line or a broken line, cannot be parallel to either. Accordingly, the lengths are not well taken by Eratosthenes. And, for that matter, the sections that stretch through the north are not well taken by him.
But let us first return to Hipparchus and see what he says next. Again fabricating assumptions on his own account he proceeds with geometrical precision to demolish what are merely the rough estimates of Eratosthenes. He says that Eratosthenes calls the distance from Babylon to the Caspian Gates six thousand seven hundred stadia, and to the frontiers of Carmania and Persis more than nine thousand stadia on a line drawn straight to the equinoctial east, and that this line comes to be perpendicular to the side that is common to the Second and the Third Sections, and that, therefore, according to Eratosthenes, a right-angled triangle is formed whose right angle lies on the frontiers of Carmania and whose hypotenuse is shorter than one of the sides that enclose the right angle; accordingly, adds Hipparchus, Eratosthenes has to make Persis a part of his Second Section! Now I have already stated in reply to this that Eratosthenes neither takes the distance from Babylon to Carmania on a parallel, nor has he spoken of the straight line that separates the two sections as a meridian line; and so in this argument Hipparchus has made no point against Eratosthenes. Neither is his subsequent conclusion correct. For, because Eratosthenes had given the distance from the Caspian Gates to Babylon as the said six thousand nine hundred stadia, and the distance from Babylon to Susa as three thousand four hundred stadia, Hipparchus, again starting from the same hypotheses, says that an obtuse-angled triangle is formed, with its vertices at the Caspian Gates, Susa and Babylon, having its obtuse angle at Susa, and having as the lengths of it sides the distances set forth by Eratosthenes. Then he draws his conclusion, namely, that it will follow according to these hypotheses that the meridian line that runs through the Caspian Gates will intersect the parallel that runs through Babylon and Susa at a point further west than the intersection of the same parallel with the straight line that runs from the Caspian Gates to the frontiers of Carmania and Persis by more than four thousand four hundred stadia; and so the line that runs through the Caspian Gates and will lean in a direction midway between the south and the equinoctial east; and that the Indus River will be parallel to this line, and that consequently this river, also, does not flow south from the mountains as Eratosthenes says it does, but between the south and the equinoctial east, precisely as it is laid down on the early maps. Who, pray, will concede that the triangle now formed by Hipparchus is obtuse-angled without also conceding that the triangle that comprehends it is right-angled? And who will concede that one of the sides which enclose the obtuse angle (the line from Babylon to Susa) lies on a parallel of latitude, without also conceding that the whole line on to Carmania does? And who will concede that the line drawn from the Caspian Gates to the frontiers of Carmania is parallel to the Indus? Yet without these concessions the argument of Hipparchus would be void. And it is without these concessions that Eratosthenes has made his statement that the shape of India is rhomboidal; and just as its eastern side has been stretched considerably eastwards (particularly at its extreme cape, which, as compared with the rest of the sea-board, is also thrown farther southwards, so, too, the side along the Indus has been stretched considerably eastwards.
In all these arguments Hipparchus speaks as a geometrician, though his test of Eratosthenes is not convincing. And though he prescribed the principles of geometry for himself, he absolves himself from them by saying that if the test showed errors amounting to only small distances, he could overlook them; but since Eratosthenes' errors clearly amount to thousands of stadia, they cannot be overlooked; and yet, continues Hipparchus, Eratosthenes himself declares that the differences of latitude are observable even within an extent of four hundred stadia; for example, between the parallels of Athens and Rhodes. Now the practice of observing differences of latitude is not confined to a single method, but one method is used where the difference is greater, another where it is lesser; where it is greater, if we rely on the evidence of the eye itself, or of the crops, or of the temperature of the atmosphere, in our judgment of the "climata"; but where it is lesser, we observe the difference by the aid of sun-dials and dioptrical instruments. Accordingly, the taking of the parallel of Athens and that of Rhodes and Caria with the sun-dial showed perceptibly (as is natural when the distance is so many stadia) the difference in latitude. But when the geographer, in dealing with a breadth of three thousand stadia and with a length of forty thousand stadia of mountain plus thirty thousand stadia of sea, takes his line from west to equinoctial east, and names the two divisions thus made the Southern Division and the Northern Division, and calls their parts "plinthia" or "sphragides," we should bear in mind what he means by these terms, and also by the terms "sides that are northern" and "that are southern," and again, "sides that are western" and "that are eastern." And if he fails to notice that which amounts to a very great error, let him be called to account therefor (for that is just); but as regards that which amounts only to a slight error, even if he has failed to notice it, he is not to be condemned. Here, however, no case is made out against Eratosthenes on either ground. For no geometrical proof would be possible where the cases involve so great a breadth of latitude; nor does Hipparchus, even where he attempts geometrical proof, use admitted assumptions, but rather fabrications which he has made for his own use.
Hipparchus discusses Eratosthenes' Fourth Section better; though here, too, he displays his propensity for fault-finding and his persistent adherence to the same, or nearly the same, assumptions. He is correct in censuring Eratosthenes for this, namely, for calling the line from Thapsacus to Egypt the length of this section — which is as if one should call the diagonal of a parallelogram its length. For Thapsacus and the coast-line of Egypt do not lie on the same parallel of latitude, but on parallels that are far part from each other; and between these two parallels the line from Thapsacus to Egypt is drawn somewhat diagonally and obliquely. But when he expresses surprise that Eratosthenes had the boldness to estimate the distance from Pelusium to Thapsacus at six thousand stadia, whereas the distance is more than eight thousand, he is incorrect. For having taken it as demonstrated that the parallel that runs through Pelusium is more than two hundred five hundred stadia farther south than the parallel that runs through Babylon, and then saying — on the authority of Eratosthenes, as he thinks — that the parallel through Thapsacus is four thousand eight hundred stadia farther north than the parallel through Babylon, he says that the distance between Pelusium and Thapsacus amounts to more than eight thousand stadia. I ask, then, how is it shown on the authority of Eratosthenes that the distance of the parallel through Babylon through the parallel through Thapsacus is as great as that? Eratosthenes has stated, indeed, that the distance from Thapsacus to Babylon is four thousand eight hundred stadia; but he has not further stated that this distance is measured from the parallel through the one place to the parallel through the other; neither indeed has he stated that Thapsacus and Babylon are on the same meridian. On the contrary, Hipparchus himself pointed out that, according to Eratosthenes, Babylon is more than two thousand stadia farther east than Thapsacus. And I have just cited the statements of Eratosthenes wherein he says that the Tigris and the Euphrates encircle Mesopotamia and Babylonia, and that the Euphrates does the greater part of the encircling, in that, 89after flowing from the north towards the south, it turns towards the east, and finally empties southwards. Now its southward course from the north lies approximately on some meridian, but its bend to the east and to Babylon is not only a deviation from the meridian but it is also not on a straight line, owing to the said encircling. It is true that Eratosthenes has stated the route to Babylon from Thapsacus to be four thousand eight hundred stadia long, though he added, as on purpose, "following the course of the Euphrates," in order that no one might interpret it as a straight line or as a measure of the distance between two parallels. If this assumption of Hipparchus be not granted, futile also is his subsequent proposition which has only the appearance of being proven, namely, that if a right-angled triangle be constructed with vertices at Pelusium, Thapsacus, and the point of intersection of the parallel of Thapsacus with the meridian of Pelusium, then one of the sides of the right angle, namely, that on the meridian, is greater than the hypotenuse, that is, the line from Thapsacus to Pelusium. Futile also is the proposition that he links with this proposition, because it is fabricated from something that is not conceded. For surely Eratosthenes has not granted the assumption that the distance from Babylon to the meridian that runs through the Caspian Gates is a matter of four thousand eight hundred stadia. I have proved that Hipparchus has fabricated this assumption from data that are not conceded by Eratosthenes; but in order to invalidate what Eratosthenes does grant, Hipparchus took as granted that the distance from Babylon to the line drawn from the Caspian Gates to the confines of Carmania just as Eratosthenes has proposed to draw it is more than nine thousand stadia, and then proceeded to show the same thing.
That, therefore, is not the criticism that should be made against Eratosthenes, but rather the criticism that his roughly-sketched magnitudes and figures require some standard of measure, and that more concession has to be made in one case, less in another. For example, if the breadth of the mountain-range that stretches toward the equinoctial east, and likewise the breadth of the sea that stretches up to the Pillars, be taken as three thousand stadia, one would more readily agree to regard as lying on a single line the parallels of that line drawn within the same breadth than he would the lines that intersect therein; and, of the intersecting lines, those that intersect within that said breadth than those that intersect without. Likewise, also, one would more readily agree to regard as lying on a single line those lines that extend within the limits of said breadth and do not reach beyond than those that reach beyond; and those lines that extend within greater lengths than those in lesser. For in such cases the inequality of the lengths and the dissimilarity of the figures would be more likely to escape notice; for instance, in the case of the breadth of the entire Taurus Range, and of the Sea up to the Pillars, if three thousand stadia be taken as hypothesis for the breadth, we can assume one single parallelogram which traces the boundary both of the entire Range and of the said Sea. Now if you divide a parallelogram lengthwise into several small parallelograms, and take the diagonal both of this whole and of its parts, then the diagonal of the whole might more easily be counted the same as (that is, both parallel and equal to) the long side than could the diagonal of any one of the small parallelograms as compared with the corresponding long side; and the smaller the parallelogram taken as a part, the more would this be true. For both the obliquity of the diagonal and the inequality of its length as compared with the long side are less easily detected in large parallelograms; so that you might not even hesitate in their case to call the diagonal the length of the figure. If, however, you make the diagonal more oblique, so that it falls exterior to both of the sides, or at least to one of them, this would no longer, in like manner, be the case. This is substantially what I mean by a standard of measurement for roughly-sketched magnitudes. But when Eratosthenes, beginning at the Caspian Gates, takes not only the line which runs through the mountains themselves, but also the line which at once diverges considerably from the mountains into Thapsacus, as though both were drawn to the Pillars on the same parallel, and when, again, he still further produces his line, on from Thapsacus to Egypt, thus taking in all this additional breadth, and then measures the length of his figure by the length of this line, he would seem to be measuring the length of his rectangle by a diagonal of a rectangle. And whenever his line is not even a diagonal but a broken line, much more he would seem to err. In fact, it is a broken line that is drawn from the Caspian Gates through Thapsacus to the Nile. So much may be said against Eratosthenes.
But against Hipparchus this too may be argued, that, as he criticised the statements of Eratosthenes, so also he should have made some sort of correction of Eratosthenes' errors — the thing that I am doing. But Hipparchus — if he has really ever taken thought of this matter — bids us to give heed to the old maps although they need much more correction than the map of Eratosthenes still needs. And his subsequent effort suffers from the same flaw. For, as I have shown by test, he takes as an admitted assumption what he has fabricated from data not granted by Eratosthenes, namely, that Babylon is not more than one thousand stadia farther east than Thapsacus; hence, if even a perfect inference is drawn by Hipparchus to the effect that Babylon is not more than two thousand four hundred stadia farther east than Thapsacus, from Eratosthenes' statement that there is a short route of two thousand four hundred stadia from Thapsacus to the Tigris River where Alexander crossed — yet if Eratosthenes also states that the Tigris and the Euphrates, after encircling Mesopotamia for a time, flow east, then turn toward the south, and finally draw near to each other and to Babylon, he has proved no absurdity in Eratosthenes' statement.
Hipparchus is also wrong in his next effort, in which he wishes to draw the inference that Eratosthenes gives the highway from Thapsacus to the Caspian Gates — a highway the length of which Eratosthenes has estimated at ten thousand stadia — as measured in a straight line, although it was not so measured, the straight line being much shorter. The attack he makes against Eratosthenes is to this effect: According to Eratosthenes himself the meridian through the Canobic mouth of the Nile and that through the Cyanean Rocks are one and the same, and this meridian is six thousand three hundred stadia distant from the meridian through Thapsacus; and the Cyanean rocks are six thousand six hundred stadia distant from Mt. Caspius, which lies at the mountain-pass that leads over from Colchis to the Caspian Sea; and hence the distance from the meridian through the Cyanean Rocks to Thapsacus is within three hundred stadia of being equal to the distance thence to Mt. Caspius; so then, practically speaking, both Thapsacus and Mt. Caspius lie on the same meridian. From this it follows, says Hipparchus, that the Caspian Gates are equidistant from Thapsacus and from Mt. Caspius; but the Caspian Gates are at a much less distance from Mt. Caspius than the ten thousand stadia which Eratosthenes says is the distance between the Caspian Gates and Thapsacus; therefore the Caspian Gates are at a much less distance from Thapsacus than the ten thousand stadia that are measured on a straight line; and therefore it is a roundabout way that measures the ten thousand stadia which Eratosthenes reckons on a straight line from the Caspian Gates to Thapsacus.Now my reply to Hipparchus will be that, although Eratosthenes takes his straight lines only roughly, as is proper to do in geography, and roughly, out of, his meridians and his lines to the equinoctial east, Hipparchus puts him to a geometrical test — just as if every one of these lines had been taken with the aid of instruments. Neither does Hipparchus himself take everything by the aid of instruments, but it is rather by conjecture that he takes the relations of both "perpendicular" and "parallel." This, then, is one of Hipparchus' mistakes. Another mistake is this, that he does not even put down the distances that are found in Eratosthenes or apply his test to them, but to those that are fabricated by himself. So, for instance, though Eratosthenes first estimated the distance from the outlet to Phasis at eight thousand stadia and added to this the six hundred stadia thence to Dioscurias, and then estimated at a five days' journey the pass that leads over to Mt. Caspius (which, according to Hipparchus himself, is conjectured to mean about one thousand stadia), so that the total distance, according to Eratosthenes, amounts to nine thousand six hundred stadia, Hipparchus has made a short cut to his result, and says that from the Cyanean Rocks to Phasis the distance is five thousand six hundred stadia, and thence to Mt. Caspius, another thousand stadia. Therefore the statement that Mt. Caspius and Thapsacus are virtually situated on the same meridian could not be based on the authority of Eratosthenes, but on that of Hipparchus himself. Well, suppose it were on the authority of Eratosthenes. How, pray, can it follow therefrom that the line from Mt. Caspius to the Caspian Gates is equal in length to the line from Thapsacus to the same point?
In his Second Book, Hipparchus again takes up the same question of Eratosthenes' division of the inhabited world along the line of the Taurus Range, about which I have already said enough; then he passes to a discussion of the Northern Division; and then he sets forth what Eratosthenes said about the countries that lie next after the Pontus, namely, that three promontories jut down from the north; one promontory, on which is the Peloponnesus; a second, the Italian; and a third the Ligurian; and that these three promontories enclose both the Adriatic and the Tyrrhenian Gulfs. After setting forth these statements of Eratosthenes in a general way, Hipparchus undertakes to test each several statement about the promontories, yet on the principles of geometry rather than those of geography. But so great is the multitude of mistakes made in case of these promontories by Eratosthenes, and by Timosthenes who wrote on The Harbours (whom Eratosthenes praises beyond all the rest, though we find him disagreeing with Timosthenes on most points), that I consider it unfitting to pass judgment either upon those men, since they both stray so very far from the facts, or upon Hipparchus. For even Hipparchus passes by some of their mistakes in silence, while yet others he does not correct, but merely shows by test that they were made falsely or captiously. We might perhaps find fault with Eratosthenes on this point too, namely, because he says "three promontories" of Europe, putting down as "one promontory" that on which is the Peloponnesus; for it is split, so to speak, into a number of promontories; for example, Sunium is a promontory just as much as is Laconia, since it reaches almost as far south as Maleae and embraces a gulf of considerable size. And the Thracian Cherronese and the promontory of Sunium cut off, between them, not only the gulf of Melasbut also all the Macedonian Gulfs that come after Melas. However, if we should pass over this objection, still, the most of the distances, which are obviously wrong, prove that Eratosthenes' ignorance of these regions is surpassing and that his ignorance requires no geometrical proofs, but only such proofs as are obvious and can be attested forthwith; for instance, that pass from Epidamnus that leads over to the Thermaic Gulf is more than two thousand stadia, though Eratosthenes says it is nine hundred; 93and that the distance from Alexandria to Carthage is more than thirteen thousand stadia, though it is not more than nine thousand — if Caria and Rhodes lies, as Eratosthenes says, on the same meridian as Alexandria, and the Strait of Sicily on the same meridian as Carthage. In fact, all agree that the voyage from Caria to the Strait of Sicily is not more than nine thousand stadia; and though, when there is some considerable distance between two places, the meridian taken for the more easterly place might be granted to be the same as the meridian which is no farther west therefrom than Carthage is west of the Strait of Sicily, yet when we are concerned with a matter of four thousand stadia the error is self-evident. And when Eratosthenes actually places Rome — which is so much farther west of the Strait of Sicily than even Carthage is — on the same meridian with Carthage, his ignorance both of these regions and of the successive regions toward the west as far as the Pillars can reach no higher extreme.
Now it would have been proper for Hipparchus, if he were not writing a work on geography but merely a review of what Eratosthenes had said in his Geography, to go further than he did in setting right in detail the mistakes of Eratosthenes; but as for me, I have thought it right to introduce in detail the appropriate discussion both in regard to the points in which Eratosthenes is right and, still more so, in regard to those in which he is wrong; and I have not merely corrected his mistakes, but where I have acquitted him of the charges brought by Hipparchus, I have also criticised Hipparchus himself, whenever he has said anything in a censorious spirit. But since in these instances I see at a glance that Eratosthenes goes entirely astray and that Hipparchus accuses him justly, I assume that it is sufficient if I correct Eratosthenes by merely stating the facts in the course of my Geography itself. Indeed, where the errors are continuous and lie on the surface, it is better not to mention them at all, except rarely and in a general way; and this is what I shall try to do in my detailed account. However, let it be said at this moment that Timosthenes and Eratosthenes and the still earlier geographers were completely ignorant of Iberia and Celtica; and vastly more ignorant of Germany and Britain, and likewise of the countries of the Getans and the Bastarnians; and they were to a considerable extent ignorant of Italy, the Adriatic Sea, the Pontus, and the regions beyond them on the north; though perhaps such statements are censorious. For, since Eratosthenes asserts that where it is a question of very remote regions he will give merely the traditional distances without vouching for them, and admits that he got them by tradition, — though at times he adds the words "in a line more or less straight" — it is not fair to apply the rigorous test to those distances which do not agree with each other. That is precisely what Hipparchus tries to do, not only in the cases mentioned above but also where he sets forth the distances round about Hyrcania up to Bactria and to the tribes on beyond, and, besides, the distances from Colchis to the Hyrcanian Sea. Indeed, in the case of the geography of the remote countries, we should not scrutinize him in the same way as we do in that of the continental sea-board and of the other regions that are as well known; nay, not even in case of the nearer regions ought we to apply the geometrical test, as I was saying, but rather the geographical. Now toward the end of his Second Book, which he has written in refutation of the Geography of Eratosthenes, Hipparchus finds fault with some of the statements of Eratosthenes about Ethiopia, and then says that in his Third Book the greater part of his speculation will be mathematical, but "to some extent" geographical also. It seems to me, however, that he did not make his theory geographical even "to some extent," but wholly mathematical — though Eratosthenes himself gives Hipparchus a good excuse for so doing. For frequently Eratosthenes digresses into discussions too scientific for the subject he is dealing with, but, after he digresses, the declarations he makes are not rigorously accurate but only vague, since, so to speak, he is a mathematician among geographers, and yet a geographer among mathematicians; and consequently on both sides he offers his opponents occasions for contradiction; and the occasions which both he and Timosthenes offer Hipparchus in this Third Book are so just that it remains for me not even to join my observations to those of Hipparchus, but merely to content myself with what Hipparchus has said about them. |
|
|
|
|
2 - 2 What Poseidonius has to say 
Now let us see what Poseidonius has to say in his treatise on Oceanus. For in it he seems to deal mainly with geography, treating it partly from the point of view of geography properly so called, and partly from a more mathematical point of view. And so it will not be out of place for me to pass judgment upon a few of Poseidonius' statements, some of them now, and others in my discussion of the individual countries, as occasion offers, always observing a kind of standard.Now it is one of the things proper to geography to take as an hypothesis that the earth as a whole is sphere-shaped,— just as we do in the case of the universe — and accept all the conclusions that follow this hypothesis, one of which is that the earth has five zones.
2 Poseidonius, then, says that Parmenides was the originator of the division into five zones, but that Parmenides represents the torrid zone as almost double its real breadth, inasmuch as it falls beyond p363both the tropics and extends into the two temperate zones, while Aristotle calls "torrid" the region between the tropics, and "temperate" the regions between the tropics and the "arctic circles." But Poseidonius censures both systems, and with justice, for by "torrid," he says, is meant only the region that is uninhabitable on account of heat; and, of the zone between the tropics, more than half is uninhabitable if we may base a conjecture upon the Ethiopians who live south of Egypt — if it be true, first, that each division of the torrid zone made by the equator is half the whole breadth of that zone and, secondly, that, of this half, the part that reaches to Meroë from Syene (which is a point on the boundary line of the summer tropic is five thousand stadia in breadth, and the part from Meroë to the parallel of the Cinnamon-producing Country, on which parallel the torrid zone begins, is three thousand stadia in breadth. Now the whole of these two parts can be measured, for they are traversed both by water and by land; but the rest of the distance, up to the equator, is shown by calculation based upon the measurement which Eratosthenes made of the earth to be eight thousand eight hundred stadia. Accordingly, as is the ratio of the sixteen thousand eight hundred stadia to the eight thousand eight hundred stadia, so would be the ratio of the distance between the two tropics to the breadth of the torrid zone. And if, of the more recent measurements of the earth, the one which makes the earth smallest in circumference be introduced — I mean that of Poseidonius, who estimates its circumference at about one hundred and eighty thousand stadia — this measurement, I say, renders the breadth of the torrid zone somewhere about half the space between the tropics, or slightly more than half, but in no wise equal to, or the same as, that space. And again, Poseidonius asks how one could determine the limits of the temperate zones, which are non-variable, by means of the "arctic circles," which are neither visible among all men nor the same everywhere. Now the fact that the "arctic circles" are not visible to all could be of no aid to his refutation of Aristotle, because the "arctic circles" must be visible to all who live in the temperate zone, with reference to whom alone the term "temperate" is in fact used. But his point that the "arctic circles" are not everywhere visible in the same way, but are subject to variations, has been well taken.
3 When Poseidonius himself divides the earth into the zones, he says that five of them are useful with reference to the celestial phenomena; of these five, two — those that lie beneath the poles and extend to the regions that have the tropics as arctic circles — are "periscian"; and the two that come next and extend to the people who live beneath the tropics are "heteroscian"; and the zone between the tropics, "amphiscian". But for purposes of human interest there are, in addition to these five zones, two other narrow ones that lie beneath the tropics and are divided into two parts by the tropics; these have the sun directly overhead for above half a month each year. These two zones, he says, have a certain peculiarity, in that they are parched in the literal sense of the word, are sandy, and produce nothing except silphium and some pungent fruits that are withered by the heat; for those regions have in their neighbourhood no mountains against which the clouds may break and produce rain, nor indeed are they coursed by rivers; 96and for this reason they produce creatures with woolly hair, crumpled horns, protruding lips, and flat noses (for their extremities are contorted by the heat); and the "fish-eaters" also live in these zones. Poseidonius says it is clear that these things are peculiar to those zones from the fact that the people who live farther south than they do have a more temperate atmosphere, and also a more fruitful, and a better-watered, country. |
|
|
|
|
2 - 3 Polybius makes six zones 
(9Polybius makes six zones: two that fall beneath the arctic circles, two between the arctic circles and the tropics, and two between the tropics and the equator. However, the division into five zones seems to me to be in harmony with physics as well as geography; with physics, in relation both to the celestial phenomena and to the temperature of the atmosphere; in relation to the celestial phenomena, because, by means of the "periscian" and the "heteroscian" and the "amphiscian" regions (the best way to determine the zone), the appearance of the constellations to our sight is at the same time determined; for thus, by a kind of rough-outline division, the constellations receive their proper variations; and in relation to the temperature of the atmosphere, because the temperature of the atmosphere, being judged with reference to the sun, is subject to three very broad differences — namely, excess of heat, lack of heat, and moderate heat, which have a strong bearing on the organisations of animals and plants, and the semi-organisations of everything else beneath the air or in the air itself. And the temperature of the atmosphere receives its proper determination by this division of the earth into five zones: for the two frigid zones imply the absence of heat, agreeing in the possession of one characteristic temperature; and in like manner the two temperate zones agree in one temperature, that of moderate heat; while the one remaining is consistent in having the remaining characteristic, in that it is one and torrid in temperature. And it is clear that this division is in harmony with geography. For geography seeks to define by boundaries that section of the earth which we inhabit by means of the one of the two temperate zones. Now on the west and on the east it is the sea that fixes its limits, but on the south and the north the nature of the air; for the air that is between these limits is well-tempered both for plants and for animals, while the air on both sides of these limits is harsh-tempered, because of excess of heat or lack of heat. It was necessary to divide the earth into five zones corresponding to these three differences of temperature; indeed, the cutting of the sphere of the earth by the equator into two hemispheres, the northern hemisphere in which we live, and the southern hemisphere, suggested the three differences of temperature. For the regions on the equator and in the torrid zone are uninhabitable because of the heat, and those near the pole are uninhabitable because of the cold; but it is the intermediate regions that are well-tempered and inhabitable. But when he adds the two zones beneath the tropics, Poseidonius does not follow the analogy of the five zones, nor yet does he employ a like criterion; but he was apparently representing zones by the ethnical criteria also, for he calls one of them the "Ethiopic zone," another the "Scythico-Celtic zone," and a third the "intermediate zone."
2 Polybius is not right in this, namely, in that he defines some of his zones by means of the arctic circles: two that fall under the arctic circles themselves, and two between the arctic circles and the tropics; for, as I have already said, non-variables must not be defined by points that are variable. And we must also not employ the tropics as boundaries of the torrid zone; this, too, I have already said. However, when he divides the torrid zone into two parts, it is clearly no foolish notion that has moved him to do so; it is by this notion that we very suitably use the equator to divide the whole earth into two parts, namely, the northern and the southern hemispheres. For it is clear that, if the torrid zone as well is divided according to this method of partition, Polybius reaches a convenient result; that is, each of the two hemispheres is composed of three whole zones, each of which is like in form to its corresponding zone in the other hemisphere. Now a partition of this kind admits of the division into six zones; but the other partition does not altogether admit of it. At all events, if you should cut the earth into two parts by means of the circle that runs through the poles, you could not reasonably divide each of the two hemispheres, the western and the eastern, into six zones, but the division into five zones would be sufficient; for the homogeneousness of the two sections of the torrid zone that are made by the equator, and the fact that they are contiguous to each other, render their partition useless and superfluous, indeed, alike in form respectively, though they are not contiguous. So, therefore, if you conceive of the whole earth as composed of hemispheres of this kind it will be sufficient to divide it into five zones. But if the country that lies under the equator is temperate, as Eratosthenes says it is (an opinion with which Polybius agrees, though he adds this, that it is the highest part of the earth, and for that reason is subject to rains, because at the season of the Etesian Winds the clouds from the north strike in great numbers against the mountain peaks in that region), it would be much better to regard it as a third temperate zone, although a narrow one, than to introduce the two zones beneath the tropics. And in accord with these circumstances are the following (which Poseidonius has already mentioned), namely, that in those regions the oblique motion of the sun is more rapid, and in the same way its daily motion from east to west; for when revolutions are accomplished within the same period of time, those on the greatest circles are the more rapid.
3 But Poseidonius objects to the statement of Polybius that the inhabited region under the equator is the highest. For, says Poseidonius, there can be no high point on a spherical surface, because the surface of a sphere is uniform all round; and indeed the country under the equator is not mountainous, but rather it is a plain that is approximately on a level with the surface of the sea; and the rains that flood the Nile come together from the mountains of Ethiopia. But although Poseidonius thus expresses himself in this passage, he concedes the view of Polybius in other passages, saying he suspects that there are mountains beneath the equator and that the clouds from the two temperate zones strike against those mountains on both sides and cause the rains. Now here the lack of consistency is obvious; but even if it be admitted that the country beneath the equator is mountainous, another inconsistency, as it seems, would arise; for these same men assert that the ocean is one continuous stream round the earth. How, pray, can they place mountains in the centre of the ocean — unless by "mountains" they refer to certain islands? But however this may be, it falls outside the province of geography; and perhaps we should give over these matters for examination to some one who proposes to write a treatise on the ocean.
4 In giving the names of those who are said to have circumnavigated Libya Poseidonius says that Herodotus believes that certain men commissioned by Neco accomplished the circumnavigation of Libya; and adds that Heracleides of Pontus in one of his Dialogues makes a certain Magus who had come to the court of Gelo assert that he had circumnavigated Libya. And, after stating that these reports are unsupported by testimony, he tells the story of a certain Eudoxus of Cyzicus, a sacred ambassador and peace herald at the festival of Persephone. Eudoxus, the story goes, came to Egypt in the reign of Euergetes the Second;1and he became associated with the king and the king's ministers, and particularly in connection with the voyages up the Nile; for he was a man inclined to admire the peculiarities of regions and was also not uninformed about them. Now it so happened, the story continues, that a certain Indian was brought to the king by the coast-guards of the recess of the Arabian Gulf, who said that they had found him half-dead and alone on a stranded ship, but that they did not know who he was or where he came from, since they did not understand his language; and the king gave the Indian into the charge of men who would teach him Greek; and when the Indian had learned Greek, he related that on his voyage from India he by a strange mischance mistook his course and reached Egypt in safety, but only after having lost all his companions by starvation; and when his story was doubted, he promised to act as guide on the trip to India for the men who had been previously selected by the King; and of this party Eudoxus, also, became a member.
So Eudoxus sailed away with presents; and he returned with a cargo of perfumes and precious stones (some of which the rivers bring down with the sands, while others are fortified by digging, being solidified from a liquid state, just as our crystals are). But Eudoxus was wholly deceived in his expectations, for Euergetes took from him his entire cargo. And after the death of Euergetes, his wife, Cleopatra, succeeded him on the throne; and so Eudoxus was again sent out, by her also, and this time with a larger outfit. But on his return voyage he was driven out of his course by the winds to the south of Ethiopia, and being driven to certain places he conciliated the people by sharing with them bread, wine, and dried figs (for they had no share of such things), and in return therefor he received a supply of fresh water and the guidance of pilots, and he also made a list of some of their words. And he found an end of a wooden prow that had come from a wrecked ship and had a horse carved on it; and when he learned that this piece of wreckage belonged to some voyagers who had been sailing from the west, he took it with him when he turned back upon his homeward voyage. And when he arrived safely in Egypt, inasmuch as Cleopatra no longer reigned but her son in her stead, he was again deprived of everything, for it was discovered that he had stolen much property. But he brought the figure-head to the market-place and showed it to the shipmasters, and learned from them that it was a figure-head from Gades; for he was told that whereas the merchants of Gades fit out large ships, the poor men fit out small ships which they call "horses" from the devices on the prows of their ships, and that they sail with these small ships on fishing voyages around the coast of Maurusia as far as the river Lixus; but some of the shipmasters, indeed, recognized the figure-head as having belonged to one of the ships that had sailed rather too far beyond the Lixus River and had not returned home safely.
And from the above-mentioned fact Eudoxus conjectured that the circumnavigation of Libya was possible, went home, placed all his property on a ship, and put out to sea. First he put in at Dicaearchia, then at Massilia, and then at the successive points along the coast until he came to Gades; and everywhere noisily proclaiming his scheme and making money by trafficking, he built a great ship and also two tow-boats like those used by pirates; and he put music-girls on board, and physicians, and other artisans, and finally set sail on the high sea on the way to India, favoured by constant western breezes. But since his companions became tired of the voyage, he sailed with a fair wind towards the land; though he did it against his will, for he feared the ebb and flow of the tides. And, indeed, what he feared actually came to pass: the p383ship ran aground, — though so gently that it was not broken up all at once, and they succeeded in bringing safely to land the cargo and also most of the ship's timbers' and from these timbers he constructed a third boat about as large as a ship of fifty oars; and he continued his voyage, until he came to people who spoke the same words that he had made a list of on the former occasion; 100and forthwith he learnt this, at least, that the men in that region belonged to the same nation as those other Ethiopians, and also that they were neighbours to the kingdom of Bogus.
Accordingly, he abandoned the voyage to India and turned back; and on the voyage along the coast, he espied and made note of an island that was well-watered and well-wooded but uninhabited. And when he reached Maurusia safely he disposed of his boats, travelled on foot to the court of Bogus, and advised him to take up this expedition on his own account; but the friends of Bogus prevailed to the contrary, inspiring in him the fear that Maurusia might in consequence be easily exposed to hostile intrigue if the way thither had once been pointed out to outsiders who wished to attack it. And when Eudoxus heard that he was being sent out, ostensibly, on the expedition as proposed by him, but in reality was going to be placed out on some desert island, he fled to the territory that was under Roman dominion, and thence crossed over to Iberia. And again he built a round ship and a long ship of fifty oars, his purpose being to keep to the open sea with his long ship and to explore the coast with the round ship. He put on board agricultural implements, seeds, and carpenters, and again set out with a view to the same circumnavigation; his intention being, in case the voyage should be delayed, to spend the winter on the island he had previously observed, to sow the seed, reap the harvest therefrom, and then finish the voyage which he had decided upon at the outset.
5 "Now I," says Poseidonius, "have traced the story of Eudoxus to this point, but what happened afterwards probably the people of Gades and Iberia know." So from all these indications he says it is shown that the ocean flows in a circle round the inhabited world: "For him no fetters of continent encompass; but he pours forth his waters boundlessly, and nothing ever sullies their purity." Now Poseidonius is a wonderful fellow in all this; for although he considers as unsupported by testimony the story of the voyage of the Magus, which Heracleides told, and of the voyage even of the emissaries of Neco, of which Herodotus gives an account, he puts down as real evidence this Bergaean story, though he either invented it himself or accepted it from others who were its inventors. For, in the first place, what plausibility is there in the "strange mischance" which the Indian tells about? Why, the Arabian Gulf is like a river in its narrowness, and it is about fifteen thousand stadia long up to its mouth, which, in its turn, is narrow throughout its entire length; and so it is not likely that the Indians who were voyaging outside this gulf were pushed out of their course into it by mistake (for its narrowness at its mouth would have shown their mistake), nor, if they sailed into the gulf on purpose, did they any longer have the excuse that they mistook their course or encountered inconstant winds. And how can it be that they permitted all their number to die of starvation with the exception of one man? And if he survived, how could he single-handed have guided the ship, which was not a small one, since at all events it could sail over open seas of so great extent? And how strange his speedy mastery of the Greek language, which enabled him to convince the king that he was competent to act as pilot of the expedition? And how strange Euergetes' scarcity of competent pilots, since the sea in that region was already known to many men? And as for that peace herald and sacred ambassador of the people of Cyzicus, how came he to abandon his native city and go sailing to India? And how did he come to be entrusted with so great an office? And although on his return everything was taken away from him, contrary to his expectation, and he was in disgrace, how did he come to be entrusted with a still greater equipment of presents? And when he returned from this second voyage and was driven out of his course to Ethiopia, why did he write down those lists of words, and why did he enquire from what source the beak of that fishing-smack had been cast ashore? For the discovery that this bit of wreckage had belonged to men who sailed from the west could have signified nothing, since he himself was to sail from the west on his homeward voyage. And so, again, upon his return to Alexandria, when it was discovered that he had stolen much property, how is it that he was not punished, and that he even went about interviewing shipmasters, at the same time showing them the figure-head of the ship? And wasn't the man that recognized the figure-head a wonderful fellow? And wasn't the man that believed him a still more wonderful fellow — the man who on the strength of a hope of that sort returned to his home land, and then changed his home to the regions beyond the Pillars? But it would not even have been permitted him to put to sea from Alexandria without a passport, least of all after he had stolen property belonging to the king. Neither could he have sailed out of the harbour secretly, since not only the harbour, but also all the other ways of issue from the city had always been kept closed under just as strong guard as I know is still kept up to this day (for I have lived a long time in Alexandria) — though at the present time, under Roman control, the watch is considerably relaxed: but under the kings, the guards were much more strict. And, again, when Eudoxus had sailed away to Gades, and in royal style had built himself ships and continued on his voyage, after his vessel had been wrecked, how could he have built a third boat in the desert? And how is it, when once more he put out to sea and found that those western Ethiopians spoke the same language as the eastern Ethiopians, that he was not eager to accomplish the rest of his voyage (inasmuch as he was so foolish in his eagerness for travels abroad, and since he had a good hope that the unexplored remainder of his voyage was but small) — but instead gave up all this and conceived a longing for the expedition that was to be carried out through the aid of Bogus? And how did he come to learn about the plot that was secretly framed against him? 102And what advantage could this have been to Bogus — I mean his causing the disappearance of the man when he might have dismissed him in other ways? But even if the man learned about the plot, p391how could he have made his escape to places of safety? For, although there is nothing impossible in any escapes of that sort, yet every one of them is difficult and rarely made even with a streak of good luck; but Eudoxus is always attended by good luck, although he is placed in jeopardies one after another. And, again, after he had escaped from Bogus, why was he not afraid to sail once more along the coast of Libya when he had an outfit large enough to colonise an island?
Now, really, all this does not fall short of the fabrications of Pytheas, Euhemerus and Antiphanes. Those men, however, we can pardon for their fabrications — since they follow precisely this as their business — just as we pardon jugglers; but who could pardon Poseidonius, master of demonstration and philosopher, whom we may almost call the claimant for first honours. So much, at least, is not well done by Poseidonius.
6 On the other hand, he correctly sets down in his work the fact that the earth sometimes rises and undergoes settling processes, and undergoes changes that result from earthquakes and the other similar agencies, all of which I too have enumerated above. And on this point he does well to cite the statement of Plato that it is possible that the story about the island of Atlantis is not a fiction. Concerning Atlantis Plato relates that Solon, after having made inquiry of the Egyptian priests, reported that Atlantis did once exist, but disappeared — an island no smaller in size than a continent; and Poseidonius thinks that it is better to put the matter in that way than to say of Atlantis: "Its inventor caused it to disappear, just as did the Poet the wall of the Achaeans." And Poseidonius also conjectures that migration of the Cimbrians and their kinsfolk from their native country occurred as the result of an inundation of the sea that came on all of a sudden. And he suspects that the length of the inhabited world, being about seventy thousand stadia, is half of the entire circle on which it has been taken, so that, says he, if you sail from the west in a straight course you will reach India within the seventy thousand stadia.
7 Then, after an attempt to find fault with those who divided the inhabited world into continents in the way they did, instead of by certain circles parallel to the equator (through means of which they could have indicated variations in animals, plants, and climates, because some of these belong peculiarly to the frigid zone and others to the torrid zone), so that the continents would be practically zones, Poseidonius again revises his own plea and withdraws his indictment, in that he again approves of the prevailing division into three continents, and thus he makes the question a mere matter of argument with no useful end in view. For such a distribution of animals, plants, and climates as exists is not the result of design — just as the differences of race, or of language, are not, either — but rather of accident and chance. And again, as regards the various arts and faculties and institutions of mankind, most of them, p395when once men have made a beginning, flourish in any latitude whatsoever and in certain instances even in spite of the latitude; so that some local characteristics of a people come by nature, others by training and habit. For instance, it was not by nature that the Athenians were fond of letters, whereas the Lacedaemonians, and also the Thebans, who are still closer to the Athenians, were not so; but rather by habit. So, also, the Babylonians and the Egyptians are philosophers, not by nature, but by training and habit. And further, the excellent qualities of horses, cattle, and other animals, are the result, not merely of locality, but of training also. But Poseidonius confounds all this. And when he approves of such a division into three continents as is now accepted, he uses as an illustration the fact that the Indians differ from the Ethiopians of Libya, for the Indians are better developed physically and less parched by the dryness of the atmosphere. And, says he, that is the reason why Homer, in speaking of the Ethiopians as a whole, divides them into two groups, "some where Hyperion sets and some where he rises." But, says Poseidonius, Crates, in introducing into the discussion the question of a second inhabited world, about which Homer knows nothing, is a slave to hypothesis, and, says Poseidonius, the passage in Homer should have been emended to read: "both where Hyperion departs," meaning where he declines from the meridian.
8 Now, in the first place, the Ethiopians that border on Egypt are themselves, also, divided into two groups; for some of them live in Asia, others in Libya, though they differ in no respect from each other. And, in the second place, Homer divides the Ethiopians into two groups, not for this reason, namely, because he knew that the Indians were physically similar to the Ethiopians (for Homer probably did not know of the Indians at all, in view of the fact that even Euergetes himself, according to that story of Eudoxus, knew nothing about India, nor the voyage that leads thither), but rather on the basis of the division of which I have spoken above. And in speaking on that subject I also expressed my opinion in regard to the reading proposed by Crates, namely, that it makes no difference whether we read the passage one way or the other; but Poseidonius says it does make a difference, and that it is better to emend the passage to read "both where Hyperion departs." Now wherein does this differ from "both where Hyperion sets"? For the whole segment of the circle from the meridian to the setting is called "the setting," just as the semi-circle of the horizon is so called. This is what Aratus means when he says: "There where the extremities of the west and of the east join with each other." And if the passage is better as Crates reads it, then one may say that it must also be better as Aristarchus reads it.
So much for Poseidonius. For in my detailed discussions many of his views will meet with fitting criticism, so far as they relate to geography; but so far as they relate to physics, I must inspect them elsewhere or else not consider them at all. For in Poseidonius there is much inquiry into causes and much imitating of Aristotle — precisely what our school avoids, on account of the obscurity of the causes. |
|
|
|
|
2 - 4 Polybius vs Dicaearchus & Eratosthenes 
1 Polybius, in his account of the geography of Europe, says he passes over the ancient geographers but examines the men who criticise them, namely, Dicaearchus, and Eratosthenes, who has written the most recent treatise on Geography; and Pytheas, by whom many have been misled; for after asserting that he travelled over the whole of Britain that was accessible Pytheas reported that the coast-line of the island was more than forty thousand stadia, and added his story about Thule and about those regions in which there was no longer either land properly so‑called, or sea, or air, but a kind of substance concreted from all these elements, resembling a sea-lungs — a thing in which, he says, the earth, the sea, and all the elements are held in suspension; and this is a sort of bond to hold all together, which you can neither walk nor sail upon. Now, as for this thing that resembles the sea-lungs, he says that he saw it himself, but that all the rest he tells from hearsay. That, then, is the narrative of Pytheas, and to it he adds that on his return from those regions he visited the whole coast-line of Europe from Gades to the Tanaïs.
2 Now Polybius says that, in the first place, it is incredible that a private individual — and a poor man too — could have travelled such distances by sea and by land; and that, though Eratosthenes was wholly at a loss whether he should believe these stories, nevertheless he has believed Pytheas' account of Britain, and the regions about Gades, and of Iberia; but he says it is far better to believe Euhemerus, the Messenian, than Pytheas. Euhemerus, at all events, asserts that he sailed only to one country, Panchaea, whereas Pytheas asserts that he explored in person the whole northern region of Europe as far as the ends of the world — an assertion which no man would believe, not even if Hermes made it. And as for Eratosthenes — adds Poseidonius — though he calls Euhemerus a Bergaean, he believes Pytheas, and that, too, though not even Dicaearchus believed him. Now that last remark, "though not even Dicaearchus believed him," is ridiculous; as if it were fitting for Eratosthenes to use as a standard the man against whom he himself directs so many criticisms. And I have already stated that Eratosthenes was ignorant concerning the western and northern parts of Europe. But while we must pardon Eratosthenes and Dicaearchus, because they had not seen those regions with their own eyes, yet who could pardon Polybius and Poseidonius? Nay, it is precisely Polybius who characterises as "popular notions" the statements made by Eratosthenes and Dicaearchus in regard to the distances in those regions and many other regions, though he does not keep himself free from the error even where he criticises them. At any rate, when Dicaearchus estimates the distance from the Peloponnesus to the Pillars at ten thousand stadia, and from the Peloponnesus to the recess of the Adriatic Sea at more than this, and when, of the distance to the Pillars, he reckons the part up to the Strait of Sicily at three thousand stadia, so that the remaining distance — the part from the Strait to the Pillars — becomes seven thousand stadia, Polybius says that he will let pass the question whether the estimate of three thousand is correctly taken or not, but, as for the seven thousand stadia, he cannot let the estimate pass from either of two points of view, namely, whether you take the measure of the coast-line or of the line drawn through the middle of the open sea. For, says he, the coast-line is very nearly like an obtuse angle, whose sides run respectively to the Strait and to the Pillars, and with Narbo as vertex; hence a triangle is formed with a base that runs straight through the open sea and with sides that form the said angle, of which sides the one from the Strait to Narbo measures more than eleven thousand two hundred stadia, the other a little less than eight thousand stadia; and, besides, it is agreed that the maximum distance from Europe to Libya across the Tyrrhenian Sea is not more than three thousand stadia, whereas the distance is reduced if measured across the Sardinian Sea. However, let it be granted, says Polybius, that the latter distance is also three thousand stadia, but let it be further assumed as a prior condition that the depth of the gulf opposite Narbo is two thousand stadia, the depth being, as it were, a perpendicular let fall from the vertex upon the base of the obtuse-angled triangle; then, says p405Polybius, it is clear from the principles of elementary geometry that the total length of the coast-line from the Strait to the Pillars exceeds the length of the straight line through the open sea by very nearly five hundred stadia. And if to this we added the three thousand stadia from the Peloponnesus to the Strait, the sum total of the stadia, merely those measured on a straight line, will be more than double the estimate given by Dicaearchus. And, according to Dicaearchus, says Polybius, it will be necessary to put the distance from the Peloponnesus to the recess of the Adriatic at more than this sum.
3 But, my dear Polybius, one might reply, just as the test based upon your own words makes evident the error of these false reckonings, namely, "from the Peloponnesus to Leucas, seven hundred stadia; from Leucas to Corcyra the same; and, again, from Corcyra to the Ceraunian Mountains the same; and the Illyrian coast-line to Iapydia on your right hand side, if you measure from the Ceraunian Mountains, six thousand one hundred and fifty stadia," so also those other reckonings are both false — both that made by Dicaearchus when he makes the distance from Strait of Sicily to the Pillars seven thousand stadia, and that which you think you have demonstrated; for most men agree in saying that the distance measured straight across the Sea is twelve thousand stadia, and this estimate agrees with the opinion rendered in regard to the length of the inhabited world. For they say that this length is about seventy thousand stadia, and that the western section thereof, that is, from the Gulf of Issus to the capes of Iberia, which are the most westerly points, is a little less than thirty thousand stadia. They arrive at this result in the following way: From the Gulf of Issus to Rhodes the distance is five thousand stadia; thence to Salmonium, which is the eastern Cape of Crete, one thousand stadia; and the length of Crete itself, from Salmonium to Criumetopon, more than two thousand stadia; thence, from Criumetopon to Pachynum in Sicily, four thousand five hundred stadia; and from Pachynum to the Strait of Sicily, more than one thousand stadia; then, the sea-passage from the Strait of Sicily to the Pillars, twelve thousand stadia; and from the Pillars to the extreme end of the Sacred Cape1of Iberia, about three thousand stadia. And Polybius has not taken even his perpendicular properly, if it be true that Narbo is situated approximately on the same parallel as that which runs through Massilia and (as Hipparchus also believes) Massilia on the same as that through Byzantium, and that the line which runs through the open Sea is on the same parallel as that through the Strait and Rhodes, and that the distance from Rhodes to Byzantium has been estimated at about five thousand stadia on the assumption that both places lies on the same meridian; for the perpendicular in question would also be five thousand stadia in length. But when they say that the longest passage across this sea from Europe to Libya, reckoned from the head of the Galatic Gulf, is approximately five thousand stadia, it seems to me that they make an erroneous statement, or else that in that region Libya projects far to the north and reaches the parallel that runs through the Pillars. And Polybius is again not right when he says that the perpendicular in question ends near Sardinia; for the line of this sea-passage is nowhere near Sardinia, but much farther west, leaving between it and Sardinia not only the Sardinian Sea, but almost the whole of the Ligurian Sea as well. And Polybius has exaggerated the length of the seaboard also, only in a lesser degree.
4 Next in order, Polybius proceeds to correct the errors of Eratosthenes; sometimes rightly, but sometimes he is even more in error than Eratosthenes. For instance, when Eratosthenes estimates the distance from Ithaca to Corcyra at three hundred stadia, Polybius says it is more than nine hundred; when Eratosthenes gives the distance from Epidamnus to Thessalonica as nine hundred stadia, Polybius says more than two thousand; and in these cases Polybius is right. But when Eratosthenes says the distance from Massilia to the Pillars is seven thousand stadia and from the Pyrenees to the Pillars six thousand stadia, Polybius himself makes a greater error in giving the distance from Massilia as more than nine thousand stadia and that from the Pyrenees a little less than eight thousand stadia; for Eratosthenes' estimates are nearer the truth. Indeed, modern authorities agree that if one cut off an allowance for the irregular windings of the roads, the whole of Iberia is not more than six thousand stadia in length from the Pyrenees to its western side. But Polybius reckons the river Tagus alone at eight thousand stadia in length from its source to its mouth — without reckoning in the windings of the river, of course (for this is a thing geography does not do) — but estimating the distance on a straight line. And yet from the Pyrenees the sources of the Tagus are more than one thousand stadia distant. On the other hand, Polybius is right when he asserts that Eratosthenes is ignorant of the geography of Iberia, that is, for the reason that he sometimes makes conflicting statements; at any rate, after he has said that the exterior coast of Iberia as far as Gades is inhabited by Gauls — if they really hold the western regions of Europe as far as Gades — he forgets that statement and nowhere mentions the Gauls in his description of Iberia.
5 Again, when Polybius sets forth that the length of Europe is less than the combined length of Libya and Asia, he does not make his comparison correctly. The outlet at the Pillars, he says, is in the equinoctial west, whereas the Tanaïs flows from the summer rising of the sun, and therefore Europe is less in length than the combined length of Libya and Asia by the space between the summer sunrise and the equinoctial sunrise; for Asia has a prior claim to this space of the northern semicircle that lies toward the equinoctial sunrise. Indeed, apart from the abstruseness which characterises Polybius when he is discussing matters that are easy of explanation, his statement that the Tanaïs flows from the summer rising of the sun is also false; for all who are acquainted with those regions say that the Tanaïs flows from the north into Lake Maeotis, and in such wise that the mouth of the river, the mouth of Lake Maeotis, and the course of the Tanaïs itself, so far as it has been explored, all lie on the same meridian.
6 Unworthy of mention are those writers who have stated that the Tanaïs rises in the regions on the Ister and flows from the west, because they have not reflected that the Tyras, the Borysthenes, and the Hypanis, all large rivers, flow between those two rivers into the Pontus, one of them parallel to the Ister and the others parallel to the Tanaïs. And since neither the sources of the Tyras, nor of the Borysthenes, nor of the Hypanis, have been explored, the regions that are farther north than they would be far less known; and therefore the argument that conducts the Tanaïs through those regions and then makes it turn from them to the Maeotis Lake (for the mouths of the Tanaïs are obviously to be seen in the most northerly parts of the Lake, which are also the most easterly parts) — such an argument, I say, would be false and inconclusive. Equally inconclusive is the argument that the Tanaïs flows through the Caucasus towards the north and then turns and flows into Lake Maeotis; for this statement has also been made. However, no one has stated that the Tanaïs flows from the east; for if it flowed from the east the more accomplished geographers would not be asserting that it flows in a direction contrary to, and in a sense diametrically opposed to, that of the Nile — meaning that the courses of the two rivers are on the same meridian or else on meridians that lie close to each other.
7 The measurement of the length of the inhabited world is made along a line parallel to the equator, because the inhabited world, in its length, stretches in the same way the equator does; and in the same way, therefore, we must take as the length of each of the continents the space that lies between two meridians. Again, the measure employed for these lengths is that by stadia; and we seek to discover the number of the stadia either by travelling through the continents themselves, or else along the roads or waterways parallel to them. But Polybius abandons this method and introduces something new, namely, a certain segment of the northern semicircle, which lies between the summer sunrise and the equinoctial sunrise. But no one employs rules and measures that are variable for things that are non-variable, nor reckonings that are made relative to one position or another for things that are absolute and unchanging. Now while the term "length" is non-variable and absolute, "equinoctial rising" and "setting" and, in the same way, "summer sunrise" and "winter sunrise," are not absolute, but relative to our individual positions; and if we shift our position to different points, the positions of sunset and sunrise, whether equinoctial or solstitial, are different, but the length of the continent remains the same. Therefore, while it is not out of place to make the Tanaïs and the Nile limits of continents, it is something new to use the summer, or the equinoctial, sunrise for this purpose.
8 Since Europe runs out into several promontories, Polybius' account of them is better than that of Eratosthenes, but it is still inadequate. For Eratosthenes spoke of only three promontories: first, the promontory that juts down to the Pillars, on which is Iberia; secondly, that to the Strait of Sicily, on which is Italy; and, thirdly, that which ends at Cape Malea, on which are all the nations that dwell between the Adriatic, the Euxine, and the Tanaïs. But Polybius explains the first two promontories in the same way and then makes a third of the promontory which ends at Cape Malea and Sunium, on which are all Greece, and Illyria, and certain parts of Thrace, and a fourth of the Thracian Chersonese, where the strait between Sestus and Abydus is, inhabited by Thracians; and still a fifth of the promontory in the region of the Cimmerian Bosporus and of the mouth of Lake Maeotis. Now we must grant the first two, because they are encompassed by simple gulfs: one of them, by the gulf that lies between Calpe and the Sacred Cape (the gulf on which Gades is situated) and also by that portion of the sea that lies between the Pillars and Sicily; the other, by the last-mentioned sea and the Adriatic — although, of course, the promontory of Iapygia, since it thrusts itself forward on the side 109and thus makes Italy have two crests, presents a sort of contradiction to my statement; but the remaining three promontories, which still more clearly are complex and composed of many members, require further division. Likewise, also, the division of Europe into six parts is open to similar objection, since it has been made in accordance with the promontories. However, in my detailed account I shall make the suitable corrections, not only of these mistakes, but also of all the other serious mistakes that Polybius has made, both in the matter of Europe and in his circuit of Libya. Brief, for the present, I shall rest satisfied with what I have here said in criticism of my predecessors — that is, of so many of them as I have thought would, if cited, make enough witnesses to prove that I too am justified in having undertaken to treat this same subject, since it stands in need of so much correction and addition. |
|
|
|
|
2 - 5 Account of the countries of the earth 
1 Since the taking in hand of my proposed task naturally follows the criticisms of my predecessors, let me make a second beginning by saying that the person who attempts to write an account of the countries of the earth must take many of the physical and mathematical principles as hypotheses and elaborate his whole treatise with reference to their intent and authority. For, as I have already said, no architect or engineer would be competent even to fix the site of a house or a city properly if he had no conception beforehand of "climata" and of the celestial phenomena, and of geometrical figures and magnitudes and heat and cold and other such things — much less a person who would fix positions for the whole of the inhabited world. For the mere drawing on one and the same plane surface of Iberia and India and the countries that lie between them and, in spite of its being a plane surface, the plotting the sun's position at its settings, risings, and in meridian, as though these positions were fixed for all the people of the world — merely this exercise gives to the man who has previously conceived of the arrangement and movement of the celestial bodies and grasped the fact that it is depicted for the moment as a plane surface for the convenience of the eye — merely this exercise, I say, gives to that man instruction that is truly geographical, but to the man not thus qualified it does not. Indeed, the case is not the same with us when we are dealing with geography as it is when we are travelling great plains (those of Babylonia, for example) or over the sea: then all that is in front of us and behind us and on either side of us is presented to our minds as a plane surface and offers no varying aspects with reference to the celestial bodies or the movements or the positions of the sun and the other stars relatively to us; but when we are dealing with geography the like parts must never present themselves to our minds in that way. The sailor on the open sea, or the man who travels through a level country, is guided by certain popular notions (and these notions impel not only the uneducated man but the man of affairs as well to act in the self-same way), because he is unfamiliar with the heavenly bodies and ignorant of the varying aspects of things with reference to them. For he sees the sun rise, pass the meridian, and set, but how it comes about he does not consider; for, indeed, such knowledge is not useful to him with reference to the task before him, any more than it is useful for him to know whether or not his body stands parallel to that of his neighbour. But perhaps he does consider these matters, and yet holds opinions opposed to the principles of mathematics — just as the natives of any given place do; for a man's place occasions such blunders. But the geographer does not write for the native of any particular place, nor yet does he write for the man of affairs of the kind who has paid no attention to the mathematical sciences properly so‑called; nor, to be sure, does he write for the harvest-hand or the ditch-digger, but for the man who can be persuaded that the earth as a whole is such as the mathematicians represent it to be, and also all that relates to such an hypothesis. And the geographer urges upon his students that they first master those principles and then consider the subsequent problems; for, he declares, he will speak only of the results which follow from those principles; and hence his students will the more unerringly make the application of his teachings if they listen as mathematicians; but he refuses to teach geography to persons not thus qualified.
2 Now as for the matters which he regards as fundamental principles of his science, the geographer must rely upon the geometricians who have measured the earth as a whole; and in their turn the geometricians must rely upon the astronomers; and again the astronomers upon the physicists. Physics is a kind of Arete; by Aretai they mean those sciences that postulate nothing but depend upon themselves, and contain within themselves their own principles as well as the proofs thereof. Now what we are taught by the physicists is as follows: The universe and the heavens are sphere-shaped. The tendency of the bodies that have weight is towards the centre. And, having taken its position about this centre in the form of a sphere, the earth remains homocentric with the heavens, as does also the axis through it, which axis extends also through the centre of the heavens. The heavens revolve round both the earth and its axis from east to west; and along with the heavens revolve the fixed stars, with the same rapidity as the vault of the heavens. Now the fixed stars move along parallel circles, and the best known parallel circles are the equator, the two tropics, and the arctic circles; whereas the planets and the sun and the moon move along certain oblique circles whose positions lie in the zodiac. Now the astronomers first accept these principles, either in whole or in part, and then work out the subsequent problems, namely, the movements of the heavenly bodies, their revolutions, their eclipses, their sizes, their respective distances, and a host of other things. And, in the same way, the geometricians, in measuring the earth as a whole, adhere to the doctrines of the physicists and the astronomers, and, in their turn, the geographers adhere to those of the geometricians.
3 Thus we must take as an hypothesis that the heavens have five zones, and that the earth also has five zones, and that the terrestrial zones have the same names as the celestial zones (I have already stated the reasons for this division into zones). The limits of the zones can be defined by circles drawn on both sides of the equator and parallel to it, namely, by two circles which enclose the torrid zone, and by two others, following upon these, which form the two temperate zones next to the torrid zone and the two frigid zones next to the temperate zones. Beneath each of the celestial circles falls the corresponding terrestrial circle which bears the same name: and, in like manner, beneath the celestial zone, the terrestrial zone. Now they call "temperate" the zones that can be inhabited; the others they call uninhabitable, the one on account of the heat, and the other on account of the cold. They proceed in the same manner with reference to the tropic and the arctic circles (that is, in countries that admit of arctic circles): they define their limits by giving the terrestrial circles the same names as the celestial — and thus they define all the terrestrial circles that fall beneath the several celestial circles. Since the celestial equator cuts the whole heavens in two, the earth also must of necessity be cut in two by the terrestrial equator. Of the two hemispheres — I refer to the two celestial as well as the two terrestrial hemispheres — one is called "the northern hemisphere" and the other "the southern hemisphere"; so also, since the torrid zone is cut in two by the same circle, the one part of it will be the northern and the other the southern. It is clear that, of the temperate zones also, the one will be northern and the other southern, each bearing the name of the hemisphere in which it lies. That hemisphere is called "northern hemisphere" which contains that temperate zone in which, as you look from the east to the west, the pole is on your right hand and the equator on your left, or in which, as you look towards the south, the west is on your right hand and the east on your left; and that hemisphere is called "southern hemisphere," in which the opposite is true; and hence it is clear that we are in one of the two hemispheres (that is, of course, in the north), and that it is impossible for us to be in both. "Between them are great rivers; first, Oceanus", and then the torrid zone. But neither is there an Oceanus in the centre of our whole inhabited world, cleaving the whole of it, nor, to be sure, is there a torrid spot in it; nor yet, indeed, is there a portion of it to be found whose "climata" are opposite to the "climata" which I have given for the northern temperate zone.
4 By accepting these principles, then, and also by making use of the sun-dial and the other helps given him by the astronomer — by means of which are found, for the several inhabited localities, both the circles that are parallel to the equator and the circles that cut the former at right angles, the latter being drawn through the poles — the geometrician can measure the inhabited portion of the earth by visiting it and the rest of the earth by his calculation of the intervals. In the same way he can find the distance from the equator to the pole, which is a fourth part of the earth's largest circle; and when he has this distance, he multiplies it by four; and this is the circumference of the earth. Accordingly, just as the man who measures the earth gets his principles from the astronomer and the astronomer his from the physicist, so, too, the geographer must in the same way first take his point of departure from the man who has measured the earth as a whole, having confidence in him and in those in whom he, in his turn, had confidence, and then explain, in the first instance, our inhabited world — its size, shape, and character, and its relations to the earth as a whole; for this is the peculiar task of the geographer. Then, secondly, he must discuss in a fitting manner the several parts of the inhabited world, both land and sea, noting in passing wherein the subject has been treated inadequately by those of our predecessors whom we have believed to be the best authorities on these matters.
5 Now let us take as hypothesis that the earth together with the sea is sphere-shaped and that the surface of the earth is one and the same with that of the high seas; for the elevations on the earth's surface would disappear from consideration, because they are small in comparison with the great size of the earth and admit of being overlooked; and so we use "sphere-shaped" for figures of this kind, not as though they were turned on a lathe, nor yet as the geometrician uses the sphere for demonstration, but as an aid to our conception of the earth — and that, too, a rather rough conception. Now let us conceive of a sphere with five zones, and let the equator be drawn as a circle upon that sphere, and let a third circle be drawn parallel thereto, bounding the frigid zone in the northern hemisphere, and let a third circle be drawn through the poles, cutting the other two circles at right angles. Then, since the northern hemisphere contains two-fourths of the earth, which are formed by the equator with the circle that passes through the poles, a quadrilateral area is cut off in each of the two fourths. The northern side of the quadrilateral is half of the parallel next to the pole; the southern side is half of the equator; and the two remaining sides are segments of the circle that runs through the poles, these segments lying opposite to each other and being equal in length. Now in one of these two quadrilaterals (it would seem to make no difference in which one) we say that our inhabited world lies, washed on all sides by the sea and like an island; for, as I have already said above, the evidence of our senses and of reason prove this. But if anyone disbelieves the evidence of reason, it would make no difference, from the point of view of the geographer, whether we make the inhabited world an island, or merely admit what experience has taught us, namely, that it is possible to sail round the inhabited world on both sides, from the east as well as from the west, with the exception of a few intermediate stretches. And, as to these stretches, it makes no difference whether they are bounded by sea or by uninhabited land; for the geographer undertakes to describe the known parts of the inhabited world, but he leaves out of consideration the unknown parts of it — just as he does what is outside of it. And it will suffice to fill out and complete the outline of what we term "the island" by joining with a straight line the extreme points reached on the coasting-voyages made on both sides of the inhabited world.
6 So let us presuppose that the island lies in the aforesaid quadrilateral. We must then take as its size the figure that is obvious to our sense, which is obtained by abstracting from the entire size of the earth our hemisphere, then from this area its half, and in turn from this half the quadrilateral in which we say the inhabited world lies and it is by an analogous process that we must form our conception of the shape of the island, accommodating the obvious shape to our hypotheses. But since the segment of the northern hemisphere that lies between the equator and the circle drawn parallel to it next to the pole is a spinning-whorl in shape, and since the circle that passes through the pole, by cutting the northern hemisphere in two, also cuts the spinning-whorl in two and thus forms the quadrilateral, it will be clear that the quadrilateral in which the Atlantic Sea lies is half of a spinning-whorl's surface; and that the inhabited world is a chlamys-shaped island in this quadrilateral, since it is less in size than half of the quadrilateral. This latter fact is clear from geometry, and also from the great extent of the enveloping sea which covers the extremities of the continents both in the east and west and contracts them to a tapering shape; and, in the third place, it is clear from the maximum length and breadth. Now the length of the inhabited world is seventy thousand stadia, being for the most part limited by a sea which still cannot be navigated because of its vastness and desolation; the breadth is less than thirty thousand stadia, being bounded by the regions that are uninhabitable on account either of heat or cold. For merely the part of the quadrilateral that is uninhabitable on account of the heat — since it has a breadth of eight thousand eight hundred stadia and a maximum length of one hundred and twenty six thousand stadia, that is, half the length of the equator — is more than half the inhabited world, and the remainder of the quadrilateral would be still more than that.
7 In essential accord with all this are the views of Hipparchus. He says that, having taken as hypothesis the measurement of the earth as stated by Eratosthenes, he must then abstract the inhabited world from the earth in his discussion; for it will not make much difference with respect to the celestial phenomena for the several inhabited places whether the measurement followed is that of Eratosthenes or that given by the later geographers. Since, then, according to Eratosthenes, the equator measures two hundred and fifty two thousand stadia, the fourth part of it would be sixty three thousand stadia; and this is the distance from the equator to the pole, namely, fifteen sixtieths of the sixty intervals into which the equator is divided. And the distance from the equator to the summer tropic is four sixtieths; and the summer tropic is the parallel drawn through Syene. Now the several distances are computed from the standard measures that are obvious to our senses. The summer tropic, for instance, must pass through Syene, because there, at the time of the summer solstice, the index of the sun-dial does not cast a shadow at noon. And the meridian through Syene is drawn approximately along the course of the Nile from Meroë to Alexandria, and this distance is about ten thousand stadia; and Syene must lie in the centre of that distance; so that the distance from Syene to Meroë is five thousand stadia. And when you have proceeded about three thousand stadia in a straight line south of Meroë, the country is no longer inhabitable on account of the heat, and therefore the parallel though these regions, being the same as that through the Cinnamon-producing Country, must be put down as the limit and the beginning of our inhabited world on the South. Since, then, the distance from Syene to Meroë is five thousand stadia, to which we have added the other three thousand stadia, the total distance from Syene to the confines of the inhabited world would be eight thousand stadia. But the distance from Syene to the equator is sixteen thousand eight hundred stadia (for that is what the four sixtieths amounts to, since each sixtieth is estimated at four thousand two hundred stadia), and therefore we should have eight thousand eight hundred stadia left as the distance from the confines of the inhabited world to the equator, and from Alexandria twenty-one thousand eight hundred. Again, all agree that the route by sea from Alexandria to Rhodes is in a straight line with the course of the Nile, as also the route thence along the coast of Caria and Ionia to the Troad, Byzantium, and the Borysthenes. Taking, therefore, the distances that are already known and sailed over, geographers inquire as to the regions beyond the Borysthenes that lie in a straight course with this line — as to how far they are inhabitable, and how far the northern parts of the inhabited world have their boundaries. Now the Roxolanians, the most remote of the known Scythians, live beyond the Borysthenes, though they are farther south than the most remote peoples of whom we have knowledge north of Britain; and the regions beyond the Roxolanians become at once uninhabitable because of the cold; and farther south than the Roxolanians are the Sarmatians who dwell beyond Lake Maeotis, and also the Scythians as far as the Eastern Scythians.
8 Now Pytheas of Massilia tells us that Thule, the most northerly of the Britannic Islands, is farthest north, and that there the circle of the summer tropic is the same as the arctic circle. But from the other writers I learn nothing on the subject — neither that there exists a certain island by the name of Thule, nor whether the northern regions are inhabitable up to the point where the summer tropic becomes the arctic circle. But in my opinion the northern limit of the inhabited world is much farther to the south than where the summer tropic becomes the arctic circle. For modern scientific writers are not able to speak of any country north of Ierne, which lies to the north of Britain and near thereto, and is the home of men who are complete savages and lead a miserable existence because of the cold; and therefore, in my opinion, the northern limit of our inhabited world is to be placed there. But if the parallel though Byzantium passes approximately through Massilia, as Hipparchus says on the testimony of Pytheas (Hipparchus says, namely, that in Byzantium the relation of the index to the shadow is the same as that which Pytheas gave for Massilia), and if the parallel through the mouth of the Borysthenes is about three thousand eight hundred stadia distant from that parallel, then, in view of the distance from Massilia to Britain, the circle drawn through the mouth of the Borysthenes would fall somewhere in Britain. But Pytheas, who misleads people everywhere else, is, I think, wholly in error here too; for it has been admitted by many writers that all the line drawn from the Pillars to the regions of Strait of Sicily and of Athens, and of Rhodes, lies on the same parallel; and it is admitted that the part of that line from the Pillars to the strait runs approximately through the middle of the sea. And further, sailors say that the longest passage from Celtica to Libya, namely, that from the Galatic Gulf, is five thousand stadia, and that this is also the greatest width of the Mediterranean sea, and therefore the distance from the line in question to the head of the gulf would be two thousand five hundred stadia and less than that to Massilia; for Massilia is farther south than the head of the gulf. But the distance from Rhodes to Byzantium is about four thousand nine hundred stadia, and therefore the parallel through Byzantium would be much farther north than that through Massilia. And the distance from Massilia to Britain may possibly correspond to that from Byzantium to the mouth of the Borysthenes; but the distance that should be set down for the stretch from Britain to Ierne is no longer a known quantity, nor is it known whether there are still inhabitable regions farther on, nor need we concern ourselves about the question if we give heed to what Hesiod said above. For, so far as science is concerned, it is sufficient to assume that, just as it was appropriate in the case of the southern regions to fix a limit of the habitable world by proceeding three thousand stadia south of Meroë (not indeed as though this were a very accurate limit, but as one that at least approximates accuracy), so in this case too we must reckon not more than three thousand stadia north of Britain, or only a little more, say, four thousand stadia. And for governmental purposesa there would be no advantage in knowing such countries and their inhabitants, and particularly if the people live in islands which are of such a nature that they can neither injure nor benefit us in any way because of their isolation. For although they could have held even Britain, the Romans scorned to do so, because they saw that there was nothing at all to fear from the Britons (for they are not strong enough to cross over and attack us), and that no corresponding advantage was to be gained by taking and holding their country. For it seems that at present more revenue is derived from the duty on their commerce than the tribute could bring in, if we deduct the expense involved in the maintenance of an army for the purpose of guarding the island and collecting the tribute; and the unprofitableness of an occupation would be still greater in the case of the other islands about Britain.
9 Now if to the distance from Rhodes to the mouth of the Borysthenes we add the distance of four thousand stadia from the mouth of the Borysthenes to the northern regions, the sum total amounts to twelve thousand seven hundred stadia, but the distance from Rhodes to the southern limit of the inhabited world is sixteen thousand six hundred stadia, and therefore the total breadth of the inhabited world would be less than thirty thousand stadia from south to north. Its length, however, is estimated at about seventy thousand stadia; and this is, from west to east, the distance from the capes of Iberia to the capes of India, measured partly by land journeys and partly by sea voyages. And that this length falls within the quadrilateral mentioned above is clear from the relation of the parallels to the equator; hence the length of the inhabited world is more than double its breadth. Its shape is described as about like that of a chlamys; for when we visit the several regions of the inhabited world, we discover a considerable contraction in its width at its extremities, and particularly at its western extremities.
We have now traced on a spherical surface the area in which we say the inhabited world is situated; and the man who would most closely approximate the truth by constructed figures must needs take for the earth a globe like that of Crates, and lay off on it the quadrilateral, and within the quadrilateral put down the map of the inhabited world. But since the need of a large globe, so that the section in question (being a small fraction of the globe) may be large enough to receive distinctly the appropriate parts of the inhabited world and to present the proper appearance to observers, it is better for him to construct a globe of adequate size, if he can do so; and let it be no less than ten feet in diameter. But if he cannot construct a globe of adequate size or not much smaller, he should sketch his map on a plane surface of at least seven feet. For it will make only a slight difference if we draw straight lines to represent the circles, that is, the parallels and meridians, by means of which we clearly indicate the "climata," the winds and the other differences, and also the positions of the parts of the earth with reference both to each other and to the heavenly bodies — drawing parallel lines for the parallels and perpendicular lines for the circles perpendicular to the parallels, for our imagination can easily transfer to the globular and spherical surface the figure or magnitude seen by the eye on a plane surface. And the same applies also, we say, to the oblique circles and their corresponding straight lines. Although the several meridians drawn through the pole all converge on the sphere toward one point, yet on our plane-surface chart it will not be a matter of importance merely to make the straight meridian lines converge slightly; for there is no necessity for this in many cases, nor are the converging straight lines, when the lines of the sphere are transferred to the plane chart and drawn as straight lines, as easily understood as are the curved lines on the sphere.
And so in what I have to say hereafter I shall assume that our drawing has been made on a plane chart. Now I shall tell what part of the land and sea I have myself visited and concerning what part I have trusted to accounts given by others by word of mouth or in writing. I have travelled westward from Armenia as far as the regions of Tyrrhenia opposite Sardinia, and southward from the Euxine Sea as far as the frontiers of Ethiopia. And you could not find another person among the writers on geography who has travelled over much more of the distances just mentioned than I; indeed, those who have travelled more than I in the western regions have not covered as much ground in the east, and those who have travelled more in the eastern countries are behind me in the western; and the same holds true in regard to the regions towards the south and north. However, the greater part of our material both they and I receive by hearsay and then form our ideas of shape and size and also other characteristics, qualitative and quantitative, precisely as the mind forms its ideas from sense impressions — for our senses report the shape, colour, and size of an apple, and also its smell, feel, and flavour; and from all this the mind forms the concept of apple. So, too, even in the case of large figures, while the senses perceive only the parts, the mind forms a concept of the whole from what the senses have perceived. And men who are eager to learn proceed in just that way: they trust as organs of sense those who have seen or wandered over any region, no matter what, some in this and some in that part of the earth, and they form in one diagram their mental image of the whole inhabited world. Why, generals, too, though they do everything themselves, are not present everywhere, but they carry out successfully most of their measures through others, trusting the reports of messengers and sending their orders around in conformity with the reports they hear. And he who claims that only those have knowledge who have actually seen abolishes the criterion of the sense of hearing, though this sense is much more important than sight for the purposes of science.
In particular the writers of the present time can give a better account of the Britons, the Germans, the peoples both north and south of the Ister, the Getans, the Tyregetans, the Bastarnians, and, furthermore, the peoples in the regions of the Caucasus, such as the Albanians and the Iberians. Information has been given us also concerning Hyrcania and Bactriana by the writers of Parthian histories (Apollodorus of Artemita and his school), in which they marked off those countries more definitely than many other writers. Again, since the Romans have recently invaded Arabia Felix with an army, of which Aelius Gallus, my friend and companion, was the commander, and since the merchants of Alexandria are already sailing with fleets by way of the Nile and of the Arabian Gulf as far as India, these regions also have become far better known to us of to‑day than to our predecessors. At any rate, when Gallus was prefect of Egypt, I accompanied him and ascended the Nile as far as Syene and the frontiers of Ethiopia, and I learned that as many as one hundred and twenty vessels were sailing from Myos Hormos to India, whereas formerly, under the Ptolemies, only a very few ventured to undertake the voyage and to carry on traffic in Indian merchandise.
Now my first and most important concern, both for the purposes of science and for the needs of the state, is this — to try to give, in the simplest possible way, the shape and size of that part of the earth which falls within our map, indicating at the same time what the nature of that part is and what portion it is of the whole earth; for this is the task proper of the geographer. But to give an accurate account of the whole earth and of the whole "spinning-whorl" of the zone of which I was speaking is the function of another science — for instance, take the question whether the "spinning-whorl" is inhabited in its other fourth also. And, indeed, if it is inhabited, it is not inhabited by men such as exist in our fourth, and we should have to regard it as another inhabited world — which is a plausible theory. It is mine, however, to describe what is in this our own inhabited world.
As I have said, the shape of the inhabited world is somewhat like a chlamys, whose greatest breadth is represented by the line that runs through the Nile, a line that begins at the parallel that runs through the Cinnamon-producing Country and the island of the fugitive Egyptians, and ends at the parallel through Ierne; its length is represented by that line drawn perpendicular thereto which runs from the west through the Pillars and the Strait of Sicily to Rhodes and the Gulf of Issus, passes along the Taurus Range, which girdles Asia, and ends at the Eastern Sea between India and the country of those Scythians who live beyond Bactriana. Accordingly, we must conceive of a parallelogram in which the chlamys-shaped figure is inscribed in such a way that the greatest length of the chlamys coincides with, and is equal to, the greatest length of the parallelogram, and likewise its greatest breadth and the breadth of the parallelogram. Now this chlamys-shaped figure is the inhabited world; and, as I said, its breadth is fixed by the parallelogram's outermost lines, which separate its inhabited and its uninhabited territory in both directions. And these sides were: in the north, the parallel through Ierne; in the torrid region, the parallel through the Cinnamon-producing Country; hence these lines, if produced both east and west as far as those parts of the inhabited world that rise opposite to them, will form a parallelogram with the meridian-lines that unite them at their extremities. Now, that the inhabited world is situated in this parallelogram is clear from this fact that neither its greatest breadth nor its greatest length fall outside thereof; and that its shape is like a chlamys is apparent from the fact that the extremities of its length, being washed away by the sea, taper off on both sides and thus diminish its width there; and this is apparent from the reports of those who have sailed around the eastern and western parts in both directions. For these navigators declare that the island called Taprobane is considerably south of India, inhabited nevertheless, and that it "rises opposite to" the Island of the Egyptians and the Cinnamon-nearing Country; and that, indeed, the temperature of the atmosphere is much the same as that of these latter places; and the region about the outlet of the Hyrcanian Sea are farther north than outermost Scythia beyond India, and the regions about Ierne are farther north still. A similar report is also made concerning the country outside the Pillars, namely, the promontory of Iberia which they call the Sacred Cape is the most westerly point of the inhabited world; and this cape lies approximately on the line that passes through Gades, the Pillars, the Strait of Sicily, and Rhodes. At all these points, they say, the shadows cast by the sun-dial agree, and the winds that blow in either direction come from the same direction, and the lengths of the longest days and nights are the same; for the longest day and the longest night have fourteen and a half equinoctial hours. Again, the constellation of the Cabeiri is sometimes seen along the coast near Gades. And Poseidonius says that from a tall house in a city about four hundred stadia distant from these regions he saw a star which he judged to be Canopus itself, so judging from the fact that those who had proceeded but a short distance south of Iberia were in agreement that they saw Canopus, and also from scientific observations made at Cnidus; for, says he, the observatory of Eudoxus at Cnidus is not much higher than the dwelling-houses, and from there, it is said, Eudoxus saw the star Canopus; and, adds Poseidonius, Cnidus lies on the parallel of Rhodes, on which lie both Gades and the coastline thereabouts.
Now as you sail to the regions of the south you come to Libya; of this country the westernmost coast extends only slightly beyond Gades; then this coast, forming a narrow promontory, recedes towards the southeast and gradually broadens out to the point where it reaches the land of the Western Ethiopians. They are the most remote people south of the territory of Carthage, and they reach the parallel that runs through the Cinnamon-producing Country. But if you sail in the opposite direction from the Sacred Cape until you come to the people called Artabrians, your voyage is northward, and you have Lusitania on your right hand. Then all the rest of your voyage is eastward, thus making an obtuse angle to your former course, until you reach the headlands of the Pyrenees that abut on the ocean. The westerly parts of Britain lie opposite these headlands towards the north; and in like manner the islands called Cassiterides, situated in the open sea approximately in the latitude of Britain, lie opposite to, and north of, the Artabrians. Therefore it is clear how greatly the east and west ends of the inhabited world have been narrowed down by the surrounding sea.
Such being the general shape of the inhabited world, it is clearly helpful to assume two straight lines that intersect each other at right angles, one of which will run through the entire greatest length and the other through the entire greatest breadth of the inhabited world; and the first line will be one of the parallels, and the second line one of the meridians; then it will be helpful to conceive of lines parallel to these two lines on either side of them and by them to divide the land and the sea with which we happen to be conversant. For thereby the shape of the inhabited world will prove more clearly to be such as I have described it, being judged by the extent of the lines, which lines are of different measurements, both those of the length and those of the breadth; and thereby too the "climata" will be better represented, both in the east and in the west, and likewise in the south and in the north. But since these straight lines must be drawn through known places, two of them have already been so drawn, I mean the two central lines mentioned above, the one representing the length and the other the breadth; and the other lines will be easily found by the help of these two. For by using these lines as "elements," so to speak, we can correlate the regions that are parallel, and the other positions, both geographical and astronomical, of inhabited places.
It is the sea more than anything else that defines the contours of the land and gives it its shape, by forming gulfs, deep seas, straits, and likewise isthmuses, peninsulas, and promontories; but both the rivers and the mountains assist the seas herein. It is through such natural features that we gain a clear conception of continents, nations, favourable positions of cities, and all the other diversified details with which our geographical map is filled. And among these details are the multitude of islands scattered both in the open seas and along the whole seaboard. And since different places exhibit different good and bad attributes, as also the advantages and inconveniences that result therefrom, some due to nature and others resulting from human design, the geographer should mention those that are due to nature; for they are permanent, whereas the adventitious attributes undergo changes. And also of the latter attributes he should indicate such as can persist for a long time, or else such as can not persist for long and yet somehow possess a certain distinction and fame, which, by enduring to later times, make a work of man, even when it no longer exists, a kind of natural attribute of a place; hence it is clear that these latter attributes must also be mentioned. Indeed, it is possible to say concerning many cities what Demosthenes said of Olynthus and the cities round about it, which have so completely disappeared, he says, that a visitor could not know even whether they had ever been founded. But nevertheless men like to visit these places as well as others, because they are eager to see at least the traces of deeds so widely famed, just as they like to visit the tombs of illustrious men. So, also, I have mentioned customs and constitutions that no longer exist, for the reason that utility urges me in their case just as it does in the case of deeds of action; that is, either to incite emulation or signal avoidance of this or that.
I now resume my first sketch of the inhabited world and say that our inhabited world, being girt by the sea, admits into itself from the exterior sea along the ocean many gulfs, of which four are very large. Of these four gulfs the northern one is called the Caspian Sea (though some call it the Hyrcanian Sea); the Persian Gulf and the Arabian Gulf pour inland from the Southern Sea, the one about opposite the Caspian Sea and the other about opposite the Pontus; and the fourth, which far exceeds the others in size, is formed by the sea which is called the Interior Sea, or Our Sea; it takes its beginning in the west at the strait at the Pillars of Heracles, and extends lengthwise towards the regions of the east, but with varying breadth, and finally divides itself and ends in two sea-like gulfs, the one on the left hand, which we call the Euxine Pontus, and the other consisting of the Egyptian, the Pamphylian, and the Issican Seas. All these aforesaid gulfs have narrow inlets from the Exterior Sea, particularly the Arabian Gulf and that at the Pillars, whereas the others are not so narrow. The land that surrounds these gulfs is divided into three parts, as I have said. Now Europe has the most irregular shape of all three; Libya has the most regular shape; while Asia occupies a sort of middle position between the other two in this respect. And the cause of their irregularity or their lack of it lies in the coastline of the Interior Sea, whereas the coastline of the Exterior Sea, with the exception of that of the aforesaid gulfs, is regular and, as I have said, like a chlamys; but I must leave out of view the other slight irregularities, for a little thing is nothing when we are dealing with great things. And further, since in the study of geography we inquire not merely into the shapes and dimensions of countries, but also, as I have said, into their positions with reference to each other, herein, too, the coast-line of the Interior Sea offers for our consideration more varied detail than that of the Exterior Sea. And far greater in extent here than there is the known portion, and the temperate portion, and the portion inhabited by well-governed cities and nations. Again, we wish to know about those parts of the world where tradition places more deeds of action, political constitutions, arts, and everything else that contributes to practical wisdom; and our needs draw us to those places with which commercial and social intercourse is attainable; and these are the places that are under government, or rather under good government. Now, as I have said, our Interior Sea has a great advantage in all these respects; and so with it I must begin my description.
I have already stated that the strait at the Pillars forms the beginning to this gulf; and the narrowest part of the strait is said to be about seventy stadia; but after you sail through the narrows, which are one hundred and twenty stadia in length, the coasts take a divergent course all at once, though the one on the left diverges more; and then the gulf assumes the aspect of a great sea. It is bounded on the right side by the coastline of Libya as far as Carthage, and on the other side, first, by Iberia and also by Celtica in the regions of Narbo and Massilia, and next by Liguria, and finally by Italy as far as the Strait of Sicily. The eastern side of this sea is formed by Sicily and the straits on either side of Sicily; the one between Italy and Sicily is seven stadia in width and the one between Sicily and Carthage is fifteen hundred stadia. But the line from the Pillars to the seven-stadia strait is a part of the line to Rhodes and the Taurus Range; it cuts the aforesaid sea approximately in the middle; and it is said to be twelve thousand stadia in length. This, then, is the length of the sea, while its greatest breadth is as much as five thousand stadia, the distance from the galatic Gulf between Massilia and Narbo to the opposite coast of Libya. The entire portion of this sea along the coast of Libya they call the Libyan Sea, and the portion that lies along the opposite coast they call, in order, the Iberian Sea, the Ligurian Sea, the Sardinian Sea, and finally, to Sicily, the Tyrrhenian Sea. There are numerous islands along the coast of the Tyrrhenian Sea as far as Liguria, and largest of all are Sardinia and Corsica, except Sicily; but Sicily is the largest and best of all the islands in our part of the world. Far behind these in size are Pandateria and Pontia, which lie in the open sea, and, lying near the land, Aethalia, Planasia, Pithecussa, Prochyta, Capreae, Leucosia, and others like them. But on the other side of the Ligurian Sea the islands off the rest of the coast up to the Pillars are not numerous, among which are the Gymnesiae and Ebysus; and those off the coasts of Libya and Sicily are not numerous, either, among which are Cossura, Aegimurus, and the Liparian Islands, which some call the Islands of Aeolus.
Beyond Sicily and the straits on both sides of it other seas join with the former sea. The first is the sea in front of the Syrtes and Cyrenaea and the two Syrtes themselves, and the second is the sea formerly called the Ausonian Sea, but now the Sicilian Sea, which is confluent with and a continuation of the first sea. Now the sea in front of the Syrtes and Cyrenaea is called the Libyan Sea, and it ends at the Egyptian Sea. Of the Syrtes, the lesser is about one thousand six hundred stadia in circumference; and the islands Meninx and Cercina lie at either side of its mouth. As for the Greater Syrtes, Eratosthenes says that its circuit is five thousand stadia, and its breadth eighteen hundred stadia, reckoning from the Hesperides to Automala and to the common boundary between Cyrenaea and the rest of Libya in that region; but others have estimated its circuit at four thousand stadia, and its breadth at fifteen hundred stadia, as much as the breadth of its mouth is. The Sicilian Sea lies in front of Sicily and Italy toward the regions of the east, and, besides, in front of the strait that lies between them — in front of the territory of Rhegium as far as Locri, and of the territory of Messina as far as Syracuse and Pachynum. Toward the regions of the east it stretches on to the headlands of Crete, and its waters also wash round most of the Peloponnesus and fill what is called the Gulf of Corinth. On the north it stretches to the Iapygian Cape and the mouth of the Ionian Gulf and to the southern parts of Epirus as far as the Ambracian Gulf and the coast that adjoins it and, with the Peloponnesus, forms the Corinthian Gulf. But the Ionian Gulf is part of what is now called the Adriatic Sea. The right side of this sea is formed by Illyria, and the left by Italy up to its head at Aquileia. It reaches up towards the north-west in a narrow and long course; and its length is about six thousand stadia, while its greatest breadth is twelve hundred stadia. There are numerous islands in this sea: off the Illyrian coast the Apsyrtides, and Cyrictica, and the Liburnides, and also Issa, Tragurium, Black Corcyra, and Pharos; and off the Italian coast the Diomedeae. The stretch of the Sicilian Sea from Pachynum to Crete, they say, measures four thousand five hundred stadia, and just as much the stretch to Taenarum in Laconia; and the stretch from the Iapygian Cape to the head of the Gulf of Corinth is less than three thousand stadia, while that from Iapygia to Libya is more than four thousand. The islands of this sea are: Corcyra and the Sybota off the coast of Epirus; and next to them, off the Gulf of Corinth, Cephallenia, Ithaca, Zacynthus, and the Echinades.
Adjoining the Sicilian Sea are the Cretan, the Saronic, and the Myrtoan Seas. The Myrtoan Sea is between Crete, Argeia and Attica; its greatest breadth, measured from Attica, is about one thousand two hundred stadia, and its length is less than double its breadth. In this sea are the islands of Cythera, Calauria, Aegina and its neighbouring isles, Salamis, and some of the Cyclades. Next beyond the Myrtoan Sea comes immediately the Aegean Sea, with the Gulf of Melas and the Hellespont; and also the Icarian and Carpathian Seas, extending to Rhodes, Crete, Carpathus, and the first regions of Asia. In the Aegean are the Cyclades, the Sporades, and the islands that lie off Caria, Ionia, and Aeolis up to the Troad — I mean Cos, Samos, Chios, Lesbos, and Tenedos; so also those that lie off Greece as far as Macedonia and Thrace the next country beyond Macedonia — namely, Euboea, Scyros, Peparethos, Lemnos, Thasos, Imbros, Samothrace, and a number of others, concerning which I shall speak in my detailed description. The length of this sea is about four thousand stadia or slightly more, and its breadth is about two thousand stadia. It is surrounded by the aforesaid regions of Asia, and by the coast-line from Sunium to the Thermaic Gulf as you sail towards the north, and by the Macedonian Gulfs up to the Thracian Chersonese.
Along this Chersonese lies the strait, seven stadia in breadth, between Sestus and Abydus, through which the Aegean Sea and the Hellespont empty northwards into another sea which they call the Propontis; and the Propontis empties into another sea termed the "Euxine"1Pontus. This latter is a double sea, so to speak: for two promontories jut out at about the middle of it, one from Europe and the northern parts, and the other, opposite to it, from Asia, thus contracting the passage between them and forming two large seas. The promontory of Europe is called Criumetopon,1and that of Asia, Carambis; and they are about two thousand five hundred stadia distant from each other. Now the western sea has a length of three thousand eight hundred stadia, reckoning from Byzantium to the mouths of the Borysthenes, and a breadth of two thousand eight hundred stadia; in this sea the island of Leuce is situated. The eastern sea is oblong and ends in a narrow head at Dioscurias; it has a length of five thousand stadia or a little more, and a breadth of about three thousand stadia. The circumference of the whole sea is approximately twenty-five thousand stadia. Some compare the shape of this circumference to that of a bent Scythian bow, likening the bow-string to the regions on what is called the right-hand side of the Pontus (that is, the ship-course along the coast from the outlet to the head at Dioscurias; for with the exception of the promontory of Carambis the whole shore has but small recesses and projections, so that it is like a straight line; and the rest they liken to the horn of the bow with its double curve, the upper curve being rounded off, while the lower curve is straighter; and thus they say the left coast forms two gulfs, of which the western is much more rounded than the other.
North of the eastern gulf lies Lake Maeotis, which has a circumference of nine thousand stadia or even a little more. It empties into the Pontus at what is called the Cimmerian Bosporus, and the Pontus empties into the Propontis at the Thracian Bosporus; for they give the name of Thracian Bosporus to the outlet at Byzantium, which is four stadia. The Propontis is said to be fifteen hundred stadia long, reckoning from the Troad to Byzantium; and its breadth is approximately the same. In it lie the island of Cyzicus and the little islands in its neighbourhood.
Such, then, is the nature and such the size of the arm of the Aegean Sea that extends towards the north. Again: the arm that begins at Rhodes and forms the Egyptian, the Pamphylian, and the Issican Seas, stretches towards the east as far as Issus in Cilicia for a distance of five thousand stadia along Lycia, Pamphylia, and the whole coastline of Cilicia. Thence, Syria, Phoenicia, and Egypt encircle the sea on the south and west as far as Alexandria. And Cyprus must lie both in the Issican and the Pamphylian Gulfs, since it borders on the Egyptian Sea. The sea-passage from Rhodes to Alexandria is, with the north wind, approximately four thousand stadia, while the coasting-voyage is double that distance. Eratosthenes says that this is merely the assumption made by navigators in regard to the length of the sea-passage, some saying it is four thousand stadia, others not hesitating to say it is even five thousand stadia, but that he himself, by means of the shadow-catching sun-dial, has discovered to be three thousand seven hundred and fifty stadia. Now the part of this sea that is next to Cilicia and Pamphylia, and the side called the right-hand side of the Pontic Sea, and the Propontis, and the sea-board next beyond as far as Pamphylia, form a great peninsula and a great isthmus belonging thereto that stretches from the sea at Tarsus to the city of Amisus, and to Themiscyra, the Plain of the Amazons. For the country within this line, as far as Caria and Ionia and the peoples that live on this side of the Halys River, is all washed by the Aegean or else by the above-mentioned parts thereof on both sides of the peninsula. And indeed we call this peninsula by the special name of Asia, the same name that is given to the whole continent.
In short, the head of the Greater Syrtis is the most southerly point of our Mediterranean Sea, and next to this Alexandria in Egypt and the mouths of the Nile; the most northerly point is the mouth of the Borysthenes, though if we add Lake Maeotis to the sea (and indeed it is a part of it, in a sense) the mouth of the Tanaïs is the most northerly point; the most westerly point is the strait at the Pillars; and the most easterly point is the above-mentioned head of the Pontus at Dioscurias; and Eratosthenes is wrong in saying that the Issican Gulf is the most easterly, for it lies on the same meridian with Amisus and Themiscyra — or, if you like, you may add in the territory of Sidene on to Pharnacia. From these regions the voyage to Dioscurias is, I might say, more than three thousand stadia eastward, as will become clearer when I describe that region in detail. Such, then, is the nature of our Mediterranean Sea.
I must also give a general description of the countries that surround this sea, beginning at the same points at which I began to describe the sea itself. Now as you sail into the strait at the Pillars, Libya lies on your right hand as far as the stream of the Nile, and on your left hand across the strait lies Europe as far as the Tanaïs. And both Europe and Libya end at Asia. But I must begin with Europe, because it is both varied in form and admirably adapted by nature for the development of excellence in men and governments, and also because it has contributed most of its own store of good things to the other continents; for the whole of it is inhabitable with the exception of a small region that is uninhabited on account of the cold. This uninhabited part borders on the country of the Wagon-Dwellers in the region of the Tanaïs, Lake Maeotis, and the Borysthenes. Of the inhabitable part of Europe, the cold mountainous regions furnish by nature only a wretched existence to their inhabitants, yet even the regions of poverty and piracy become civilised as soon as they get good administrators. Take the case of the Greeks: though occupying mountains and rocks, they used to live happily, because they took forethought for good government, for the arts, and in general for the science of living. The Romans, too, took over many nations that were naturally savage owing to the regions they inhabited, because those regions were either rocky or without harbours or cold or for some other reason ill-suited to habitation by many, and thus not only brought into communication with each other peoples who had been isolated, but also taught the more savage how to live under forms of government. But all of Europe that is level and has a temperate climate has nature to coöperate with her toward these results; for while in a country that is blessed by nature everything tends to peace, in a disagreeable country everything tends to make men warlike and courageous; and so both kinds of country receive benefits from each other, for the latter helps with arms, the former with products of the soil, with arts, and with character-building. But the harm that they receive from each other, if they are not mutually helpful, is also apparent; and the might of those who are accustomed to carry arms will have some advantage unless it be controlled by the majority. However, this continent has a natural advantage to meet this condition also; for the whole of it is diversified with plains and mountains, so that throughout its entire extent the agricultural and civilised element dwells side by side with the warlike element; but of the two elements the one that is peace-loving is more numerous and therefore keeps control over the whole body; and the leading p489nations, too — formerly the Greeks and later the Macedonians and the Romans — have taken hold and helped. And for this reason Europe is most independent of other countries as regards both peace and war; for the warlike population which she possesses is abundant and also that which tills her soils and holds her cities secure. She excels also in this respect, that she produces the fruits that are best and that are necessary for life, and all the useful metals, while she imports from abroad spices and precious stones — things that make the life of persons who have only a scarcity of them fully as happy as that of persons who have them in abundance. So, also, Europe offers an abundance of various kinds of cattle, but a scarcity of wild animals. Such, in a general way, is the nature of this continent.
If, however, we look at the separate parts of it, the first of all its countries, beginning from the west, is Iberia, which in shape is like an ox-hide, whose "neck" parts, so to speak, fall over into the neighbouring Celtica; and these are the parts that lie towards the east, and within these parts the eastern side of Iberia is cut off by a mountain, the so‑called Pyrenees, but all the rest is surrounded by the sea; on the south, as far as the Pillars, it is surrounded by our Sea, and on the other side, as far as the northern headlands of the Pyrenees, by the Atlantic. The greatest length of this country is about six thousand stadia; and breadth, five thousand.
Next to Iberia towards the east lies Celtica, which extends to the River Rhine. On its northern p491side it is washed by the whole British Channel (for the whole island of Britain lies over against and parallel to the whole of Celtica and stretches lengthwise about five thousand stadia); on its eastern side it is bounded by the River Rhine, whose stream runs parallel to the Pyrenees; and on its southern side it is bounded, on the stretch that begins at the Rhine, by the Alps, and by our sea itself in the region where the so‑called Galatic Gulf widens out — the region in which Massilia and Narbo are situated, very famous cities. Opposite this gulf, and facing in the opposite direction, lies another gulf that is also called Galatic Gulf; and it looks toward the north and Britain; and it is between these two gulfs that Celtica has its least breadth; for it is contracted into an isthmus of less than three thousand, but more than two thousand, stadia. Between these two gulfs a mountain range, the so‑called Cemmenus Mountain, runs at right angles to the Pyrenees and comes to an end in the very centre of the plains of Celtica. As for the Alps (which are extremely high mountains that form the arc of a circle), their convex side is turned towards the plains of Celtica just mentioned and the Cemmenus Mountain, while their concave side is turned toward Liguria and Italy. Many tribes occupy these mountains, all Celtic except the Ligurians; but while these Ligurians belong to a different race, still they are similar to the Celts in their modes of life. They live in the part of the Alps that joins the Apennines, and they occupy a part of the Apennines also. The Apennines form a mountain range running through the whole length of Italy from the north to the south and ending at the Strait of Sicily.
The first parts of Italy are the plains that lie at the foot of the Alps and extend as far as the head of the Adriatic and the regions near it, but the rest of Italy is a narrow and long promontory in the form of a peninsula, through which, as I have said, the Apennines extend lengthwise for about seven thousand stadia, but with varying breadth. The seas that make Italy a peninsula are the Tyrrhenian (which begins at the Ligurian Sea), the Ausonian, and the Adriatic.
After Italy and Celtica come the remaining, or eastern, countries of Europe, which are cut in two by the River Ister. This river flows from the west towards the east and the Euxine Sea; it leaves on its left the whole of Germany (which begins at the Rhine), all the country of the Getans, and the country of the Tyregetans, Bastarnians, and Sarmatians as far as the River Tanaïs and Lake Maeotis; and it leaves on its right the whole of Thrace, Illyria, and, lastly and finally, Greece. The islands which I have already mentioned1lie off Europe; outside the Pillars: Gades, the Cassiterides, and the Britannic islands; and inside the Pillars: the Gymnesiae and other little islands of the Phoenicians, and those off Massilia and Liguria, and the islands of Italy up to the Islands of Aeolus and to Sicily, and all the islands round about Epirus and Greece and as far as Macedonia and the Thracian Chersonese.
After the Tanaïs and Lake Maeotis come the regions of Asia — the Cis-Tauran regions which are contiguous to the Tanaïs and Lake Maeotis, and following upon these regions come the Trans-Tauran regions. For since Asia is divided in two by the Taurus Range, which stretches from the capes of Pamphylia to the eastern sea at India and farther Scythia, the Greeks gave the name of Cis-Tauran to that part of the continent which looks towards the north, and the name of Trans-Tauran to that part which looks towards the south; accordingly, the parts of Asia that are contiguous to lake Maeotis and the Tanaïs belong to the Cis-Tauran regions. The first of these regions are those that lie between the Caspian Sea and the Euxine Pontus, and they come to an end, in one direction, at the Tanaïs and the ocean, that is, both at the exterior ocean and at that part of it which forms the Hyrcanian Sea, and, in the other direction, at the isthmus, at the point where the distance from the head of the Pontus to the Caspian Sea is least. Then come those Cis-Tauran regions that are north of Hyrcania, which reach all the way to the sea at India and farther Scythia, and to Mt. Imaeus. These regions inhabited, partly, by the Maeotic Sarmatians, and by the Sarmatians that dwell between the Hyrcanian Sea and the Pontus as far as the Caucasus and the countries of the Iberians and the Albanians, and by Scythians, Achaeans, Zygians, and Heniochians; and, partly, beyond the Hyrcanian Sea, by Scythians, Hyrcanians, Parthians, Bactrians, Sogdianians, and also by the inhabitants of the regions that lie beyond India on the north. And to the south of the Hyrcanian Sea, in part, and of the whole of the isthmus between this sea and the Pontus lie the greater part of Armenia, Colchis, the whole of Cappadocia up to the Euxine and to the Tibaranian tribes, and also the so‑called Cis-Halys country, which embraces, first next to the Pontus and to the Propontis, Paphlagonia, Bithynia, Mysia, the so‑called "Phrygia on the Hellespont" (of which the Troad is a part); and, secondly, next to the Aegean and to the sea that forms its continuation, Aeolis, Ionia, Caria, Lycia; and, thirdly, in the interior, Phrygia (of which both the so‑called "Galatia of the Gallo-Grecians" and "Phrygia Epictetus" form a part), Lycaonia, and Lydia.
Following immediately upon the Cis-Tauran peoples come the peoples that inhabit the mountains: the Paropamisadae, the tribes of the Parthians, of the Medes, of the Armenians, and of the Cilicians, and the Cataonians and the Pisidians. Next after the mountaineers come the Trans-Tauran regions. The first of them is India,1which is the greatest of all nations and the happiest in lot, a nation whose confines reach both to the eastern sea and to the southern sea of the Atlantic. In this southern sea, off the coast of India, lies an island, Taprobane, which is not less than Britain. Then, if we turn from India toward the western regions and keep the mountains on our right, we come to a vast country, which owing to the poverty of the soil, furnishes only a wretched livelihood to men who are wholly barbarians and belong to different races. They call this country Aria, and it extends from the mountains as far as Gedrosia and Carmania. Next after Aria, toward the sea, are Persia, Susiana, Babylonia (countries which reach down to the Persian Sea), and the small tribes that dwell on the frontiers of those countries; while the peoples who live near the mountains or in the mountains themselves are the Parthians, the Medes, the Armenians and the tribe adjoining them, and the Mesopotamians. After Mesopotamia come the countries this side of the Euphrates. These are: the whole of Arabia Felix (which is bounded by the whole extent of the Arabian Gulf and by the Persian Gulf), and all the country occupied by the Tent-Dwellers and by the Sheikh-governed tribes (which reaches to the Euphrates and Syria). Then come the peoples who live on the other side of the Arabian Gulf and as far as the Nile, namely, the Ethiopians and the Arabs, and the Egyptians who live next to them, and the Syrians, and the Cilicians (including the so‑called "Trachiotae"), and finally the Pamphylians.
After Asia comes Libya, which is a continuation of Egypt and Ethiopia. Its shore that lies opposite to us runs in a straight line almost to the Pillars, beginning at Alexandria, except for the Syrtes and perhaps other moderate bends of gulfs and projections of the promontories that form these gulfs; but its coastline on the ocean from Ethiopia to a certain point is approximately parallel to the former line, and then it draws in on the south and forms a sharp promontory, which projects slightly outside the Pillars and thus gives to Libya approximately the shape of a trapezium. And Libya is — as the others show, and indeed as Cnaeus Piso, who was once the prefect of that country, told me — like a leopard's skin; for it is spotted with inhabited places that are surrounded by waterless and desert land. The Egyptians call such inhabited places "auases." But though Libya is thus peculiar, it has some other peculiarities, which give it a threefold division. In the first place, most of its coastline that lies opposite to us is extremely fertile, and especially Cyrenaea and the country about Carthage up to Maurusia and to the Pillars of Heracles; secondly, even its coastline on the ocean affords only moderate sustenance, and thirdly, its interior region, which produces silphium, affords only a wretched sustenance, being, for the most part, a rocky and sandy desert; and the same is also true of the straight prolongation of this region through Ethiopia, the Troglodyte Country, Arabia, and Gedrosia where the Fish-Eaters live. The most of the peoples of Libya are unknown to us; for not much of it is visited by armies, nor yet by men of outside tribes; and not only do very few of the natives from far inland ever visit us, but what they tell is not trustworthy or complete either. But still the following is based on what they say. They call the most southerly peoples Ethiopians; those who live next north of the Ethiopians they call, in the main, Garamantians, Pharusians, and Nigritans; those who live still north of these latter, Gaetulans; those who live near the sea, or even on the seacoast, next to Egypt and as far as Cyrenaea, Marmaridans; while they call those beyond Cyrenaea and the Syrtes, Psyllians, Nasamonians, and certain of the Gaetulans, and then Asbystians and Byzacians, whose territory reaches to that of Carthage. The territory of Carthage is large, and beyond it comes that of the Nomads;203 the best known of these are called, some of them, Masylians, and others Masaesylians. And last of all come the Maurusians. The whole country from Carthage to the Pillars is fertile, though full of wild beasts, as is also the whole of the interior of Libya. So it is not unlikely that some of these peoples were also called Nomads for the reason that in early times they were not able to cultivate the soil on account of the multitude of wild animals. But the Nomads of to‑day not only excel in the skill of hunting (and the Romans take a hand in this with them because of their fondness for fights with wild animals), but they have mastered farming as well as the chase. This, then, is what I have to say about the continents.
It remains for me to speak about the "climata" (which is likewise a subject that involves only a general sketch), taking my beginning at those lines which I have called "elements" — I mean the two lines that mark off the greatest length and breadth of the inhabited world, but more particularly the breadth-line. Astronomers, of course, must treat this subject more at length, just as Hipparchus has treated it. For, as he himself says, he recorded the different aspects of the celestial bodies for all the different regions of the earth that are found in our Fourth — I mean the regions between the equator and the north pole. The geographer, however, need not busy himself with what lies outside of our inhabited world; and even in the case of the parts of the inhabited world the man of affairs need not be taught the nature and number of the different aspects of the celestial bodies, because this is dry reading for him. But it will be sufficient for me to set forth the significant and simplest differences noted by Hipparchus, taking as a hypothesis, just as he does, that the magnitude of the earth is two hundred and fifty-two thousand stadia, the figure rendered by Eratosthenes also. For the variation from this reckoning will not be large, so far as the celestial phenomena are concerned, in the distances between the inhabited places. If, then, we cut the greatest circle of the earth into three hundred and sixty sections, each of these sections will have seven hundred stadia. Now it is this that Hipparchus uses as a measure for the distances to be fixed on the aforesaid meridian through Meroë. So he begins with the inhabitants of the equator, and after that, proceeding along the said meridian to the inhabited places, one after another, with an interval each time of seven hundred stadia, he tries to give the celestial phenomena for each place; but for me the equator is not the place to begin. For if these regions are inhabitable, as some think, they constitute a peculiar kind of inhabited country, stretching as a narrow strip through the centre of the country that is uninhabitable on account of the heat, and not forming a part of our inhabited world. But the geographer takes into his purview only this our inhabited world; and its limits are marked off on the south by the parallel through the Cinnamon-producing Country and on the north by the parallel through Ierne; and, keeping in mind the scope of my geography, I am neither required to enumerate all the many inhabited places that the said intervening distance suggests to me, nor to fix all the celestial phenomena; but I must begin with the southern parts, as Hipparchus does.
Now Hipparchus says that the people who live on the parallel that runs through the Cinnamon-producing Country (this parallel is three thousand stadia south of Meroë and from it the equator is distant eight thousand eight hundred stadia), have their home very nearly midway between the equator and the summer tropic which passes through Syene; for Syene is five thousand stadia distant from Meroë. The Cinnamon-producing Country are the first to whom the Little Bear is wholly inside the arctic circle and always visible; for the bright star at the tip of the tail, the most southerly in the constellation, is situated on the very circumference of the arctic circle, so that it touches the horizon. The Arabian Gulf lies approximately parallel to the meridian in question, to the east of it; and where this gulf pours outside into the exterior sea is the Cinnamon-producing Country, where in ancient times they used to hunt the elephant. But this parallel passes outside the inhabited world, running, on the one side, to the south of Taprobane, or else to its farthermost inhabitants, and, on the other side, to the most southerly regions of Libya.
In the regions of Meroë, and of the Ptolemaïs in the country of the Troglodytes, the longest day has thirteen equinoctial hours; and this inhabited country is approximately midway between the equator and the parallel that runs through Alexandria (the stretch to the equator being eighteen hundred stadia more). And the parallel through Meroë passes, on the one side, through unknown regions, and, on the other, through the capes of India. At Syene, at Berenice on the Arabian Gulf, and in the country of the Troglodytes, the sun stands in the zenith at the time of the summer solstice, and the longest day has thirteen and one half equinoctial hours; and almost the whole of the Great Bear is also visible in the arctic circle, and one of the stars in the square. And the parallel through Syene passes, on the one side, through the country of the Fish-Eaters in Gedrosia, and through India, and, on the other side, through the regions that are almost five thousand stadia south of Cyrene.
In all the regions that lie between the tropic and the equator the shadows fall in both directions, that is, toward the north and toward the north; but, beginning at the regions of Syene and the summer tropic, the shadows fall toward the north at noon; and the inhabitants of the former region are called Amphiscians, and of the latter, Heteroscians. There is still another distinctive characteristic of the regions beneath the tropic, which I have mentioned before in speaking of the zones, namely, the soil itself is very sandy, silphium-producing, and dry, whereas the regions to the south of it are well-watered and very fruitful.
In the region approximately four hundred stadia farther south than the parallel through Alexandria and Cyrene, where the longest day has fourteen equinoctial hours, Arcturus stands in the zenith, though he declines a little toward the south. At Alexandria the relation of the index of the sun-dial to the shadow on the day of the equinox is five to three. But the region in question is thirteen hundred stadia farther south than Carthage — if it be true that at Carthage the relation of the index to the shadow on the day of the equinox is as eleven to seven. But our parallel through Alexandria passes, in one direction, through Cyrene and the regions nine hundred stadia south of Carthage and central Maurusia, and, in the other direction, it passes through Egypt, Coelesyria, Upper Syria, Babylonia, Susiana, Persia, Carmania, Upper Gedrosia, and India.
At the Ptolemaïs in Phoenicia, at Sidon, and at Tyre, and the regions thereabouts, the longest day has fourteen and one quarter equinoctial hours; and these regions are about sixteen hundred stadia farther north than Alexandria and about seven hundred stadia farther north than Carthage. But in the Peloponnesus, in the regions about the centre of Rhodes, about Xanthus of Lycia or a little south of Xanthus, and also in the regions four hundred stadia south of Syracuse, — here, I say, the longest day has fourteen and one half equinoctial hours. These regions are three thousand six hundred and forty stadia distant in latitude from Alexandria; and, according to Eratosthenes, this parallel runs through Caria, Lycaonia, Cataonia, Media, the Caspian Gates, and the parts of India along the Caucasus.
At the Alexandria in the Troad and the regions thereabouts, at Amphipolis, at the Apollonia in Epirus, and in the regions south of Rome but north of Neapolis, the longest day has fifteen equinoctial hours. This parallel is about seven thousand stadia north of the parallel through the Alexandria in Egypt, and more than twenty-eight thousand eight hundred stadia distant from the equator, and three thousand four hundred stadia distant from the parallel through Rhodes, and one thousand five hundred stadia south of Byzantium, Nicaea, Massilia, and the regions thereabouts; and a little north of it lies the parallel through Lysimachia, which, says Eratosthenes, passes through Mysia, Paphlagonia, Sinope, and the regions thereabouts, Hyrcania, and Bactra.
At Byzantium and the regions thereabouts the longest day has fifteen and one quarter equinoctial hours, and the ratio of the index of the sun-dial to the shadow at the time of summer solstice is that of one hundred and twenty to forty-two minus one fifth. These regions are about four thousand nine hundred stadia distant from the parallel through the centre of Rhodes and about thirty thousand three hundred stadia distant from the equator. If you sail into the Pontus and proceed about fourteen hundred stadia toward the north, the longest day becomes fifteen and one half equinoctial hours. These regions are equidistant from the pole and from the equator, and there the arctic circle is in the zenith; and the star on the neck of Cassiopeia lies on the arctic circle, while the star on the right elbow of Perseus is a little north of it.
In the regions about three thousand eight hundred stadia north of Byzantium the longest day has sixteen equinoctial hours; and therefore Cassiopeia moves within the arctic circle. These are the regions about the Borysthenes and the southern parts of Lake Maeotis, and they are about thirty-four thousand one hundred stadia distant from the equator. There the northern part of the horizon is dimly illuminated by the sun throughout almost the entire night in the summer-time, the sun's light making a reverse movement from west back to east. For the summer tropic is seven-twelfths of a zodiacal sign distant from the horizon; and accordingly the sun at midnight is just that distance below the horizon. And in our own regions also, when the sun is so far as that from the horizon before sunrise and after sunset, it illumines the skies in the east and in the west. And in those regions in the winter-days the sun attains an elevation of at most nine cubits. Eratosthenes says that these regions are a little more than twenty-three thousand stadia from Meroë, since the distance from Meroë to the parallel through the Hellespont is eighteen thousand stadia, and thence to the Borysthenes, five thousand. In the regions about six thousand three hundred stadia distant from Byzantium north of Lake Maeotis, in the winter-days, the sun attains an elevation of at most six cubits, and there the longest day has seventeen equinoctial hours.
Since the regions beyond already lie near territory rendered uninhabitable by the cold, they are without value to the geographer. But if any one wishes to learn about these regions also, and about all the other astronomical matters that are treated by Hipparchus, but omitted by me as being already too clearly treated to be discussed in the present treatise, let him get them from Hipparchus. And what Poseidonius says about the Periscians and Amphiscians and Heteroscians is too clear to be repeated here; nevertheless, I must mention these terms at sufficient length to explain the idea and to show wherein it is useful for geography and wherein useless. Now since the point in question concerns the shadows cast by the sun, and since, on the evidence of our senses, the sun moves along a circle parallel to the revolution of the universe, it follows that, wherever each revolution of the universe produces a day and a night (because at one time the sun moves beneath the earth and at another time above the earth), the people are thought of as either Amphiscians or Heteroscians, — as Amphiscians, all whose shadows at noon sometimes fall toward the north, namely, when the sun strikes from the south the index (which is perpendicular to the horizontal surface beneath), and, at other times, fall in the opposite direction, namely, when the sun revolves round to the opposite side (this is the result for only those who live between the tropics), but as Heteroscians, all whose shadows either always fall toward the north, as is the case with us, or always toward the south, as is the case with the inhabitants of the other temperate zone. And this is the result for every man whose arctic circle is smaller than the tropic circle. But wherever the arctic circle is the same as, or greater than, the tropic, there the Periscians begin and they extend to the people who live beneath the pole.For since, in those regions, the sun moves above the earth throughout the whole revolution of the universe, it is clear that the shadow will move in a circle round the index of the sun-dial; and that is the reason why Poseidonius called them Periscians, although they are non-existent as far as geography is concerned; for all those regions uninhabitable on account of the cold, as I have already stated in my criticism of Pytheas. Therefore I need not concern myself, either, with the extent of this uninhabited region, apart from assuming that those regions which have the tropic-arctic circle lie beneath the circle described by the pole of the zodiac in the diurnal revolution of the universe — that is, on the hypothesis that the distance between the equator and the tropic is four-sixtieths of the greatest circle. |
|
|
|
|
3 Iberia 5 115 1:50 
|
3 - 1 Introduction 
1 Now that I have given the first general outline of geography, it is proper for me to discuss next the several parts of the inhabited world; indeed, I have promised to do so, and I think that thus far my treatise has been correctly apportioned. But I must begin again with Europe and with those parts of Europe with which I began at first, and for the same reasons.
2 As I was saying, the first part of Europe is the western, namely, Iberia. Now of Iberia the larger part affords but poor means of livelihood; for most of the inhabited country consists of mountains, forests, and plains whose soil is thin — and even that not uniformly well-watered. And Northern Iberia, in addition to its ruggedness, not only is extremely cold, but lies next to the ocean, and thus has acquired its characteristic of inhospitality and aversion to intercourse with other countries; consequently, it is an exceedingly wretched place to live in. Such, then, is the character of the northern parts; but almost the whole of Southern Iberia is fertile, particularly the region outside the Pillars. This will become clear in the course of my detailed description of Iberia. But first I must briefly describe its shape and give its dimensions.
3 Iberia is like an ox-hide extending in length from west to east, its fore-parts toward the east, and in breadth from north to south. It is six thousand stadia in length all told, and five thousand stadia in its greatest breadth; though in some places it is much less than three thousand stadia in breadth, particularly near the Pyrenees, which form its eastern side. That is, an unbroken chain of mountains, stretching from north to south, forms the boundary line between Celtica and Iberia; and since Celtica, as well as Iberia, varies in breadth, the part of each country that is narrowest in breadth between Our Sea and the ocean is that which lies nearest to the Pyrenees, on either side of those mountains, and forms gulfs both at the ocean and at Our Sea. The Celtic gulfs, however, which are also called Galatic, are larger, and the isthmus which they form is narrower as compared with that of Iberia. So the eastern side of Iberia is formed by the Pyrenees; the southern side is formed in part by Our Sea, from the Pyrenees to the Pillars, and from that point on by the ocean, up to what is called the Sacred Cape; the third is the western side, which is approximately parallel to the Pyrenees and extends from the Sacred Cape to that Cape of the Artabrians which is called Nerium; and the fourth side extends from Cape Nerium up to the northern headlands of the Pyrenees.
4 But, to resume, let me describe Iberia in detail, beginning with the Sacred Cape. This cape is the most westerly point, not only of Europe, but of the whole inhabited world; for, whereas the inhabited world comes to an end in the west with the two continents (in the one hand, at the headlands of Europe, and in the other, at the extremities of Libya, of which regions the Iberians occupy the one, and the Maurusians the other), the headlands of Iberia project at the aforementioned cape about fifteen hundred stadia beyond those of Libya. Moreover, the country adjacent to this cape they call in the Latin language "Cuneus," meaning thereby to indicate its wedge-shape. But as for the cape itself, which projects into the sea, Artemidorus (who visited the place, as he says) likens it to a ship; and he says that three little islands help to give it this shape, one of these islands occupying the position of a ship's beak, and the other two, which have fairly good places of anchorage, occupying the position of cat-heads. But as for Heracles, he says, there is neither a temple of his to be seen on the cape (as Ephorus wrongly states), nor an altar to him, or to any other god either, but only stones in many spots, lying in groups of three or four, which in accordance with a native custom are turned round by those who visit the place, and then, after the pouring of a libation, are moved back again. And it is not lawful, he adds, to offer sacrifice there, nor, at night, even to set foot on the place, because the gods, the people say, occupy it at that time; but those who come to see the place spend the night in a neighbouring village, and then enter the place by day, taking water with them, for there is no water there.
5 Now these assertions of Artemidorus are allowable, and we should believe them; but the stories which he has told in agreement with the common crowd of people are by no means to be believed. For example, it is a general saying among the people, according to Poseidonius, that in the regions along the coast of the ocean the sun is larger when it sets, and that it sets with a noise much as if the sea were sizzling to extinguish it because of its falling into the depths. But, says Poseidonius, this is false, as also the statement that night follows instantly upon sunset; for night does not come on instantly, but after a slight interval, just as it does on the coasts of the other large seas. For in regions where the sun sets behind mountains, he says, the daylight lasts a longer time after sunset, as a result of the indirect light; but on the sea-coasts no considerable interval ensues, albeit the darkness does not come on instantly, either, any more than it does on the great plains. And, he says, the visual impression of the size of the sun increases alike both at sunset and sunrise on the seas, because at those times a greater amount of vapour rises from the water; that is, the visual rays, in passing through this vapour as through a lens, are broken, and therefore the visual impression is magnified, just as it is when the setting or the rising sun, or moon, is seen through a dry, thin cloud, at which time the heavenly body also appears somewhat ruddy. He convinced himself, he says, of the falsity of the above assertions during his stay of thirty days in Gades, when he observed the settings of the sun. Nevertheless, Artemidorus says that the sun sets a hundred times larger than usual, and that night comes on immediately! However, if we look closely at his declaration, we are obliged to assume that he did not himself see this phenomenon at the Sacred Cape, for he states that no one sets foot on the place by night; and hence no one could set foot on it while the sun was setting, either, if it be true that night comes on immediately. Neither, in fact, did he see it at any other point on the ocean-coast, for Gades is also on the ocean, and Poseidonius and several others bear witness against him.
6 The coastline adjacent to the Sacred Cape, on the west, is the beginning of the western side of Iberia as far as the mouth of the Tagus River, and, on the south, the beginning of the southern side as far as another river, the Anas, and its mouth. Both rivers flow from the eastern regions; the Tagus, which is a much larger stream than the other, flows straight westward to its mouth, whereas the Anas turns south, and marks off a boundary of the interfluvial region, which is inhabited for the most part by Celtic peoples, and by certain of the Lusitanians who were transplanted thither by the Romans from the other side of the Tagus. But in the regions farther inland dwell Carpetanians, Oretanians, and large numbers of Vettonians. This country, to be sure, has only a moderately happy lot, but that which lies next to it on the east and south takes pre-eminence in comparison with the entire inhabited world in respect of fertility and of the goodly products of land and sea. This is the country through which the Baetis flows, which rises in the same districts as both the Anas and the Tagus, and in size is about midway between the other two rivers. Like the Anas, however, it at first flows towards the west, and then turns south, and empties on the same coast as the Anas. They call the country Baetica for the river, and also Turdetania after the inhabitants; yet they call the inhabitants both Turdetanians and Turdulians, some believing that they are the same people, others that they are different. Among the latter is Polybius, for he states that the Turdulians are neighbours of the Turdetanians on the north; but at the present time there is no distinction to be seen among them. The Turdetanians are ranked as the wisest of the Iberians; and they make use of an alphabet, and possess records of their ancient history, poems, and laws written in verse that are six thousand years old, as they assert. And also the other Iberians use an alphabet, though not letters of one and the same character, for their speech is not one and the same, either. Now Turdetania, the country this side the Anas, stretches eastward as far as Oretania, and southward as far as the coastline that extends from the mouths of the Anas to the Pillars. But I must describe it and the regions that are close to it at greater length, telling all that contributes to our knowledge of their natural advantages and happy lot.
7 Between this stretch of coastline, on which both the Baetis and the Anas empty, and the limits of Maurusia, the Atlantic Ocean breaks in and thus forms the strait at the Pillars, and by this strait the interior sea connects with the exterior sea. Now at this strait there is a mountain belonging to those Iberians that are called Bastetanians, who are also called Bastulians; I mean Calpe, which, although its circumference is not great, rises to so great a height and is so steep that from a distance it looks like an island. So when you sail from Our Sea into the exterior sea, you have this mountain on your right hand; and near it, within a distance of forty stadia, is the city Calpe, an important and ancient city, which was once a naval station of the Iberians. And some further say that it was founded by Heracles, among whom is Timosthenes, who says that in ancient times it was also called Heracleia, and that its great city-walls and its docks are still to be seen.
8 Then comes Menlaria, with its establishments for salting fish; and next, the city and river of Belon. It is from Belon that people generally take ship for the passage across to Tingis in Maurusia; and at Belon there are trading-places and establishments for salting fish. There used to be a city of Zelis, also, a neighbour of Tingis, but the Romans transplanted it to the opposite coast of Iberia, taking along some of the inhabitants of Tingis; and they also sent some of their own people thither as colonists and named the city "Julia Ioza." Then comes Gades, an island separated from Turdetania by a narrow strait, and distant from Calpe about seven hundred and fifty stadia (though some say eight hundred). This island does not differ at all from the others except that, because of the daring of its inhabitants as sailors, and because of their friendship for the Romans, it has made such advances in every kind of prosperity that, although situated at the extremity of the earth, it is the most famous of them all. But I shall tell about Gades when I discuss the other islands.
9 Next in order comes what is called the Port of Menestheus, and then the estuary at Asta and Nabrissa. (The name of estuaries is given to hollows that are covered by the sea at the high tides, and, like rivers, afford waterways into the interior and to the cities on their shores.) Then immediately comes the outlet of the Baetis, which has a twofold division; and the island that is enclosed by the two mouths has a coastal boundary of one hundred stadia, or, as some say, still more than that. Hereabouts is the oracle of Menestheus; and also the tower of Caepio, which is situated upon a rock that is washed on all sides by the waves, and, like the Pharos tower, is a marvellous structure built for the sake of the safety of mariners; for not only do the alluvial deposits that are discharged by the river form shallows, but the region in front of it is full of reefs, so that there is need of a conspicuous beacon. Thence is the waterway up the Baetis, and the city of Ebura, and the shrine of Phosphorus, which they call "Lux Dubia." Then come the waterways up to the estuaries; and after that the Anas River, which also has two mouths, and the waterway from both mouths into the interior. Then, finally, comes the Sacred Cape, which is less than two thousand stadia distant from Gades. Some, however, say that the distance from the Sacred Cape to the mouth of the Anas is sixty miles, and thence to the mouth of the Baetis, a hundred, and then, to Gades, seventy. |
|
|
|
|
3 - 2 Boundaries 
1 At all events, it is above the coast this side the Anas that Turdetania lies, and through it flows the Baetis River. And its boundary is marked off on the west and north by the Anas River, on the east by a part of Carpetania and by Oretania, and on the south by those of the Bastetanians who occupy a narrow stretch of coast between Calpe and Gades and by the sea next to that stretch as far as the Anas. But these Bastetanians of whom I have just spoken also belong to Turdetania, and so do those Bastetanians beyond the Anas, and most of its immediate neighbours. The extent of this country is not more than two thousand stadia, that is, in length or breadth, but it contains a surpassing number of cities — as many, indeed, as two hundred, it is said. The best known are those situated on the rivers, on the estuaries, and on the sea; and this is due to their commercial intercourse. But the two that have grown most in fame and in power are Corduba, which was founded by Marcellus, and the city of the Gaditanians: the latter, because of its maritime commerce and because it associated itself with the Romans as an ally; the former because of the excellence of its soil and the extent of its territory, though the Baetis River has also contributed in great measure to its growth; and it has been inhabited from the beginning by picked men of the Romans and of the native Iberians; what is more, the first colony which the Romans sent to these regions was that to Corduba. After Corduba and the city of the Gaditanians, Hispalis, itself also a colony of the Romans, is most famous, and still remains the trade-centre of the district; yet, in the matter of distinction, that is, in the fact that the soldiers of Caesar have recently colonised it, Baetis ranks higher, albeit a city not notable for its population.
2 After these cities come Italica and Ilipa, both near the Baetis River; and Astigis, farther away from the river, and Carmo, and Obulco, and, besides these, the cities in which the sons of Pompey were defeated, namely, Munda, Ategua, Urso, Tuccis, Ulia, and Aegua; and all of these cities are not far from Corduba. In a way, Munda has become the capital city of this region. Munda is one thousand four hundred stadia distant from Carteia, whither Gnaeus fled after his defeat; he sailed away from there, and disembarked into a certain mountainous region overlooking the sea, where he was put to death. But his brother Sextus escaped from Corduba, carried on war for a short time in Iberia, and later on caused Sicily to revolt; then, driven out of Sicily into Asia, he was captured by the generals of Antony, and ended his life at Miletus. In the country of the Celti, Conistorgis is the best known city; but on the estuaries Asta is the best known, where the Gaditanians of to‑day usually hold their assemblies, and it is situated not much more than one hundred stadia beyond the seaport of the island.
3 The Baetis has a large population along its shores, and is navigable for approximately one thousand two hundred stadia from the sea up to Corduba and the regions a little higher up. Furthermore, the land along the river, and the little islands in the river, are exceedingly well cultivated. And besides that, there is the charm of the scenery, for the farms are fully improved with groves and gardens of the various plants. Now, up to Hispalis, the river is navigable for merchant-vessels of considerable size, that is, for a distance not much short of five hundred stadia; to the cities higher up the stream as far as Ilipa, for the smaller merchant vessels; and, as far as Corduba, for the river-boats (at the present time these are builded boats, whereas in antiquity they were merely dugout canoes); but above Corduba, in the direction of Castalo, the river is not navigable. On the north, there are some mountain-ridges which extend parallel to the river, approaching it closely, sometimes more so, sometimes less, and they are full of mines. Silver, however, is the most plentiful in the regions about Ilipa, and in those about Sisapo — I mean what is called the Old Sisapo as well as the New Sisapo; and at the place called Cotinae both copper and gold are mined at the same time. Now on your left, as you sail up the river, are these mountains, while on your right is a large plain, high, very productive, with lofty trees, and affording good pasturage. The Anas also is navigable, though neither for such large vessels nor for so great a distance. Beyond the Anas, too, lie mountains that contain ores, and these mountains reach down to the Tagus River. Now the regions which contain ores are necessarily rugged as well as rather poor in soil, precisely as are the regions that join Carpetania, and still more so those that join Celtiberia. And such is the nature of Baeturia also, which contains arid plains that stretch along the Anas.
4 Turdetania itself is marvellously blessed by nature; and while it produces all things, and likewise great quantities of them, these blessings are doubled by the facilities of exportation; for its surplus products are bartered off with ease because of the large number of the merchant vessels. This is made possible by the rivers, and by the estuaries as well, which, as I have said, resemble rivers, and, like rivers, are navigable inland from the sea, not only for small boats but also for large ones, to the cities of the interior. For the whole country beyond the seaboard that lies between the Sacred Cape and the Pillars is a plain for a considerable distance inland. And here, at a large number of places, are inlets which run up from the sea into the interior, resembling moderate-sized ravines or simply river-beds, and extending for many stadia; and these inlets are filled by the overflows of the sea at the flood-tides, so that one can sail inland thereon as readily as on the rivers — in fact, better, for it is like sailing down the rivers, not only because there is no opposing current, but because, on account of the flood-tide, the sea wafts you onwards just as the river-current does. And the overflows are greater on this coast than in the other regions, because the sea, coming from the great ocean, is compressed into the narrow strait which Maurusia forms with Iberia, there meets resistance, and then easily rushes to those parts of the land that yield to it. Now, while a number of the inlets of this kind are emptied at the ebb-tides (though some of them do not become wholly dry), yet a number of them enclose islands within themselves. Such, then, are the estuaries between the Sacred Cape and the Pillars, for they have an excessive rise of tide as compared with those in the other regions. A rise of tide like this affords a certain advantage to be utilised by sailors, namely, the estuaries are made more numerous and larger, oftentimes being navigable even for a distance of eight stadia; so that, after a fashion, it renders the whole country navigable and convenient both for exporting and importing merchandise. And yet it also affords a certain annoyance; for, on account of the vehemence of the flood-tides, which press with superior force against the current of the rivers, navigation on the rivers is attended by no small danger to the vessels, alike in their descent and ascent. But in the case of the estuaries the ebb-tides too are harmful; for the ebb-tides too grow violent in proportion to the strength of the flood-tides, and on account of their swiftness have oftentimes even left the ship stranded on dry land. Again, the cattle which cross over to the islands that lie off the rivers or the estuaries have at times actually been engulfed; at other times they have merely been cut off, and in their struggle to get back to the land lacked the strength to do so, and perished. But the cows, they say, are by observation actually aware of what happens, wait for the retirement of the sea, and then make off for the mainland.
5 At any rate, it was because the people had learned the character of these regions and that the estuaries could subserve the same purpose as the rivers, that they built cities and other settlements on their banks, just as on the rivers. Among these cities are Asta, Nabrissa, Onoba, Ossonoba, Maenoba, and several others. Again, canals that have been dug in a number of places are an additional aid, since many are the points thereon from which and to which the people carry on their traffic, not only with one another but also with the outside world. And further, the meetings of the waters when the flood-tides reach far inland are likewise helpful, for the waters pour across over the isthmuses that separate the waterways, thus rendering the isthmuses navigable also; so that one can cross over by boat from the rivers into the estuaries and from the estuaries into the rivers. But all the foreign trade of the country is carried on with Italy and Rome, since the voyage as far as the Pillars is good, except, perhaps, for a certain difficulty in passing the strait, and also the voyage on the high seas of Our Sea. For the sea-routes all pass through a zone of fair weather, particularly if the sailor keeps to the high seas; and this fact is advantageous to the merchant-freighters. And further, the winds on the high seas are regular. Added to that, too, is the present peace, because all piracy has been broken up, and hence the sailors feel wholly at ease. Poseidonius says that he observed a peculiar circumstance on his return voyage from Iberia, namely, that the east winds on that sea, as far as the gulf of Sardinia, blew at a fixed time each year; and that this was why he barely reached Italy even in three months; for he was driven out of his course in both directions, not only near to the Gymnesian Islands and Sardinia, but also to the different parts of Libya opposite to these islands.
6 There are exported from Turdetania large quantities of grain and wine, and also olive oil, not only in large quantities, but also of best quality. And further, wax, honey, and pitch are exported from there, and large quantities of kermes, and ruddle which is not inferior to the Sinopian earth. And they build up their ships there out of native timber; and they have salt quarries in their country, and not a few streams of salt water; and not unimportant, either, is the fish-salting industry that is carried on, not only from this county,º but also from the rest of the seaboard outside the Pillars; and the product is not inferior to that of the Pontus. Formerly much cloth came from Turdetania, but now, wool, rather of the raven-black sort. And it is surpassingly beautiful; at all events, the rams are bought for breeding purposes at a talent apiece. Surpassing, too, are the delicate fabrics which are woven by the people of Salacia. Turdetania also has a great abundance of cattle of all kinds, and of game. But there are scarcely any destructive animals, except the burrowing hares, by some called "peelers"; for they damage both plants and seeds by eating the roots. This pest occurs throughout almost the whole of Iberia, and extends even as far as Massilia, and infests the islands as well. The inhabitants of the Gymnesian Islands, it is said, once sent an embassy to Rome to ask for a new place of abode, for they were being driven out by these animals, because they could not hold out against them on account of their great numbers. Now perhaps such a remedy is needed against so great a warfare (which is not always the case, but only when there is some destructive plague like that of snakes or field-mice), but, against the moderate pest, several methods of hunting have been discovered; more than that, they make a point of breeding Libyan ferrets, which they muzzle and send into the holes. The ferrets with their claws drag outside all the rabbits they catch, or else force them to flee into the open, where men, stationed at the hole, catch them as they are driven out. The abundance of the exports of Turdetania is indicated by the size and the number of the ships; for merchantmen of the greatest size sail from this country to Dicaearchia, and to Ostia, the seaport of Rome; and their number very nearly rivals that of the Libyan ships.
7 Although the interior of Turdetania is so productive, it will be found that the seaboard vies with it in its goodly products from the sea. For the various kinds of oysters as well as mussels are in general surpassing, both in their number and in their size, along the whole of the exterior sea; but especially so here, inasmuch as the flood-tides and the ebb-tides have increased power here, and these tides, it is reasonable to suppose, are, on account of the exercise they give, responsible both for the number and the size of them. So it is, in the same way, with respect to all the cetaceans; narwhals, "phalaenae" and spouting-whales; when these spout, the distant observer seems to see a cloud-like pillar. And further, the conger-eels become monsters, far exceeding in size those of Our Sea; and so do the lampreys and several other edible fish of the kind. And at Carteia, it is said, there are shells of trumpet-fish and purple-fish which hold ten cotylae, and in the regions farther out to sea the lamprey and the conger-eel weigh even more than eighty minae, the sea-polypus a talent, the cuttle-fish are two cubits long — and other things in like proportion. Again, large numbers of plump, fat tunny-fish congregate hither from the other coast, namely, that outside the Pillars. And they feed on the acorns of a certain very stunted oak that grows at the bottom of the sea and produces very large fruit. This oak also grows in abundance on the dry land, in Iberia; and although its roots are large like those of a full-grown oak, yet it does not grow as high as a low bush. But the sea-oak brings forth so much fruit that, after the ripening, the seacoast, both inside and outside the Pillars, is covered with the acorns, for they are cast ashore by the tides. However, those inside the Pillars are always smaller, and are to be found in greater quantities. Polybius tells us that the sea casts these acorns ashore even as far as Latium, unless perhaps, says he, also Sardinia and the neighbouring land produce them. And further, the nearer the tunny-fish approach the Pillars, in coming from the exterior sea, the leaner they become, since their food fails them. This creature, says Polybius, is therefore a sea-hog, for it is fond of the acorn and gets exceedingly fat on it; and whenever the sea-oak has produced a large crop of acorns, there is also a large crop of tunny-fish.
8 Now, although the aforesaid country has been endowed with so many good things, still one might welcome and admire, not least of all, but even most of all, its natural richness in metals. For the whole country of the Iberians is full of metals, although not all of it is so rich in fruit, or so fertile either, and in particular that part of it which is well supplied with metals. It is rare for a country to be fortunate in both respects, and it is also rare for the same country to have within a small area an abundance of all kinds of metals. But as for Turdetania and the territory adjoining it, there is no worthy word of praise left to him who wishes to praise their excellence in this respect. Up to the present moment, in fact, neither gold, nor silver, nor yet copper, nor iron, has been found anywhere in the world, in a natural state, either in such quantity or of such good quality. And the gold is not only mined, but is also washed down; that is, the gold-bearing sand is carried down by the rivers and the torrents, although it is often found in the waterless districts also; but in these districts it cannot be seen, whereas in the flooded districts the gold-dust glitters. Besides, they flood the waterless districts by conducting water thither, and thus they make the gold-dust glitter; and they also get the gold out by digging pits, and by inventing other means for washing the sand; and the so‑called "gold-washeries" are now more numerous than the gold mines. The Galatae hold that their own mines, both those in the Cemmenus Mountains and those situated at the foot of the Pyrenees themselves, are equal to those of Turdetania; the metals from the latter, however, are held in greater esteem. And in the gold-dust, they say, nuggets weighing as much as half a pound are some found, which are called "palae," and they need but little refining. They further say that when stones are split they find in them small nuggles resembling nipples, and when the gold is smelted and refined by means of a sort of styptic earth the residuum thereof is "electrum"; and, again, that when this electrum, which contains a mixture of silver and gold, is smelted, the silver is burned away, while the gold remains. For the alloy-type is easily fused and stone-like. For this reason, too, the gold is preferably melted with chaff-fire, because the flame, on account of its softness, is suitable to a substance that yields and fuses easily; but the charcoal-fire consumes much of it because, owing to its intensity, it over-melts the gold and carries it off as vapour.a The soil is carried along in the streams, and is washed in by troughs; or else a pit is dug, and the soil that has been accumulated is there washed. They build the silver-smelting furnaces with high chimneys, so that the gas from the ore may be carried high into the air; for it is heavy and deadly. Some of the copper-mines are called gold-mines, and from this fact it is inferred that in former times gold was mined from them.
9 Poseidonius, in praising the quantity and the excellence of these ores, does not abstain from his usual rhetorical speech; indeed, he enthusiastically concurs with the extravagant stories told; for example, he does not discredit the story, he says, that, when on a time the forests had been burned, the soil, since it was composed of silver and gold ores, melted and boiled out over the surface, because, as he says, every mountain and every hill is bullion heaped up there by some prodigal fortune. And, in general, he says, anyone who had seen these regions would declare that they are everlasting storehouses of nature, or a never-failing treasury of an empire. For the country was, he adds, not only rich, but also rich down below; and with the Turdetanians it is verily Pluto, and not Hades, who inhabits the region down below. Such, then, are the flowery utterances of Poseidonius on this subject — himself drawing much of his language from a mine, as it were. Again, in speaking of the industry of the miners, he cites the statement of Demetrius of Phalerum. Demetrius, he says, states in reference to the Attic silver-mines, that the people dig as strenuously as if they expected to bring up Pluto himself. So Poseidonius implies that the energy and industry of the Turdetanian miners is similar, since they cut their shafts aslant and deep, and, as regards the streams that meet them in the shafts, oftentimes draw them off with the Egyptian screw. However, the whole affair, he says, is never the same for these miners as for the Attic miners; indeed, for the latter, mining is like a riddle: "What they took up," he says, "they did not take, yet what they had, they lost"; but, for the Turdetanians, mining is profitable beyond measure, since one-fourth of the ore brought out by their copper-workers is pure copper, while some of their private adventurers who search for silver pick up within three days a Euboean talent of silver. Tin, however, is not found there on the surface of the ground, he says, as the historians continually repeat, but is dug up; and it is produced both in the country of the barbarians who live beyond Lusitania, and in the Cassiterides Islands; and tin is brought to Massilia from the British Islands also. But among the Artabrians, who live farthest on the north-west of Lusitania, the soil "effloresces," he says, with silver, tin, and "white gold" (for it is mixed with silver). This soil, however, he adds, is brought by the streams; and the women scrape it up with shovels and wash it in sieves woven basket-like. Such, then, is what Poseidonius has said about the mines.
Polybius, in mentioning the silver-mines of New Carthage, says that they are very large; that they are distant from the city about twenty stadia and embrace an area four hundred stadia in circuit; and that forty thousand workmen stay there, who (in his time) bring into the Roman exchequer a daily revenue of twenty-five thousand drachmae. But as for the processes of the work, I omit all he says about it (for it is a long story) except what he says of the silver-bearing ore that is carried along in the streams, namely, that it is crushed and by means of sieves disengaged in water; then the sediment is again crushed, and again strained through (the waters meantime being poured off), and crushed; then the fifth sediment is smelted, and, after the lead has been poured off, yields the pure silver. The silver-mines are still being worked at the present time; they are not state-property, however, either at New Carthage or anywhere else, but have passed over to private ownership. But the majority of the gold-mines are state-property. Both in Castalo and elsewhere there is a special metal of mined lead; this, too, has a slight quantity of silver mixed with it, though not enough to make the refining of it profitable.
Not very far from Castalo is also the mountain in which the Baetis is said to rise; it is called "Silver Mountain" on account of the silver-mines that are in it. According to Polybius, however, both this river and the Anas, though distant from each other as much as nine hundred stadia, rise in Celtiberia; for, as a result of their growth in power, the Celtiberians caused the whole neighbouring country to have the same name as their own. The ancients seem to have called the Baetis River "Tartessus"; and to have called Gades and the adjoining islands "Erytheia"; and this is supposed to be the reason why Stesichorus spoke as he did about the neat-herd of Geryon, namely, that he was born "about opposite famous Erytheia, beside the unlimited, silver-rooted springs of the river Tartessus, in a cavern of a cliff." Since the river had two mouths, a city was planted on the intervening territory in former times, it is said, — a city which was called "Tartessus," after the name of the river; and the country, which is now occupied by Turdulians, was called "Tartessis." Further, Eratosthenes says that the country adjoining Calpe is called "Tartessis," and that Erytheia is called "Blest Isle." Eratosthenes is contradicted by Artemidorus, who says that this is another false statement of Eratosthenes, like his statement that the distance from Gades to the Sacred Cape is a five days' sail (although it is not more than one thousand seven hundred stadia), and his statement that the tides come to an end at the Sacred Cape (although the tides take place round the whole circuit of the inhabited world), and his statement that the northerly parts of Iberia afford an easier passage to Celtica than if you sail thither by the ocean; and, in fact, every other statement which he had made in reliance upon Pytheas, on account of the latter's false pretensions.
The poet, man of many voices, so to speak, and of wide information, affords us grounds for the argument that even these regions were not unheard of by him, if one were only willing to argue scientifically from both statements that are made about these regions, not only from the worse, but also from the better and more truthful. Worse, namely, the statement that Tartessus was known by hearsay as "farthermost in the west," where, as the poet himself says, falls into Oceanus "the sun's bright light, drawing black night over earth, the grain-giver." Now, that night is a thing of evil omen and associated with Hades, is obvious; also that Hades is associated with Tartarus. Accordingly, one might reasonably suppose that Homer, because he heard about Tartessus, named the farthermost of the nether-regions Tartarus after Tartessis, with a slight alteration of letters; and that he also added a mythical element, thus conserving the creative quality of poetry. Just as the poet, because he knew that the Cimmerians had taken their abode in northern and gloomy regions about the Bosporus, settled them in the neighbourhood of Hades, though perhaps he did it also in accordance with a certain common hatred of the Ionians for this tribe (indeed, it was in the time of Homer, or shortly before his time, they say, that that Cimmerian invasion which reached as far as Aeolis and Ionia took place). Again, the poet modelled his "Planctae" after the "Cyaneae," always bringing in his myths from some historical fact or other. For example, he tells a mythical story of certain rocks that are dangerous, just as they say the Cyaneae are (from which fact the Cyaneae are also called "Symplegades"), and this is the reason why he cited Jason's voyage through them. But both the strait at the Pillars and that at Sicily suggested to him the myth about the Planctae. As regards that worse statement, therefore, one might get a hint from the mythical invention of Tartarus that Homer had in mind the regions about Tartessus.
As regards the latter, on the other hand, one might get hints from the following: In the first place, the expeditions of Heracles and of the Phoenicians, since they both reached as far as Iberia, suggested to Homer that the people of Iberia were in some way rich, and led a life of ease. Indeed, these people became so utterly subject to the Phoenicians that the greater number of the cities in Turdetania and of the neighbouring places are now inhabited by the Phoenicians. Secondly, the expedition of Odysseus, as it seems to me, since it actually had been made to Iberia, and since Homer had learned about it through inquiry, gave him an historical pretext; and so he also transferred the Odyssey, just as he had already transferred the Iliad, from the domain of historical fact to that of creative art, and to that of mythical invention so familiar to the poets. For not only do the regions about Italy and Sicily and certain other regions betray signs of such facts, but in Iberia also a city of Odysseia is to be seen, and a temple of Athene, and countless other traces, not only of the wanderings of Odysseus, but also of other wanderings which took place thither after the Trojan War and afflicted the capturers of Troy quite as much as it did the vanquished (for the capturers, as it happened, carried off only a Cadmean victory). And since the Trojan homes were in ruins, and the booty that came to each Greek was but small, the result was that the surviving Trojans, after having escaped from the perils of the war, turned to acts of piracy, as did also the Greeks; the Trojans, because their city was now in utter ruins; the Greeks, for shame, since every Greek took it for granted that it was "verily shameful to wait long" far from his kindred "and then" back to them "empty-handed go." Thirdly, the wanderings of Aeneas are a traditional fact, as also those of Antenor, and those of the Henetians;similarly, also, those of Diomedes, Menelaus, Odysseus, and several others. So then, the poet, informed through his inquiries of so many expeditions to the outermost parts of Iberia, and learning by hearsay about the wealth and the other good attributes of the country (for the Phoenicians were making these facts known), in fancy placed the abode of the blest there, and also the Elysian Plain, where Proteus says Menelaus will go and make his home: "But the deathless gods will escort thee to the Elysian Plain and the ends of the earth, where is Rhadamanthys of the fair hair, where life is easiest. No snow is there, nor yet great storm, nor ever any p57rain; but always Oceanus sendeth forth the breezes of clear-blowing Zephyrus." For both the pure air and the gentle breezes of Zephyrus properly belong to this country, since the country is not only in the west but also warm; and the phrase "at the ends of the earth" properly belongs to it, where Hades has been "mythically placed," as we say. And Homer's citing of Rhadamanthys suggests the region that is near Minos, concerning whom he says: "There it was I saw Minos, glorious son of Zeus, holding a golden sceptre, rendering decisions to the dead." Furthermore, the poets who came after Homer keep dinning into our ears similar stories: the expedition of Heracles in quest of the kine of Geryon and likewise the expedition which he made in quest of the golden apples of the Hesperides — even calling by name certain Isles of the Blest, which, as we know, are still now pointed out, not very far from the headlands of Maurusia that lie opposite to Gades.
The Phoenicians, I say, were the informants of Homer; and these people occupied the best of Iberia and Libya before the age of Homer, and continued to be masters of those regions until the Romans broke up their empire. The wealth of Iberia is further evidenced by the following facts: the Carthaginians who, along with Barcas, made a campaign against Iberia found the people in Turdetania, as the historians tell us, using silver feeding-troughs and wine-jars. And one might assume that it was from their great prosperity that the people there got the additional name of "Macraeones," and particularly the chieftains; and that this is why Anacreon said as follows: "I, for my part, should neither wish the horn of Amaltheia, nor to be king of Tartessus for one hundred and fifty years"; and why Herodotus recorded even the name of the king, whom he called Arganthonius. For one might either take the phrase of Anacreon literally or as meaning "a time equal to the king's," or else in a more general way, "nor the king of Tartessus for a long time." Some, however, call Tartessus the Carteia of to‑day.
Along with the happy lot of their country, the qualities of both gentleness and civility have come to the Turdetanians; and to the Celtic peoples, too, on account of their being neighbours to the Turdetanians, as Polybius has said, or else on account of their kinship; but less so the Celtic peoples, because for the most part they live in mere villages. The Turdetanians, however, and particularly those that live about the Baetis, have completely changed over to the Roman mode of life, not even remembering their own language any more. And most of them have become Latins, and they have received Romans as colonists, so that they are not far from being all Romans. And the present jointly-settled cities, Pax Augusta in the Celtic country, Augusta Emerita in the country of the Turdulians, Caesar-Augusta near Celtiberia, and some other settlements, manifest the change to the aforesaid civil modes of life. Moreover, all those Iberians who belong to this class are called "Togati." And among these are the Celtiberians, who were once regarded the most brutish of all. So much for the Turditanians. |
|
|
|








|
3 - 3 Polybius makes six zones 
Polybius makes six zones: two that fall beneath the arctic circles, two between the arctic circles and the tropics, and two between the tropics and the geography; with physics, in relation both to the celestial phenomena and to the temperature of the atmosphere; in relation to the celestial phenomena, because, by means of the "periscian" and the "heteroscian" and the "amphiscian" regions (the best way to determine the zone), the appearance of the constellations to our sight is at the same time determined; for thus, by a kind of rough-outline division, the constellations receive their proper variations; and in relation to the temperature of the atmosphere, because the temperature of the atmosphere, being judged with reference to the sun, is subject to three very broad differences — namely, excess of heat, lack of heat, and moderate heat, which have a strong bearing on the organisations of animals and plants, and the semi-organisations of everything else beneath the air or in the air itself. And the temperature of the atmosphere receives its proper determination by this division of the earth into five zones: for the two frigid zones imply the absence of heat, agreeing in the possession of one characteristic temperature; and in like manner the two temperate zones agree in one temperature, that of moderate heat; while the one remaining is consistent in having the remaining characteristic, in that it is one and torrid in temperature. And it is clear that this division is in harmony with geography. For geography seeks to define by boundaries that section of the earth which we inhabit by means of the one of the two temperate zones. Now on the west and on the east it is the sea that fixes its limits, but on the south and the north the nature of the air; for the air that is between these limits is well-tempered both for plants and for animals, while the air on both sides of these limits is harsh-tempered, because of excess of heat or lack of heat. It was necessary to divide the earth into five zones corresponding to these three differences of temperature; indeed, the cutting of the sphere of the earth by the equator into two hemispheres, the northern hemisphere in which we live, and the southern hemisphere, suggested the three differences of temperature. For the regions on the equator and in the torrid zone are uninhabitable because of the heat, and those near the pole are uninhabitable because of the cold; but it is the intermediate regions that are well-tempered and inhabitable. But when he adds the two zones beneath the tropics, Poseidonius does not follow the analogy of the five zones, nor yet does he employ a like criterion; but he was apparently representing zones by the ethnical criteria also, for he calls one of them the "Ethiopic zone," another the "Scythico-Celtic zone," and a third the "intermediate zone."
2 Polybius is not right in this, namely, in that he defines some of his zones by means of the arctic circles: two that fall under the arctic circles themselves, and two between the arctic circles and the tropics; for, as I have already said, non-variables must not be defined by points that are variable. And we must also not employ the tropics as boundaries of the torrid zone; this, too, I have already said. However, when he divides the torrid zone into two parts, it is clearly no foolish notion that has moved him to do so; it is by this notion that we very suitably use the equator to divide the whole earth into two parts, namely, the northern and the southern hemispheres. For it is clear that, if the torrid zone as well is divided according to this method of partition, Polybius reaches a convenient result; that is, each of the two hemispheres is composed of three whole zones, each of which is like in form to its corresponding zone in the other hemisphere. Now a partition of this kind admits of the division into six zones; but the other partition does not altogether admit of it. At all events, if you should cut the earth into two parts by means of the circle that runs through the poles, you could not reasonably divide each of the two hemispheres, the western and the eastern, into six zones, but the division into five zones would be sufficient; for the homogeneousness of the two sections of the torrid zone that are made by the equator, and the fact that they are contiguous to each other, render their partition useless and superfluous, indeed, alike in form respectively, though they are not contiguous. So, therefore, if you conceive of the whole earth as composed of hemispheres of this kind it will be sufficient to divide it into five zones. But if the country that lies under the equator is temperate, as Eratosthenes says it is (an opinion with which Polybius agrees, though he adds this, that it is the highest part of the earth, and for that reason is subject to rains, because at the season of the Etesian Winds the clouds from the north strike in great numbers against the mountain peaks in that region), it would be much better to regard it as a third temperate zone, although a narrow one, than to introduce the two zones beneath the tropics. And in accord with these circumstances are the following (which Poseidonius has already mentioned), namely, that in those regions the oblique motion of the sun is more rapid, and in the same way its daily motion from east to west; for when revolutions are accomplished within the same period of time, those on the greatest circles are the more rapid.
3 But Poseidonius objects to the statement of Polybius that the inhabited region under the equator is the highest. For, says Poseidonius, there can be no high point on a spherical surface, because the surface of a sphere is uniform all round; and indeed the country under the equator is not mountainous, but rather it is a plain that is approximately on a level with the surface of the sea; and the rains that flood the Nile come together from the mountains of Ethiopia. But although Poseidonius thus expresses himself in this passage, he concedes the view of Polybius in other passages, saying he suspects that there are mountains beneath the equator and that the clouds from the two temperate zones strike against those mountains on both sides and cause the rains. Now here the lack of consistency is obvious; but even if it be admitted that the country beneath the equator is mountainous, another inconsistency, as it seems, would arise; for these same men assert that the ocean is one continuous stream round the earth. How, pray, can they place mountains in the centre of the ocean — unless by "mountains" they refer to certain islands? But however this may be, it falls outside the province of geography; and perhaps we should give over these matters for examination to some one who proposes to write a treatise on the ocean.
4 In giving the names of those who are said to have circumnavigated Libya Poseidonius says that Herodotus believes that certain men commissioned by Neco accomplished the circumnavigation of Libya; and adds that Heracleides of Pontus in one of his Dialogues makes a certain Magus who had come to the court of Gelo assert that he had circumnavigated Libya. And, after stating that these reports are unsupported by testimony, he tells the story of a certain Eudoxus of Cyzicus, a sacred ambassador and peace herald at the festival of Persephone. Eudoxus, the story goes, came to Egypt in the reign of Euergetes the Second;1and he became associated with the king and the king's ministers, and particularly in connection with the voyages up the Nile; for he was a man inclined to admire the peculiarities of regions and was also not uninformed about them. Now it so happened, the story continues, that a certain Indian was brought to the king by the coast-guards of the recess of the Arabian Gulf, who said that they had found him half-dead and alone on a stranded ship, but that they did not know who he was or where he came from, since they did not understand his language; and the king gave the Indian into the charge of men who would teach him Greek; and when the Indian had learned Greek, he related that on his voyage from India he by a strange mischance mistook his course and reached Egypt in safety, but only after having lost all his companions by starvation; and when his story was doubted, he promised to act as guide on the trip to India for the men who had been previously selected by the King; and of this party Eudoxus, also, became a member.
So Eudoxus sailed away with presents; and he returned with a cargo of perfumes and precious stones (some of which the rivers bring down with the sands, while others are fortified by digging, being solidified from a liquid state, just as our crystals are). But Eudoxus was wholly deceived in his expectations, for Euergetes took from him his entire cargo. And after the death of Euergetes, his wife, Cleopatra, succeeded him on the throne; and so Eudoxus was again sent out, by her also, and this time with a larger outfit. But on his return voyage he was driven out of his course by the winds to the south of Ethiopia, and being driven to certain places he conciliated the people by sharing with them bread, wine, and dried figs (for they had no share of such things), and in return therefor he received a supply of fresh water and the guidance of pilots, and he also made a list of some of their words. And he found an end of a wooden prow that had come from a wrecked ship and had a horse carved on it; and when he learned that this piece of wreckage belonged to some voyagers who had been sailing from the west, he took it with him when he turned back upon his homeward voyage. And when he arrived safely in Egypt, inasmuch as Cleopatra no longer reigned but her son in her stead, he was again deprived of everything, for it was discovered that he had stolen much property. But he brought the figure-head to the market-place and showed it to the shipmasters, and learned from them that it was a figure-head from Gades; for he was told that whereas the merchants of Gades fit out large ships, the poor men fit out small ships which they call "horses" from the devices on the prows of their ships, and that they sail with these small ships on fishing voyages around the coast of Maurusia as far as the river Lixus; but some of the shipmasters, indeed, recognized the figure-head as having belonged to one of the ships that had sailed rather too far beyond the Lixus River and had not returned home safely.
And from the above-mentioned fact Eudoxus conjectured that the circumnavigation of Libya was possible, went home, placed all his property on a ship, and put out to sea. First he put in at Dicaearchia, then at Massilia, and then at the successive points along the coast until he came to Gades; and everywhere noisily proclaiming his scheme and making money by trafficking, he built a great ship and also two tow-boats like those used by pirates; and he put music-girls on board, and physicians, and other artisans, and finally set sail on the high sea on the way to India, favoured by constant western breezes. But since his companions became tired of the voyage, he sailed with a fair wind towards the land; though he did it against his will, for he feared the ebb and flow of the tides. And, indeed, what he feared actually came to pass: the ship ran aground, — though so gently that it was not broken up all at once, and they succeeded in bringing safely to land the cargo and also most of the ship's timbers' and from these timbers he constructed a third boat about as large as a ship of fifty oars; and he continued his voyage, until he came to people who spoke the same words that he had made a list of on the former occasion; and forthwith he learnt this, at least, that the men in that region belonged to the same nation as those other Ethiopians, and also that they were neighbours to the kingdom of Bogus.
Accordingly, he abandoned the voyage to India and turned back; and on the voyage along the coast, he espied and made note of an island that was well-watered and well-wooded but uninhabited. And when he reached Maurusia safely he disposed of his boats, travelled on foot to the court of Bogus, and advised him to take up this expedition on his own account; but the friends of Bogus prevailed to the contrary, inspiring in him the fear that Maurusia might in consequence be easily exposed to hostile intrigue if the way thither had once been pointed out to outsiders who wished to attack it. And when Eudoxus heard that he was being sent out, ostensibly, on the expedition as proposed by him, but in reality was going to be placed out on some desert island, he fled to the territory that was under Roman dominion, and thence crossed over to Iberia. And again he built a round ship and a long ship of fifty oars, his purpose being to keep to the open sea with his long ship and to explore the coast with the round ship. He put on board agricultural implements, seeds, and carpenters, and again set out with a view to the same circumnavigation; his intention being, in case the voyage should be delayed, to spend the winter on the island he had previously observed, to sow the seed, reap the harvest therefrom, and then finish the voyage which he had decided upon at the outset.
5 "Now I," says Poseidonius, "have traced the story of Eudoxus to this point, but what happened afterwards probably the people of Gades and Iberia know." So from all these indications he says it is shown that the ocean flows in a circle round the inhabited world: "For him no fetters of continent encompass; but he pours forth his waters boundlessly, and nothing ever sullies their purity." Now Poseidonius is a wonderful fellow in all this; for although he considers as unsupported by testimony the story of the voyage of the Magus, which Heracleides told, and of the voyage even of the emissaries of Neco, of which Herodotus gives an account, he puts down as real evidence this Bergaean story, though he either invented it himself or accepted it from others who were its inventors. For, in the first place, what plausibility is there in the "strange mischance" which the Indian tells about? Why, the Arabian Gulf is like a river in its narrowness, and it is about fifteen thousand stadia long up to its mouth, which, in its turn, is narrow throughout its entire length; and so it is not likely that the Indians who were voyaging outside this gulf were pushed out of their course into it by mistake (for its narrowness at its mouth would have shown their mistake), nor, if they sailed into the gulf on purpose, did they any longer have the excuse that they mistook their course or encountered inconstant winds. And how can it be that they permitted all their number to die of starvation with the exception of one man? And if he survived, how could he single-handed have guided the ship, which was not a small one, since at all events it could sail over open seas of so great extent? And how strange his speedy mastery of the Greek language, which enabled him to convince the king that he was competent to act as pilot of the expedition? And how strange Euergetes' scarcity of competent pilots, since the sea in that region was already known to many men? And as for that peace herald and sacred ambassador of the people of Cyzicus, how came he to abandon his native city and go sailing to India? And how did he come to be entrusted with so great an office? And although on his return everything was taken away from him, contrary to his expectation, and he was in disgrace, how did he come to be entrusted with a still greater equipment of presents? And when he returned from this second voyage and was driven out of his course to Ethiopia, why did he write down those lists of words, and why did he enquire from what source the beak of that fishing-smack had been cast ashore? For the discovery that this bit of wreckage had belonged to men who sailed from the west could have signified nothing, since he himself was to sail from the west on his homeward voyage. And so, again, upon his return to Alexandria, when it was discovered that he had stolen much property, how is it that he was not punished, and that he even went about interviewing shipmasters, at the same time showing them the figure-head of the ship? And wasn't the man that recognized the figure-head a wonderful fellow? And wasn't the man that believed him a still more wonderful fellow — the man who on the strength of a hope of that sort returned to his home land, and then changed his home to the regions beyond the Pillars? But it would not even have been permitted him to put to sea from Alexandria without a passport, least of all after he had stolen property belonging to the king. Neither could he have sailed out of the harbour secretly, since not only the harbour, but also all the other ways of issue from the city had always been kept closed under just as strong guard as I know is still kept up to this day (for I have lived a long time in Alexandria) — though at the present time, under Roman control, the watch is considerably relaxed: but under the kings, the guards were much more strict. And, again, when Eudoxus had sailed away to Gades, and in royal style had built himself ships and continued on his voyage, after his vessel had been wrecked, how could he have built a third boat in the desert? And how is it, when once more he put out to sea and found that those western Ethiopians spoke the same language as the eastern Ethiopians, that he was not eager to accomplish the rest of his voyage (inasmuch as he was so foolish in his eagerness for travels abroad, and since he had a good hope that the unexplored remainder of his voyage was but small) — but instead gave up all this and conceived a longing for the expedition that was to be carried out through the aid of Bogus? And how did he come to learn about the plot that was secretly framed against him? And what advantage could this have been to Bogus — I mean his causing the disappearance of the man when he might have dismissed him in other ways? But even if the man learned about the plot, how could he have made his escape to places of safety? For, although there is nothing impossible in any escapes of that sort, yet every one of them is difficult and rarely made even with a streak of good luck; but Eudoxus is always attended by good luck, although he is placed in jeopardies one after another. And, again, after he had escaped from Bogus, why was he not afraid to sail once more along the coast of Libya when he had an outfit large enough to colonise an island?
Now, really, all this does not fall short of the fabrications of Pytheas, Euhemerus and Antiphanes. Those men, however, we can pardon for their fabrications — since they follow precisely this as their business — just as we pardon jugglers; but who could pardon Poseidonius, master of demonstration and philosopher, whom we may almost call the claimant for first honours. So much, at least, is not well done by Poseidonius.
6 On the other hand, he correctly sets down in his work the fact that the earth sometimes rises and undergoes settling processes, and undergoes changes that result from earthquakes and the other similar agencies, all of which I too have enumerated above. And on this point he does well to cite the statement of Plato that it is possible that the story about the island of Atlantis is not a fiction. Concerning Atlantis Plato relates that Solon, after having made inquiry of the Egyptian priests, reported that Atlantis did once exist, but disappeared — an island no smaller in size than a continent; and Poseidonius thinks that it is better to put the matter in that way than to say of Atlantis: "Its inventor caused it to disappear, just as did the Poet the wall of the Achaeans." And Poseidonius also conjectures that migration of the Cimbrians and their kinsfolk from their native country occurred as the result of an inundation of the sea that came on all of a sudden. And he suspects that the length of the inhabited world, being about seventy thousand stadia, is half of the entire circle on which it has been taken, so that, says he, if you sail from the west in a straight course you will reach India within the seventy thousand stadia.
7 Then, after an attempt to find fault with those who divided the inhabited world into continents in the way they did, instead of by certain circles parallel to the equator (through means of which they could have indicated variations in animals, plants, and climates, because some of these belong peculiarly to the frigid zone and others to the torrid zone), so that the continents would be practically zones, Poseidonius again revises his own plea and withdraws his indictment, in that he again approves of the prevailing division into three continents, and thus he makes the question a mere matter of argument with no useful end in view. For such a distribution of animals, plants, and climates as exists is not the result of design — just as the differences of race, or of language, are not, either — but rather of accident and chance. And again, as regards the various arts and faculties and institutions of mankind, most of them, when once men have made a beginning, flourish in any latitude whatsoever and in certain instances even in spite of the latitude; so that some local characteristics of a people come by nature, others by training and habit. For instance, it was not by nature that the Athenians were fond of letters, whereas the Lacedaemonians, and also the Thebans, who are still closer to the Athenians, were not so; but rather by habit. So, also, the Babylonians and the Egyptians are philosophers, not by nature, but by training and habit. And further, the excellent qualities of horses, cattle, and other animals, are the result, not merely of locality, but of training also. But Poseidonius confounds all this. And when he approves of such a division into three continents as is now accepted, he uses as an illustration the fact that the Indians differ from the Ethiopians of Libya, for the Indians are better developed physically and less parched by the dryness of the atmosphere. And, says he, that is the reason why Homer, in speaking of the Ethiopians as a whole, divides them into two groups, "some where Hyperion sets and some where he rises." But, says Poseidonius, Crates, in introducing into the discussion the question of a second inhabited world, about which Homer knows nothing, is a slave to hypothesis, and, says Poseidonius, the passage in Homer should have been emended to read: "both where Hyperion departs," meaning where he declines from the meridian.
8 Now, in the first place, the Ethiopians that border on Egypt are themselves, also, divided into two groups; for some of them live in Asia, others in Libya, though they differ in no respect from each other. And, in the second place, Homer divides the Ethiopians into two groups, not for this reason, namely, because he knew that the Indians were physically similar to the Ethiopians (for Homer probably did not know of the Indians at all, in view of the fact that even Euergetes himself, according to that story of Eudoxus, knew nothing about India, nor the voyage that leads thither), but rather on the basis of the division of which I have spoken above. And in speaking on that subject I also expressed my opinion in regard to the reading proposed by Crates, namely, that it makes no difference whether we read the passage one way or the other; but Poseidonius says it does make a difference, and that it is better to emend the passage to read "both where Hyperion departs." Now wherein does this differ from "both where Hyperion sets"? For the whole segment of the circle from the meridian to the setting is called "the setting," just as the semi-circle of the horizon is so called. This is what Aratus means when he says: "There where the extremities of the west and of the east join with each other." And if the passage is better as Crates reads it, then one may say that it must also be better as Aristarchus reads it.
So much for Poseidonius. For in my detailed discussions many of his views will meet with fitting criticism, so far as they relate to geography; but so far as they relate to physics, I must inspect them elsewhere or else not consider them at all. For in Poseidonius there is much inquiry into causes and much imitating of Aristotle — precisely what our school avoids, on account of the obscurity of the causes. |
|
|
|

|
3 - 4 
Polybius, in his account of the geography of Europe, says he passes over the ancient geographers but examines the men who criticise them, namely, Dicaearchus, and Eratosthenes, who has written the most recent treatise on Geography; and Pytheas, by whom many have been misled; for after asserting that he travelled over the whole of Britain that was accessible Pytheas reported that the coast-line of the island was more than forty thousand stadia, and added his story about Thule and about those regions in which there was no longer either land properly so‑called, or sea, or air, but a kind of substance concreted from all these elements, resembling a sea-lungs — a thing in which, he says, the earth, the sea, and all the elements are held in suspension; and this is a sort of bond to hold all together, which you can neither walk nor sail upon. Now, as for this thing that resembles the sea-lungs, he says that he saw it himself, but that all the rest he tells from hearsay. That, then, is the narrative of Pytheas, and to it he adds that on his return from those regions he visited the whole coast-line of Europe from Gades to the Tanaïs.
2 Now Polybius says that, in the first place, it is incredible that a private individual — and a poor man too — could have travelled such distances by sea and by land; and that, though Eratosthenes was wholly at a loss whether he should believe these stories, nevertheless he has believed Pytheas' account of Britain, and the regions about Gades, and of Iberia; but he says it is far better to believe Euhemerus, the Messenian, than Pytheas. Euhemerus, at all events, asserts that he sailed only to one country, Panchaea, whereas Pytheas asserts that he explored in person the whole northern region of Europe as far as the ends of the world — an assertion which no man would believe, not even if Hermes made it. And as for Eratosthenes — adds Poseidonius — though he calls Euhemerus a Bergaean, he believes Pytheas, and that, too, though not even Dicaearchus believed him. Now that last remark, "though not even Dicaearchus believed him," is ridiculous; as if it were fitting for Eratosthenes to use as a standard the man against whom he himself directs so many criticisms. And I have already stated that Eratosthenes was ignorant concerning the western and northern parts of Europe. But while we must pardon Eratosthenes and Dicaearchus, because they had not seen those regions with their own eyes, yet who could pardon Polybius and Poseidonius? Nay, it is precisely Polybius who characterises as "popular notions" the statements made by Eratosthenes and Dicaearchus in regard to the distances in those regions and many other regions, though he does not keep himself free from the error even where he criticises them. At any rate, when Dicaearchus estimates the distance from p403the Peloponnesus to the Pillars at ten thousand stadia, and from the Peloponnesus to the recess of the Adriatic Sea at more than this, and when, of the distance to the Pillars, he reckons the part up to the Strait of Sicily at three thousand stadia, so that the remaining distance — the part from the Strait to the Pillars — becomes seven thousand stadia, Polybius says that he will let pass the question whether the estimate of three thousand is correctly taken or not, but, as for the seven thousand stadia, he cannot let the estimate pass from either of two points of view, namely, whether you take the measure of the coast-line or of the line drawn through the middle of the open sea. For, says he, the coast-line is very nearly like an obtuse angle, whose sides run respectively to the Strait and to the Pillars, and with Narbo as vertex; hence a triangle is formed with a base that runs straight through the open sea and with sides that form the said angle, of which sides the one from the Strait to Narbo measures more than eleven thousand two hundred stadia, the other a little less than eight thousand stadia; and, besides, it is agreed that the maximum distance from Europe to Libya across the Tyrrhenian Sea is not more than three thousand stadia, whereas the distance is reduced if measured across the Sardinian Sea. However, let it be granted, says Polybius, that the latter distance is also three thousand stadia, but let it be further assumed as a prior condition that the depth of the gulf opposite Narbo is two thousand stadia, the depth being, as it were, a perpendicular let fall from the vertex upon the base of the obtuse-angled triangle; then, says Polybius, it is clear from the principles of elementary geometry that the total length of the coast-line from the Strait to the Pillars exceeds the length of the straight line through the open sea by very nearly five hundred stadia. And if to this we added the three thousand stadia from the Peloponnesus to the Strait, the sum total of the stadia, merely those measured on a straight line, will be more than double the estimate given by Dicaearchus. And, according to Dicaearchus, says Polybius, it will be necessary to put the distance from the Peloponnesus to the recess of the Adriatic at more than this sum.
3 But, my dear Polybius, one might reply, just as the test based upon your own words makes evident the error of these false reckonings, namely, "from the Peloponnesus to Leucas, seven hundred stadia; from Leucas to Corcyra the same; and, again, from Corcyra to the Ceraunian Mountains the same; and the Illyrian coast-line to Iapydia on your right hand side, if you measure from the Ceraunian Mountains, six thousand one hundred and fifty stadia," so also those other reckonings are both false — both that made by Dicaearchus when he makes the distance from Strait of Sicily to the Pillars seven thousand stadia, and that which you think you have demonstrated; for most men agree in saying that the distance measured straight across the Sea is twelve thousand stadia, and this estimate agrees with the opinion rendered in regard to the length of the inhabited world. For they say that this length is about seventy thousand stadia, and that the western section thereof, that is, from the Gulf of Issus to the capes of Iberia, which are the most westerly points, is a little less than thirty thousand stadia. They arrive at this result in the following way: From the Gulf of Issus to Rhodes the distance is five thousand stadia; thence to Salmonium, which is the eastern Cape of Crete, one thousand stadia; and the length of Crete itself, from Salmonium to Criumetopon, more than two thousand stadia; thence, from Criumetopon to Pachynum in Sicily, four thousand five hundred stadia; and from Pachynum to the Strait of Sicily, more than one thousand stadia; then, the sea-passage from the Strait of Sicily to the Pillars, twelve thousand stadia; and from the Pillars to the extreme end of the Sacred Cape1of Iberia, about three thousand stadia. And Polybius has not taken even his perpendicular properly, if it be true that Narbo is situated approximately on the same parallel as that which runs through Massilia and (as Hipparchus also believes) Massilia on the same as that through Byzantium, and that the line which runs through the open Sea is on the same parallel as that through the Strait and Rhodes, and that the distance from Rhodes to Byzantium has been estimated at about five thousand stadia on the assumption that both places lies on the same meridian; for the perpendicular in question would also be five thousand stadia in length. But when they say that the longest passage across this sea from Europe to Libya, reckoned from the head of the Galatic Gulf, is approximately five thousand stadia, it seems to me that they make an erroneous statement, or else that in that region Libya projects far to the north and reaches the parallel that runs through the Pillars. And Polybius is again not right when he says that the perpendicular in question ends near Sardinia; for the line of this sea-passage is nowhere near Sardinia, but much farther west, leaving between it and Sardinia not only the Sardinian Sea, but almost the whole of the Ligurian Sea as well. And Polybius has exaggerated the length of the seaboard also, only in a lesser degree.
4 Next in order, Polybius proceeds to correct the errors of Eratosthenes; sometimes rightly, but sometimes he is even more in error than Eratosthenes. For instance, when Eratosthenes estimates the distance from Ithaca to Corcyra at three hundred stadia, Polybius says it is more than nine hundred; when Eratosthenes gives the distance from Epidamnus to Thessalonica as nine hundred stadia, Polybius says more than two thousand; and in these cases Polybius is right. But when Eratosthenes says the distance from Massilia to the Pillars is seven thousand stadia and from the Pyrenees to the Pillars six thousand stadia, Polybius himself makes a greater error in giving the distance from Massilia as more than nine thousand stadia and that from the Pyrenees a little less than eight thousand stadia; for Eratosthenes' estimates are nearer the truth. Indeed, modern authorities agree that if one cut off an allowance for the irregular windings of the roads, the whole of Iberia is not more than six thousand stadia in length from the Pyrenees to its western side. But Polybius reckons the river Tagus alone at eight thousand stadia in length from its source to its mouth — without reckoning in the windings of the river, of course (for this is a thing geography does not do) — but estimating the distance on a straight line. And yet from the Pyrenees the sources of the Tagus are more than one thousand stadia distant. On the other hand, Polybius is right when he asserts that Eratosthenes is ignorant of the geography of Iberia, that is, for the reason that he sometimes makes conflicting statements; at any rate, after he has said that the exterior coast of Iberia as far as Gades is inhabited by Gauls — if they really hold the western regions of Europe as far as Gades — he forgets that statement and nowhere mentions the Gauls in his description of Iberia.
5 Again, when Polybius sets forth that the length of Europe is less than the combined length of Libya and Asia, he does not make his comparison correctly. The outlet at the Pillars, he says, is in the equinoctial west, whereas the Tanaïs flows from the summer rising of the sun, and therefore Europe is less in length than the combined length of Libya and Asia by the space between the summer sunrise and the equinoctial sunrise; for Asia has a prior claim to this space of the northern semicircle that lies toward the equinoctial sunrise. Indeed, apart from the abstruseness which characterises Polybius when he is discussing matters that are easy of explanation, his statement that the Tanaïs flows from the summer rising of the sun is also false; for all who are acquainted with those regions say that the Tanaïs flows from the north into Lake Maeotis, and in such wise that the mouth of the river, the mouth of Lake Maeotis, and the course of the Tanaïs itself, so far as it has been explored, all lie on the same meridian.
6 Unworthy of mention are those writers who have stated that the Tanaïs rises in the regions on the Ister and flows from the west, because they have not reflected that the Tyras, the Borysthenes, and the Hypanis, all large rivers, flow between those two rivers into the Pontus, one of them parallel to the Ister and the others parallel to the Tanaïs. And since neither the sources of the Tyras, nor of the Borysthenes, nor of the Hypanis, have been explored, the regions that are farther north than they would be far less known; and therefore the argument that conducts the Tanaïs through those regions and then makes it turn from them to the Maeotis Lake (for the mouths of the Tanaïs are obviously to be seen in the most northerly parts of the Lake, which are also the most easterly parts) — such an argument, I say, would be false and inconclusive. Equally inconclusive is the argument that the Tanaïs flows through the Caucasus towards the north and then turns and flows into Lake Maeotis; for this statement has also been made. However, no one has stated that the Tanaïs flows from the east; for if it flowed from the east the more accomplished geographers would not be asserting that it flows in a direction contrary to, and in a sense diametrically opposed to, that of the Nile — meaning that the courses of the two rivers are on the same meridian or else on meridians that lie close to each other.
7 The measurement of the length of the inhabited world is made along a line parallel to the equator, because the inhabited world, in its length, stretches in the same way the equator does; and in the same way, therefore, we must take as the length of each of the continents the space that lies between two meridians. Again, the measure employed for these lengths is that by stadia; and we seek to discover the number of the stadia either by travelling through the continents themselves, or else along the roads or waterways parallel to them. But Polybius abandons this method and introduces something new, namely, a certain segment of the northern semicircle, which lies between the summer sunrise and the equinoctial sunrise. But no one employs rules and measures that are variable for things that are non-variable, nor reckonings that are made relative to one position or another for things that are absolute and unchanging. Now while the term "length" is non-variable and absolute, "equinoctial rising" and "setting" and, in the same way, "summer sunrise" and "winter sunrise," are not absolute, but relative to our individual positions; and if we shift our position to different points, the positions of sunset and sunrise, whether equinoctial or solstitial, are different, but the length of the continent remains the same. Therefore, while it is not out of place to make the Tanaïs and the Nile limits of continents, it is something new to use the summer, or the equinoctial, sunrise for this purpose.
8 Since Europe runs out into several promontories, Polybius' account of them is better than that of Eratosthenes, but it is still inadequate. For Eratosthenes spoke of only three promontories: first, the promontory that juts down to the Pillars, on which is Iberia; secondly, that to the Strait of Sicily, on which is Italy; and, thirdly, that which ends at Cape Malea, on which are all the nations that dwell between the Adriatic, the Euxine, and the Tanaïs. But Polybius explains the first two promontories in the same way and then makes a third of the promontory which ends at Cape Malea and Sunium, on which are all Greece, and Illyria, and certain parts of Thrace, and a fourth of the Thracian Chersonese, where the strait between Sestus and Abydus is, inhabited by Thracians; and still a fifth of the promontory in the region of the Cimmerian Bosporus and of the mouth of Lake Maeotis. Now we must grant the first two, because they are encompassed by simple gulfs: one of them, by the gulf that lies between Calpe and the Sacred Cape (the gulf on which Gades is situated) and also by that portion of the sea that lies between the Pillars and Sicily; the other, by the last-mentioned sea and the Adriatic — although, of course, the promontory of Iapygia, since it thrusts itself forward on the side and thus makes Italy have two crests, presents a sort of contradiction to my statement; but the remaining three promontories, which still more clearly are complex and composed of many members, require further division. Likewise, also, the division of Europe into six parts is open to similar objection, since it has been made in accordance with the promontories. However, in my detailed account I shall make the suitable corrections, not only of these mistakes, but also of all the other serious mistakes that Polybius has made, both in the matter of Europe and in his circuit of Libya. Brief, for the present, I shall rest satisfied with what I have here said in criticism of my predecessors — that is, of so many of them as I have thought would, if cited, make enough witnesses to prove that I too am justified in having undertaken to treat this same subject, since it stands in need of so much correction and addition. |
|
|
|


|
3 - 5 Islands of Iberia: Baleares, Cassiterides, Gades 
1 Since the taking in hand of my proposed task naturally follows the criticisms of my predecessors, let me make a second beginning by saying that the person who attempts to write an account of the countries of the earth must take many of the physical and mathematical principles as hypotheses and elaborate his whole treatise with reference to their intent and authority. For, as I have already said, no architect or engineer would be competent even to fix the site of a house or a city properly if he had no conception beforehand of "climata" and of the celestial phenomena, and of geometrical figures and magnitudes and heat and cold and other such things — much less a person who would fix positions for the whole of the inhabited world. For the mere drawing on one and the same plane surface of Iberia and India and the countries that lie between them and, in spite of its being a plane surface, the plotting the sun's position at its settings, risings, and in meridian, as though these positions were fixed for all the people of the world — merely this exercise gives to the man who has previously conceived of the arrangement and movement of the celestial bodies and grasped the fact that it is depicted for the moment as a plane surface for the convenience of the eye — merely this exercise, I say, gives to that man instruction that is truly geographical, but to the man not thus qualified it does not. Indeed, the case is not the same with us when we are dealing with geography as it is when we are travelling great plains (those of Babylonia, for example) or over the sea: then all that is in front of us and behind us and on either side of us is presented to our minds as a plane surface and offers no varying aspects with reference to the celestial bodies or the movements or the positions of the sun and the other stars relatively to us; but when we are dealing with geography the like parts must never present themselves to our minds in that way. The sailor on the open sea, or the man who travels through a level country, is guided by certain popular notions (and these notions impel not only the uneducated man but the man of affairs as well to act in the self-same way), because he is unfamiliar with the heavenly bodies and ignorant of the varying aspects of things with reference to them. For he sees the sun rise, pass the meridian, and set, but how it comes about he does not consider; for, indeed, such knowledge is not useful to him with reference to the task before him, any more than it is useful for him to know whether or not his body stands parallel to that of his neighbour. But perhaps he does consider these matters, and yet holds opinions opposed to the principles of mathematics — just as the natives of any given place do; for a man's place occasions such blunders. But the geographer does not write for the native of any particular place, nor yet does he write for the man of affairs of the kind who has paid no attention to the mathematical sciences properly so‑called; nor, to be sure, does he write for the harvest-hand or the ditch-digger, but for the man who can be persuaded that the earth as a whole is such as the mathematicians represent it to be, and also all that relates to such an hypothesis. And the geographer urges upon his students that they first master those principles and then consider the subsequent problems; for, he declares, he will speak only of the results which follow from those principles; and hence his students will the more unerringly make the application of his teachings if they listen as mathematicians; but he refuses to teach geography to persons not thus qualified.
2 Now as for the matters which he regards as fundamental principles of his science, the geographer must rely upon the geometricians who have measured the earth as a whole; and in their turn the geometricians must rely upon the astronomers; and again the astronomers upon the physicists. Physics is a kind of Arete; by Aretai they mean those sciences that postulate nothing but depend upon themselves, and contain within themselves their own principles as well as the proofs thereof. Now what we are taught by the physicists is as follows: The universe and the heavens are sphere-shaped. The tendency of the bodies that have weight is towards the centre. And, having taken its position about this centre in the form of a sphere, the earth remains homocentric with the heavens, as does also the axis through it, which axis extends also through the centre of the heavens. The heavens revolve round both the earth and its axis from east to west; and along with the heavens revolve the fixed stars, with the same rapidity as the vault of the heavens. Now the fixed stars move along parallel circles, and the best known parallel circles are the equator, the two tropics, and the arctic circles; whereas the planets and the sun and the moon move along certain oblique circles whose positions lie in the zodiac. Now the astronomers first accept these principles, either in whole or in part, and then work out the subsequent problems, namely, the movements of the heavenly bodies, their revolutions, their eclipses, their sizes, their respective distances, and a host of other things. And, in the same way, the geometricians, in measuring the earth as a whole, adhere to the doctrines of the physicists and the astronomers, and, in their turn, the geographers adhere to those of the geometricians.
3 Thus we must take as an hypothesis that the heavens have five zones, and that the earth also has five zones, and that the terrestrial zones have the same names as the celestial zones (I have already stated the reasons for this division into zones). The limits of the zones can be defined by circles drawn on both sides of the equator and parallel to it, namely, by two circles which enclose the torrid zone, and by two others, following upon these, which form the two temperate zones next to the torrid zone and the two frigid zones next to the temperate zones. Beneath each of the celestial circles falls the corresponding terrestrial circle which bears the same name: and, in like manner, beneath the celestial zone, the terrestrial zone. Now they call "temperate" the zones that can be inhabited; the others they call uninhabitable, the one on account of the heat, and the other on account of the cold. They proceed in the same manner with reference to the tropic and the arctic circles (that is, in countries that admit of arctic circles): they define their limits by giving the terrestrial circles the same names as the celestial — and thus they define all the terrestrial circles that fall beneath the several celestial circles. Since the celestial equator cuts the whole heavens in two, the earth also must of necessity be cut in two by the terrestrial equator. Of the two hemispheres — I refer to the two celestial as well as the two terrestrial hemispheres — one is called "the northern hemisphere" and the other "the southern hemisphere"; so also, since the torrid zone is cut in two by the same circle, the one part of it will be the northern and the other the southern. It is clear that, of the temperate zones also, the one will be northern and the other southern, each bearing the name of the hemisphere in which it lies. That hemisphere is called "northern hemisphere" which contains that temperate zone in which, as you look from the east to the west, the pole is on your right hand and the equator on your left, or in which, as you look towards the south, the west is on your right hand and the east on your left; and that hemisphere is called "southern hemisphere," in which the opposite is true; and hence it is clear that we are in one of the two hemispheres (that is, of course, in the north), and that it is impossible for us to be in both. "Between them are great rivers; first, Oceanus", and then the torrid zone. But neither is there an Oceanus in the centre of our whole inhabited world, cleaving the whole of it, nor, to be sure, is there a torrid spot in it; nor yet, indeed, is there a portion of it to be found whose "climata" are opposite to the "climata" which I have given for the northern temperate zone.
4 By accepting these principles, then, and also by making use of the sun-dial and the other helps given him by the astronomer — by means of which are found, for the several inhabited localities, both the circles that are parallel to the equator and the circles that cut the former at right angles, the latter being drawn through the poles — the geometrician can measure the inhabited portion of the earth by visiting it and the rest of the earth by his calculation of the intervals. In the same way he can find the distance from the equator to the pole, which is a fourth part of the earth's largest circle; and when he has this distance, he multiplies it by four; and this is the circumference of the earth. Accordingly, just as the man who measures the earth gets his principles from the astronomer and the astronomer his from the physicist, so, too, the geographer must in the same way first take his point of departure from the man who has measured the earth as a whole, having confidence in him and in those in whom he, in his turn, had confidence, and then explain, in the first instance, our inhabited world — its size, shape, and character, and its relations to the earth as a whole; for this is the peculiar task of the geographer. Then, secondly, he must discuss in a fitting manner the several parts of the inhabited world, both land and sea, noting in passing wherein the subject has been treated inadequately by those of our predecessors whom we have believed to be the best authorities on these matters.
5 Now let us take as hypothesis that the earth together with the sea is sphere-shaped and that the surface of the earth is one and the same with that of the high seas; for the elevations on the earth's surface would disappear from consideration, because they are small in comparison with the great size of the earth and admit of being overlooked; and so we use "sphere-shaped" for figures of this kind, not as though they were turned on a lathe, nor yet as the geometrician uses the sphere for demonstration, but as an aid to our conception of the earth — and that, too, a rather rough conception. Now let us conceive of a sphere with five zones, and let the equator be drawn as a circle upon that sphere, and let a third circle be drawn parallel thereto, bounding the frigid zone in the northern hemisphere, and let a third circle be drawn through the poles, cutting the other two circles at right angles. Then, since the northern hemisphere contains two-fourths of the earth, which are formed by the equator with the circle that passes through the poles, a quadrilateral area is cut off in each of the two fourths. The northern side of the quadrilateral is half of the parallel next to the pole; the southern side is half of the equator; and the two remaining sides are segments of the circle that runs through the poles, these segments lying opposite to each other and being equal in length. Now in one of these two quadrilaterals (it would seem to make no difference in which one) we say that our inhabited world lies, washed on all sides by the sea and like an island; for, as I have already said above, the evidence of our senses and of reason prove this. But if anyone disbelieves the evidence of reason, it would make no difference, from the point of view of the geographer, whether we make the inhabited world an island, or merely admit what experience has taught us, namely, that it is possible to sail round the inhabited world on both sides, from the east as well as from the west, with the exception of a few intermediate stretches. And, as to these stretches, it makes no difference whether they are bounded by sea or by uninhabited land; for the geographer undertakes to describe the known parts of the inhabited world, but he leaves out of consideration the unknown parts of it — just as he does what is outside of it. And it will suffice to fill out and complete the outline of what we term "the island" by joining with a straight line the extreme points reached on the coasting-voyages made on both sides of the inhabited world.
6 So let us presuppose that the island lies in the aforesaid quadrilateral. We must then take as its p435size the figure that is obvious to our sense, which is obtained by abstracting from the entire size of the earth our hemisphere, then from this area its half, and in turn from this half the quadrilateral in which we say the inhabited world lies and it is by an analogous process that we must form our conception of the shape of the island, accommodating the obvious shape to our hypotheses. But since the segment of the northern hemisphere that lies between the equator and the circle drawn parallel to it next to the pole is a spinning-whorl in shape, and since the circle that passes through the pole, by cutting the northern hemisphere in two, also cuts the spinning-whorl in two and thus forms the quadrilateral, it will be clear that the quadrilateral in which the Atlantic Sea lies is half of a spinning-whorl's surface; and that the inhabited world is a chlamys-shaped island in this quadrilateral, since it is less in size than half of the quadrilateral. This latter fact is clear from geometry, and also from the great extent of the enveloping sea which covers the extremities of the continents both in the east and west and contracts them to a tapering shape; and, in the third place, it is clear from the maximum length and breadth. Now the length of the inhabited world is seventy thousand stadia, being for the most part limited by a sea which still cannot be navigated because of its vastness and desolation; the breadth is less than thirty thousand stadia, being bounded by the regions that are uninhabitable on account either of heat or cold. For merely the part of the quadrilateral that is uninhabitable on account of the heat — since it has a breadth of eight thousand eight hundred stadia and a maximum length of one hundred and twenty six thousand stadia, that is, half the length of the equator — is more than half the inhabited world, and the remainder of the quadrilateral would be still more than that.
7 In essential accord with all this are the views of Hipparchus. He says that, having taken as hypothesis the measurement of the earth as stated by Eratosthenes, he must then abstract the inhabited world from the earth in his discussion; for it will not make much difference with respect to the celestial phenomena for the several inhabited places whether the measurement followed is that of Eratosthenes or that given by the later geographers. Since, then, according to Eratosthenes, the equator measures two hundred and fifty two thousand stadia, the fourth part of it would be sixty three thousand stadia; and this is the distance from the equator to the pole, namely, fifteen sixtieths of the sixty intervals into which the equator is divided. And the distance from the equator to the summer tropic is four sixtieths; and the summer tropic is the parallel drawn through Syene. Now the several distances are computed from the standard measures that are obvious to our senses. The summer tropic, for instance, must pass through Syene, because there, at the time of the summer solstice, the index of the sun-dial does not cast a shadow at noon. And the meridian through Syene is drawn approximately along the course of the Nile from Meroë to Alexandria, and this distance is about ten thousand stadia; and Syene must lie in the centre of that distance; so that the distance from Syene to Meroë is five thousand stadia. And when you have proceeded about three thousand stadia in a straight line south of Meroë, the country is no longer inhabitable on account of the heat, and therefore the parallel though these regions, being the same as that through the Cinnamon-producing Country, must be put down as the limit and the beginning of our inhabited world on the South. Since, then, the distance from Syene to Meroë is five thousand stadia, to which we have added the other three thousand stadia, the total distance from Syene to the confines of the inhabited world would be eight thousand stadia. But the distance from Syene to the equator is sixteen thousand eight hundred stadia (for that is what the four sixtieths amounts to, since each sixtieth is estimated at four thousand two hundred stadia), and therefore we should have eight thousand eight hundred stadia left as the distance from the confines of the inhabited world to the equator, and from Alexandria twenty-one thousand eight hundred. Again, all agree that the route by sea from Alexandria to Rhodes is in a straight line with the course of the Nile, as also the route thence along the coast of Caria and Ionia to the Troad, Byzantium, and the Borysthenes. Taking, therefore, the distances that are already known and sailed over, geographers inquire as to the regions beyond the Borysthenes that lie in a straight course with this line — as to how far they are inhabitable, and how far the northern parts of the inhabited world have their boundaries. Now the Roxolanians, the most remote of the known Scythians, live beyond the Borysthenes, though they are farther south than the most remote peoples of whom we have knowledge north of Britain; and the regions beyond the Roxolanians become at once uninhabitable because of the cold; and farther south than the Roxolanians are the Sarmatians who dwell beyond Lake Maeotis, and also the Scythians as far as the Eastern Scythians.
8 Now Pytheas of Massilia tells us that Thule, the most northerly of the Britannic Islands, is farthest north, and that there the circle of the summer tropic is the same as the arctic circle. But from the other writers I learn nothing on the subject — neither that there exists a certain island by the name of Thule, nor whether the northern regions are inhabitable up to the point where the summer tropic becomes the arctic circle. But in my opinion the northern limit of the inhabited world is much farther to the south than where the summer tropic becomes the arctic circle. For modern scientific writers are not able to speak of any country north of Ierne, which lies to the north of Britain and near thereto, and is the home of men who are complete savages and lead a miserable existence because of the cold; and therefore, in my opinion, the northern limit of our inhabited world is to be placed there. But if the parallel though Byzantium passes approximately through Massilia, as Hipparchus says on the testimony of Pytheas (Hipparchus says, namely, that in Byzantium the relation of the index to the shadow is the same as that which Pytheas gave for Massilia), and if the parallel through the mouth of the Borysthenes is about three thousand eight hundred stadia distant from that parallel, then, in view of the distance from Massilia to Britain,1the circle drawn through the mouth of the Borysthenes would fall somewhere in Britain. But Pytheas, who misleads people everywhere else, is, I think, wholly in error here too; for it has been admitted by many writers that all the line drawn from the Pillars to the regions of Strait of Sicily and of Athens, and of Rhodes, lies on the same parallel; and it is admitted that the part of that line from the Pillars to the strait runs approximately through the middle of the sea. And further, sailors say that the longest passage from Celtica to Libya, namely, that from the Galatic Gulf, is five thousand stadia, and that this is also the greatest width of the Mediterranean sea, and therefore the distance from the line in question to the head of the gulf would be two thousand five hundred stadia and less than that to Massilia; for Massilia is farther south than the head of the gulf. But the distance from Rhodes to Byzantium is about four thousand nine hundred stadia, and therefore the parallel through Byzantium would be much farther north than that through Massilia. And the distance from Massilia to Britain may possibly correspond to that from Byzantium to the mouth of the Borysthenes; but the distance that should be set down for the stretch from Britain to Ierne is no longer a known quantity, nor is it known whether there are still inhabitable regions farther on, nor need we concern ourselves about the question if we give heed to what Hesiod said above. For, so far as science is concerned, it is sufficient to assume that, just as it was appropriate in the case of the southern regions to fix a limit of the habitable world by proceeding three thousand stadia south of Meroë (not indeed as though this were a very accurate limit, but as one that at least approximates accuracy), so in this case too we must reckon not more than three thousand stadia north of Britain, or only a little more, say, four thousand stadia. And for governmental purposesa there would be no advantage in knowing such countries and their inhabitants, and particularly if the people live in islands which are of such a nature that they can neither injure nor benefit us in any way because of their isolation. For although they could have held even Britain, the Romans scorned to do so, because they saw that there was nothing at all to fear from the Britons (for they are not strong enough to cross p447over and attack us), 116and that no corresponding advantage was to be gained by taking and holding their country. For it seems that at present more revenue is derived from the duty on their commerce than the tribute could bring in, if we deduct the expense involved in the maintenance of an army for the purpose of guarding the island and collecting the tribute; and the unprofitableness of an occupation would be still greater in the case of the other islands about Britain.
9 Now if to the distance from Rhodes to the mouth of the Borysthenes we add the distance of four thousand stadia from the mouth of the Borysthenes to the northern regions, the sum total amounts to twelve thousand seven hundred stadia, but the distance from Rhodes to the southern limit of the inhabited world is sixteen thousand six hundred stadia, and therefore the total breadth of the inhabited world would be less than thirty thousand stadia from south to north. Its length, however, is estimated at about seventy thousand stadia; and this is, from west to east, the distance from the capes of Iberia to the capes of India, measured partly by land journeys and partly by sea voyages. And that this length falls within the quadrilateral mentioned above is clear from the relation of the parallels to the equator; hence the length of the inhabited world is more than double its breadth. Its shape is described as about like that of a chlamys; for when we visit the several regions of the inhabited world, we discover a considerable contraction in its width at its extremities, and particularly at its western extremities.
We have now traced on a spherical surface the area in which we say the inhabited world is situated; and the man who would most closely approximate the truth by constructed figures must needs take for the earth a globe like that of Crates, and lay off on it the quadrilateral, and within the quadrilateral put down the map of the inhabited world. But since the need of a large globe, so that the section in question (being a small fraction of the globe) may be large enough to receive distinctly the appropriate parts of the inhabited world and to present the proper appearance to observers, it is better for him to construct a globe of adequate size, if he can do so; and let it be no less than ten feet in diameter. But if he cannot construct a globe of adequate size or not much smaller, he should sketch his map on a plane surface of at least seven feet. For it will make only a slight difference if we draw straight lines to represent the circles, that is, the parallels and meridians, by means of which we clearly indicate the "climata," the winds and the other differences, and also the positions of the parts of the earth with reference both to each other and to the heavenly bodies — drawing parallel lines for the parallels and perpendicular lines for the circles perpendicular to the parallels, for our imagination can easily transfer to the globular and spherical surface the figure or magnitude seen by the eye on a plane surface. And the same applies also, we say, to the oblique circles and their corresponding straight lines. Although the several meridians drawn through the pole all converge on the sphere toward one point, yet on our plane-surface chart it will not be a matter of importance merely to make the straight meridian lines converge slightly; for there is no necessity for this in many cases, nor are the converging straight lines, when the lines of the sphere are transferred to the plane chart and drawn as straight lines, as easily understood as are the curved lines on the sphere.
And so in what I have to say hereafter I shall assume that our drawing has been made on a plane chart. Now I shall tell what part of the land and sea I have myself visited and concerning what part I have trusted to accounts given by others by word of mouth or in writing. I have travelled westward from Armenia as far as the regions of Tyrrhenia opposite Sardinia, and southward from the Euxine Sea as far as the frontiers of Ethiopia. And you could not find another person among the writers on geography who has travelled over much more of the distances just mentioned than I; indeed, those who have travelled more than I in the western regions have not covered as much ground in the east, and those who have travelled more in the eastern countries are behind me in the western; and the same holds true in regard to the regions towards the south and north. However, the greater part of our material both they and I receive by hearsay and then form our ideas of shape and size and also other characteristics, qualitative and quantitative, precisely as the mind forms its ideas from sense impressions — for our senses report the shape, colour, and size of an apple, and also its smell, feel, and flavour; and from all this the mind forms the concept of apple. So, too, even in the case of large figures, while the senses perceive only the parts, the mind forms a concept of the whole from what the senses have perceived. And men who are eager to learn proceed in just that way: they trust as organs of sense those who have seen or wandered over any region, no matter what, some in this and some in that part of the earth, and they form in one diagram their mental image of the whole inhabited world. Why, generals, too, though they do everything themselves, are not present everywhere, but they carry out successfully most of their measures through others, trusting the reports of messengers and sending their orders around in conformity with the reports they hear. And he who claims that only those have knowledge who have actually seen abolishes the criterion of the sense of hearing, though this sense is much more important than sight for the purposes of science.
In particular the writers of the present time can give a better account of the Britons, the Germans, the peoples both north and south of the Ister, the Getans, the Tyregetans, the Bastarnians, and, furthermore, the peoples in the regions of the Caucasus, such as the Albanians and the Iberians. Information has been given us also concerning Hyrcania and Bactriana by the writers of Parthian histories (Apollodorus of Artemita and his school), in which they marked off those countries more definitely than many other writers. Again, since the Romans have recently invaded Arabia Felix with an army, of which Aelius Gallus, my friend and companion, was the commander, and since the merchants of Alexandria are already sailing with fleets by way of the Nile and of the Arabian Gulf as far as India, these regions also have become far better known to us of to‑day than to our predecessors. At any rate, when Gallus was prefect of Egypt, I accompanied him and ascended the Nile as far as Syene and the frontiers of Ethiopia, and I learned that as many as one hundred and twenty vessels were sailing from Myos Hormos to India, whereas formerly, under the Ptolemies, only a very few ventured to undertake the voyage and to carry on traffic in Indian merchandise.
Now my first and most important concern, both for the purposes of science and for the needs of the state, is this — to try to give, in the simplest possible way, the shape and size of that part of the earth which falls within our map, indicating at the same time what the nature of that part is and what portion it is of the whole earth; for this is the task proper of the geographer. But to give an accurate account of the whole earth and of the whole "spinning-whorl" of the zone of which I was speaking is the function of another science — for instance, take the question whether the "spinning-whorl" is inhabited in its other fourth also. And, indeed, if it is inhabited, it is not inhabited by men such as exist in our fourth, and we should have to regard it as another inhabited world — which is a plausible theory. It is mine, however, to describe what is in this our own inhabited world.
As I have said, the shape of the inhabited world is somewhat like a chlamys, whose greatest breadth is represented by the line that runs through the Nile, a line that begins at the parallel that runs through the Cinnamon-producing Country and the island of the fugitive Egyptians, and ends at the parallel through Ierne; its length is represented by that line drawn perpendicular thereto which runs from the west through the Pillars and the Strait of Sicily to Rhodes and the Gulf of Issus, passes along the Taurus Range, which girdles Asia, and ends at the Eastern Sea between India and the country of those Scythians who live beyond Bactriana. Accordingly, we must conceive of a parallelogram in which the chlamys-shaped figure is inscribed in such a way that the greatest length of the chlamys coincides with, and is equal to, the greatest length of the parallelogram, and likewise its greatest breadth and the breadth of the parallelogram. Now this chlamys-shaped figure is the inhabited world; and, as I said, its breadth is fixed by the parallelogram's outermost lines, which separate its inhabited and its uninhabited territory in both directions. And these sides were: in the north, the parallel through Ierne; in the torrid region, the parallel through the Cinnamon-producing Country; hence these lines, if produced both east and west as far as those parts of the inhabited world that rise opposite to them, will form a parallelogram with the meridian-lines that unite them at their extremities. Now, that the inhabited world is situated in this parallelogram is clear from this fact that neither its greatest breadth nor its greatest length fall outside thereof; and that its shape is like a chlamys is apparent from the fact that the extremities of its length, being washed away by the sea, taper off on both sides and thus diminish its width there; and this is apparent from the reports of those who have sailed around the eastern and western parts in both directions. For these navigators declare that the island called Taprobane is considerably south of India, inhabited nevertheless, and that it "rises opposite to" the Island of the Egyptians and the Cinnamon-nearing Country; and that, indeed, the temperature of the atmosphere is much the same as that of these latter places; and the region about the outlet of the Hyrcanian Sea are farther north than outermost Scythia beyond India, and the regions about Ierne are farther north still. A similar report is also made concerning the country outside the Pillars, namely, the promontory of Iberia which they call the Sacred Cape is the most westerly point of the inhabited world; and this cape lies approximately on the line that passes through Gades, the Pillars, the Strait of Sicily, and Rhodes. At all these points, they say, the shadows cast by the sun-dial agree, and the winds that blow in either direction come from the same direction, and the lengths of the longest days and nights are the same; for the longest day and the longest night have fourteen and a half equinoctial hours. Again, the constellation of the Cabeiri is sometimes seen along the coast near Gades. And Poseidonius says that from a tall house in a city about four hundred stadia distant from these regions he saw a star which he judged to be Canopus itself, so judging from the fact that those who had proceeded but a short distance south of Iberia were in agreement that they saw Canopus, and also from scientific observations made at Cnidus; for, says he, the observatory of Eudoxus at Cnidus is not much higher than the dwelling-houses, and from there, it is said, Eudoxus saw the star Canopus; and, adds Poseidonius, Cnidus lies on the parallel of Rhodes, on which lie both Gades and the coastline thereabouts.
Now as you sail to the regions of the south you come to Libya; of this country the westernmost coast extends only slightly beyond Gades; then this coast, forming a narrow promontory, recedes towards the southeast and gradually broadens out to the point where it reaches the land of the Western Ethiopians. They are the most remote people south of the territory of Carthage, and they reach the parallel that runs through the Cinnamon-producing Country. But if you sail in the opposite direction from the Sacred Cape until you come to the people called Artabrians, your voyage is northward, and you have Lusitania on your right hand. Then all the rest of your voyage is eastward, thus making an obtuse angle to your former course, until you reach the headlands of the Pyrenees that abut on the ocean. The westerly parts of Britain lie opposite these headlands towards the north; and in like manner the islands called Cassiterides, situated in the open sea approximately in the latitude of Britain, lie opposite to, and north of, the Artabrians. Therefore it is clear how greatly the east and west ends of the inhabited world have been narrowed down by the surrounding sea.
Such being the general shape of the inhabited world, it is clearly helpful to assume two straight lines that intersect each other at right angles, one of which will run through the entire greatest length and the other through the entire greatest breadth of the inhabited world; and the first line will be one of the parallels, and the second line one of the meridians; then it will be helpful to conceive of lines parallel to these two lines on either side of them and by them to divide the land and the sea with which we happen to be conversant. For thereby the shape of the inhabited world will prove more clearly to be such as I have described it, being judged by the extent of the lines, which lines are of different measurements, both those of the length and those of the breadth; and thereby too the "climata" will be better represented, both in the east and in the west, and likewise in the south and in the north. But since these straight lines must be drawn through known places, two of them have already been so drawn, I mean the two central lines mentioned above, the one representing the length and the other the breadth; and the other lines will be easily found by the help of these two. For by using these lines as "elements," so to speak, we can correlate the regions that are parallel, and the other positions, both geographical and astronomical, of inhabited places.
It is the sea more than anything else that defines the contours of the land and gives it its shape, by forming gulfs, deep seas, straits, and likewise isthmuses, peninsulas, and promontories; but both the rivers and the mountains assist the seas herein. It is through such natural features that we gain a clear conception of continents, nations, favourable positions of cities, and all the other diversified details with which our geographical map is filled. And among these details are the multitude of islands scattered both in the open seas and along the whole seaboard. And since different places exhibit different good and bad attributes, as also the advantages and inconveniences that result therefrom, some due to nature and others resulting from human design, the geographer should mention those that are due to nature; for they are permanent, whereas the adventitious attributes undergo changes. And also of the latter attributes he should indicate such as can persist for a long time, or else such as can not persist for long and yet somehow possess a certain distinction and fame, which, by enduring to later times, make a work of man, even when it no longer exists, a kind of natural attribute of a place; hence it is clear that these latter attributes must also be mentioned. Indeed, it is possible to say concerning many cities what Demosthenes said of Olynthus and the cities round about it, which have so completely disappeared, he says, that a visitor could not know even whether they had ever been founded. But nevertheless men like to visit these places as well as others, because they are eager to see at least the traces of deeds so widely famed, just as they like to visit the tombs of illustrious men. So, also, I have mentioned customs and constitutions that no longer exist, for the reason that utility urges me in their case just as it does in the case of deeds of action; that is, either to incite emulation or signal avoidance of this or that.
I now resume my first sketch of the inhabited world and say that our inhabited world, being girt by the sea, admits into itself from the exterior sea along the ocean many gulfs, of which four are very large. Of these four gulfs the northern one is called the Caspian Sea (though some call it the Hyrcanian Sea); the Persian Gulf and the Arabian Gulf pour inland from the Southern Sea, the one about opposite the Caspian Sea and the other about opposite the Pontus; and the fourth, which far exceeds the others in size, is formed by the sea which is called the Interior Sea, or Our Sea; it takes its beginning in the west at the strait at the Pillars of Heracles, and extends lengthwise towards the regions of the east, but with varying breadth, and finally divides itself and ends in two sea-like gulfs, the one on the left hand, which we call the Euxine Pontus, and the other consisting of the Egyptian, the Pamphylian, and the Issican Seas. All these aforesaid gulfs have narrow inlets from the Exterior Sea, particularly the Arabian Gulf and that at the Pillars, whereas the others are not so narrow. The land that surrounds these gulfs is divided into three parts, as I have said. Now Europe has the most irregular shape of all three; Libya has the most regular shape; while Asia occupies a sort of middle p469position between the other two in this respect. And the cause of their irregularity or their lack of it lies in the coastline of the Interior Sea, whereas the coastline of the Exterior Sea, with the exception of that of the aforesaid gulfs, is regular and, as I have said, like a chlamys; but I must leave out of view the other slight irregularities, for a little thing is nothing when we are dealing with great things. And further, since in the study of geography we inquire not merely into the shapes and dimensions of countries, but also, as I have said, into their positions with reference to each other, herein, too, the coast-line of the Interior Sea offers for our consideration more varied detail than that of the Exterior Sea. And far greater in extent here than there is the known portion, and the temperate portion, and the portion inhabited by well-governed cities and nations. Again, we wish to know about those parts of the world where tradition places more deeds of action, political constitutions, arts, and everything else that contributes to practical wisdom; and our needs draw us to those places with which commercial and social intercourse is attainable; and these are the places that are under government, or rather under good government. Now, as I have said, our Interior Sea has a great advantage in all these respects; and so with it I must begin my description.
I have already stated that the strait at the Pillars forms the beginning to this gulf; and the narrowest part of the strait is said to be about seventy stadia; but after you sail through the narrows, which are one hundred and twenty stadia in length, the coasts take a divergent course all at once, though the one on the left diverges more; and then the gulf assumes the aspect of a great sea. It is bounded on the right side by the coastline of Libya as far as Carthage, and on the other side, first, by Iberia and also by Celtica in the regions of Narbo and Massilia, and next by Liguria, and finally by Italy as far as the Strait of Sicily. The eastern side of this sea is formed by Sicily and the straits on either side of Sicily; the one between Italy and Sicily is seven stadia in width and the one between Sicily and Carthage is fifteen hundred stadia. But the line from the Pillars to the seven-stadia strait is a part of the line to Rhodes and the Taurus Range; it cuts the aforesaid sea approximately in the middle; and it is said to be twelve thousand stadia in length. This, then, is the length of the sea, while its greatest breadth is as much as five thousand stadia, the distance from the galatic Gulf between Massilia and Narbo to the opposite coast of Libya. The entire portion of this sea along the coast of Libya they call the Libyan Sea, and the portion that lies along the opposite coast they call, in order, the Iberian Sea, the Ligurian Sea, the Sardinian Sea, and finally, to Sicily, the Tyrrhenian Sea. There are numerous islands along the coast of the Tyrrhenian Sea as far as Liguria, and largest of all are Sardinia and Corsica, except Sicily; but Sicily is the largest and best of all the islands in our part of the world. Far behind these in size are Pandateria and Pontia, which lie in the open sea, and, lying near the land, Aethalia, Planasia, Pithecussa, Prochyta, Capreae, Leucosia, and others like them. But on the other side of the Ligurian Sea the islands off the rest of the coast up to the Pillars are not numerous, among which are the Gymnesiae and Ebysus; and those off the coasts of Libya and Sicily are not numerous, either, among which are Cossura, Aegimurus, and the Liparian Islands, which some call the Islands of Aeolus.
Beyond Sicily and the straits on both sides of it other seas join with the former sea. The first is the sea in front of the Syrtes and Cyrenaea and the two Syrtes themselves, and the second is the sea formerly called the Ausonian Sea, but now the Sicilian Sea, which is confluent with and a continuation of the first sea. Now the sea in front of the Syrtes and Cyrenaea is called the Libyan Sea, and it ends at the Egyptian Sea. Of the Syrtes, the lesser is about one thousand six hundred stadia in circumference; and the islands Meninx and Cercina lie at either side of its mouth. As for the Greater Syrtes, Eratosthenes says that its circuit is five thousand stadia, and its breadth eighteen hundred stadia, reckoning from the Hesperides to Automala and to the common boundary between Cyrenaea and the rest of Libya in that region; but others have estimated its circuit at four thousand stadia, and its breadth at fifteen hundred stadia, as much as the breadth of its mouth is. The Sicilian Sea lies in front of Sicily and Italy toward the regions of the east, and, besides, in front of the strait that lies between them — in front of the territory of Rhegium as far as Locri, and of the territory of Messina as far as Syracuse and Pachynum. Toward the regions of the east it stretches on to the headlands of Crete, and its waters also wash round most of the Peloponnesus and fill what is called the Gulf of Corinth. On the north it stretches to the Iapygian Cape and the mouth of the Ionian Gulf and to the southern parts of Epirus as far as the Ambracian Gulf and the coast that adjoins it and, with the Peloponnesus, forms the Corinthian Gulf. But the Ionian Gulf is part of what is now called the Adriatic Sea. The right side of this sea is formed by Illyria, and the left by Italy up to its head at Aquileia. It reaches up towards the north-west in a narrow and long course; and its length is about six thousand stadia, while its greatest breadth is twelve hundred stadia. There are numerous islands in this sea: off the Illyrian coast the Apsyrtides, and Cyrictica, and the Liburnides, and also Issa, Tragurium, Black Corcyra, and Pharos; and off the Italian coast the Diomedeae. The stretch of the Sicilian Sea from Pachynum to Crete, they say, measures four thousand five hundred stadia, and just as much the stretch to Taenarum in Laconia; and the stretch from the Iapygian Cape to the head of the Gulf of Corinth is less than three thousand stadia, while that from Iapygia to Libya is more than four thousand. The islands of this sea are: Corcyra and the Sybota off the coast of Epirus; and next to them, off the Gulf of Corinth, Cephallenia, Ithaca, Zacynthus, and the Echinades.
Adjoining the Sicilian Sea are the Cretan, the Saronic, and the Myrtoan Seas. The Myrtoan Sea is between Crete, Argeia and Attica; its greatest breadth, measured from Attica, is about one thousand two hundred stadia, and its length is less than double its breadth. In this sea are the islands of Cythera, Calauria, Aegina and its neighbouring isles, Salamis, and some of the Cyclades. Next beyond the Myrtoan Sea comes immediately the Aegean Sea, with the Gulf of Melas and the Hellespont; and also the Icarian and Carpathian Seas, extending to Rhodes, Crete, Carpathus, and the first regions of Asia. In the Aegean are the Cyclades, the Sporades, and the islands that lie off Caria, Ionia, and Aeolis up to the Troad — I mean Cos, Samos, Chios, Lesbos, and Tenedos; so also those that lie off Greece as far as Macedonia and Thrace the next country beyond Macedonia — namely, Euboea, Scyros, Peparethos, Lemnos, Thasos, Imbros, Samothrace, and a number of others, concerning which I shall speak in my detailed description. The length of this sea is about four thousand stadia or slightly more, and its breadth is about two thousand stadia. It is surrounded by the aforesaid regions of Asia, and by the coast-line from Sunium to the Thermaic Gulf as you sail towards the north, and by the Macedonian Gulfs up to the Thracian Chersonese.
Along this Chersonese lies the strait, seven stadia in breadth, between Sestus and Abydus, through which the Aegean Sea and the Hellespont empty northwards into another sea which they call the Propontis; and the Propontis empties into another sea termed the "Euxine" Pontus. This latter is a double sea, so to speak: for two promontories jut out at about the middle of it, one from Europe and the northern parts, and the other, opposite to it, from Asia, thus contracting the passage between them and forming two large seas. The promontory of Europe is called Criumetopon, and that of Asia, Carambis; and they are about two thousand five hundred stadia distant from each other. Now the western sea has a length of three thousand eight hundred stadia, reckoning from Byzantium to the mouths of the Borysthenes, and a breadth of two thousand eight hundred stadia; in this sea the island of Leuce is situated. The eastern sea is oblong and ends in a narrow head at Dioscurias; it has a length of five thousand stadia or a little more, and a breadth of about three thousand stadia. The circumference of the whole sea is approximately twenty-five thousand stadia. Some compare the shape of this circumference to that of a bent Scythian bow, likening the bow-string to the regions on what is called the right-hand side of the Pontus (that is, the ship-course along the coast from the outlet to the head at Dioscurias; for with the exception of the promontory of Carambis the whole shore has but small recesses and projections, so that it is like a straight line; and the rest they liken to the horn of the bow with its double curve, the upper curve being rounded off, while the lower curve is straighter; and thus they say the left coast forms two gulfs, of which the western is much more rounded than the other.
North of the eastern gulf lies Lake Maeotis, which has a circumference of nine thousand stadia or even a little more. It empties into the Pontus at what is called the Cimmerian Bosporus, and the Pontus empties into the Propontis at the Thracian Bosporus; for they give the name of Thracian Bosporus to the outlet at Byzantium, which is four stadia. The Propontis is said to be fifteen hundred stadia long, reckoning from the Troad to Byzantium; and its breadth is approximately the same. In it lie the island of Cyzicus and the little islands in its neighbourhood.
Such, then, is the nature and such the size of the arm of the Aegean Sea that extends towards the north. Again: the arm that begins at Rhodes and forms the Egyptian, the Pamphylian, and the Issican Seas, stretches towards the east as far as Issus in Cilicia for a distance of five thousand stadia along Lycia, Pamphylia, and the whole coastline of Cilicia. Thence, Syria, Phoenicia, and Egypt encircle the sea on the south and west as far as Alexandria. And Cyprus must lie both in the Issican and the Pamphylian Gulfs, since it borders on the Egyptian Sea. The sea-passage from Rhodes to Alexandria is, with the north wind, approximately four thousand stadia, while the coasting-voyage is double that distance. Eratosthenes says that this is merely the assumption made by navigators in regard to the length of the sea-passage, some saying it is four thousand stadia, others not hesitating to say it is even five thousand stadia, but that he himself, by means of the shadow-catching sun-dial, has discovered to be three thousand seven hundred and fifty stadia. Now the part of this sea that is next to Cilicia and Pamphylia, and the side called the right-hand side of the Pontic Sea, and the Propontis, and the sea-board next beyond as far as Pamphylia, form a great peninsula and a great isthmus belonging thereto that stretches from the sea at Tarsus to the city of Amisus, and to Themiscyra, the Plain of the Amazons. For the country within this line, as far as Caria and Ionia and the peoples that live on this side of the Halys River, is all washed by the Aegean or else by the above-mentioned parts thereof on both sides of the peninsula. And indeed we call this peninsula by the special name of Asia, the same name that is given to the whole continent.
In short, the head of the Greater Syrtis is the most southerly point of our Mediterranean Sea, and next to this Alexandria in Egypt and the mouths of the Nile; the most northerly point is the mouth of the Borysthenes, though if we add Lake Maeotis to the sea (and indeed it is a part of it, in a sense) the mouth of the Tanaïs is the most northerly point; the most westerly point is the strait at the Pillars; and the most easterly point is the above-mentioned head of the Pontus at Dioscurias; and Eratosthenes is wrong in saying that the Issican Gulf is the most easterly, for it lies on the same meridian with Amisus and Themiscyra — or, if you like, you may add in the territory of Sidene on to Pharnacia. From these regions the voyage to Dioscurias is, I might say, more than three thousand stadia eastward, as will become clearer when I describe that region in detail. Such, then, is the nature of our Mediterranean Sea.
I must also give a general description of the countries that surround this sea, beginning at the same points at which I began to describe the sea itself. Now as you sail into the strait at the Pillars, Libya lies on your right hand as far as the stream of the Nile, and on your left hand across the strait lies Europe as far as the Tanaïs. And both Europe and Libya end at Asia. But I must begin with Europe, because it is both varied in form and admirably adapted by nature for the development of excellence in men and governments, and also because it has contributed most of its own store of good things to the other continents; for the whole of it is inhabitable with the exception of a small region that is uninhabited on account of the cold. This uninhabited part borders on the country of the Wagon-Dwellers in the region of the Tanaïs, Lake Maeotis, and the Borysthenes. Of the inhabitable part of Europe, the cold mountainous regions furnish by nature only a wretched existence to their inhabitants, yet even the regions of poverty and piracy become civilised as soon as they get good administrators. Take the case of the Greeks: though occupying mountains and rocks, they used to live happily, because they took forethought for good government, for the arts, and in general for the science of living. The Romans, too, took over many nations that were naturally savage owing to the regions they inhabited, because those regions were either rocky or without harbours or cold or for some other reason ill-suited to habitation by many, and thus not only brought into communication with each other peoples who had been isolated, but also taught the more savage how to live under forms of government. But all of Europe that is level and has a temperate climate has nature to coöperate with her toward these results; for while in a country that is blessed by nature everything tends to peace, in a disagreeable country everything tends to make men warlike and courageous; and so both kinds of country receive benefits from each other, for the latter helps with arms, the former with products of the soil, with arts, and with character-building. But the harm that they receive from each other, if they are not mutually helpful, is also apparent; and the might of those who are accustomed to carry arms will have some advantage unless it be controlled by the majority. However, this continent has a natural advantage to meet this condition also; for the whole of it is diversified with plains and mountains, so that throughout its entire extent the agricultural and civilised element dwells side by side with the warlike element; but of the two elements the one that is peace-loving is more numerous and therefore keeps control over the whole body; and the leading p489nations, too — formerly the Greeks and later the Macedonians and the Romans — have taken hold and helped. And for this reason Europe is most independent of other countries as regards both peace and war; for the warlike population which she possesses is abundant and also that which tills her soils and holds her cities secure. She excels also in this respect, that she produces the fruits that are best and that are necessary for life, and all the useful metals, while she imports from abroad spices and precious stones — things that make the life of persons who have only a scarcity of them fully as happy as that of persons who have them in abundance. So, also, Europe offers an abundance of various kinds of cattle, but a scarcity of wild animals. Such, in a general way, is the nature of this continent.
If, however, we look at the separate parts of it, the first of all its countries, beginning from the west, is Iberia, which in shape is like an ox-hide, whose "neck" parts, so to speak, fall over into the neighbouring Celtica; and these are the parts that lie towards the east, and within these parts the eastern side of Iberia is cut off by a mountain, the so‑called Pyrenees, but all the rest is surrounded by the sea; on the south, as far as the Pillars, it is surrounded by our Sea, and on the other side, as far as the northern headlands of the Pyrenees, by the Atlantic. The greatest length of this country is about six thousand stadia; and breadth, five thousand.
Next to Iberia towards the east lies Celtica, which extends to the River Rhine. On its northern p491side it is washed by the whole British Channel (for the whole island of Britain lies over against and parallel to the whole of Celtica and stretches lengthwise about five thousand stadia); on its eastern side it is bounded by the River Rhine, whose stream runs parallel to the Pyrenees; and on its southern side it is bounded, on the stretch that begins at the Rhine, by the Alps, and by our sea itself in the region where the so‑called Galatic Gulf widens out — the region in which Massilia and Narbo are situated, very famous cities. Opposite this gulf, and facing in the opposite direction, lies another gulf that is also called Galatic Gulf; and it looks toward the north and Britain; and it is between these two gulfs that Celtica has its least breadth; for it is contracted into an isthmus of less than three thousand, but more than two thousand, stadia. Between these two gulfs a mountain range, the so‑called Cemmenus Mountain, runs at right angles to the Pyrenees and comes to an end in the very centre of the plains of Celtica. As for the Alps (which are extremely high mountains that form the arc of a circle), their convex side is turned towards the plains of Celtica just mentioned and the Cemmenus Mountain, while their concave side is turned toward Liguria and Italy. Many tribes occupy these mountains, all Celtic except the Ligurians; but while these Ligurians belong to a different race, still they are similar to the Celts in their modes of life. They live in the part of the Alps that joins the Apennines, and they occupy a part of the Apennines also. The Apennines form a mountain range running through the whole length of Italy from the north to the south and ending at the Strait of Sicily.
The first parts of Italy are the plains that lie at the foot of the Alps and extend as far as the head of the Adriatic and the regions near it, but the rest of Italy is a narrow and long promontory in the form of a peninsula, through which, as I have said, the Apennines extend lengthwise for about seven thousand stadia, but with varying breadth. The seas that make Italy a peninsula are the Tyrrhenian (which begins at the Ligurian Sea), the Ausonian, and the Adriatic.
After Italy and Celtica come the remaining, or eastern, countries of Europe, which are cut in two by the River Ister. This river flows from the west towards the east and the Euxine Sea; it leaves on its left the whole of Germany (which begins at the Rhine), all the country of the Getans, and the country of the Tyregetans, Bastarnians, and Sarmatians as far as the River Tanaïs and Lake Maeotis; and it leaves on its right the whole of Thrace, Illyria, and, lastly and finally, Greece. The islands which I have already mentioned lie off Europe; outside the Pillars: Gades, the Cassiterides, and the Britannic islands; and inside the Pillars: the Gymnesiae and other little islands of the Phoenicians, and those off Massilia and Liguria, and the islands of Italy up to the Islands of Aeolus and to Sicily, and all the islands round about Epirus and Greece and as far as Macedonia and the Thracian Chersonese.
After the Tanaïs and Lake Maeotis come the regions of Asia — the Cis-Tauran regions which are contiguous to the Tanaïs and Lake Maeotis, and following upon these regions come the Trans-Tauran regions. For since Asia is divided in two by the Taurus Range, which stretches from the capes of Pamphylia to the eastern sea at India and farther Scythia, the Greeks gave the name of Cis-Tauran to that part of the continent which looks towards the north, and the name of Trans-Tauran to that part which looks towards the south; accordingly, the parts of Asia that are contiguous to lake Maeotis and the Tanaïs belong to the Cis-Tauran regions. The first of these regions are those that lie between the Caspian Sea and the Euxine Pontus, and they come to an end, in one direction, at the Tanaïs and the ocean, that is, both at the exterior ocean and at that part of it which forms the Hyrcanian Sea, and, in the other direction, at the isthmus, at the point where the distance from the head of the Pontus to the Caspian Sea is least. Then come those Cis-Tauran regions that are north of Hyrcania, which reach all the way to the sea at India and farther Scythia, and to Mt. Imaeus. These regions inhabited, partly, by the Maeotic Sarmatians, and by the Sarmatians that dwell between the Hyrcanian Sea and the Pontus as far as the Caucasus and the countries of the Iberians and the Albanians, and by Scythians, Achaeans, Zygians, and Heniochians; and, partly, beyond the Hyrcanian Sea, by Scythians, Hyrcanians, Parthians, Bactrians, Sogdianians, and also by the inhabitants of the regions that lie beyond India on the north. And to the south of the Hyrcanian Sea, in part, and of the whole of the isthmus between this sea and the Pontus lie the greater part of Armenia, Colchis, the whole of Cappadocia up to the Euxine and to the Tibaranian tribes, and also the so‑called Cis-Halys country, which embraces, first next to the Pontus and to the Propontis, Paphlagonia, Bithynia, Mysia, the so‑called "Phrygia on the Hellespont" (of which the Troad is a part); and, secondly, next to the Aegean and to the sea that forms its continuation, Aeolis, Ionia, Caria, Lycia; and, thirdly, in the interior, Phrygia (of which both the so‑called "Galatia of the Gallo-Grecians" and "Phrygia Epictetus" form a part), Lycaonia, and Lydia.
Following immediately upon the Cis-Tauran peoples come the peoples that inhabit the mountains: the Paropamisadae, the tribes of the Parthians, of the Medes, of the Armenians, and of the Cilicians, and the Cataonians and the Pisidians. Next after the mountaineers come the Trans-Tauran regions. The first of them is India, which is the greatest of all nations and the happiest in lot, a nation whose confines reach both to the eastern sea and to the southern sea of the Atlantic. In this southern sea, off the coast of India, lies an island, Taprobane, which is not less than Britain. Then, if we turn from India toward the western regions and keep the mountains on our right, we come to a vast country, which owing to the poverty of the soil, furnishes only a wretched livelihood to men who are wholly barbarians and belong to different races. They call this country Aria, and it extends from the mountains p499as far as Gedrosia and Carmania. Next after Aria, toward the sea, are Persia, Susiana, Babylonia (countries which reach down to the Persian Sea), and the small tribes that dwell on the frontiers of those countries; while the peoples who live near the mountains or in the mountains themselves are the Parthians, the Medes, the Armenians and the tribe adjoining them, and the Mesopotamians. After Mesopotamia come the countries this side of the Euphrates. These are: the whole of Arabia Felix (which is bounded by the whole extent of the Arabian Gulf and by the Persian Gulf), and all the country occupied by the Tent-Dwellers and by the Sheikh-governed tribes (which reaches to the Euphrates and Syria). Then come the peoples who live on the other side of the Arabian Gulf and as far as the Nile, namely, the Ethiopians and the Arabs, and the Egyptians who live next to them, and the Syrians, and the Cilicians (including the so‑called "Trachiotae"), and finally the Pamphylians.
After Asia comes Libya, which is a continuation of Egypt and Ethiopia. Its shore that lies opposite to us runs in a straight line almost to the Pillars, beginning at Alexandria, except for the Syrtes and perhaps other moderate bends of gulfs and projections of the promontories that form these gulfs; but its coastline on the ocean from Ethiopia to a certain point is approximately parallel to the former line, and then it draws in on the south and forms a sharp promontory, which projects slightly outside the Pillars and thus gives to Libya approximately p501the shape of a trapezium. And Libya is — as the others show, and indeed as Cnaeus Piso, who was once the prefect of that country, told me — like a leopard's skin; for it is spotted with inhabited places that are surrounded by waterless and desert land. The Egyptians call such inhabited places "auases." But though Libya is thus peculiar, it has some other peculiarities, which give it a threefold division. In the first place, most of its coastline that lies opposite to us is extremely fertile, and especially Cyrenaea and the country about Carthage up to Maurusia and to the Pillars of Heracles; secondly, even its coastline on the ocean affords only moderate sustenance, and thirdly, its interior region, which produces silphium, affords only a wretched sustenance, being, for the most part, a rocky and sandy desert; and the same is also true of the straight prolongation of this region through Ethiopia, the Troglodyte Country, Arabia, and Gedrosia where the Fish-Eaters live. The most of the peoples of Libya are unknown to us; for not much of it is visited by armies, nor yet by men of outside tribes; and not only do very few of the natives from far inland ever visit us, but what they tell is not trustworthy or complete either. But still the following is based on what they say. They call the most southerly peoples Ethiopians; those who live next north of the Ethiopians they call, in the main, Garamantians, Pharusians, and Nigritans; those who live still north of these latter, Gaetulans; those who live near the sea, or even on the seacoast, next to Egypt and as far as Cyrenaea, Marmaridans; while they call those beyond Cyrenaea and the Syrtes, Psyllians, Nasamonians, and certain of the Gaetulans, and then Asbystians and Byzacians, whose territory reaches to that of Carthage. The territory of Carthage is large, and beyond it comes that of the Nomads; the best known of these are called, some of them, Masylians, and others Masaesylians. And last of all come the Maurusians. The whole country from Carthage to the Pillars is fertile, though full of wild beasts, as is also the whole of the interior of Libya. So it is not unlikely that some of these peoples were also called Nomads for the reason that in early times they were not able to cultivate the soil on account of the multitude of wild animals. But the Nomads of to‑day not only excel in the skill of hunting (and the Romans take a hand in this with them because of their fondness for fights with wild animals), but they have mastered farming as well as the chase. This, then, is what I have to say about the continents.
It remains for me to speak about the "climata" (which is likewise a subject that involves only a general sketch), taking my beginning at those lines which I have called "elements" — I mean the two lines that mark off the greatest length and breadth of the inhabited world, but more particularly the breadth-line. Astronomers, of course, must treat this subject more at length, just as Hipparchus has treated it. For, as he himself says, he recorded the different aspects of the celestial bodies for all the different regions of the earth that are found in our Fourth — I mean the regions between the equator and the north pole. The geographer, however, need not busy himself with what lies outside of our inhabited world; and even in the case of the parts of the inhabited world the man of affairs need not be taught the nature and number of the different aspects of the celestial bodies, because this is dry reading for him. But it will be sufficient for me to set forth the significant and simplest differences noted by Hipparchus, taking as a hypothesis, just as he does, that the magnitude of the earth is two hundred and fifty-two thousand stadia, the figure rendered by Eratosthenes also. For the variation from this reckoning will not be large, so far as the celestial phenomena are concerned, in the distances between the inhabited places. If, then, we cut the greatest circle of the earth into three hundred and sixty sections, each of these sections will have seven hundred stadia. Now it is this that Hipparchus uses as a measure for the distances to be fixed on the aforesaid meridian through Meroë. So he begins with the inhabitants of the equator, and after that, proceeding along the said meridian to the inhabited places, one after another, with an interval each time of seven hundred stadia, he tries to give the celestial phenomena for each place; but for me the equator is not the place to begin. For if these regions are inhabitable, as some think, they constitute a peculiar kind of inhabited country, stretching as a narrow strip through the centre of the country that is uninhabitable on account of the heat, and not forming a part of our inhabited world. But the geographer takes into his purview only this our inhabited world; and its limits are marked off on the south by the parallel through the Cinnamon-producing Country and on the north by the parallel through Ierne; and, keeping in mind the scope of my geography, I am neither required to enumerate all the many inhabited places that the said intervening distance suggests to me, nor to fix all the celestial phenomena; but I must begin with the southern parts, as Hipparchus does.
Now Hipparchus says that the people who live on the parallel that runs through the Cinnamon-producing Country (this parallel is three thousand stadia south of Meroë and from it the equator is distant eight thousand eight hundred stadia), have their home very nearly midway between the equator and the summer tropic which passes through Syene; for Syene is five thousand stadia distant from Meroë. The Cinnamon-producing Country are the first to whom the Little Bear is wholly inside the arctic circle and always visible; for the bright star at the tip of the tail, the most southerly in the constellation, is situated on the very circumference of the arctic circle, so that it touches the horizon. The Arabian Gulf lies approximately parallel to the meridian in question, to the east of it; and where this gulf pours outside into the exterior sea is the Cinnamon-producing Country, where in ancient times they used to hunt the elephant. But this parallel passes outside the inhabited world, running, on the one side, to the south of Taprobane, or else to its farthermost inhabitants, and, on the other side, to the most southerly regions of Libya.
In the regions of Meroë, and of the Ptolemaïs in the country of the Troglodytes, the longest day has thirteen equinoctial hours; and this inhabited country is approximately midway between the equator and the parallel that runs through Alexandria (the stretch to the equator being eighteen hundred stadia more). And the parallel through Meroë passes, on the one side, through unknown regions, and, on the other, through the capes of India. At Syene, at Berenice on the Arabian Gulf, and in the country of the Troglodytes, the sun stands in the zenith at the time of the summer solstice, and the longest day has thirteen and one half equinoctial hours; and almost the whole of the Great Bear is also visible in the arctic circle, and one of the stars in the square. And the parallel through Syene passes, on the one side, through the country of the Fish-Eaters in Gedrosia, and through India, and, on the other side, through the regions that are almost five thousand stadia south of Cyrene.
In all the regions that lie between the tropic and the equator the shadows fall in both directions, that is, toward the north and toward the north; but, beginning at the regions of Syene and the summer tropic, the shadows fall toward the north at noon; and the inhabitants of the former region are called Amphiscians, and of the latter, Heteroscians. There is still another distinctive characteristic of the regions beneath the tropic, which I have mentioned before in speaking of the zones, namely, the soil itself is very sandy, silphium-producing, and dry, whereas the regions to the south of it are well-watered and very fruitful.
In the region approximately four hundred stadia farther south than the parallel through Alexandria and Cyrene, where the longest day has fourteen equinoctial hours, Arcturus stands in the zenith, though he declines a little toward the south. At Alexandria the relation of the index of the sun-dial to the shadow on the day of the equinox is five to three. But the region in question is thirteen hundred stadia farther south than Carthage — if it be true that at Carthage the relation of the index to the shadow on the day of the equinox is as eleven to seven. But our parallel through Alexandria passes, in one direction, through Cyrene and the regions nine hundred stadia south of Carthage and central Maurusia, and, in the other direction, it passes through Egypt, Coelesyria, Upper Syria, Babylonia, Susiana, Persia, Carmania, Upper Gedrosia, and India.
At the Ptolemaïs in Phoenicia, at Sidon, and at Tyre, and the regions thereabouts, the longest day has fourteen and one quarter equinoctial hours; and these regions are about sixteen hundred stadia farther north than Alexandria and about seven hundred stadia farther north than Carthage. But in the Peloponnesus, in the regions about the centre of Rhodes, about Xanthus of Lycia or a little south of Xanthus, and also in the regions four hundred stadia south of Syracuse, — here, I say, the longest day has fourteen and one half equinoctial hours. These regions are three thousand six hundred and forty stadia distant in latitude from Alexandria; and, according to Eratosthenes, this parallel runs through Caria, Lycaonia, Cataonia, Media, the Caspian Gates, and the parts of India along the Caucasus.
At the Alexandria in the Troad and the regions thereabouts, at Amphipolis, at the Apollonia in Epirus, and in the regions south of Rome but north of Neapolis, the longest day has fifteen equinoctial hours. This parallel is about seven thousand stadia north of the parallel through the Alexandria in Egypt, and more than twenty-eight thousand eight hundred stadia distant from the equator, and three thousand four hundred stadia distant from the parallel through Rhodes, and one thousand five hundred stadia south of Byzantium, Nicaea, Massilia, and the regions thereabouts; and a little north of it lies the parallel through Lysimachia, which, says Eratosthenes, passes through Mysia, Paphlagonia, Sinope, and the regions thereabouts, Hyrcania, and Bactra.
At Byzantium and the regions thereabouts the longest day has fifteen and one quarter equinoctial hours, and the ratio of the index of the sun-dial to the shadow at the time of summer solstice is that of one hundred and twenty to forty-two minus one fifth. These regions are about four thousand nine hundred stadia distant from the parallel through the centre of Rhodes and about thirty thousand three hundred stadia distant from the equator. If you sail into the Pontus and proceed about fourteen hundred stadia toward the north, the longest day becomes fifteen and one half equinoctial hours. These regions are equidistant from the pole and from the equator, and there the arctic circle is in the zenith; and the star on the neck of Cassiopeia lies on the arctic circle, while the star on the right elbow of Perseus is a little north of it.
In the regions about three thousand eight hundred stadia north of Byzantium the longest day has sixteen equinoctial hours; and therefore Cassiopeia moves within the arctic circle. These are the regions about the Borysthenes and the southern parts of Lake Maeotis, and they are about thirty-four thousand one hundred stadia distant from the equator. There the northern part of the horizon is dimly illuminated by the sun throughout almost the entire night in the summer-time, the sun's light making a reverse movement from west back to east. For the summer tropic is seven-twelfths of a zodiacal sign distant from the horizon; and accordingly the sun at midnight is just that distance below the horizon. And in our own regions also, when the sun is so far as that from the horizon before sunrise and after sunset, it illumines the skies in the east and in the west. And in those regions in the winter-days the sun attains an elevation of at most nine cubits. Eratosthenes says that these regions are a little more than twenty-three thousand stadia from Meroë, since the distance from Meroë to the parallel through the Hellespont is eighteen thousand stadia, and thence to the Borysthenes, five thousand. In the regions about six thousand three hundred stadia distant from Byzantium north of Lake Maeotis, in the winter-days, the sun attains an elevation of at most six cubits, and there the longest day has seventeen equinoctial hours.
Since the regions beyond already lie near territory rendered uninhabitable by the cold, they are without value to the geographer. But if any one wishes to learn about these regions also, and about all the other astronomical matters that are treated by Hipparchus, but omitted by me as being already too clearly treated to be discussed in the present treatise, let him get them from Hipparchus. And what Poseidonius says about the Periscians and Amphiscians and Heteroscians is too clear to be repeated here; nevertheless, I must mention these terms at sufficient length to explain the idea and to show wherein it is useful for geography and wherein useless. Now since the point in question concerns the shadows cast by the sun, and since, on the evidence of our senses, the sun moves along a circle parallel to the revolution of the universe, it follows that, wherever each revolution of the universe produces a day and a night (because at one time the sun moves beneath the earth and at another time above the earth), the people are thought of as either Amphiscians or Heteroscians, — as Amphiscians, all whose shadows at noon sometimes fall toward the north, namely, when the sun strikes from the south the index (which is perpendicular to the horizontal surface beneath), and, at other times, fall in the opposite direction, namely, when the sun revolves round to the opposite side (this is the result for only those who live between the tropics), but as Heteroscians, all whose shadows either always fall toward the north, as is the case with us, or always toward the south, as is the case with the inhabitants of the other temperate zone. And this is the result for every man whose arctic circle is smaller than the tropic circle. But wherever the arctic circle is the same as, or greater than, the tropic, there the Periscians begin and they extend to the people who live beneath the pole.For since, in those regions, the sun moves above the earth throughout the whole revolution of the universe, it is clear that the shadow will move in a circle round the index of the sun-dial; and that is the reason why Poseidonius called them Periscians, although they are non-existent as far as geography is concerned; for all those regions uninhabitable on account of the cold, as I have already stated in my criticism of Pytheas. Therefore I need not concern myself, either, with the extent of this uninhabited region, apart from assuming that those regions which have the tropic-arctic circle lie beneath the circle described by the pole of the zodiac in the diurnal revolution of the universe — that is, on the hypothesis that the distance between the equator and the tropic is four-sixtieths of the greatest circle. |
|
|
|
|
4 Transalpine Gaul 6 71 1:50 
|
4 - 1 Transalpine Gaul: Narbonensis 
1 Next, in order,1 comes Transalpine Celtica. I have already indicated roughly both the shape and the size of this country; but now I must speak of it in detail. Some, as we know, have divided it into three parts, calling its inhabitants Aquitani, Belgae, and Celtae. The Aquitani, they said, are wholly different, not only in respect to their language but also in respect to their physique — more like the Iberians than the Galatae; while the rest of the inhabitants are Galatic in appearance, although not all speak the same language, but some make slight variations in their languages. Furthermore, their governments and their modes of life are slightly different. Now by "Aquitani" and "Celtae" they meant the two peoples (separated from each other by the Cemmenus Mountain) who live next to the Pyrenees; for, as has already been said, this Celtica is bounded on the west by the Pyrenees Mountains, which join the sea on either side, that is, both the inner and the outer sea; on the east, by the River Rhenus, which is parallel to the Pyrenees; as for the parts on the north and the south, those on the north are surrounded by the ocean (beginning at the northern headlands of the Pyrenees) as far as the mouths of the Rhenus, while those on the opposite side are surrounded by the sea that is about Massilia and Narbo, and by the Alps (beginning at Liguria) as far as the sources of the Rhenus. The Cemmenus Mountain has been drawn at right angles to the Pyrenees, through the midst of the plains; and it comes to an end about the centre of these plains, near Lugdunum, with an extent of about two thousand stadia. So, then, by "Aquitani" they meant the people who occupy the northern parts of the Pyrenees and, from the country of the Cemmenus on to the ocean, the parts this side the Garumna River; by "Celtae" they meant the people whose territory extends in the other direction; — down to the sea that is about Massilia and Narbo — and also joins some of the Alpine Mountains; and by "Belgae" they meant the rest of the people who live beside the Rhenus and the Alps. Thus the Deified Caesar, also, has put it in his "Commentaries." Augustus Caesar, however, divided Transalpine Celtica into four parts: the Celtae he designated as belonging to the province of Narbonitis; the Aquitani he designated as the former Caesar had already done, although he added to them fourteen tribes of the peoples who dwell between the Garumna and the Liger Rivers; the rest of the country he divided into two parts: one part he included within the boundaries of Lugdunum as far as the upper districts of the Rhenus, while the other he included within the boundaries of the Belgae. Now although the geographer should tell of all the physical and ethnic distinctions which have been made, whenever they are worth recording, yet, as for the diversified political divisions which are made by the rulers (for they suit their government to the particular times), it is sufficient if one state them merely in a summary way; and the scientfic treatment of them should be left to others.
2 Now the whole of this country is watered by rivers: some of them flow down from the Alps, the others from the Cemmenus and the Pyrenees; and some of them are discharged into the ocean, the others into Our Sea. Further, the districts through which they flow are plains, for the most part, and hilly lands with navigable water-courses. The river-beds are by nature so well situated with reference to one another that there is transportation from either sea into the other; for the cargoes are transported only a short distance by land, with an easy transit through plains, but most of the way they are carried on the rivers — on some into the interior, on the others to the sea. The Rhodanus offers an advantage in this regard; for not only is it a stream of many tributaries, as has been stated, but it also connects with Our Sea, which is better than the outer sea, and traverses a country which is the most favoured of all in that part of the world. For example, the same fruits are produced by the whole of the province of Narbonitis as by Italy. As you proceed towards the north and the Cemmenus Mountain, the olive-planted and fig-bearing land indeed ceases, but the other things still grow. Also the vine, as you thus proceed, does not easily bring its fruit to maturity. All the rest of the country produces grain in large quantities, and millet, and nuts, and all kinds of live stock. And none of the country is untilled except parts where tilling is precluded by swamps and woods. Yet these parts too are thickly peopled — more because of the largeness of the populationthan because of the industry of the people; for the women are not only prolific, but good nurses as well, while the men are fighters rather than farmers. But at the present time they are compelled to till the soil, now that they have laid down their arms. However, although I am here speaking only in a general way of the whole of outer Celtica, let me now take each of the fourth parts separately and tell about them, describing them only in rough outline. And first, Narbonitis.
3 The figure of Narbonitis is approximately a parallelogram, since, on the west, it is traced by the Pyrenees, and, on the north, by the Cemmenus; as for the remaining sides, the southern is formed by the sea between the Pyrenees and Massilia, the eastern by the Alps, partly, and also by the intervening distance (taken in a straight line with the Alps) between the Alps and those foot-hills of the Cemmenus that reach down to the Rhodanus and form a right angle with the aforesaid straight line from the Alps. To the southern part there belongs an addition to the aforesaid figure, I mean the seaboard that follows next which is inhabited by the Massiliotes and the Sallyes, as far as the Ligures, to those parts that lie towards Italy and to the Varus River. This river is, as I stated before,the boundary between this Province and Italy. It is only a small river in summer, but in winter it broadens out to a breadth of as much as seven stadia. Now from this river the seaboard extends as far as the temple of the Pyrenaean Aphrodite. This temple, moreover, marks the boundary between the province of Narbonitis and the Iberian country, although some represent the place where the Trophies of Pompey are as marking the boundary between Iberia and Celtica. The distance thence to Narbo is sixty-three miles, from here to Nemausus eighty-eight, from Nemausus through Ugernum and Tarusco to the hot waters that are called "Sextian," which are near Massilia, fifty-three, and thence to Antipolis and the Varus River seventy-three; so that the sum total amounts to two hundred and seventy-seven miles. Some, however, have recorded the distance from the temple of Aphrodite on to the Varus River as two thousand six hundred stadia, while others add two hundred more; for there is disagreement with respect to the distances. But if you go by the other road — that leads through the country of the Vocontii and that of Cottius: from Nemausus the road is identical with the former road 179as far as Ugernum and Tarusco, but thence it runs across the Druentia River and through Caballio sixty-three miles to the frontiers of the Vocontii and the beginning of the ascent of the Alps; and thence, again, ninety-nine miles to the other frontiers of the Vocontii, at the country of Cottius, to the village of Ebrodunum; then, another ninety-nine through the village of Brigantium and Scingomagus and the pass that leads over the Alps to Ocelum, the end of the land of Cottius. Moreover, from Scingomagus on you begin to call the country Italy; and the distance from here to Ocelum is twenty-eight miles.
4 Massilia was founded by the Phocaeans,a and it is situated on a rocky place. Its harbour lies at the foot of a theatre-like rock which faces south. And not only is the rock itself well fortified, but also the city as a whole, though it is of considerable size. It is on the headland, however, that the Ephesium and also the temple of the Delphinian Apollo are situated. The latter is shared in common by all Ionians, whereas the Ephesium is a temple dedicated solely to the Ephesian Artemis: for when the Phocaeans were setting sail from their homeland an oracle was delivered to them, it is said, to use for their voyage a guide received from the Ephesian Artemis; accordingly, some of them put in at Ephesus and inquired in what way they might procure from the goddess what had been enjoined in a dream. Now the goddess, in a dream, it is said, had stood beside Aristarcha, one of the women held in very high honour, and commanded her to sail away with the Phocaeans, taking with her a certain reproduction which was among the sacred images; this done and the colony finally settled, they not only established the temple but also did Aristarcha the exceptional honour of appointing her priestess; further, in the colonial cities the people everywhere do this goddess honours of the first rank, and they preserve the artistic design of the "xoanon" the same, and all the other usages precisely the same as is customary in the mother-city.
5 The government under which the Massiliotes lives is aristocratic, and of all aristocracies theirs is the best ordered, since they have established an Assembly of six hundred men, who hold the honour of that office for life; these they call Timouchoi. Over the Assembly are set fifteen of its number, and to these fifteen it is given to carry on the immediate business of the government. And, in turn, three, holding the chief power, preside over the fifteen. However, a Timouchos cannot become one of these three unless he has children or is a descendant of persons who have been citizens for three generations. Their laws are Ionic, and are published to the people. They possess a country which, although planted with olive-trees and vines, is, on account of its ruggedness, too poor for grain; so that, trusting the sea rather than the land, they preferred their natural fitness for a seafaring life. 180Later, however, their valour enabled them to take in some of the surrounding plains, thanks to the same military strength by which they founded their cities, I mean their stronghold-cities, namely, first, those which they founded in Iberia as strongholds against the Iberians (they also taught the Iberians the sacred rites of the Ephesian Artemis, as practised in the fatherland, so that they sacrifice by the Greek ritual); secondly, Rhoë Agathe, as a stronghold against the barbarians who live round about the River Rhodanus; thirdly, Tauroentium, Olbia, Antipolis, and Nicaea, against the tribe of the Sallyes and against those Ligures who live in the Alps. There are also dry-docks and an armoury among the Massiliotes. In earlier times they had a good supply of ships, as well as of arms and instruments that are useful for the purposes of navigation and for sieges; and thanks to these they not only held out against the barbarians, but also acquired the Romans as friends, and many times not only themselves rendered useful service to the Romans, but also were aided by the Romans in their own aggrandizement. At any rate, Sextius, who defeated the Sallyes, after founding not very far from Massilia a city which bears his own name and that of the "hot waters" (some of which, they say, have changed to cold waters), not only settled a garrison of Romans there, but also drove back the barbarians out of the seaboard which leads from Massilia into Italy, since the Massiliotes could not entirely keep them back. Yet not even Sextius could effect more than merely this — that at those parts of the coast where there were good harbours the barbarians retired for a distance of only twelve stadia, and at the rugged parts, only eight. And the country thus abandoned by them he has given over to the Massiliotes. And in their citadel are set up great quantities of the first fruits of their victories, which they captured by defeating in naval battles those who from time to time unjustly disputed their claim to the mastery of the sea. In earlier times, then, they were exceptionally fortunate, not only in everything else, but also in their friendship with the Romans, of which one may detect many signs; what is more, the "xoanon" of that Artemis which is on the Aventine Hill was constructed by the Romans on the same artistic design as the "xoanon" which the Massiliotes have. But at the time of Pompey's sedition against Caesar they joined the conquered party and thus threw away the greater part of their prosperity. Nevertheless traces of their ancient zeal are still left among the people, especially in regard to the making of instruments and to the equipment of ships. But since, on account of the overmastery of the Romans, the barbarians who are situated beyond the Massiliotes became more and more subdued as time went on, and instead of carrying on war have already turned to civic life and farming, it may also be the case that the Massiliotes themselves no longer occupy themselves so earnestly with the pursuits aforementioned. Their present state of life makes this clear; for all the men of culture turn to the art of speaking and the study of philosophy; so that the city, although a short time ago it was given over as merely a training-school for the barbarians and was schooling the Galatae to be fond enough of the Greeks to write even their contracts in Greek, at the present time has attracted also the most notable of the Romans, if eager for knowledge, to go to school there instead of making their foreign sojourn at Athens. Seeing these men and at the same time living at peace, the Galatae are glad to adapt their leisure to such modes of life, not only as individuals, but also in a public way; at any rate, they welcome sophists, hiring some at private expense, but others in common, as cities, just as they do physicians. And the following might be set down as not the least proof of the simplicity of the modes of life, and of the self-restraint, of the Massiliotes: the maximum dowry among them is a hundred gold pieces, and five for dress, and five for golden ornaments; but more than this is not permitted. Both Caesar and the commanders who succeeded him, mindful of the former friendship, acted in moderation with reference to the wrongs done in the war, and preserved to the city the autonomy which it had had from the beginning; so that neither Massilia nor its subjects are subject to the praetors who are sent to the province. So much for Massilia.
6 While the mountainous country of the Sallyes inclines more and more from the west to the north and retires little by little from the sea, the coastline bends round to the west; but after extending a short distance from the city of the Massiliotes, about a hundred stadia, to a fair-sized promontory near some stone-quarries, the coastline then begins to curve inland and to form with the precincts of Aphrodite (that is, the headland of the Pyrenees) the Galatic Gulf, which is also called the Gulf of Massilia. The Gulf is double, for, in the same circuit, Mount Setium, with the help of the Isle of Blascon, which is situated near by, juts out and thus marks off two gulfs. Of the two gulfs, the larger, into which the mouth of the Rhodanus discharges, is again called, in the proper sense of the term, "Galatic Gulf"; the smaller is opposite Narbo and extends as far as the Pyrenees. Now Narbo lies above the outlets of the Atax and the Lake of Narbonitis, and it is the greatest of the emporiums in this country, though there is a city near the Rhodanus which is no small emporium, namely, Arelate. These emporiums are about an equal distance from each other and from the aforesaid headlands — Narbo from the precincts of Aphrodite, and Arelate from Massilia. On either side of Narbo there flow other rivers — some from the Cemmenus Mountains, the others from the Pyrenees — and they have cities to which voyages of no considerable length are made in small ships. From the Pyrenees flow both the Ruscino and the Ilibirris, each of them having a city of like name; and, as for the Ruscino, there is not only a lake near by, but also, a short distance above the sea, a marshy district, full of salt-springs, which contains the "dug mullets"; for if one digs only two or three feet and thrusts his trident down into the muddy water, it is possible to spit a fish that is notable for its size; and it feeds on the mud just as the eels do. These, then, are the rivers which flow from the Pyrenees between Narbo and the precincts of Aphrodite; while on the other size of Narbo there flow to the sea from the Cemmenus (from which the Atax flows) both the Orbis and the Arauris. On the former of these rivers is situated Baetera, a safe city, near Narbo, and on the other, Agathe, founded by the Massiliotes.
7 Now the aforesaid seaboard has not merely one marvel, namely, that of the "dug mullets," but also another which one might say is greater than that, about which I shall now speak: Between Massilia and the outlets of the Rhodanus there is a plain, circular in shape, which is as far distant from the sea as a hundred stadia, and is also as much as that in diameter. It is called Stony Plain from the fact that it is full of stones as large as you can hold in your hand, although from beneath the stones there is a growth of wild herbage which affords abundant pasturage for cattle. In the middle of the plain stand water and salt springs, and also lumps of salt. Now although the whole of the country which lies beyond, as well as this, is exposed to the winds, the Black North, a violent and chilly wind, descends upon this plain with exceptional severity; at any rate, it is said that some of the stones are swept and rolled along, and that by the blasts the people are dashed from their vehicles and stripped of both weapons and clothing. Now Aristotle says that the stones, after being vomited to the surface by those earthquakes that are called "Brastae," rolled together into the hollow places of the districts. But Poseidonius says that, since it was a lake, it solidified while the waves were dashing, and because of this was parted into a number of stones — as are the river-rocks and the pebbles on the sea-shore; and by reason of the similarity of origin, the former, like the latter, are both smooth and equal in size. And an account of the cause has been given by both men. Now the argument in both treatises is plausible; for of necessity the stones that have been assembled together in this way cannot separately, one by one, either have changed from liquid to solid or have been detached from great masses of rock that received a succession of fractures. What was difficult to account for, however, Aeschylus, who closely studied the accounts or else received them from another source, removed to the realm of myth. At any rate, Prometheus, in Aeschylus' poem, in detailing to Heracles the route of the roads from the Caucasus to the Hesperides says: "And thou wilt come to the undaunted host of the Ligurians, where thou wilt not complain of battle, I clearly know, — impetuous fighter though thou art; because there it is fated that even thy missiles shall fail thee, and no stone from the ground shalt thou be able to choose, since the whole district is soft ground. But Zeus, seeing thee without means to fight, will have pity upon thee, and, supplying a cloud with a snow-like shower of round stones, will put the soil under cover; and with these stones, thereupon, thou wilt pelt, and easily push thy way through, the Ligurian host." Just as if it were not better, says Poseidonius, for Zeus to have cast the stones upon the Ligures themselves and to have buried the whole host than to represent Heracles as in need of so many stones. Now, as for the number ("so many"), he needed them all if indeed the poet was speaking with reference to a throng that was very numerous; so that in this, at least, the writer of the myth is more plausible than the man who revises the myth. Furthermore, by saying "it is fated," the poet forbids one to find fault in a captious way with anything else in the p189passage — "captious," I say, for one might also find in the discussions on "Providence" and "Presdestination" many instances among the affairs of men and among the natural occurrences of such a kind that, in reference to them, one might say that it were much better for this to have taken place than that; for example, for Egypt to be well-watered by rains, rather than that Ethiopia should soak its soil with water; and for Paris to have met his reversal by shipwreck on the voyage to Sparta, instead of later carrying off Helen and paying the penalty to those whom he had wronged, after he had effected all that ruin of Greeks and barbarians — a ruin which Euripides attributed to Zeus: "For Zeus, the father, willing not only evil for the Trojans but also sorrow for the Greeks, resolved upon all this."
8 With respect to the mouths of the Rhodanus: Polybius reproves Timaeus by saying that there are not five but two; Artemidorus says three; Marius, later, seeing that, in consequence of the silting, its mouths were becoming stopped up and difficult of entrance, cut a new channel, and, upon admitting the greater part of the river here, presented it to the Massiliotes as a meed of their valour in the war against the Ambrones and Toÿgeni; and the wealth they carried off from this source was considerable, because they exacted tolls from all who sailed up and all who sailed down it. Nevertheless, the mouths still remain difficult of entrance for ships, not only on account of the impetuosity of the river and the silting up, but also of the lowness of the country, so that in foul weather one cannot descry the land even when close to it. Wherefore the Massiliotes set up towers as beacons, because they were in every way making the country their own; and, in truth, they also established a temple of the Ephesian Artemis there, after first enclosing a piece of land which is made an island by the mouths of the river. Beyond the outlets of the Rhodanus lies a sea-water marsh; it is called "Stomalimne," and it has a very great quantity of oysters, and, besides that, is well supplied with fish. This lake was by some counted in with the mouths of the Rhodanus, and particularly by those who said there were seven mouths, although they were right in neither the latter nor the former; for there is a mountain intervening which separates the lake from the river. This, then, is approximately the nature and the extent of the seaboard from the Pyrenees to Massilia.
9 Again, the seaboard which extends from Massilia to the Varus River and to those Ligures who live in the region of the river has not only the following cities of the Massiliotes, namely, Tauroentium, Olbia, Antipolis, and Nicaea, but also that naval-station of Caesar Augustus which is called Forum Julium. This naval-station is situated between Olbia and Antipolis, at a distance of about six hundred stadia from Massilia. The Varus is between Antipolis and Nicaea, at a distance of about twenty stadia from the latter and sixty from the former, so that, according to what is now the declared boundary, Nicaea becomes a part of Italy, although it belongs to the Massiliotes; for the Massiliotes founded these places as strongholds against those barbarians who were situated beyond, wishing at least to keep free the sea, since the land was controlled by the barbarians; for it is mountainous and also strong for defence, since, although next to Massilia it leaves a strip of level land of moderate width, yet as you proceed towards the east it squeezes the strip off altogether towards the sea, and scarcely leaves the road itself passable. Now the first of these districts are occupied by the Sallyes, but the last by those Ligures whose territory connects with Italy, concerning whom I shall speak hereafter. But at present I need add only this, that, although Antipolis is situated among the parts that belong to Narbonitis, and Nicaea among those that belong to Italy, Nicaea remains subject to the Massiliotes and belongs to the Province, while Antipolis is classed among the Italiote cities, having been so adjudged in a suit against the Massiliotes and thereby freed from their orders.
Lying off these narrow stretches of coast, if we begin at Massilia, are the five Stoechades Islands, three of them of considerable size, but two quite small; they are tilled by Massiliotes. In early times the Massiliotes had also a garrison, which they placed there to meet the onsets of the pirates, whence the islands were well supplied with harbours. Next, after the Stoechades, are the islands of Planasia and Lero, which have colonial settlements. In Lero there is also a hero-temple, namely, that in honour of Lero; this island lies off Antipolis. And, besides, there are isles that are not worth mentioning, some off Massilia itself and the others off the rest of the aforesaid shore. As for the harbours, the one that is at the naval-station is of considerable size, and so is that of the Massiliotes, whereas the others are only of moderate size; among these latter is the harbour that is called Oxybius, so named after the Oxybian Ligures. This is what I have to say about the seaboard.
As for the country that lies beyond the seaboard, its geographical limits are, in a general way, traced by the mountains that lie round about it, and also by the rivers — by the Rhodanus River especially, for it not only is the largest but also affords the most navigation inland, since the number of the streams from which it is filled is large. However, I must tell about all these regions in order. If you begin, then, at Massilia, and proceed towards the country that is between the Alps and the Rhodanus: Up to the Druentia River the country is inhabited by the Sallyes for a distance of five hundred stadia; but if you cross the river by ferry into the city of Caballio, the whole country next thereafter belongs to the Cavari, up to the confluence of the Isar with the Rhodanus; this is also approximately where the Cemmenus Mountain joins the Rhodanus; the length of your journey from Druentia up to this place is seven hundred stadia. Now the Sallyes occupy — I mean in their own country — not only the plains but also the mountains that lie above the plains, whereas above the Cavari are situated the Vocontii, Tricorii, Iconii, and Medulli. Between the Druentia and the Isar there are still other rivers which flow from the Alps to the Rhodanus, namely, two that flow round a city of the Cavaran Vari, and coming together in a common stream empty into the Rhodanus; and a third, the Sulgas, which mingles its waters with the Rhodanus near the city of Undalum, where in a great battle Gnaeus Ahenobarbus turned many myriads of Celti to flight. And there are in the intervening space the cities of Avenio, Arausio, and Aeria — "an 'Aeria' in reality," says Artemidorus, "because it is situated on a lofty elevation." All the country, however, is level and good for pasturage, except that the stretch from Aeria to Durio has mountainous passes that are narrow and wooded. But where the Isar River and the Rhodanus and the Cemmenus Mountain meet, Quintus Fabius Maximus Aemilianus, with less than thirty thousand men all told, cut down two hundred thousand Celti; and on the spot he set up a trophy of white marble, and also two temples, one in honour of Ares, the other in honour of Heracles. From the Isar to Vienna, the metropolis of the Allobroges, situated on the Rhodanus, the distance is three hundred and twenty stadia. Near Vienna, and beyond it, is situated Lugdunum, at which the Arar and the Rhodanus mingle with one another; and the distance to Lugdunum in stadia is, if you go by foot through the territory of the Allobroges, about two hundred, but if by voyage up the river, slightly more than that. Formerly the Allobroges kept up warfare with many myriads of men, whereas now they till the plains and the glens that are in the Alps, and all of them live in villages, except that the most notable of them, inhabitants of Vienna (formerly a village, but called, nevertheless, the "metropolis" of the tribe), have built it up into a city. It is situated on the Rhodanus. This river runs from the Alps in great volume and impetuosity — since on its way out, while passing through the Lemenna Lake, its stream is clearly visible for many stadia. And after coming down into the plains of the country of the Allobroges and Segusiavi, it meets the Arar at Lugdunum, a city of the Segusiavi. The Arar, too, flows from the Alps, since it separates the Sequani from the Aedui and the Lingones; then, later, taking on the waters of the Dubis — a navigable river that runs from the same mountains — it prevails over the Dubis with its name, and though made up of both mingles with the Rhodanus as the "Arar." And, in its turn, the Rhodanus prevails, and runs to Vienna. So the result is, that at first the three rivers run northwards, and then westwards; and then, immediately after they have joined together into one bed, the stream again takes another turn and runs a southerly course as far as its outlets (although before this it has received the other rivers), and from there begins to make the remainder of its course as far as the sea. Such, then, is approximately the nature of the country which lies between the Alps and the Rhodanus.
As for the country which lies on the other side of the river, most of it is occupied by those Volcae who are called Arecomisci. Narbo is spoken of as the naval-station of these people alone, though it would be fairer to add "and of the rest of Celtica" — so greatly has it surpassed the others in the number of people who use it as a trade-centre. Now, although the Volcae border on the Rhodanus, with the Sallyes and also the Cavari stretching along parallel to them on the opposite side of the river, the name of the Cavari prevails, and people are already calling by that name all the barbarians in that part of the country — no, they are no longer barbarians, but are, for the most part, transformed to the type of the Romans, both in their speech and in their modes of living, and some of them in their civic life as well. Again, situated alongside the Arecomisci as far as the Pyrenees, are other tribes, which are without repute and small. Now the metropolis of the Arecomisci is Nemausus, which, although it comes considerably short of Narbo in its throng of foreigners and of merchants, surpasses Narbo in that of citizens; for it has, subject to its authority, twenty-four villages, which are exceptional in their supply of strong men, of stock like its own, and contribute towards its expenses; and it has also what is called the "Latin right," so that those who have been thought worthy of the offices of aedile and quaestor at Nemausus are by that preferment Roman citizens, and, on account of this fact, this tribe too is not subject to the orders of the praetors who are sent out from Rome.The city is situated on the road that leads from Iberia into Italy, which, although it is easy to travel in summer, is muddy and also flooded by the rivers in winter and spring. Now some of the streams are crossed by ferries, others by bridges — some made of timber, others of stone. But it is the torrents that cause the annoying difficulties that result from the waters, since, after the melting away of the snows, they sometimes rush down from the Alps even till the summer-time. Of the aforesaid road, the branchthat leads straight to the Alps is, as I stated, the short cut through the territory of the Vocontii, whereas that through the Massilian and Ligurian seaboard is indeed longer, although the passes it affords over into Italy are easier since the mountains begin to lower there. The distance of Nemausus from the Rhodanus — reckoning from a point opposite the town of Tarusco, on the other side of the river — is about a hundred stadia; but from Narbo, seven hundred and twenty. Again, in territory that joins the Cemmenus Mountain, and that takes in also the southern side of the mountain as far as its summits, there live that people of the Volcae who are called Tectosages and also certain others. About these others I shall speak later on.
The people who are called Tectosages closely approach the Pyrenees, though they also reach over small parts of the northern side of the Cemmenus; and the land they occupy is rich in gold. It appears that at one time they were so powerful and had so large a stock of strong men that, when a sedition broke out in their midst, they drove a considerable number of their own people out of the homeland; again, that other persons from other tribes made common lot with these exiles; and that among these are also those people who have taken possession of that part of Phrygia which has a common boundary with Cappadocia and the Paphlagonians.Now as proof of this we have the people who are still, even at the present time, called Tectosages; for, since there are three tribes, one of them — the one that lives about the city of Ancyra — is called "the tribe of the Tectosages," while the remaining two are the Trocmi and the Tolistobogii. As for these latter peoples, although the fact of their racial kinship with the Tectosages indicates that they emigrated from Celtica, I am unable to tell from what districts they set forth; for I have not learned of any Trocmi or Tolistobogii who now live beyond the Alps, or within them, or this side of them. But it is reasonable to suppose that nothing has been left of them in Celtica on account of their thoroughgoing migrations — just as is the case with several other peoples. For example, some say that the second Brennus who made an invasion against Delphi was a Prausan, but I am unable to say where on earth the Prausans formerly lived, either. And it is further said that the Tectosages shared in the expedition to Delphi; and even the treasures that were found among them in the city of Tolosa by Caepio, a general of the Romans, were, it is said, a part of the valuables that were taken from Delphi, although the people, in trying to consecrate them and propitiate the god, added thereto out of their personal properties, and it was on account of having laid hands on them that Caepio ended his life in misfortunes — for he was cast out by his native land as a temple-robber, and he left behind as his heirs female children only, who, as it turned out, became prostitutes, as Timagenes has said, and therefore perished in disgrace. However, the account of Poseidonius is more plausible: for he says that the treasure that was found in Tolosa amounted to about fifteen thousand talents (part of it in sacred lakes), unwrought, that is, merely gold and silver bullion; whereas the temple at Delphi was in those times already empty of such treasure, because it had been robbed at the time of the sacred war by the Phocians; but even if something was left, it was divided by many among themselves; neither is it reasonable to suppose that they reached their homeland in safety, since they fared wretchedly after their retreat from Delphi and, because of their dissensions, were scattered, some in one direction, others in another. But, as has been said both by Poseidonius and several others, since the country was rich in gold, and also belonged to people who were god-fearing and not extravagant in their ways of living, it came to have treasures in many places in Celtica; but it was the lakes, most of all, that afforded the treasures their inviolability, into which the people let down heavy masses of silver or even of gold. At all events, the Romans, after they mastered the regions, sold the lakes for the public treasury, and many of the buyers found in them hammered mill-stones of silver. And, in Tolosa, the temple too was hallowed, since it was very much revered by the inhabitants of the surrounding country, and on this account the treasures there were excessive, for numerous people had dedicated them and no one dared to lay hands on them.
Tolosa is situated on the narrowest part of the isthmus which separates the ocean from the sea that is at Narbo, which isthmus, according to Poseidonius is less than three thousand stadia in width. But it is above all worth while to note again a characteristic of this region which I have spoken of before — the harmonious arrangement of the country with reference, not only to the rivers, but also to the sea, alike both the outer sea and the inner; for one might find, if he set his thoughts upon the matter, that this is not the least factor in the excellence of the regions — I mean the fact that the necessities of life are with ease interchanged by every one with every one else and that the advantages which have arisen therefrom are common to all; but especially so at present, when being at leisure from the weapons of war, the people are tilling the country diligently, and are devising for themselves modes of life that are civil. Therefore, in the cases of this sort, one might believe that there is confirmatory evidence for the workings of Providence, since the regions are laid out, not in a fortuitous way, but as though in accordance with some calculated plan. In the first place, the voyage which the Rhodanus affords inland is a considerable one, even for vessels of great burden, and reaches numerous parts of the country, on account of the fact that the rivers which fall into it are navigable, and in their turns receive most of the traffic. Secondly, the Rhodanus is succeeded by the Arar, and by the Dubis (which empties into the Arar); then the traffic goes by land as far as the Sequana River; and thence it begins its voyage down to the ocean, and to the Lexobii and Caleti; and from these peoples it is less than a day's run to Britain. But since the Rhodanus is swift and difficult to sail up, some of the traffic from here preferably goes by land on the wagons, that is, all the traffic that is conveyed to the Arvernians and the Liger River — albeit in a part of its course the Rhodanus draws close to these also; still, the fact that the road is level and not long (about eight hundred stadia)is an inducement not to use the voyage upstream, since it is easier to go by land; from here, however, the road is naturally succeeded by the Liger; and it flows from the Cemmenus Mountain to the ocean. Thirdly, from Narbo traffic goes inland for a short distance by the Atax River, and then a greater distance by land to the Garumna River; and this latter distance is about eight hundred or seven hundred stadia. And the Garumna, too, flows to the ocean. This, then, is what I have to say about the people who inhabit the dominion of Narbonitis, whom the men of former times named "Celtae"; and it was from the Celtae, I think, that the Galatae as a whole were by the Greeks called "Celti" — on account of the fame of the Celtae, or it may also be that the Massiliotes, as well as other Greek neighbours, contributed to this result, on account of their proximity. |
|
|
|
|
4 - 2 Transalpine Gaul: Aquitania 
Next, I must discuss the Aquitani, and the tribes which have been included within their boundaries, namely, the fourteen Galatic tribes which inhabit the country between the Garumna and the Liger, some of which reach even to the river-land of the Rhone and to the plains of Narbonitis. For, speaking in a general way, the Aquitani differ from the Galatic race in the build of their bodies as well as in their speech; that is, they are more like the Iberians. Their country is bounded by the Garumna River, since they live between this and the Pyrenees. There are more than twenty tribes of the Aquitani, but they are small and lacking in repute; the majority of the tribes live along the ocean, while the others reach up into the interior and to the summits of the Cemmenus Mountains, as far as the Tectosages. But since a country of this size was only a small division, they added to it the country which is between the Garumna and the Liger. These rivers are approximately parallel to the Pyrenees and form with the Pyrenees two parallelograms, since they are bounded on their other sides by the ocean and the Cemmenus Mountains. And the voyage on either of the rivers is, all told, two thousand stadia. The Garumna, after being increased by the waters of three rivers, discharges its waters into the region that is between those Bituriges that are surnamed "Vivisci" and the Santoni — both of them Galatic tribes; for the tribe of these Bituriges is the only tribe of different race that is situated among the Aquitani; and it does than pay tribute to them, though it has an emporium, Burdigala, which is situated on a lagoon that is formed by the outlets of the river. The Liger, however, discharges its waters between the Pictones and the Namnitae. Formerly there was an emporium on this river, called Corbilo, with respect to which Polybius, calling to mind the fabulous stories of Pytheas, has said: "Although no one of all the Massiliotes who conversed with Scipio was able, when questioned by Scipio about Britain, to tell anything worth recording, nor yet any one of the people from Narbo or of those from Corbilo, though these were the best of all the cities in that country, still Pytheas had the hardihood to tell all those falsehoods about Britain." The city of the Santoni, however, is Mediolanium. Now the most of the ocean-coast of the Aquitani is sandy and thin-soiled, thus growing millet, but it is rather unproductive in respect of the other products. Here too is the gulf which, along with that Galatic Gulf which is within the coastline of Narbonitis, forms the isthmus (itself too, like the latter gulf, having the name "Galatic"). The gulf is held by the Tarbelli, in whose land the gold mines are most important of all; for in pits dug only to a slight depth they find slabs of gold as big as the hand can hold, which at times require but little refining; but the rest is gold dust and nuggets, the nuggets too requiring no great amount of working. The interior and mountainous country, however, has better soil: first, next to the Pyrenees, the country of the "Convenae" (that is, "assembled rabble"), in which are the city of Lugdunum and the hot springsa of the Onesii — most beautiful springs of most potable waters; and, secondly, the country of the Auscii also has good soil.
2 Those tribes between the Garumna and the Liger that belong to Aquitania are, first, the Elui, whose territory begins at the Rhodanus, and then, after them, the Vellavii, who were once included within the boundaries of the Arverni, though they are now ranked as autonomous; then the Arverni, the Lemovices, and the Petrocorii; and, next to these, the Nitiobriges, the Cadurci, and those Bituriges that are called "Cubi"; and, next to the ocean, both the Santoni and the Pictones, the former living along the Garumna, as I have said, the latter along the Liger; but the Ruteni and the Gabales closely approach Narbonitis. Now among the Petrocorii there are fine iron-works, and also among the Bituriges Cubi; among the Cadurci, linen factories; among the Ruteni, silver mines; and the Gabales, also, have silver mines. The Romans have given the "Latin right" to certain of the Aquitani just as they have done in the case of the Auscii and the Convenae.
3 The Arverni are situated on the Liger; their metropolis is Nemossus, a city situated on the Liger. This river, after flowing past Cenabum (the emporium of the Carnutes at about the middle of the voyage, an emporium that is jointly peopled), discharges its waters towards the ocean. As for their former power, the Arverni hold out as a great proof thereof the fact that they oftentimes warred against the Romans, at times with two hundred thousand men, and again, with double that number — with double that number, for example, when they, with Vercingetorix, struggled to a finish against the Deified Caesar; and, before that, also, with two hundred thousand against Maximus Aemilianus, and also, in like manner, against Dometius Ahenobarbus. Now the struggles against Caesar took place near Gergovia (a city of the Arverni, situated on a high mountain), where Vercingetorix was born, and also near Alesia (a city of the Mandubii — a tribe which has a common boundary with the Arverni — and this city too is situated on a high hill, although it is surrounded by mountains and two rivers), in which not only the commander was captured but the war had its end. But the struggles against Maximus Aemilianus took place at the confluence of the Isar and the Rhodanus, where the Cemmenus Mountain approaches closely the Rhodanus; and against Dometius Ahenobarbus, at a place still lower down the Rhodanus, at the confluence of the Sulgas and the Rhodanus. Again, the Arverni not only had extended their empire as far as Narbo and the boundaries of Massiliotis, but they were also masters of the tribes as far as the Pyrenees, and as far as the ocean and the Rhenus. Luerius, the father of the Bituitus who warred against Maximus and Dometius, is said to have been so exceptionally rich and extravagant that once, when making a display of his opulence to his friends, he rode on a carriage through a plain, scattering gold and silver coins here and there, for his followers to pick up. |
|
|
|
|
4 - 3 Transalpine Gaul: Lugdunensis 
The country next in order after the Aquitanian division and Narbonitis reaches as far as the whole of the Rhenus, extending from the Liger River and also from the Rhodanus at the point where the Rhodanus, after it runs down from its source, touches Lugdunum. Now of this country the upper parts that are next to the sources of the rivers (the Rhenus and the Rhodanus), extending as far, approximately, as the centre of the plains, have been classified under Lugdunum; whereas the remaining parts, including the parts along the ocean, have been classified under another division, I mean that division which is specifically assigned to the Belgae. As for me, however, I shall point out the separate parts in a rather general way.
2 Lugdunum itself, then, (a city founded at the foot of a hill at the confluence of the River Arar and the Rhodanus), is occupied by the Romans. And it is the most populous of all the cities of Celtica except Narbo; for not only do people use it as an emporium, but the Roman governors coin their money there, both the silver and the gold.a Again, the temple that was dedicated to Caesar Augustus by all the Galatae in common is situated in front of this city at the junction of the rivers. And in it is a noteworthy altar, bearing an inscription of the names of the tribes, sixty in number; and also images from these tribes, one from each tribe, and also another large altar. The city of Lugdunum presides over the tribe of the Segusiavi, which tribe is situated between the Rhodanus and the Dubis. The tribes that come next in order after the Segusiavi, I mean those which together stretch towards the Rhenus, are bounded partly by the Dubis and partly by the Arar. Now these rivers too, as I have said before,first run down from the Alps, and then, falling into one stream, run down into the Rhodanus; and there is still another river, Sequana by name, which likewise has its sources in the Alps.b It flows into the ocean, however, running parallel to the Rhenus, through a tribe of like name,whose country joins the Rhenus in its eastern parts, but in the opposite parts, the Arar; and it is from their country that the finest of salted hog-meat is brought down and shipped to Rome. Now between the Dubis and the Arar dwells the tribe of the Aedui, with their city of Cabyllinum, on the Arar, and their garrison of Bibracte. (The Aedui were not only called kinsmen of the Romans, but they were also the first of the peoples in that country to apply for their friendship and alliance.) But across the Arar dwell the Sequani, who, for a long time, in fact, had been at variance with the Romans as well as with the Aedui. This was because they often joined forces with the Germans in their attacks upon Italy; aye, and they demonstrated that theirs was no ordinary power: they made the Germans strong when they took part with them and weak when they stood aloof. As regards the Aedui, not only were the Sequani at variance with them for the same reasons, but their hostility was intensified by the strife about the river that separates them, since each tribe claimed that the Arar was its private property and that the transportation tolls belonged to itself. Now, however, everything is subject to the Romans.
3 As for the country that is on the Rhenus, the first of all the peoples who live there are the Elvetii, in whose territory, on Mount Adula, are the sources of the river. Mount Adula is a part of the Alps, and from it flows also the River Addua, in the opposite direction, that is, towards Cisalpine Celtica, and fills Lake Larius (near which the city of Comum has been founded), and then, flowing on from Lake Larius, contributes its waters to those of the Padus (matters about which I shall speak later on). The Rhenus, too, spreads into great marshes and a great lake, which lake is touched by the territory of both the Rhaeti and the Vindelici (certain of the peoples who live in the Alps and also beyond the Alps). Asinius says that the length of the river is six thousand stadia, but it is not. In fact, it could only slightly exceed the half of that in a straight line, while the addition of one thousand stadia would be quite sufficient for the windings. For not only is it swift, and on this account also hard to bridge, but after its descent from the mountains runs the rest of the way with even slope through the plains. How, then, could it remain swift and violent, if to the even slope of the river we added numerous long windings? He further says it has only two mouths, after first finding fault with those who say it has more than that. So then, both this river and the Sequana encircle somewhat of territory within their windings, but not so much as that. Both rivers flow from the southern parts towards the north; and in front of them lies Britain, which is near enough to the Rhenus for Cantium, which is the eastern cape of the island, to be visible from it, though it is slightly farther off from the Sequana. Here, too, the Deified Caesar established his navy-yard when he sailed to Britain. The part of the Sequana that is navigated by those who receive the cargoes from the Arar is slightly longer than that of the Liger and that of the Garumna; but the distance from Lugdunum to the Sequana is a thousand stadia, and that from the mouths of the Rhodanus to Lugdunum is less than double this distance. It is said also that the Elvetii, although rich in gold, none the less turned themselves to robbery upon seeing the opulence of the Cimbri; but that on their campaigns two of their tribes (there were three) were obliterated. But still the number of the descendants from what was left of them was shown by their war against the Deified Caesar, in which about four hundred thousand lives were destroyed, although Caesar allowed the rest of them, about eight thousand, to escape, so as not to abandon the country, destitute of inhabitants, to the Germans, whose territory bordered on theirs.
4 After the Elvetii, along the Rhenus, dwell the Sequani and the Mediomatrici, in whose territory are situated the Tribocchi, a Germanic tribe which crossed the river from their homeland. Mount Jura is in the territory of the Sequani; it marks the boundary between the Elvetii and the Sequani. So it is beyond the Elvetii and the Sequani, towards the west, that the Aedui and the Lingones dwell; and beyond the Mediomatrici, that the Leuci and a part of the Lingones dwell. But those tribes between the Liger and the Sequana Rivers that are on the far side of the Rhodanus and the Arar are situated side by side, towards the north, with both the Allobroges and the people round Lugdunum; and of these tribes the most conspicuous are those of the Arverni and the Carnutes, through both of whose territories the Liger runs on its way out to the ocean. The passage across to Britain from the rivers of Celtica is three hundred and twenty stadia; for if you put to sea on the ebb-tide at nightfall, you land upon the island about the eighth hour on the following day. After the Mediomatrici and the Tribocchi, along the Rhenus, dwell the Treveri, near whom the bridge has been built by the Roman officers who are now conducting the Germanic war. The Ubii used to live opposite this region, across the Rhenus, though by their own consent they were transferred by Agrippa to the country this side the Rhenus. Next after the Treveri are the Nervii, who are also a Germanic tribe. Last come the Menapii, who dwell on both sides of the river near its mouths, in marshes and woods (not of tall timber, but dense and thorny). It is opposite to these that the Sugambri are situated, a Germanic people. But beyond this whole river-country are those Germans who are called the Suevi and excel all the others in power and numbers (the people driven out by the Suevi in our time have been fleeing for refuge to this side of the Rhenus). And other peoples, also, lord it in different places, and in their turn take up the tinders of war, but the foremost are always put down.
5 West of the Treveri and the Nervii dwell the Senones and the Remi, and farther on, the Atrebatii and the Eburones; and after the Menapii, on the sea, are, in their order, the Morini, the Bellovaci, the Ambiani, the Suessiones, and the Caleti, as far as the outlet of the Sequana River. Both the country of the Morini and that of the Atrebatii and Eburones resemble that of the Menapii; for much of it, though not so much as the historians have said (four thousand stadia), is a forest, consisting of trees that are not tall; the forest is called Arduenna. At the time of hostile onsets they used to intertwine the withes of the brushwood, since the withes were thorny, and thus block the passage of the enemy. In some places they also used to fix stakes in the ground — themselves, with their whole families, slinking away into the depths of the forest, for they had small islands in their marshes. Now although the refuge they took was safe for them in the rainy seasons, they were easily captured in the dry seasons. But as it is, all the peoples this side the Rhenus are living in a state of tranquillity and are submissive to the Romans. The Parisii live round about the Sequana River, having an island in the river and a city called Lucotocia; and so do the Meldi and the Lexovii — these latter beside the ocean. But the most noteworthy of all the tribes in this region of Celtica is that of the Remi; their metropolis, Duricortora, is most thickly settled and is the city that entertains the Roman governors. |
|
|
|
|
4 - 4 Transalpine Gaul: W Lugdunensis and Belgica 
After the aforesaid tribes, the rest are tribes of those Belgae who live on the ocean-coast. Of the Belgae, there are, first, the Veneti who fought the naval battle with Caesar; for they were already prepared to hinder his voyage to Britain, since they were using the emporium there. But he easily defeated them in the naval battle, making no use of ramming (for the beams were thick), but when the Veneti bore down upon him with the wind, the Romans hauled down their sails by means of pole-hooks; for, on account of the violence of the winds, the sails were made of leather, and they were hoisted by chains instead of ropes. Because of the ebb-tides, they make their ships with broad bottoms, high sterns, and high prows; they make them of oak (of which they have a plentiful supply), and this is why they do not bring the joints of the planks together but leave gaps; they stuff the gaps full of sea-weed, however, so that the wood may not, for lack of moisture, become dry when the ships are hauled up, because the sea-weed is naturally rather moist, whereas the oak is dry and without fat. It is these Veneti, I think, who settled the colony that is on the Adriatic (for about all the Celti that are in Italy migrated from the transalpine land, just as did the Boii and Senones), although, on account of the likeness of name, people call them Paphlagonians. I do not speak positively, however, for with reference to such matters probability suffices. Secondly, there are the Osismii (whom Pytheas calls the Ostimii), who live on a promontory that projects quite far out into the ocean, though not so far as he and those who have trusted him say. But of the tribes that are between the Sequana and the Liger, some border on the Sequani, others on the Arverni.
2 The whole race which is now called both "Gallic" and "Galatic" is war-mad, and both high-spirited and quick for battle, although otherwise simple and not ill-mannered. And therefore, if roused, they come together all at once for the struggle, both openly and without circumspection, so that for those who wish to defeat them by stratagem they become easy to deal with (in fact, irritate them when, where, or by what chance pretext you please, and you have them ready to risk their lives, with nothing to help them in the struggle but might and daring); whereas, if coaxed, they so easily yield to considerations of utility that they lay hold, not only of training in general, but of language-studies as well. As for their might, it arises partly from their large physique and partly from their numbers. And on account of their trait of simplicity and straightforwardness they easily come together in great numbers, because they always share in the vexation of those of their neighbours whom they think wronged. At the present time they are all at peace, since they have been enslaved and are living in accordance with the commands of the Romans who captured them, but it is from the early times that I am taking this account of them, and also from the customs that hold fast to this day among the Germans. For these peoples are not only similar in respect to their nature and their governments, but they are also kinsmen to one another; and, further, they live in country that has a common boundary, since it is divided by the River Rhenus, and the most of its regions are similar (though Germany is more to the north), if the southern regions be judged with reference to the southern and also the northern with reference to the northern. But it is also on account of this trait that their migrations easily take place, for they move in droves, army and all, or rather they make off, households and all, whenever they are cast out by others stronger than themselves. Again, the Romans conquered these people much more easily than they did the Iberians; in fact, the Romans began earlier, and stopped later, carrying on war with the Iberians, but in the meantime defeated all these — I mean all the peoples who live between the Rhenus and the Pyrenees Mountains. For, since the former were wont to fall upon their opponents all at once and in great numbers, they were defeated all at once, but the latter would husband their resources and divide their struggles, carrying on war in the manner of brigands, different men at different times and in separate divisions. Now although they are all fighters by nature, they are better as cavalry than as infantry; and the best cavalry-force the Romans have comes from these people. However, it is always those who live more to the north and along the ocean-coast that are the more warlike.
3 Of these people, they say, the Belgae are bravest (who have been divided into fifteen tribes, the tribes that live along the ocean between the Rhenus and the Liger); consequently they alone could hold out against the onset of the Germans — the Cimbri and Teutones. But of the Belgae themselves, they say, the Bellovaci are bravest, and after them the Suessiones. As for the largeness of the population, this is an indication: it is found upon inquiry, they say, that there are as many as three hundred thousand of those Belgae (of former times) who are able to bear arms; and I have already told the number of the Elvetii, and of the Arverni, and of their allies, — from all of which the largeness of the population is manifest, as is also the thing of which I spoke above — the excellence of the women in regard to the bearing and nursing of children. The Gallic people wear the "sagus," let their hair grow long, and wear tight breeches; instead of tunics they wear slit tunics that have sleeves and reach as far as their private parts and the buttocks. The wool of their sheep, from which they weave the coarse "sagi" (which they call "laenae"), is not only rough, but also flocky at the surface; the Romans, however, even in the most northerly parts raise skin-clothed flocks with wool that is sufficiently fine. The Gallic armour is commensurate with the large size of their bodies: a long sabre, which hangs along the right side, and a long oblong shield, and spears in proportion, and a "madaris," a special kind of javelin. But some of them also use bows and slings. There is also a certain wooden instrument resembling the "grosphus" (it is hurled by hand, not by thong, and ranges even farther than an arrow), which they use particularly for the purposes of bird-hunting. Most of them, even to the present time, sleep on the ground, and eat their meals seated on beds of straw. Food they have in very great quantities, along with milk and flesh of all sorts, but particularly the flesh of hogs, both fresh and salted. Their hogs run wild, and they are of exceptional height, boldness, and swiftness; at any rate, it is dangerous for one unfamiliar with their ways to approach them, and likewise, also, for a wolf. As for their houses, which are large and dome-shaped, they make them of planks and wicker, throwing up over them quantities of thatch. And their flocks of sheep and herds of swine are so very large that they supply an abundance of the "sagi" and the salt-meat, not only to Rome, but to most parts of Italy as well. The greater number of their governments used to be aristocratic — although in the olden time only one leader was chosen, annually; and so, likewise, for war, only one man was declared general by the common people. But now they give heed, for the most part, to the commands of the Romans. There is a procedure that takes place in their assemblies which is peculiar to them: if a man disturbs the speaker and heckles him, the sergeant-at‑arms approaches him with drawn sword, and with a threat commands him to be silent; if he does not stop, the sergeant-at‑arms does the same thing a second time, and also a third time, but at last cuts off enough of the man's "sagus" to make it useless for the future. But as for their custom relating to the men and the women (I mean the fact that their tasks have been exchanged, in a manner opposite to what obtains among us), it is one which they share in common with many other barbarian peoples.
4 Among all the Gallic peoples, generally speaking, there are three sets of men who are held in exceptional honour; the Bards, the Vates and the Druids. The Bards are singers and poets; the Vates, diviners and natural philosophers; while the Druids, in addition to natural philosophy, study also moral philosophy. The Druids are considered the most just of men, and on this account they are entrusted with the decision, not only of the private disputes, but of the public disputes as well; so that, in former times, they even arbitrated cases of war and made the opponents stop when they were about to line up for battle, and the murder cases, in particular, had been turned over to them for decision. Further, when there is a big yield from these cases, there is forthcoming a big yield from the land too, as they think. However, not only the Druids, but others as well, say that men's souls, and also the universe, are indestructible, although both fire and water will at some time or other prevail over them.
5 In addition to their trait of simplicity and high-spiritedness, that of witlessness and boastfulness is much in evidence, and also that of fondness for ornaments; for they not only wear golden ornaments — both chains round their necks and bracelets round their arms and wrists — but their dignitaries wear garments that are dyed in colours and sprinkled with gold. And by reason of this levity of character they not only look insufferable when victorious, but also scared out of their wits when worsted.a Again, in addition to their witlessness, there is also that custom, barbarous and exotic, which attends most of the northern tribes — I mean the fact that when they depart from the battle they hang the heads of their enemies from the necks of their horses, and, when they have brought them home, nail the spectacle to the entrances of their homes. At any rate, Poseidonius says that he himself saw this spectacle in many places, and that, although at first he loathed it, afterwards, through his familiarity with it, he could bear it calmly. The heads of enemies of high repute, however, they used to embalm in cedar-oil and exhibit to strangers, and they would not deign to give them back even for a ransom of an equal weight of gold. But the Romans put a stop to these customs, as well as to all those connected with the sacrifices and divinations that are opposed to our usages. They used to strike a human being, whom they had devoted to death, in the back with a sabre, and then divine from his death-struggle. But they would not sacrifice without the Druids. We are told of still other kinds of human sacrifices; for example, they would shoot victims to death with arrows, or impale them in the temples, or, having devised a colossus of straw and wood, throw into the colossus cattle and wild animals of all sorts and human beings, and then make a burnt-offering of the whole thing.
6 In the ocean, he says, there is a small island, not very far out to sea, situated off the outlet of the Liger River; and the island is inhabited by women of the Samnitae, and they are possessed by Dionysus and make this god propitious by appeasing him with mystic initiations as well as other sacred performances; and no man sets foot on the island, although the women themselves, sailing from it, have intercourse with the men and then return again. And, he says, it is a custom of theirs once a year to unroof the temple and roof it again on the same day before sunset, each woman bringing her load to add to the roof; but the woman whose load falls out of her arms is rent to pieces by the rest, and they carry the pieces round the temple with the cry of "Ev-ah," and do not cease until their frenzy ceases; and it is always the case, he says, that some one jostles the woman who is to suffer this fate. But the following story which Artemidorus has told about the case of the crows is still more fabulous: there is a certain harbour on the ocean-coast, his story goes, which is surnamed "Two Crows," and in this harbour are to be seen two crows, with their right wings somewhat white; so the men who have disputes about certain things come here, put a plank on an elevated place, and then throw on barley cakes, each man separately; the birds fly up, eat some of the barley cakes, scatter the others; and the man whose barley cakes are scattered wins his dispute. Now although this story is more fabulous, his story about Demeter and Core is more credible. He says that there is an island near Britain on which sacrifices are performed like those sacrifices in Samothrace that have to do with Demeter and Core. And the following, too, is one of the things that are believed, namely, that in Celtica there grows a tree like a fig-tree, and that it brings forth a fruit similar to a Corinthian-wrought capital of a column; and that, if an incision be made, this fruit exudes a sap which, as used for the smearing of arrows, is deadly. And the following, too, is one of the things that are repeated over and over again, namely, that not only are all Celti fond of strife, but among them it is considered no disgrace for the young men to be prodigal of their youthful charms. Ephorus, in his account, makes Celtica so excessive in its size that he assigns to the regions of Celtic most of the regions, as far as Gades, of what we now call Iberia; further, he declares that the people are fond of the Greeks, and specifies many things about them that do not fit the facts of to‑day. The following, also, is a thing peculiar to them, that they endeavour not to grow fat or pot-bellied, and any young man who exceeds the standard measure of the girdle is punished. So much for Transalpine Celtica. |
|
|
|
|
4 - 5 Britain, Ireland, and Thule 
1 Britain is triangular in shape; and its longest side stretches parallel to Celtica, neither exceeding nor falling short of the length of Celtica; for each of the two lengths is about four thousand three hundred — or four hundred — stadia: the Celtic length that extends from the outlets of the Rhenus as far as those northern ends of the Pyrenees that are near Aquitania, as also the length that extends from Cantium (which is directly opposite the outlets of the Rhenus), the most easterly point of Britain, as far as that westerly end of the island which lies opposite the Aquitanian Pyrenees. This, of course, is the shortest distance from the Pyrenees to the Rhenus, since, as I have already said, the greatest distance is as much as five thousand stadia; yet it is reasonable to suppose that there is a convergence from the parallel position which the river and the mountains occupy with reference to each other, since at the ends where they approach the ocean there is a curve in both of them.
2 There are only four passages which are habitually used in crossing from the mainland to the island, those which begin at the mouths of the rivers — the Rhenus, the Sequana, the Liger, and the Garumna. However, the people who put to sea from the regions that are near the Rhenus make the voyage, not from the mouths themselves, but from the coast of those Morini who have a common boundary with the Menapii. (On their coast, also, is Itium, which the Deified Caesar used as a naval station when he set sail for the island. He put to sea by night and landed on the following day about the fourth hour, thus having completed three hundred and twenty stadia in his voyage across; and he found the grain still in the fields.) Most of the island is flat and overgrown with forests, although many of its districts are hilly. It bears grain, cattle, gold, silver, and iron. These things, accordingly, are exported from the island, as also hides, and slaves, and dogs that are by nature suited to the purposes of the chase; the Celti, however, use both these and the native dogs for the purposes of war too. The men of Britain are taller than the Celti, and not so yellow-haired, although their bodies are of looser build. The following is an indication of their size: I myself, in Rome, saw mere lads towering as much as half a foot above the tallest people in the city, although they were bandy-legged and presented no fair lines anywhere else in their figure. Their habits are in part like those of the Celti, but in part more simple and barbaric — so much so that, on account of their inexperience, some of them, although well supplied with milk, make no cheese; and they have no experience in gardening or other agricultural pursuits. And they have powerful chieftains in their country. For the purposes of war they use chariots for the most part, just as some of the Celti do. The forests are their cities; for they fence in a spacious circular enclosure with trees which they have felled, and in that enclosure make huts for themselves and also pen up their cattle — not, however, with the purpose of staying a long time. Their weather is more rainy than snowy; and on the days of clear sky fog prevails so long a time that throughout a whole day the sun is to be seen for only three or four hours round about midday. And this is the case also among the Morini and the Menapii and all the neighbours of the latter.
3 The Deified Caesar crossed over to the island twice, although he came back in haste, without accomplishing anything great or proceeding far into the island, not only on account of the quarrels that took place in the land of the Celti, among the barbarians and his own soldiers as well, but also on account of the fact that many of his ships had been lost at the time of the full moon, since the ebb-tides and the flood-tides got their increase at that time. However, he won two or three victories over the Britons, albeit he carried along only two legions of his army; and he brought back hostages, slaves, and quantities of the rest of the booty. At present, however, some of the chieftains there, after procuring the friendship of Caesar Augustus by sending embassies and by paying court to him,1have not only dedicated offerings in the Capitol, but have also managed to make the whole of the island virtually Roman property. Further, they submit so easily to heavy duties, both on the exports from there to Celtica and on the imports from Celtica (these latter are ivorya chains and necklaces, and amber-gems and glass vessels and other petty wares of that sort), that there is no need of garrisoning the island; for one legion, at the least, and some cavalry would be required in order to carry off tribute from them, and the expense of the army would offset the tribute-money; in fact, the duties must necessarily be lessened if tribute is imposed, and, at the same time, dangers be encountered, if force is applied.
4 Besides some small islands round about Britain, there is also a large island, Ierne, which stretches parallel to Britain on the north, its breadth being greater than its length. Concerning this island I have nothing certain to tell, except that its inhabitants are more savage than the Britons, since they are man-eaters as well as heavy eaters, and since, further, they count it an honourable thing, when their fathers die, to devour them, and openly to have intercourse, not only with the other women, but also with their mothers and sisters; but I am saying this only with the understanding that I have no trustworthy witnesses for it; and yet, as for the matter of man-eating, that is said to be a custom of the Scythians also, and, in cases of necessity forced by sieges, the Celti, the Iberians, and several other peoples are said to have practised it.
5 Concerning Thule our historical information is still more uncertain, on account of its outside position; for Thule, of all the countries that are named, is set farthest north. But that the things which Pytheas has told about Thule, as well as the other places in that part of the world, have indeed been fabricated by him, we have clear evidence from the districts that are known to us, for in most cases he has falsified them, as I have already said before, and hence he is obviously more false concerning the districts which have been placed outside the inhabited world. And yet, if judged by the science of the celestial phenomena and by mathematical theory, he might possibly seem to have made adequate use of the facts as regards the people who live close to the frozen zone, when he says that, of the animals and domesticated fruits, there is an utter dearth of some and a scarcity of the others, and that the people live on millet and other herbs, and on fruits and roots; and where there are grain and honey, the people get their beverage, also, from them. As for the grain, he says, — since they have no pure sunshine — they pound it out in large storehouses, after first gathering in the ears thither; for the threshing floors become useless because of this lack of sunshine and because of the rains. |
|
|
|
|
4 - 6 Cisalpine Gaul (Northern Italy) 
After Transalpine Celtica and the tribes which hold this country, I must tell about the Alps themselves and the people who inhabit them, and then about the whole of Italy, keeping the same order in my description as is given me by the nature of the country. The beginning, then, of the Alps is not at the Port of Monoecus, as some have told us, but at the same districts as the beginning of the Apennine mountains, namely, near Genua, the emporium of the Ligures, and what is called Vada (that is, "Shoals") Sabatorum: for the Apennines begin at Genua, and the Alps have their beginning at Sabata; and the distance, in stadia, between Genua and Sabata is two hundred and sixty; then, after three hundred and seventy stadia from Sabata, comes the town of Albingaunum (its inhabitants are called Ligures Ingauni); and thence, to the Port of Monoecus, four hundred and eighty stadia. Further, in this last interval there is a city of fair size, Albium Intemelium, and its occupants are called Intemelii. And indeed it is on the strength of these names that writers advance a proof that the Alps begin at Sabata; for things "Alpian" were formerly called "Albian," as also things "Alpionian," and, in fact, writers add that still to‑day the high mountain among the Iapodes which almost joins Mount Ocra and the Alps is called "Albius," thus implying that the Alps have stretched as far as that mountain.
2 Since, then, the Ligures were partly Ingauni and partly Intemelii, writers add, it was reasonable for their settlements on the sea to be named, the one, Albium (the equivalent of Alpium) Intemelium, and the other, more concisely, Albingaunum. Polybius,a however, adds to the two aforesaid tribes of the Ligures both that of the Oxybii and that of the Decietae. Speaking generally, this whole coastline, from the Port of Monoecus as far as Tyrrhenia, is not only exposed to the wind but harbourless as well, except for shallow mooring-places and anchorages. And lying above it are the enormous beetling cliffs of the mountains, which leave only a narrow pass next to the sea. This country is occupied by the Ligures, who live on sheep, for the most part, and milk, and a drink made of barley; they pasture their flocks in the districts next to the sea, but mainly in the mountains. They have there in very great quantities timber that is suitable for ship-building, with trees so large that the diameter of their thickness is sometimes found to be •eight feet. And many of these trees, even in the variegation of the grain, are not inferior to the thyine wood for the purposes of table-making. These, accordingly, the people bring down to the emporium of Genua, as well as flocks, hides and honey, and receive therefor a return-cargo of olive oil and Italian wine (the little wine they have in their country is mixed with pitch, and harsh). And this is the country from which come not only the so‑called "ginni" — both horses and mules, — but also the Ligurian tunics and "sagi." And they also have in their country excessive quantities of amber, which by some is called "electrum."b And although, in their campaigns, they are no good at all as cavalrymen, they are excellent heavy-armed soldiers and skirmishers; and, from the fact that they use bronze shields, some infer that they are Greeks.
3 The Port of Monoecus affords a mooring-place for no large ships, nor yet for a considerable number; and it has a temple of Heracles "Monoecus," as he is called; and it is reasonable to conjecture from the name that the coastal voyages of the Massiliotes reach even as far as the Port of Monoecus. The distance from the Port of Monoecus to Antipolis is a little more than two hundred stadia. As for the stretch of country which begins at Antipolis and extends as far as Massilia or a little farther, the tribe of the Sallyes inhabits the Alps that lie above the seaboard and also — promiscuously with the Greeks — certain parts of the same seaboard. But though the early writers of the Greeks call the Sallyes "Ligues," and the country which the Massiliotes hold, "Ligustica," later writers name them "Celtoligures," and attach to their territory all the level country as far as Luerio and the Rhodanus, the country from which the inhabitants, divided into ten parts, used to send forth an army, not only of infantry, but of cavalry as well. These were the first of the Transalpine Celti that the Romans conquered, though they did so only after carrying on war with both them and the Ligures for a long time — because the latter had barred all the passes leading to Iberia that ran through the seaboard. And, in fact, they kept making raids both by land and sea, and were so powerful that the road was scarcely practicable even for great armies. And it was not until the eightieth year of the war that the Romans succeeded, though only with difficulty, in opening up the road for a breadth of only twelve stadia to those travelling on public business. After this, however, they defeated them all, and, having imposed a tribute upon them, administered the government themselves.
4 After the Sallyes come the Albienses and the Albioeci and the Vocontii, who occupy the northerly parts of the mountains. But the Vocontii, stretching alongside the others, reach as far as the Allobroges; they have glens in the depths of their mountainous country that are of considerable size and not inferior to those which the Allobroges have. Now the Allobroges and the Ligures are ranked as subject to the praetors who come to Narbonitis, but the Vocontii (as I said of the Volcae who live round about Nemausus) are ranked as autonomous. Of the Ligures who live between the Varus River and Genua, those who live on the sea are the same as the Italiotes, whereas to the mountaineers a praefect of equestrian rank is sent — as is done in the case of other peoples who are perfect barbarians.
5 After the Vocontii come the Iconii and the Tricorii; and after them the Medulli, who hold the loftiest peaks. At any rate, the steepest height of these peaks is said to involve an ascent of a hundred stadia, and an equal number the descent thence to the boundaries of Italy. And up in a certain hollowed-out region stands a large lake, and also two springs which are not far from one another. One of these springs is the source of the Druentia, a torrential river which dashes down towards the Rhodanus, and also of the Durias, which takes the opposite direction, since it first courses down through the country of the Salassi into Cisalpine Celtica and then mingles with the Padus; while from the other spring there issues forth, considerably lower than the region above-mentioned, the Padus itself, large and swift, although as it proceeds it becomes larger and more gentle in its flow; for from the time it reaches the plains it is increased from many streams and is thus widened out; and so, because of the spreading out of its waters, the force of its current is dispersed and blunted; then it empties into the Adriatic Sea, becoming the largest of all the rivers in Europe except the Ister. The situation of the Medulli is, to put it in a general way, above the confluence of the Isar and the Rhodanus.
6 Towards the other parts (I mean the parts which slope towards Italy) of the aforesaid mountainous country dwell both the Taurini, a Ligurian tribe, and other Ligures; to these latter belongs what is called the land of Donnus and Cottius. And after these peoples and the Padus come the Salassi; and above them, on the mountain-crests, the Ceutrones, Catoriges, Varagri, Nantuates, Lake Lemenna (through which the Rhodanus courses), and the source of the Rhodanus. And not far from these are also the sources of the Rhenus, and Mount Adula, whence flows not only, towards the north, the Rhenus, but also, in the opposite direction, the Addua, emptying into Lake Larius, which is near Comum. And beyond Comum, which is situated near the base of the Alps, lie, on the one side, with its slope towards the east, the land of the Rhaeti and the Vennones, and, on the other, the land of the Lepontii, Tridentini, Stoni, and several other small tribes, brigandish and resourceless, which in former times held the upper hand in Italy; but as it is, some of the tribes have been wholly destroyed, while the others have been so completely subdued that the passes which lead through their territory over the mountain, though formerly few and hard to get through, are now numerous, and safe from harm on the part of the people, and easily passable — so far as human device can make them so. For in addition to his putting down the brigands Augustus Caesar built up the roads as much as he possibly could; for it was not everywhere possible to overcome nature by forcing a way through masses of rock and enormous beetling cliffs, which sometimes lay above the road and sometimes fell away beneath it, and consequently, if one made even a slight misstep out of the road, the peril was one from which there was no escape, since the fall reached to chasms abysmal. And at some places the road there is so narrow that it brings dizziness to all who travel it afoot — not only to men, but also to all beasts of burden that are unfamiliar with it; the native beasts, however, carry the burdens with sureness of foot. Accordingly, these places are beyond remedy; and so are the layers of ice that slide down from above — enormous layers, capable of intercepting a whole caravan or of thrusting them all together into the chasms that yawn below; for there are numerous layers resting upon another, because there are congelations upon congelations of snow that have become ice-like, and the congelations that are on the surface are from time to time easily released from those beneath before they are completely dissolved in the rays of the sun.
7 Most of the country of the Salassi lies in a deep glen, the district being shut in by both mountains, whereas a certain part of their territory stretches up to the mountain-crests that lie above. Accordingly, the road for all who pass over the mountains from Italy runs through the aforesaid glen. Then the road forks; and one fork runs through what is called Poeninus (a road which, for wagons, is impassable near the summits of the Alps), while the other runs more to the west, through the country of the Ceutrones. The country of the Salassi has gold mines also, which in former times, when the Salassi were powerful, they kept possession of, just as they were also masters of the passes. The Durias River was of the greatest aid to them in their mining — I mean in washing the gold; and therefore, in making the water branch off to numerous places, they used to empty the common bed completely. But although this was helpful to the Salassi in their hunt for the gold, it distressed the people who farmed the plains below them, because their country was deprived of irrigation; for, since its bed was on favourable ground higher up, the river could give the country water. And for this reason both tribes were continually at war with each other. But after the Romans got the mastery, the Salassi were thrown out of their gold-works and country too; however, since they still held possession of the mountains, they sold water to the publicans who had contracted to work the gold mines; but on account of the greediness of the publicans Salassi were always in disagreement with them too. And in this way it resulted that those of the Romans who from time to time wished to lead armies and were sent to the regions in question were well provided with pretexts for war. Until quite recently, indeed, although at one time they were being warred upon by the Romans and at another were trying to bring to an end their war against the Romans, they were still powerful, and, in accordance with their custom of brigandage, inflicted much damage upon those who passed through their country over the mountains; at any rate, they exacted even from Decimus Brutus, on his flight from Mutina, a toll of a drachma per man; and when Messala was wintering near their country, he had to pay for wood, cash down, not only for his fire-wood but also for the elm-wood used for javelins and the wood used for gymnastic purposes. And once these men robbed even Caesar of money and threw crags upon his legions under the pretext that they were making roads or bridging rivers. Later on, however, Augustus completely overthrew them, and sold all of them as booty, after carrying them to Eporedia, a Roman colony; and although the Romans had colonised this city because they wished it to be a garrison against the Salassi, the people there were able to offer only slight opposition until the tribe, as such, was wiped out. Now although the number of the other persons captured proved to be thirty-six thousand and, of the fighting men, eight thousand, Terentius Varro, the general who overthrew them, sold all of them under the spear. And Caesar sent three thousand Romans and founded the city of Augusta in the place where Varro had pitched his camp, and at the present time peace is kept by all the neighbouring country as far as the highest parts of the passes which lead over the mountain.
8 Next, in order, come those parts of the mountains that are towards the east, and those that bend round towards the south: the Rhaeti and the Vindelici occupy them, and their territories join those of the Elvetii and the Boii; for their territories overlook the plains of those peoples. Now the Rhaeti reach down as far as that part of Italy which is above Verona and Comum (moreover, the "Rhaetic" wine, which has the repute of not being inferior to the approved wines of the Italic regions, is made in the foot-hills of the Rhaetic Alps), and also extend as far as the districts through which the Rhenus runs; the Lepontii, also, and Camuni, belong to this stock. But the Vindelici and Norici occupy the greater part of the outer side of the mountain, along with the Breuni and the Genauni, the two peoples last named being Illyrians. All these peoples used to overrun, from time to time, the neighbouring parts, not only of Italy, but also of the country of the Elvetii, the Sequani, the Boii and the Germans. The Licattii, the Clautenatii, and the Vennones proved to be the boldest warriors of all the Vindelici, as did the Rucantii and the Cotuantii of all the Rhaeti. The Estiones, also, belong to the Vindelici, and so do the Brigantii, and their cities, Brigantium and Cambodunum, and also Damasia, the acropolis, as it were, of the Licattii. The stories of the severity of these brigands towards the Italiotes are to this effect: When they capture a village or city, they not only murder all males from youths up but they also go on and kill the male infants, and they do not stop there either, but also kill all the pregnant women who their seers say are pregnant with male children.
9 Directly after these people come the peoples that dwell near the recess of the Adriatic and the districts round about Aquileia, namely, the Carni as well as certain of the Norici; the Taurisci, also, belong to the Norici. But Tiberius and his brother Drusus stopped all of them from their riotous incursions by means of a single summer-campaign; so that now for thirty-three years they have been in a state of tranquillity and have been paying their tributes regularly. Now throughout the whole of the mountainous country of the Alps there are, indeed, not only hilly districts which admit of good farming, but also glens which have been well built up by settlers; the greater part, however (and, in particular, in the neighbourhood of the mountain-crests, where, as we know, the brigands used to congregate) is wretched and unfruitful, both on account of the frosts and of the ruggedness of the soil. It was because of scarcity, therefore, of both food and other things that they sometimes would spare the people in the plains, in order that they might have people to supply their wants; and in exchange they would give resin, pitch, torch-pine, wax, honey, and cheese — for with these things they were well supplied. Above the Carni lies the Apennine Mountain, which has a lake that issues forth into the River Isaras, which, after having received another river, the Atagis, empties into the Adriatic. But there is also another river, called the Atesinus, which flows into the Ister from the same lake. The Ister too, in fact, takes it beginning in these mountains, for they are split into many parts and have many peaks; that is, from Liguria, up to this point, the lofty parts of the Alps run in an unbroken stretch and then break up and diminish in height, and in turn rise again, into more and more parts, and more and more crests. Now the first of these is that ridge, on the far side of the Rhenus and the lake, which leans towards the east — a ridge only moderately high, in which, near the Suevi and the Hercynian Forest, are the sources of the Ister. And there are other ridges which bend round towards Illyria and the Adriatic, among which are the Apennine Mountain above-mentioned and also the Tullum and Phligadia, the mountains which lie above the Vindelici, whence flow the Duras and Clanis and several other torrential rivers which join the stream of the Ister.
And further, the Iapodes (we now come to this mixed tribe of Illyrii and Celti) dwell round about these regions; and Mount Ocra is near these people. The Iapodes, then, although formerly they were well supplied with strong men and held as their homeland both sides of the mountain208 and by their business of piracy held sway over these regions, have been vanquished and completely outdone by Augustus Caesar. Their cities are: Metulum, Arupini, Monetium, and Vendo. After the Iapodes comes Segestica, a city in the plain, past which flows the River Saüs, which empties into the Ister. The situation of the city is naturally well-suited for making war against the Daci. The Ocra is the lowest part of the Alps in that region in which the Alps join the country of the Carni, and through which the merchandise from Aquileia is conveyed in wagons to what is called Nauportus (over a road of not much more than four hundred stadia); from here, however, it is carried down by the rivers as far as the Ister and the districts in that part of the country; for there is, in fact, a river which flows past Nauportus; it runs out of Illyria, is navigable, and empties into the Saüs, so that the merchandise is easily carried down to Segestica and the country of the Pannonii and Taurisci. And the Colapis too joins the Saüs near the city; both are navigable and flow from the Alps. The Alps have both cattle and wild horses. Polybius says that there is also produced in the Alps an animal of special form; it is like a deer in shape, except for its neck and growth of hair (in these respects, he says, it resembles a boar), and beneath its chin it has a sac about a span long with hair at the tip, the thickness of a colt's tail.
Among the passes which lead over from Italy to the outer — or northerly — Celtica, is the one that leads through the country of the Salassi, to Lugdunum; it is a double pass, one branch, that through the Ceutrones, being practicable for wagons through the greater part of its length, while the other, that through the Poeninus, is steep and narrow, but a short cut. Lugdunum is in the centre of the country — an acropolis, as it were, not only because the rivers meet there, but also because it is near all parts of the country. And it was on this account, also, that Agrippa began at Lugdunum when he cut his roads — that which passes through the Cemmenus Mountains as far as the Santoni and Aquitania, and that which leads to the Rhenus, and, a third, that which leads to the ocean (the one that runs by the Bellovaci and the Ambiani); and, a fourth, that which leads to Narbonitis and the Massilian seaboard. And there is also, again, in the Poeninus itself (if you leave on your left Lugdunum and the country that lies above it), a bye-road which, after you cross the Rhodanus or Lake Lemenna, leads into the plains of the Helvetii; and thence there is a pass through the Jura Mountain over to the country of the Sequani and also to that of the Lingones; moreover, the thoroughfares through these countries branch off both ways — both towards the Rhenus and towards the ocean.
Polybius further says that in his own time there was found, about opposite Aquileia in the country of the Noric Taurisci, a gold mine so well-suited for mining that, if one scraped away the surface-soil for a depth of only two feet, he found forthwith dug-gold, and that the diggings were never deeper than fifteen feet; and he goes on to say that part of the gold is immediately pure, in sizes of a bean or a lupine, when only the eighth part is boiled away, and that although the rest needs more smelting, the smelting is very profitable; and that two months after the Italiotes joined them in working the mine, the price of gold suddenly became a third less throughout the whole of Italy, but when the Taurisci learned this they cast out their fellow-workers and carried on a monopoly. Now, however, all the gold mines are under the control of the Romans. And here, too, just as in Iberia, in addition to the dug-gold, gold-dust is brought down by the rivers — not, however, in such quantities as there. The same man, in telling about the size and the height of the Alps, contrasts with them the greatest mountains among the Greeks: Taygetus, Lycaeus, Parnassus, Olympus, Pelion, Ossa; and in Thrace: Haemus, Rhodope, Dunax; and he says it is possible for people who are unencumbered to ascend any one of them on the same day, whereas one cannot ascend the Alps even in five days; and their length is two thousand two hundred stadia, that is, their length at the side, along the plains. But he only names four passes over the mountains: the pass through the Ligures (the one that is nearest the Tyrrhenian Sea), then that through the Taurini, which Hannibal crossed, then that through the Salassi, and the fourth, that through the Rhaeti, — all of them precipitous passes. And as for lakes, he says that there are several in the mountains, but that only three are large: one of these, Lake Benacus, has a length of five hundred stadia and a breadth of thirty, from which flows the Mincius River; the next, lake Verbanus, four hundred in length, and narrower in breadth than the former, which sends forth the River Addua; and, third, Lake Larius, in length nearly three hundred stadia, and in breadth thirty, which sends forth a large river, the Ticinus; and all three rivers flow into the Padus. This, then, is what I have to say about the Alpine Mountains. |
|
|
|
|
5 North Italy 4 89 1:50 

|
5 - 1 Northern Italy proper (roughly Emilia-Romagna) 
1 After the foothills of the Alps comes the beginning of what is now Italy. For the ancients used to call only Oenotria Italy, although it extended from the Strait of Sicily only as far as the Gulfs of Tarentum and Poseidonia, but the name of Italy prevailed and advanced even as far as the foothills of the Alps, and also took in, not only those parts of Ligustica which extend from the boundaries of Tyrrhenia as far as the Varus River and the sea there, but also those parts of Istria which extend as far as Pola. One might guess that it was because of their prosperity that the people who were the first to be named Italians imparted the name to the neighbouring peoples, and then received further increments in this way until the time of the Roman conquest. At some late time or other after the Romans had shared with the Italiotes the equality of civil rights, they decided to allow the same honour both to the Cisalpine Galatae3 and to the Heneti, and to call all of them Italiotes as well as Romans, and, further, to send forth many colonies amongst them, some earlier and some later, than which it is not easy to call any other set of colonies better.
2 Now it is not easy geometrically to outline what is now Italy, as a whole, by means of a single figure, and yet they say it is a triangular promontory extending towards the south and the winter-risings of the sun, with its vertex at the Strait of Sicily, and with the Alps as its base. I must concede also one of the sides, namely, that which ends at the strait and is washed by the Tyrrhenian Sea. But "triangle" is the specific name for the rectilinear figure, whereas in this case both the base and the side are curved, so that, if I say "I must concede," I must put down both the base and the side as belonging to a curved-line figure, and I must concede also the slant of this side, namely, the slant towards the risings. But as for the rest of the description given by these writers, it is inadequate, because they have assumed only a single side extending from the recess of the Adriatic to the strait; for by "side" we mean the line that has no angle, and a line has no angle when its parts either do not converge towards one another or else not much. But the line from Ariminum to the Iapygian Cape and that from the strait to the same cape converge very much. And the same holds true, I think, with the line from the recess of the Adriatic and that from Iapygia; for, meeting in the regions round about Ariminum and Ravenna, they form an angle, or, if not an angle, at least a considerable curve. Hence this stretch might perhaps be one side (I mean the coasting-voyage from the recess to Iapygia), though the side would not be straight; and the rest of the stretch, thence to the strait, might suggest another side, though this side would not be straight, either. In this sense one might call the figure "four-sided" rather than "three-sided," but in no sense whatever a "triangle," except by an abuse of the term. It is better, however, to confess that the representation of non-geometrical figures is not easy to describe.
3 Taking the parts severally, however, we can speak as follows: as for the Alps, their base is curved and gulf-like, with the cavities turned towards Italy; the central gulf are near the Salassi, while the extremities take a turn, the one as far as Ocra and the recess of the Adriatic, the other to the Ligurian seaboard as far as Genua (the emporium of the Ligures), where the Apennine Mountains join the Alps. But immediately at the base of the Alps there lies a considerable plain, with its length and its breadth about equal, namely, two thousand one hundred stadia; its southern side is shut in both by the seaboard of the Heneti and by those Apennine Mountains which reach down to the neighbourhood of Ariminum and Ancona; for these mountains, after beginning in Liguria, enter Tyrrhenia, leaving only a narrow seaboard, and then, withdrawing into the interior little by little, when they come to be opposite the territory of Pisa, bend towards the east and towards the Adriatic until they reach the regions round about Ariminum and Ancona, there joining in a straight line the seaboard of the Heneti. Cisalpine Celtica, accordingly, is shut in by these boundaries; and although the length of the seaboard, together with that of the mountains, is as much as six thousand three hundred stadia, the breadth is slightly less than one thousand. The remainder of Italy, however, is narrow and elongated, terminating in two heads, one at the Sicilian Strait and the other at Iapygia; and it is pinched in on both sides, on one by the Adriatic and on the other by the Tyrrhenian Sea. The shape and the size of the Adriatic are like that part of Italy which is marked off by the Apennine Mountains and by both seas as far as Iapygia and that isthmus which is between the Gulfs of Tarentum and Poseidonia; for the maximum breadth of each is about one thousand three hundred stadia, and the length not much less than six thousand. The remainder of Italy, however, is all the country occupied by the Brettii and certain of the Leucani. Polybius says that, if you go by foot, the seaboard from Iapygia to the strait is as much as three thousand stadia, and that it is washed by the Sicilian Sea, but that, if you go by sea, it is as much as five hundred stadia short of that. The Apennine Mountains, after joining the regions round about Ariminum and Ancona, that is, after marking off the breadth of Italy there from sea to sea, again take a turn, and cut the whole country lengthwise. As far, then, as the territory of the Peucetii and that of the Leucani they do not recede much from the Adriatic, but after joining the territory of the Leucani they bend off more towards the other sea and then, for the rest of the way, passing throughout the centre of the territory of the Leucani and Brettii, end at what is called Leucopetra in the district of Rhegium. Thus much, then, I have said about what is now Italy, as a whole, in a merely rough-outline way, but I shall now go back and try to tell about the several parts in detail; and first about the parts at the base of the Alps.
4 This country is a plain that is very rich in soil and diversified by fruitful hills. The plain is divided almost at its very centre by the Padus; and its parts are called, the one Cispadana, the other Transpadana. Cispadana is all the part that lies next to the Apennine Mountains and Liguria, while Transpadana is the rest. The latter is inhabited by the Ligurian and the Celtic tribes, who live partly in the mountains, partly in the plains, whereas the former is inhabited by the Celti and Heneti. Now these Celti are indeed of the same race as the Transalpine Celti, but concerning the Heneti there are two different accounts: Some say that the Heneti too are colonists of those Celti of like name who live on the ocean-coast; while others say that certain of the Heneti of Paphlagonia escaped hither with Antenor from the Trojan war, and, as testimony in this, adduce their devotion to the breeding of horses — a devotion which now, indeed, has wholly disappeared, although formerly it was prized among them, from the fact of their ancient rivalry in the matter of producing mares for mule-breeding. Homer, too, recalls this fact: "From the land of the Heneti, whence the breed of the wild mules." Again, Dionysius, the tyrant of Sicily, collected his stud of prize-horses from here, and consequently not only did the fame of the Henetian foal-breeding reach the Greeks but the breed itself was held in high esteem by them for a long time.
5 Now this whole country is filled with rivers and marshes, but particularly the part that belongs to the Heneti. And this part, furthermore, is also affected by the behaviour of the sea; for here are almost the only parts of Our Sea that behave like the ocean, and both the ebb-tides and the flood-tides produced here are similar to those of the ocean, since by them the greater part of the plain is made full of lagoons. But, like what is called Lower Egypt, it has been intersected by channels and dikes; and while some parts have been relieved by drainage and are being tilled, others afford voyages across their waters. Of the cities here, some are wholly island, while others are only partly surrounded by water. As for all the cities that are situated above the marshes in the interior, the inland voyages afforded thereto by the rivers are wonderful, but particularly by the Padus; for not only is it the largest of these rivers but it is oftentimes filled by both the rains and the snow, although, as the result of separating into many streams near the outlets, the mouth is choked with mud and hard to enter. But even the greatest difficulties are overcome by experience.
6 In early times, then, as I was saying, the country round about the Padus was inhabited for the most part by the Celti. And the largest tribes of the Celti were the Boii, the Insubri, and those Senones who, along with the Gaezatae, once seized the territory of the Romans at the first assault. These two peoples, it is true, were utterly destroyed by the Romans later on, but the Boii were merely driven out of the regions they occupied; and after migrating to the regions round about the Ister, lived with the Taurisci, and carried on war against the Daci until they perished, tribe and all — and thus they left their country, which was a part of Illyria, to their neighbours as a pasture-ground for sheep. The Insubri, however, are still in existence. They had as metropolis Mediolanium, which, though long ago only a village (for they all used to dwell only in villages), is now a notable city; it is across the Padus, and almost adjoins the Alps. Near by is Verona also (this, too, a large city), and, smaller than these two, the cities of Brixia, Mantua, Regium, and Comum. Comum used to be only a moderate-sized settlement, but, after its ill treatment by the Rhaeti who are situated above it, Pompey Strabo, father of Pompey the Great, settled a Roman colony there; then Gaius Scipio added three thousand colonists; then the Deified Caesar further settled it with five thousand, among whom the five hundred Greeks were the most notable; and to these latter he not only gave the rights of citizenship but also enrolled them among the colonists. The Greeks did not, however, take up their abode there, though they at least left to the settlement the name; for the colonists were, as a whole, called "Neo-Comitae" — that is, if interpreted in Latin, "Novum Comum." Near this place is what is called Lake Larius; it is fed by the River Addua. The river then issues forth from the lake into the Padus; it has its original sources, however, in Mount Adula, in which also the Rhenus has its sources.
7 These cities, then, are situated considerably above the marshes; and near them is Patavium, the best of all the cities in that part of the country, since this city by recent census, so it is said, had five hundred knights, and, besides, in ancient times used to send forth an army of one hundred and twenty thousand. And the quantities of manufactured goods which Patavium sends to Rome to market — clothing of all sorts and many other things — show what a goodly store of men it has and how skilled they are in the arts. Patavium offers an inland voyage from the sea by a river which runs through the marshes, two hundred and fifty stadia from a large harbour; the harbour, like the river, is called Medoacus. The largest city in the marshes, however, is Ravenna, a city built entirely of wood and coursed by rivers, and it is provided with thoroughfares by means of bridges and ferries. At the tides the city receives no small portion of the sea, so that, since the filth is all washed out by these as well as the rivers, the city is relieved of foul air. At any rate, the place has been found to be so healthful that the rulers have given orders to feed and train the gladiators there. Now this is indeed one of the marvellous things at Ravenna, I mean the fact that the air in a marsh is harmless (compare the Egyptian Alexandria, where, in summer, the lake loses its baneful qualities by reason of the overflow of the Nile and the disappearance of the standing waters), but the behaviour of the vine is also a thing fit to marvel at; for although the marshes support it and make it fruit quickly and in great quantities, it dies within four or five years. Altinum too is in a marsh, for the portion it occupies is similar to that of Ravenna. Between the two cities is Butrium, a town belonging to Ravenna, and also Spina, which though now only a small village, long ago was a Greek city of repute.a At any rate, a treasury of the Spinitae is to be seen at Delphi; and everything else that history tells about them shows that they were once masters of the sea. Moreover, it is said that Spina was once situated by the sea, although at the present time the place is in the interior, about ninety stadia distant from the sea. Furthermore, it has been said that Ravenna was founded by the Thessalians; but since they could not bear the wanton outrages of the Tyrrhenians, they voluntarily took in some of the Ombrici, which latter still now hold the city, whereas the Thessalians themselves returned home. These cities, then, are for the most part surrounded by the marshes, and hence subject to inundations.
8 But Opitergium, Concordia, Atria, Vicetia, and other small towns like them are less hemmed in by the marshes, though they are connected with the sea by small waterways. It is said that Atria was once an illustrious city, and that the Adriatic Gulf got its name therefrom, with only a slight change in the spelling. Aquileia, which is nearest of all to the recess of the Gulf, was founded by the Romans as a fortress against the barbarians who were situated above it; and there is an inland voyage thither for merchant-vessels, by way of the River Natiso, for a distance of more than sixty stadia. Aquileia has been given over as an emporium for those tribes of the Illyrians that live near the Ister; the latter load on wagons and carry inland the products of the sea, and wine stored in wooden jars, and also olive-oil, whereas the former get in exchange slaves, cattle, and hides. But Aquileia is outside the boundaries of the Heneti. The boundary between the two peoples is marked by a river flowing from the Alps, which affords an inland voyage of as much as twelve hundred stadia to the city of Noreia, near which Gnaeus Carbo clashed to no effect with the Cimbri. This region has places that are naturally well-suited to gold-washing, and has also iron-works. And in the very recess of the Adriatic there is also a temple of Diomedes that is worth recording, "the Timavum"; for it has a harbour, and a magnificent precinct, and seven fountains of potable waters which immediately empty into the sea in one broad, deep river. According to Polybius, all the fountains except one are of salt water, and what is more, the natives call the place the source and mother of the sea. But Poseidonius says that a river, the Timavus, runs out of the mountains, falls down into a chasm, and then, after running underground about a hundred and thirty stadia, makes its exit near the sea.
9 As for the dominion of Diomedes in the neighbourhood of this sea, not only the "Islands of Diomedes" bear witness thereto, but also the historical accounts of the Daunii and Argos Hippium, which I shall relate insofar as they may be historically useful; but I must disregard most of the mythical or false stories, as, for example, the stories of Phaethon, and of the Heliades that were changed into poplar-trees near the Eridanus (the Eridanus that exists nowhere on earth, although it is spoken of as near the Padus), and of the Electrides Islands that lie off the Padus, and of the guinea-fowls on them; for not one of these things is in that region, either. It is an historical fact, however, that among the Heneti certain honours have been decreed to Diomedes; and, indeed, a white horse is still sacrificed to him, and two precincts are still to be seen — one of them sacred to the Argive Hera and the other to the Aetolian Artemis. But some mythical elements, of course, have been added: namely, that in these sacred precincts the wild animals become tame, and deer herd with wolves, and they allow the people to approach and caress them, and any that are being pursued by dogs are no longer pursued when they have taken refuge here. And it is said that one of the prominent men, who was known for his fondness for giving bail for people and was twitted for this, fell in with some hunters who had a wolf in their nets, and, upon their saying in jest that if he would give bail for the wolf, and agree to settle all the damage the wolf should do, they would set the wolf free from the toils, he agreed to the proposal; and the wolf, when set free, drove off a considerable herd of unbranded horses and brought them to the steading of the man who was fond of giving bail; and the man who received the favour not only branded all the mares with a wolf, but also called them the "wolf-breed" — mares exceptional for speed rather than beauty; and his successors kept not only the brand but also the name for the breed of the horses, and made it a custom not to sell a mare to outsiders, in order that the genuine breed might remain in their family alone, since horses of that breed had become famous. But, at the present time, as I was saying, the practice of horse-breeding has wholly disappeared. After the Timavum comes the seaboard of the Istrii as far as Pola, which belongs to Italy. Between the Timavum and Pola lies the stronghold of Tergeste, at a distance of one hundred and eighty stadia from Aquileia. As for Pola, it is situated in a harbour-like gulf which has isles with good mooring-places and with fruitful soil; it was founded in early times by those Colchians who were sent forth in quest of Medea, but failed in their undertaking and thus condemned themselves to exile: "which a Greek would call 'the city of the exiles,' " as Callimachus has said, "but their tongue hath named it Polae." The Transpadane districts, then, are occupied both by the Heneti and by the peoples who extend as far as Pola; and, above the Heneti, by the Carni, the Cenomani, the Medoaci, and the Symbri; of these peoples, some were once enemies of the Romans, but the Cenomani and the Heneti used to help the Romans in their battles, not only before the campaign of Hannibal (I mean when the Romans were making war upon the Boii and the Symbri), but thereafter as well.
But the Cispadane peoples occupy all that country which is encircled by the Apennine Mountains towards the Alps as far as Genua and Sabata. The greater part of the country used to be occupied by the Boii, Ligures, Senones, and Gaezatae; but since the Boii have been driven out, and since both the Gaezatae and the Senones have been annihilated, only the Ligurian tribes and the Roman colonies are left. The Romans, however, have been intermingled with the stock of the Ombrici and also, in some places, with that of the Tyrrheni; for both these tribes, before the general aggrandizement of the Romans, carried on a sort of competition with one another for the primacy, and since they had only the River Tiber between them could easily cross over against one another. And if, as I suppose, one of the two peoples went forth on a campaign against a third people, the other of the two conceived a contentious desire not to fail to make an expedition to the same places; and so, too, when the Tyrrheni had sent forth an army into the midst of the barbarians round about the Padus and had fared well, and then on account of their luxurious living were quickly cast out again, the other of the two made an expedition against those who had cast them out; and then, in turns, disputing over the places, the two, in the case of many of the settlements, made some Tyrrhenian and some Ombrican — the greater number, however, Ombrican, for the Ombrici were nearer. But the Romans, upon taking control and sending settlers to many places, helped to preserve also the stocks of the earlier settlers. And at the present time, although they are all Romans, they are none the less called, some "Ombri," and some "Tyrrheni," as is the case with the Heneti, the Ligures, and the Insubri.
There are some famous cities in Cispadana and in the neighbourhood of the Padus: first, Placentia and Cremona, which are very near each other and are at about the centre of the country; and secondly — between these two and Ariminum — Parma, Mutina, and Bononia (once in Bononia you are near Ravenna), and also some small towns scattered between these three which also lie on the road to Rome — I mean Ancara, Regium Lepidum, Macri Campi where a public festival is held every year, Claterna, and Forum Cornelium; and then, Faventia and Caesena, near the River Sapis and the Rubicon, where, at last, you are on the borders of Ariminum. Ariminum is a settlement of the Ombri, just as Ravenna is, although each of them has received Roman colonists. And Ariminum has a harbour and a river of like name. From Placentia to Ariminum the distance is one thousand three hundred stadia. Beyond Placentia, towards the boundaries of the land of Cottius, there lies, within a distance of thirty-six miles from Placentia, the city of Ticinum (and also the river of like name that flows past it and joins the Padus), and also, on a road which runs slightly to one side, there lie Clastidium, Derton and Aquae Statiellae. But the direct road to Ocelum runs along the Padus and the River Durias, the greater part of it over ravines, since, besides these two, it has several other rivers to cross, among which is the Druentia, a distance of about sixty miles. And this is where the Alps Mountains and Celtica begin.
Near those mountains which lie above Luna is a city, Luca, although some of the people here live only in villages; nevertheless the country has a goodly store of men, and the greater part of the soldiery comes from here, and also the majority of those men of equestrian rank from whom the Senate recruits its ranks. Derton is a considerable city, and it is situated about midway of the road which runs from Genua to Placentia, being four hundred stadia distant from each; and this is the road on which Aquae Statiellae is situated. Of the distance from Placentia to Ariminum I have already spoken; there is also a voyage thence by the Padus down to Ravenna which takes two days and nights. Now a considerable part of Cispadana too used to be covered by marshes (through which Hannibal, on his advance against Tyrrhenia, passed only with difficulty); but Scaurus drained the plains by running navigable canals from the Padus as far as Parma; for near Placentia the Padus is joined by the Trebia, as also before that by several other rivers, and is thus made excessively full. This Scaurus is the man who constructed the Aemilian Way which runs through Pisa and Luna as far as Sabata and thence through Derton; there is another Aemilian Way, however — I mean the one which succeeds the Flaminian. For Marcus Lepidus and Gaius Flaminius were consuls together; and, upon subjugating the Ligures, the latter constructed the Flaminian Way from Rome through Tyrrhenia and Ombrica as far as the regions of Ariminum, and the former the succeeding road that runs as far as Bononia, and from there, along the base of the Alps, thus encircling the marshes, to Aquileia. Now the boundary of all this country which we call Cisalpine Celtica — I mean the boundary between it and the remainder of Italy — was once designated by that part of the Apennine Mountains which is beyond Tyrrhenia, and also by the River Aesis, but later on by the Rubicon; both these rivers empty into the Adriatic.
As for the excellence of the regions, it is evidenced by their goodly store of men, the size of the cities and their wealth, in all which respects the Romans in that part of the world have surpassed the rest of Italy. For not only does the tilled land bring forth fruits in large quantities and of all sorts, but the forests have acorns in such quantities that Rome is fed mainly on the herds of swine that come from there. And the yield of millet is also exceptional, since the soil is well-watered; and millet is the greatest preventive of famine, since it withstands every unfavourable weather, and can never fail, even though there be scarcity of every other grain. The country has wonderful pitch-works, also; and as for the wine, the quantity is indicated by the jars, for the wooden ones are larger than houses; and the good supply of the pitch helps much towards the excellent smearing the jars receive. As for wool, the soft kind is produced by the regions round Mutina and the River Scultenna (the finest wool of all); the coarse, by Liguria and the country of the Symbri, from which the greater part of the households of the Italiotes are clothed; and the medium, by the regions round Patavium, from which are made the expensive carpets and covers and everything of this kind that is woolly either on both sides or only on one. But as for the mines, at the present time they are not being worked here as seriously as before — perhaps on account of the fact that those in the country of the Transalpine Celti and in Iberia are more profitable; formerly, however, they were seriously worked, for there was a gold mine at Vercelli too; Vercelli is a village near Ictumuli (this too a village), and both are near Placentia. So much, then, my geographical description of the First Portion of Italy. |
|
|
|

|
5 - 2 Tyrrhenia and Umbria (Tuscany, Umbria, and the N Marche) 
1 Let us call the Second Portion that Liguria which is in the Apennines themselves, situated between that Celtica which I have just described and Tyrrhenia. It contains nothing worthy of detailed p335description except that the people live only in villages, plowing and digging rough land, or rather, as Poseidonius says, quarrying stones. The Third Portion is contiguous to the Second — I mean the country of the Tyrrheni, who hold the plains that extend as far as the River Tiber and whose country is washed, on its eastern side (generally speaking), by the river as far as its mouth, and on the other side by the Tyrrhenian and Sardinian Sea. But the Tiber flows from the Apennine Mountains, and is fed by many rivers; for a part of its course it runs through Tyrrhenia itself, and in its course thereafter separates from Tyrrhenia, first, Ombrica, then, the country of the Sabini and also that part of Latium which is near Rome and extends as far as the coastline. These three latter lie approximately parallel to the river and Tyrrhenia in their breadth and also to one another in their length; and they reach up to those parts of the Apennine Mountains which closely approach the Adriatic, in this order: first, Ombrica, then, after Ombrica, the country of the Sabini, and, last, Latium, — all of them beginning at the river. Now the country of the Latini lies between the coastline that stretches from Ostia as far as the city of Sinuessa and the country of the Sabini (Ostia is the port-town of the Roman navy — the port into which the Tiber, after flowing past Rome, empties), although it extends lengthwise as far as Campania and the mountains of the Samnitae. But the country of the Sabini lies between that of the Latini and that of the Ombrici, although it too extends to the mountains of the Samnitae, or rather it joins that part of the Apennines which is in the country of the Vestini, the Peligni, and the Marsi. And the country of the Ombrici lies between the country of the Sabini and Tyrrhenia, although it extends over the mountains as far as Ariminum and Ravenna. And Tyrrhenia, beginning at its proper sea and the Tiber, ceases at the very foot of those mountains which enclose it from Liguria to the Adriatic. I shall treat the several parts, however, in detail, beginning with the Tyrrheni themselves.
2 The Tyrrheni, then, are called among the Romans "Etrusci" and "Tusci". The Greeks, however, so the story goes, named them thus after Tyrrhenus, the son of Atys, who sent forth colonists hither from Lydia: At a time of famine and dearth of crops, Atys, one of the descendants of Heracles and Omphale, having only two children, by a casting of lots detained one of them, Lydus, and, assembling the greater part of the people with the other, Tyrrhenus, sent them forth. And when Tyrrhenus came, he not only called the country Tyrrhenia after himself, but also put Tarco in charge as "coloniser," and founded twelve cities; Tarco, I say, after whom the city of Tarquinia is named, who, on account of his sagacity from boyhood, is said by the myth-tellers to have been born with grey hair. Now at first the Tyrrheni, since they were subject to the orders of only one ruler, were very strong, but in later times, it is reasonable to suppose, their united government was dissolved, and the Tyrrheni, yielding to the violence of their neighbours, were broken up into separate cities; for otherwise they would not have given up a happy land and taken to the sea as pirates, different bands turning to different parts of the high seas; indeed, in all cases where they acted in concert, they were able, not only to defend themselves against those who attacked them, but also to attack in turn and to make long expeditions. But it was after the founding of Rome that Demaratus arrived, bringing with him a host of people from Corinth; and, since he was received by the Tarquinians, he married a native woman, by whom he begot Lucumo. And since Lucumo had proved a friend to Ancus Marcius, the king of the Romans, he was made king, and his name was changed to Lucius Tarquinius Priscus. Be that as it may, he too adorned Tyrrhenia, as his father had done before him — the father by means of the goodly supply of artisans who had accompanied him from home and the son by means of the resources supplied by Rome. It is further said that the triumphal, and consular, adornment, and, in a word, that of all the rulers, was transferred to Rome from Tarquinii, as also fasces, axes, trumpets, sacrificial rites, divination, and all music publicly used by the Romans. This Tarquinius was the father of the second Tarquinius, the "Superbus," who was the last of the kings and was banished. Porsinas, the king of Clusium, a Tyrrhenian city, undertook to restore him to the throne by force of arms, but was unable to do so, although he broke up the personal enmity against himself and departed as friend, along with honour and large gifts.
3 Thus much for the lustre of the Tyrrheni. And still to be recorded are the achievements of the Caeretani: they defeated in war those Galatae who had captured Rome, having attacked them when they were in the country of the Sabini on their way back, and also took away as booty from the Galatae, against their will, what the Romans had willingly given them; in addition to this, they saved all who fled to them for refuge from Rome, and the immortal fire, and the priestesses of Vesta. The Romans, it is true, on account of the bad managers which the city had at the time, do not seem to have remembered the favour of the Caeretani with sufficient gratitude, for, although they gave them the right of citizenship, they did not enroll them among the citizens, and even used to relegate all others who had no share in the equal right to "the Tablets of the Caeretani." Among the Greeks, however, this city was in good repute both for bravery and for righteousness; for it not only abstained from all piracy, but also set up at Pytho what is called "the treasury of the Agyllaei"; for what is now Caerea was formerly called Agylla, and is said to have been founded by Pelasgi who had come from Thessaly. But when those Lydians whose name was changed to Tyrrheni marched against the Agyllaei, one of them approached the wall and inquired what the name of the city was, and when one of the Thessalians on the wall, instead of replying to the inquiry, saluted him with a "Chaere," the Tyrrheni accepted the omen, and, on capturing the city, changed its name accordingly. But the city, once so splendid and illustrious, now preserves mere traces of its former self; and the hot springs near by, which are called Caeretanian Springs, have a greater population than it has — because of those who visit the Springs for the cure.
4 As for the Pelasgi, almost all agree, in the first place, that some ancient tribe of that name spread throughout the whole of Greece, and particularly among the Aeolians of Thessaly. Again, Ephorus says that he is of the opinion that, since they were originally Arcadians, they chose a military life, and that, in converting many peoples to the same mode of life, they imparted their name to all, and thus acquired great glory, not only among the Greeks, but also among all other people whithersoever they had chanced to come. For example, they prove to have been colonisers of Crete, as Homer says; at any rate, Odysseus says to Penelope: "But one tongue with others is mixed; there dwell Achaeans, there Cretans of the old stock, proud of heart, there Cydonians, and Dorians too, of waving plumes, and goodly Pelasgians." And Thessaly is called "the Pelasgian Argos" (I mean that part of it which lies between the outlets of the Peneius River and Thermopylae as far as the mountainous country of Pindus), on account of the fact that the Pelasgi extended their rule over these regions. Further, the Dodonaean Zeus is by the poet himself named "Pelasgian": "O Lord Zeus, Dodonaean, Pelasgian." And many have called also the tribes of Epirus "Pelasgian," because in their opinion the Pelasgi extended their rule even as far as that. And, further, because many of the heroes were called "Pelasgi" by name, the people of later times have, from those heroes, applied the name to many of the tribes; for example, they have called the island of Lesbos "Pelasgia," and Homer has called "Pelasgi" the people that were neighbours to those Cilicians who lived in the Troad: "And Hippothous led the tribes of spear-fighting Pelasgi, those Pelasgi who inhabited deep-soiled Larissa."But Ephorus' authority for the statement that this race originated in Arcadia was Hesiod; for Hesiod says: "And sons were born of god-like Lycaon, who, on a time, was begotten by Pelasgus." Again, Aeschylus, in his Suppliants, or else his Danaan Women, says that the race of the Pelasgi originated in that Argos which is round about Mycenae. And the Peloponnesus too, according to Ephorus, was called "Pelasgia." And Euripides too, in his Archelaus, says: "Danaus, the father of fifty daughters, on coming into Argos, took up his abode in the city of Inachus, and throughout Greece he laid down a law that all people hitherto named Pelasgians were to be called Danaans." And again, Anticleides says that they were the first to settle the regions round about Lemnos and Imbros, and indeed that some of these sailed away to Italy with Tyrrhenus the son of Atys. And the compilers of the histories of The Land of Atthis give accounts of the Pelasgi, believing that the Pelasgi were in fact at Athens too, although the Pelasgi were by the Attic people called "Pelargi," the compilers add, because they were wanderers and, like birds, resorted to those places whither chance led them.
5 They say that the maximum length of Tyrrhenia — the coastline from Luna as far as Ostia — is about two thousand five hundred stadia, and its breadth (I mean its breadth near the mountains) less than half its length. Now from Luna to Pisa the distance is more than four hundred stadia; and thence to Volaterrae, two hundred and eighty; again, from here to Poplonium, two hundred and seventy; and from Poplonium to Cosa, nearly eight hundred, though some say six hundred. Polybius, however, says the total number of stadia is not so much as one thousand three hundred and thirty. Of these, take first Luna; it is a city and also a harbour, and the Greeks call the city as well as the harbour "Harbour of Selene." The city, indeed, is not large, but the harbour is both very large and very beautiful, since it includes within itself several harbours, all of them deep up to the very shore, — just such a place as would naturally become the naval base of a people who were masters of the sea for so long a time. And the harbour is shut in all round by high mountains, from which the high seas are to be seen, as also Sardo, and a considerable stretch of the shore on either side. And the quarries of marble, both white and mottled bluish-grey marble, are so numerous, and of such quality (for they yield monolithic slabs and columns), that the material for most of the superior works of artin Rome and the rest of the cities are supplied therefrom; and, indeed, the marble is easy to export, since the quarries lie above the sea and near it, and since the Tiber in its turn takes up the cargo from the sea and conveys it to Rome. And the wooden material for the buildings, in beams that are very straight and very long, is for the most part supplied by Tyrrhenia, since by means of the river it can be brought down directly from the mountains. Now between Luna and Pisa is the Macras, which many of the historians have used as the boundary between Tyrrhenia and Liguria. As for Pisa, it was founded by those Pisatae who lived in the Peloponnesus, who made the expedition to Ilium with Nestor and on the return voyage went astray, some to Metapontum, and others to the territory of Pisa, although all of them were called Pylians. Pisa is situated between, and at the very confluence of, two rivers, the Arnus and the Ausar, of which the former runs from Arretium, with great quantities of water (not all in one stream, but divided into three streams), and the latter from the Apennine Mountains; and when they unite and form one stream they heave one another up so high by their mutual resistance that two persons standing on the opposite banks cannot even see each other;a and hence, necessarily, voyages inland from the sea are difficult to make; the length of the voyage is about twenty stadia. And the following fable is told: when these rivers first began to flow down from the mountains, and their course was being hindered by the natives for fear that they would unite in one stream and deluge the country, the rivers promised not to deluge it and kept their pledge. Again, Pisa is reputed to have been prosperous on a time, and at the present time it is not without repute, on account of its fertility, its stone-quarries, and its timber for ship-building; in ancient times, indeed, they utilised this latter material to meet the perils that faced them on the sea (for they were, to begin with, more warlike than the Tyrrheni, and their warlike spirit was sharpened by the Ligures, bad neighbours living at their flank), but at the present time most of it is being used up on the buildings at Rome, and also at the villas, now that people are devising palaces of Persian magnificence.
6 As for the Volaterrani, their country is washed by the sea and their settlement is in a deep ravine; in the ravine there is a high hill, which is precipitous on all sides and flat on the crest, and it is on this hill that the walls of the city are situated. The ascent from the base to the crest is fifteen stadia, an ascent that is sharp all the way up, and difficult to make. This is where some of the Tyrrheni and of those who had been proscribed by Sulla assembled; and, on filling out four battalions, they withstood a siege for two years, and even then retired from the place only under a truce. As for Poplonium, it is situated on a high promontory that makes an abrupt descent into the sea and forms a peninsula; it too sustained a siege at about the same time as Volaterrae. Now although the town is wholly desert except for the temples and a few dwellings, the port-town, which has a little harbour and two docks p355at the base of the mountain, is better peopled; and in my opinion this is the only one of the ancient Tyrrhenian cities that was situated on the sea itself; and my reason is the country's lack of harbours — precisely the reason why the founders would avoid the sea altogether, or else would throw forward defences towards the sea, so as not to be exposed, a ready prey, to any who might sail against them. Again, beneath the promontory there is a place for watching the tunny-fish. And in looking down from the city you can see, albeit from afar and with difficulty, the island of Sardo, and, nearer, the island of Cyrnus (about sixty stadia distant from Sardo), and much better than these, the island of Aethalia; Aethalia is closer to the mainland, since it is distant only about three hundred stadia, the same as its distance from Cyrnus. This place is the best point of departure from the mainland to the three aforesaid islands. I myself saw these islands when I went up to Poplonium, and also some mines out in the country that had failed. And I also saw the people who work the iron that is brought over from Aethalia; for it cannot be brought into complete coalescence by heating in the furnaces on the island; and it is brought over immediately from the mines to the mainland. However, this is not the only remarkable thing about the island; there is also the fact that the diggings which have been mined are in time filled up again, as is said to be the case with the ledges of rocks in Rhodes, the marble-rock in Paros, and, according to Cleitarchus, the salt-rock in India. Neither, then, is Eratosthenes correct, when he says that neither Cyrnus nor Sardo can be seen from the mainland, nor Artemidorus, when he says that both islands lie in the high sea within twelve hundred stadia; for even supposing they were visible to some people at that distance, they could not have been so to me, at least, or else not to the extent of their being seen clearly, and particularly Cyrnus. Again, there is at Aethalia a Portus Argous, from the ship "Argo," as they say; for when Jason, the story goes, was in quest of the abode of Circe, because Medea wished to see the goddess, he sailed to this port; and, what is more, because the scrapings, which the Argonauts formed when they used their •strigils, became congealed, the pebbles on the shore remain variegated still to this day. Now mythical stories of this sort are proofs of what I have been saying: that Homer was not wont to fabricate everything on his own account, but, because he heard many such stories told over and over again, he was wont on his own account to add to them by lengthening the distances and making the settings more remote; and that, just as he threw the setting of his Odysseus out into the ocean, so similarly he threw the setting of his Jason there, because a wandering had actually taken place in the life of Jason as well as in that of Odysseus — just as also in that of Menelaus. So much, then, for the island of Aethalia.
7 But Cyrnus is by the Romans called Corsica. It affords such a poor livelihood — being not only rough but in most of its parts absolutely impracticable for travel — that those who occupy the mountains and live from brigandage are more savage than wild animals. At any rate, whenever the Roman generals have made a sally, and, falling suddenly upon the strongholds, have taken a large number of the people as slaves, you can at Rome see, and marvel at, the extent to which the nature of wild beasts, as also that of battening cattle, is manifested in them; for either they cannot endure to live in captivity, or, if they live, they so irritate their purchasers by their apathy and insensibility, that, even to the purchasers may have paid for them no more than an insignificant sum, nevertheless they repent the purchase. But still there are some habitable parts in the island, and what might be called towns, namely, Blesinon, Charax, Eniconiae and Vapanes. The length of the island, says the Chorographer, is one hundred and sixty miles, and the breadth seventy; but the length of Sardinia is two hundred and twenty, and the breadth ninety-eight. According to others, however, the perimeter of Cyrnus is called about three thousand two hundred stadia, and of Sardo as much as four thousand. The greater part of Sardo is rugged and not at peace, though much of it has also soil that is blessed with all products — especially with grain. As for cities, there are indeed several, but only Caralis and Sulchi are noteworthy. But the excellence of the places is offset by a serious defect, for in summer the island is unhealthful, particularly in the fruitful districts; and it is precisely these districts that are continually ravaged by those mountaineers who are now called Diagesbes; in earlier times, however, their name was Iolaës; for Iolaüs, it is said, came hither, bringing with him some of the children of Heracles, and took up his abode with the barbarians who held the island (the latter were Tyrrheni). Later on, the Phoenicians of Carthage got the mastery over them, and along with them carried on war against the Romans; but upon the defeat of the Phoenicians, everything became subject to the Romans. There are four tribes of the mountaineers, the Parati, the Sossinati, the Balari, and the Aconites, and they live in caverns; but if they do hold a bit of land that is fit for sowing, they do not sow even this diligently; instead, they pillage the lands of the farmers — not only of the farmers on the island, but they actually sail against the people on the opposite coast, the Pisatae in particular. Now the military governors who are sent to the island resist the mountaineers part of the time, but sometimes they grow weary of it — when it is not profitable continuously to maintain a camp in unhealthful places, and then the only thing left for them is to employ stratagems; and so, having observed a certain custom of the barbarians (who come together after their forays for a general celebration extending over several days), attack them at that time and overpower many of them. Again, Sardo produces the rams that grow goat-hair instead of wool; they are called, however, "musmones," and it is with the hides of these that the people there make their cuirasses. They also use a small leather shield and a small dagger.
8 The islands can be seen clearly enough from any part of the country between Poplonium and Pisa; they are oblong and approximately parallel, all three of them, and they point towards the south and Libya; Aethalia, however, falls considerably short of the others in size. Further, the shortest passage to Sardo from Libya, according to the Chorographer, is three hundred miles. After Poplonium comes Cossa, a city slightly above the sea; that is, there is a high hill at the head of a gulf, and the settlement is on this hill; and beneath lies the Harbour of Heracles and near it is a lagoon and, along the promontory that lies above the gulf, a station for observing the tunny-fish; for along the shore the tunny-fish follow not only the acorns but also the purple fish, beginning their course at the outer sea and going even as far as Sicily. As one sails along the coast from Cossa to Ostia one comes to some small towns: Gravisci, Pyrgi, Alsium and Fregena. To Gravisci, then, the distance is three hundred stadia; and in the interval is a place called Regis Villa. History tells us that this was once the palace of Maleos, the Pelasgian, who, it is said, although he held dominion in the places mentioned, along with the Pelasgi who helped him to colonise them, departed thence to Athens. And this is also the stock to which people belong who have taken and now hold Agylla. Again, from Gravisci to Pyrgi the distance is a little less than one hundred and eighty stadia; it is the port-town of the Caeretani, thirty stadia away.b And Pyrgi has a temple of Eilethyia, an establishment of the Pelasgi; it was once rich, but it was robbed by Dionysius, the tyrant of the Sicilians, on his expedition to Cyrnus. And again, from Pyrgi to Ostia the distance is two hundred and sixty stadia; and in the interval are Alsium and Fregena. Thus much for the coastline of Tyrrhenia.
9 In the interior there are still other cities besides those already mentioned — Arretium, Perusia, Volsinii, and Sutrium; and, besides these, numerous small towns — Blera, Ferentinum,c Falerii, Faliscum, Nepeta, Statonia, and several others; some of them are constituted as of old, while others the Romans have colonised, or else have brought low, as they did Veii, which had oftentimes gone to war with them, and as they did Fidenae. Some, however, call the Falerii, not "Tyrrheni," but "Falisci," a special and distinct tribe; again, others call Faliscum a city with a special language all its own; and others mean by Faliscum "Aequum Faliscum," which is situated on the Flaminian Way between Ocriclid and Rome. The city of Feronia is at the foot of Mount Soracte, with the same name as a certain native goddess, a goddess greatly honoured by the surrounding peoples; her sacred precinct is in the place; and it has remarkable ceremonies, for those who are possessed by this goddess walk with bare feet through a great heap of embers and ashes without suffering; and a multitude of people come together at the same time, for the sake not only of attending the festal assembly, which is held here every year, but also of seeing the aforesaid sight. But Arretium, which is near the mountains, is farthest of all in the interior; at any rate, it is twelve hundred stadia distant from Rome, while Clusium is only eight hundred; and Perusia is near these two. The lakes, too, contribute to the prosperity of Tyrrhenia, being both large and numerous; for they are navigable, and also give food to quantities of fish and to the various marsh-birds; quantities of cat-tail, too, and papyrus, and downy plumes of the reed, are transported by rivers into Rome — rivers which are sent forth by the lakes as far as the Tiber; and among these are the Ciminian Lake, the lake near Volsinii, the lake near Clusium, and the lake that is nearest Rome and the sea — Lake Sabata. But the lake that is farthest away and that is near Arretium is Trasumenna, near which is the pass by which an army may debouch into Tyrrhenia from Celtica, the very pass which Hannibal used; there are two, however, this one and the one towards Ariminum through Ombrica. Now the one towards Ariminum is better, since the mountains become considerably lower there; and yet, since the defiles on this pass were carefully guarded, Hannibal was forced to choose the more difficult pass, but, for all that, he got control of it, after having conquered Flaminius in great battles. Furthermore, there are abundant hot springs in Tyrrhenia, and, because of the fact that they are near Rome, they have a population not less than the springs at Baiae, which are by far the most widely renowned of all.
Alongside Tyrrhenia, on the part toward the east, lies Ombrica; it takes its beginning at the Apennines and extends still farther beyond as far as the Adriatic; for it is at Ravenna that the Ombrici begin, and they occupy the nearby territory and also, in order thereafter, Sarsina, Ariminum, Sena, Camarinum. Here, too, is the Aesis River, and Mount Cingulum, and Sentinum, and the Metaurus River, and the Temple of Fortune. Indeed, it is near these places that the boundary between the Italy of former days and Celtica passed (I mean the boundary at the part next to the Adriatic Sea), albeit the boundary has often been changed by the rulers; at least they formerly made the Aesis the boundary and then in turn the Rubicon. The Aesis is between Ancona and Sena, the Rubicon between Ariminum and Ravenna, and both empty into the Adriatic. But as it is, now that the whole of the country as far as the Alps has been designated Italy, we should disregard these boundaries, but none the less agree, as is agreed by all, that Ombrica, properly so‑called, extends all the way to Ravenna; for Ravenna is inhabited by these people. From Ravenna, then, to Ariminum the distance is, they say, about three hundred stadia; and if you travel from Ariminum toward Rome along the Flaminian Way through Ombrica your whole journey, as far as Ocricli and the Tiber, is thirteen hundred and fifty stadia. This, then, is the length of Ombrica, but the breadth is uneven. The cities this side the Apennine Mountains that are worthy of mention are: first, on the Flaminian Way itself: Ocricli, near the Tiber and theº Larolon, and Narna, through which the Nar River flows (it meets the Tiber a little above Ocricli, and is navigable, though only for small boats); then, Carsuli, and Mevania, past which flows the Teneas (this too brings the products of the plain down to the Tiber on rather small boats); and, besides, still other settlements, which have become filled up with people rather on account of the Way itself than of political organisation; these are Forum Flaminium, and Nuceria (the place where the wooden utensils are made), and Forum Sempronium. Secondly, to the right of the Way, as you travel from Ocricli to Ariminum, is Interamna, and Spoletium, and Aesium, and Camertes (in the very mountains that mark the boundary of the Picentine country); and, on the other side of the Way, Ameria, and Tuder (a well-fortified city), and Hispellum, and Iguvium, the last-named lying near the passes that lead over the mountain. Now as a whole Ombrica is blessed with fertility, though it is a little too mountainous and nourishes its people with spelt rather than with wheat. The Sabine country also, which comes next in order after Ombrica, is mountainous, and it lies alongside Ombrica in the same way that Ombrica lies alongside Tyrrhenia; and further, all parts of the Latin country that are near to these parts and to the Apennine Mountains are rather rugged. These two tribes begin, then, at the Tiber and Tyrrhenia, and extend to that stretch of the Apennine Mountains near the Adriatic which slants slightly inland, although Ombrica passes on beyond the mountains, as I have said, as far as the Adriatic. So much, then, for the Ombrici. |
|
|
|










|
5 - 3 Sabine lands and Latium 
The country the Sabini live in is narrow, but taken lengthwise it reaches even a thousand stadia from the Tiber and the little town of Nomentum, as far as the country of the Vestini. They have but few cities and even these have been brought low on account of the continual wars; they are Amiternum, and Reate (near which is the village of Interocrea, and also the cold springs of Cotiliae,1where people cure their diseases, not only by drinking from the springs but also by sitting down in them). Foruli too belongs to the Sabini — a rocky elevation naturally suited to the purposes of a revolt rather than habitation. As for Cures, it is now only a small village,a but it was once a city of significance, since it was the original home of two kings of Rome, Titius Tatius and Numa Pompilius; hence, the title "Curites" by which the public orators address the Romans. Trebula, Eretum, and other such settlements might be ranked as villages rather than cities. As a whole the land of the Sabini is exceptionally well-planted with the olive and the vine, and it also produces acorns in quantities; it is important, also, for its domestic cattle of every kind; and in particular the fame of the Reate-breed of mules is remarkably widespread. In a word, Italy as a whole is an excellent nurse both of young animals and of fruits, although different species in different parts take the first prize. The Sabini not only are a very ancient race but are also the indigenous inhabitants (and both the Picentini and the Samnitae are colonists from the Sabini, and the Leucani from the Samnitae, and the Brettii from the Leucani). And the old-fashioned ways of the Sabini might be taken as evidence of bravery, and of those other excellent qualities which have enabled them to hold out to the present time. Fabius, the historian, says that the Romans realised their wealth for the first time when they became established as masters of this tribe. As for the roads that have been constructed through their country, there is not only the Via Salaria (though it does not run far) but also the Via Nomentana which unites with it at Eretum (a village of the Sabine country, situated beyond the Tiber), though it begins above the same gate, Porta Collina.
2 Next comes the Latin country, in which the city of the Romans is situated, though it now comprises also many cities of what was formerly non-Latin country. For the Aeci, the Volsci, the Hernici, and also the aborigines who lived near Rome itself, the Rutuli who held the old Ardea, and other groups, greater or less, who lived near the Romans of that time, were all in existence when the city was first founded; and some of these groups, since they were ranked under no common tribe, used to be allowed to live autonomously in separate villages. It is said that Aeneas, along with his father Anchises and his son Ascanius, after putting in at Laurentum, which was on the shore near Ostia and the Tiber, founded a city a little above the sea, within about twenty-four stadia from it; and Latinus, the king of the aborigines, who lived in this place where Rome now is, on making them a visit, used Aeneas and his people as allies against the neighbouring Rutuli who occupied Ardea (the distance from Ardea to Rome is one hundred and sixty stadia), and after his victory founded a city near by, naming it after his daughter Lavinia; and when the Rutuli joined battle again, Latinus fell, but Aeneas was victorious, became king, and called his subjects "Latini"; and after the death of both Aeneas and his father Anchises, Ascanius founded Alba and Mount Albanus, which Mount is the same distance from Rome as Ardea. Here the Romans in company with the Latini — I mean the joint assembly of all their magistrates — offered sacrifice to Zeus; and the assembly put one of the young nobles in charge of the city as governor for the time of the sacrifice. But it is four hundred years later that the stories about Amollius and his brother Numitor are placed — stories partly fabulous but partly closer to the truth. In the first place, both brothers succeeded to the rule of Alba (which extended as far as the Tiber) from the descendants of Ascanius; but Amollius, the younger, elbowed the elder out and reigned alone; but since Numitor had a son and a daughter, Amollius treacherously murdered the son while on a hunt, and appointed the daughter, in order that she might remain childless, a priestess of Vesta, so as to keep her a virgin (she is called Rhea Silvia); then, on discovering that she had been ruined (for she gave birth to twins), instead of killing her, he merely incarcerated her, to gratify his brother, and exposed the twins on the banks of the Tiber in accordance with an ancestral custom. In mythology, however, we are told that the boys were begotten by Ares, and that after they were exposed people saw them being suckled by a she-wolf; but Faustulus, one of the swineherds near the place, took them up and reared them (but we must assume that it was some influential man, a subject of Amollius, that took them and reared them), and called one Romulus and the other Romus; and upon reaching manhood they attacked Amollius and his sons, and upon the defeat of the latter and the reversion of the rule to Numitor, they went back home and founded Rome — in a place which was suitable more as a matter of necessity than of choice; for neither was the site naturally strong, nor did it have enough land of its own in the surrounding territory to meet the requirements of a city, nor yet, indeed, people to join with the Romans as inhabitants; for the people who lived thereabouts were wont to dwell by themselves (though their territory almost joined the walls of the city that was being founded), not even paying any attention to the Albani themselves. And there was Collatia, and Antemnae, and Fidenae, and Labicum, and other such places — then little cities, but now mere villages, or else estates of private citizens — all at a distance from Rome of thirty stadia, or a little more. At any rate, between the fifth and the sixth of those stones which indicate the miles from Rome there is a place called "Festi," and this, it is declared, is a boundary of what was then the Roman territory; and, further, the priests celebrate sacrificial festivals, called "Ambarvia," on the same day, both there and at several other places, as being boundaries. Be this as it may, a quarrel arose at the time of the founding of the city, and as a result Remus was slain. After the founding Romulus set about collecting a promiscuous rabble by designating as an asylum a sacred precinct between the Arx and the Capitol, and by declaring citizens all the neighbours who fled thither for refuge. But since he could not obtain the right of intermarriage for these, he announced one horse-race, sacred to Poseidon, the rite that is still to‑day performed; and when numerous people, but mostly Sabini, had assembled, he bade all who wanted a wife to seize the maidens who had come to the race. Titus Tatius, the king of the Curites, went to avenge1the outrage by force of arms, but compromised with Romulus on the basis of partnership in the throne and state. But Tatius was treacherously murdered in Lavinium, and then Romulus, with the consent of the Curites, reigned alone. After Romulus, Numa Pompilius, a fellow-citizen of Tatius, succeeded to the throne, receiving it from his subjects by their own choice. This, then, is the best accredited story of the founding of Rome.
3 But there is another one, older and fabulous, in which we are told that Rome was an Arcadian colony and founded by Evander:— When Heracles was driving the cattle of Geryon he was entertained by Evander; and since Evander had learned from his mother Nicostrate (she was skilled in the art of divination, the story goes) that Heracles was destined to become a god after he had finished his labours, he not only told this to Heracles but also consecrated to him a precinct and offered a sacrifice to him after the Greek ritual, which is still to this day kept up in honour of Heracles. And Coelius himself, the Roman historian, puts this down as proof that Rome was founded by Greeks — the fact that at Rome the hereditary sacrifice to Heracles is after the Greek ritual. And the Romans honour also the mother of Evander, regarding her as one of the nymphs, although her name has been changed to Carmentis.
4 Be that as it may, the Latini at the outset were few in number and most of them would pay no attention to the Romans; but later on, struck with amazement at the prowess both of Romulus and of the kings who came after him, they all became subjects. And after the overthrow of the Aequi,1of the Volsci, and of the Hernici, and, still before that, of both the Rutuli and the aborigines (and besides these, certain of the Rhaeci, as also of the Argyrusci and the Preferni), the whole country that belonged to these peoples was called Latium. The Pomptine Plain, on the confines of the Latini, and the city of Apiola, which was destroyed by Tarquinius Priscus, used to belong to the Volsci. The Aequi are the nearest neighbours of the Curites; their cities, too, were sacked by Tarquinius Priscus; and his son captured Suessa, the metropolis of the Volsci. The Hernici used to live near Lanuvium, Alba, and Rome itself; and Aricia, also, and Tellenae and Antium were not far away. At the outset the Albani lived in harmony with the Romans, since they spoke the same language and p389were Latini, and though they were each, as it happened, ruled by kings, separate and apart, none the less they not only had the right of intermarriage with one another, but also held sacrifices — those at Alba — and other political rights in common; later on, however, war arose between them, with the result that all Alba was destroyed except the temple, and that the Albani were adjudged Roman citizens. As for the other neighbouring cities, some of them too were destroyed, and others humiliated, for their disobedience, while some were made even stronger than they were because of their loyalty. Now at the present time the seaboard is called Latium from Ostia as far as the city of Sinuessa, but in earlier times Latium had extended its seaboard only as far as Circaeum. Further, in earlier times Latium did not include much of the interior, but later on it extended even as far as Campania and the Samnitae and the Peligni and other peoples who inhabit the Apennines.
5 All Latium is blest with fertility and produces everything, except for a few districts that are on the seaboard — I mean all those districts that are marshy and sickly (such as those of the Ardeatae, and those between Antium and Lanuvium as far as the Pomptine Plain, and certain districts in the territory of Setia and the country round about Tarracina and the Circaeum), or any districts that are perhaps mountainous and rocky; and yet even these are not wholly untilled or useless, but afford rich pasture grounds, or timber, or certain fruits that grow in marshy or rocky ground (the Caecuban Plain, although marshy, supports a vine that produces the best of wine, I mean the tree-vine). The seaboard cities belonging to the Latii are, first, Ostia: it is harbourless on account of the silting up which is caused by the Tiber, since the Tiber is fed by numerous streams. Now although it is with peril that the merchant-ships anchor far out in the surge, still, the prospect of gain prevails; and in fact the good supply of the tenders which receive the cargoes and bring back cargoes in exchange makes it possible for the ships to sail away quickly before they touch the river, or else, after being partly relieved of their cargoes, they sail into the Tiber and run inland as far as Rome, one hundred and ninety stadia. Ostia was founded by Ancus Marcius. Such, then, is this city of Ostia. Next comes Antium, it also being a harbourless city. It is situated on masses of rock, and is about two hundred and sixty stadia distant from Ostia. Now at the present time Antium is given over to the rulers for their leisure and relief from the cares of state whenever they get the opportunity, and therefore, for the purposes of such sojourns, many very costly residences have been built in the city; but in earlier times the people of Antium used to possess ships and to take part with the Tyrrheni in their acts of piracy, although at that time they were already subjects of the Romans. It is for this reason that Alexander, in earlier times, sent in complaints, and that Demetrius, later on, when he sent back to the Romans what pirates he had captured, said that, although he was doing the Romans the favour of sending back the captives because of the kinship between the Romans and the Greeks, he did not deem it right for men to be sending out bands of pirates at the same time that they were in command of Italy, or to build in their Forum a temple in honour of the Dioscuri, and to worship them, whom all call Saviours, and yet at the same time send to Greece people who would plunder the native land of the Dioscuri. And the Romans put a stop to such practices. Midway between these two cities is Lavinium, which has a temple of Aphrodite that is common to all the Latini, though the Ardeatae, through attendants, have the care of it. Then comes Laurentum. And beyond these cities lies Ardea, a settlement of the Rutuli, seventy stadia inland from the sea. Near Ardea too there is a temple of Aphrodite, where the Latini hold religious festivals. But the places were devastated by the Samnitae; and although only traces of cities are left, those traces have become famous because of the sojourn which Aeneas made there and because of those sacred rites which, it is said, have been handed down from those times.
6 After Antium, within a distance of two hundred and ninety stadia, comes Circaeum, a mountain which has the form of an island, because it is surrounded by sea and marshes. They further say that Circaeum is a place that abounds in roots — perhaps because they associate it with the myth about Circe. It has a little city and a temple of Circe and an altar of Athene, and people there show you a sort of bowl which, they say, belonged to Odysseus. Between Antium and Circaeum is the River Storas, and also, near it, an anchoring-place. Then comes a stretch of coast that is exposed to the south-west wind, with no shelter except a little harbour near Circaeum itself. Beyond this coast, in the interior, is the Pomptine Plain. The country that joins this latter was formerly inhabited by the Ausones, who also held Campania. After these come the Osci; they too had a share in Campania; but now everything belongs to the Latini as far as Sinuessa, as I said. A peculiar thing has taken place in the case of the Osci and the tribe of the Ausones. Although the Osci have disappeared, their dialect still remains among the Romans, so much so that, at the time of a certain traditional competition, poems in that dialect are brought on the stage and recited like mimes; again, although the Ausones never once lived on the Sicilian Sea, still the high sea is called "Ausonian." Next, within one hundred stadia of Circaeum, is Tarracina, which was formerly called "Trachine" from its actual character. In front of Tarracina lies a great marsh, formed by two rivers; the larger one is called Aufidus. It is here that the Appian Way first touches the sea; it has been constructed from Rome as far as Brentesium and is the most travelled of all; but of the cities on the sea it touches only these: Tarracina, and those that come next in order after it, Formiae, Minturnae, and Sinuessa, and those at the end — Taras and Brentesium. Near Tarracina, as you go toward Rome, there is a canal which runs alongside the Appian Way, and is fed at numerous places by waters from the marshes and the rivers. People navigate the canal, preferably by night (so that if they embark in the evening they can disembark early in the morning and go the rest of their journey by the Way), but they also navigate it by day. The boat is towed by a mule. Next after Tarracina comes Formiae, founded by the Laconians, and formerly called "Hormiae" because of its good "hormos." And those people also named the intervening gulf "Caietas," for the Laconians call all hollow things "Caietas"; but some say the gulf was named after the nurse of Aeneas. It has a length of one hundred stadia, beginning at Tarracina and extending as far as the promontory of like name. There are wide-open caverns of immense size at this place, which have been occupied by large and very costly residences; from here to Formiae the distance is forty stadia. Midway between Formiae and Sinuessa is Minturnae, which is about eighty stadia distant from each. Through Minturnae flows the River Liris, formerly called the "Clanis." It runs from the interior, out of the Apennine Mountains and the country of the Vestini, past Fregellae,º a village (it was formerly a famous city), and empties into a sacred precinct which is much revered by the people in Minturnae; the precinct is situated below the city. In the high sea, off the caverns and visible thence most of the time, are situated two islands, Pandateria and Pontia, which, though small, are well peopled; they are not far distant from one another, but they are two hundred and fifty stadia from the mainland. The Caecuban Plain borders on the Gulf of Caietas; and next to the plain comes Fundi, situated on the Appian Way. All these places produce exceedingly good wine; indeed, the Caecuban and the Fundanian and the Setinian belong to the class of wines that are widely famed, as is the case with the Falernian and the Alban and the Statanian. Sinuessa is situated in the Caietan "Kolpos," and hence its name; for "Kolpos" means "Sinus"; and near Sinuessa are hot baths, which are most efficacious for certain diseases. These, then, are the cities of the Latini on the sea.
7 In the interior, the first city above Ostia is Rome, and it is the only city that is situated on the Tiber. With regard to this city, I have already said that it was founded there as a matter of necessity, not as a matter of choice; and I must add that even those who afterwards added certain districts to the settlement could not as masters take the better course, but as slaves must needs accommodate themselves to what had already been founded. The first founders walled the Capitolium and the Palatium and the Quirinal Hill, which last was so easy for outsiders to ascend that Titus Tatius took it at the first onset, making his attack at the time when he came to avenge the outrage of the seizure of the maidens. Again, Ancus Marcius took in Mt. Caelium and Mt. Aventine, and the plain between them, which were separated both from one another and from the parts that were already walled, but he did so only from necessity; for, in the first place, it was not a good thing to leave hills that were so well fortified by nature outside the walls for any who wished strongholds against the city, and, secondly, he was unable to fill out the whole circuit of hills as far as the Quirinal. Servius, however, detected the gap, for he filled it out by adding both the Esquiline Hill and the Viminal Hill. But these too are easy for outsiders to attack; and for this reason they dug a deep trench and took the earth to the inner side of the trench, and extended a mound about six stadia on the inner brow of the trench, and built thereon a wall with towers from the Colline Gate to the Esquiline. Below the centre of the mound is a third gate, bearing the same name as the Viminal Hill. Such, then, are the fortifications of the city, though they need a second set of fortifications. And, in my opinion, the first founders took the same course of reasoning both for themselves and for their successors, namely, that it was appropriate for the Romans to depend for their safety and general welfare, not on their fortifications, but on their arms and their own valour, in the belief that it is not walls that protect men but men that protect walls. At the outset, then, since the fertile and extensive country round about them belonged to others, and since the terrain of the city was so easy to attack, there was nothing fortunate in their position to call for congratulation, but when by their valour and their toil they had made the country their own property, there was obviously a concourse, so to speak, of blessings that surpassed all natural advantages; and it is because of this concourse of blessings that the city, although it has grown to such an extent, holds out in the way it does, not only in respect to food, but also in respect to timber and stones for the building of houses, which goes on unceasingly in consequence of the collapses and fires and repeated sales (these last, too, going on unceasingly); and indeed the sales are intentional collapses, as it were, since the purchasers keep on tearing down the houses and build new ones, one after another, to suit their wishes. To meet these requirements, then, the Romans are afforded a wonderful supply of materials by the large number of mines, by the timber, and by the rivers which bring these down: first, the Anio, which flows from Alba, the Latin city next to the Marsi, through the plain that is below Alba to its confluence with the Tiber; and then the Nar and the Teneas, the rivers which run through Ombrica down to the same river, the Tiber; and also the Clanis, which, however, runs down thither through Tyrrhenia and the territory of Clusium. Now Augustus Caesar concerned himself about such impairments of the city, organising for protection against fires a militia composed of freedmen, whose duty it was to render assistance, and also to provide against collapses, reducing the heights of the new buildings and forbidding that any structure on the public streets should rise as high as seventy feet; but still his constructive measures would have failed by now were it not that the mines and the timber and the easy means of transportation by water still hold out.
8 So much, then, for the blessings with which nature supplies the city; but the Romans have added still others, which are the result of their foresight; for if the Greeks had the repute of aiming most happily in the founding of cities, in that they aimed at beauty, strength of position, harbours, and productive soil, the Romans had the best foresight in those matters which the Greeks made but little account of, such as the construction of roads and aqueducts, and of sewers that could wash out the filth of the city into the Tiber. Moreover, they have so constructed also the roads which run throughout the country, by adding both cuts through hills and embankments across valleys, that their wagons can carry boat-loads; and the sewers, vaulted with close-fitting stones, have in some places left room enough for wagons loaded with hay to pass through them. And water is brought into the city through the aqueducts in such quantities that veritable rivers flow through the city and the sewers; and almost every house has cisterns, and service-pipes, and copious fountains — with which Marcus Agrippa concerned himself most, though he also adorned the city with p407many other structures. In a word, the early Romans made but little account of the beauty of Rome, because they were occupied with other, greater and more necessary, matters; whereas the later Romans, and particularly those of to‑day and in my time, have not fallen short in this respect either — indeed, they have filled the city with many beautiful structures. In fact, Pompey, the Deified Caesar, Augustus, his sons and friends, and wife and sister, have outdone all others in their zeal for buildings and in the expense incurred. The Campus Martius contains most of these, and thus, in addition to its natural beauty, it has received still further adornment as the result of foresight. Indeed, the size of the Campus is remarkable, since it affords space at the same time and without interference, not only for the chariot-races and every other equestrian exercise, but also for all that multitude of people who exercise themselves by ball-playing, hoop-trundling, and wrestling; and the works of art situated around the Campus Martius, and the ground, which is covered with grass throughout the year, and the crowns of those hills that are above the river and extend as far as its bed, which present to the eye the appearance of a stage-painting — all this, I say, affords a spectacle that one can hardly draw away from. And near this campus is there is another campus, with colonnades round about it in very great numbers, and sacred precincts, and three theatres, and an amphitheatre, p409and very costly temples, in close succession to one another, giving you the impression that they are trying, as it were, to declare the rest of the city a mere accessory. For this reason, in the belief that this place was holiest of all, the Romans have erected in it the tombs of their most illustrious men and women. The most noteworthy is what is called the Mausoleum, a great mound near the river on a lofty foundation of white marble, thickly covered with ever-green trees to the very summit. Now on top is a bronze image of Augustus Caesar; beneath the mound are the tombs of himself and his kinsmen and intimates; behind the mound is a large sacred precinct with wonderful promenades; and in the centre of the Campus is the wall (this too of white marble) round his crematorium; the wall is surrounded by a circular iron fence and the space within the wall is planted with black poplars. And again, if, on passing to the old Forum, you saw one forum after another ranged along the old one, and basilicas, and temples, and saw also the Capitolium and the works of art there and those of the Palatium and Livia's Promenade, you would easily become oblivious to everything else outside. Such is Rome.
9 As for the rest of the cities of Latium, their positions may be defined, some by a different set of distinctive marks, and others by the best known roads that have been constructed through Latium; for they are situated either on these roads, or near them, or between them. The best known of the roads are the Appian Way, the Latin Way, and the Valerian Way. The Appian Way marks off, as far as Sinuessa, those parts of Latium that are next to the sea, and the Valerian Way, as far as the Marsi, those parts that are next to the Sabine country; while the Latin Way is between the two — the Way that unites with the Appian Way at Casilinum, a city nineteen stadia distant from Capua. The Latin Way begins, however, at the Appian Way, since near Rome it turns off from it to the left, and then, passing through the Tusculan Mountain, and over it at a point between the city of Tusculum and the Alban Mountain, runs down to the little city of Algidum and the Inns of Pictae;2and then it is joined by the Labican Way. This latter begins at the Esquiline Gate, as also does the Praenestine Way, but it leaves both the Praenestine Way and the Esquiline Plain to the left and runs on for more than one hundred and twenty stadia, and, on drawing near to Labicum (a city founded in early times, once situated on an eminence, but now demolished), leaves both it and Tusculum on the right and comes to an end at Pictae and the Latin Way; the distance of this place from Rome is two hundred and ten stadia. Then in order, as you proceed on the Latin Way itself, you come to important settlements and the cities of Ferentinum, Frusino (past which the Cosa flows), Fabrateria (past which the Trerus flows), Aquinum (it is a large city, and past it flows a large river, the Melpis), Interamnium (which is situated at the confluence of two rivers, the Liris and another), and Casinum (this too a noteworthy city), which is the last city of Latium; for what is called Teanum "Sidicinum," which is situated next in order after Casinum, shows clearly from its epithet that it belongs to the Sidicini. These people are Osci, a tribe of Campani that has disappeared; and therefore this city might be called a part of Campania, although it is the largest of the cities on the Latin Way, as also might the city that comes next after it, that of the Caleni (this too a noteworthy city), although its territory joins that of Casilinum.
Then take the cities on either side of the Latin Way. On the right are those between it and the Appian Way, namely, Setia and Signia, which produce wine, the former, one of the costly wines, and the latter, the best for checking the bowels (what is called the "Signine" wine). And farther on, beyond Signia, is Privernum, and Cora, and Suessa, and also Trapontium, Velitrae, and Aletrium; and besides these, Fregellae (past which the Liris flows, the river that empties at Minturnae), which is now merely a village, although it was once a noteworthy city and formerly held as dependencies most of the surrounding cities just mentioned (and at the present time the inhabitants of these cities meet at Fregellae both to hold markets and to perform certain sacred rites), but, having revolted, it was demolished by the Romans. Most of these cities, as also of those on the Latin Way and of those on the far side of it, are situated in the country of the Hernici, the Aeci, and the Volsci, though all were founded by the Romans. Again, on the left of the Latin Way are the cities between it and the Valerian Way: first, Gabii, situated on the Praenestine Way, with a rock-quarry that is more serviceable to Rome than any other, and equidistant — about one hundred stadia — from Rome and Praeneste; then Praeneste, about which I shall speak presently; then the cities in those mountains that are above Praeneste: Capitulum, the little city of the Hernici, and Anagnia, a noteworthy city, and Cereate, and Sora (past which the Liris flows as it issues from the mountains and comes to Fregellae and Minturnae); and then certain other places, and Venafrum, whence comes the finest olive-oil. Now the city of Venafrum is situated on an eminence, and past the base of the hill flows the Volturnus River, which runs past Casilinum also and empties into the sea at the city of like name. But when you come to the cities of Aesernia and Allifae you are already in Samnitic territory; the former was destroyed in the Marsic War, while the latter still endures.
The Valerian Way has its beginning at Tibur, and leads to the country of the Marsi, and to Corfinium, the metropolis of the Peligni. On the Valerian Way are the following cities of Latium: Varia, Carseoli, and Alba, and also, near by, the city of Cuculum. Tibur, Praeneste, and Tusculum are all visible from Rome. First, Tibur: it possesses the temple of Heracles, and also the waterfall formed by the Anio, a navigable river which falls down from a great height into a deep, wooded2ravine near the city itself. Thence the river flows out through a very fruitful plain past the quarries of the Tiburtine stone, and of the stone of Gabii, what is called "red stone"; so that the delivery from the quarries and the transportation by water are perfectly easy — most of the works of art2at Rome being constructed of stone brought thence. In this plain, also, flow what are called the Albula waters — cold waters from many springs, helpful, both as drinking-water and as baths, in the cure of various diseases; and such, also, are the Labana waters, not far from the former, on the Nomentan Way and in the neighbourhood of Eretum. Secondly, Praeneste: here is the temple of Fortuna, noted for its oracles. Both of these cities are situated near the same mountain range, and they are about one hundred stadia distant from one another; but from Rome Praeneste is as much as double that distance, whereas Tibur is less than double. Both are called Greek cities; in any case Praeneste, they say, was formerly called "Polystephanos." Now each is well fortified by nature, but Praeneste is much more so, since it has for a citadel2a high mountain which not only rises above the city but also in the rear is disjoined from the unbroken mountain range by a neck of land above which it rises as much as two stadia in a perpendicular ascent. And in addition to its natural strength, subterranean passages have been bored through it from all sides as far as the plains — some for water-supply, others for secret exits (it was in one of these that Marius was put to death when he was being besieged). Now although in the case of all other cities, generally speaking, good defences are accounted a blessing, in the case of the Praenestini they have proved to be a misfortune, because of the seditions among the Romans. For all who have attempted a revolution take refuge in Praeneste; and, if forced by a siege to surrender, the inhabitants, in addition to the damage done to their city, meet with the further misfortune that their territory is alienated, the guilt being transferred to the guiltless. The Verestis River flows through the territory in question. The aforesaid cities are to the east of Rome.
But still closer to Rome than the mountainous country where these cities lie, there is another ridge, which leaves a valley (the valley near Algidum) between them and is high as far as Mt. Albanus. It is on this chain that Tusculum is situated, a city with no mean equipment of buildings; and it is adorned by the plantings and villas encircling it, and particularly by those that extend below the city in the general direction of the city of Rome; for here Tusculum is a fertile and well-watered hill, which in many places rises gently into crests and admits of magnificently devised royal palaces. Adjoining this hill are also the foothills of Mt. Albanus, with the same fertility and the same kind of palaces. Then, next, come the plains, some connecting with Rome and its suburbs, and others with the sea. Now although the plains that connect with the sea are less healthful, the others are both pleasant to dwell in and decked out in similar manner. After Mt. Albanus comes Aricia, a city on the Appian Way; it is one hundred and sixty stadia distant from Rome. Aricia lies in a hollow, but for all that it has a naturally strong citadel. Above Aricia lies, first, on the right hand side of the Appian Way, Lanuvium, a city of the Romans, from which both the sea and Antium are visible, and, secondly, to the left of the Way as you go up from Aricia, the Artemisium, which they call Nemus. The temple of the Arician, they say, is a copy of that of the Tauropolos. And in fact a barbaric, and Scythian, element predominates in the sacred usages, for the people set up as priest merely a run-away slave who has slain with his own hand the man previously consecrated to that office; accordingly the priest is always armed with a sword, looking around for the attacks, and ready to defend himself. The temple is in a sacred grove, and in front of it is a lake which resembles an open sea, and round about it in a circle lies an unbroken and very high mountain-brow, which encloses both the temple and the water in a place that is hollow and deep. You can see the springs, it is true, from which the lake is fed (one of them is "Egeria," as it is called from a certain deity), but the outflows at the lake itself are not apparent, though they are pointed out to you at a distance outside the hollow, where they rise to the surface.
Near these places is also Mt. Albanus, which rises considerably above the Artemisium and the mountain-brows round about it, though they too are high and rather steep. This mountain also has a lake, much larger than the one at the Artemisium. The previously mentioned cities of Latium are farther away than these places. But of all the cities of Latium, Alba is the farthest in the interior, since it is on the confines of the Marsi; it is situated on a lofty rock, near Lake Fucinus,2which in size is like an open sea. The lake is used mostly by the Marsi and all the neighbouring peoples. They say that it not only fills up sometimes as far as the mountainous country, but also lowers again enough to permit the places which have been converted into marshes to get dry and to be tilled — whether it be that changes take place, sporadically and in a way that is not apparent, in the flow of the waters down in the depths, and that they flow back together again, or that the springs completely fail and then by pressure are brought together again — as is said to be the case with the Amenanus, the river that flows through Catana, for it fails for many years and then flows again. It is from Lake Fucinus, the story goes, that the springs of the Aqua Marcia come, which brings drinking-water to Rome and has the highest repute as compared with the other waters. Because of the fact that Alba is situated deep in the interior of the country, and is also well-walled, the Romans often used it for a prison, shutting up therein those who have to be kept under guard. |
|
|
|

|
5 - 4 Picenum (S Marche) and Campania 
1 I began with the tribes that live next to the Alps, and with that part of the Apennine Mountains which lies next to them, and then, passing over that part, traversed all the country on this side which lies between the Tyrrhenian Sea and that part of the Apennine Mountains which bends towards the Adriatic and stretches to the countries of the Samnitae and the Campani; I shall now, therefore, go back and indicate the tribes that live in these mountains, and also in the foothills both of the country outside the mountains, as far as the Adriatic seaboard, and of the country this side. But I must begin again with the Celtic boundaries.
2 Next after those cities of the Ombrici that are between Ariminum and Ancona comes the Picentine country. The Picentini are originally from the Sabine country, a woodpecker having led the way for their progenitors; and hence their name, for they call this bird "picus," and consider it sacred to Mars. The country they live in begins at the mountains and extends as far as the plains and the sea, thus having increased in length more than breadth; it is good for every use to which it may be put, though better for fruits than for grain. Its breadth — that from the mountains to the sea — taken at the different intervals, is irregular, while its length, by a voyage along the coast from the Aesis River to Castrum, is eight hundred stadia. Its cities are, first Ancona, a Greek city, founded by the Syracusans who fled from the tyranny of Dionysius; it is situated on a promontory, which by its curve towards the north encloses a harbour; and it is exceedingly productive of wine and wheat. Near it is the city of Auxumum, which is a short distance above the sea; then Septempeda, Pneuentia, Potentia and Firmum Picenum (its port-town is Castellum). Next in order comes the temple of Cupra, which was established, and founded as a city, by the Tyrrheni, who call Hera "Cupra"; then, the River Truentinus and the city named after it; then Castrum Novum, and the River Matrinus (which flows from the city of the Adriani), on which is Adria's port-town, named after the river. Not only is Adria in the interior, but also Asculum Picenum, a place that is well fortified by nature, not only where the wall is situated — but also the mountains that lie round about it are impassable for armies. Beyond the Picentine country are the Vestini, the Marsi, the Peligni, the Marrucini, and the Frentani (a Samnitic tribe); they occupy the mountain-country there, their territory touching upon the sea for only short stretches. These tribes are small, it is true, but they are very brave and oftentimes have exhibited this virtue to the Romans: first, when they went to war against them; a second time, when they took the field with them as allies; and a third time when, begging for freedom and political rights without getting them, they revolted and kindled what is called the Marsic War, for they proclaimed Corfinium (the metropolis of the Peligni) the common city for all the Italiotes, instead of Rome, making it their base of operations for the war and changing its name to Italica; and here it was that they mustered all their followers and elected consuls and praetors. And they persisted in the war for two years, until they achieved the partnership for which they went to war. The war was named "Marsic" after the people who began the revolt, Pompaedius in particular. Now these peoples live in villages, generally speaking, but they also have cities: first, above the sea, Corfinium, Sulmon, Maruvium, and Teate, the metropolis of the Marrucini. And, secondly, on the sea itself, Aternum, which borders on the Picentine country and is of like name with the river that separates the Vestine country from the Marrucine; for it flows from the territory of Amiternum, and through the Vestine country, leaving on its right that part of the Marrucine country which lies above the Peligni (it may be crossed by a pontoon-bridge). But although the little city that is named after the river belongs to the Vestini, it is used as a common port by the Peligni and the Marrucini. The pontoon-bridge is twenty-four stadia distant from Corfinium. After Aternum comes Orton, the port-town of the Frentani, and then Buca (it too belongs to the Frentani), whose territory borders on that of Teanum Apulum. Ortonium is in the country of the Frentani, a cliff-town belonging to pirates, whose dwellings are pieced together from the wreckage of ships; and in every other respect they are said to be a bestial folk. Between Orton and Aternum is the Sagrus River, which separates the country of the Frentani from that of the Peligni. The voyage along the coast from the Picentine country to the country of those Apuli whom the Greeks call "Daunii" is about four hundred and ninety stadia.
3 Next in order after Latium come both Campania, which stretches along the sea, and, above Campania, in the interior, the Samnite country, which extends as far as the country of the Frentani and the Daunii; then the Daunii themselves, and the rest of the tribes on to the Sicilian Strait. But I must first speak of Campania. There is a fair-sized gulf which, beginning at Sinuessa, extends along the coast next thereafter as far as Misenum, and also another gulf, much larger than the first, which begins at Misenum; they call the latter the "Crater," and the "Crater" forms a bay between the two capes of Misenum and Athenaeum. Above these coasts lies the whole of Campania; it is the most blest of all plains, and round about it lie fruitful hills, and the mountains of the Samnitae and of the Osci. Antiochus, it is true, says that the Opici once lived in this country and that "they are also called Ausones," but Polybius clearly believes that they are two different tribes, for he says "the Opici and the Ausones live in this country round about the Crater." Again, others say that, although at first it was inhabited by the Opici, and also by the Ausones, later on it was taken by the Sidicini, an Oscan tribe, but the Sidicini were ejected by the Cumaei, and in turn the Cumaei by the Tyrrheni. For on account of its fertility, they continue, the plain became an object of contention; and the Tyrrheni founded twelve cities in the country and named their capital city "Capua"; but on account of their luxury living they became soft, and consequently, just as they had been made to get out of the country round about the Padus, so now they had to yield this country to the Samnitae; and in turn the Samnitae were ejected by the Romans. A proof of the fruitfulness of the country is that it produces the finest grain — I mean the wheat from which groats are made, which is superior, not only to every kind of rice, but also to almost every kind of grain-food. It is reported that, in the course of one year, some of the plains are seeded twice with spelt, the third time with millet, and others still the fourth time with vegetables. And indeed it is from here that the Romans obtain their best wine, namely, the Falernian, the Statanian, and the Calenian, though already the Sorrentine wine is taking its place as a rival of the three, for recent tests show that it admits of aging. And so, in the same way, all the country round about Venafrum, which is on the border of the plains, is well-supplied with the olive.
4 The cities on the sea after Sinuessa are: Liternum, where is the tomb of Scipio, the one first to be called "Africanus"; for he spent his last days here, giving up the affairs of state, so strong was his hatred for certain persons. A river of like name flows by the city. And so, likewise, the Vulturnus has a name like that of the city which is situated beside it and which comes next in order after Sinuessa; this river flows through Venafrum and the centre of Campania. Next in order after these two cities comes Cumae, a city founded in most ancient times by people from Chalcis and Cumae; for it is the oldest of all the Sicilian and the Italiote cities. However, the men who led the expedition, Hippocles of Cumae and Megasthenes of Chalcis, made an agreement with one another that the city should be a colony of Chalcis, and a namesake of Cumae; and, hence, although the city is now called Cumae, it is reputed to have been founded by the Chalcidians alone. In earlier times, then, the city was prosperous, and so was what is called the Phlegraean Plain, which mythology has made the setting of the story of the Giants — for no other reason, it would seem, than that the land, on account of its excellence, was a thing to fight for; but later on, when the Campani became established as masters of the city, they committed numerous outrages against the people in general, and, what is more, cohabited with the wives of the citizens. Nevertheless, many traces of the Greek decorum and usages are still preserved there. But according to some, "Cumae" is named after the "Kumata"; for the neighbouring shore is surfy and exposed to the wind. And Cumae also has the best fisheries for the catching of large fish. Moreover, on this gulf there is a forest of scrub trees, extending for many stadia over a waterless and sandy tract, which they call "Silva Gallinaria." Here it was that the admirals of Sextus Pompeius assembled bands of pirates at that critical time when he caused Sicily to revolt.
5 Near Cumae is Cape Misenum, and between them is the Acherusian Lake, a kind of shoal-water estuary of the sea. After you double Cape Misenum you immediately come to a harbour, at the base of the cape, and, after the harbour, to a stretch of coast which runs inland and forms a deeply indented gulf — the coast on which is situated Baiae, and those hot springs that are suited both to the taste of the fastidious and to the cure of disease. Contiguous to Baiae is Gulf Lucrinus, and also, behind this gulf, Gulf Avernus, which forms a peninsula of the land that is cut off as far as Misenum, beginning from the transverse line which runs between Cumae and Avernus, for there remains an isthmus only a few stadia broad, that is, reckoning straight through the tunnel to Cumae itself and to the sea next to Cumae. The people prior to my time were wont to make Avernus the setting of the fabulous story of the Homeric "Necyia"; and, what is more, writers tell us that there actually was an oracle of the dead here and that Odysseus visited it. Now Gulf Avernus is deep up to the very shore and has a clear outlet; and it has both the size and character of a harbour, although it is useless as a harbour because of the fact that Gulf Lucrinus lies before it and is somewhat shallow as well as considerable in extent. Again, Avernus is enclosed round about by steep hill-brows that rise above it on all sides except where you sail into it (at the present time they have been brought by the toil of man into cultivation, though in former times they were thickly covered with a wild and untrodden forest of large trees); and these hill-brows, because of the superstition of man, used to make the gulf a shadowy place. And the natives used to add the further fable that all birds that fly over it fall down into the water, being killed by the vapours that rise from it, as in the case of all the Plutonia. And people used to suppose that this too was a Plutonian place and that the Cimmerians had actually been there. At any rate, only those who had sacrificed beforehand and propitiated the nether deities could sail into Avernus, and priests who held the locality on lease it were there to give directions in all such matters; and there is a fountain of potable water at this place, on the sea, but people used to abstain from it because they regarded it as the water of the Styx; and the oracle, too, is situated somewhere near it; and further, the hot springs near by and Lake Acherusia betokened the River Pyriphlegethon. Again, Ephorus, in the passage where he claims the locality in question for the Cimmerians, says: They live in underground houses, which they call "argillae," and it is through tunnels that they visit one another, back and forth, and also admit strangers to the oracle, which is situated far beneath the earth; and they live on what they get from mining, and from those who consult the oracle, and from the king of the country, who has appointed them fixed allowances; and those who live about the oracle have an ancestral custom, that no one should see the sun, but should go outside the caverns only during the night; and it is for this reason that the poet speaks of them as follows: "And never does the shining sun look upon them"; but later on the Cimmerians were destroyed by a certain king, because the response of the oracle did not turn out in his favour; the seat of the oracle, however, still endures, although it has been removed to another place. Such, then, are the stories the people before my time used to tell, but now that the forest round about Avernus has been cut down by Agrippa, and the tracts of land have been built up with houses, and the tunnel has been cut from Avernus to Cumae, all those stories have proven be mere myths; and yet the Cocceius who made, not only this tunnel, but also the one from Dicaearchia (near Baiae) to Neapolis, was pretty well acquainted with the story just now related about the Cimmerians, and it may very well be that he also deemed it an ancestral custom, for this region, that its roads should run through tunnels.
6 Gulf Lucrinus broadens out as far as Baiae; and it is shut off from the outer sea by a mound eight stadia in length and broad as a wagon-road. This mound is said to have been brought to completion by Heracles, when he was driving the cattle of Geryon. But since it admitted the waves over its surface in times of storm, so that it could not easily be traversed on foot, Agrippa built it up higher. The gulf affords entrance to light boats only; and, though useless as a place to moor boats, it affords most abundant catches of oysters. And some say that this gulf itself is Lake Acherusia, while Artemidorus says that Gulf Avernus itself is that lake. But Baiae is said to be named after one of the companions of Odysseus, Baius; and also Misenum. Next in order come the headlands that are in the neighbourhood of Dicaearchia, and then the city itself. In earlier times it was only a port-town of the Cumaeans, situated on the brow of a hill, but at the time of Hannibal's expedition the Romans settled a colony there, and changed its name to Puteoli from the wells there — though some say that it was from the foul smell of the waters, since the whole district, as far as Baiae and Cumae, has a foul smell, because it is full of sulphur and fire and hot waters. And some believe that it is for this reason that the Cumaean country was called "Phlegra," and that it is the wounds of the fallen giants, inflicted by the thunderbolts, that pour forth those streams of fire and water. And the city has become a very great emporium, since it has havens that have been made by the hand of man — a thing made possible by the natural qualities of the sand, for it is in proper proportion to the lime, and takes a firm set and solidity. And therefore, by mixing the sand-ash with the lime, they can run jetties out into the sea and thus make the wide-open shores curve into the form of bays, so that the greatest merchant-ships can moor therein with safety. Immediately above the city lies the Forum of Hephaestus, a plain shut in all round by exceedingly hot ridges, which in numerous places have fumaroles that are like chimneys and that have a rather noisome smell; and the plain is full of drifted sulphur.
7 After Dicaearchia comes Neapolis, a city of the Cumaeans. At a later time it was re-colonised by Chalcidians, and also by some Pithecussaeans and Athenians, and hence, for this reason, was called Neapolis. A monument of Parthenope, one of the Sirens, is pointed out in Neapolis, and in accordance with an oracle a gymnastic contest is celebrated there. But at a still later time, as the result of a dissension, they admitted some of the Campani as fellow-inhabitants, and thus they were forced to treat their worst enemies as their best friends, now that they had alienated their proper friends. This is disclosed by the names of their demarchs, for the earliest names are Greek only, whereas the later are Greek mixed with Campanian. And very many traces of Greek culture are preserved there — gymnasia, ephebeia, phratriae, and Greek names of things, although the people are Romans. And at the present time a sacred contest is celebrated among them every four years, in music as well as gymnastics; it lasts for several days, and vies with the most famous of those celebrated in Greece. Here, too, there is a tunnel — the mountain between Dicaearchia and Neapolis having been tunneled like the one leading to Cumae, and a road having been opened up for a distance of many stadia that is wide enough to allow teams going in opposite directions to pass each other. And windows have been cut out at many places, and thus the light of day is brought down from the surface of the mountain along shafts that are of considerable depth. Furthermore, Neapolis has springs of hot water and bathing-establishments that are not inferior to those at Baiae, although it is far short of Baiae in the number of people, for at Baiae, where palace on palace has been built, one after another, a new city has arisen, not inferior to Dicaearchia. And greater vogue is given to the Greek mode of life at Neapolis by the people who withdraw thither from Rome for the sake of rest — I mean the class who have made their livelihood by training the young, or still others who, because of old age or infirmity, long to live in relaxation; and some of the Romans, too, taking delight in this way of living and observing the great number of men of the same culture as themselves sojourning there, gladly fall in love with the place and make it their permanent abode.
8 Next after Neapolis comes the Heracleian Fortress, with a promontory which runs out into the sea and so admirably catches the breezes of the southwest wind that it makes the settlement a p453healthful place to live in. Both this settlement and the one next after it, Pompaia (past which flows the River Sarnus), were once held by the Osci; then, by the Tyrrheni and the Pelasgi; and after that, by the Samnitae; but they, too, were ejected from the places. Pompaia, on the River Sarnus — a river which both takes the cargoes inland and sends them out to sea — is the port-town of Nola, Nuceria, and Acherrae (a place with name like that of the settlement Cremona). Above these places lies Mt. Vesuvius, which, save for its summit, has dwellings all round, on farm-lands that are absolutely beautiful. As for the summit, a considerable part of it is flat, but all of it is unfruitful, and looks ash-coloured, and it shows pore-like cavities in masses of rock that are soot-coloured on the surface, these masses of rock looking as though they had been eaten out by fire; and hence one might infer that in earlier times this district was on fire and had craters of fire, and then, because the fuel gave out, was quenched. Perhaps, too, this is the cause of the fruitfulness of the country all round the mountain; just as at Catana, it is said, that part of the country which had been covered with ash-dust from the hot ashes carried up into the air by the fire of Aetna made the land suited to the vine; for it contains the substance that fattens both the soil which is burnt out and that which produces the fruits; so then, when it acquired plenty of fat, it was suited to burning out, as is the case with all sulphur-like substances, and then when it had been evaporated and quenched and reduced to ash-dust, it passed into a state of fruitfulness. Next after Pompaia comes Surrentum, a city of the Campani, whence the Athenaeum juts forth into the sea, which some call the Cape of the Sirenussae. There is a sanctuary of Athene, built by Odysseus, on the tip of the Cape. It is only a short voyage from here across to the island of Capreae; and after doubling the cape you come to desert, rocky isles, which are called the Sirens. On the side of the Cape toward Surrentum people show you a kind of temple, and offerings dedicated there long ago, because the people in the neighbourhood hold the place in honour. Here, then, the gulf that is called the "Crater" comes to an end, being marked off by two capes that face the south, namely, Misenum and Athenaeum. And the whole of the gulf is garnished, in part by the cities which I have just mentioned, and in part by the residences and plantations, which, since they intervene in unbroken succession, present the appearance of a single city.
9 The island of Prochyta lies off Cape Misenum, and it is a fragment broken off of Pithecussae. Pithecussae was once settled by Eretrians and also Chalcidians, who, although they had prospered there on account of the fruitfulness of the soil and on account of the gold mines, forsook the island as the result of a quarrel; later on they were also driven out of the island by earthquakes, and by eruptions of fire, sea, and hot waters; for the island has "fistulas" of this sort, and it was these that caused also the people sent thither by Hiero the tyrant of Syracuse to forsake the island and the fortress they had erected there; and then the Neapolitans came over and took possession. Hence, also, the myth according to which Typhon lies beneath this island, and when he turns his body the flames and the waters, and sometimes even small islands containing boiling water, spout forth. But what Pindar says is more plausible, since he starts with the actual phenomena; for this whole channel, beginning at the Cumaean country and extending as far as Sicily, is full of fire, and has caverns deep down in the earth that form a single whole, connecting not only with one another but also with the mainland; and therefore, not only Aetna clearly has such a character as it is reported by all to have, but also the Lipari Islands, and the districts round about Dicaearchia, Neapolis, and Baiae, and the island of Pithecussae. This, I say, is Pindar's thought when he says that Typhon lies beneath the whole region: "Now, however, both Sicily and the sea-fenced cliffs beyond Cumae press hard upon his shaggy breast." And Timaeus, also, says that many marvellous things are told by the ancients about Pithecussae, and that only shortly before his own time the hill called Epopeus, in the centre of the island, on being shaken by earthquakes, cast forth fire and shoved the part between it and the sea back to the open sea; and the part of the land that had been burned to ashes, on being lifted high into the air, crashed down again upon the island like a whirlwind; and the sea retreated for three stadia, but not long after retreating turned back and with its reverse current deluged the island; and consequently, the fire in the island was quenched, but the noise was such that the people on the mainland fled from the coast into Campania. The hot springs in the island are thought to cure those who have gall-stones. Capreae had two small towns in ancient times, though later on only one. The Neapolitans took possession of this island too; and although they lost Pithecussae in war, they got it back again, Augustus Caesar giving it to them, though he appropriated Capreae to himself personally and erected buildings on it. Such, then, are the seaboard cities of Campania and the islands that lie off it.
In the interior, take first Capua: It is the capital city — a "capital" in reality, as the etymology of its name implies, for in comparison with it all the rest might be regarded as only small towns, except Teanum Sidicinum, which is indeed a noteworthy city. It, too, lies on the Appian Way, and so do the three cities which, among the rest, lead from it to Brentesium, namely, Calatia, Caudium, and Beneventum. But Casilinum is situated towards Rome, on the River Vulturnus; it was here that five hundred and forty of the Praenestini held out against Hannibal — then at the height of his strength — for so long that, by reason of famine, a "medimnus" was sold for two hundred "drachmae," and the man who sold it died of hunger, whereas the man who bought it escaped with his life. And when Hannibal saw them sowing turnips near the wall, he wondered, and with reason, at their long-suffering — that they expected to hold out long enough for the turnips to get ripe; and in fact they all survived, it is said, except a few who perished either because of hunger or in the battles.
But in addition to the cities aforesaid, the following (to which I have adverted before) are also Campanian cities — Cales and Teanum Sidicinum, whose territories are separated by the two temples of Fortune situated on either side of the Latin Way; and so are Suessula, Atella, Nola, Nuceria, Acherrae, Abella, and other settlements (some of which are said to be Samnite) that are still smaller than these. As for the Samnitae: In earlier times they made expeditions even as far as that part of the Latin country which is about Ardea, and then, after that, ravaged Campania itself, and therefore they must have possessed considerable power (indeed, the Campani, since they were already schooled in the obedience of other despots, quickly submitted to the new commands); but now they have been completely worn out — first by others and last of all by Sulla, who became dictator of the Romans; for when, on putting down the insurrection of the Italiotes by many battles, he saw that the Samnitae, almost alone, were holding together and, in like manner as before, were on the border, ready actually to march against Rome itself, he joined battle with them before the walls; and some of them he cut down in the battle (for he had ordered that none be taken alive), while the rest, who had flung their arms (about three or four thousand men, it is said) he brought down to the Villa Publica in the Campus Martius and imprisoned; three days later, however, he let soldiers loose upon them and thus slaughtered them all; and further, he would not stop making proscriptions until either he had destroyed all Samnitae of importance or banished them from Italy. And to those who found fault with him for such excessive wrath he said he had realised from experience that not a Roman could ever live in peace so long as the Samnitae held together as a separate people. And verily their cities have now come to be mere villages (though some have utterly vanished), I mean Bovianum, Aesernia, Panna, Telesia (close to Venafrum), and others like them. No one of these deserves to be regarded as a city, but I, for my part, am thus going into detail, within due bounds, because of the glory and power of Italy. Beneventum, however, has held up very well, and so has Venusia.
Concerning the Samnitae there is another story current to this effect: The Sabini, since they had long been at war with the Ombrici, vowed (just as some of the Greeks do) to dedicate everything that was produced that year; and, on winning the victory, they partly sacrificed and partly dedicated all that was produced; then a dearth ensued, and some one said that they ought to have dedicated the babies too; this they did, and devoted to Mars all the children born that year; and these children, when grown to manhood, they sent away as colonists, and a bull led the way; and when the bull lay down to rest in the land of the Opici (who, as it chanced, were living only in villages), the Sabini ejected them and settled on the spot, and, in accordance with the utterance of their seers, slaughtered the bull as a sacrifice to Mars who had given it for a guide. It is reasonable to suppose therefore that their name "Sabelli" is a nickname derived from the name of their forefathers, while their name "Samnitae" (the Greeks say "Saunitae") is due to a different cause. Some say, moreover, that a colony of Laconians joined the Samnitae, and that for this reason the Samnitae actually became philhellenes, and that some of them were even called "Pitanatae." But it is thought that the Tarantini simply fabricated this, to flatter, and at the same time to win the friendship of, a powerful people on their borders; because, on a time, the Samnitae were wont to send forth an army of as many as eighty thousand infantry and eight thousand cavalry. And they say that among the Samnitae there is a law which is indeed honourable and conducive to noble qualities; for they are not permitted to give their daughters in marriage to whom they wish, but every year ten virgins and ten young men, the noblest of each sex, are selected, and, of these, the first choice of the virgins is given to the first choice of the young men, and the second to the second, and so on to the end; but if the young man who wins the meed of honour changes and turns out bad, they disgrace him and take away from him the woman given him. Next after the Samnitae come the Hirpini, and they too are Samnitae; they got their name from the wolf that led the way for their colony (for "hirpus" is what the Samnitae call the wolf); and their territory adjoins that of those Leucani who live in the interior. So much, then, for the Samnitae.
As for the Campani, it was their lot, because of the fertility of their country, to enjoy in equal degree both evil things and good. For they were so extravagant that they would invite gladiators, in pairs, to dinner, regulating the number by the importance of the dinners; and when, on their instant submission to Hannibal, they received his army into winter-quarters, the soldiers became so effeminate because of the pleasures afforded them that Hannibal said that, although victor, he was in danger of falling into the hands of his foes, because the soldiers he had got back were not his men, but only women. But when the Romans got the mastery, they brought them to their sense by many severe lessons, and, last of all, portioned out to Roman settlers a part of the land. Now, however, they are living in prosperity, being of one mind with the new settlers, and they preserve their old-time reputation, in respect to both the size of their city and the high quality of its men. After Campania, and the Samnite country (as far as the Frentani), on the Tyrrhenian Sea dwells the tribe of the Picentini, a small offshoot of those Picentini who dwell on the Adriatic, which has been transplanted by the Romans to the Poseidonian Gulf; this gulf is now called the Paestan Gulf; and the city of Poseidonia, which is situated in the centre of the gulf, is now called Paestus. The Sybaritae, it is true, had erected fortifications on the sea, but the settlers removed them farther inland; later on, however, the Leucani took the city away from the Sybaritae, and, in turn, the Romans took it away from the Leucani. But the city is rendered unhealthy by a river that spreads out into marshes in the neighbourhood. Between the Sirenussae and Poseidonia lies Marcina, a city founded by the Tyrrheni and now inhabited by Samnitae. From here to Pompaia, by way of Nuceria, the distance across the isthmus is not more than one hundred and twenty stadia. The country of the Picentes extends as far as the River Silaris, which separates the old Campania from this country. In regard to this river, writers report the following as a special characteristic, that although its water is potable, any plant that is let down into it turns to stone, though it keeps its colour and its shape. Picentia first belonged to the Picentes, as metropolis, but at the present time they live only in villages, having been driven away by the Romans because they had made common cause with Hannibal. And instead of doing military service, they were at that time appointed to serve the State as couriers and letter-carriers (as were also, for the same reasons, both the Leucani and the Brettii); and for the sake of keeping watch over the Picentes the Romans fortified Salernum against them, a city situated only a short distance above the sea. The distance from the Sirenussae to the Silaris is two hundred and sixty stadia. |
|
|
|
|
6 South Italy 4 74 1:50 






|
6 - 1 
1 After the mouth of the Silaris one comes to Leucania, and to the temple of the Argoan Hera, built by Jason, and near by, within fifty stadia, to Poseidonia. Thence, sailing out past the gulf, one comes to Leucosia,1 an island, from which it is only a short voyage across to the continent. The island is named after one of the Sirens, who was cast ashore here after the Sirens had flung themselves, as the myth has it, into the depths of the sea. In front of the island lies that promontory which is opposite the Sirenussae and with them forms the Poseidonian Gulf. On doubling this promontory one comes immediately to another gulf, in which there is a city which was called "Hyele" by the Phocaeans who founded it, and by others "Ele," after a certain spring, but is called by the men of to‑day "Elea." This is the native city of Parmenides and Zeno, the Pythagorean philosophers. It is my opinion that not only through the influence of these men but also in still earlier times the city was well governed; and it was because of this good government that the people not only held their own against the Leucani and the Poseidoniatae, but even returned victorious, although they were inferior to them both in extent of territory and in population. At any rate, they are compelled, on account of the poverty of their soil, to busy themselves mostly with the sea and to establish factories for the salting of fish, and other such industries. According to Antiochus, after the capture of Phocaea by Harpagus, the general of Cyrus, all the Phocaeans who could do so embarked with their entire families on their light boats and, under the leadership of Creontiades, sailed first to Cyrnus and Massalia, but when they were beaten off from those places founded Elea. Some, however, say that the city took its name from the River Elees. It is about two hundred stadia distant from Poseidonia. After Elea comes the promontory of Palinurus. Off the territory of Elea are two islands, the Oenotrides, which have anchoring-places. After Palinurus comes Pyxus — a cape, harbour, and river, for all three have the same name. Pyxus was peopled with new settlers by Micythus, the ruler of the Messene in Sicily, but all the settlers except a few sailed away again. After Pyxus comes another gulf, and also Laüs — a river and city; it is the last of the Leucanian cities, lying only a short distance above the sea, is a colony of the Sybaritae, and the distance thither from Ele is four hundred stadia. The whole voyage along the coast of Leucania is six hundred and fifty stadia. Near Laüs is the hero-temple of Draco, one of the companions of Odysseus, in regard to which the following oracle was given out to the Italiotes "Much people will one day perish about Laïan Draco." And the oracle came true, for, deceived by it, the peoples who made campaigns against Laüs, that is, the Greek inhabitants of Italy, met disaster at the hands of the Leucani.
2 These, then, are the places on the Tyrrhenian seaboard that belong to the Leucani. As for the other sea, they could not reach it at first; in fact, the Greeks who held the Gulf of Tarentum were in control there. Before the Greeks came, however, the Leucani were as yet not even in existence, and the regions were occupied by the Chones and the Oenotri. But after the Samnitae had grown considerably in power, and had ejected the Chones and the Oenotri, and had settled a colony of Leucani in this portion of Italy, while at the same time the Greeks were holding possession of both seaboards as far as the Strait, the Greeks and the barbarians carried on war with one another for a long time. Then the tyrants of Sicily, and afterwards the Carthaginians, at one time at war with the Romans for the possession of Sicily and at another for the possession of Italy itself, maltreated all the peoples in this part of the world, but especially the Greeks. Later on, beginning from the time of the Trojan war, the Greeks had taken away from the earlier inhabitants much of the interior country also, and indeed had increased in power to such an extent that they called this part of Italy, together with Sicily, Magna Graecia. But to‑day all parts of it, except Taras, Rhegium, and Neapolis, have become p9completely barbarised, and some parts have been taken and are held by the Leucani and the Brettii, and others by the Campani — that is, nominally by the Campani but in truth by the Romans, since the Campani themselves have become Romans. However, the man who busies himself with the description of the earth must needs speak, not only of the facts of the present, but also sometimes of the facts of the past, especially when they are notable. As for the Leucani, I have already spoken of those whose territory borders on the Tyrrhenian Sea, while those who hold the interior are the people who live above the Gulf of Tarentum. But the latter, and the Brettii, and the Samnitae themselves (the progenitors of these peoples) have so utterly deteriorated that it is difficult even to distinguish their several settlements; and the reason is that no common organisation longer endures in any one of the separate tribes; and their characteristic differences in language, armour, dress, and the like, have completely disappeared; and, besides, their settlements, severally and in detail, are wholly without repute.
3 Accordingly, without making distinctions between them, I shall only tell in a general way what I have learned about the peoples who live in the interior, I mean the Leucani and such of the Samnitae as are their next neighbours. Petelia, then, is regarded as the metropolis of the Chones, and has been rather populous down to the present day. It was founded by Philoctetes after he, as the result of a political quarrel, had fled from Meliboea. It has so strong a position by nature that the Samnitae once fortified it against the Thurii. And the old Crimissa, which is near the same regions, was also founded by Philoctetes. Apollodorus, in his work On Ships, in mentioning Philoctetes, says that, according to some, when Philoctetes arrived at the territory of Croton, he colonised the promontory Crimissa, and, in the interior above it, the city Chone, from which the Chonians of that district took their name, and that some of his companions whom he had sent forth with Aegestes the Trojan to the region of Eryx in Sicily fortified Aegesta. Moreover, Grumentum and Vertinae are in the interior, and so are Calasarna and some other small settlements, until we arrive at Venusia, a notable city; but I think that this city and those that follow in order after it as one goes towards Campania are Samnite cities. Beyond Thurii lies also the country that is called Tauriana. The Leucani are Samnite in race, but upon mastering the Poseidoniatae and their allies in war they took possession of their cities. At all other times, it is true, their government was democratic, but in times of war they were wont to choose a king from those who held magisterial offices. But now they are Romans.
4 The seaboard that comes next after Leucania, as far as the Sicilian Strait and for a distance of thirteen hundred and fifty stadia, is occupied by the Brettii. According to Antiochus, in his treatise On Italy, this territory (and this is the territory which he says he is describing) was once called Italy, although in earlier times it was called Oenotria. And he designates as its boundaries, first, on the Tyrrhenian Sea, the same boundary that I have assigned to the country of the Brettii — the River Laüs; and secondly, on the Sicilian Sea, Metapontium. But as for the country of the Tarantini, which borders on Metapontium, he names it as outside of Italy, and calls its inhabitants Iapyges. And at a time more remote, according to him, the names "Italians" and "Oenotrians" were applied only to the people who lived this side the isthmus in the country that slopes toward the Sicilian Strait. The isthmus itself, one hundred and sixty stadia in width, lies between two gulfs — the Hipponiate (which Antiochus has called Napetine) and the Scylletic. The coasting-voyage round the country comprised between the isthmus and the Strait is two thousand stadia. But after that, he says, the name of "Italy" and that of the "Oenotrians" was further extended as far as the territory of Metapontium and that of Seiris, for, he adds, the Chones, a well-regulated Oenotrian tribe, had taken up their abode in these regions and had called the land Chone. Now Antiochus had spoken only in a rather simple and antiquated way, without making any distinctions between the Leucani and the Brettii. In the first place, Leucania lies between the Tyrrhenian and Sicilian coast-lines, the former coast-line from the River Silaris as far as Laüs, and the latter, from Metapontium as far as Thurii; in the second place, on the mainland, from the country of the Samnitae as far as the isthmus which extends from Thurii to Cerilli (a city near Laüs), the isthmus is three hundred stadia in width. But the Brettii are situated beyond the Leucani; they live on a peninsula, but this peninsula includes another peninsula which has the isthmus that extends from Scylletium to the Hipponiate Gulf. The name of the tribe was given to it by the Leucani, for the Leucani call all revolters "brettii." The Brettii revolted, so it is said (at first they merely tended flocks for the Leucani, and then, by reason of the indulgence of their masters, began to act as free men), at the time when Dio made his expedition against Dionysius and aroused all peoples against all others. So much, then, for my general description of the Leucani and the Brettii.
5 The next city after Laüs belongs to Brettium, and is named Temesa, though the men of to‑day call it Tempsa; it was founded by the Ausones, but later on was settled also by the Aetolians under the leadership of Thoas; but the Aetolians were ejected by the Brettii, and then the Brettii were crushed by Hannibal and by the Romans. Near Temesa, and thickly shaded with wild olive trees, is the hero-temple of Polites, one of the companions of Odysseus, who was treacherously slain by the barbarians, and for that reason became so exceedingly wroth against the country that, in accordance with an oracle, the people of the neighbourhood collected tribute for him; and hence, also, the popular saying applied to those who are merciless, that they are "beset by the hero of Temesa." But when the Epizephyrian Locrians captured the city, Euthymus, the pugilist, so the story goes, entered the lists against Polites, defeated him in the fight and forced him to release the natives from the tribute. People say that Homer has in mind this Temesa, not the Tamassus in Cyprus (the name is spelled both ways), when he says "to Temesa, in quest of copper." And in fact copper mines are to be seen in the neighbourhood, although now they have been abandoned. Near Temesa is Terina, which Hannibal destroyed, because he was unable to guard it, at the time when he had taken refuge in Brettium itself. Then comes Consentia, the metropolis of the Brettii; and a little above this city is Pandosia, a strong fortress, near which Alexander the Molossian was killed. He, too, was deceived by the oracle at Dodona, which bade him be on his guard against Acheron and Pandosia; for places which bore these names were pointed out to him in Thesprotia, but he came to his end here in Brettium. Now the fortress has three summits, and the River Acheron flows past it. And there was another oracle that helped to deceive him: "Three-hilled Pandosia, much people shalt thou kill one day"; for he thought that the oracle clearly meant the destruction of the enemy, not of his own people. It is said that Pandosia was once the capital of the Oenotrian Kings. After Consentia comes Hipponium, which was founded by the Locrians. Later on, the Brettii were in possession of Hipponium, but the Romans took it away from them and changed its name to Vibo Valentia. And because the country round about Hipponium has luxuriant meadows abounding in flowers, people have believed that Core used to come hither from Sicily to gather flowers; and consequently it has become the custom among the women of Hipponium to gather flowers and to weave them into garlands, so that on festival days it is disgraceful to wear bought garlands. Hipponium has also a naval station, which was built long ago by Agathocles, the tyrant of the Siciliotes, when he made himself master of the city. Thence one sails to the Harbour of Heracles, which is the point where the headlands of Italy near the Strait begin to turn towards the west. And on this voyage one passes Medma, a city of the same Locrians aforementioned, which has the same name as a great fountain there, and possesses a naval station near by, called Emporium. Near it is also the Metaurus River, and a mooring-place bearing the same name. Off this coast lie the islands of the Liparaei, at a distance of two hundred stadia from the Strait. According to some, they are the islands of Aeolus, of whom the Poet makes mention in the Odyssey. They are seven in number and are all within view both from Sicily and from the continent near Medma. But I shall tell about them when I discuss Sicily. After the Metaurus River comes a second Metaurus. Next after this river comes Scyllaeum, a lofty rock which forms a peninsula, its isthmus being low and affording access to ships on both sides. This isthmus Anaxilaüs, the tyrant of the Rhegini, fortified against the Tyrrheni, building a naval station there, and thus deprived the pirates of their passage through the strait. For Caenys, too, is near by, being two hundred and fifty stadia distant from Medma; it is the last cape, and with the cape on the Sicilian side, Pelorias, forms the narrows of the Strait. Cape Pelorias is one of the three capes that make the island triangular, and it bends towards the summer sunrise, just as Caenys bends towards the west, each one thus turning away from the other in the opposite direction. Now the length of the narrow passage of the Strait from Caenys as far as the Poseidonium, or the Columna Rheginorum, is about six stadia, while the shortest passage across is slightly more; and the distance is one hundred stadia from the Columna to Rhegium, where the Strait begins to widen out, as one proceeds towards the east, towards the outer sea, the sea which is called the Sicilian Sea.
6 Rhegium was founded by the Chalcidians who, it is said, in accordance with an oracle, were dedicated, one man out of every ten Chalcidians, to Apollo, because of a dearth of crops, but later on emigrated hithera from Delphi, taking with them still others from their home. But according to Antiochus, the Zanclaeans sent for the Chalcidians and appointed Antimnestus their founder-in‑chief. To this colony also belonged the refugees of the Peloponnesian Messenians who had been defeated by the men of the opposing faction. These men were unwilling to be punished by the Lacedaemonians for the violation of the maidens which took place at Limnae, though they were themselves guilty of the outrage done to the maidens, who had been sent there for a religious rite, and had also killed those who came to their aid. So the refugees, after withdrawing to Macistus, sent a deputation to the oracle of the god to find fault with Apollo and Artemis if such was to be their fate in return for their trying to avenge those gods, and also to enquire how they, now utterly ruined, might be saved. Apollo bade them go forth with the Chalcidians to Rhegium, and to be grateful to his sister; for, he added, they were not ruined, but saved, inasmuch as they were surely not to perish along with their native land, which would be captured a little later by the Spartans. They obeyed; and therefore the rulers of the Rhegini down to Anaxilas were always appointed from the stock of the Messenians. According to Antiochus, the Siceli and Morgetes had in early times inhabited the whole of this region, but later on, being ejected by the Oenotrians, had crossed over into Sicily. According to some, Morgantium also took its name from the Morgetes of Rhegium. The city of Rhegium was once very powerful and had many dependencies in the neighbourhood; and it was always a fortified outpost threatening the island, not only in earlier times but also recently, in our own times, when Sextus Pompeius caused Sicily to revolt. It was named Rhegium, either, as Aeschylus says, because of the calamity that had befallen this region, for, as both he and others state, Sicily was once "rent" from the continent by earthquakes, "and so from this fact," he adds, "it is called Rhegium." They infer from the occurrences about Aetna and in other parts of Sicily, and in Lipara and in the islands about it, and also in the Pithecussae and the whole of the coast of the adjacent continent, that it is not unreasonable to suppose that the rending actually took place. Now at the present time the earth about the Strait, they say, is but seldom shaken by earthquakes, because the orifices there, through which the fire is blown up and the red-hot masses and the waters are ejected, are open. At that time, however, the fire that was smouldering beneath the earth, together with the wind, produced violent earthquakes, because the passages to the surface were all blocked up, and the regions thus heaved up yielded at last to the force of the blasts of wind, were rent asunder, and then received the sea that was on either side, both here and between the other islands in that region. And, in fact, Prochyte and the Pithecussae are fragments broken off from the continent, as also Capreae, Leucosia, the Sirenes, and the Oenotrides. Again, there are islands which have arisen from the high seas, a thing that even now happens in many places; for it is more plausible that the islands in the high seas were heaved up from the deeps, whereas it is more reasonable to think that those lying off the promontories and separated merely by a strait from the mainland have been rent therefrom. However, the question which of the two explanations is true, whether Rhegium got its name on account of this or on account of its fame (for the Samnitae might have called it by the Latin word for "royal," because their progenitors had shared in the government with the Romans and used the Latin language to a considerable extent), is open to investigation. Be this as it may, it was a famous city, and not only founded many cities but also produced many notable men, some notable for their excellence as statesmen and others for their learning; nevertheless, Dionysius demolished it, they say, on the charge that when he asked for a girl in marriage they proffered the daughter of the public executioner; but his son restored a part of the old city and called it Phoebia. Now in the time of Pyrrhus the garrison of the Campani broke the treaty and destroyed most of the inhabitants, and shortly before the Marsic war much of the settlement was laid in ruins by earthquakes; but Augustus Caesar, after ejecting Pompeius from Sicily, seeing that the city was in want of population, gave it some men from his expeditionary forces as new settlers, and it is now fairly populous.
7 As one sails from Rhegium towards the east, and at a distance of fifty stadia, one comes to Cape Leucopetra (so called from its colour), in which, it is said, the Apennine Mountain terminates. Then comes Heracleium, which is the last cape of Italy and inclines towards the south; for on doubling it one immediately sails with the southwest wind as far as Cape Iapygia, and then veers off, always more and more, towards the northwest in the direction of the Ionian Gulf. After Heracleium comes a cape belonging to Locris, which is called Zephyrium; its harbour is exposed to the winds that blow from the west, and hence the name. Then comes the city Locri Epizephyrii, a colony of the Locri who live on the Crisaean Gulf, which was led out by Evanthes only a little while after the founding of Croton and Syracuse. Ephorus is wrong in calling it a colony of the Locri Opuntii. However, they lived only three or four years at Zephyrium, and then moved the city to its present site, with the cooperation of Syracusans for at the same time the latter, among whom . . . And at Zephyrium there is a spring, called Locria, where the Locri first pitched camp. The distance from Rhegium to Locri is six hundred stadia. The city is situated on the brow of a hill called Epopis.
8 The Locri Epizephyrii are believed to have been the first people to use written laws. After they had lived under good laws for a very long time, Dionysius, on being banished from the country of the Syracusans,abused them most lawlessly of all men. For he would sneak into the bed-chambers of the girls after they had been dressed up for their wedding, and lie with them before their marriage; and he would gather together the girls who were ripe for marriage, let loose doves with cropped wings upon them in the midst of the banquets, and then bid the girls waltz around unclad, and also bid some of them, shod with sandals that were not mates (one high and the other low), chase the doves around — all for the sheer indecency of it. However, he paid the penalty after he went back to Sicily again to resume his government; for the Locri broke up his garrison, set themselves free, and thus became masters of his wife and children. These children were his two daughters, and the younger of his two sons (who was already a lad), for the other, Apollocrates, was helping his father to effect his return to Sicily by force of arms. And although Dionysius — both himself and the Tarantini on his behalf — earnestly begged the Locri to release the prisoners on any terms they wished, they would not give them up; instead, they endured a siege and a devastation of their country. But they poured out most of their wrath upon his daughters, for they first made them prostitutes and then strangled them, and then, after burning their bodies, ground up the bones and sank them in the sea. Now Ephorus, in his mention of the written legislation of the Locri which was drawn up by Zaleucus from the Cretan, the Laconian, and the Areopagite usages, says that Zaleucus was among the first to make the following innovation — that whereas before his time it had been left to the judges to determine the penalties for the several crimes, he defined them in the laws, because he held that the opinions of the judges about the same crimes would not be the same, although they ought to be the same. And Ephorus goes on to commend Zaleucus for drawing up the laws on contracts in simpler language. And he says that the Thurii, who later on wished to excel the Locri in precision, became more famous, to be sure, but morally inferior; for, he adds, it is not those who in their laws guard against all the wiles of false accusers that have good laws, but those who abide by laws that are laid down in simple language. And Plato has said as much — that where there are very many laws, there are also very many lawsuits and corrupt practices, just as where there are many physicians, there are also likely to be many diseases.
9 The Halex River, which marks the boundary between the Rhegian and the Locrian territories, passes out through a deep ravine; and a peculiar thing happens there in connection with the grasshoppers, that although those on the Locrian bank sing, the others remain mute. As for the cause of this, it is conjectured that on the latter side the region is so densely shaded that the grasshoppers, being wet with dew, cannot expand their membranes, whereas those on the sunny side have dry and horn-like membranes and therefore can easily produce their song. And people used to show in Locri a statue of Eunomus, the cithara-bard, with a locust seated on the cithara. Timaeus says that Eunomus and Ariston of Rhegium were once contesting with each other at the Pythian games and fell to quarrelling about the casting of the lots; so Ariston begged the Delphians to cooperate with him, for the reason that his ancestors belonged to the god and that the colony had been sent forth from there; and although Eunomus said that the Rhegini had absolutely no right even to participate in the vocal contests, since in their country even the grasshoppers, the sweetest-voiced of all creatures, were mute, Ariston was none the less held in favour and hoped for the victory; and yet Eunomus gained the victory and set up the aforesaid image in his native land, because during the contest, when one of the chords broke, a grasshopper lit on his cithara and supplied the missing sound. The interior above these cities is held by the Brettii; here is the city Mamertium, and also the forest that produces the best pitch, the Brettian. This forest is called Sila, is both well wooded and well watered, and is seven hundred stadia in length.
After Locri comes the Sagra, a river which has a feminine name. On its banks are the altars of the Dioscuri, near which ten thousand Locri, with Rhegini, clashed with one hundred and thirty thousand Crotoniates and gained the victory — an occurrence which gave rise, it is said, to the proverb we use with incredulous people, "Truer than the result at Sagra." And some have gone on to add the fable that the news of the result was reported on the same day to the people at the Olympia when the games were in progress, and that the speed with which the news had come was afterwards verified. This misfortune of the Crotoniates is said to be the reason why their city did not endure much longer, so great was the multitude of men who fell in the battle. After the Sagra comes a city founded by the Achaeans, Caulonia, formerly called Aulonia, because of the glen which lies in front of it. It is deserted, however, for those who held it were driven out by the barbarians to Sicily and founded the Caulonia there. After this city comes Scylletium, a colony of the Athenians who were with Menestheus (and now called Scylacium). Though the Crotoniates held it, Dionysius included it within the boundaries of the Locri. The Scylletic Gulf, which, with the Hipponiate Gulf forms the aforementioned isthmus, is named after the city. Dionysius undertook also to build a wall across the isthmus when he made war upon the Leucani, on the pretext, indeed, that it would afford security to the people inside the isthmus from the barbarians outside, but in truth because he wished to break the alliance which the Greeks had with one another, and thus command with impunity the people inside; but the people outside came in and prevented the undertaking.
After Scylletium comes the territory of the Crotoniates, and three capes of the Iapyges; and after these, the Lacinium, a temple of Hera, which at one time was rich and full of dedicated offerings. As for the distances by sea, writers give them without satisfactory clearness, except that, in a general way, Polybius gives the distance from the strait to Lacinium as two thousand three hundred stadia, and the distance thence across to Cape Iapygia as seven hundred. This point is called the mouth of the Tarantine Gulf. As for the gulf itself, the distance around it by sea is of considerable length, two hundred and forty miles, as the Chorographer says, but Artemidorus says three hundred and eighty for a man well-girded, although he falls short of the real breadth of the mouth of the gulf by as much. The gulf faces the winter-sunrise; and it begins at Cape Lacinium, for, on doubling it, one immediately comes to the cities of the Achaeans, which, except that of the Tarantini, no longer exist, and yet, because of the fame of some of them, are worthy of rather extended mention.
The first city is Croton, within one hundred and fifty stadia from the Lacinium; and then comes the River Aesarus, and a harbour, and another river, the Neaethus. The Neaethus got its name, it is said, from what occurred there: Certain of the Achaeans who had strayed from the Trojan fleet put in there and disembarked for an inspection of the region, and when the Trojan women who were sailing with them learned that the boats were empty of men, they set fire to the boats, for they were weary of the voyage, so that the men remained there of necessity, although they at the same time noticed that the soil was very fertile. And immediately several other groups, on the strength of their racial kinship, came and imitated them, and thus arose many settlements, most of which took their names from the Trojans; and also a river, the Neaethus, took its appellation from the aforementioned occurrence. According to Antiochus, when the god told the Achaeans to found Croton, Myscellus departed to inspect the place, but when he saw that Sybaris was already founded — having the same name as the river near by — he judged that Sybaris was better; at all events, he questioned the god again when he returned whether it would be better to found this instead of Croton, and the god replied to him (Myscelluswas a hunchback as it happened): "Myscellus, short of back, in searching else outside thy track, thou hunt'st for morsels only; 'tis right that what one giveth thee thou do approve;"and Myscellus came back and founded Croton, having as an associate Archias, the founder of Syracuse, who happened to sail up while on his way to found Syracuse. The Iapyges used to live at Croton in earlier times, as Ephorus says. And the city is reputed to have cultivated warfare and athletics; at any rate, in one Olympian festival the seven men who took the lead over all others in the stadium-race were all Crotoniates, and therefore the saying "The last of the Crotoniates was the first among all other Greeks" seems reasonable. And this, it is said, is what gave rise to the other proverb, "more healthful than Croton," the belief being that the place contains something that tends to health and bodily vigour, to judge by the multitude of its athletes. Accordingly, it had a very large number of Olympic victors, although it did not remain inhabited a long time, on account of the ruinous loss of its citizens who fell in such great numbers at the River Sagra. And its fame was increased by the large number of its Pythagorean philosophers, and by Milo, who was the most illustrious of athletes, and also a companion of Pythagoras, who spent a long time in the city. It is said that once, at the common mess of the philosophers, when a pillar began to give way, Milo slipped in under the burden and saved them all, and then drew himself from under it and escaped. And it is probably because he relied upon this same strength that he brought on himself the end of his life as reported by some writers; at any rate, the story is told that once, when he was travelling through a deep forest, he strayed rather far from the road, and then, on finding a large log cleft with wedges, thrust his hands and feet at the same time into the cleft and strained to split the log completely asunder; but he was only strong enough to make the wedges fall out, whereupon the two parts of the log instantly snapped together; and caught in such a trap as that, he became food for wild beasts.
Next in order, at a distance of two hundred stadia, comes Sybaris, founded by the Achaeans; it is between two rivers, the Crathis and the Sybaris. Its founder was Is of Helice. In early times this city was so superior in its good fortune that it ruled over four tribes in the neighbourhood, had twenty-five subject cities, made the campaign against the Crotoniates with three hundred thousand men, and its inhabitants on the Crathis alone completely filled up a circuit of fifty stadia. However, by reason of luxury and insolence they were deprived of all their felicity by the Crotoniates within seventy days; for on taking the city these conducted the river over it and submerged it. Later on, the survivors, only a few, came together and were making it their home again, but in time these too were destroyed by Athenians and other Greeks, who, although they came there to live with them, conceived such a contempt for them that they not only slew them but removed the city to another place near by and named it Thurii, after a spring of that name. Now the Sybaris River makes the horses that drink from it timid, and therefore all herds are kept away from it; whereas the Crathis makes the hair of persons who bathe in it yellow or white, and besides it cures many afflictions. Now after the Thurii had prospered for a long time, they were enslaved by the Leucani, and when they were taken away from the Leucani by the Tarantini, they took refuge in Rome, and the Romans sent colonists to supplement them, since their population was reduced, and changed the name of the city to Copiae.
After Thurii comes Lagaria, a stronghold, bounded by Epeius and the Phocaeans; thence comes the Lagaritan wine, which is sweet, mild, and extremely well thought of among physicians. That of Thurii, too, is one of the famous wines. Then comes the city Heracleia, a short distance above the sea; and two navigable rivers, the Aciris and the Siris. On the Siris there used to be a Trojan city of the same name, but in time, when Heracleia was colonised thence by the Tarantini, it became the port of the Heracleotes. It is twenty-four stadia distant from Heracleia and about three hundred and thirty from Thurii. Writers produce as proof of its settlement by the Trojans the wooden image of the Trojan Athene which is set up there — the image that closed its eyes, the fable goes, when the suppliants were dragged away by the Ionians who captured the city; for these Ionians came there as colonists when in flight from the dominion of the Lydians, and by force took the city, which belonged to the Chones, and called it Polieium; and the image even now can be seen closing its eyes. It is a bold thing, to be sure, to tell such a fable and to say that the image not only closed its eyes (just as they say the image in Troy turned away at the time Cassandra was violated) but can also be seen closing its eyes; and yet it is much bolder to represent as brought from Troy all those images which the historians say were brought from there; for not only in the territory of Siris, but also at Rome, at Lavinium, and at Luceria, Athene is called "Trojan Athena," as though brought from Troy. And further, the daring deed of the Trojan women is current in numerous places, and appears incredible, although it is possible. According to some, however, both Siris and the Sybaris which is on the Teuthras were founded by the Rhodians. According to Antiochus, when the Tarantini were at war with the Thurii and their general Cleandridas, an exile from Lacedaemon, for the possession of the territory of Siris, they made a compromise and peopled Siris jointly, although it was adjudged the colony of the Tarantini; but later on it was called Heracleia, its site as well as its name being changed.
Next in order comes Metapontium, which is one hundred and forty stadia from the naval station of Heracleia. It is said to have been founded by the Pylians who sailed from Troy with Nestor; and they so prospered from farming, it is said, that they dedicated a golden harvest at Delphi. And writers produce as a sign of its having been founded by the Pylians the sacrifice to the shades of the sons of Neleus. However, the city was wiped out by the Samnitae. According to Antiochus: Certain of the Achaeans were sent for by the Achaeans in Sybaris and resettled the place, then forsaken, but they were summoned only because of a hatred which the Achaeans who had been banished from Laconia had for the Tarantini, in order that the neighbouring Tarantini might not pounce upon the place; there were two cities, but since, of the two, Metapontium was nearer to Taras, the new-comers were persuaded by the Sybarites to take Metapontium and hold it, for, if they held this, they would also hold the territory of Siris, whereas, if they turned to the territory of Siris, they would add Metapontium to the territory of the Tarantini, which latter was on the very flank of Metapontium; and when, later on, the Metapontians were at war with the Tarantini and the Oenotrians of the interior, a reconciliation was effected in regard to a portion of the land — that portion, indeed, which marked the boundary between the Italy of that time and Iapygia. Here, too, the fabulous accounts place Metapontus, and also Melanippe the prisoner and her son Boeotus. In the opinion of Antiochus, the city Metapontium was first called Metabum and later on its name was slightly altered, and further, Melanippe was brought, not to Metabus, but to Dius, as is proved by a hero-temple of Metabus, and also by Asius the poet, when he says that Boeotus was brought forth "in the halls of Dius by shapely Melanippe," meaning that Melanippe was brought to Dius, not to Metabus. But, as Ephorus says, the coloniser of Metapontium was Daulius, the tyrant of the Crisa which is near Delphi. And there is this further account, that the man who was sent by the Achaeans to help colonise it was Leucippus, and that after procuring the use of the place from the Tarantini for only a day and night he would not give it back, replying by day to those who asked it back that he had asked and taken it for the next night also, and by night that he had taken and asked it also for the next day.
Next in order comes Taras and Iapygia; but before discussing them I shall, in accordance with my original purpose, give a general description of the islands that lie in front of Italy; for as from time to time I have named also the islands which neighbour upon the several tribes, so now, since I have traversed Oenotria from beginning to end, which alone the people of earlier times called Italy, it is right that I should preserve the same order in traversing Sicily and the islands round about it. |
|
|





|

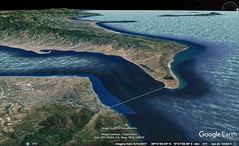


|
6 - 2 Sicily 
Sicily is triangular in shape; and for this reason it was at first called "Trinacria," though later the name was changed to the more euphonious "Thrinacis." Its shape is defined by three capes: Pelorias, which with Caenys and Columna Rheginorum forms the strait, and Pachynus, which lies out towards the east and is washed by the Sicilian Sea, thus facing towards the Peloponnesus and the sea-passage to Crete, and, third, Lilybaeum, the cape that is next to Libya, thus facing at the same time towards Libya and the winter sunset. As for the sides which are marked off by the three capes, two of them are moderately concave, 266whereas the third, the one that reaches from Lilybaeum to Pelorias, is convex; and this last is the longest, being one thousand seven hundred stadia in length, as Poseidonius states, though he adds twenty stadia more. Of the other two sides, the one from Lilybaeum to Pachynus is longer than the other, and the one next to the strait and Italy, from Pelorias to Pachynus, is shortest, being about one thousand one hundred and thirty stadia long. And the distance round the island by sea, as declared by Poseidonius, is four thousand stadia. But in the Chorography the distances given are longer, marked off in sections and given in miles: from Pelorias to Mylae, twenty-five miles; the same from Mylae to Tyndaris; then to Agathyrnum thirty, and the same to Alaesa, and again the same to Cephaloedium, these being small towns; and eighteen to the River Himera, which flows through the middle of Sicily; then to Panormus thirty-five, and thirty-two to the Emporium of the Aegestes, and the rest of the way, to Lilybaeum, thirty-eight. Thence, on doubling Lilybaeum, to the adjacent side, to the Heracleium seventy-five miles, and to the Emporium of the Acragantini twenty, and another twenty to Camarina; and then to Pachynus fifty. Thence again along the third side: to Syracuse thirty-six, and to Catana sixty; then to Tauromenium thirty-three; and then to Messene thirty. On foot, however, the distance from Pachynus to Pelorias is one hundred and sixty-eight miles, and from Messene to Lilybaeum by the Valerian Way two hundred and thirty-five. But some writers have spoken in a more general way, as, for example, Ephorus: "At any rate, the voyage round the island takes five days and nights." Further, Poseidonius, in marking off the boundaries of the island by means of the "climata," puts Pelorias towards the north, Lilybaeum towards the south, and Pachynus towards the east. But since the "climata" are each divided off into parallelograms, necessarily the triangles that are inscribed (particularly those which are scalene and of which no side fits on any one of the sides of the parallelogram) cannot, because of their slant, be fitted to the "climata." However this may be, one p61might fairly say, in the case of the "climata" of Sicily, which is situated south of Italy, that Pelorias is the most northerly of the three corners; and therefore the side that joins Pelorias to Pachynus will lie out towards the east, thus facing towards the north, and also will form the side that is on the strait. But this side must take a slight turn toward the winter sunrise, for the shore bends aside in this direction as one proceeds from Catana to Syracuse and Pachynus. Now the distance from Pachynus across to the mouth of the Alpheiusis four thousand stadia; but when Artemidorus says that it is four thousand six hundred stadia from Pachynus to Taenarum and one thousand one hundred and thirty from the Alpheius to the Pamisus, he seems to me to afford us reason for suspecting that his statement is not in agreement with that of the man who says that the distance to the Alpheius from Pachynus is four thousand stadia. Again, the side that extends from Pachynus to Lilybaeum, which is considerably farther west than Pelorias, should itself also be made to slant considerably from its southernmost point towards the west, and should face at the same time towards the east and towards the south, one part being washed by the Sicilian Sea and the other by the Libyan Sea that reaches from Carthaginia to the Syrtes. The shortest passage from Lilybaeum across to Libya in the neighbourhood of Carthage is one thousand five hundred stadia; and on this passage, it is said, some man of sharp vision, from a look-out, used to report to the men in Lilybaeum the number of ships that were putting to sea from Carthage. Again, the side that extends from Lilybaeum to Pelorias necessarily slants towards the east, and faces towards the region that is between the west and the north, having Italy on the north and on the west the Tyrrhenian Sea and the Islands of Aeolus.
2 The cities along the side that forms the Strait are, first, Messene, and then Tauromenium, Catana, and Syracuse; but those that were between Catana and Syracuse have disappeared — Naxusand Megara; and on this coast are the outlets of the Symaethus and all rivers that flow down from Aetna and have good harbours at their mouths; and here too is the promontory of Xiphonia. According to Ephorus these were the earliest Greek cities to be founded in Sicily, that is, in the tenth generation after the Trojan war; for before that time men were so afraid of the bands of Tyrrhenian pirates and the savagery of the barbarians in this region that they would not so much as sail thither for trafficking; but though Theocles, the Athenian, borne out of his course by the winds to Sicily, clearly perceived both the weakness of the peoples and the excellence of the soil, yet, when he went back, he could not persuade the Athenians, and hence took as partners a considerable number of Euboean Chalcidians and some Ionians and also some Dorians (most of whom were Megarians) and made the voyage; so the Chalcidians founded Naxus, whereas the Dorians founded Megara, which in earlier times had been called Hybla. The cities no longer exist, it is true, but the name of Hybla still endures, because of the excellence of the Hyblaean honey.
3 As for the cities that still endure along the aforementioned side: Messene is situated in a gulf of Pelorias, which bends considerably towards the east and forms an armpit, so to speak; but though the distance across to Messene from Rhegium is only sixty stadia, it is much less from Columna. Messene was founded by the Messenians of the Peloponnesus, who named it after themselves, changing its name; for formerly it was called Zancle, on account of the crookedness of the coast (anything crooked was called "zanclion"), having been founded formerly by the Naxians who lived near Catana. But the Mamertini, a tribe of the Campani, joined the colony later on. Now the Romans used it as a base of operations for their Sicilian war against the Carthaginians; and afterwards Pompeius Sextus, when at war with Augustus Caesar, kept his fleet together there, and when ejected from the island also made his escape thence. And in the ship-channel, only a short distance off the city, is to be seen Charybdis, a monstrous deep, into which the ships are easily drawn by the refluent currents of the strait and plunged prow-foremost along with a mighty eddying of the whirlpool; and when the ships are gulped down and broken to pieces, the wreckage is swept along to the Tauromenian shore, which, from this occurrence, is called Copria. The Mamertini prevailed to such an extent among the Messenii that they got control of the city; and the people are by all called Mamertini rather than Messenii; and further, since the country is exceedingly productive of wine, the wine is called, not Messenian, but Mamertine, and it rivals the best of the Italian wines. The city is fairly populous, though Catana is still more so, and in fact has received Romans as inhabitants; but Tauromenium is less populous than either. Catana, moreover, was founded by the same Naxians, whereas Tauromenium was founded by the Zanclaeans of Hybla; but Catana lost its original inhabitants when Hiero, tyrant of Syracuse, established a different set of colonists there and called it Aetna instead of Catana. And Pindar too calls him the founder of Aetna when he says: "Attend to what I say to thee, O Father, whose name is that of the holy sacrifices, founder of Aetna." But at the death of Hiero the Catanaeans came back, ejected the inhabitants, and demolished the tomb of the tyrant.And the Aetnaeans, on withdrawing, took up their abode in a hilly district of Aetna called Innesa, and called the place, which is eighty stadia from Catana, Aetna, and declared Hiero its founder. Now the city of Aetna is situated in the interior about over Catana, and shares most in the devastation caused by the action of the craters; in fact the streams of lava rush down very nearly as far as the territory of Catana; and here is the scene of the act of filial piety, so often recounted, of Amphinomus and Anapias, who lifted their parents on their shoulders and saved them from the doom that was rushing upon them. According to Poseidonius, when the mountain is in action, the fields of the Catanaeans are covered with ash-dust to a great depth. Now although the ash is an affliction at the time, it benefits the country in later times, for it renders it fertile and suited to the vine, the rest of the country not being equally productive of good wine; further, the roots produced by the fields that have been covered with ash-dust make the sheep so fat, it is said, that they choke; and this is why blood is drawn from their ears every four or five days — a thing of which I have spoken before as occurring near Erytheia. But when the lava changes to a solid, it turns the surface of the earth into stone to a considerable depth, so that quarrying is necessary on the part of any who wish to uncover the original surface; for when the mass of rock in the craters melts and then is thrown up, the liquid that is poured out over the top is black mud and flows down the mountain, and then, solidifying, becomes millstone, keeping the same colour it had when in a liquid state. And ash is also produced when the stones are burnt, as from wood; therefore, just as wood-ashes nourish rue, so the ashes of Aetna, it is reasonable to suppose, have some quality that is peculiarly suited to the vine.
4 Syracuse was founded by Archias, who sailed from Corinth about the same time that Naxus and Megara were colonised. It is said that Archias went to Delphi at the same time as Myscellus, and when they were consulting the oracle, the god asked them whether they chose wealth or health; now Archias chose wealth, and Myscellus health; accordingly, the god granted to the former to found Syracuse, and to the latter Croton. And it actually came to pass that the Crotoniates took up their abode in a city that was exceedingly healthful, as I have related, and that Syracuse fell into such exceptional wealth that the name of the Syracusans was spread abroad in a proverb applied to the excessively extravagant — "the tithe of the Syracusans would not be sufficient for them." And when Archias, the story continues, was on his voyage to Sicily, he left Chersicrates, of the race of the Heracleidae, with a part of the expedition to help colonise what is now called Corcyra, but was formerly called Scheria; Chersicrates, however, ejected the Liburnians, who held possession of the island, and colonised it with new settlers, whereas Archias landed at Zephyrium, found that some Dorians who had quit the company of the founders of Megara and were on their way back home had arrived there from Sicily, took them up and in common with them founded Syracuse. And the city grew, both on account of the fertility of the soil and on account of the natural excellence of its harbours. Furthermore, the men of Syracuse proved to have the gift of leadership, with the result that when the Syracusans were ruled by tyrants they lorded it over the rest, and when set free themselves they set free those who were oppressed by the barbarians. As for these barbarians, some were native inhabitants, whereas others came over from the mainland. The Greeks would permit none of them to lay hold of the seaboard, but were not strong enough to keep them altogether away from the interior; indeed, to this day the Siceli, the Sicani, the Morgetes, and certain others have continued to live in the island, among whom there used to be Iberians, who, according to Ephorus, were said to be the first barbarian settlers of Sicily. Morgantium, it is reasonable to suppose, was settled by the Morgetes; it used to be a city, but now it does not exist. When the Carthaginians came over they did not cease to abuse both these people and the Greeks, but the Syracusans nevertheless held out. But the Romans later on ejected the Carthaginians and took Syracuse by siege. And in our own time, because Pompeius abused, not only the other cities, but Syracuse in particular, Augustus Caesar sent a colony and restored a considerable part of the old settlement; for in olden times it was a city of five towns, with a wall of one hundred and eighty stadia. Now it was not at all necessary to fill out the whole of this circuit, but it was necessary, he thought, to build up in a better way only the part that was settled — the part adjacent to the Island of Ortygia which had a sufficient circuit to make a notable city. Ortygia is connected with the mainland, near which it lies, by a bridge, and has the fountain of Arethusa, which sends forth a river that empties immediately into the sea.
People tell the mythical story that the river Arethusa is the Alpheius, which latter, they say, rises in the Peloponnesus, flows underground through the sea as far as Arethusa, and then empties thence once more into the sea. And the kind of evidence they adduce is as follows: a certain cup, they think, was thrown out into the river at Olympia and was discharged into the fountain; and again, the fountain was discoloured as the result of the sacrifices of oxen at Olympia. Pindar follows these reports when he says: "O resting-place august of Alpheius, Ortygia, scion of famous Syracuse." And in agreement with Pindar Timaeus the historian also declares the same thing. Now if the Alpheius fell into a pit before joining the sea, there would be some plausibility in the view that the stream extends underground from Olympia as far as Sicily, thereby preserving its potable water unmixed with the sea; but since the mouth of the river empties into the sea in full view, and since near this mouth, on the transit, there is no mouth visible that swallows up the stream of the river (though even so the water could not remain fresh; yet it might, the greater part of it at least, if it sank into the underground channel), the thing is absolutely impossible. For the water of Arethusa bears testimony against it, since it is potable; and that the stream of the river should hold together through so long a transit without being diffused with the sea-water, that is, until it falls into the fancied underground passage, is utterly mythical. Indeed, we can scarcely believe this in the case of the Rhodanus, although its stream does hold together when it passes through a lake, keeping its course visible; in this case, however, the distance is short and the lake does not rise in waves, whereas in case of the sea in question, where there are prodigious storms and surging waves, the tale is foreign to all plausibility. And the citing of the story of the cup only magnifies the falsehood, for a cup does not of itself readily follow the current of any stream, to say nothing of a stream that flows so great a distance and through such passages.
Now there are many rivers in many parts of the world that flow underground, but not for such a distance; and even if this is possible, the stories aforesaid, at least, are impossible, and those concerning the river Inachus are like a myth: "For it flows from the heights of Pindus," says Sophocles, "and from Lacmus, from the land of the Perrhaebians, into the lands of the Amphilochians and Acarnanians, and mingles with the waters of Acheloüs," and, a little below, he adds, "whence it cleaves the waves to Argos and comes to the people of Lyrceium." Marvellous tales of this sort are stretched still further by those who make the Inopus cross over from the Nile to Delos. And Zoïlus the rhetorician says in his Eulogy of the Tenedians that the Alpheius rises in Tenedos — the man who finds fault with Homer as a writer of myths! And Ibycus says that the Asopus in Sicyon rises in Phrygia. But the statement of Hecataeus is better, when he says that the Inachus among the Amphilochians, which flows from Lacmus, as does also the Aeas, is different from the river of Argos, and that it was named by Amphilochus, the man who called the city Argos Amphilochicum. Now Hecataeus says that this river does empty into the Acheloüs, but that the Aeas flows towards the west into Apollonia.
On either side of the island of Ortygia is a large harbour; the larger of the two is eighty stadia in circuit. Caesar restored this city and also Catana; and so, in the same way, Centoripa, because it contributed much to the overthrow of Pompeius. p81Centoripa lies above Catana, bordering on the Aetnaean mountains, and on the Symaethus River, which flows into the territory of Catana.
5 Of the remaining sides of Sicily, that which extends from Pachynus to Lilybaeum has been utterly deserted, although it preserves traces of the old settlements, among which was Camarina, a colony of the Syracusans; Acragas, however, which belongs to the Geloans, and its seaport, and also Lilybaeum still endure. For since this region was most exposed to attack on the part of Carthaginia, most of it was ruined by the long wars that arose one after another. The last and longest side is not populous either, but still it is fairly well peopled; in fact, Alaesa, Tyndaris, the Emporium of the Aegestes, and Cephaloedis are all cities, and Panormus has also a Roman settlement. Aegestaea was founded, it is said, by those who crossed over with Philoctetes to the territory of Croton, as I have stated in my account of Italy; they were sent to Sicily by him along with Aegestes the Trojan.
6 In the interior is Enna, where is the temple of Demeter, with only a few inhabitants; it is situated on a hill, and is wholly surrounded by broad plateaus that are tillable. It suffered most at the hands of Eunus and his runaway slaves, who were besieged there and only with difficulty were dislodged by the Romans. The inhabitants of Catana and Tauromenium and also several other peoples suffered this same fate.
Eryx, a lofty hill, is also inhabited. It has a temple of Aphrodite that is held in exceptional honour, and in early times was full of female temple-slaves, who had been dedicated in fulfillment of vows not only by the people of Sicily but also by many people from abroad; but at the present time, just as the settlement itself, so the temple is in want of men, and the multitude of temple-slaves has disappeared. In Rome, also, there is a reproduction of this goddess, I mean the temple before the Colline Gate which is called that of Venus Erycina and is remarkable for its shrine and surrounding colonnade.
But the rest of the settlements as well as most of the interior have come into the possession of shepherds; for I do not know of any settled population still living in either Himera, or Gela, or Callipolis or Selinus or Euboea or several other places. Of these cities Himera was founded by the Zanclaeans of Mylae, Callipolis by the Naxians, Selinus by the Megarians of the Sicilian Megara, and Euboea by the Leontines. Many of the barbarian cities, also, have been wiped out; for example Camici, the royal residence of Cocalus, at which Minos is said to have been murdered by treachery. The Romans, therefore, taking notice that the country was deserted, took possession of the mountains and most of the plains and then gave them over to horseherds, cowherds, and shepherds; and by these herdsmen the island was many times put in great danger, because, although at first they only turned to brigandage in a sporadic way, later they both assembled in great numbers and plundered the settlements, as, for example, when Eunus and his men took possession of Enna. And recently, in my own time, a certain Selurus, called the "son of Aetna," was sent up to Rome because he had put himself at the head of an army and for a long time had overrun the regions round about Aetna with frequent raids; I saw him torn to pieces by wild beasts at an appointed combat of gladiators in the Forum; for he was placed on a lofty scaffold, as though on Aetna, and the scaffold was made suddenly to break up and collapse, and he himself was carried down with it into cages of wild-beasts — fragile cages that had been prepared beneath the scaffold for that purpose.
7 As for the fertility of the country, why should I speak of it, since it is on the lips of all men, who declare that it is no whit inferior to that of Italy? And in the matter of grain, honey, saffron, and certain other products, one might call it even superior. There is, furthermore, its propinquity; for the island is a part of Italy, as it were, and readily and without great labour supplies Rome with everything it has, as though from the fields of Italy. And in fact it is called the storehouse of Rome, for everything it produces is brought hither except a few things that are consumed at home, and not the fruits only, but also cattle, hides, wool, and the like. Poseidonius says that Syracuse and Eryx are each situated like an acropolis by the sea, whereas Enna lies midway between the two above the encircling plains.
The whole of the territory of Leontini, also, which likewise belonged to the Naxians of Sicily, has been devastated; for although they always shared with the Syracusans in their misfortunes, it was not always so with their good fortunes.
8 Near Centoripa is the town of Aetna, which was mentioned a little above, whose people entertain and conduct those who ascend the mountain; for the mountain-summit begins here. The upper districts are bare and ash-like and full of snow during the winter, whereas the lower are divided up by forests and plantations of every sort. The topmost parts of the mountain appear to undergo many changes because of the way the fire distributes itself, for at one time the fire concentrates in one crater, but at another time divides, while at one time the mountain sends forth lava, at another, flames and fiery smoke, and at still other times it also emits red-hot masses; and the inevitable result of these disturbances is that not only the underground passages, but also the orifices, sometimes rather numerous, which appear on the surface of the mountain all round, undergo changes at the same time. Be this as it may, those who recently made the ascent gave me the following account: They found at the top a level plain, about twenty stadia in circuit, enclosed by a rim of ashes the height of a house-wall, so that any who wished to proceed into the plain had to leap down from the wall; they saw in the centre of the plain a mound of the colour of ashes, in this respect being like the surface of the plain as seen from above, and above the mound a perpendicular cloud rising straight up to a height of about two hundred feet, motionless (for it was a windless day) and resembling smoke; and two of the men had the hardihood to proceed into the plain, but because the sand they were walking on got hotter and deeper, they turned back, and so were unable to tell those who were observing from a distance anything more than what was already apparent. But they believed, from such a view as they had, that many of the current stories are mythical, and particularly those which some tell about Empedocles, that he leaped down into the crater and left behind, as a trace of the fate he suffered, one of the brazen sandals which he wore; for it was found, they say, a short distance outside the rim of the crater, as though it had been thrown up by the force of the fire. Indeed, the place is neither to be approached nor to be seen, according to my informants; and further, they surmised that nothing could be thrown down into it either, owing to the contrary blasts of the winds arising from the p91depths, and also owing to the heat, which, it is reasonable to suppose, meets one long before one comes near the mouth of the crater; but even if something should be thrown down into it, it would be destroyed before it could be thrown up in anything like the shape it had when first received; and although it is not unreasonable to assume that at times the blasts of the fire die down when at times the fuel is deficient, yet surely this would not last long enough to make possible the approach of man against so great a force. Aetna dominates more especially the seaboard in the region of the Strait and the territory of Catana, but also that in the region of the Tyrrhenian Sea and the Liparaean Islands. Now although by night a brilliant light shines from the summit, by day it is covered with smoke and haze.
9 Over against Aetna rise the Nebrodes Mountains, which, though lower than Aetna, exceed it considerably in breadth. The whole island is hollow down beneath the ground, and full of streams and of fire, as is the case with the Tyrrhenian Sea, as far as the Cumaean country, as I have said before. At all events, the island has at many places springs of hot waters which spout up, of which those of Selinus and those of Himera are brackish, whereas those of Aegesta are potable. Near Acragas are lakes which, though they have the taste of sea-water, are different in nature; for even people who cannot swim do not sink, but float on the surface like wood. The territory of the Palici has craters that spout up water in a dome-like jet and receive it back again into the same recess. The cavern near Mataurus contains an immense gallery through which a river flows invisible for a considerable distance, and then emerges to the surface, as is the case with the Orontes in Syria, which sinks into the chasm (called Charybdis) between Apameia and Antiocheia and rises again forty stadia away. Similar, too, are the cases both of the Tigris in Mesopotamia and of the Nile in Libya, only a short distance from their sources. And the water in the territory of Stymphalus first flows underground for two hundred stadia and then issues forth in Argeia as the Erasinus River; and again, the water near the Arcadian Asea is first forced below the surface and then, much later, emerges as both the Eurotas and the Alpheius; and hence the belief in a certain fabulous utterance, that if two wreaths be dedicated separately to each of the two rivers and thrown into the common stream, each will reappear, in accordance with the dedication, in the appropriate river. And I have already mentioned what is told about the Timavus River.
Phenomena akin both to these and to those in Sicily are to be seen about the Liparaean Islands and Lipara itself. The islands are seven in number, but the largest is Lipara (a colony of the Cnidians), which, Thermessa excepted, lies nearest to Sicily. It was formerly called Meligunis; and it not only commanded a fleet, but for a long time resisted the incursions of the Tyrrheni, for it held in obedience all the Liparaean Islands, as they are now called, though by some they are called the Islands of Aeolus. Furthermore, it often adorned the temple of Apollo at Delphi with dedications from the first fruits of victory. It has also a fruitful soil, and a mine of styptic earth that brings in revenues, and hot springs, and fire blasts. Between Lipara and Sicily is Thermessa, which is now called Hiera of Hephaestus; the whole island is rocky, desert, and fiery, and it has three fire blasts, rising from three openings which one might call craters. From the largest the flames carry up also red-hot masses, which have already choked up a considerable part of the Strait. From observation it has been believed that the flames, both here and on Aetna, are stimulated along with the winds and that when the winds cease the flames cease too. And this is not unreasonable, for the winds are begotten by the evaporations of the sea and after they have taken their beginning are fed thereby; and therefore it is not permissible for any who have any sort of insight into such matters to marvel if the fire too is kindled by a cognate fuel or disturbance. According to Polybius, one of the three craters has partially fallen in, whereas the others remain whole; and the largest has a circular rim five stadia in circuit, but it gradually contracts to a diameter of fifty feet; and the altitude of this crater above the level of the sea is a stadium, so that the crater is visible on windless days. But if all this is to be believed, perhaps one should also believe the mythical story about Empedocles. Now if the south wind is about to blow, Polybius continues, a cloud-like mist pours down all round the island, so that not even Sicily is visible in the distance; and when the north wind is about to blow, pure flames rise aloft from the aforesaid crater and louder rumblings are sent forth; but the west wind holds a middle position, so to speak, between the two; but though the two other craters are like the first in kind, they fall short in the violence of their spoutings; accordingly, both the difference in the rumblings, and the place whence the spoutings and the flames and the fiery smoke begin, signify beforehand the wind that is going to blow again three days afterward; at all events, certain of the men in Liparae, when the weather made sailing impossible, predicted, he says, the wind that was to blow, and they were not mistaken; from this fact, then, it is clear that that saying of the Poet which is regarded as most mythical of all was not idly spoken, but that he hinted at the truth when he called Aeolus "steward of the winds." However, I have already discussed these matters sufficiently. It is the close attention of the Poet to vivid description, one might call it, . . . for both are equally present in rhetorical composition and vivid description; at any rate, pleasure is common to both. But I shall return to the topic which follows that at which I digressed.
Of Lipara, then, and Thermessa I have already spoken. As for Strongyle, it is so called from its shape, and it too is fiery; it falls short in the violence of its flame, but excels in the brightness of its light; and this is where Aeolus lived, it is said. The fourth island is Didyme, and it too is named after its shape. Of the remaining islands, Ericussa and Phoenicussa have been so called from their plants, and are given over to pasturage of flocks. The seventh is Euonymus, which is farthest out in the high sea and is desert; it is so named because it is more to the left than the others, to those who sail from Lipara to Sicily. Again, many times flames have been observed running over the surface of the sea round about the islands when some passage had been opened up from the cavities down in the depths of the earth and the fire had forced its way to the outside. Poseidonius says that within his own recollection, one morning at daybreak about the time of the summer solstice, the sea between Hiera and Euonymus was seen raised to an enormous height, and by a sustained blast remained puffed up for a considerable time, and then subsided; and when those who had the hardihood to sail up to it saw dead fish driven by the current, and some of the men were stricken ill because of the heat and stench, they took flight; one of the boats, however, approaching more closely, lost some of its occupants and barely escaped to Lipara with the rest, who would at times become senseless like epileptics, and then afterwards would recur to their proper reasoning faculties; and many days later mud was seen forming on the surface of the sea, and in many places flames, smoke, and murky fire broke forth, but later the scum hardened and became as hard as mill-stone; and the governor of Sicily, Titus Flaminius, reported the event to the Senate, and the Senate sent a deputation to offer propitiatory sacrifices, both in the islet and in Liparae, to the gods both of the underworld and of the Sea. Now, according to the Chorographer, the distance from Ericodes to Phoenicodes is ten miles, and thence to Didyme thirty, and thence to the northern part of Lipara twenty-nine, and thence to Sicily nineteen, but from Strongyle sixteen. Off Pachynus lie Melita, whence come the little dogs called Melitaean, and Gaudos, both eighty-eight miles distant from the Cape. Cossura lies off Lilybaeum, and off Aspis, a Carthaginian city whose Latin name is Clupea; it lies midway between the two, and is the aforesaid distance from either. Aegimurus, also, and other small islands lie off Sicily and Libya. So much for the islands. |
|
|
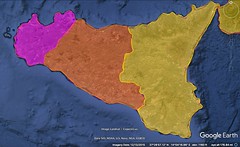
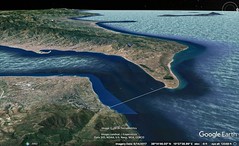
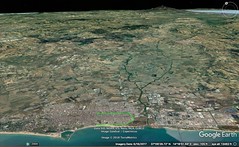


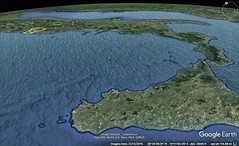
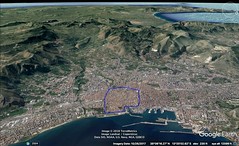
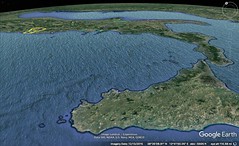

|


|
6 - 3 Iapygia 
Now that I have traversed the regions of Old Italy as far as Metapontium, I must speak of those that border on them. And Iapygia borders on them. The Greeks call it Messapia, also, but the natives, dividing it into two parts, call one part (that about the Iapygian Cape) the country of the Salentini, and the other the country of the Calabri. Above these latter, on the north, are the Peucetii and also those people who in the Greek language are called Daunii, but the natives give the name Apulia to the whole country that comes after that of the Calabri, though some of them, particularly the Peucetii, are called Poedicli also. Messapia forms a sort of peninsula, since it is enclosed by the isthmus that extends from Brentesium as far as Taras, three hundred and ten stadia. And the voyage thither around the Iapygian Cape is, all told, about four hundred stadia. The distance from Metapontium is about two hundred and twenty stadia, and the voyage to it is towards the rising sun. But though the whole Tarantine Gulf, generally speaking, is harbourless, yet at the city there is a very large and beautiful harbour, which is enclosed by a large bridge and is one hundred stadia in circumference. In that part of the harbour which lies towards the innermost recess, the harbour, with the outer sea, forms an isthmus, and therefore the city is situated on a peninsula; and since the neck of land is low-lying, the ships are easily hauled overland from either side. The ground of the city, too, is low-lying, but still it is slightly elevated where the acropolis is. The old wall has a large circuit, but at the present time the greater part of the city — the part that is near the isthmus — has been forsaken, but the part that is near the mouth of the harbour, where the acropolis is, still endures and makes up a city of noteworthy size. And it has a very beautiful gymnasium, and also a spacious market-place, in which is situated the bronze colossus of Zeus, the largest in the world except the one that belongs to the Rhodians. Between the market-place and the mouth of the harbour is the acropolis, which has but few remnants of the dedicated objects that in early times adorned it, for most of them were either destroyed by the Carthaginians when they took the city or carried off as booty by the Romans when they took the place by storm. Among this booty is the Heracles in the Capitol, a colossal bronze statue, the work of Lysippus, dedicated by Maximus Fabius, who captured the city.
2 In speaking of the founding of Taras, Antiochus says: After the Messenian war broke out, those of the Lacedaemonians who did not take part in the expedition were adjudged slaves and were named Helots, and all children who were born in the time of the expedition were called Partheniae and judicially deprived of the rights of citizenship, but they would not tolerate this, and since they were numerous formed a plot against the free citizens; and when the latter learned of the plot they sent secretly certain men who, through a pretence of friendship, were to report what manner of plot it was; among these was Phalanthus, who was reputed to be their champion, but he was not pleased, in general, with those who had been named to take part in the council. It was agreed, however, that p109the attack should be made at the Hyacinthian festival in the Amyclaeum when the games were being celebrated, at the moment when Phalanthus should put on his leather cap (the free citizens were recognizable by their hair); but when Phalanthus and his men had secretly reported the agreement, and when the games were in progress, the herald came forward and forbade Phalanthus to put on a leather cap; and when the plotters perceived that the plot had been revealed, some of them began to run away and others to beg for mercy; but they were bidden to be of good cheer and were given over to custody; Phalanthus, however, was sent to the temple of the god to consult with reference to founding a colony; and the god responded, "I give to thee Satyrium, both to take up thine abode in the rich land of Taras and to become a bane to the Iapygians." Accordingly, the Partheniae went thither with Phalanthus, and they were welcomed by both the barbarians and the Cretans who had previously taken possession of the place. These latter, it is said, are the people who sailed with Minos to Sicily, and, after his death, which occurred at the home of Cocalus in Camici, set sail from Sicily; but on the voyage back they were driven out of their course to Taras, although later some of them went afoot around the Adrias as far as Macedonia and were called Bottiaeans. But all the people as far as Daunia, it is said, were called Iapyges, after Iapyx, who is said to have been the son of Daedalus by a Cretan woman and to have been the leader of the Cretans. The city of Taras, however, was named after some hero.
3 But Ephorus describes the founding of the city thus: The Lacedaemonians were at war with the Messenians because the latter had killed their king Teleclus when he went to Messene to offer sacrifice, and they swore that they would not return home again until they either destroyed Messene or were all killed; and when they set out on the expedition, they left behind the youngest and the oldest of the citizens to guard the city; but later on, in the tenth year of the war, the Lacedaemonian women met together and sent certain of their own number to make complaint to their husbands that they were carrying on the war with the Messenians on unequal terms, for the Messenians, staying in their own country, were begetting children, whereas they, having abandoned their wives to widowhood, were on an expedition in the country of the enemy, and they complained that the fatherland was in danger of being in want of men; and the Lacedaemonians, both keeping their oath and at the same time bearing in mind the argument of the women, sent the men who were most vigorous and at the same time youngest, for they knew that these had not taken part in the oaths, because they were still children when they went out to war along with the men who were of military age; and they ordered them to cohabit with the maidens, every man with every maiden, thinking that thus the maidens would bear many more children; and when this was done, the children were named Partheniae. But as for Messene, it was captured after a war of nineteen years, as Tyrtaeus says: "About it they fought for nineteen years, relentlessly, with heart ever steadfast, did the fathers of our fathers, spearmen they; and in the twentieth the people forsook their fertile farms and fled from the great mountains of Ithome." Now the Lacedaemonians divided up Messenia among themselves, but when they came on back home they would not honour the Partheniae with civic rights like the rest, on the ground that they had been born out of wedlock; and the Partheniae, leaguing with the Helots, formed a plot against the Lacedaemonians and agreed to raise a Laconian cap in the market-place as a signal for the attack. But though some of the Helots had revealed the plot, the Lacedaemonians decided that it would be difficult to make a counter-attack against them, for the Helots were not only numerous but were all of one mind, regarding themselves as virtually brothers of one another, and merely charged those who were about to raise the signal to go away from the market-place. So the plotters, on learning that the undertaking had been betrayed, held back, and the Lacedaemonians persuaded them, through the influence of their fathers, to go forth and found a colony, and if the place they took possession of sufficed them, to stay there, but if not, to come on back and divide among themselves the fifth part of Messenia. And they, thus sent forth, found the Achaeans at war with the barbarians, took part in their perils, and founded Taras.
4 At one time the Tarantini were exceedingly powerful, that is, when they enjoyed a democratic government; for they not only had acquired the largest fleet of all peoples in that part of the world but were wont to send forth an army of thirty thousand infantry, three thousand cavalry, and one thousand commanders of cavalry. Moreover, the Pythagorean philosophy was embraced by them, but especially by Archytas, who presided over the city for a considerable time. But later, because of their prosperity, luxury prevailed to such an extent that the public festivals celebrated among them every year were more in number than the days of the year; and in consequence of this they also were poorly governed. One evidence of their bad policies is the fact that they employed foreign generals; for they sent for Alexander the Molossian to lead them in their war against the Messapians and Leucanians, and, still before that, for Archidamus, the son of Agesilaüs, and, later on, for Cleonymus, and Agathocles, and then for Pyrrhus, at the time when they formed a league with him against the Romans. And yet even to those whom they called in they could not yield a ready obedience, and would set them at enmity. At all events, it was out of enmity that Alexander tried to transfer to Thurian territory the general festival assembly of all Greek peoples in that part of the world — the assembly which was wont to meet at Heracleia in Tarantine territory, and that he began to urge that a place for the meetings be fortified on the Acalandrus River. Furthermore, it is said that the unhappy end which befell him was the result of their ingratitude. Again, about the time of the wars with Hannibal, they were deprived of their freedom, although later they received a colony of Romans, and are now living at peace and better than before. In their war against the Messapians for the possession of Heracleia, they had the co-operation of the king of the Daunians and the king of the Peucetians.
5 That part of the country of the Iapygians which comes next is fine, though in an unexpected way; for although on the surface it appears rough, it is found to be deep-soiled when ploughed, and although it is rather lacking in water, it is manifestly none the less good for pasturage and for trees. The whole of this district was once extremely populous; and it also had thirteen cities; but now, with the exception of Taras and Brentesium, all of them are so worn out by war that they are merely small towns. The Salentini are said to be a colony of the Cretans. The temple of Athene, once so rich, is in their territory, as also the look‑out-rock called Cape Iapygia, a huge rock which extends out into the sea towards the winter sunrise, though it bends approximately towards the Lacinium, which rises opposite to it on the west and with it bars the mouth of the Tarantine Gulf. And with it the Ceraunian Mountains, likewise, bar the mouth of the Ionian Gulf; the passage across from it both to the Ceraunian Mountains and to the Lacinium is about seven hundred stadia. But the distance by sea from Taras around to Brentesium is as follows: First, to the small town of Baris, six hundred stadia; Baris is called by the people of to‑day Veretum, is situated at the edge of the Salentine territory, and the trip thither from Taras is for the most part easier to make on foot than by sailing. Thence to Leuca eighty stadia; this, too, is a small town, and in it is to be seen a fountain of malodorous water; the mythical story is told that those of the Giants who survived at the Campanian Phlegra and are called the Leuternian Giants were driven out by Heracles, and on fleeing hithera for refuge were shrouded by Mother Earth, and the fountain gets its malodorous stream from the ichor of their bodies; and for this reason, also, the seaboard here is called Leuternia. Again, from Leuca to Hydrus, a small town, one hundred and fifty stadia. Thence to Brentesium four hundred; and it is an equal distance to the island Sason,1which is situated about midway of the distance across from Epeirus to Brentesium. And therefore those who cannot accomplish the straight voyage sail to the left of Sason and put in at Hydrus; and then, watching for a favorable wind, they hold their course towards the harbours of the Brentesini, although if they disembark, they go afoot by a shorter route by way of Rodiae, a Greek city, where the poet Ennius was born. So then, the district one sails around in going from Taras to Brentesium resembles a peninsula, and the overland journey from Brentesium to Taras, which is only a one day's journey for a man well-girt, forms the isthmus of the aforesaid peninsula; and this peninsula most people call by one general name Messapia, or Iapygia, or Calabria, or Salentina, although some divide it up, as I have said before. So much, then, for the towns on the sea-coast.
6 In the interior are Rodiae and Lupiae, and, slightly above the sea, Aletia; and at the middle of the isthmus, Uria, in which is still to be seen the palace of one of the chieftains. When Herodotus states that Hyria is in Iapygia and was founded by the Cretans who strayed from the fleet of Minos when on its way to Sicily, we must understand Hyria to be either Uria or Veretum. Brentesium, they say, was further colonised by the Cretans, whether by those who came over with Theseus from Cnossus or by those who set sail from Sicily with Iapyx (the story is told both ways), although they did not stay together there, it is said, but went off to Bottiaea. Later on, however, when ruled by kings, the city lost much of its country to the Lacedaemonians who were under the leadership of Phalanthus; but still, when he was ejected from Taras, he was admitted by the Brentesini, and when he died was counted by them worthy of a splendid burial. Their country is better than that of the Tarantini, for, though the soil is thin, it produces good fruits, and its honey and wool are among those that are strongly commended. Brentesium is also better supplied with harbours; for here many harbours are closed in by one mouth; and they are sheltered from the waves, because bays are formed inside in such a way as to resemble in shape a stag's horns; and hence the name, for, along with the city, the place very much resembles a stag's head, and in the Messapian language the head of the stag is called "brentesium." But the Tarantine harbour, because of its wide expanse, is not wholly sheltered from the waves; and besides there are some shallows in the innermost part of it.
7 In the case of those who sail across from Greece or Asia, the more direct route is to Brentesium, and, in fact, all who propose to go to Rome by land put into port here. There are two roads from here: one, a mule-road through the countries of the Peucetii (who are called Poedicli), the Daunii, and the Samnitae as far as Beneventum; on this road is the city of Egnatia, and then, Celia, Netium, Canusium, and Herdonia. But the road by way of Taras, lying slightly to the left of the other, though as much as one day's journey out of the way when one has made the circuit, what is called the Appian Way, is better for carriages. On this road are the cities of Uria and Venusia, the former between Taras and Brentesium and the latter on the confines of the Samnitae and the Leucani. Both the roads from Brentesium meet near Beneventum and Campania. And the common road from here on, as far as Rome, is called the Appian Way, and passes through Caudium, Calatia, Capua, and Casilinum to Sinuessa. And the places from there on I have already mentioned. The total length of the road from Rome to Brentesium is three hundred and sixty miles. But there is also a third road, which runs from Rhegium through the countries of the Brettii, the Leucani, and the Samnitae into Campania, where it joins the Appian Way; it passes through the Apennine Mountains and it requires three or four days more than the road from Brentesium.
8 The voyage from Brentesium to the opposite mainland is made either to the Ceraunian Mountains and those parts of the seaboard of Epeirus and of Greece which come next to them, or else to Epidamnus; the latter is longer than the former, for it is one thousand eight hundred stadia. And yet the latter is the usual route, because the city has a good position with reference both to the tribes of the Illyrians and to those of the Macedonians. As one sails from Brentesium along the Adriatic seaboard, one comes to the city of Egnatia, which is the common stopping-place for people who are travelling either by sea or land to Barium; and the voyage is made with the south wind. The country of the Peucetii extends only thus far on the sea, but in the interior as far as Silvium. All of it is rugged and mountainous, since it embraces a large portion of the Apennine Mountains; and it is thought to have admitted Arcadians as colonists. From Brentesium to Barium is about seven hundred stadia, and Taras is about an equal distance from each. The adjacent country is inhabited by the Daunii; and then come the Apuli, whose country extends as far as that of the Frentani. But since the terms "Peucetii" and "Daunii" are not at all used by the native inhabitants, except in early times, and since this country as a whole is now called Apulia, necessarily the boundaries of these tribes cannot be told to a nicety either, and for this reason neither should I myself make positive assertions about them.
9 From Barium to the Aufidus River, on which is the Emporium of the Canusitae is four hundred stadia and the voyage inland to Emporium is ninety. Near by is also Salapia, the seaport of the Argyrippini. For not far above the sea (in the plain, at all events) are situated two cities, Canusium and Argyrippa, which in earlier times were the largest of the Italiote cities, as is clear from the circuits of their walls. Now, however, Argyrippa is smaller; it was called Argos Hippium at first, then Argyrippa, and then by the present name Arpi. Both are said to have been founded by Diomedes. And as signs of the dominion of Diomedes in these regions are to be seen the Plain of Diomedes and many other things, among which are the old votive offerings in the temple of Athene at Luceria — a place which likewise was in ancient times a city of the Daunii, but is now reduced — and, in the sea near by, two islands that are called the Islands of Diomedes, of which one is inhabited, while the other, it is said, is desert; on the latter, according to certain narrators of myths, Diomedes was caused to disappear, and his companions were changed to birds, and to this day, in fact, remain tame and live a sort of human life, not only in their orderly ways but also in their tameness towards honorable men and in their flight from wicked and knavish men. But I have already mentioned the stories constantly told among the Heneti about this hero and the rites which are observed in his honour. It is thought that Sipus also was founded by Diomedes, which is about one hundred and forty stadia distant from Salapia; at any rate it was named "Sepius" in Greek after the "sepia" that are cast ashore by the waves. Between Salapia and Sinus is a navigable river, and also a large lake that opens into the sea; and the merchandise from Sipus, particularly grain, is brought down on both. In Daunia, on a hill by the name of Drium, are to be seen two hero-temples: one, to Calchas, on the very summit, where those who consult the oracle sacrifice to his shade a black ram and sleep in the hide, and the other, to Podaleirius, down near the base of the hill, this temple being about one hundred stadia distant from the sea; and from it flows a stream which is a cure-all for diseases of animals. In front of this gulf is a promontory, Garganum, which extends towards the east for a distance of three hundred stadia into the high sea; doubling the headland, one comes to a small town, Urium, and off the headland are to be seen the Islands of Diomedes. This whole country produces everything in great quantity, and is excellent for horses and sheep; but though the wool is softer than the Tarantine, it is not so glossy. And the country is well sheltered, because the plains lie in hollows. According to some, Diomedes even tried to cut a canal as far as the sea, but left behind both this and the rest of his undertakings only half-finished, because he was summoned home and there ended his life. This is one account of him; but there is also a second, that he stayed here till the end of his life; and a third, the aforesaid mythical account, which tells of his disappearance in the island; and as a fourth one might set down the account of the Heneti, for they too tell a mythical story of how he in some way came to his end in their country, and they call it his apotheosis.
Now the above distances are put down in accordance with the data of Artemidorus; but according to the Chorographer, the distances from Brentesium as far as Garganum amount to one hundred and sixty-five miles, whereas according to Artemidorus they amount to more; and thence to Ancona two hundred and fifty-four miles according to the former, whereas according to Artemidorus the distance to the Aesis River, which is near Ancona, is one thousand two hundred and fifty stadia, a much shorter distance. Polybius states that the distance from Iapygia has been marked out by miles, and that the distance to the city of Sena is five hundred and sixty-two miles, and thence to Aquileia one hundred and seventy-eight. And they do not agree with the commonly accepted distance along the Illyrian coast-line, from the Ceraunian Mountains to the recess of the Adrias, since they represent this latter coasting-voyage as over six thousand stadia, thus making it even longer than the former, although it is much shorter. However, every writer does not agree with every other, particularly about the distances, as I often say. As for myself, where it is possible to reach a decision, I set forth my opinion, but where it is not, I think that I should make known the opinions of others. And when I have no opinion of theirs, there is no occasion for surprise if I too have passed something by, especially when one considers the character of my subject; for I would not pass by anything important, while as for little things, not only do they profit one but slightly if known, but their omission escapes unnoticed, and detracts not at all, or else not much, from the completeness of the work.
The intervening space, immediately after Cape Garganum, is taken up by a deep gulf; the people who live around it are called by the special name of Apuli, although they speak the same language as the Daunii and the Peucetii, and do not differ from them in any other respect either, at the present time at least, although it is reasonable to suppose that in early times they differed and that this is the source of the three diverse names for them that are now prevalent. In earlier times this whole country was prosperous, but it was laid waste by Hannibal and the later wars. And here too occurred the battle of Cannae, in which the Romans and their allies suffered a very great loss of life. On the gulf is a lake; and above the lake, in the interior, is Teanum Apulum, which has the same name as Teanum Sidicinum. At this point the breadth of Italy seems to be considerably contracted, since from here to the region of Dicaearcheia an isthmus is left of less than one thousand stadia from sea to sea. After the lake comes the voyage along the coast to the country of the Frentani and to Buca; and the distance from the lake either to Buca or to Cape Garganum is two hundred stadia. As for the places that come next after Buca, I have already mentioned them. |
|
|
|
|
6 - 4 Summary remarks on Italy and the expansion of Rome 
1 Such, indeed, is the size and such the character of Italy. And while I have already mentioned many things which have caused the Romans at the present time to be exalted to so great a height, I shall now indicate the most important things. One is, that, like an island, Italy is securely guarded by the seas on all sides, except in a few regions, and even these are fortified by mountains that are hardly passable. A second is that along most of its coast it is harbourless and that the harbours it does have are large and admirable. The former is useful in meeting attacks from the outside, while the latter is helpful in making counter-attacks and in promoting an abundant commerce. A third is that it is characterised by many differences of air and temperature, on which depend the greater variation, whether for better or for worse, in animals, plants, and, in short, everything that is useful for the support of life. Its length extends from north to south, generally speaking, and Sicily counts as an addition to its length, already so great. Now mild temperature and harsh temperature of the air are judged by heat, cold, and their intermediates; and so from this it necessarily follows that what is now Italy, situated as it is between the two extremes and extending to such a length, shares very largely in the temperate zone and in a very large number of ways. And the following is still another advantage which has fallen to the lot of Italy; since the Apennine Mountains extend through the whole of its length and leave on both sides plains and hills which bear fine fruits, there is no part of it which does not enjoy the blessings of both mountain and plain. And add also to this the size and number of its rivers and its lakes, and, besides these, the fountains of water, both hot and cold, which in many places nature has provided as an aid to health, and then again its good supply of mines of all sorts. Neither can one worthily describe Italy's abundant supply of fuel, and of food both for men and beast, and the excellence of its fruits. Further, since it lies intermediate between the largest races on the one hand, and Greece and the best parts of Libya on the other, it not only is naturally well-suited to hegemony, because it surpasses the countries that surround it both in the valour of its people and in size, but also can easily avail itself of their services, because it is close to them.
2 Now if I must add to my account of Italy a summary account also of the Romans who took possession of it and equipped it as a base of operations for the universal hegemony, let me add as follows: After the founding of Rome, the Romans wisely continued for many generations under the rule of kings. Afterwards, because the last Tarquinius was a bad ruler, they ejected him, framed a government which was a mixture of monarchy and aristocracy, and dealt with the Sabini and Latini as with partners. But since they did not always find either them or the other neighbouring peoples well intentioned, they were forced, in a way, to enlarge their own country by the dismemberment of that of the others. And in this way, while they were advancing and increasing little by little, it came to pass, contrary to the expectation of all, that they suddenly lost their city, although they also got it back contrary to expectation. This took place, as Polybius says, in the nineteenth year after the naval battle at Aegospotami, at the time of the Peace of Antalcidas After having rid themselves of these enemies, the Romans first made all the Latini their subjects; then stopped the Tyrrheni and the Celti who lived about the Padus from their wide and unrestrained licence; then fought down the Samnitae, and, after them, the Tarantini and Pyrrhus; and then at last also the remainder of what is now Italy, except the part that is about the Padus. And while this part was still in a state of war, the Romans crossed over to Sicily, and on taking it away from the Carthaginians came back again to attack the peoples who lived about the Padus; and it was while that war was still in progress that Hannibal invaded Italy. This latter is the second war that occurred against the Carthaginians; and not long afterwards occurred the third, in which Carthage was destroyed; and at the same time the Romans acquired, not only Libya, but also as much of Iberia as they had taken away from the Carthaginians. But the Greeks, the Macedonians, and those peoples in Asia who lived this side the Halys River and the Taurus Mountains joined the Carthaginians in a revolution, and therefore at the same time the Romans were led on to a conquest of these peoples, whose kings were Antiochus, Philip, and Perseus. Further, those of the Illyrians and Thracians who were neighbours to the Greeks and the Macedonians began to carry on war against the Romans and kept on warring until the Romans had subdued all the tribes this side the Ister and this side the Halys. And the Iberians, Celti, and all the remaining peoples which now give ear to the Romans had the same experience. As for Iberia, the Romans did not stop reducing it by force of arms until they had subdued the whole of it, first, by driving out the Nomantini, and, later on, by destroying Viriathus and Sertorius, and, last of all, the Cantabri, who were subdued by Augustus Caesar. As for Celtica (I mean Celtica as a whole, both the Cisalpine and Transalpine, together with Liguria), the Romans at first brought it over to their side only part by part, from time to time, but later the Deified Caesar, and afterwards Caesar Augustus, acquired it all at once in a general war. But at the present time the Romans are carrying on war against the Germans, setting out from the Celtic regions as the most appropriate base of operations, and have already glorified the fatherland with some triumphs over them. As for Libya, so much of it as did not belong to the Carthaginians was turned over to kings who were subject to the Romans, and, if they ever revolted, they were deposed. But at the present time Juba has been invested with the rule, not only of Maurusia, but also of many parts of the rest of Libya, because of his loyalty and his friendship for the Romans. And the case of Asia was like that of Libya. At the outset it was administered through the agency of kings who were subject to the Romans, but from that time on, when their line failed, as was the case with the Attalic, Syrian, Paphlagonian, Cappadocian, and Egyptian kings, or when they would revolt and afterwards be deposed, as was the case with Mithridates Eupator and the Egyptian Cleopatra, all parts of it this side the Phasis and the Euphrates, except certain parts of Arabia, have been subject to the Romans and the rulers appointed by them. As for the Armenians, and the peoples who are situated above Colchis, both Albanians and Iberians, they require the presence only of men to lead them, and are excellent subjects, but because the Romans are engrossed by other affairs, they make attempts at revolution — as is the case with all the peoples who live beyond the Ister in the neighbourhood of the Euxine, except those in the region of the Bosporus and the Nomads, for the people of the Bosporus are in subjection, whereas the Nomads, on account of their lack of intercourse with others, are of no use for anything and only require watching. Also the remaining parts of Asia, generally speaking, belong to the Tent-dwellers and the Nomads, who are very distant peoples. But as for the Parthians, although they have a common border with the Romans and also are very powerful, they have nevertheless yielded so far to the preeminence of the Romans and of the rulers of our time that they have sent to Rome the trophies which they once set up as a memorial of their victory over the Romans, and, what is more, Phraates has entrusted to Augustus Caesar his children and also his children's children, thus obsequiously making sure of Caesar's friendship by giving hostages; and the Parthians of to‑day have often gone to Rome in quest of a man to be their king, and are now about ready to put their entire authority into the hands of the Romans. As for Italy itself,a though it has often been torn by factions, at least since it has been under the Romans, and as for Rome itself, they have been prevented by the excellence of their form of government and of their rulers from proceeding too far in the ways of error and corruption. But it were a difficult thing to administer so great a dominion otherwise than by turning it over to one man, as to a father; at all events, never have the Romans and their allies thrived in such peace and plenty as that which was afforded them by Augustus Caesar, from the time he assumed the absolute authority, and is now being afforded them by his son and successor, Tiberius, who is making Augustus the model of his administration and decrees, as are his children, Germanicus and Drusus, who are assisting their father. |
|
|
|
|
7 Central Europe 8 114 1:50 
|
7 - 1 Germany 
1 Now that I have described Iberia and the Celtic and Italian tribes, along with the islands near by, it will be next in order to speak of the remaining parts of Europe, dividing them in the approved manner. The remaining parts are: first, those towards the east, being those which are across the Rhenus and extend as far as the Tanaïs and the mouth of Lake Maeotis, and also all those regions lying between the Adrias and the regions on the left of the Pontic Sea that are shut off by the Ister4 and extend towards the south as far as Greece and the Propontis; for this river divides very nearly the whole of the aforesaid land into two parts. It is the largest of the European rivers, at the outset flowing towards the south and then turning straight from the west towards the east and the Pontus. It rises in the western limits of Germany, as also near the recess of the Adriatic (at a distance from it of about one thousand stadia), and comes to an end at the Pontus not very far from the outlets of the Tyras and the Borysthenes, bending from its easterly course approximately towards the north. Now the parts that are beyond the Rhenus and Celtica are to the north of the Ister; these are the territories of the Galatic and the Germanic tribes, extending as far as the Bastarnians and the Tyregetans and the River Borysthenes. And the territories of all the tribes between this river and the Tanaïs and the mouth of Lake Maeotis extend up into the interior as far as the ocean and are washed by the Pontic Sea. But both the Illyrian and the Thracian tribes, and all tribes of the Celtic or other peoples that are mingled with these, as far as Greece, are to the south of the Ister. But let me first describe the parts outside the Ister, for they are much simpler than those on the other side.
2 Now the parts beyond the Rhenus, immediately after the country of the Celti, slope towards the east and are occupied by the Germans, who, though they vary slightly from the Celtic stock in that they are wilder, taller, and have yellower hair, are in all other respects similar, for in build, habits, and modes of life they are such as I have said the Celti are. And I also think that it was for this reason that the Romans assigned to them the name "Germani," as though they wished to indicate thereby that they were "genuine" Galatae, for in the language of the Romans "germani" means "genuine."
3 The first parts of this country are those that are next to the Rhenus, beginning at its source and extending as far as its outlet; and this stretch of river-land taken as a whole is approximately the breadth of the country on its western side. Some of the tribes of this river-land were transferred by the Romans to Celtica, whereas the others anticipated the Romans by migrating deep into the country, for instance, the Marsi; and only a few people, including a part of the Sugambri, are left. After the people who live along the river come the other tribes that live between the Rhenus and the River Albis, which latter flows approximately parallel to the former, towards the ocean, and traverses no less territory than the former. Between the two are other navigable rivers also (among them the Amasias, on which Drusus won a naval victory over the Bructeri), which likewise flow from the south towards the north and the ocean; for the country is elevated towards the south and forms a mountain chain that connects with the Alps and extends towards the east as though it were a part of the Alps; and in truth some declare that they actually are a part of the Alps, both because of their aforesaid position and of the fact that they produce the same timber; however, the country in this region does not rise to a sufficient height for that. Here, too, is the Hercynian Forest, and also the tribes of the Suevi, some of which dwell inside the forest, as, for instance, the tribes of the Coldui, in whose territory is Boihaemum, the domain of Marabodus, the place whither he caused to migrate, not only several other peoples, but in particular the Marcomanni, his fellow-tribesmen; for after his return from Rome this man, who before had been only a private citizen, was placed in charge of the affairs of state, for, as a youth he had been at Rome and had enjoyed the favour of Augustus, and on his return he took the rulership and acquired, in addition to the peoples aforementioned, the Lugii (a large tribe), the Zumi, the Butones, the Mugilones, the Sibini, and also the Semnones, a large tribe of the Suevi themselves. However, while some of the tribes of the Suevi dwell inside the forest, as I was saying, others dwell outside of it, and have a common boundary with the Getae. Now as for the tribe of the Suevi, it is the largest, for it extends from the Rhenus to the Albis; and a part of them even dwell on the far side of the Albis, as, for instance, the Hermondori and the Langobardi; 1and at the present time these latter, at least, have, to the last man, been driven in flight out of their country into the land on the far side of the river. It is a common characteristic of all the peoples in this part of the world that they migrate with ease, because of the meagerness of their livelihood and because they do not till the soil or even store up food, but live in small huts that are merely temporary structures; and they live for the most part off their flocks, as the Nomads do, so that, in imitation of the Nomads, they load their household belongings on their wagons and with their beasts turn whithersoever they think best. But other German tribes are still more indigent. I mean the Cherusci, the Chatti, the Gamabrivii and the Chattuarii,a and also, near the ocean, the Sugambri, the Chaubi, the Bructeri, and the Cimbri, and also the Cauci, the Caülci, the Campsiani, and several others. Both the Visurgis and the Lupias Rivers run in the same direction as the Amasias, the Lupias being about six hundred stadia distant from the Rhenus and flowing through the country of the Lesser Bructeri. Germany has also the Salas River; and it was between the Salas and the Rhenus that Drusus Germanicus, while he was successfully carrying on the war, came to his end. He had subjugated, not only most of the tribes, but also the islands along the coast, among which is Burchanis, which he took by siege.
4 These tribes have become known through their wars with the Romans, in which they would either yield and then later revolt again, or else quit their settlements; and they would have been better known if Augustus had allowed his generals to cross the Albis in pursuit of those who emigrated thither. But as a matter of fact he supposed that he could conduct the war in hand more successfully if he should hold off from those outside the Albis, who were living in peace, and should not incite them to make common cause with the others in their enmity against him. It was the Sugambri, who live near the Rhenus, that began the war, Melo being their leader; and from that time on different peoples at different times would cause a breach, first growing powerful and then being put down, and then revolting again, betraying both the hostages they had given and their pledges of good faith. In dealing with these peoples distrust has been a great advantage, whereas those who have been trusted have done the greatest harm, as, for instance, the Cherusci and their subjects, in whose country three Roman legions, with their general Quintilius Varus, were destroyed by ambush in violation of the treaty. But they all paid the penalty, and afforded the younger Germanicus a most brilliant triumph — that triumph in which their most famous men and women were led captive, I mean Segimuntus, son of Segestes and chieftain of the Cherusci, and his sister Thusnelda, the wife of Armenius, the man who at the time of the violation of the treaty against Quintilius Varus was commander-in‑chief of the Cheruscan army and even to this day is keeping up the war, and Thusnelda's three-year‑old son Thumelicus; and also Sesithacus, the son of Segimerus and chieftain of the Cherusci, and Rhamis, his wife, and a daughter of Ucromirus chieftain of the Chatti, and Deudorix, a Sugambrian, the son of Baetorix the brother of Melo. But Segestes, the father-in‑law of Armenius, who even from the outset had opposed the purpose of Armenius, and, taking advantage of an opportune time, had deserted him, was present as a guest of honour at the triumph over his loved ones. And Libes too, a priest of the Chatti, marched in the procession, as also other captives from the plundered tribes — the Caülci, Campsani, Bructeri, Usipi, Cherusci, Chatti, Chattuarii, Landi, Tubattii. Now the Rhenus is about three thousand stadia distant from the Albis, if one had straight roads to travel on, but as it is one must go by a circuitous route, which winds through a marshy country and forests.
5 The Hercynian Forest is not only rather dense, but also has large trees, and comprises a large circuit within regions that are fortified by nature; in the centre of it, however, lies a country (of which I have already spoken) that is capable of affording an excellent livelihood. And near it are the sources of both the Ister and the Rhenus, as also the lake between the two sources, and the marshes into which the Rhenus spreads. The perimeter of the lake is more than three hundred stadia, while the passage across it is nearly two hundred. There is also an island in it which Tiberius used as a base of operations in his naval battle with the Vindelici. This lake is south of the sources of the Ister, as is also the Hercynian Forest, so that necessarily, in going from Celtica to the Hercynian Forest, one first crosses the lake and then the Ister, and from there on advances through more passable regions — plateaus — to the forest. Tiberius had proceeded only a day's journey from the lake when he saw the sources of the Ister. The country of the Rhaeti adjoins the lake for only a short distance, whereas that of the Helvetii and the Vindelici, and also the desert of the Boii, adjoin the greater part of it. All the peoples as far as the Pannonii, but more especially the Helvetii and the Vindelici, inhabit plateaus. But the countries of the Rhaeti and the Norici extend as far as the passes over the Alps and verge toward Italy, a part thereof bordering on the country of the Insubri and a part on that of the Carni and the legions about Aquileia. And there is also another large forest, Gabreta; it is on this side of the territory of the Suevi, whereas the Hercynian Forest, which is also held by them, is on the far side. |
|
|
|
|
7 - 2 Germans and the Cimbri or Cimmerians 
1 As for the Cimbri, some things that are told about them are incorrect and others are extremely improbable. For instance, one could not accept such a reason for their having become a wandering and piratical folk as this — that while they were dwelling on a Peninsula they were driven out of their habitations by a great flood-tide; for in fact they still hold the country which they held in earlier times; and they sent as a present to Augustus the most sacred kettle in their country, with a plea for his friendship and for an amnesty of their earlier offences, and when their petition was granted they set sail for home; and it is ridiculous to suppose that they departed from their homes because they were incensed on account of a phenomenon that is natural and eternal, occurring twice every day. And the assertion that an excessive flood-tide once occurred looks like a fabrication, for when the ocean is affected in this way it is subject to increases and diminutions, but these are regulated and periodical. And the man who said that the Cimbri took up arms against the flood-tides was not right, either; nor yet the statement that the Celti, as a training in the virtue of fearlessness, meekly abide the destruction of their homes by the tides and then rebuild them, and that they suffer a greater loss of life as the result of water than of war, as Ephorus says. Indeed, the regularity of the flood-tides and the fact that the part of the country subject to inundations was known should have precluded such absurdities; for since this phenomenon occurs twice every day, it is of course improbable that the Cimbri did not so much as once perceive that the reflux was natural and harmless, and that it occurred, not in their country alone, but in every country that was on the ocean. Neither is Cleitarchus right; for he says that the horsemen, on seeing the onset of the sea, rode away, and though in full flight came very near being cut off by the water. Now we know, in the first place, that the invasion of the tide does not rush on with such speed as that, but that the sea advances imperceptibly; and, secondly, that what takes place daily and is audible to all who are about to draw near it, even before they behold it, would not have been likely to prompt in them such terror that they would take to flight, as if it had occurred unexpectedly.a
2 Poseidonius is right in censuring the historians for these assertions, and his conjecture is not a bad one, that the Cimbri, being a piratical and wandering folk, made an expedition even as far as the region of Lake Maeotis, and that also the "Cimmerian" Bosporus was named after them, being equivalent to "Cimbrian," the Greeks naming the Cimbri "Cimmerii." And he goes off to say that in earlier times the Boii dwelt in the Hercynian Forest, and that the Cimbri made a sally against this place, but on being repulsed by the Boii, went down to the Ister and the country of the Scordiscan Galatae, then to the country of the Teuristae and Taurisci (these, too, Galatae), and then to the country of the Helvetii — men rich in gold but peaceable; however, when the Helvetii saw that the wealth which the Cimbri had got from their robberies surpassed that of their own country, they, and particularly their tribes of Tigyreni and of Toygeni, were so excited that they sallied forth with the Cimbri. All, however, were subdued by the Romans, both the Cimbri themselves and those who had joined their expeditions, in part after they had crossed the Alps into Italy and in part while still on the other side of the Alps.
3 Writers report a custom of the Cimbri to this effect: Their wives, who would accompany them on their expeditions, were attended by priestesses who were seers; these were grey-haired, clad in white, with flaxen cloaks fastened on with clasps, girt with girdles of bronze, and bare-footed; now sword in hand these priestesses would meet with the prisoners of war throughout the camp, and having first crowned them with wreaths would lead them to a brazen vessel of about twenty amphorae; and they had a raised platform which the priestess would mount, and then, bending over the kettle, would cut the throat of each prisoner after he had been lifted up; and from the blood that poured forth into the vessel some of the priestesses would draw a prophecy, while still others would split open the body and from an inspection of the entrails would utter a prophecy of victory for their own people; and during the battles they would beat on the hides that were stretched over the wicker-bodies of the wagons and in this way produce an unearthly noise.
4 Of the Germans, as I have said, those towards the north extend along the ocean; and beginning at the outlets of the Rhenus, they are known as far as the Albis; and of these the best known are the Sugambri and the Cimbri; but those parts of the country beyond the Albis that are near the ocean are wholly unknown to us. For of the men of earlier times I know of no one who has made this voyage along the coast to the eastern parts that extend as far as the mouth of the Caspian Sea; and the Romans have not yet advanced into the parts that are beyond the Albis; and likewise no one has made the journey by land either. However, it is clear from the "climata" and the parallel distances that if one travels longitudinally towards the east, one encounters the regions that are about the Borysthenes and that are to the north of the Pontus; but what is beyond Germany and what beyond the countries which are next after Germany — whether one should say the Bastarnae, as most writers suspect, or say that others lie in between, either the Iazyges, or the Roxolani, or certain other of the wagon-dwellers— it is not easy to say; nor yet whether they extend as far as the ocean along its entire length, or whether any part is uninhabitable by reason of the cold or other cause, or whether even a different race of people, succeeding the Germans, is situated between the sea and the eastern Germans. And this same ignorance prevails also in regard to the rest of the peoples that come next in order on the north; for I know neither the Bastarnae, nor the Sauromatae, nor, in a word, any of the peoples who dwell above the Pontus, nor how far distant they are from the Atlantic Sea, nor whether their countries border upon it. |
|
|
|


|
7 - 3 Mysia, Dacia, and the Danube (SE Europe) 
1 As for the southern part of Germany beyond the Albis, the portion which is just contiguous to that river is occupied by the Suevi; then immediately adjoining this is the land of the Getae, which, though narrow at first, stretching as it does along the Ister on its southern side and on the opposite side along the mountain-side of the Hercynian Forest (for the land of the Getae also embraces a part of the mountains), afterwards broadens out towards the north as far as the Tyregetae; but I cannot tell the precise boundaries. It is because of men's ignorance of these regions that any heed has been given to those who created the mythical "Rhipaean Mountains" and "Hyperboreans," and also to all those false statements made by Pytheas the Massalian regarding the country along the ocean, wherein he uses as a screen his scientific knowledge of astronomy and mathematics. So then, those men should be disregarded; in fact, if even Sophocles, when in his role as a tragic poet he speaks of Oreithyia, tells how she was snatched up by "Boreas" and carried "over the whole sea to the ends of the earth and to the sources of night and to the unfoldings of heaven and to the ancient garden of Phoebus," his story can have no bearing on the present inquiry, but should be disregarded, just as it is disregarded by Socrates in the Phaedrus. But let us confine our narrative to what we have learned from history, both ancient and modern.
2 Now the Greeks used to suppose that the Getae were Thracians; and the Getae lived on either side the Ister, as did also the Mysi, these also being Thracians and identical with the people who are now called Moesi; from these Mysi sprang also the Mysi who now live between the Lydians and the Phrygians and Trojans. And the Phrygians themselves are Brigians, a Thracian tribe, as are also the Mygdonians, the Bebricians, the Medobithynians, the Bithynians, and the Thynians, and, I think, also the Mariandynians. These peoples, to be sure, have all utterly quitted Europe, but the Mysi have remained there. And Poseidonius seems to me to be correct in his conjecture that Homer designates the Mysi in Europe (I mean those in Thrace) when he says, "But back he turned his shining eyes, and looked far away towards the land of the horse-tending Thracians, and of the Mysi, hand-to‑hand fighters" for surely, if one should take Homer to mean the Mysi in Asia, the statement would not hang together. Indeed, when Zeus turns his eyes away from the Trojans towards the land of the Thracians, it would be the act of a man who confuses the continents and does not understand the poet's phraseology to connect with Thrace the land of the Asiatic Mysi, who are not "far away," but have a common boundary with the Troad and are situated behind it and on either side of it, and are separated from Thrace by the broad Hellespont; for "back he turned" generally means "to the rear," and he who transfers his gaze from the Trojans to the people who are either in the rear of the Trojans or on their flanks, does indeed transfer his gaze rather far, but not at all "to the rear." Again, the appended phrase is testimony to this very view, because the poet connected with the Mysi the "Hippemolgi" and "Galactophagi" and "Abii," who are indeed the wagon-dwelling Scythians and Sarmatians. For at the present time these tribes, as well as the Bastarnian tribes, are mingled with the Thracians (more indeed with those outside the Ister, but also with those inside). And mingled with them are also the Celtic tribes — the Boii, the Scordisci, and the Taurisci. However, the Scordisci are by some called "Scordistae"; and the Taurisci are called also "Ligurisci" and "Tauristae."
3 Poseidonius goes on to say of the Mysians that in accordance with their religion they abstain from eating any living thing, and therefore from their flocks as well; and that they use as food honey and milk and cheese, living a peaceable life, and for this reason are called both "god-fearing" and "capnobatae"; and there are some of the Thracians who live apart from woman-kind; these are called "Ctistae," and because of the honour in which they are held, have been dedicated to the gods and live with freedom from every fear; accordingly, Homer speaks collectively of all these peoples as "proud Hippemolgi, Galactophagi and Abii, men most just," but he calls them "Abii" more especially for this reason, that they live apart from women, since he thinks that a life which is bereft of woman is only half-complete (just as he thinks the "house of Protesilaüs" is only "half complete," because it is so bereft); and he speaks of the Mysians as "hand-to‑hand fighters" because they were indomitable, as is the case with all brave warriors; and Poseidonius adds that in the Thirteenth Book one should read "Moesi, hand-to‑hand fighters" instead of "Mysi, hand-to‑hand fighters."
4 However, it is perhaps superfluous to disturb the reading that has had approval for so many years; for it is much more credible that the people were called Mysi at first and that later their name was changed to what it is now. And as for the term "Abii," one might interpret it as meaning those who are "without hearths" and "live on wagons" quite as well as those who are "bereft"; for since, in general, injustices arise only in connection with contracts and a too high regard for property, so it is reasonable that those who, like the Abii, live cheaply, on slight resources, should have been called "most just." In fact, the philosophers who put justice next to self-restraint strive above all things for frugality and personal independence; and consequently extreme self-restraint diverts some of them to the Cynical mode of life. But as for the statement that they live "bereft of women," the poet suggests nothing of the sort, and particularly in the country of the Thracians and p183of those of their number who are Getae. And see the statement of Menander about them, which, as one may reasonably suppose, was not invented by him but taken from history: "All the Thracians, and most of all we Getae (for I too boast that I am of this stock) are not very continent;" and a little below he sets down the proofs of their incontinence in their relations with women: "For every man of us marries ten or eleven women, and some, twelve or more; but if anyone meets death before he has married more than four or five, he is lamented among the people there as a wretch without bride and nuptial song." Indeed, these facts are confirmed by the other writers as well. Further, it is not reasonable to suppose that the same people regard as wretched a life without many women, and yet at the same time regard as pious and just a life that is wholly bereft of women.a And of course to regard as "both god-fearing and capnobatae" those who are without women is very much opposed to the common notions on that subject; for all agree in regarding the women as the chief founders of religion, and it is the women who provoke the men to the more attentive worship of the gods, to festivals, and to supplications, and it is a rare thing for a man who lives by himself to be found addicted to these things. See again what the same poet says when he introduces as speaker the man who is vexed by the money spent by the women in connection with the sacrifices: "The gods are the undoing of us, especially us married men, for we must always be celebrating some festival;" and again when he introduces the Woman-hater, who complains about these very things: "we used to sacrifice five times a day, and seven female attendants would beat the cymbals all round us, while others would cry out to the gods." So, then, the interpretation that the wifeless men of the Getae are in a special way reverential towards the gods is clearly contrary to reason, whereas the interpretation that zeal for religion is strong in this tribe, and that because of their reverence for the gods the people abstain from eating any living thing, is one which, both from what Poseidonius and from what the histories in general tell us, should not be disbelieved.
5 In fact, it is said that a certain man of the Getae, Zamolxis by name, had been a slave to Pythagoras, and had learned some things about the heavenly bodies from him, as also certain other things from the Egyptians, for in his wanderings he had gone even as far as Egypt; and when he came on back to his home-land he was eagerly courted by the rulers and the people of the tribe, because he could make predictions from the celestial signs; and at last he persuaded the king to take him as a partner in the government, on the ground that he was competent to report the will of the gods; and although at the outset he was only made a priest of the god who was most honoured in their country, 298yet afterwards he was even addressed as god, and having taken possession of a certain cavernous place that was inaccessible to anyone else he spent his life there, only rarely meeting with any people outside except the king and his own attendants; and the king cooperated with him, because he saw that the people paid much more attention to himself than before, in the belief that the decrees which he promulgated were in accordance with the counsel of the gods. This custom persisted even down to our own time, because some man of that character was always to be found, who, though in fact only a counsellor to the king, was called god among the Getae. And the people took up the notion that the mountain was sacred and they so call it, but its name is Cogaeonum, like that of the river which flows past it. So, too, at the time when Byrebistas, against whom already the Deified Caesar had prepared to make an expedition, was reigning over the Getae, the office in question was held by Decaeneus, and somehow or other the Pythagorean doctrine of abstention from eating any living thing still survived as taught by Zamolxis.
6 Now although such difficulties as these might fairly be raised concerning what is found in the text of Homer about the Mysians and the "proud Hippemolgi," yet what Apollodorus states in the preface to the Second Book of his work On Ships can by no means be asserted; for he approves the declaration of Eratosthenes, that although both Homer and the other early authors knew the Greek places, they were decidedly unacquainted with those that were far away, since they had no experience either in making long journeys by land or in making voyages by sea. And in support of this Apollodorus says that Homer calls Aulis "rocky" (and so it is), and Eteonus "place of many ridges," and Thisbe "haunt of doves," and Haliartus "grassy," but, he says, neither Homer nor the others knew the places that were far away. At any rate, he says, although about forty rivers flow into the Pontus, Homer mentions not a single one of those that are the most famous, as, for example, the Ister, the Tanaïs, the Borysthenes, the Hypanis, the Phasis, the Thermodon, the Halys; and, besides, he does not mention the Scythians, but invents certain "proud Hippemolgi" and "Galactophagi" and "Abii"; and as for the Paphlagonians of the interior, he reports what he has learned from those who have approached the regions afoot, but he is ignorant of the seaboard, and naturally so, for at that time this sea was not navigable, and was called Axine because of its wintry storms and the ferocity of the tribes that lived around it, and particularly the Scythians, in that they sacrificed strangers, ate their flesh, and used their skulls as drinking-cups; but later it was called "Euxine," when the Ionians founded cities on the seaboard. And, likewise, Homer is also ignorant of the facts about Egypt and Libya, as, for example, about the risings of the Nile and the silting up of the sea, things which he nowhere mentions; neither does he mention the isthmus between the Erythraean and the Egyptian Seas, nor the regions of Arabia and Ethiopia and the ocean, unless one should give heed to Zeno the philosopher when he writes, "And I came to the Ethiopians and Sidonians and Arabians." But this ignorance in Homer's case is not amazing, for those who have lived later than he have been ignorant of many things and have invented marvellous tales: Hesiod, when he speaks of "men who are half-dog," of "long-headed men," and of "Pygmies"; and Alcman, when he speaks of "web-footed men"; and Aeschylus, when he speaks of "dog-headed men," of "men with eyes in their breasts", and of "one-eyed men" (in his Prometheus it is said); and a host of other tales. From these men he proceeds against the historians who speak of the "Rhipaean Mountains," and of "Mt. Ogyium," and of the settlement of the Gorgons and Hesperides, and of the "Land of Meropis" in Theopompus, and the "City of Cimmeris" in Hecataeus, and the "Land of Panchaea" in Euhemerus, and in Aristotle "the river-stones, which are formed of sand but are melted by the rains." And in Libya, Apollodorus continues, there is a "City of Dionysus" which it is impossible for the same man ever to find twice. He censures also those who speak of the Homeric wanderings of Odysseus as having been in the neighbourhood of Sicily; for in that case, says he, one should go on and say that, although the wanderings took place there, the poet, for the sake of mythology, placed them out in Oceanus. And, he adds, the writers in general can be pardoned, but Callimachus cannot be pardoned at all, because he makes a pretence of being a scholar; for he calls Gaudos the "Isle of Calypso" and Corcyra "Scheria." And others he charges with falsifying about "Gerena," and "Acacesium," and "Demus" in Ithaca, and about "Pelethronium" in Pelion, and about Glaucopium in Athens. To these criticisms Apollodorus adds some petty ones of like sort and then stops, but he borrowed most of them from Eratosthenes, and as I have remarked before they are wrong. For while one must concede to Eratosthenes and Apollodorus that the later writers have shown themselves better acquainted with such matters than the men of early times, yet to proceed beyond all moderation as they do, and particularly in the case of Homer, is a thing for which, as it seems to me, one might justly rebuke them and make the reverse statement: that where they are ignorant themselves, there they reproach the poet with ignorance. However, what remains to be said on this subject meets with appropriate mention in my detailed descriptions of the several countries, as also in my general description.
7 Just now I was discussing the Thracians, and the "Mysians, hand-to‑hand fighters, and the proud Hippemolgi, Galactophagi, and Abii, men most just," because I wished to make a comparison between the statements made by Poseidonius and myself and those made by the two men in question. Take first the fact that the argument which they have attempted is contrary to the proposition which they set out to prove; for although they set out to prove that the men of earlier times were more ignorant of regions remote from Greece than the men of more recent times, they showed the reverse, not only in regard to regions remote, but also in regard to places in Greece itself. However, as I was saying, let me put off everything else and look to what is now before me: they say that the poet through ignorance fails to mention the Scythians, or their savage dealings with strangers, in that they sacrifice them, eat their flesh, and use their skulls as drinking-cups, although it was on account of the Scythians that the Pontus was called "Axine," but that he invents certain "proud Hippemolgi, Galactophagi, and Abii, men most just" — people that exist nowhere on earth. How, then, could they call the sea "Axine" if they did not know about the ferocity or about the people who were most ferocious? And these, of course, are the Scythians. And were the people who lived beyond the Mysians and Thracians and Getae not also "Hippemolgi," not also "Galactophagi" and "Abii"? In fact, even now there are Wagon-dwellers and Nomads, so called, who live off their herds, and on milk and cheese, and particularly on cheese made from mare's milk, and know nothing about storing up food or about peddling merchandise either, except the exchange of wares for wares. How, then, could the poet be ignorant of the Scythians if he called certain people "Hippemolgi and Galactophagi"? For that the people of his time were wont to call the Scythians "Hippemolgi," Hesiod, too, is witness in the words cited by Eratosthenes: "The Ethiopians, the Ligurians, and also the Scythians, Hippemolgi." Now wherein is it to be wondered at that, because of the widespread injustice connected with contracts in our country, Homer called "most just" and "proud" those who by no means spend their lives on contracts and money-getting but actually possess all things in common except sword and drinking-cup, and above all things have their wives and their children in common, in the Platonic way? Aeschylus, too, is clearly pleading the cause of the poet when he says about the Scythians: "But the Scythians, law-abiding, eaters of cheese made of mare's milk." And this assumption even now still persists among the Greeks; for we regard the Scythians the most straightforward of men and the least prone to mischief, as also far more frugal and independent of others than we are. And yet our mode of life has spread its change for the worse to almost all peoples, introducing amongst them luxury and sensual pleasures and, to satisfy these vices, base artifices that lead to innumerable acts of greed. So then, much wickedness of this sort has fallen on the barbarian peoples also, on the Nomads as well as the rest; for as the result of taking up a seafaring life they not only have become morally worse, indulging in the practice of piracy and of slaying strangers, but also, because of their intercourse with many peoples, have partaken of the luxury and the peddling habits of those peoples. But though these things seem to conduce strongly to gentleness of manner, they corrupt morals and introduce cunning instead of the straightforwardness which I just now mentioned.
8 Those, however, who lived before our times, and particularly those who lived near the time of Homer, were — and among the Greeks were assumed to be — some such people as Homer describes. And see what Herodotus says concerning that king of the Scythians against whom Dareius made his expedition, and the message which the king sent back to him. See also what Chrysippus says concerning the kings of the Bosporus, the house of Leuco. And not only the Persian letters are full of references to that straightforwardness of which I am speaking but also the memoirs written by the Egyptians, Babylonians, and Indians. And it was on this account that Anacharsis, Abaris, and other men of the sort were in fair repute among the Greeks, because they displayed a nature characterized by complacency, frugality, and justice. But why should I speak of the men of olden times? For when Alexander, the son of Philip, on his expedition against the Thracians beyond the Haemus, invaded the country of the Triballians and saw that it extended as far as the Ister and the island of Peuce in the Ister, and that the parts on the far side were held by the Getae, he went as far as that, it is said, but could not disembark upon the island because of scarcity of boats (for Syrmus, the king of the Triballi had taken refuge there and resisted his attempts); he did, however, cross over to the country of the Getae, took their city, and returned with all speed to his home-land, after receiving gifts from the tribes in question and from Syrmus. And Ptolemaeus, the son of Lagus, says that on this expedition the Celti who lived about the Adriatic joined Alexander for the sake of establishing friendship and hospitality, and that the king received them kindly and asked them when drinking what it was that they most feared, thinking they would say himself, but that they replied they feared no one, unless it were that Heaven might fall on them, although indeed they added that they put above everything else the friendship of such a man as he. And the following are signs of the straightforwardness of the barbarians: first, the fact that Syrmus refused to consent to the debarkation upon the island and yet sent gifts and made a compact of friendship; and, secondly, that the Celti said that they feared no one, and yet valued above everything else the friendship of great men. Again, Dromichaetes was king of the Getae in the time of the successors of Alexander. Now he, when he captured Lysimachus alive, who had made an expedition against him, first pointed out the poverty both of himself and of his tribe and likewise their independence of others, and then bade him not to carry on war with people of that sort but rather to deal with them as friends; and after saying this he first entertained him as a guest, and made a compact of friendship, and then released him. Moreover, Plato in his Republic thinks that those who would have a well-governed city should flee as far as possible from the sea, as being a thing that teaches wickedness, and should not live near it.
9 Ephorus, in the fourth book of his history, the book entitled Europe (for he made the circuit of Europe as far as the Scythians), says towards the end that the modes of life both of the Sauromatae and of the other Scythians are unlike, for, whereas some are so cruel that they even eat human beings, others abstain from eating any living creature whatever. Now the other writers, he says, tell only about their savagery, because they know that the terrible and the marvellous are startling, but one should tell the opposite facts too and make them patterns of conduct, and he himself, therefore, will tell only about those who follow "most just" habits, for there are some of the Scythian Nomads who feed only on mare's milk, and excel all men in justice; and they are mentioned by the poets: by Homer, when he says that Zeus espies the land "of the Galactophagi and Abii, men most just," and by Hesiod, in what is called his Circuit of the Earth, when he says that Phineus is carried by the Storm Winds "to the land of the Galactophagi, who have their dwellings in wagons." Then Ephorus reasons out p207the cause as follows: since they are frugal in their ways of living and not money-getters, they not only are orderly towards one another, because they have all things in common, their wives, children, the whole of their kin and everything, but also remain invincible and unconquered by outsiders, because they have nothing to be enslaved for. And he cites Choerilus also, who, in his The Crossing of the Pontoon-Bridge which was constructed by Dareius, says, "the sheep-tending Sacae, of Scythian stock; but they used to live in wheat-producing Asia; however, they were colonists from the Nomads, law-abiding people." And when he calls Anacharsis "wise," Ephorus says that he belongs to this race, and that he was considered also one of Seven Wise Men because of his perfect self-control and good sense. And he goes on to tell the inventions of Anacharsis — the bellows, the two-fluked anchor and the potter's wheel. These things I tell knowing full well that Ephorus himself does not tell the whole truth about everything; and particularly in his account of Anacharsis (for how could the wheel be his invention, if Homer, who lived in earlier times, knew of it? "As when a potter his wheel that fits in his hands," and so on); but as for those other things, I tell them because I wish to make my point clear that there actually was a common report, which was believed by the men of both early and of later times, that a part of the Nomads, I mean those who had settled the farthest away from the rest of mankind, were "galactophagi," "abii," and "most just," and that they were not an invention of Homer.
It is but fair, too, to ask Apollodorus to account for the Mysians that are mentioned in the verses of Homer, whether he thinks that these too are inventions (when the poet says, "and the Mysians, hand-to‑hand fighters and the proud Hippemolgi"), or takes the poet to mean the Mysians in Asia. Now if he takes the poet to mean those in Asia, he will misinterpret him, as I have said before, but if he calls them an invention, meaning that there were no Mysians in Thrace, he will contradict the facts; for at any rate, even in our own times, Aelius Catus transplanted from the country on the far side of the Ister into Thrace fifty thousand persons from among the Getae, a tribe with the same tongue as the Thracians. And they live there in Thrace now and are called "Moesi" — whether it be that their people of earlier times were so called and that in Asia the name was changed to "Mysi," or (what is more apposite to history and the declaration of the poet) that in earlier times their people in Thrace were called "Mysi." Enough, however, on this subject. I shall now go back to the next topic in the general description.
As for the Getae, then, their early history must be left untold, but that which pertains to our own times is about as follows: Boerebistas a Getan, on setting himself in authority over the tribe, restored the people, who had been reduced to an evil plight by numerous wars, and raised them to such a height through training, sobriety, and obedience to his commands that within only a few years he had established a great empire and subordinated to the Getae most of the neighbouring peoples. And he began to be formidable even to the Romans, because he would cross the Ister with impunity and plunder Thrace as far as Macedonia and the Illyrian country; and he not only laid waste the country of the Celti who were intermingled with the Thracians and the Illyrians, but actually caused the complete disappearance of the Boii who were under the rule of Critasirus, and also of the Taurisci. To help him secure the complete obedience of his tribe he had as his coadjutor Decaeneus, a wizard, a man who not only had wandered through Egypt, but also had thoroughly learned certain prognostics through which he would pretend to tell the divine will; and within a short time he was set up as god (as I said when relating the story of Zamolxis). The following is an indication of their complete obedience: they were persuaded to cut down their vines and to live without wine. However, certain men rose up against Boerebistas and he was deposed before the Romans sent an expedition against him; and those who succeeded him divided the empire into several parts. In fact, only recently, when Augustus Caesar sent an expedition against them, the number of parts into which the empire had been divided was five, though at the time of the insurrection it had been four. Such divisions, to be sure, are only temporary and vary with the times.
But there is also another division of the country which has endured from early times, for some of the people are called Daci, whereas others are called Getae — Getae, those who incline towards the Pontus and the east, and Daci, those who incline in the opposite direction towards Germany and the sources of the Ister. The Daci, I think, were called Daï in early times; whence the slave names "Geta" and "Daüs" which prevailed among the Attic people; for this is more probable than that "Daüs" is from those Scythians who are called "Daae," for they live far away in the neighbourhood of Hyrcania, and it is not reasonable to suppose that slaves were brought into Attica from there; for the Attic people were wont either to call their slaves by the same names as those of the nations from which they were brought (as "Lydus" or "Syrus"), or addressed them by names that were prevalent in their countries (as "Manes" or else "Midas" for the Phrygian, or "Tibius" for the Paphlagonian). But though the tribe was raised to such a height by Boerebistas, it has been completely humbled by its own seditions and by the Romans; nevertheless, they are capable, even to‑day, of sending forth an army of forty thousand men.
The Marisus River flows through their country into the Danuvius, on which the Romans used to convey their equipment for war; the "Danuvius" I say, for so they used to call the upper part of the river from near its sources on to the cataracts, I mean the part which in the main flows through the country, of the Daci, although they give the name "Ister" to the lower part, from the cataracts on to the Pontus, the part which flows past the country of the Getae. The language of the Daci is the same as that of the Getae. Among the Greeks, however, the Getae are better known because the migrations they make to either side of the Ister are continuous, and because they are intermingled with the Thracians and Mysians. And also the tribe of the Triballi, likewise Thracian, has had this same experience, for it has admitted migrations into this country, because the neighbouring peoples force them to emigrate into the country of those who are weaker; that is, the Scythians and Bastarnians and Sauromatians on the far side of the river often prevail to the extent that they actually cross over to attack those whom they have already driven out, and some of them remain there, either in the islands or in Thrace, whereas those on the other side are generally overpowered by the Illyrians. Be that as it may, although the Getae and Daci once attained to very great power, so that they actually could send forth an expedition of two hundred thousand men, they now find themselves reduced to as few as forty thousand, and they have come close to the point of yielding obedience to the Romans, though as yet they are not absolutely submissive, because of the hopes which they base on the Germans, who are enemies to the Romans.
In the intervening space, facing that part of the Pontic Sea which extends from the Ister to the Tyras, lies the Desert of the Getae, wholly flat and waterless, in which Dareius the son of Hystaspis was caught on the occasion when he crossed the Ister to attack the Scythians and ran the risk of perishing from thirst, army and all; however, he belatedly realised his error and turned back. And, later on, Lysimachus, in his expedition against the Getae and King Dromichaetes, not only ran the risk but actually was captured alive; but he again came off safely, because he found the barbarian kind-hearted, as I said before.
Near the outlets of the Ister River is a great island called Peuce; and when the Bastarnians took possession of it they received the appellation of Peucini. There are still other islands which are much smaller; some of these are farther inland than Peuce, while others are near the sea, for the river has seven mouths. The largest of these mouths is what is called the Sacred Mouth, on which one can sail inland a hundred and twenty stadia to Peuce. It was at the lower part of Peuce that Dareius made his pontoon-bridge, although the bridge could have been constructed at the upper part also. The Sacred Mouth is the first mouth on the left as one sails into the Pontus; the others come in order thereafter as one sails along the coast towards the Tyras; and the distance from it to the seventh mouth is about three hundred stadia. Accordingly, small islands are formed between the mouths. Now the three mouths that come next in order after the Sacred Mouth are small, but the remaining mouths are much smaller than it, but larger than any one of the three. According to Ephorus, however, the Ister has only five mouths. Thence to the Tyras, a navigable river, the distance is nine hundred stadia. 306And in the interval are two large lakes — one of them opening into the sea, so that it can also be used as a harbour, but the other mouthless.
At the mouth of the Tyras is what is called the Tower of Neoptolemus, and also what is called the village of Hermonax. And on sailing inland one hundred and forty stadia one comes to two cities, one on each side, Niconia on the right and Ophiussa on the left. But the people who live near the river speak of a city one hundred and twenty stadia inland. Again, at a distance of five hundred stadia from the mouth is the island called Leuce, which lies in the high sea and is sacred to Achilles.
Then comes the Borysthenes River, which is navigable for a distance of six hundred stadia; and, near it, another river, the Hypanis, and off the mouth of the Borysthenes, an island with a harbour. On sailing up the Borysthenes two hundred stadia one comes to a city of the same name as the river, but the same city is also called Olbia; it is a great trading centre and was founded by Milesians. Now the whole country that lies above the said seaboard between the Borysthenes and the Ister consists, first, of the Desert of the Getae; then the country of the Tyregetans; and after it the country of the Iazygian Sarmatians and that of the people called the Basileians and that of the Urgi, who in general are nomads, though a few are interested also in farming; these people, it is said, dwell also along the Ister, often on both sides. In the interior dwell, first, those Bastarnians whose country borders on that of the Tyregetans and Germans — they also being, one might say, of Germanic stock; and they are divided up into several tribes, for a part of them are called Atmoni and Sidoni, while those who took possession of Peuce, the island in the Ister, are called "Peucini," whereas the "Roxolani" (the most northerly of them all) roam the plains between the Tanaïs and the Borysthenes. In fact, the whole country towards the north from Germany as far as the Caspian Sea is, so far as we know it, a plain, but whether any people dwell beyond the Roxolani we do not know. Now the Roxolani, under the leadership of Tasius, carried on war even with the generals of Mithridates Eupator; they came for the purpose of assisting Palacus, the son of Scilurus, as his allies, and they had the reputation of being warlike; yet all barbarian races and light-armed peoples are weak when matched against a well-ordered and well-armed phalanx. At any rate, those people, about fifty thousand strong, could not hold out against the six thousand men arrayed with Diophantus, the general of Mithridates, and most of them were destroyed. They use helmets and corselets made of raw ox-hides, carry wicker shields, and have for weapons spears, bow, and sword; and most of the other barbarians are armed in this way. As for the Nomads, their tents, made of felt, are fastened on the wagons in which they spend their lives; and round about the tents are the herds which afford the milk, cheese, and meat on which they live; and they follow the grazing herds, from time to time moving to other places that have grass, living only in the marsh-meadows about Lake Maeotis in winter, but also in the plains in summer.
The whole of the country has severe winters as far as the regions by the sea that are between the Borysthenes and the mouth of Lake Maeotis; but of the regions themselves that are by the sea the most northerly are the mouth of the Maeotis and, still more northerly, the mouth of the Borysthenes, and the recess of the Gulf of Tamyraces, or Carcinites, which is the isthmus of the Great Chersonesus. The coldness of these regions, albeit the people live in plains, is evident, for they do not breed asses, an animal that is very sensitive to cold; and as for their cattle, some are born without horns, while the horns of others are filed off, for this part of the animal is sensitive to cold; and the horses are small, whereas the sheep are large; and bronze water-jars burst and their contents freeze solid. But the severity of the frosts is most clearly evidenced by what takes place in the region of the mouth of Lake Maeotis: the waterway from Panticapaeum across to Phanagoria is traversed by wagons, so that it is both ice and roadway. And fish that become caught in the ice are obtained by digging with an implement called the "gangame," and particularly the antacaei, which are about the size of dolphins. It is said of Neoptolemus, the general of Mithridates, that in the same strait he overcame the barbarians in a naval engagement in summer and in a cavalry engagement in winter. And it is further said that the vine in the Bosporus region is buried during the winter, the people heaping quantities of earth upon it. And it is said that the heat too becomes severe, perhaps because the bodies of the people are unaccustomed to it, or perhaps because no winds blow on the plains at that time, or else because the air, by reason of its density, becomes superheated (like the effect of the parhelia in the clouds). It appears that Ateas, who waged war with Philip the son of Amyntas, ruled over most of the barbarians in this part of the world.
After the island that lies off the Borysthenes, and next towards the rising sun, one sails to the cape of the Race Course of Achilles, which, though a treeless place, is called Alsos and is sacred to Achilles. Then comes the Race Course of Achilles, a peninsula that lies flat on the sea; it is a ribbon-like stretch of land, as much as one thousand stadia in length, extending towards the east; its maximum breadth is only two stadia, and its minimum only four plethra, and it is only sixty stadia distant from the mainland that lies on either side of the neck. It is sandy, and water may be had by digging. The neck of the isthmus is near the centre of the peninsula and is about forty stadia wide. It terminates in a cape called Tamyrace, which has a mooring-place that faces the mainland. And after this cape comes the Carcinites Gulf. It is a very large gulf, reaching up towards the north as far as one thousand stadia; some say, however, that the distance to its recess is three times as much. The people there are called Taphrians. The gulf is also called Tamyrace, the same name as that of the cape. |
|
|
|
|
7 - 4 Tauric Chersonese (Crimea) 
1 Here is the isthmus which separates what is called Lake Sapra from the sea; it is forty stadia in width and forms what is called the Tauric, or Scythian, Chersonese. Some, however, say that the breadth of the isthmus is three hundred and sixty stadia. But though Lake Sapra is said to be as much as four thousand stadia, it is only a part, the western part, of Lake Maeotis, for it is connected with the latter by a wide mouth. It is very marshy and is scarcely navigable for sewn boats, for the winds readily uncover the shallow places and then cover them with water again, and therefore the marshes are impassable for the larger boats. The gulf contains three small islands, and also some shoals and a few reefs along the coast.
2 As one sails out of the gulf, one comes, on the left, to a small city and another harbour belonging to the Chersonesites. For next in order as one sails along the coast is a great cape which projects towards the south and is a part of the Chersonesus as a whole; and on this cape is situated a city of the Heracleotae, a colony of the Heracleotae who live on the Pontus, and this place itself is called Chersonesus, being distant as one sails along the coast four thousand four hundred stadia from the Tyras. In this city is the temple of the Parthenos, a certain deity; and the cape which is in front of the city, at a distance of one hundred stadia, is also named after this deity, for it is called the Parthenium, and it has a shrine and xoanon of her. Between the city and the cape are three harbours. Then comes the Old Chersonesus, which has been razed to the ground; and after it comes a narrow-mouthed harbour, where, generally speaking, the Tauri, a Scythian tribe, used to assemble their bands of pirates in order to attack all who fled thither for refuge. It is called Symbolon Limen. This harbour forms with another harbour called Ctenus Limen an isthmus forty stadia in width; and this is the isthmus that encloses the Little Chersonesus, which, as I was saying, is a part of the Great Chersonesus and has on it the city of Chersonesus, which bears the same name as the peninsula.
3 This city was at first self-governing, but when it was sacked by the barbarians it was forced to choose Mithridates Eupator as protector. He was then leading an army against the barbarians who lived beyond the isthmus as far as the Borysthenes and the Adrias; this, however, was preparatory to a campaign against the Romans. So, then, in accordance with these hopes of his he gladly sent an army to Chersonesus, and at the same time carried on war against the Scythians, not only against Scilurus, but also the sons of Scilurus — Palacus and the rest — who, according to Poseidonius were fifty in number, but according to Apollonides were eighty. At the same time, also, he not only subdued all these by force, but also established himself as lord of the Bosporus, receiving the country as a voluntary gift from Parisades who held sway over it. So from that time on down to the present the city of the Chersonesites has been subject to the potentates of the Bosporus. Again, Ctenus Limen is equidistant from the city of the Chersonesites and Symbolon Limen. And after Symbolon Limen, as far as the city Theodosia, lies the Tauric seaboard, which is about one thousand stadia in length. It is rugged and mountainous, and is subject to furious storms from the north. And in front of it lies a promontory which extends far out towards the high sea and the south in the direction of Paphlagonia and the city Amastris; it is called Criumetopon. And opposite it lies that promontory of the Paphlagonians, Carambis, which, by means of the strait, which is contracted on both sides, divides the Euxine Pontus into two seas. Now the distance from Carambis to the city of the Chersonesites is two thousand five hundred stadia, but the number to Criumetopon is much less; at any rate, many who have sailed across the strait say that they have seen both promontories, on either side, at the same time. In the mountainous district of the Taurians is also the mountain Trapezus, which has the same name as the city in the neighbourhood of Tibarania and Colchis. And near the same mountainous district is also another mountain, Cimmerius, so called because the Cimmerians once held sway in the Bosporus; and it is because of this fact that the whole of the strait which extends to the mouth of Lake Maeotis is called the Cimmerian Bosporus.
4 After the aforesaid mountainous district is the city Theodosia. It is situated in a fertile plain and has a harbour that can accommodate as many as a hundred ships; this harbour in earlier times was a boundary between the countries of the Bosporians and the Taurians. And the country that comes next after that of Theodosia is also fertile, as far as Panticapaeum. Panticapaeum is the metropolis of the Bosporians and is situated at the mouth of Lake Maeotis. The distance between Theodosia and Panticapaeum is about five hundred and thirty stadia; the district is everywhere productive of grain, and it contains villages, as well as a city called Nymphaeum, which possesses a good harbour. Panticapaeum is a hill inhabited on all sides in a circuit of twenty stadia. To the east it has a harbour, and docks for about thirty ships; and it also has an acropolis. It is a colony of the Milesians. For a long time it was ruled as a monarchy by the dynasty of Leuco, Satyrus, and Parisades, as were p239also all the neighbouring settlements near the mouth of Lake Maeotis on both sides, until Parisades gave over the sovereignty to Mithridates. They were called tyrants, although most of them, beginning with Parisades and Leuco, proved to be equitable rulers. And Parisades was actually held in honour as god. The last of these monarchs also bore the name Parisades, but he was unable to hold out against the barbarians, who kept exacting greater tribute than before, and he therefore gave over the sovereignty to Mithridates Eupator. But since the time of Mithridates the kingdom has been subject to the Romans. The greater part of it is situated in Europe, although a part of it is situated in Asia.
5 The mouth of Lake Maeotis is called the Cimmerian Bosporus. It is rather wide at first — about seventy stadia — and it is here that people cross over from the regions of Panticapaeum to Phanagoria, the nearest city of Asia; but it ends in a much narrower channel. This strait separates Asia from Europe; and so does the Tanaïs River, which is directly opposite and flows from the north into the lake and then into the mouth of it. The river has two outlets into the lake which are about sixty stadia distant from one another. There is also a city which has the same name as the river, and next to Panticapaeum is the greatest emporium of the barbarians. On the left, as one sails into the p241Cimmerian Bosporus, is a little city, Myrmecium, at a distance of twenty stadia from Panticapaeum. And twice this distance from Myrmecium is the village of Parthenium; here the strait is narrowest — about twenty stadia — and on the opposite side, in Asia, is situated a village called Achilleium. Thence, if one sails straight to the Tanaïs and the islands near its outlets, the distance is two thousand two hundred stadia, but if one sails along the coast of Asia, the distance slightly exceeds this; if, however, one sails on the left as far as the Tanaïs, following the coast where the isthmus is situated, the distance is more than three times as much. Now the whole of the seaboard along this coast, I mean on the European side, is desert, but the seaboard on the right is not desert; and, according to report, the total circuit of the lake is nine thousand stadia. The Great Chersonesus is similar to the Peloponnesus both in shape and in size. It is held by the potentates of the Bosporus, though the whole of it has been devastated by continuous wars. But in earlier times only a small part of it — that which is close to the mouth of Lake Maeotis and to Panticapaeum and extends as far as Theodosia — was held by the tyrants of the Bosporians, whereas most of it, as far as the isthmus and the Gulf of Carcinites, was held by the Taurians, a Scythian tribe. And the whole of this country, together with about all the country outside the isthmus as far as the Borysthenes, was called Little Scythia. But on account of the large number of people who left Little Scythia and crossed both the Tyras and the Ister and took up their abode in the land beyond, no small portion of Thrace as well came to be called Little Scythia; the Thracians giving way to them partly as the result of force and partly because of the bad quality of the land, for the greater part of the country is marshy.
6 But the Chersonesus, except for the mountainous district that extends along the sea as far as Theodosia, is everywhere level and fertile, and in the production of grain it is extremely fortunate. At any rate, it yields thirty-fold if furrowed by any sort of a digging-instrument. Further, the people of this region, together with those of the Asiatic districts round about Sindice, used to pay as tribute to Mithridates one hundred and eighty thousand medimni and also two hundred talents of silver. And in still earlier times the Greeks imported their supplies of grain from here, just as they imported their supplies of salt-fish from the lake. Leuco, it is said, once sent from Theodosia to Athens two million one hundred thousand medimni. These same people used to be called Georgi, in the literal sense of the term, because of the fact that the people who were situated beyond them were Nomads and lived not only on meats in general but also on the meat of horses, as also on cheese made from mare's milk, on mare's fresh milk, and on mare's sour milk, which last, when prepared in a particular way, is much relished by them. And this is why the poet calls all the people in that part of the world "Galactophagi." Now although the Nomads are warriors rather than brigands, yet they go to war only for the sake of the tributes due them; for they turn over their land to any people who wish to till it, and are satisfied if they receive in return for the land the tribute they have assessed, which is a moderate one, assessed with a view, not to an abundance, but only to the daily necessities of life; but if the tenants do not pay, the Nomads go to war with them. And so it is that the poet calls these same men at the same time both "just" and "resourceless"; for if the tributes were paid regularly, they would never resort to war. But men who are confident that they are powerful enough either to ward off attacks easily or to prevent any invasion do not pay regularly; such was the case with Asander, who, according to Hypsicrates, walled off the isthmus of the Chersonesus which is near Lake Maeotis and is three hundred and sixty stadia in width, and set up ten towers for every stadium. But though the Georgi of this region are considered to be at the same time both more gentle and civilised, still, since they are money-getters and have to do with the sea, they do not hold aloof from acts of piracy, nor yet from any other such acts of injustice and greed.
7 In addition to the places in the Chersonesus which I have enumerated, there were also the three forts which were built by Scilurus and his sons — the forts which they used as bases of operations against the generals of Mithridates — I mean Palacium, Chabum, and Neapolis. There was also a Fort Eupatorium, founded by Diophantus when he was leading the army for Mithridates. There is a cape about fifteen stadia distant from the wall of the Chersonesites; it forms a very large gulf which inclines towards the city. And above this gulf is situated a lagoon which has salt-works. And here, too, was the Ctenus Harbour. Now it was in order that they might hold out that the besieged generals of the king fortified the place, established a garrison on the cape aforesaid, and filled up that part of the mouth of the gulf which extends as far as the city, so that there was now an easy journey on foot and, in a way, one city instead of two. Consequently, they could more easily beat off the Scythians. But when the Scythians made their attack, near Ctenus, on the fortified wall that extends across the isthmus, and daily filled up the trench with straw, the generals of the king set fire by night to the part thus bridged by day, and held out until they finally prevailed over them. And to‑day everything is subject to whatever kings of the Bosporians the Romans choose to set up.
8 It is a peculiarity of the whole Scythian and Sarmatian race that they castrate their horses to make them easy to manage; for although the horses are small, they are exceedingly quick and hard to manage. As for game, there are deer and wild boars in the marshes, and wild asses and roe deer in the plains. Another peculiar thing is the fact that the eagle is not found in these regions. And among the quadrupeds there is what is called the "colos"; it is between the deer and ram in size, is white, is swifter than they, and drinks through its nostrils into its head, and then from this storage supplies itself for several days, so that it can easily live in the waterless country. Such, then, is the nature of the whole of the country which is outside the Ister between the Rhenus and the Tanaïs Rivers as far as the Pontic Sea and Lake Maeotis. |
|
|
|
|
7 - 5 Illyria and Pannonia 
1 The remainder of Europe consists of the country which is between the Ister and the encircling sea, beginning at the recess of the Adriatic and extending as far as the Sacred Mouth of the Ister. In this country are Greece and the tribes of the Macedonians and of the Epeirotes, and all those tribes above them whose countries reach to the Ister and to the seas on either side, both the Adriatic and the Pontic — to the Adriatic, the Illyrian tribes, and to the other sea as far as the Propontis and the Hellespont, the Thracian tribes and whatever Scythian or Celtic tribes are intermingled with them. But I must make my beginning at the Ister, speaking of the parts that come next in order after the regions which I have already encompassed in my description. These are the parts that border on Italy, on the Alps, and on the counties of the Germans, Dacians, and Getans. This country also might be divided into two parts, for, in a way, the Illyrian, Paeonian, and Thracian mountains are parallel to the Ister, thus completing what is almost a straight line that reaches from the Adrias as far as the Pontus; and to the north of this line are the parts that are between the Ister and the mountains, whereas to the south are Greece and the barbarian country which borders thereon and extends as far as the mountainous country. Now the mountain called Haemus is near the Pontus; it is the largest and highest of all mountains in that part of the world, and cleaves Thrace almost in the centre. Polybius says that both seas are visible from the mountain, but this is untrue, for the distance to the Adrias is great and the things that obscure the view are many. On the other hand, almost the whole of Ardia is near the Adrias. But Paeonia is in the middle, and the whole of it too is high country. Paeonia is bounded on either side, first, towards the Thracian parts, by Rhodope, a mountain next in height to the Haemus, and secondly, on the other side, towards the north, by the Illyrian parts, both the country of the Autariatae and that of the Dardanians. So then, let me speak first of the Illyrian parts, which join the Ister and that part of the Alps which lies between Italy and Germany and begins at the lake which is near the country of the Vindelici, Rhaeti, and Toenii.
2 A part of this country was laid waste by the Dacians when they subdued the Boii and Taurisci, Celtic tribes under the rule of Critasirus. They alleged that the country was theirs, although it was separated from theirs by the River Parisus, which flows from the mountains to the Ister near the country of the Scordisci who are called Galatae, for these too lived intermingled with the Illyrian and the Thracian tribes. But though the Dacians destroyed the Boii and Taurisci, they often used the Scordisci as allies. The remainder of the country in question is held by the Pannonii as far as Segestica and the Ister, on the north and east, although their territory extends still farther in the other directions. The city Segestica, belonging to the Pannonians, is at the confluence of several rivers, all of them navigable, and is naturally fitted to be a base of operations for making war against the Dacians; for it lies beneath that part of the Alps which extends as far as the country of the Iapodes, a tribe which is at the same time both Celtic and Illyrian. And thence, too, flow rivers which bring down into Segestica much merchandise both from other countries and from Italy. For if one passes over Mount Ocra from Aquileia to Nauportus, a settlement of the Taurisci, whither the wagons are brought, the distance is three hundred and fifty stadia, though some say five hundred. Now the Ocra is the lowest part of that portion of the Alps which extends from the country of the Rhaeti to that of the Iapodes. Then the mountains rise again, in the country of the Iapodes, and are called "Albian." In like manner, also, there is a pass which leads over Ocra from Tergeste, a Carnic village, to a marsh called Lugeum. Near Nauportus there is a river, the Corcoras, which receives the cargoes. Now this river empties into the Saüs, and the Saüs into the Dravus, and the Dravus into the Noarus near Segestica. Immediately below Nauportus the Noarus is further increased in volume by the Colapis, which flows from the Albian Mountain through the country of the Iapodes and meets the Danuvius near the country of the Scordisci. The voyage on these rivers is, for the most part, towards the north. The road from Tergeste to the Danuvius is about one thousand two hundred stadia. Near Segestica, and on the road to Italy, are situated both Siscia, a fort, and Sirmium.
3 The tribes of the Pannonii are: the Breuci, the Andizetii, the Ditiones, the Peirustae, the Mazaei, and the Daesitiatae, whose leader is Bato, and also other small tribes of less significance which extend as far as Dalmatia and, as one goes south, almost as far as the land of the Ardiaei. The whole of the mountainous country that stretches alongside Pannonia from the recess of the Adriatic as far as the Rhizonic Gulf and the land of the Ardiaei is Illyrian, falling as it does between the sea and the Pannonian tribes. But this is about where I should begin my continuous geographical circuit — though first I shall repeat a little of what I have said before. I was saying in my geographical circuit of Italy that the Istrians were the first people on the Illyrian seaboard; their country being a continuation of Italy and the country of the Carni; and it is for this reason that the present Roman rulers have advanced the boundary of Italy as far as Pola, an Istrian city. Now this boundary is about eight hundred stadia from the recess, and the distance from the promontory in front of Pola to Ancona, if one keeps the Henetic country on the right, is the same. And the entire distance along the coast of Istria is one thousand three hundred stadia.
4 Next in order comes the voyage of one thousand stadia along the coast of the country of the Iapodes; for the Iapodes are situated on the Albian Mountain, which is the last mountain of the Alps, is very lofty, and reaches down to the country of the Pannonians on one side and to the Adrias on the other. They are indeed a war-mad people, but they have been utterly worn out by Augustus. Their cities are Metulum, Arupini, Monetium, and Vendo. Their lands are poor, the people living for the most part on spelt and millet. Their armour is Celtic, and they are tattooed like the rest of the Illyrians and the Thracians. After the voyage along the coast of the country of the Iapodes comes that along the coast of the country of the Liburni, the latter being five hundred stadia longer than the former; on this voyage is a river, which is navigable inland for merchant-vessels as far as the country of the Dalmatians, and also a Liburnian city, Scardo.
5 There are islands along the whole of the aforesaid seaboard: first, the Apsyrtides, where Medeia is said to have killed her brother Apsyrtus who was pursuing her; and then, opposite the country of the Iapodes, Cyrictica, then the Liburnides, about forty in number; then other islands, of which the best known are Issa, Tragurium (founded by the people of Issa), and Pharos (formerly Paros, founded by the Parians), the native land of Demetrius the Pharian. Then comes the seaboard of the Dalmatians, and also their sea-port, Salo. This tribe is one of those which carried on war against the Romans for a long time; it had as many as fifty noteworthy settlements; and some of these were cities — Salo, Priamo, Ninia, and Sinotium (both the Old and the New), all of which were set on fire by Augustus. And there is Andretium, a fortified place; and also Dalmium (whence the name of the tribe), which was once a large city, but because of the greed of the people Nasica reduced it to a small city and made the plain a mere sheep-pasture. The Dalmatians have the peculiar custom of making a redistribution of land every seven years; and that they make no use of coined money is peculiar to them as compared with the other peoples in that part of the world, although as compared with many other barbarian peoples it is common. And there is Mount Adrium, which cuts the Dalmatian country through the middle into two parts, one facing the sea and the other in the opposite direction. Then come the River Naro and the people who live about it — the Daorizi, the Ardiaei, and the Pleraei. An island called the Black Corcyra and also a city founded by the Cnidians are close to the Pleraei, while Pharos (formerly called Paros, for it was founded by Parians) is close to the Ardiaei.
6 The Ardiaei were called by the men of later times "Vardiaei." Because they pestered the sea through their piratical bands, the Romans pushed them back from it into the interior and forced them to till the soil. But the country is rough and poor and not suited to a farming population, and therefore the tribe has been utterly ruined and in fact has almost been obliterated. And this is what befell the rest of the peoples in that part of the world; for those who were most powerful in earlier times were utterly humbled or were obliterated, as, for example, among the Galatae the Boii and the Scordistae, and among the Illyrians the Autariatae, Ardiaei, and Dardanii, and among the Thracians the Triballi; 316that is, they were reduced in warfare by one another at first and then later by the Macedonians and the Romans.
7 Be this as it may, after the seaboard of the Ardiaei and the Pleraei come the Rhizonic Gulf, and the city Rhizo, and other small towns and also the River Drilo, which is navigable inland towards the east as far as the Dardanian country. This country borders on the Macedonian and the Paeonian tribes on the south, as do also the Autariatae and the Dassaretii — different peoples on different sides being contiguous to one another and to the Autariatae. To the Dardaniatae belong also the Galabrii, among whom is an ancient city, and the Thunatae, whose country joins that of the Medi, a Thracian tribe on the east. The Dardanians are so utterly wild that they dig caves beneath their dung-hills and live there, but still they care for music, always making use of musical instruments, both flutes and stringed instruments. However, these people live in the interior, and I shall mention them again later.
8 After the Rhizonic Gulf comes the city of Lissus, and Acrolissus, and Epidamnus, founded by the Corcyraeans, which is now called Dyrrachium, like the peninsula on which it is situated. Then comes the Apsus River; and then the Aoüs, on which is situated Apollonia, an exceedingly well-governed city, founded by the Corinthians and the Corcyraeans, and ten stadia distant from the river and sixty from the sea. The Aoüs is called "Aeas" by Hecataeus, who says that both the Inachus and the Aeas flow from the same place, the region of Lacmus, or rather from the same subterranean recess, the former towards the south into Argos and the latter towards the west and towards the Adrias. In the country of the Apolloniates is a place called Nymphaeum; it is a rock that gives forth fire; and beneath it flow springs of warm water and asphalt — probably because the clods of asphalt in the earth are burned by the fire. And near by, on a hill, is a mine of asphalt; and the part that is trenched is filled up again in the course of time, since, as Poseidonius says, the earth that is poured into the trenches changes to asphalt. He also speaks of the asphaltic vine-earth which is mined at the Pierian Seleuceia as a cure for the infested vine; for, he says, if it is smeared on together with olive oil, it kills the insects before they can mount the sprouts of the roots; and, he adds, earth of this sort was also discovered in Rhodes when he was in office there as Prytanis, but it required more olive oil. After Apollonia comes Bylliaca, and Oricum and its seaport Panormus, and the Ceraunian Mountains, where the mouth of the Ionian Gulf and the Adrias begins.
9 Now the mouth is common to both, but the Ionian is different in that it is the name of the first part of this sea, whereas Adrias is the name of the inside part of the sea as far as the recess; at the present time, however, Adrias is also the name of the sea as a whole. According to Theopompus, the first name came from a man, a native of Issa, who once ruled over the region, whereas the Adrias was named after a river. The distance from the country of the Liburnians to the Ceraunian Mountains is slightly more than two thousand stadia Theopompus states that the whole voyage from the recess takes six days, and that on foot the length of the Illyrian country is as much as thirty days, though in my opinion he makes the distance too great. And he also says other things that are incredible: first, that the seas are connected by a subterranean passage, from the fact that both Chian and Thasian pottery are found in the Naro River; secondly, that both seas are visible from a certain mountain; and thirdly, when he puts down a certain one of the Liburnides islands as large enough to have a circuit of five hundred stadia; and fourthly, that the Ister empties by one of its mouths into the Adrias. In Eratosthenes, also, are some false hearsay statements of this kind — "popular notions," as Polybius calls them when speaking of him and the other historians.
Now the whole Illyrian seaboard is exceedingly well supplied with harbours, not only on the continuous coast itself but also in the neighbouring islands, although the reverse is the case with that part of the Italian seaboard which lies opposite, since it is harbourless. But both seaboards in like manner are sunny and good for fruits, for the olive and the vine flourish there, except, perhaps, in places here or there that are utterly rugged. But although the Illyrian seaboard is such, people in earlier times made but small account of it — perhaps in part owing to their ignorance of its fertility, though mostly because of the wildness of the inhabitants and their piratical habits. But the whole of the country situated above this is mountainous, cold, and subject to snows, especially the northerly part, so that there is a scarcity of the vine, not only on the heights but also on the levels. These latter are the mountain-plains occupied by the Pannonians; on the south they extend as far as the country of the Dalmatians and the Ardiaei, on the north they end at the Ister, while on the east they border on the country of the Scordisci, that is, on the country that extends along the mountains of the Macedonians and the Thracians.
Now the Autariatae were once the largest and best tribe of the Illyrians. In earlier times they were continually at war with the Ardiaei over the salt-works on the common frontiers. The salt was made to crystallise out of water which in the spring-time flowed at the foot of a certain mountain-glen; for if they drew off the water and stowed it away for five days the salt would become thoroughly crystallised. They would agree to use the salt-works alternately, but would break the agreements and go to war. At one time when the Autariatae had subdued the Triballi, whose territory extended from that of the Agrianes as far as the Ister, a journey of fifteen days, they held sway also over the rest of the Thracians and the Illyrians; but they were overpowered, at first by the Scordisci, and later on by the Romans, who also subdued the Scordisci themselves, after these had been in power for a long time.
The Scordisci lived along the Ister and were divided into two tribes called the Great Scordisci and the Little Scordisci. The former lived between two rivers that empty into the Ister — the Noarus, which flows past Segestica, and the Margus (by some called the Bargus), whereas the Little Scordisci lived on the far side of this river, and their territory bordered on that of the Triballi and the Mysi. The Scordisci also held some of the islands; and they increased to such an extent that they advanced as far as the Illyrian, Paeonian, and Thracian mountains; accordingly, they also took possession of most of the islands in the Ister. And they also had two cities — Heorta and Capedunum. After the country of the Scordisci, along the Ister, comes that of the Triballi and the Mysi (whom I have mentioned before), and also the marshes of that part of what is called Little Scythia which is this side the Ister (these too I have mentioned). These people, as also the Crobyzi and what are called the Troglodytae, live above the region round about Callatis, Tomis, and Ister. Then come the peoples who live in the neighbourhood of the Haemus Mountain and those who live at its base and extend as far as the Pontus — I mean the Coralli, the Bessi, and some of the Medi and Dantheletae. Now these tribes are very brigandish themselves, but the Bessi, who inhabit the greater part of the Haemus Mountain, are called brigands even by the brigands. The Bessi live in huts and lead a wretched life; and their country borders on Mount Rhodope, on the country of the Paeonians, and on that of two Illyrian peoples — the Autariatae, and the Dardanians. Between these and the Ardiaei are the Dassaretii, the Hybrianes, and other insignificant tribes, which the Scordisci kept on ravaging until they had depopulated the country and made it full of trackless forests for a distance of several days' journey. |
|
|
|
|
7 - 6 Eastern Dacia and the north shore of the Propontis 
1 The remainder of the country between the Ister and the mountains on either side of Paeonia consists of that part of the Pontic seaboard which extends from the Sacred Mouth of the Ister as far as the mountainous country in the neighbourhood of the Haemus and as far as the mouth at Byzantium. And just as, in traversing the Illyrian seaboard, I proceeded as far as the Ceraunian Mountains, because, although they fall outside the mountainous country of Illyria, they afford an appropriate limit, and just as I determined the positions of the tribes of the interior by these mountains, because I thought that marks of this kind would be more significant as regards both the description at hand and what was to follow, so also in this case the seaboard, even though it falls beyond the mountain-line, will nevertheless end at an appropriate limit — the mouth of the Pontus — as regards both the description at hand and that which comes next in order. So, then, if one begins at the Sacred Mouth of the Ister and keeps the continuous seaboard on the right, one comes, at a distance of five hundred stadia, to a small town, Ister, founded by the Milesians; then, at a distance of two hundred and fifty stadia, to a second small town, Tomis; then, at two hundred and eighty stadia, to a city Callatis, a colony of the Heracleotae; then, at one thousand three hundred stadia, to Apollonia, a colony of the Milesians. The greater part of Apollonia was founded on a certain isle, where there is a temple of Apollo, from which Marcus Lucullus carried off the colossal statue of Apollo, a work of Calamis, which he set up in the Capitolium. In the interval between Callatis and Apollonia come also Bizone, of which a considerable part was engulfed by earthquakes, Cruni, Odessus, a colony of the Milesians, and Naulochus, a small town of the Mesembriani. Then comes the Haemus Mountain, which reaches the sea here; then Mesembria, a colony of the Megarians, formerly called "Menebria" (that is, "city of Menas," because the name of its founder was Menas, while "bria" is the word for "city" in the Thracian language. In this way, also, the city of Selys is called Selybria and Aenus was once called Poltyobria). Then come Anchiale, a small town belonging to the Apolloniatae, and Apollonia itself. On this coast-line is Cape Tirizis, a stronghold, which Lysimachus once used as a treasury. Again, from Apollonia to the Cyaneae the distance is about one thousand five hundred stadia; and in the interval are Thynias, a territory belonging to the Apolloniatae (Anchiale, which also belongs to the Apolloniatae), and also Phinopolis and Andriaca, which border on Salmydessus. Salmydessus is a desert and stony beach, harbourless and wide open to the north winds, and in length extends as far as the Cyaneae, a distance of about seven hundred stadia; and all who are cast ashore on this beach are plundered by the Astae, a Thracian tribe who are situated above it. The Cyaneae are two islets near the mouth of the Pontus, one close to Europe and the other to Asia; they are separated by a channel of about twenty stadia and are twenty stadia distant both from the temple of the Byzantines and from the temple of the Chalcedonians. And this is the narrowest part of the mouth of the Euxine, for when one proceeds only ten stadia farther one comes to a headland which makes the strait only five stadia in width, and then the strait opens to a greater width and begins to form the Propontis.
2 Now the distance from the headland that makes the strait only five stadia wide to the harbour which is called "Under the Fig-tree" is thirty-five stadia; and thence to the Horn of the Byzantines, five stadia. The Horn, which is close to the wall of the Byzantines, is a gulf that extends approximately towards the west for a distance of sixty stadia; it resembles a stag's horn, for it is split into numerous gulfs — branches, as it were. The pelamydes rush into these gulfs and are easily caught — because of their numbers, the force of the current that drives them together, and the narrowness of the gulfs; in fact, because of the narrowness of the area, they are even caught by hand. Now these fish are hatched in the marshes of Lake Maeotis, and when they have gained a little strength they rush out through the mouth of the lake in schools and move along the Asian shore as far as Trapezus and Pharnacia. It is here that the catching of the fish first takes place, though the catch is not considerable, for the fish have not yet grown to their normal size. But when they reach Sinope, they are mature enough for catching and salting. Yet when once they touch the Cyaneae and pass by these, the creatures take such fright at a certain white rock which projects from the Chalcedonian shore that they forthwith turn to the opposite shore. There they are caught by the current, and since at the same time the region is so formed by nature as to turn the current of the sea there to Byzantium and the Horn at Byzantium, they naturally are driven together thither and thus afford the Byzantines and the Roman people considerable revenue. But the Chalcedonians, though situated near by, on the opposite shore, have no share in this abundance, because the pelamydes do not approach their harbours; hence the saying that Apollo, when the men who founded Byzantium at a time subsequent to the founding of Chalcedon by the Megarians consulted the oracle, ordered them to "make their settlement opposite the blind," thus calling the Chalcedonians "blind", because, although they sailed the regions in question at an earlier time, they failed to take possession of the country on the far side, with all its wealth, and chose the poorer country.
I have now carried my description as far as Byzantium, because a famous city, lying as it does very near to the mouth, marked a better-known limit to the coasting-voyage from the Ister. And above Byzantium is situated the tribe of the Astae, in whose territory is a city Calybe, where Philip the son of Amyntas settled the most villainous people of his kingdom. |
|
|
|
|
7 - Epirus 
These alone, then, of all the tribes that are marked off by the Ister and by the Illyrian and Thracian mountains, deserve to be mentioned, occupying as they do the whole of the Adriatic seaboard beginning at the recess, and also the seaboard that is called "the left parts of the Pontus," and extends from the Ister River as far as Byzantium. But there remain to be described the southerly parts of the aforesaid mountainous country and next thereafter the districts that are situated below them, among which are both Greece and the adjacent barbarian country as far as the mountains. Now Hecataeus of Miletus says of the Peloponnesus that before the time of the Greeks it was inhabited by barbarians. Yet one might say that in the ancient times the whole of Greece was a settlement of barbarians, if one reasons from the traditions themselves: Pelops brought over peoples from Phrygia to the Peloponnesus that received its name from him; and Danaüs from Egypt; whereas the Dryopes, the Caucones, the Pelasgi, the Leleges, and other such peoples, apportioned among themselves the parts that are inside the isthmus — and also the parts outside, for Attica was once held by the Thracians who came with Eumolpus, Daulis in Phocis by Tereus, Cadmeia by the Phoenicians who came with Cadmus, and Boeotia itself by the Aones and Temmices and Hyantes. According to Pindar, there was a time when the Boeotian tribe was called "Syes." Moreover, the barbarian origin of some is indicated by their names — Cecrops, Codrus, Aïclus, Cothus, Drymas, and Crinacus. And even to the present day the Thracians, Illyrians, and Epeirotes live on the flanks of the Greeks (though this was still more the case formerly than now); indeed most of the country that at the present time is indisputably Greece is held by the barbarians — Macedonia and certain parts of Thessaly by the Thracians, and the parts above Acarnania and Aetolia by the Thesproti, the Cassopaei, the Amphilochi, the Molossi, and the Athamanes — Epeirotic tribes.
2 As for the Pelasgi, I have already discussed them. As for the Leleges, some conjecture that they are the same as the Carians, and others that they were only fellow-inhabitants and fellow-soldiers of these; and this, they say, is why, in the territory of Miletus, certain settlements are called settlements of the Leleges, and why, in many places of Caria, tombs of the Leleges and deserted forts, known as "Lelegian forts," are so called. However, the whole of what is now called Ionia used to be inhabited by Carians and Leleges; but the Ionians themselves expelled them and took possession of the country, although in still earlier times the captors of Troy had driven the Leleges from the region about Ida that is near Pedasus and the Satnioïs River. So then, the very fact that the Leleges made common cause with the Carians might be considered a sign that they were barbarians. And Aristotle, in his Polities, also clearly indicates that they led a wandering life, not only with the Carians, but also apart from them, and from earliest times; for instance, in the Polity of the Acarnanians he says that the Curetes held a part of the country, whereas the Leleges, and then the Teleboae, held the westerly part; and in the Polity of the Aetolians (and likewise in that of the Opuntii and the Megarians) he calls the Locri of to‑day Leleges and says that they took possession of Boeotia too; again, in the Polity of the Leucadians he names a certain indigenous Lelex, and also Teleboas, the son of a daughter of Lelex, and twenty-two sons of Teleboas, some of whom, he says, dwelt in Leucas. But in particular one might believe Hesiod when he says concerning them: "For verily Locrus was chieftain of the peoples of the Leleges, whom once Zeus the son of Cronus, who knoweth devices imperishable, gave to Deucalion — peoples picked out of earth"; for by his etymology he seems to me to hint that from earliest times they were a collection of mixed peoples and that this was why the tribe disappeared. And the same might be said of the Caucones, since now they are nowhere to be found, although in earlier times they were settled in several places.
3 Now although in earlier times the tribes in question were small, numerous, and obscure, still, because of the density of their population and because they lived each under its own king, it was not at all difficult to determine their boundaries; but now that most of the country has become depopulated and the settlements, particularly the cities, have disappeared from sight, it would do no good, even if one could determine their boundaries with strict accuracy, to do so, because of their obscurity and their disappearance. This process of disappearing began a long time ago, and has not yet entirely ceased in many regions because the people keep revolting; indeed, the Romans, after being set up as masters by the inhabitants, encamp in their very houses. Be this as it may, Polybius says that Paulus, after his subjection of Perseus and the Macedonians, destroyed seventy cities of the Epeirotes (most of which, he adds, belonged to the Molossi), and reduced to slavery one hundred and fifty thousand people. Nevertheless, I shall attempt, in so far as it is appropriate to my description and as my knowledge reaches, to traverse the several different parts, beginning at the seaboard of the Ionian Gulf — that is, where the voyage out of the Adrias ends.
4 Of this seaboard, then, the first parts are those about Epidamnus and Apollonia. From Apollonia to Macedonia one travels the Egnatian Road, towards the east; it has been measured by Roman miles and marked by pillars as far as Cypsela and the Hebrus River — a distance of five hundred and thirty-five miles. Now if one reckons as most people do, eight stadia to the mile, there would be four thousand two hundred and eighty stadia, whereas if one reckons as Polybius does, who adds two plethra, which is a third of a stadium, to the eight stadia, one must add one hundred and seventy-eight stadia — the third of the number of miles. And it so happens that travellers setting out from Apollonia and Epidamnus meet at an equal distance from the two places on the same road.408 Now although the road as a whole is called the Egnatian Road, the first part of it is called the Road to Candavia (an Illyrian mountain) and passes through Lychnidus, a city, and Pylon, a place on the road which marks the boundary between the Illyrian country and Macedonia. From Pylon the road runs to Barnus through Heracleia and the country of the Lyncestae and that of the Eordi into Edessa and Pella and as far as Thessaloniceia; and the length of this road in miles, according to Polybius, is two hundred and sixty-seven. So then, in travelling this road from the region of Epidamnus and Apollonia, one has on the right the Epeirotic tribes whose coasts are washed by the Sicilian Sea and extend as far as the Ambracian Gulf, and, on the left, the mountains of Illyria, which I have already described in detail, and those tribes which live along them and extend as far as Macedonia and the country of the Paeonians. Then, beginning at the Ambracian Gulf, all the districts which, one after another, incline towards the east and stretch parallel to the Peloponnesus belong to Greece; they then leave the whole of the Peloponnesus on the right and project into the Aegaean Sea. But the districts which extend from the beginning of the Macedonian and the Paeonian mountains as far as the Strymon4River are inhabited by the Macedonians, the Paeonians, and by some of the Thracian mountaineers; whereas the districts beyond the Strymon, extending as far as the mouth of the Pontus and the Haemus, all belong to the Thracians, except the seaboard. This seaboard is inhabited by Greeks, some being situated on the Propontis, others on the Hellespont and the Gulf of Melas, and others on the Aegaean. The Aegaean Sea washes Greece on two sides: first, the side that faces towards the east and stretches from Sunium, towards the north as far as the Thermaean Gulf and Thessaloniceia, a Macedonian city, which at the present time is more populous than any of the rest; and secondly, the side that faces towards the south, I mean the Macedonian country, extending from Thessaloniceia as far as the Strymon. Some, however, also assign to Macedonia the country that extends from the Strymon as far as the Nestus River, since Philip was so specially interested in these districts that he appropriated them to himself, and since he organized very large revenues from the mines and the other natural resources of the country. But from Sunium to the Peloponnesus lie the Myrtoan, the Cretan, and the Libyan Seas, together with their gulfs, as far as the Sicilian Sea; and this last fills out the Ambracian, the Corinthian, and the Crisaean Gulfs.
5 Now as for the Epeirotes, there are fourteen tribes of them, according to Theopompus, but of these the Chaones and the Molossi are the most famous, because of the fact that they once ruled over the whole of the Epeirote country — the Chaones earlier and later the Molossi; and the Molossi grew to still greater power, partly because of the kinship of their kings, who belonged to the family of the Aeacidae, and partly because of the fact that the oracle at Dodona was in their country, an oracle both ancient and renowned. Now the Chaones and the Thesproti and, next in order after these, the Cassopaei (these, too, are Thesproti) inhabit the seaboard which extends from the Ceraunian Mountains as far as the Ambracian Gulf, and they have a fertile country. The voyage, if one begins at the country of the Chaones and sails towards the rising sun and towards the Ambracian and Corinthian Gulfs, keeping the Ausonian Sea on the right and Epeirus on the left, is one thousand three hundred stadia, that is, from the Ceraunian Mountains to the mouth of the Ambracian Gulf. In this interval is Panormus, a large harbour at the centre of the Ceraunian Mountains, and after these mountains one comes to Onchesmus, another harbour, opposite which lie the western extremities of Corcyraea, and then still another harbour, Cassiope, from which the distance to Brentesium is one thousand seven hundred stadia. And the distance to Taras from another cape, which is farther south than Cassiope and is called Phalacrum, is the same. After Onchesmus comes Poseidium, and also Buthrotum (which is at the mouth of what is called Pelodes Harbour, and has alien settlers consisting of Romans), and the Sybota. The Sybota are small islands situated only a short distance from the mainland and opposite Leucimma, the eastern headland of Corcyraea. And there are still other small islands as one sails along this coast, but they are not worth mentioning. Then comes Cape Cheimerium, and also Glycys Limen, into which the River Acheron empties. The Acheron flows from the Acherusian Lake and receives several rivers as tributaries, so that it sweetens the waters of the gulf. And also the Thyamis flows near by. Cichyrus, the Ephyra of former times, a city of the Thesprotians, lies above this gulf, whereas Phoenice lies above that gulf which is at Buthrotum. Near Cichyrus is Buchetium, a small town of the Cassopaeans, which is only a short distance above the sea; also Elatria, Pandosia, and Batiae, which are in the interior, though their territory reaches down as far as the gulf. Next in order after Glycys Limen come two other harbours — Comarus, the nearer and smaller of the two, which forms an isthmus of sixty stadia with the Ambracian Gulf, and Nicopolis, a city founded by Augustus Caesar, and the other, the more distant and larger and better of the two, which is near the mouth of the gulf and is about twelve stadia distant from Nicopolis.
6 Next comes the mouth of the Ambracian Gulf. Although the mouth of this gulf is but slightly more than four stadia wide, the circumference is as much as three hundred stadia; and it has good harbours everywhere. That part of the country which is on the right as one sails in is inhabited by the Greek Acarnanians. Here too, near the mouth, is the sacred precinct of the Actian Apollo — a hill on which the temple stands; and at the foot of the hill is a plain which contains a sacred grove and a naval station, the naval station where Caesar dedicated as first fruits of his victory the squadron of ten ships — from vessel with single bank of oars to vessel with ten; however, not only the boats, it is said, but also the boat-houses have been wiped out by fire. On the left of the mouth are Nicopolis and the country of the Epeirote Cassopaeans, which extends as far as the recess of the gulf near Ambracia. Ambracia lies only a short distance above the recess; it was founded by Gorgus, the son of Cypselus. The River Aratthus flows past Ambracia; it is navigable inland for only a few stadia, from the sea to Ambracia, although it rises in Mount Tymphe and the Paroraea. Now this city enjoyed an exceptional prosperity in earlier times (at any rate the gulf was named after it), and it was adorned most of all by Pyrrhus, who made the place his royal residence. In later times, however, the Macedonians and the Romans, by their continuous war, so completely reduced both this and the other Epeirote cities because of their disobedience that finally Augustus, seeing that the cities had utterly failed, settled what inhabitants were left in one city together — the city on this gulf which was called by him Nicopolis; and he so named it after the victory which he won in the naval battle before the mouth of the gulf over Antonius and Cleopatra the queen of the Egyptians, who was also present at the fight. Nicopolis is populous, and its numbers are increasing daily, since it has not only a considerable territory and the adornment taken from the spoils of the battle, but also, in its suburbs, the thoroughly equipped sacred precinct — one part of it being in a sacred grove that contains a gymnasium and a stadium for the celebration of the quinquennial games, the other part being on the hill that is sacred to Apollo and lies above the grove. These games — the Actia, sacred to Actian Apollo — have been designated as Olympian, and they are superintended by the Lacedaemonians. The other settlements are dependencies of Nicopolis. In earlier times also the Actian Games were wont to be celebrated in honour of the god by the inhabitants of the surrounding country — games in which the prize was a wreath — but at the present time they have been set in greater honour by Caesar.
7 After Ambracia comes Argos Amphilochicum, founded by Alcmaeon and his children. According to Ephorus, at any rate, Alcmaeon, after the expedition of the Epigoni against Thebes, on being invited by Diomedes, went with him into Aetolia and helped him acquire both this country and Acarnania; and when Agamemnon summoned them to the Trojan war, Diomedes went, but Alcmaeon stayed in Acarnania, founded Argos, and named it Amphilochicum after his brother; and he named the river which flows through the country into the Ambracian Gulf "Inachus," after the river in the Argeian country. But according to Thucydides, Amphilochus himself, after his return from Troy, being displeased with the state of affairs at Argos, passed on into Acarnania, and on succeeding to his brother's dominion founded the city that is named after him.
8 The Amphilochians are Epeirotes; and so are the peoples who are situated above them and border on the Illyrian mountains, inhabiting a rugged country — I mean the Molossi, the Athamanes, the Aethices, the Tymphaei, the Orestae, and also the Paroraei and the Atintanes, some of them being nearer to the Macedonians and others to the Ionian Gulf. It is said that Orestes once took possession of Orestias — when in exile on account of the murder of his mother — and left the country bearing his name; and that he also founded a city and called it Argos Oresticum. But the Illyrian tribes which are near the southern part of the mountainous country and those which are above the Ionian Gulf are intermingled with these peoples; for above Epidamnus and Apollonia as far as the Ceraunian Mountains dwell the Bylliones, the Taulantii, the Parthini, and the Brygi. Somewhere near by are also the silver mines of Damastium, around which the Dyestae and the Enchelii (also called Sesarethii) together established their dominion; and near these people are also the Lyncestae, the territory Deuriopus, Pelagonian Tripolitis, the Eoerdi, Elimeia, and Eratyra. In earlier times these peoples were ruled separately, each by its own dynasty. For instance, it was the descendants of Cadmus and Harmonia who ruled over the Enchelii; and the scenes of the stories told about them are still pointed out there. These people, I say, were not ruled by men of native stock; and the Lyncestae became subject to Arrabaeus, who was of the stock of the Bacchiads (Eurydice, the mother of Philip, Amyntas' son, was Arrabaeus' daughter's daughter and Sirra was his daughter); and again, of the Epeirotes, the Molossi became subject to Pyrrhus, the son of Neoptolemus the son of Achilles, and to his descendants, who were Thessalians. But the rest were ruled by men of native stock. Then, because one tribe or another was always getting the mastery over others, they all ended in the Macedonian empire, except a few who dwelt above the Ionian Gulf. And in fact the regions about Lyncus, Pelagonia, Orestias, and Elimeia, used to be called Upper Macedonia, though later on they were by some also called Free Macedonia. But some go so far as to call the whole of the country Macedonia, as far as Corcyra, at the same time stating as their reason that in tonsure, language, short cloak, and other things of the kind, the usages of the inhabitants are similar, although, they add, some speak both languages. But when the empire of the Macedonians was broken up, they fell under the power of the Romans. And it is through the country of these tribes that the Egnatian Road runs, which begins at Epidamnus and Apollonia. Near the Road to Candavia are not only the lakes which are in the neighbourhood of Lychnidus, on the shores of which are salt-fish establishments that are independent of other waters, but also a number of rivers, some emptying into the Ionian Gulf and others flowing in a southerly direction — I mean the Inachus, the Aratthus, the Acheloüs and the Evenus (formerly called the Lycormas); the Aratthus emptying into the Ambracian Gulf, the Inachus into the Acheloüs, the Acheloüs itself and the Evenus into the sea — the Acheloüs after traversing Acarnania and the Evenus after traversing Aetolia. But the Erigon, after receiving many streams from the Illyrian mountains and from the countries of the Lyncestae, Brygi, Deuriopes, and Pelagonians, empties into the Axius.
9 In earlier times there were also cities among these tribes; at any rate, Pelagonia used to be called Tripolitis, one of which was Azorus; and all the cities of the Deuriopes on the Erigon River were populous, among which were Bryanium, Alalcomenae, and Stubara. And Cydrae belonged to the Brygi, while Aeginium, on the border of Aethicia and Tricca, belonged to the Tymphaei. When one is already near to Macedonia and to Thessaly, and in the neighbourhood of the Poeus and the Pindus Mountains, one comes to the country of the Aethices and to the sources of the Peneius River, the possession of which is disputed by the Tymphaei and those Thessalians who live at the foot of the Pindus, and to the city Oxineia, situated on the Ion River one hundred and twenty stadia from Azorus in Tripolitis. Near by are Alalcomenae, Aeginium, Europus, and the confluence of the Ion River with the Peneius. Now although in those earlier times, as I have said, all Epeirus and the Illyrian country were rugged and full of mountains, such as Tomarus and Polyanus and several others, still they were populous; but at the present time desolation prevails in most parts, while the parts are still inhabited survive only in villages and in ruins. And even the oracle at Dodona, like the rest, is virtually extinct.
This oracle, according to Ephorus, was founded by the Pelasgi. And the Pelasgi are called the earliest of all peoples who have held dominion in Greece. And the poet speaks in this way: "O Lord Zeus, Dodonaean, Pelasgian"; and Hesiod: "He came to Dodona and the oak-tree, seat of the Pelasgi." The Pelasgi I have already discussed in my description of Tyrrhenia; and as for the people who lived in the neighbourhood of the temple of Dodona, Homer too makes it perfectly clear from their mode of life, when he calls them "men with feet unwashen, men who sleep upon the ground," that they were barbarians; but whether one should call them "Helli," as Pindar does, or "Selli," as is conjectured to be the true reading in Homer, is a question to which the text, since it is doubtful, does not permit a positive answer. Philochorus says that the region round about Dodona, like Euboea, was called Hellopia, and that in fact Hesiod speaks of it in this way: "There is a land called Hellopia, with many a corn-fieldº and with goodly meadows; on the edge of this land a city called Dodona hath been built." It is thought, Apollodorus says, that the land was so called from the marshes around the temple; as for the poet, however, Apollodorus takes it for granted that he did not call the people who lived about the temple "Helli," but "Selli," since (Apollodorus adds) the poet also named a certain river Selleeïs. He names it, indeed, when he says, "From afar, out of Ephyra, from the River Selleeïs"; however, as Demetrius of Scepsis says, the poet is not referring to the Ephyra among the Thesprotians, but to that among the Eleians, for the Selleeïs is among the Elians, he adds, and there is no Selleeïs among the Thesprotians, nor yet among the Molossi. And as for the myths that are told about the oak-tree and the doves, and any other myths of the kind, although they, like those told about Delphi, are in part more appropriate to poetry, yet they also in part properly belong to the present geographical description.
In ancient times, then, Dodona was under the rule of the Thesprotians; and so was Mount Tomarus, or Tmarus (for it is called both ways), at the base of which the temple is situated. And both the tragic poets and Pindar have called Dodona "Thesprotian Dodona." But later on it came under the rule of the Molossi. And it is after the Tomarus, people say, that those whom the poet calls interpreters of Zeus — whom he also calls "men with feet unwashen, men who sleep upon the ground" — were called "tomouroi"; and in the Odyssey some so write the words of Amphinomus, when he counsels the wooers not to attack Telemachus until they inquire of Zeus: "If the tomouroi of great Zeus approve, I myself shall slay, and I shall bid all the rest to aid, whereas if god averts it, I bid you stop." For it is better, they argue, to write "tomouroi" than "themistes"; at any rate, nowhere in the poet are the oracles called "themistes," but it is the decrees, statutes, and laws that are so called; and the people have been called "tomouroi" because "tomouroi" is a contraction of "tomarouroi," the equivalent of "tomarophylakes." Now although the more recent critics say "tomouri," yet in Homer one should interpret "themistes" (and also "boulai") in a simpler way, though in a way that is a misuse of the term, as meaning those orders and decrees that are oracular, just as one also interprets "themistes" as meaning those that are made by law. For example, such is the case in the following: "to give ear to the decree of Zeus from the oak-tree of lofty foliage."
At the outset, it is true, those who uttered the prophecies were men (this too perhaps the poet indicates, for he calls them "hypophetae," and the prophets might be ranked among these), but later on three old women were designated as prophets, after Dione also had been designated as temple-associate of Zeus. Suidas, however, in his desire to gratify the Thessalians with mythical stories, says that the temple was transferred from Thessaly, from the part of Pelasgia which is about Scotussa (and Scotussa does belong to the territory called Thessalia Pelasgiotis), and also that most of the women whose descendants are the prophetesses of to‑day went along at the same time; and it is from this fact that Zeus was also called "Pelasgian." But Cineas tells a story that is still more mythical. . . .
The rest of Book VII, containing the description of Macedonia and Thrace, has been lost, but the following fragments, gathered chiefly from the Vatican and Palatine Epitomes and from Eustathius, seem to preserve most of the original matter. |
|
|
|
|
7 - 8 Fragments 
0 Cineas says that there was a city in Thessaly, and that an oak-tree and the oracle of Zeus were transferred from there to Epeirus.
In Earlier times the oracle was in the neighbourhood of Scotussa, a city of Pelasgiotis; but when the tree was set on fire by certain people the oracle was transferred in accordance with an oracle which Apollo gave out at Dodona. However, he gave out the oracle, not through words, but through certain symbols, as was the case at the oracle of Zeus Ammon in Libya. Perhaps there was something exceptional about the flight of the three pigeons from which the priestesses were wont to make observations and to prophesy. It is further said that in the language of the Molossians and the Thesprotians old women are called "peliai" and old men "pelioi." And perhaps the much talked of Peleiades were not birds, but three old women who busied themselves about the temple.
I mentioned Scotussa also in my description of Dodona and of the oracle in Thessaly, because the oracle was originally in the latter region.
According to the Geographer, a sacred oak-tree is revered in Dodona, because it was thought to be the earliest plant created and the first to supply men with food. And the same writer also says in reference to the oracular doves there, as they are called, that the doves are observed for the purposes of augury, just as there were some seers who divined from ravens.
Among the Thesprotians and the Molossians old women are called "peliai" and old men "pelioi," as is also the case among the Macedonians; at any rate, those people call their dignitaries "peligones" (compare the "gerontes" among the Laconians and the Massaliotes). And this, it is said, is the origin of the myth about the pigeons in the Dodonaean oak-tree.
3 The proverbial phrase, "the copper vessel in Dodona," originated thus: In the temple was a copper vessel with a statue of a man situated above it and holding a copper scourge, dedicated by the Corcyraeans; the scourge was three-fold and wrought in chain fashion, with bones strung from it; and these bones, striking the copper vessel continuously when they were swung by the winds, would produce tones so long that anyone who measured the time from the beginning of the tone to the end could count to four hundred. Whence, also, the origin of the proverbial term, "the scourge of the Corcyraeans."
4 1 Paeonia is on the east of these tribes and on the west of the Thracian mountains, but it is situated on the north of the Macedonians; and, by the road that runs through the city Gortynium and Stobi, it affords a passage to . . . (through which the Axius flows, and thus makes difficult the passage from Paeonia to Macedonia — just as the Peneius flows through Tempe and thus fortifies Macedonia on the side of Greece). And on the south Paeonia borders on the countries of the Autariatae, the Dardanii, and the Ardiaei; and it extends as far as the Strymon.
5 1 The Haliacmon flows into the Thermaean Gulf.
6 1 Orestis is of considerable extent, and has a large mountain which reaches as far as Mount Corax in Aetolia and Mount Parnassus. About this mountain dwell the Orestae themselves, the Tymphaei, and the Greeks outside the isthmus that are in the neighbourhood of Parnassus, Oeta, and Pindus. As a whole the mountain is called by a general name, Boëum, but taken part by part it has many names. People say that from the highest peaks one can see both the Aegaean Sea and the Ambracian and Ionian Gulfs, but they exaggerate, I think. Mount Pteleum, also, is fairly high; it is situated around the Ambracian Gulf, extending on one side as far as the Corcyraean country and on the other to the sea at Leucas.
7 1 Corcyra is proverbially derided as a joke because it was humbled by its many wars.
8 1 Corcyra in early times enjoyed a happy lot and had a very large naval force, but was ruined by certain wars and tyrants. And later on, although it was set free by the Romans, it got no commendation, but instead, as an object of reproach, got a proverb: "Corcyra is free, dung where thou wilt."
9 1 There remain of Europe, first, Macedonia and the parts of Thrace that are contiguous to it and extend as far as Byzantium; secondly, Greece; and thirdly, the islands that are close by. Macedonia, of course, is a part of Greece, yet now, since I am following the nature and shape of the places geographically, I have decided to classify it apart from the rest of Greece and to join it with that part of Thrace which borders on it and extends as far as the mouth of the Euxine and the Propontis. Then, a little further on, Strabo mentions Cypsela and the Hebrus River, and also describes a sort of parallelogram in which the whole of Macedonia lies.
1 Macedonia is bounded, first, on the west, by the coastline of the Adrias; secondly, on the east, by the meridian line which is parallel to this coastline and runs through the outlets of the Hebrus River and through the city Cypsela; thirdly, on the north, by the imaginary straight line which runs through the Bertiscus Mountain, the Scardus, the Orbelus, the Rhodope, and the Haemus; for these mountains, beginning at the Adrias, extend on a straight line as far as the Euxine, thus forming towards the south a great peninsula which comprises Thrace together with Macedonia, Epeirus, and Achaea; and fourthly, on the south, by the Egnatian Road, which runs from the city Dyrrhachium towards the east as far as Thessaloniceia. And thus the shape of Macedonia is very nearly that of a parallelogram.
What is now called Macedonia was in earlier times called Emathia. And it took its present name from Macedon, one of its early chieftains. And there was also a city Emathia close to the sea. Now a part of this country was taken and held by certain of the Epeirotes and the Illyrians, but most of it by the Bottiaei and the Thracians. The Bottiaei came from Crete originally, so it is said, along with Botton as chieftain. As for the Thracians, the Pieres inhabited Pieria and the region about Olympus; the Paeones, the region on both sides of the Axius River, which on that account is called Amphaxitis; the Edoni and Bisaltae, the rest of the country as far as the Strymon. Of these two peoples the latter are called Bisaltae alone, whereas a part of the Edoni are called Mygdones, a part Edones, and a part Sithones. But of all these tribes the Argeadae, as they are called, established themselves as masters, and also the Chalcidians of Euboea; for the Chalcidians of Euboea also came over to the country of the Sithones and jointly peopled about thirty cities in it, although later on the majority of them were ejected and came together into one city, Olynthus; and they were named the Thracian Chalcidians.
a The ethnic of Botteia is spelled with the i, according to Strabo in his Seventh Book. And the city is called after Botton the Cretan.
b Amphaxion. Two parts of speech. A city. The ethnic of Amphaxion is Amphaxites.
1 The Peneius forms the boundary between Lower Macedonia, or that part of Macedonia which is close to the sea, and Thessaly and Magnesia; the Haliacmon forms the boundary of Upper Macedonia; and the Haliacmon also, together with the Erigon and the Axius and another set of rivers, form the boundary of the Epeirotes and the Paeonians.
1For if, according to the Geographer, Macedonia stretches from the Thessalian Pelion and Peneius towards the interior as far as Paeonia and the Epeirote tribes, and if the Greeks had at Troy an allied force from Paeonia, it is difficult to conceive that an allied force came to the Trojans from the aforesaid more distant part of Paeonia.
1 Of the Macedonian coastline, beginning at the recess of the Thermaean Gulf and at Thessaloniceia, there are two parts — one extending towards the south as far as Sunium and the other towards the east as far as the Thracian Chersonese, thus forming at the recess a sort of angle. Since Macedonia extends in both directions, I must begin with the part first mentioned. The first portion, then, of this part — I mean the region of Sunium — has above it Attica together with the Megarian country as far as the Crisaean Gulf; after this is that Boeotian coastline which faces Euboea, and above this coastline lies the rest of Boeotia, extending in the direction of the west, parallel to Attica. And he says that the Egnatian Road, also, beginning at the Ionian Gulf, ends at Thessaloniceia.
1 As for the ribbon-like stretches of land, he says, I shall first mark off the boundary of the peoples who live in the one which is beside the sea near the Peneius and the Haliacmon. Now the Peneius flows from the Pindus Mountain through the middle of Thessaly towards the east; and after it passes through the cities of the Lapithae and some cities of the Perrhaebians, it reaches Tempe, after having received the waters of several rivers, again which is the Europus, which the poet called Titaresius, since it has its sources in the Titarius Mountain; the Titarius Mountain joins Olympus, and thence Olympus begins to mark the boundary between Macedonia and Thessaly; for Tempe is a narrow glen between Olympus and Ossa, and from these narrows the Peneius flows for a distance of forty stadia with Olympus, the loftiest mountain in Macedonia, on the left, and with Ossa, near the outlets of the river, on the right. So then, Gyrton, the Perrhaebian and Magnetan city in which Periothoüs and Ixion reigned, is situated near the outlets of the Peneius on the right; and the city of Crannon lies at a distance of as much as one hundred stadia from Gyrton; and writers say that when the poet says, "Verily these twain from Thrace" and what follows, he means by "Ephyri" the Crannonians and by "Phlegyae" the Gyrtonians. But Pieria is on the other side of the Peneius.
1 The Peneius River rises in the Pindus Mountain and flows through Tempe and through the middle of Thessaly and of the countries of the Lapithae and the Perrhaebians, and also receives the waters of the Europus River, which Homer called Titaresius it marks the boundary between Macedonia on the north and Thessaly on the south. But the source-waters of the Europus rise in the Titarius Mountain, which is continuous with Olympus. And Olympus belongs to Macedonia, whereas Ossa and Pelion belong to Thessaly.
a The Peneius rises, according to the Geographer, in that part of the Pindus Mountain about which the Perrhaebians live. . . . And Strabo also makes the following statements concerning the Peneius: The Peneius rises in the Pindus; and leaving Tricca on the left it flows around Atrax and Larissa, and after receiving the rivers in Thessaly passes on through Tempe. And he says that the Peneius flows through the centre of Thessaly, receiving many rivers, and that in its course it keeps Olympus on the left and Ossa on the right. And at its outlets, on the right, is a Magnetan city, Gyrton, in which Perithoüs and Ixion reigned; and not far from Gyrton is a city Crannon, whose citizens were called by a different name, "Ephyri," just as the citizens of Gyrton were called "Phlegyae."
1 Below the foot-hills of Olympus, along the Peneius River, lies Gyrton, the Perrhaebian and Magnetan city, in which Perithoüs and Ixion ruled; and Crannon is at a distance of one hundred stadia from Gyrton, and writers say that when the poet says, "Verily these twain from Thrace," he means by "Ephyri" the Crannonians and by "Phlegyae" the Gyrtonians.
1The city of Crannon is at a distance of one hundred stadia from Cyrton, according to Strabo.
1Homolium, a city of Macedonia and Magnesia. Strabo in his Seventh Book.
1I have said in my description of Macedonia that Homolium is close to Ossa and is where the Peneius, flowing through Tempe, begins to discharge its waters.
1There were several different Ephyrae, if indeed the Geographer counts as many as nine.
1He (the Geographer) speaks of a city Gyrton, a Magnetan city near the outlets of the Peneius.
1 The city Dium, in the foot-hills of Olympus, is not on the shore of the Thermaean Gulf, but is at a distance of as much as seven stadia from it. And the city Dium has a village near by, Pimpleia, where Orpheus lived.
1 At the base of Olympus is a city Dium. And it has a village near by, Pimpleia. Here lived Orpheus, the Ciconian, it is said — a wizard who at first collected money from his music, together with his soothsaying and his celebration of the orgies connected with the mystic initiatory rites, but soon afterwards thought himself worthy of still greater things and procured for himself a throng of followers and power. Some, of course, received him willingly, but others, since they suspected a plot and violence, combined against him and killed him. And near here, also, is Leibethra.
1 In the early times the soothsayers also practised music.
1 After Dium come the outlets of the Haliacmon; then Pydna, Methone, Alorus, and the Erigon and Ludias Rivers. The Erigon flows from the country of the Triclari through that of the Orestae and through Pellaea, leaves the city on the left, and meets the Axius; the Ludias is navigable inland to Pella, a distance of one hundred and twenty stadia. Methone, which lies between the two cities, is about forty stadia from Pydna and seventy from Alorus. Alorus is in the inmost recess of the Thermaean Gulf, and it is called Thessaloniceia because of its fame. Now Alorus is regarded as a Bottiaean city, whereas Pydna is regarded as a Pierian. Pella belongs to Lower Macedonia, which the Bottiaei used to occupy; in early times the treasury of Macedonia was here. Philip enlarged it from a small city, because he was reared in it. It has a headland in what is called Lake Ludias; and it is from this lake that the Ludias River issues, and the lake itself is supplied by an offshoot of the Axius. The Axius empties between Chalastra and Therma; and on this river lies a fortified place which now is called Abydon, though Homer5calls it Amydon, and says that the Paeonians went to the aid of Troy from there, "from afar, out of Amydon, from wide-flowing Axius." The place was destroyed by the Argeadae.
20a Abydon, Abydonis; a place in Macedonia, according to Strabo.
1 The Axius is a muddy stream; but Homer calls it "water most fair," perhaps on account of the spring called Aea, which, since it empties purest water into the Axius, proves that the present current reading of the passage in the poet is faulty. After the Axius, at a distance of twenty stadia, is the Echedorus; then, forty stadia farther on, Thessaloniceia, founded by Cassander, and also the Egnatian Road. Cassander named the city after his wife Thessalonice, daughter of Philip son of Amyntas, after he had rased to the ground the towns in Crusis and those on the Thermaean Gulf, about twenty-six in number, and had settled all the inhabitants together in one city; and this city is the metropolis of what is now Macedonia. Among those included in the settlement were Apollonia, Chalastra, Therma, Garescus, Aenea, and Cissus; and of these one might suspect that Cissus belonged to Cisses, whom the poet mentions in speaking of Iphidamas, "whom Cisses reared."
1 Crusis; a portion out of Mygdonia. Strabo in his Seventh Book.
2Chalastra: a city of Thrace near the Thermaean Gulf — though Strabo, in his Seventh Book, calls it a city of Macedonia.
1 After the city Dium comes the Haliacmon River, which empties into the Thermaean Gulf. The part after this, the seaboard of the gulf towards the north as far as the Axius River, is called Pieria, in which is the city Pydna, now called Citrum. Then come the cities Methone and Alorus. Then the Rivers Erigon and Ludias; and from Ludias to the city of Pella the river is navigable, a distance of one hundred and twenty stadia. Methone is forty stadia distant from Pydna and seventy stadia from Alorus. Now Pydna is a Pierian city, whereas Alorus is Bottiaean. Now it was in the plain before Pydna that the Romans defeated Perseus in war and destroyed the kingdom of the Macedonians, and it was in the plain before Methone that Philip the son of Amyntas, during the siege of the city, had the misfortune to have his right eye knocked out by a bolt from a catapult.
1 As for Pella, though it was formerly small, Philip greatly enlarged it, because he was reared in it. It has a lake before it; and it is from this lake that the Ludias River flows, and the lake is supplied by an offshoot of the Axius. Then the Axius, dividing both Bottiaea and the land called Amphaxitis, and receiving the erigon River, discharges its waters between Chalastra and Therma. And on the Axius River lies the place which Homer calls Amydon, saying that the Paeonians went to the aid of Troy from there, "from afar, out of Amydon, from wide-flowing Axius." But since the Axius is muddy and since a certain spring rises in Amydon and mingles "water most fair" with it, therefore the next line, "Axius, whose water most fair is spread o'er Aea," is changed to read thus, "Axius, o'er which is spread Aea's water most fair"; for it is not the "water most fair" of the Axius that is spread over the face of the earth, but that of the spring o'er the Axius.
a In the phrase 'spread o'er Aiai,' or 'Aian,' (for it is written in two ways), some are of the opinion that 'Aea' means, not the earth, but a certain spring, as is clear from what the Geographer says, namely: the Amydon in Homer was later called Abydon, but it was destroyed; and there is a spring near Amydon called Aea, which empties purest water into the Axius; and this river, since it is filled from many rivers, flows muddy. Therefore, he says, the current reading, 'Axius's water most fair spreads o'er Aea,' is faulty, because it is clearly not the water of the Axius that spread o'er the spring, but the reverse. Then the Geographer goes on somewhat gruffly to find fault with the opinion that Aea refers to the earth, and appears disposed to eject such diction from the Homeric poem altogether.
1 After the Axius River comes Thessalonica, a city which in earlier times was called Therma. It was founded by Cassander, who named it after his wife, the daughter of Philip the son of Amyntas. And he transferred to it the towns in the surrounding country, as, for instance, Chalastra, Aenea, Cissus, and also some others. And one might suspect that it was from this Cissus that Homer's Iphidamas came, whose grandfather Cisseus "reared him," Homer says, in Thrace, which now is called Macedonia.
1 Mt. Bermium, also, is somewhere in this region; in earlier times it was occupied by Briges, a tribe of Thracians; some of these crossed over into Asia and their name was changed to Phryges. After Thessaloniceia come the remaining parts of the Thermaean Gulf as far as Canastraeum; this is a headland which forms a peninsula and rises opposite to Magnetis. The name of the peninsula is Pallene; and it has an isthmus five stadia in width, through which a canal is cut. On the isthmus is situated a city founded by the Corinthians, which in earlier times was called Potidaea, although later on it was called Cassandreia, after the same King Cassander, who restored it after it had been destroyed. The distance by sea around this peninsula is five hundred and seventy stadia. And further, writers say that in earlier times the giants lived here and that the country was named Phlegra; the stories of some are mythical, but the account of others is more plausible, for they tell of a certain barbarous and impious tribe which occupied the place but was broken up by Heracles when, after capturing Troy, he sailed back to his home-land. And here, too, the Trojan women were guilty of their crime, it is said, when they set the ships on fire in order that they might not be slaves to the wives of their captors.
2The Geographer points out that the Phrygians too were called Brigians.
1 The city Beroea lies in the foot-hills of Mt. Bermium.
1 The peninsula Pallene, on whose isthmus is situated the city formerly called Potidaea and now Cassandreia, was called Phlegra in still earlier times. It used to be inhabited by the giants of whom the myths are told, an impious and lawless tribe, whom Heracles destroyed. It has four cities, Aphytis, Mende, Scione, Sane.
2The Scepsian apparently accepts the opinion neither of this man nor of those who suppose them to be the Halizoni near Pallene, whom I have mentioned in my description of Macedonia.
1 Olynthus was seventy stadia distant from Potidaea.
1 The naval station of Olynthus is Macyperna, on the Toronaean Gulf.
1 Near Olynthus is a hollow place which is called Cantharolethron from what happens there; for when the insect called the Cantharos, which is found all over the country, touches that place, it dies.
1 After Cassandreia, in order, comes the remainder of the seaboard of the Toronic Gulf, extending as far as Derrhis. Derrhis is a headland that rises opposite to Canastraeum and forms the gulf; and directly opposite Derrhis, towards the east, are the capes of Athos; and between is the Singitic Gulf, which is named after Singus, the ancient city that was on it, now in ruins. After this city comes Acanthus, a city situated on the isthmus of Athos; it was founded by the Andrii, and from it many call the gulf the Acanthian Gulf.
1 Opposite Canastrum, a cape of Pallene, is Derrhis, a headland near Cophus Harbour; and these two mark off the limits of the Toronaean Gulf. And towards the east, again, lies the cape of Athos, which marks off the limit of the Singitic Gulf. And so the gulfs of the Aegaean Sea lie in order, though at some distance from one another, towards the north, as follows: the Maliac, the Pagasitic, the Thermaean, the Toronaean, the Singitic, the Strymonic. The capes are, first, Poseidium, the one between the Maliac and the Pegasitics; secondly, the next one towards the north, Sepias; then the one on Pallene, Canastrum; then Derrhis; then come Nymphaeum, on Athos on the Singitic Gulf, and Acrathos, the cape that is on the Strymonic Gulf (Mt. Athos is between these two capes, and Lemnos is to the east of Mt. Athos); on the north, however, the limit of the Strymonic Gulf is marked by Neapolis.
1 Acanthus, a city on the Singitic Gulf, is on the coast near the canal of Xerxes. Athos has five cities, Dium, Cleonae, Thyssus, Olophyxis, Acrothoï; and Acrothoï is near the crest of Athos. Mt. Athos is breast-shaped, has a very sharp crest, and is very high, since those who live on the crest see the sun rise three hours before it rises on the seaboard. And the distance by sea around the peninsula from the city Acanthus as far as Stageirus, the city of Aristotle, is four hundred stadia. On this coast is a harbour, Caprus by name, and also an isle with the same name as the harbour. Then come the outlets of the Strymon; then Phagres, Galepsus, Apollonia, all cities; then the mouth of the Nestus, which is the boundary between Macedonia and Thrace as fixed by Philip and his son Alexander in their times. There is also another set of cities about the Strymonic Gulf, as, for instance, Myrcinus, Argilus, Drabescus, and Datum. The last named has not only excellent and fruitful soil but also dock-yards and gold mines; and hence the proverb, "a Datum of good things," like that other proverb, "spools of good things."
1 There are very many gold mines in Crenides, where the city Philippi now is situated, near Mt. Pangaeum. And Mt. Pangaeum as well has gold and silver mines, as also the country across, and the country this side, the Strymon River as far as Paeonia. And it is further said that the people who plough the Paeonian land find nuggets of gold.
Mt. Athos is high and breast-shaped; so high that on its crests the sun is up and that the people are weary of ploughing by the time cock-crow begins among the people who live on the shore. It was on this shore that Thamyris the Thracian reigned, who was a man of the same pursuits as Orpheus. Here, too, is to be seen a canal, in the neighbourhood of Acanthus, where Xerxes dug a canal across Athos, it is said, and, by admitting the sea into the canal, brought his fleet across from the Strymonic Gulf through the isthmus. Demetrius of Scepsis, however, does not believe that this canal was navigable, for, he says, although as far as ten stadia the ground is deep-soiled and can be dug, and in fact a canal one plethrum in width has been dug, yet after that it is a flat rock, almost a stadium in length, which is too high and broad to admit of being quarried out through the whole of the distance as far as the sea; but even if it were dug thus far, certainly it should not be dug deep enough to make a navigable passage; this, he adds, is where Alexarchus, the son of Antipater, laid the foundation of Uranopolis, with its circuit of thirty stadia. Some of the Pelasgi from Lemnos took up their abode on this peninsula, and they were divided into five cities, Cleonae, Olophyxis, Acrothoï, Dium, Thyssus. After Athos comes the Strymonic Gulf extending as far as the Nestus, the river which marks off the boundary of Macedonia as fixed by Philip and Alexander; to be accurate, however, there is a cape which with Athos forms the Strymonic Gulf, I mean the cape which has had on it a city called Apollonia. The first city on this gulf after the harbour of the Acanthians is Stageira, the native city of Aristotle, now deserted; this too belongs to the Chalcidians and so do its harbour, Caprus, and an isle bearing the same name as the harbour. Then come the Strymon and the inland voyage of twenty stadia to Amphipolis. Amphipolis was founded by the Athenians and is situated in that place which is called Ennea Hodoi.5Then come Galepsus and Apollonia, which were rased to the ground by Philip.
1 From the Peneius, he says, to Pydna is one hundred and twenty stadia. Along the seaboard of the Strymon and the Dateni are, not only the city Neapolis, but also Datum itself, with its fruitful plains, lake, rivers, dock-yards, and profitable gold mines; and hence the proverb, "a Datum of good things," like that other proverb, "spools of good things." Now the country that is on the far side of the Strymon, I mean that which is near the sea and those places that are in the neighbourhood of Datum, is the country of the Odomantes and the Edoni and the Bisaltae, both those who are indigenous and those who crossed over from Macedonia, amongst whom Rhesus reigned. Above Amphipolis, however, and as far as the city Heracleia, is the country of the Bisaltae, with its fruitful valley; this valley is divided into two parts by the Strymon, which has its source in the country of the Agrianes who live round about Rhodope; and alongside this country lies Parorbelia, a district of Macedonia, which has in its interior, along the valley that begins at Eidomene, the cities Callipolis, Orthopolis, Philippopolis, Garescus.
If one goes up the Strymon, one comes to Berge; it, too, is situated in the country of the Bisaltae, and is a village about two hundred stadia distant from Amphipolis. And if one goes from Heracleia towards the north and the narrows through which the Strymon flows, keeping the river on the right, one has Paeonia and the region around Doberus, Rhodope, and the Haemus Mountain on the left, whereas on the right one has the region round about Haemus, This side the Strymon are Scotussa, near the river itself, and Arethusa, near Lake Bolbe. Furthermore, the name Mygdones is applied especially to the people round about the lake. Not only the Axius flows out of the country of the Paeonians, but also the Strymon, for its flows out of the country of the Agrianes through that of the Medi and Sinti and empties into the parts that are between the Bisaltae and the Odomantes.
1 The Strymon River rises in the country of the Agrianes who live round about Rhodope.
1 Some represent the Paeonians as colonists from the Phrygians, while others represent them as independent founders. And it is said that Paeonia has extended as far as Pelagonia and Pieria; that Pelagonia was called Orestia in earlier times, that Asteropaeus, one of the leaders who made the expedition from Paeonia to Troy, was not without good reason called "son of Pelegon," and that the Paeonians themselves were called Pelagonians.
1 The Homeric "Atersopaeus son of Pelegon" was, as history tells us, from Paeonia in Macedonia; wherefore "son of Pelegon," for the Paeonians were called Pelagonians.
1 Since the "apeanismos" of the Thracians is called "titanismos" by the Greeks, in imitation of the cry uttered in paeans, the Titans too were called Pelagonians.
1 It is clear that in early times, as now, the Paeonians occupied much of what is now Macedonia, so that they could not only lay siege to Perinthus but also bring under their power all Crestonia and Mygdonis and the country of the Agrianes as far as Pangaeum. Philippi and the region about Philippi lie above that part of the seaboard of the Strymonic Gulf which extends from Galepsus as far as Nestus. In earlier times Philippi was called Crenides, and was only a small settlement, but it was enlarged after the defeat of Brutus and Cassius.
(4 What is now the city Philippi was called Crenides in early times.
(4 Off this seaboard lie two islands, Lemnos and Thasos. And after the strait of Thasos one comes to Abdera and the scene of the myths connected with Abderus. It was inhabited by the Bistonian Thracians over whom Diomedes ruled. The Nestus River does not always remain in the same bed, but oftentimes floods the country. Then come Dicaea, a city situated on a gulf, and a harbour. Above these lies the Bistonis, a lake which has a circuit of about two hundred stadia. It is said that, because this plain was altogether a hollow and lower than the sea, Heracles, since he was inferior in horse when he came to get the mares of Diomedes, dug a canal through the shore and let in the water of the sea upon the plain and thus mastered his adversaries. One is shown also the royal residence of Diomedes, which, because of its naturally strong position and from what is actually the case, is called Cartera Come. After the lake, which is midway between, come Xantheia, Maroneia, and Ismarus, the cities of the Cicones. Ismarus, however, is now called Ismara; it is near Maroneia. And near here, also, Lake Ismaris sends forth its stream; this stream is called Odysseium. And here, too, are what are called the Thasiôn Cephalae. But the people situated in the interior are Sapaei.
(4Topeira is near Abdera and Maroneia.
4The aforesaid Ismarus, in later times called Ismara, is, they say, a city of the Cicones; it is near Maroneia, where is also a lake, the stream of which is called Odysseium; here too is a hero-temple of Maron, as the Geographer records.
(4The Sinti, a Thracian tribe, inhabit the island Lemnos; and from this fact Homer calls them Sinties, when he says, "where me the Sinties . . ."
4Lemnos: first settled by the Thracians who were called Sinties, according to Strabo.
(4After the Nestus River, towards the east, is the city Abdera, named after Abderus, whom the horses of Diomedes devoured; then, near by, the city Dicaea, above which lies a great lake, Bistonis; then the city Maroneia.
(4Thrace as a whole consists of twenty-two tribes. But although it has been devastated to an exceptional degree, it can send into the field fifteen thousand cavalry and also two hundred thousand infantry. After Maroneia one comes to the city Orthagoria and to the region about Serrhium (a rough coasting-voyage) and to Tempyra, the little town of the Samothracians, and to Caracoma, another little town, off which lies the island Samothrace, and to Imbros, which is not very far from Samothrace; Thasos, however, is more than twice as far from Samothrace as Imbros is. From Caracoma one comes to Doriscus, where Xerxes enumerated his army; then to the Hebrus, which is navigable inland to Cypsela, a distance of one hundred and twenty stadia. This, he says, was the boundary of Macedonia which the Romans first took away from Perseus and afterwards from the Pseudo-Philip. Now Paulus, who captured Perseus, annexed the Epeirotic tribes to Macedonia, divided the country into four parts for purposes of administration, and apportioned one part to Amphipolis, another to Thessaloniceia, another to Pella, and another to the Pelagonians. Along the Hebrus live the Corpili, and, still farther up the river, the Brenae, and then, farthermost of all, the Bessi, for the river is navigable thus far. All these tribes are given to brigandage, but most of all the Bessi, who, he says, are neighbours to the Odrysae and the Sapaei. Bizye was the royal residence of the Astae. The term "Odrysae" is applied by some to all the peoples living above the seaboard from the Hebrus and Cypsela as far as Odessus — the peoples over whom Amadocus, Cersobleptes, Berisades, Seuthes and Cotys reigned as kings.
4Odrysae: a tribe of Thrace; Strabo in his Seventh Book.
4The Geographer, in pointing out the great extent of Thrace, says also that Thrace as a whole consists of twenty-two tribes.
The river in Thrace that is now called Rheginia used to be called Erigon.
Iasion and Dardanus, two brothers, used to live in Samothrace. But when Iasion was struck by a thunderbolt because of his sin against Demeter, Dardanus sailed away from Samothrace, went and took up his abode at the foot of Mount Ida, calling the city Dardania, and taught the Trojans the Samothracian Mysteries. In earlier times, however, Samothrace was called Samos.
Many writers have identified the gods that are worshipped in Samothrace with the Cabeiri, though they cannot say who the Cabeiri themselves are, just as the Cyrbantes and Corybantes, and likewise the Curetes and the Idaean Dactyli, are identified with them.
a this Thracian island, according to the Geographer, is called Samos because of its height; for "samoi," he said, means "heights." . . . And from Mycale settled in the island, which had been deserted because of a dearth of crops, and that in this way it was called Samos. . . . And the Geographer records also that in earlier times Samothrace was called Melite, as also that it was rich; for Cilician pirates, he says, secretly broke into the temple in Samothrace, robbed it, and carried off more than a thousand talents.
5Near the outlet of the Hebrus, which has two mouths, lies the city Aenus, on the Melas Gulf; it was founded by Mitylenaeans and Cumaeans, though in still earlier times by Alopeconnesians. Then comes Cape Sarpedon; then what is called the Thracian Chersonesus, which forms the Propontis and the Melas Gulf and the Hellespont; for it is a cape which projects towards the south-east, thus connecting Europe with Asia by the strait, seven stadia wide, which is between Abydus and Sestus, and thus having on the left the Propontis and on the right the Melas Gulf — so called, just as Herodotus and Eudoxus say, from the Melas River which empties into it. But Herodotus, he says, states that this stream was not sufficient to supply the army of Xerxes. The aforesaid cape is closed in by an isthmus forty stadia wide. Now in the middle of the isthmus is situated the city Lysimacheia, named after the king who founded it; and on either side of it lies a city — on the Melas Gulf, Cardia, the largest of the cities on the Chersonesus, founded by Milesians and Clazomenians but later refounded by Athenians, and on the Propontis, Pactye. And after Cardia come Drabus and Limnae; then Alepeconnesus, in which the Melas Gulf comes approximately to an end; then the large headland, Mazusia; then, on a gulf, Eleus, where is the temple of Protesilaus, opposite which, forty stadia distant, is Sigeium, a headland of the Troad; and this is about the most southerly extremity of the Chersonesus, being slightly more than four hundred stadia from Cardia; and if one sails around the rest of the circuit, towards the other side of the isthmus, the distance is slightly more than this.
5Aenus; a city of Thrace, called Apsinthus. Strabo in his Seventh Book. The city Aenus is in the outlet of the hebrus, which has two mouths, and was founded by Cumaeans; and it was so called because there was an Aenius River and also a village of the same name near Ossa.
The Thracian Chersonese forms three seas: the Propontis in the north, the Hellespont in the east, and the Melas Gulf in the south, into which empties the Melas River, which bears the same name as the gulf.
On the isthmus of the Chersonesus are situated three cities: near the Melas Gulf, Cardia, and near the Propontis, Pactye, and near the middle, Lysimacheia. The length of the isthmus is forty stadia.
The name of the city Eleus is masculine; and perhaps also that of the city Trapezus.
On this voyage along the coast of the Chersonesus after leaving Eleus, one comes first to the entrance which leads through the narrows into the Propontis; and this entrance is called the beginning of the Hellespont. And here is the cape called the Cynos-Sema; though some call it Hecabe's Sema, and in fact her tomb is pointed out after one has doubled the cape. Then one comes to Madytus, and to Cape Sestias, where the pontoon-bridge of Xerxes was built; and, after these, to Sestus. The distance from Eleus to the place of the pontoon-bridge is one hundred and seventy stadia. After Sestus one comes to Aegospotami, eighty stadia, a town which has been rased to the ground, where it is said, the stone fell at the time of the Persian war. Then comes Callipolis, from which the distance across to Lampsacus in Asia is forty stadia; then Crithote, a little town which has been rased to the ground; then Pactye; then Macron Teichos,º Leuce Acte, Hieron Oros, and Perinthus, founded by the Samians: then Selybria. Above these places lies Silta; and the Hieron Oros is revered by all the natives and is a sort of acropolis of the country. The hieron Oros discharges asphalt into the sea, near the place where the Proconnesus, only one hundred and twenty stadia distant, is nearest to the land; and the quarry of white marble in the Proconnesus is both large and excellent. After Selybria come the Rivers Athyras and Bathynias; and then, Byzantium and the places which come in order thereafter as far as the Cyanean Rocks.
5As for Sestus and the whole of the Chersonesus, I have already discussed them in my description of the regions of Thrace.
5Sestus, a colony of the Lesbians, as is also Madytus, as the Geographer says, is a Chersonesian city thirty stadia distant from Abydus, from harbour to harbour.
The distance from Perinthus to Byzantium is six hundred and thirty stadia; but from the Hebruion Cypseal to Byzantium, as far as the Cyanean Rocks, three thousand one hundred, as Artemidorus says; and the entire distance from the Ionian Gulf at Apollonia as far as Byzantium is seven thousand three hundred and twenty stadia, though Polybius adds one hundred and eighty more, since he adds a third of a stadium to the eight stadia in the mile. Demetrius of Scepsis, however, in his work On the Martiallingº of the Trojan Forces calls the distance from Perinthus to Byzantium six hundred stadia and the distance to Parium equal thereto; and he represents the Propontis as one thousand four hundred stadia in length and five hundred in breadth; while as for the Hellespont, he calls its narrowest breadth seven stadia and its length four hundred.
There is no general agreement in the definition of the term "Hellespont": in fact, there are several opinions concerning it. For some writers call "Hellespont" the whole of the Propontis; others, that part of the Propontis which is this side Perinthus; others go on to add that part of the outer sea which faces the Melas Gulf and the open waters of the Aegaean Sea, and these writers in turn each comprise different sections in their definitions, some the part from Sigeium to Lampsacus and Cyzicus, or Parium, or Priapus, another going on to add the part which extends from Sigrium in the Lesbian Isle. And some do not shrink even from applying the name Hellespont to the whole of the high sea as far as the Myrtoan Sea, since, as Pindar says in his hymns, those who were sailing with Heracles from Troy through Helle's maidenly strait, on touching the Myrtoan Sea, ran back again to Cos, because Zephyrus blew contrary to their course. And in this way, also, they require that the whole of the Aegaean Sea as far as the Thermaean Gulf and the sea which is about Thessaly and Macedonia should be called Hellespont, invoking Homer also as witness; for Homer says, "thou shalt see, if thou dost wish and hast a care therefor, my ships sailing o'er the fishy Hellespont at very early morn"; but such an argument is refuted by those other lines, "the hero, son of Imbrasus, who, as we know, had come from Aenus," but he was the leader of the Thracians, "all who are shut in by strong-flowing Hellespont"; that is, Homer would represent those who are situated next after these as situated outside the Hellespont; that is, Aenus lies in what was formerly called Apsinthis, though now called Corpilice, whereas the country of the Cicones lies next thereafter towards the west.
1 Corpili: certain of the Thracians. Strabo, Seventh Book; their country is called Corpilice; for Aenus lies in what was formerly called Apsinthis, though now called Corpilice.
Tetrachoritae: the Bessi, according to Strabo in his Seventh Book. These are also called Tetracomi.
For he says in the Seventh Book of the same work that he knew Poseidonius, the Stoic philosopher.º
There is also a river Arisbus in Thrace, as I have said before, and near this the Cebrenian Thracians.
1 Perhaps Rhipe is also called Rhipae, in the plural, if Strabo means Rhipe when he says that Rhipae is not inhabited. And they call the country Rhipis. But elsewhere Strabo says very clearly: "Rhipe and Stratie and Enispe not only are hard to find, but when found are of no use because of their desolation."
The geographer says also that the tribe of the Cauconians has been completely destroyed. And the Geographer further says that the Cauconians in the Peloponnesus, the Arcadian portion, could not endure to be ruled by the house of Lepreus — Lepreus was a bad man — and so they sailed away from there to Lycia.
Porphyrius records that the people from the Methone that was subject to Menelaus were called Phthians. But the Geographer says that the people about Methone were not the only people who were called Phthians, but, as has been said before, the peoples subject to Achilles, Protesilaüs, and Philoctetes were so called in common with them.
6The same Geographer says also that the Ister was once called the "Matoas" — that is, in Greek, "Asius"; and that, although the Scythians had often crossed over it without suffering any mishap, yet, when once a misfortune befell them, its name was changed to Danubis or Daüsis, as though it were to blame for their mistake.
The Geographer also says that Hades was much revered there. |
|
|
|
|
8 Peloponnesus. 8 112 1:50 
|
8 - 1 Greece, generalities 
1 I began my description by going over all the western parts of Europe comprised between the inner and the outer sea;1 and now that I have encompassed in my survey all the barbarian tribes in Europe as far as the Tanaïs and also a small part of Greece, Macedonia, I now shall give an account of the remainder of the geography of Greece. This subject was first treated by Homer; and then, after him, by several others, some of whom have written special treatises entitled Harbours, or Coasting Voyages, or General Descriptions of the Earth, or the like; and in these is comprised also the description of Greece. Others have set forth the topography of the continents in separate parts of their general histories, for instance, Ephorus and Polybius. Still others have inserted certain things on this subject in their treatises on physics and mathematics, for instance, Poseidonius and Hipparchus. Now although the statements of the others are easy to pass judgment upon, yet those of Homer require critical inquiry, since he speaks poetically, and not of things as they now are, but of things as they were in antiquity, which for the most part have been p5obscured by time. Be this as it may, as far as I can I must undertake the inquiry; and I shall begin where I left off. My account ended, on the west and the north, with the tribes of the Epeirotes and of the Illyrians, and, on the east, with those of the Macedonians as far as Byzantium. After the Epeirotes and the Illyrians, then, come the following peoples of the Greeks: the Acarnanians, the Aetolians, and the Ozolian Locrians; and, next, the Phocians and Boeotians; and opposite these, across the arm of the sea, is the Peloponnesus, which with these encloses the Corinthian Gulf, and not only shapes the gulf but also is shaped by it; and after Macedonia, the Thessalians (extending as far as the Malians) and the countries of the rest of the peoples outside the Isthmus, as also of those inside.
2 There have been many tribes in Greece, but those which go back to the earliest times are only as many in number as the Greek dialects which we have learned to distinguish. But though the dialects themselves are four in number, we may say that the Ionic is the same as the ancient Attic, for the Attic people of ancient times were called Ionians, and from that stock sprang those Ionians who colonised Asia and used what is now called the Ionic speech; and we may say that the Doric dialect is the same as the Aeolic, for all the Greeks outside the Isthmus, except the Athenians and the Megarians and the Dorians who live about Parnassus, are to this day still called Aeolians. And it is reasonable to suppose that the Dorians too, since they were few in number and lived in a most p7rugged country, have, because of their lack of intercourse with others, changed their speech and their other customs to the extent that they are no longer a part of the same tribe as before. And this was precisely the case with the Athenians; that is, they lived in a country that was both thin-soiled and rugged, and for this reason, according to Thucydides, their country remained free from devastation, and they were regarded as an indigenous people, who always occupied the same country, since no one drove them out of their country or even desired to possess it. This, therefore, as one may suppose, was precisely the cause of their becoming different both in speech and in customs, albeit they were few in number. And just as the Aeolic element predominated in the parts outside the Isthmus, so too the people inside the Isthmus were in earlier times Aeolians; and then they became mixed with other peoples, since, in the first place, Ionians from Attica seized the Aegialus, and, secondly, the Heracleidae brought back the Dorians, who founded both Megara and many of the cities of the Peloponnesus. The Ionians, however, were soon driven out again by the Achaeans, an Aeolic tribe; and so there were left in the Peloponnesus only the two tribes, the Aeolian and the Dorian. Now all the peoples who had less intercourse with the Dorians — as was the case with the Arcadians and with the Eleians, since the former were wholly mountaineers and had no share in the allotments of territory, while the latter were regarded as sacred to the Olympian Zeus and hence p9have long lived to themselves in peace, especially because they belonged to the Aeolic stock and had admitted the army which came back with Oxylus about the time of the return of the Heracleidae — these peoples, I say, spoke the Aeolic dialect, whereas the rest used a sort of mixture of the two, some leaning more to the Aeolic and some less. And, I might almost say, even now the people of each city speaks a different dialect, although, because of the predominance which has been gained by the Dorians, one and all are reputed to speak the Doric. Such, then, are the tribes of the Greeks, and such in general terms is their ethnographical division. Let me now take them separately, following the appropriate order, and tell about them.
3 Ephorus says that, if one begins with the western parts, Acarnania is the beginning of Greece; for, he adds, Acarnania is the first to border on the tribes of the Epeirotes. But just as Ephorus, using the sea-coast as his measuring-line, begins with Acarnania (for he decides in favour of the sea as a kind of guide in his description of places, because otherwise he might have represented parts that border on the land of the Macedonians and the Thessalians as the beginning), so it is proper that I too, following the natural character of the regions, should make the sea my counsellor. Now this sea, issuing forth out of the Sicilian Sea, on one side stretches to the Corinthian Gulf, and on the other forms a large peninsula, the Peloponnesus, which is closed by a narrow isthmus. Thus Greece consists of two very large bodies of land, the part inside the Isthmus, and the part outside, which extends through Pylae as far as the outlet of the Peneius (this latter is the Thessalian part of Greece);but the part inside the Isthmus is both larger and more famous. I might almost say that the Peloponnesus is the acropolis of Greece as a whole; for, apart from the splendour and power of the tribes that have lived in it, the very topography of Greece, diversified as it is by gulfs, many capes, and, what are the most significant, large peninsulas that follow one another in succession, suggests such hegemony for it. The first of the peninsulas is the Peloponnesus which is closed by an isthmus forty stadia in width. The second includes the first; and its isthmus extends in width from Pagae in Megaris to Nisaea, the naval station of the Megarians, the distance across being •one hundred and twenty stadia from sea to sea. The third likewise includes the second; and its isthmus extends in width from the recess of the Crisaean Gulf as far as Thermopylae — the imaginary straight line, •about five hundred and eight stadia in length, enclosing within the peninsula the whole of Boeotia and cutting obliquely Phocis and the country of the Epicnemidians. The fourth is the peninsula whose isthmus extends from the Ambracian Gulf through Oeta and Trachinia to the Maliac Gulf and Thermopylae — the isthmus being •about eight hundred stadia in width. But there is another isthmus, •more than one thousand stadia in width, extending from the same Ambracian Gulf through the countries of the Thessalians and the Macedonians to the recess of the Thermaean Gulf. So then, the succession of the peninsulas suggests a kind of order, and not a bad one, for me to follow in my description; and I should begin with the smallest, but most famous, of them. |
|
|
|


|
8 - 2 Peloponnesus 
1 Now the Peloponnesus is like a leaf of a plane tree in shape, its length and breadth being almost equal, that is, about fourteen hundred stadia. Its length is reckoned from the west to the east, that is, from Chelonatas through Olympia and Megalopolis to the Isthmus; and its width, from the south towards the north, that is, from Maleae through Arcadia to Aegium. The perimeter, not following the sinuosities of the gulfs, is four thousand stadia, according to Polybius, although Artemidorus adds four hundred more; but following the sinuosities of the gulfs, it is more than five thousand six hundred. The width of the Isthmus at the "Diolcus," where the ships are hauled overland from one sea to the other, is forty stadia, as I have already said.
2 The western part of this peninsula is occupied by the Eleians and the Messenians, whose countries are washed by the Sicilian Sea. In addition, they also hold a part of the sea-coast in both directions, for the Eleian country curves towards the north and the beginning of the Corinthian Gulf as far as Cape Araxus (opposite which, across the straits, lie Acarnania and the islands off its coast — Zacynthos, Cephallenia, Ithaca, and also the Echinades, among which is Dulichium), whereas the greater part of the Messenian country opens up towards the south and the Libyan Sea as far as what is called Thyrides, near Taenarum. Next after the Eleian country comes the tribe of the Achaeans, whose country faces towards the north and stretches along the Corinthian Gulf, ending at Sicyonia. Then come in succession Sicyon and Corinth, the territory of the latter extending as far as the Isthmus. After the Messenian country come the Laconian and the Argive, the latter also extending as far as the Isthmus. The gulfs on this coast are: first, the Messenian; second, the Laconian; third, the Argolic; fourth, the Hermionic; and fifth, the Saronic, by some called the Salaminiac. Of these gulfs the first two are filled by the Libyan Sea, and the others by the Cretan and Myrtoan Seas. Some, however, call the Saronic Gulf "Strait" or "Sea." In the interior of the peninsula is Arcadia, which touches as next door neighbour the countries of all those other tribes.
3 The Corinthian Gulf begins, on the one side, at the outlets of the Evenus (though some say at the outlets of the Acheloüs, the river that separates the Acarnanians and the Aetolians), and, on the other, at Araxus; for here the shores on either side first draw notably nearer to one another; then in their advance they all but meet at Rhium and Antirrhium, where they leave between them a strait only about five stadia in width. Rhium, belonging to the Achaeans, is a low-lying cape; it bends inwards (and it is in fact called "Sickle "). It lies between Patrae and Aegium, and possesses a temple of Poseidon. Antirrhium is situated on the common boundary of Aetolia and Locris; and people call it Molycrian Rhium. Then, from here, the shoreline on either side again draws moderately apart, and then, advancing into the Crisaean Gulf, it comes to an end there, being shut in by the westerly limits of Boeotia and Megaris. The perimeter of the Corinthian Gulf if one measures from the Evenus to Araxus, is two thousand two hundred and thirty stadia; but if one measures from the Acheloüs, it is about a hundred stadia more. Now from the Acheloüs to the Evenus the coast is occupied by Acarnanians; and thence to Antirrhium, by Aetolians; but the remaining coast, as far as the Isthmus, belongs to the Phocians, the Boeotians and Megaris — a distance of one thousand one hundred and eighteen stadia. The sea from Antirrhium as far as the Isthmus is called Alcyonian, it being a part of the Crisaean Gulf. Again, from the Isthmus to Araxus the distance is one thousand and thirty stadia. Such, then, in general terms, is the position and extent of the Peloponnesus, and of the land that lies opposite to it across the arm of the sea as far as the recess; and such, too, is the character of the gulf that lies between the two bodies of land. Now I shall describe each part in detail, beginning with the Eleian country. |
|
|
|






|
8 - 3 Elea 
1 At the present time the whole of the seaboard that lies between the countries of the Achaeans and the Messenians, and extends inland to the Arcadian districts of Pholoë, of the Azanes, and of the Parrhasians, is called the Eleian country. But in early times this country was divided into several domains; and afterwards into two — that of the Epeians and that under the rule of Nestor the son of Neleus; just as Homer, too, states, when he calls the land of the Epeians by the name of "Elis" ("and passed goodly Elis, where the Epeians hold sway"), and the land under the rule of Nestor, "Pylus," through which, he says, the Alpheius flows ("of the Alpheius, that floweth in wide stream through the land of the Pylians"). Of course Homer also knew of Pylus as a city ("and they reached Pylus, the well-built city of Nestor"), but the Alpheius does not flow through the city, nor past it either; in fact, another river flows past it, a river which some call "Pamisus" and others "Amathus" (whence, apparently, the epithet "Emathoëis" which has been applied to this Pylus), but the Alpheius flows through the Pylian country.
2 What is now the city of Elis had not yet been founded in Homer's time; in fact, the people of the country lived only in villages. And the country was called Coelê Elis from the fact in the case, for the most and best of it was "Coelê." It was only relatively late, after the Persian wars, that people came together from many communities into what is now the city of Elis. And I might almost say that, with only a few exceptions, the other Peloponnesian places named by the poet were also named by him, not as cities, but as countries, each country being composed of several communities, from which in later times the well-known cities were settled. For instance, in Arcadia, Mantineia was settled by Argive colonists from five communities; and Tegea from nine; and also Heraea from nine, either by Cleombrotus or by Cleonymus. And in the same way the city Aegium was made up of seven or eight communities; the city Patrae of seven; and the city Dymê of eight. And in this way the city Elis was also made up of the communities of the surrounding country (one of these . . . the Agriades). The Peneius River flows through the city past the gymnasium. And the Eleians did not make this gymnasium until a long time after the districts that were under Nestor had passed into their possession.
3 These districts were Pisatis (of which Olympia was a part), Triphylia, and the country of the Cauconians. The Triphylians were so called from the fact that three tribes of people had come together in that country — that of the Epeians, who were there at the outset, and that of the Minyans, who later settled there, and that of the Eleians, who last dominated the country. But some name the Arcadians in the place of the Minyans, since the Arcadians had often disputed the possession of the country; and hence the same Pylus was called both Arcadian Pylus and Triphylian Pylus. Homer calls this whole country as far as Messenê "Pylus," giving it the same name as the city. But Coelê Elis was distinct from the places subject to Nestor, as is shown in the Catalogue of Ships by the names of the chieftains and of their abodes. I say this because I am comparing present conditions with those described by Homer; for we must needs institute this comparison because of the fame of the poet and because of our familiarity with him from our childhood, since all of us believe that we have not successfully treated any subject which we may have in hand until there remains in our treatment nothing that conflicts with what the poet says on the same subject, such confidence do we have in his words. Accordingly, I must give conditions as they now are, and then, citing the words of the poet, in so far as they bear on the matter, take them also into consideration.
4 In the Eleian country, on the north, is a cape, Araxus, sixty stadia distant from Dymê, an Achaean city. This cape, then, I put down as the beginning of the seaboard of the Eleians. After this cape, as one proceeds towards the west, one comes to the naval station of the Eleians, Cyllenê, from which there is a road leading inland to the present city Elis, a distance of one hundred and twenty stadia. Homer, too, mentions this Cyllenê when he says, "Otus, a Cyllenian, a chief of the Epeians," for we would not have represented a chieftain of the Epeians as being from the Arcadian mountain. Cyllenê is a village of moderate size; and it has the Asclepius made by Colotes — an ivory image that is wonderful to behold. After Cyllenê one comes to the promontory Chelonatas, the most westerly point of the Peloponnesus. Off Chelonatas lies an isle, and also some shallows that are on the common boundary between Coelê Elis and the country of the Pisatae; and from here the voyage to Cephallenia is not more than eighty stadia. Somewhere in this neighbourhood, on the aforesaid boundary-line, there also flows the River Elison or Elisa.
5 It is between Chelonatas and Cyllenê that the River Peneus empties; as also the River Sellëeis, which is mentioned by the poet and flows out of Pholoê. On the Sellëeis is situated a city Ephyra, which is to be distinguished from the Thesprotian, Thessalian, and Corinthian Ephyras; it is a fourth Ephyra, and is situated on the road that leads to Lasion, being either the same city as Boenoa (for thus Oenoê is usually called), or else near that city, at a distance of one hundred and twenty stadia from the city of the Eleians. This, apparently, is the Ephyra which Homer calls the home of the mother of Tlepolemus the son of Heracles (for the expeditions of Heracles were in this region rather than in any of the other three) when he says, "whom he had brought out of Ephyra, from the River Sellëeis; and there is no River Sellëeis near the other Ephyras. Again, he says of the corselet of Meges: "this corselet Phyleus once brought out of Ephyra, from the River Sellëeis." And thirdly, the man-slaying drugs: for Homer says that Odysseus came to Ephyra "in search of a man-slaying drug, that he might have wherewithal to smear his arrows"; and in speaking of Telemachus the wooers say: "or else he means to go to the fertile soil of Ephyra, that from there he may bring deadly drugs"; for Nestor, in his narrative of his war against the Epeians, introduces the daughter of Augeas, the king of the Epeians, as a mixer of drugs: "I was the first that slew a man, even the spearman Mulius; he was a son-in‑law of Augeias, having married his eldest daughter, and she knew all drugs that are nourished by the wide earth." But there is another River Sellëeis near Sicyon, and near the river a village Ephyra. And in the Agraean district of Aetolia there is a village Ephyra; its inhabitants are called Ephyri. And there are still other Ephyri, I mean the branch of the Perrhaebians who live near Macedonia (the Crannonians), as also those Thesprotian Ephyri of Cichyrus, which in earlier times was called Ephyra.
6 Apollodorus, in teaching us how the poet is wont to distinguish between places of the same name, says that as the poet, in the case of Orchomenus, for instance, refers to the Arcadian Orchomenus as "abounding in flocks" and to the Boeotian Orchomenus as "Minyeian," and refers to Samos as the Thracian Samos by connecting it with a neighbouring island, "betwixt Samos and Imbros," in order to distinguish it from Ionian Samos — so too, Apollodorus says, the poet distinguishes the Thesprotian Ephyra both by the word "distant" and by the phrase "from the River Sellëeis." In this, however, Apollodorus is not in agreement with what Demetrius of Scepsis says, from whom he borrows most of his material; for Demetrius says that there is no River Sellëeis among the Thesprotians, but says that it is in the Eleian country and flows past the Ephyra there, as I have said before. In this statement, therefore, Apollodorus was in want of perception; as also in his statement concerning Oechalia, because, although Oechalia is the name of not merely one city, he says that there is only one city of Eurytus the Oechalian, namely, the Thessalian Oechalia, in reference to which Homers says: "Those that held Oechalia, city of Eurytus the Oechalian." What Oechalia, pray, was it from which Thamyris had set out when, near Dorium, the Muses met Thamyris the Thracian and put a stop to his singing"? For Homer adds: "as he was on his way from Oechalia, from Eurytus the Oechalian." For if it was the Thessalian Oechalia, Demetrius of Scepsis is wrong again when he says that it was a certain Arcadian Oechalia, which is now called Andania; but if Demetrius is right, Arcadian Oechalia was also called "city of Eurytus," and therefore there was not merely one Oechalia; but Apollodorus says that there was one only.
7 It was between the outlets of the Peneius and the Sellëeis, near the Scollium, that Pylus was situated; not the city of Nestor, but another Pylus which has nothing in common with the Alpheius, nor with the Pamisus (or Amathus, if we should call it that). Yet there are some who do violence to Homer's words, seeking to win for themselves the fame and noble lineage of Nestor; for, since history mentions three Pyluses in the Peloponnesus (as is stated in this verse: "There is a Pylus in front of Pylus; yea, and there is still another Pylus"), the Pylus in question, the Lepreatic Pylus in Triphylia and Pisatis, and a third, the Messenian Pylus near Coryphasium, the inhabitants of each try to show that the Pylus in their own country is "emathoëis" and declare that it is the native place of Nestor. However, most of the more recent writers, both historians and poets, say that Nestor was a Messenian, thus adding their support to the Pylus which has been preserved down to their own times. But the writers who follow the words of Homer more closely say that the Pylus of Nestor is the Pylus through whose territory the Alpheius flows. And the Alpheius flows through Pisatis and Triphylia. However, the writers from Coelê Elis have not only supported their own Pylus with a similar zeal, but have also attached to it tokens of recognition, pointing out a place called Gerenus, a river called Geron, and another river called Geranius, and then confidently asserting that Homer's epithet for Nestor, "Gerenian," was derived from these. But the Messenians have done the self-same thing, and their argument appears at least more plausible; for they say that their own Gerena is better known, and that p35it was once a populous place. Such, then, is the present state of affairs as regards Coelê Elis.
8 But when the poet divides this country into four parts and also speaks of the leaders as four in number, his statement is not clear: "And they too that inhabited both Buprasium and goodly Elis, so much thereof as is enclosed by Hyrminê and Myrsinus on the borders, and by Olenian Rock and Aleisium, — of these men, I say, there were four leaders, and ten swift ships followed each leader, and many Epeians embarked thereon." For when he speaks of both the Buprasians and the Eleians as Epeians, but without going on and calling the Buprasians Eleians, it would seem that he is not dividing the Eleian country into four parts, but rather the country of the Epeians, which he had already divided into only two parts; and thus Buprasium would not be a part of Elis but rather of the country of the Epeians. For it is clear that he calls the Buprasians Epeians; "as when the Epeians were burying lord Amarynces at Buprasium." But Buprasium now appears to have been a territory of the Eleian country, having in it a settlement of the same name, which was also a part of Elis. And again, when he names the two together, saying "both Buprasium and goodly Elis," and then divides the country into four parts, it seems as though he is classifying the four parts under the general designation "both Buprasium and goodly Elis." It seems likely that at one time there was a considerable settlement which is no longer in existence (indeed, only that territory which is on the road that leads to Dymê from the present city of Elis is now so called); and one might suppose that at that time Buprasium had a certain pre-eminence as compared with Elis, just as the Epeians had in comparison with the Eleians; but later on the people were called Eleians instead of Epeians. And though Buprasium was a part of Elis, they say that Homer, by a sort of poetic figure, names the part with the whole, as for instance when he says: "throughout Hellas and mid-Argos," and "throughout Hellas and Phthia," and "the Curetes fought and the Aetolians," and "the men of Dulichium and the holy Echinades," for Dulichium is one of the Echinades. And more recent poets also use this figure; for instance, Hipponax, when he says: "to those who have eaten the bread of the Cyprians and the wheaten bread of the Amathusians," for the Amathusians were also Cyprians; and Alcman, when he says: "when she had left lovely Cypros and sea-girt Paphos"; and Aeschylus, when he says: "since thou dost possess the whole of Cypros and Paphos as thine allotment." But if Homer nowhere calls the Buprasians Eleians, I will say that there are many other facts also that he does not mention; yet this is no proof that they are not facts, but merely that he has not mentioned them.
9 But Hecataeus of Miletus says that the Epeians are a different people from the Eleians; that, at any rate, the Epeians joined Heracles in his expedition against Augeas and helped him to destroy both Augeas and Elis. And he says, further, that Dymê is an Epeian and an Achaean city. However, the early historians say many things that are not true, because they were accustomed to falsehoods on account of the use of myths in their writings; and on this account, too, they do not agree with one another concerning the same things. Yet it is not incredible that the Epeians, even if they were once at variance with the Eleians and belonged to a different race, later became united with the Eleians as the result of prevailing over them, and with them formed one common state; and that they prevailed even as far as Dymê. For although the poet has not named Dymê, it is not unreasonable to suppose that in his time Dymê belonged to the Epeians, and later to the Ionians, or, if not to them, at all events to the Achaeans who took possession of their country. Of the four parts, inside which Buprasium is situated, only Hyrminê and Myrsinus belong to the Eleian country, whereas the remaining two are already on the frontiers of Pisatis, as some writers think.
Now Hyrminê was a small town. It is no longer in existence, but near Cyllenê there is a p41mountain promontory called Hormina or Hyrmina. Myrsinus is the present Myrtuntium, a settlement that extends down to the sea, and is situated on the road which runs from Dymê into Elis, and is seventy stadia distant from the city of the Eleians. The Olenian Rock is surmised to be what is now called Scollis;for we are obliged to state what is merely probable, because both the places and the names have undergone changes, and because in many cases the poet does not make himself very clear. Scollis is a rocky mountain common to the territories of the Dymaeans, the Tritaeans, and the Eleians, and borders on another Arcadian mountain called Lampeia, which is one hundred and thirty stadia distant from Elis, one hundred from Tritaea, and the same from Dymê; the last two are Achaean cities. Aleisium is the present Alesiaeum, a territory in the neighbourhood of Amphidolis, in which the people of the surrounding country hold a monthly market. It is situated on the mountain-road that runs from Elis to Olympia. In earlier times it was a city of Pisatis, for the boundaries have varied at different times on account of the change of rulers. The poet also calls Aleisium "Hill of Aleisium," when he says: "until we caused our horses to set foot on Buprasium, rich in wheat, and on the Olenian Rock, and of Aleisium where is the place called Hill" (we must interpret the words as a case of hyperbaton, that is, as equivalent to "and where is the place called Hill of Aleisium"). Some writers point also to a river Aleisius.
Since certain people in Triphylia near Messenia are called Cauconians, and since Dymê also is called Cauconian by some writers, and since in the Dymaean territory between Dymê and Tritaea there is also a river which is called Caucon, in the feminine gender, writers raise the question whether there are not two different sets of Cauconians, one in the region of Triphylia, and the other in the region of Dymê, Elis, and the River Caucon. This river empties into another river which is called Teutheas, in the masculine gender; Teutheas has the same name as one of the little towns which were incorporated into Dymê, except that the name of this town, "Teuthea," is in the feminine gender, and is spelled without the s and with the last syllable long. In this town is the temple of the Nemydian Artemis. The Teutheas empties into the Acheloüs which flows by Dymêº and has the same name as the Acarnanian river. It is also called the "Peirus"; by Hesiod, for instance, when he says: "he dwelt on the Olenian Rock along the banks of a river, wide Peirus." Some change the reading to "Pierus," wrongly. They raise that question about the Cauconians, they say, because, when Athenê in the guise of Mentor, in the Odyssey, says to Nestor, "but in the morning I will go to the great-hearted Cauconians, where a debt is due me, in no way new or small. But do thou send this man on his way with a chariot and with thy son, since he has come to thy house, and give him horses," the poet seems to designate a certain territory in the country of the Epeians which was held by the Cauconians, these Cauconians being a different set from those in Triphylia and perhaps extending as far as the territory of Dymê. Indeed, one should not fail to inquire both into the origin of the epithet of Dymê, "Cauconian," and into the origin of the name of the river "Caucon," because the question who those Cauconians were to whom Athenê says she is going in order to recover the debt offers a problem; for if we should interpret the poet as meaning the Cauconians in Triphylia near Lepreum, I do not see how his account can be plausible. Hence some read: "where a debt is due me in goodly Elis, no small one." But this question will be investigated with clearer results when I describe the country that comes next after this, I mean Pisatis and Triphylia as far as the borders of the country of the Messenians.
After Chelonatas comes the long sea-shore of the Pisatans; and then Cape Pheia. And there was also a small town called Pheia: "beside the walls of Pheia, about the streams of Iardanus," for there is also a small river near by. According to some, Pheia is the beginning of Pisatis. Off Pheia lie a little island and a harbour, from which the nearest distance from the sea to Olympia is one hundred and twenty stadia. Then comes another cape, Ichthys, which, like Chelonatas, projects for a considerable distance towards the west; and from it the distance to Cephallenia is again one hundred and twenty stadia. Then comes the mouth of the Alpheius, which is distant two hundred and eighty stadia from Chelonatas, and five hundred and forty-five from Araxus. It flows from the same regions as the Eurotas, that is, from a place called Asea, a village in the territory of Megalopolis, where there are two springs near one another from which the rivers in question flow. They sink and flow beneath the earth for many stadiaand then rise again; and then they flow down, one into Laconia and the other into Pisatis. The stream of the Eurotas reappears where the district called Bleminatis begins, and then flows past Sparta itself, traverses a long glen near Helus (a place mentioned by the poet), and empties between Gythium, the naval station of Sparta, and Acraea. But the Alpheius, after receiving the waters of the Ladon, the Erymanthus, and other rivers of less significance, flows through Phrixa, Pisatis, and Triphylia past Olympia itself to the Sicilian Sea, into which it empties between Pheia and Epitalium. Near the outlet of the river is the sacred precinct of Artemis Alpheionia or Alpheiusa (for the epithet is spelled both ways), which is about eighty stadia distant from Olympia. An annual festival is also celebrated at Olympia in honour of this goddess as well as in honour of Artemis Elaphia and Artemis Daphnia. The whole country is full of temples of Artemis, Aphroditê, and the Nymphs, being situated in sacred precincts that are generally full of flowers because of the abundance of water. And there are also numerous shrines of Hermes on the road-sides, and temples of Poseidon on the capes. In the temple of Artemis Alpheionia are very famous paintings by two Corinthians, Cleanthes and Aregon: by Cleanthes the "Capture of Troy" and the "Birth of Athenê," and by Aregon the "Artemis Borne Aloft on a Griffin."
Then comes the mountain of Triphylia that sees Macistia from Pisatis; then another river called Chalcis, and a spring called Cruni, and a settlement called Chalcis, and, after these, Samicum, where is the most highly revered temple of the Samian Poseidon. About the temple is a sacred precinct full of wild olive-trees. The people of Macistum used to have charge over it; and it was they, too, who used to proclaim the armistice-day called "Samian." But all the Triphylians contribute to the maintenance of the temple.
In the general neighbourhood of these temples, above the sea, at a distance of thirty stadia or slightly more, is situated the Triphylian Pylus, also called the Lepreatic Pylus, which Homer calls "emathoëis" and transmits to posterity as the fatherland of Nestor, as one might infer from his words, whether it be that the river that flows past Pylus towards the north (now called Mamaüs, or Arcadicus) was called Amathus in earlier times, so that Pylus got its epithet "emathoëis" from "Amathus," or that this river was called Pamisus, the same as two rivers in Messenia, and that the derivation of the epithet of the city is uncertain; it is false, they say, that either the river or the country about it is "amathodes." And also the temple of Athenê Scilluntia at Scillus, in the neighbourhood of Olympia near Phellon, is one of the famous temples. Near Pylus, towards the east, is a mountain named after Minthê, who, according to myth, became the concubine of Hades, was trampled under foot by Corê, and was transformed into garden-mint, the plant which some call Hedyosmos. Furthermore, near the mountain is a precinct sacred to Hades, which is revered by the Macistians too, and also a grove sacred to Demeter, which is situated above the Pylian plain. This plain is fertile; it borders on the sea and stretches along the whole distance between Samicum and the River Neda. But the shore of the sea is narrow and sandy, so that one could not refuse to believe that Pylus got is epithet "emathoëis" therefrom.
Towards the north, on the borders of Pylus, were two little Triphylian cities, Hypana and Tympaneae; the former of these was incorporated into Elis, whereas the latter remained as it was. And further, two rivers flow near these places, the Dalion and the Acheron, both of them emptying into the Alpheius. The Acheron has been so named by virtue of its close relation to Hades; for, as we know, not only the temples of Demeter and Corê have been held in very high honour there, but also those of Hades, perhaps because of "the contrariness of the soil," to use the phrase of Demetrius of Scepsis. For while Triphylia brings forth good fruit, it breeds red-rust and produces rush; and therefore in this region it is often the case that instead of a large crop there is no crop at all.
To the south of Pylus is Lepreum. This city, too, was situated above the sea, at a distance of forty stadia; and between Lepreum and the Annius is the temple of the Samian Poseidon, at a distance of one hundred stadia from each. This is the temple at which the poet says Telemachus found the Pylians performing the sacrifice: "And they came to Pylus, the well-built city of Neleus; and the people were doing sacrifice on the sea-shore, slaying bulls that were black all over, to the dark-haired Earth-shaker." Now it is indeed allowable for the poet even to fabricate what is not true, but when practicable he should adapt his words to what is true and preserve his narrative; but the more appropriate thing was to abstain from what was not true. The Lepreatans held a fertile territory; and that of the Cyparissians bordered on it. Both these districts were taken and held by the Cauconians; and so was the Macistus (by some called Platanistus). The name of the town is the same as that of the territory. It is said that there is a tomb of Caucon in the territory of Lepreum — whether Caucon was a progenitor of the tribe or one who for some other reason had the same name as the tribe.
There are several accounts of the Cauconians; for it is said that, like the Pelasgians, they were an Arcadian tribe, and, again like the Pelasgians, that they were a wandering tribe. At any rate, the poet tells us that they came to Troy as allies of the Trojans. But he does not say whence they come, though they seem to have come from Paphlagonia; for in Paphlagonia there is a people called Cauconiatae whose territory borders on that of the Mariandyni, who are themselves Paphlagonians. But I shall speak of them at greater length when I come to my description of that region. At present I must add the following to my account of the Cauconians in Triphylia. Some say that the whole of what is now called Eleia, from Messenia as far as Dymê, was called Cauconia. Antimachus, at any rate, calls all the inhabitants both Epeians and Cauconians. Others, however, say that the Cauconians did not occupy the whole of Eleia, but lived there in two separate divisions, one division in Triphylia near Messenia, and the other in Buprasis and Coelê Elis near Dymê. And Aristotle has knowledge of their having been established at this latter place especially. And in fact the last view agrees better with what Homer says, and furnishes a solution of the question asked above, for in this view it is assumed that Nestor lived in the Triphylian Pylus, and that the parts towards the south and east (that is, the parts that are contiguous to Messenia and the Laconian country) were subject to him; and these parts were held by the Cauconians, so that if one went by land from Pylus to Lacedaemon his journey necessarily must have been made through the territory of the Cauconians; and yet the temple of the Samian Poseidon and the mooring-place near it, where Telemachus landed, lie off towards the north-west. So then, if the Cauconians live only here, the account of the poet is not conserved; for instance, Athenê, according to Sotades, bids Nestor to send Telemachus to Lacedaemon "with chariot and son" to the parts that lie towards the east, and yet she says that she herself will go to the ship to spend the night, towards the west, and back the same way she came, and she goes on to say that "in the morning" she will go "amongst the great-hearted Cauconians" to collect a debt, that is, she will go forward again. How, pray? For Nestor might have said: "But the Cauconians are my subjects and live near the road that people travel to Lacedaemon. Why, therefore, do you not travel with Telemachus and his companions instead of going back the same way you came?" And at the same time it would have been proper for one who was going to people subject to Nestor to collect a debt — "no small debt," as she says — to request aid from Nestor, if there should be any unfairness (as is usually the case) in connection with the contract; but this she did not do. If, then, the Cauconians lived only there, the result would be absurd; but if some of the Cauconians had been separated from the rest and had gone to the regions near Dymê in Eleia, than Athenê would be speaking of her journey thither, and there would no longer be anything incongruous either in her going down to the ship or in her withdrawing from the company of travellers, because their roads lay in opposite directions. And similarly, too, the puzzling questions raised in regard to Pylus may find an appropriate solution when, a little further on in my chorography, I reach the Messenian Pylus.
A part of the inhabitants of Triphylia were called Paroreatae; they occupied mountains, in the neighbourhood of Lepreum and Macistum, that reach down to the sea near the Samian Poseidium.
At the base of these mountains, on the seaboard, are two caves. One is the cave of the nymphs called Anigriades; the other is the scene of the stories of the daughters of Atlas and of the birth of Dardanus. And here, too, are the sacred precincts called the Ionaeum and the Eurycydeium. Samicum is now only a fortress, though formerly there was also a city which was called Samus, perhaps because of its lofty situation; for they used to call lofty places "Samoi." And perhaps Samicum was the acropolis of Arenê, which the poet mentions in the Catalogue: "And those who dwelt in Pylus and lovely Arenê." For while they cannot with certainty discover Arenê anywhere, they prefer to conjecture that this is its site; and the neighbouring River Anigrus, formerly called Minyeius, gives no slight indication of the truth of the conjecture, for the poet says: "And there is a River Minyeius which falls into the sea near Arenê." For near the cave of the nymphs called Anigriades is a spring which makes the region that lies below it swampy and marshy. The greater part of the water is received by Anigrus, a river so deep and so sluggish that it forms a marsh; and since the region is muddy, it emits an offensive odour for a distance of twenty stadia, and makes the fish unfit to eat. In the mythical accounts, however, this is attributed by some writers to the fact that certain of the Centaurs here washed off the poison they got from the Hydra, and by others to the fact that Melampus used these cleansing waters for the purification of the Proetides. The bathing-water from here cures leprosy, elephantiasis, and scabies. It is said, also, that the Alpheius was so named from its being a cure for leprosy. At any rate, since both the sluggishness of the Anigrus and the back-wash from the sea give p63fixity rather than current to its waters, it was called the "Minyeius" in earlier times, so it is said, though some have perverted the name and made it "Minteius" instead. But the word had other sources of derivation, either from the people who went forth with Chloris, the mother of Nestor, from the Minyeian Orchomenus, or from the Minyans, who, being descendants of the Argonauts, were first driven out of Lemnos into Lacedaemon, and thence into Triphylia, and took up their abode about Arenê in the country which is now called Hypaesia, though it no longer has the settlements of the Minyans. Some of these Minyans sailed with Theras, the son of Autesion, who was a descendant of Polyneices, to the island which is situated between Cyrenaea and Crete ("Callistê its earlier name, but Thera its later," as Callimachus says), and founded Thera, the mother-city of Cyrenê, and designated the island by the same name as the city.
Between the Anigrus and the mountain from which it flows are to be seen the meadow and tomb of Iardanus, and also the Achaeae, which are abrupt cliffs of that same mountain above which, as I was saying, the city Samus was situated. However, Samus is not mentioned at all by the writers of the Circumnavigations — perhaps because it had long since been torn down and perhaps also because of its position; for the Poseidium is a sacred precinct, as I have said, near the sea, and above it is situated a lofty hill which is in front of the Samicum of to‑day, on the site of which Samus once stood, and therefore Samus was not visible from the sea. Here, too, is a plain called Samicum; and from this one might get more conclusive proof that there was once a city called Samus. And further, the poem entitled Rhadinê (of which Stesichorus is reputed to be the author), which begins, "Come, thou clear-voiced Muse, Erato, begin thy song, voicing to the tune of thy lovely lyre the strain of the children of Samus," refers to the children of the Samus in question; for Rhadinê, who had been betrothed to a tyrant of Corinth, the author says, set sail from Samus (not meaning, of course, the Ionian Samus) while the west wind was blowing, and with the same wind her brother, he adds, went to Delphi as chief of an embassy; and her cousin, who was in love with her, set out for Corinth in his chariot to visit her. And the tyrant killed them both and sent their bodies away on a chariot, but repented, recalled the chariot, and buried their bodies.
From this Pylus and Lepreum to the Messenian Pylus and Coryphasium (a fortress situated on the sea) and to the adjacent island Sphagia, the distance is about four hundred stadia; from the Alpheius seven hundred and fifty; and from Chelonatas one thousand and thirty. In the intervening space are both the temple of the Macistian Heracles and the Acidon River. The Acidon flows past the tomb of Iardanus and past Chaa — a city that was once in existence near Lepreum, where is also the Aepasian Plain. It was for the possession of this Chaa, some say, that the war between the Arcadians and Pylians, of which Homer tells us, arose in a dispute; and they think that one should write, "Would that I were in the bloom of my youth, as when the Pylians and the Arcadians gathered together and fought at the swift-flowing Acidon, beside the walls of Chaa" — instead of "Celadon" and "Pheia"; for this region, they say, is nearer than the other to the tomb of Iardanus and to the country of the Arcadians.
Cyparissia is on the Triphylian Sea, and so are Pyrgi, and the Acidon and Neda Rivers. At the present time the stream of the Neda is the boundary between Triphylia and Messenia (an impetuous stream that comes down from Lycaeus, an Arcadian mountain, out of a spring, which, according to the myth, Rhea, after she had given birth to Zeus, caused to break forth in order to have water to bathe in); and it flows past Phigalia, opposite the place where the Pyrgetans, last of the Triphylians, border on the Cyparissians, first of the Messenians; but in the early times the division between the two countries was different, so that some of the territories across the Neda were subject to Nestor — not only Cyparissëeis, but also some other parts on the far side. Just so, too, the poet prolongs the Pylian Sea as far as the seven cities which Agamemnon promised to Achilles; "and all are situated near the sea of sandy Pylus"; for this phrase is equivalent to "near the Pylian Sea."
Be that as it may, next in order after sailing past Cyparissëeis towards the Messenian Pylus and Coryphasium one comes to Erana, which some wrongly think was in earlier times called Arenê, by the same name as the Pylian Arenê, and also to Cape Platamodes, from which the distance to Coryphasium and to what is now called Pylus is one hundred stadia. Here, too, is a small island, Protê, and on it a town of the same name. Perhaps I would not be examining at such length things that are ancient, and would be content merely to tell in detail how things now are, if there were not connected with these matters legends that have been taught us from boyhood; and since different men say different things, I must act as arbiter. In general, it is the most famous, the oldest, and the most experienced men who are believed; and since it is Homer who has surpassed all others in these respects, I must likewise both inquire into his words and compare them with things as they now are, as I was saying a little while ago.
I have already inquired into Homer's words concerning Coelê Elis and Buprasium. Concerning the country that was subject to Nestor, Homer speaks as follows: "And those who dwelt in Pylus and lovely Arenê and Thryum, fording-place of the Alpheius, and well-built Aepy, and also those who were inhabitants of Cyparissëeis and Amphigeneia and Pteleus and Helus and Dorium, at which place the Muses met Thamyris the Thracian, and put a stop to his singing while he was on his way from Oechalia from Eurytus the Oechalian." It is Pylus, then, with which our investigation is concerned, and about it we shall make inquiry presently. About Arenê I have already spoken. The city which the poet now calls Thryum he elsewhere calls Thryoessa: "There is a certain city, Thryoessa, a steep hill, far away on the Alphaeus." He calls it "fording-place of the Alpheius" because the river could be crossed on foot, as it seems, at this place. But it is now called Epitalium (a small place in Macistia). As for "well-built Aepy," some raise the question which of the two words is the epithet and which is the city, and whether it is the Margalae of to‑day, in Amphidolia. Now Margalae is not a natural stronghold, but another place is pointed out which is a natural stronghold, in Macistia. The man, therefore, who suspects that the latter place is meant by Homer calls the name of the city "Aepy" from what is actually the case in nature (compare Helus, Aegialus, and several other names of places); whereas the man who suspects that "Margala" is meant does the reverse perhaps. Thryum, or Thryoessa, they say, is Epitalium, because the whole of this country is full of rushes, particularly the rivers; and this is still more conspicuous at the fordable places of the stream. But perhaps, they say, Homer called the ford "Thryum" and called Epitalium "well-built Aepy"; for Epitalium is fortified by nature. And in fact he speaks of a "steep hill" in other places: "There is a certain city, Thryoessa, a steep hill, far away on the Alpheius, last city of sandy Pylus."
Cyparissëeis is in the neighbourhood of the Macistia of earlier times (when Macistia still extended across the Neda), but it is no longer inhabited, as is also the case with Macistum. But there is another, the Messenian Cyparissia; it, too, is now called by the same name as the Macistian and in like manner, namely, Cyparissia, in the singular number and in the feminine gender, whereas only the river is now called Cyparissëeis. And Amphigeneia, also, is in Macistia, in the neighbourhood of the Hypsöeis River, where is the temple of Leto. Pteleum was a settlement of the colony from the Thessalian Pteleum, for, as Homer tells us, there was a Pteleum in Thessaly too: "and Antrum, near the sea, and grassy Pteleum"; but now it is a woody, uninhabited place, and is called Pteleasium. As for Helus, some call it a territory in the neighbourhood of the Alpheius, while others go on to call it a city, as they do the Laconian Helus: "and Helus, a city near the sea"; but others call it a marsh, the marsh in the neighbourhood of Alorium, where is the temple of the Heleian Artemis, whose worship was under the management of the Arcadians, for this people had the priesthood. As for Dorium, some call it a mountain, while others call it a plain, but nothing is now to be seen; and yet by some the Aluris of to‑day, or Alura, situated in what is called the Aulon of Messenia, is called Dorium. And somewhere in this region is also the Oechalia of Eurytus (the Andania of to‑day, a small Arcadian town, with the same name as the towns in Thessaly and Euboea), whence, according to the poet, Thamyris the Thracian came to Dorium and was deprived of the art of singing.
From these facts, then, it is clear that the country subject to Nestor, all of which the poet calls "land of the Pylians," extends on each side of the Alphaeus; but the Alpheius nowhere touches either Messenia or Coelê Elis. For the fatherland of Nestor is in this country which we call Triphylian, or Arcadian, or Leprean, Pylus. And the truth is that, whereas the other places called Pylus are to be seen on the sea, this Pylus is more than thirty stadia above the sea — a fact that is also clear from the verses of Homer, for, in the first place, a messenger is sent to the boat after the companions of Timomachus to invite them to an entertainment, and, secondly, Telemachus on his return from Sparta does not permit Peisistratus to drive to the city, but urges him to turn aside towards the ship, knowing that the road towards the city is not the same as that towards the place of anchorage. And thus the return voyage of Telemachus might be spoken of appropriately in these words: "And they went past Cruni and fair-flowing Chalcis. And the sun set and all the ways grew dark; and the ship, rejoicing in the breeze of Zeus, drew near to Phea, and on past goodly Elis, where the Epeians held sway." Thus far, then, the voyage is towards the north, but thence it bends in the direction of the east. That is, the ship abandons the voyage that was set out upon at first and that led straight to Ithaca, because there the wooers had set the ambush "in the strait between Ithaca and Samos." "And thence again he steered for the islands that are thoai"; but by "thoai" the poet means the islands that are "pointed." These belong to the Echinades group and are near the beginning of the Corinthian Gulf and the outlets of the Acheloüs. Again, after passing by Ithaca far enough to put it south of him, Telemachus turns round towards the proper course between Acarnania and Ithaca and makes his landing on the other side of the island — not at the Cephallenian strait which was being guarded by the wooers.
At any rate, if one should conceive the notion that the Eleian Pylus is the Pylus of Nestor, the poet could not appropriately say that the ship, after putting to sea from there, was carried past Cruni and Chalcis before sunset, then drew near to Phea by night, and then sailed past Eleia; for these places are to the south of Eleia: first, Phea, then Chalcis, then Cruni, and then the Triphylian Pylus and Samicum. This, then, would be the voyage for one who is sailing towards the south from Eleian Pylus, whereas one who is sailing towards the north, where Ithaca is, leaves all these parts behind him, and also must sail past Eleia itself — and that before sunset, though the poet says after sunset. And further, if one should go on to make a second supposition, that the Messenian Pylus and Coryphasium are the beginning of the voyage from Nestor's, the distance would be considerable and would require more time. At any rate, merely the distance to Triphylian Pylus and the Samian Poseidium is four hundred stadia; and the first part of the coasting-voyage is not "past Cruni and Chalcis" and Phea (names of obscure rivers, or rather creeks), but past the Neda; then past the Acidon; and then past the Alpheius and the intervening places. And on this supposition those other places should have been mentioned later, for the voyage was indeed made past them too.
Furthermore, the detailed account which Nestor recites to Patroclus concerning the war that took place between the Pylians and the Eleians pleads for what I have been trying to prove, if one observes the verses of the poet. For in them the poet says that, since Heracles had ravaged the Pylian country to the extent that all the youth were slain and that of all the twelve sons of Neleus only Nestor, then in his earliest youth, had been left, and since the Epeians had conceived a contempt for Neleus because of his old age and lack of defenders, they began to treat the Pylians in an arrogant and wanton manner. So, in return for this treatment, Nestor gathered together all he could of the people of his home-land, made an attack, he says, upon Eleia, and herded together very much booty, "fifty herds of cattle, and as many flocks of sheep, and as many droves of swine," and also as many herds of goats, and one hundred and fifty sorrel mares, most of them with foals beneath them. "And these," he says, "we drove within Neleian Pylus, to the city, in the night," meaning, first, that it was in the day-time that the driving away of the booty and the rout of those who came to the rescue took place (when he says he killed Itymoneus), and, secondly, that it was in the night-time that the return took place, so that it was night when they arrived at the city. And while the Pylians were busied with the distribution of the booty and with offering sacrifice, the Epeians, on the third day, after assembling in numbers, both footmen and horsemen, came forth in their turn against the Pylians and encamped around Thryum, which is situated on the Alpheius River. And when the Pylians learned this, they forthwith set out to the rescue; they passed the night in the neighbourhood of the Minyeius River near Arenê, and thence arrived at the Alpheius "in open sky," that is, at midday. And after they offered sacrifice to the gods and passed the night near the river, they joined battle at early dawn; and after the rout took place, they did not stop pursuing and slaying the enemy until they set foot on Buprasium "and on the Olenian Rock and where is the place called Hill of Aleisium, whence Athenê turned the people back again"; and a little further on the poet says: "But the Achaeans drove back their swift horses from Buprasium to Pylus."
From all this, then, how could one suppose that either the Eleian or Messenian Pylus is meant? Not the Eleian Pylus, because, if this Pylus was being ravaged by Heracles, the country of the Epeians was being ravaged by him at the same time; but this is the Eleian country. How, pray, could a people whose country had been ravaged at the same time and were of the same stock, have acquired such arrogance and wantonness towards a people who had been wronged at the same time? And how could they overrun and plunder their own homeland? And how could both Augeas and Neleus be rulers of the same people at the same time if they were personal enemies? If to Neleus "a great debt was owing in goodly Elis. Four horses, prize-winners, with their chariots, had come to win prizes and were to run for a tripod; but these Augeas, lord of men, detained there, though he sent away the driver." And if this is where Neleus lived, Nestor too must have lived there. How, pray, could the poet say of the Eleians and the Buprasians, "there were four rulers of them, and ten swift ships followed each man, and many Epeians embarked"? And the country, too, was divided into four parts; yet Nestor ruled over no one of these, but over them "that dwelt in Pylus and in lovely Arenê," and over the places that come after these as far as Messenê. Again, how could the Epeians, who in their turn went forth to attack the Pylians, set out for the Alpheius and Thryum? And how, after the battle took place there, after they were routed, could they flee towards Buprasium? And again, if it was the Messenian Pylus which Heracles had ravaged, how could a people so far distant as the Epeians act wantonly towards them, and how could the Epeians have been involved in numerous contracts with them and have defaulted these by cancelling them, so that the war resulted on that account? And how could Nestor, when he went forth to plunder the country, when he herded together so much booty consisting of both swine and cattle, none of which could travel fast or far, have accomplished a journey of more than one thousand stadia to that Pylus which is near Coryphasium? Yet on the third day they all came to Thryoessa and the River Alpheius to besiege the stronghold! And how could these places belong to those who were in power in Messenia, when they were held by Cauconians and Triphylians and Pisatans? And as for Gerena, or Gerenia (for the word is spelled in both ways), perhaps some people named it that to suit a purpose, though it is also possible that the place was by chance so named. And, in general, since Messenia was classified as subject to Menelaüs, as was also the Laconian country (as will be clear from what I shall say later), and since the Pamisus and the Nedon flow through Messenia, whereas the Alpheius nowhere touches it (the Alpheius "that floweth in broad stream through the land of the Pylians," over which Nestor ruled), what plausibility could there be in an account which lands Nestor in a foreign realm and robs him of the cities that are attributed to him in the Catalogue, and thus makes everything subject to Menelaüs?
It remains for me to tell about Olympia, and how everything fell into the hands of the Eleians. The temple is in Pisatis, less than three hundred stadia distant from Elis. In front of the temple is situated a grove of wild olive-trees, and the stadium is in this grove. Past the temple flows the Alpheius, which, rising in Arcadia, flows between the west and the south into the Triphylian Sea. At the outset the temple got fame on account of the oracle of the Olympian Zeus; and yet, after the oracle failed to respond, the glory of the temple persisted none the less, and it received all that increase of fame of which we know, on account both of the festal assembly and of the Olympian Games, in which the prize was a crown and which were regarded as sacred, the greatest games in the world. The temple was adorned by its numerous offerings, which were dedicated there from all parts of Greece. Among these was the Zeus of beaten gold dedicated by Cypselus the tyrant of Corinth. But the greatest of these was the image of Zeus made by Pheidias of Athens, son of Charmides; it was made of ivory, and it was so large that, although the temple was very large, the artist is thought to have missed the proper symmetry, for he showed Zeus seated but almost touching the roof with his head, thus making the impression that if Zeus arose and stood erect he would unroof the temple. Certain writers have recorded the measurements of the image, and Callimachus has set them forth in an iambic poem. Panaenus the painter, who was the nephew and collaborator of Pheidias, helped him greatly in decorating the image, particularly the garments, with colours. And many wonderful paintings, works of Panaenus, are also to be seen round the temple. It is related of Pheidias that, when Panaenus asked him after what model he was going to make the likeness of Zeus, he replied that he was going to make it after the likeness set forth by Homer in these words "Cronion spake, and nodded assent with his dark brows, and then the ambrosial locks flowed streaming from the lord's immortal head, and he caused great Olympus to quake." A noble description indeed, as appears not only from the "brows" but from the other details in the passage, because the poet provokes our imagination to conceive the picture of a mighty personage and a mighty power worthy of a Zeus, just as he does in the p91case of Hera, at the same time preserving what is appropriate in each; for of Hera he says, "she shook herself upon the throne, and caused lofty Olympus to quake." What in her case occurred when she moved her whole body, resulted in the case of Zeus when he merely "nodded with his brows," although his hair too was somewhat affected at the same time. This, too, is a graceful saying about the poet, that "he alone has seen, or else he alone has shown, the likenesses of the gods." The Eleians above all others are to be credited both with the magnificence of the temple at Olympia and with the honour in which it was held. In the times of the Trojan war, it is true, or even before those times, they were not a prosperous people, since they had been humbled by the Pylians, and also, later on, by Heracles when Augeas their king was overthrown. The evidence is this: "The Eleians sent only forty ships to Troy, whereas the Pylians and Nestor sent ninety. But later on, after the return of the Heracleidae, the contrary was the case, for the Aetolians, having returned with the Heracleidae under the leadership of Oxylus, and on the strength of ancient kinship having taken up their abode with the Epeians, enlarged Coelê Elis, and not only seized much of Pisatis but also got Olympia under their power. What is more, the Olympian Games are an invention of theirs; and it was they who celebrated the first Olympiads, for one should disregard the ancient stories both of the founding of the temple and of the establishment of the games — some alleging that it was Heracles, one of the Idaean Dactyli, who was the originator of both, and others, that it was Heracles the son of Alcmenê and Zeus, who also was the first to contend in the games and win the victory; for such stories are told in many ways, and no faith at all is to be put in them. It is nearer the truth to say that from the first Olympiad, in which the Eleian Coroebus won the stadium-race, until the twenty-sixth Olympiad, the Eleians had charge both of the temple and of the games. But in the times of the Trojan War, either there were no games in which the prize was a crown or else they were not famous, neither the Olympian nor any other of those that are now famous. In the first place, Homer does not mention any of these, though he mentions another kind — funeral games. And yet some think that he mentions the Olympian Games when he says that Augeas deprived the driver of "four horses, prize-winners, that had come to win prizes." And they say that the Pisatans took no part in the Trojan War because they were regarded as sacred to Zeus. But neither was the Pisatis in which Olympia is situated subject to Augeas at that time, but only the Eleian country, nor were the Olympian Games celebrated even once in Eleia, but always in Olympia. And the games which I have just cited from Homer clearly took place in Elis, where the debt was owing: "for a debt was owing to him in goodly Elis, four horses, prize-winners." And these were not games in which the prize was a crown (for the horses were to run for a tripod), as was the case at Olympia. After the twenty-sixth Olympiad, when they had got back their home-land, the Pisatans themselves went to celebrating the games because they saw that these were held in high esteem. But in later times Pisatis again fell into the power of the Eleians, and thus again the direction of the games fell to them. The Lacedaemonians also, after the last defeat of the Messenians, co-operated with the Eleians, who had been their allies in battle, whereas the Arcadians and the descendants of Nestor had done the opposite, having joined with the Messenians in war. And the Lacedaemonians co-operated with them so effectually that the whole country as far as Messenê came to be called Eleia, and the name has persisted to this day, whereas, of the Pisatans, the Triphylians, and the Cauconians, not even a name has survived. Further, the Eleians settled the inhabitants of "sandy Pylus" itself in Lepreum, to gratify the Lepreatans, who had been victorious in a war, and they broke up many other settlements, and also exacted tribute of as many as they saw inclined to act independently.
Pisatis first became widely famous on account of its rulers, who were most powerful: they were Oenomaüs, and Pelops who succeeded him, and the numerous sons of the latter. And Salmoneus, too, is said to have reigned there; at any rate, one of the eight cities into which Pisatis is divided is called Salmonê. So for these reasons, as well as on account of the temple at Olympia, the country has gained wide repute. But one should listen to the old accounts with reserve, knowing that they are not very commonly accepted; for the later writers hold new views about many things and even tell the opposite of the old accounts, as when they say that Augeas ruled over Pisatis, but Oenomaüs and Salmoneus over Eleia; and some writers combine the two tribes into one. But in general one should follow only what is commonly accepted. Indeed, the writers do not even agree as to the derivation of the name Pisatis; for some derive it from a city Pisa, which bears the same name as the spring; the spring, they say, was called "Pisa," the equivalent of "pistra," that is "potistra"; and they point out the site of the city on a lofty place between Ossa and Olympus, two mountains that bear the same name as those in Thessaly. But some say that there was no city by the name of Pisa (for if there had been, it would have been one of the eight cities), but only a spring, now called Bisa, near Cicysium, the largest of the eight cities; and Stesichorus, they explain, uses the term "city" for the territory called Pisa, just as Homer calls Lesbos the "city of Macar"; so Euripides in his Ion, "there is Euboea, a neighbouring city to Athens"; and in his Rhadamanthys, "who hold the Euboean land, a neighbouring city"; and Sophocles in his Mysians, "The whole country, stranger, is called Asia, but the city of the Mysians is called Mysia."
Salmonê is situated near the spring of that name from which flows the Enipeus River. The river empties into the Alpheius, and is now called the Barnichius. It is said that Tyro fell in love with Enipeus: "She loved a river, the divine Enipeus." For there, it is said, her father Salmoneus reigned, just as Euripides also says in his Aeolus. Some write the name of the river in Thessaly "Eniseus"; it flows from Mount Othrys, and receives the Apidanus, which flows down out of Pharsalus. Near Salmonê is Heracleia, which is also one of the eight cities; it is about forty stadia distant from Olympia and is situated on the Cytherius River, where is the temple of the Ioniades Nymphs, who have been believed to cure diseases with their waters. Near Olympia is Arpina, also one of the eight cities, through which flows the River Parthenias, on the road that leads up to Pheraea. Pheraea is in Arcadia, and it is situated above Dymaea and Buprasium and Elis, that is, to the north of Pisatis. Here, too, is Cicysium, one of the eight cities; and also Dyspontium, which is situated in a plain and on the road that leads from Elis to Olympia; but it was destroyed, and most of its inhabitants emigrated to Epidamnus and Apollonia. Pholoê, an Arcadian mountain, is also situated above Olympia, and very close to it, so that its foot-hills are in Pisatis. Both the whole of Pisatis and most parts of Triphylia border on Arcadia; and on this account most of the Pylian districts mentioned in the Catalogue are thought to be Arcadian; the well-informed, however, deny this, for they say that the Erymanthus, one of the rivers that empty into the Alpheius, forms a boundary of Arcadia and that the districts in question are situated outside that river.
Ephorus says that Aetolus, after he had been driven by Salmoneus, the king of the Epeians and the Pisatans, out of Eleia into Aetolia, named the country after himself and also united the cities there under one metropolis; and Oxylus, a descendant of Aetolus and a friend of Temenus and the Heracleidae who accompanied him, acted as their guide on their way back to the Peloponnesus, and apportioned among them that part of the country which was hostile to them, and in general made suggestions regarding the conquest of the country; and in return for all this he received as a favour the permission to return to Eleia, his ancestral land; and he collected an army and returned from Aetolia to attack the Epeians who were in possession of Elis; but when the Epeians met them with arms, and it was found that the two forces were evenly matched, Pyraechmes the Aetolian and Degmenus the Epeians, in accordance with an ancient custom of the Greeks, advanced to single combat. Degmenus was lightly armed with a bow, thinking that he would easily overcome a heavy-armed opponent at long range, but Pyraechmes armed himself with a sling and a bag of stones, after he had noticed his opponent's ruse (as it happened, the sling had only recently been invented by the Aetolians); and since the sling had longer range, Degmenus fell, and the Aetolians drove out the Epeians and took possession of the land; and they also assumed the superintendence, then in the hands of the Achaeans, of the temple at Olympia; and because of the friendship of Oxylus with the Heracleidae, a sworn agreement was promptly made by all that the Eleians should be sacred to Zeus, 358and that p105whoever invaded that country with arms should be under a curse, and that whoever did not defend it to the extent of his power should be likewise under a curse; consequently those who later founded the city of the Eleians left it without a wall, and those who go through the country itself with an army give up their arms and then get them back again after they have passed out of its borders; and Iphitus celebrated1the Olympian Games, the Eleians now being a sacred people; for these reasons the people flourished, for whereas the other peoples were always at war with one another, the Eleians alone had profound peace, not only they, but their alien residents as well, and so for this reason their country became the most populous of all; but Pheidon the Argive, who was the tenth in descent from Temenus and surpassed all men of his time in ability (whereby he not only recovered the whole inheritance of Temenus, which had been broken up into several parts, but also invented the measures called "Pheidonian," and weights, and coinage struck from silver and other metals) — Pheidon, I say, in addition to all this, also attacked the cities that had been captured previously by Heracles, and claimed for himself the right to celebrate all the games that Heracles had instituted. And he said that the Olympian Games were among these; and so he forcibly invaded Eleia and celebrated the games himself, the Eleians, because of the peace, having no arms wherewith to resist him, and all the others being under his domination; however, the Eleians did not record this celebration in their public register, but because of his action they also procured arms and began to defend themselves; and the Lacedaemonians co-operated with them, either because they envied them the prosperity which they had enjoyed on account of the peace, or because they thought that they would have them as allies in destroying the power of Pheidon, for he had deprived them of the hegemony over the Peloponnesus which they had formerly held; and the Eleians did help them to destroy the power of Pheidon, and the Lacedaemonians helped the Eleians to bring both Pisatis and Triphylia under their sway. The length of the voyage along the coast of the Eleia of to‑day, not counting the sinuosities of the gulfs, is, all told, twelve hundred stadia. So much for Eleia. |
|
|
|
|
8 - 4 Messenia 
1 Messenia borders on Eleia; and for the most part it inclines round towards the south and the Libyan Sea. Now in the time of the Trojan War this country was classed as subject to Menelaüs, since it was a part of Laconia, and it was called Messenê, but the city now named Messenê, whose acropolis was Ithomê, had not yet been founded; but after the death of Menelaüs, when those who succeeded to the government of Laconia had become enfeebled, the Neleidae began to rule over Messenia. And indeed at the time of the return of the Heracleidae and of the division of the country which then took place, Melanthus was king of the Messenians, who were an autonomous people, although formerly they had been subject to Menelaüs. An indication of this is as follows: The seven cities which Agamemnon promised to give to Achilles were on the Messenian Gulf and the adjacent Asinaean Gulf, so called after the Messenian Asinê; these cities were "Cardamylê and Enopê and grassy Hirê and sacred Pherae and deep-meadowed Antheia and beautiful Aepeia and vine-clad Pedasus;" and surely Agamemnon would not have promised cities that belonged neither to himself nor to his brother. And the poet makes it clear that men from Pherae did accompany Menelaüs on the expedition; and in the Laconian Catalogue he includes Oetylus, which is situated on the Messenian Gulf. Messenê comes after Triphylia; and there is a cape which is common to both; and after this cape come Cyparissia and Coryphasium. Above Coryphasium and the sea, at a distance of seven stadia, lies a mountain, Aegaleum.
2 Now the ancient Messenian Pylus was a city at the foot of Aegaleum; but after this city was torn down some of its inhabitants took up their abode on Cape Coryphasium; and when the Athenians under the leadership of Eurymedon and Stratocles were sailing on the second expedition to Sicily, they reconstructed the city as a fortress against the Lacedaemonians. Here, too, is the Messenian Cyparissia, and the island called Protê, and the island called Sphagia that lies off the coast near Pylus (the same is also called Sphacteria), on which the Lacedaemonians lost by capture three hundred of their own men, who were besieged and forced to surrender by the Athenians. Opposite this sea-coast of the Cyparissians, out in the high sea, lie two islands called Strophades; and they are distant, I should say, about four hundred stadia from the mainland, in the Libyan and Southern Sea. Thucydides says that this Pylus was the naval station of the Messenians. It is four hundred stadia distant from Sparta.
3 Next comes Methonê. This, they say, is what the poet calls Pedasus, one of the seven cities which Agamemnon promised to Achilles. It was here that Agrippa, during the war of Actium, after he had taken the place by an attack from the sea, put to death Bogus, the king of the Maurusians, who belonged to the faction of Antony.
4 Adjacent to Methonê is Acritas, which is the beginning of the Messenian Gulf. But this is also called the Asinaean Gulf, from Asinê, which is the first town on the gulf and bears the same name as the Hermionic town. Asinê, then, is the beginning of the gulf on the west, while the beginning on the east is formed by a place called Thyrides, which borders on that part of the Laconia of to‑day which is near Cynaethius and Taenarum. Between Asinê and Thyrides, beginning at Thyrides, one comes to Oetylus (by some called Baetylus); then to Leuctrum, a colony of the Leuctri in Boeotia; then to Cardamylê, which is situated on a rock fortified by nature; then to Pherae, which borders on Thuria and Gerena, the place from which Nestor got his epithet "Gerenian," it is said, because his life was saved there, as I have said before. In Gerenia is to be seen a temple of Triccaean Asclepius, a reproduction of the one in the Thessalian Tricca. It is said that Pelops, after he had given his sister Niobê in marriage to Amphion, founded Leuctrum, Charadra, and Thalami (now called Boeoti), bringing with him certain colonists from Boeotia. Near Pherae is the mouth of the Nedon River; it flows through Laconia and is a different river from the Neda. It has a notable temple of Athena Nedusia. In Poeäessa, also, there is a temple of Athena Nedusia, named after some place called Nedon, from which Teleclus is said to have colonised Poeäessa and Echeiae and Tragium.
5 Of the seven cities which Agamemnon tendered to Achilles, I have already spoken about Cardamylê and Pherae and Pedasus. As for Enopê, some say that it is Pellana, others that it is some place near Cardamylê, and others that it is Gerenia. As for Hirê, it is pointed out near the mountain that is near Megalopolis in Arcadia, on the road that leads to Andania, the city which, as I have said, the poet called Oechalia; but others say that what is now Mesola, which extends to the gulf between Taÿgetus and Messenia, is called Hirê. And Aepeia is now called Thuria, which, as I have said, borders on Pharae; it is situated on a lofty hill, and hence the name. From Thuria is derived the name of the Thuriates Gulf, on which there was but one city, Rhium by name, opposite Taenarum. And as for Antheia, some say that it is Thuria itself, and that Aepeia is Methonê; but others say that of all the Messenian cities the epithet "deep-meadowed" was most appropriately applied to the intervening Asinê, in whose territory on the sea is a city called Coronê; moreover, according to some writers, it was Coronê that the poet called Pedasus. "And all are close to the salt sea," Cardamylê on it, Pharae only five stadia distant (with an anchoring place in summer), while the others are at varying distances from the sea.
6 It is near Coronê, at about the centre of the gulf, that the river Pamisus empties. The river has on its right Coronê and the cities that come in order after it (of these latter the farthermost towards the west are Pylus and Cyparissia, and between these is Erana, which some have wrongly thought to be the Arenê of earlier time), and it has Thuria and Pharae on its left. It is the largest of the rivers inside the Isthmus, although it is no more than a hundred stadia in length from its sources, from which it flows with an abundance of water through the Messenian plain, that is, through Macaria, as it is called. The river stands at a distance of fifty stadia from the present city of the Messenians. There is also another Pamisus, a small torrential stream, which flows near the Laconian Leuctrum; and it was over Leuctrum that the Messenians got into a dispute with the Lacedaemonians in the time of Philip. Of the Pamisus which some called the Amathus I have already spoken.
7 According to Ephorus: When Cresphontes took Messenia, he divided it into five cities; and so, since Stenyclarus was situated in the centre of this country, he designated it as a royal residence for himself, while as for the others — Pylus, Rhium, Mesola, and Hyameitis — he sent kings to them, after conferring on all the Messenians equal rights with the Dorians; but since this irritated the Dorians, he changed his mind, gave sanction to Stenyclarus alone as a city, and also gathered into it all the Dorians.
8 The city of the Messenians is similar to Corinth; for above either city lies a high and precipitous mountain that is enclosed by a common wall, so that it is used as an acropolis, the one mountain being called Ithomê and the other Acrocorinthus. And so Demetrius of Pharos seems to have spoken aptly to Philip the son of Demetrius when he advised him to lay hold of both these cities if he coveted the Peloponnesus, "for if you hold both horns," he said, "you will hold down the cow," meaning by "horns" Ithomê and Acrocorinthus, and by "cow" the Peloponnesus. And indeed it is because of their advantageous position that these cities have been objects of contention. Corinth was destroyed and rebuilt again by the Romans; and Messenê was destroyed by the Lacedaemonians but restored by the Thebans and afterward by Philip the son of Amyntas. The citadels, however, remained uninhabited.
9 The temple of Artemis at Limnae, at which the Messenians are reputed to have outraged the maidens who had come to the sacrifice, is on the boundaries between Laconia and Messenia, where both peoples held assemblies and offered sacrifice in common; and they say that it was after the outraging of the maidens, when the Messenians refused to give satisfaction for the act, that the war took place. And it is after this Limnae, also, that the Limnaeum, the temple of Artemis in Sparta, has been named.
Often, however, they went to war on account of the revolts of the Messenians. Tyrtaeus says in his poems that the first conquest of Messenia took place in the time of his fathers' fathers; the second, at the time when the Messenians chose the Argives, Eleians, Pisatans, and Arcadians as allies and revolted — the Arcadians furnishing Aristocrates the king of Orchomenus as general and the Pisatae furnishing Pantaleon the son of Omphalion; at this time, he says, he himself was the Lacedaemonian general in the war, for in his elegy entitled Eunomia he says that he came from there: "For the son of Cronus, spouse of Hera of the beautiful crown, Zeus himself, hath given this city to the Heracleidae, in company with whom I left windy Erineus, and came to the broad island of Pelops." Therefore either these verses of the elegy must be denied authority or we must discredit Philochorus, who says that Tyrtaeus was an Athenian from the deme of Aphidnae, and also Callisthenes and several other writers, who say that he came from Athens when the Lacedaemonians asked for him in accordance with an oracle which bade them to get a commander from the Athenians. So the second war was in the time of Tyrtaeus; but also a third and fourth war took place, they say, in which the Messenians were defeated. The voyage round the coast of Messenia, following the sinuosities of the gulfs, is, all told, about eight hundred stadia in length.
However, I am overstepping the bounds of moderation in recounting the numerous stories told about a country the most of which is now deserted; in fact, Laconia too is now short of population as compared with its large population in olden times, for outside of Sparta the remaining towns are only about thirty in number, whereas in olden times it was called, they say, "country of the hundred cities"; and it was on this account, they say, that they held annual festivals in which one hundred cattle were sacrificed. |
|
|
|



|
8 - 5 Laconia 
1 Be this as it may, after the Messenian Gulf comes the Laconian Gulf, lying between Taenarum and Maleae, which bends slightly from the south towards the east; and Thyrides, a precipitous rock exposed to the currents of the sea, is in the Messenian Gulf at a distance of one hundred and thirty stadia from Taenarum. Above Thyrides lies Taÿgetus; it is a lofty and steep mountain, only a short distance from the sea, and it connects in its northerly parts with the foothills of the Arcadian mountains in such a way that a glen is left in between, where Messenia borders on Laconia. Below Taÿgetus, in the interior, lies Sparta, and also Amyclae, where is the temple of Apollo, and Pharis. Now the site of Sparta is in a rather hollow district, although it includes mountains within its limits; yet no part of it is marshy, though in olden times the suburban part was marshy, and this part they called Limnae; and the temple of Dionysus in Limnae stood on wet ground, though now its foundations rest on dry ground. In the bend of the seaboard one comes, first, to a headland that projects into the sea, Taenarum, with its temple of Poseidon situated in a grove; and secondly, near by, to the cavern through which, according to the myth writers, Cerberus was brought up from Hades by Heracles. From here the passage towards the south across the sea to Phycus, a cape in Cyrenaea, is three thousand stadia; and the passage towards the west to Pachynus, the promontory of Sicily, is four thousand six hundred, though some say four thousand; and towards the east to Maleae, following the sinuosities of the gulfs, six hundred and seventy; and to Onugnathus, a low-lying peninsula somewhat this side of Maleae, five hundred and twenty; off Onugnathus and opposite it, at a distance of forty stadia, lies Cythera, an island with a good harbour, containing a city of the same name, which Eurycles, the ruler of the Lacedaemonians in our times, seized as his private property; and round it lie several small islands, some near it and others slightly farther away; and to Corycus, a cape in Crete, the shortest voyage is seven hundred stadia.
2 After Taenarum, on the voyage to Onugnathus and Maleae, one comes to the city Psamathus; then to Asinê, and to Gythium, the seaport of Sparta, situated at a distance of two hundred and forty stadia from Sparta. The roadstead of the seaport was dug by the hand of man, so it is said. Then one comes to the Eurotas, which empties between Gythium and Acraea. Now for a time the voyage is along the shore, for about two hundred and forty stadia; then comes a marshy district situated above the gulf, and also a village called Helus. In earlier times Helus was a city, just as Homer says: "And they that held Amyclae, and Helus, a city by the sea." It is said to have been founded by Helius, a son of Perseus. And one comes also to a plain called Leucê; then to a city Cyparissia, which is situated on a peninsula and has a harbour; then to Onugnathus, which has a harbour; then to the city Boea; and then to Maleae. And the distance from Onugnathus to Maleae is one hundred and fifty stadia; and there is also a city Asopus in Laconia.
3 They say that one of the places mentioned in Homer's Catalogue, Messê, is nowhere to be seen; and that Messoa was not a part of the country but of Sparta, as was the case with Limnaeum, . . . But some take "Messê" as an apocopated form of "Messenê," for, as I have said, Messenê too was a part of Laconia. As examples of apocope from the poet himself, writers cite "krī," "do," and "maps," and also the passage "the heroes Automedon and Alcimus," for "Alcimedon"; then from Hesiod, who uses "bri" for "brithu" or "briaron"; and Sophocles and Ion, "rha" for "rhadion"; and Epicharmus, "li" for "lian," and "Syracō" for "Syracuse"; and in Empedocles, "ops" for "opsis": "the 'ops' of both becomes one;" and in Antimachus, "the sacred 'ops' of the Eleusinian Demeter," and "alphi" for "alphiton"; and Euphorion even uses "hēl" for "hēlos"; and in Philetas, "eri" for "erion": "maidservants bring white 'eri' and put it in baskets;" and Aratus says "pēda" for "pēdalia": "the 'pēda' towards the wind"; and Simmias, "Dodo" for "Dodona." As for the rest of the places listed by the poet, some have been destroyed; of others traces are still left; and of others the names have been changed, for example, Augeiae to Aegaeae; for the Augeiae in Locris no longer exists at all. As for Las, the story goes, the Dioscuri once captured it by siege, and it was from this fact that they got the appellation "Lapersae." And Sophocles says, "by the two Lapersae, I swear, by Eurotas third, by the gods in Argos and about Sparta."
4 According to Ephorus: Eurysthenes and Procles, the Heracleidae, took possession of Laconia, divided the country into six parts, and founded cities; now one of the divisions, Amyclae, they selected and gave to the man who had betrayed Laconia to them and who had persuaded the ruler who was in possession of it to accept their terms and emigrate with the Achaeans to Ionia; Sparta they designated as a royal residence for themselves; to the other divisions they sent kings, and because of the sparsity of the population gave them permission to receive as fellow inhabitants any strangers who wished the privilege; and they used Las as a naval station because of its good harbour, and Aegys as a base of operations against their enemies (for its territory bordered on those of the surrounding peoples) and Pharis as a treasury, because it afforded security against outsiders; . . . but though the neighbouring peoples, one and all, were subject to the Spartiatae, still they had equal rights, sharing both in the rights of citizenship and in the offices of state, and they were called Helots; but Agis, the son of Eurysthenes, deprived them of the equality of rights and ordered them to pay tribute to Sparta; now all obeyed except the Heleians, the occupants of Helus, who, because they revolted, were forcibly reduced in a war, and were condemned to slavery, with the express reservation that no slaveholder should be permitted either to set them free or to sell them outside the borders of the country; and this war was called the War against the Helots. One may almost say that it was Agis and his associates who introduced the whole system of Helot-slavery that persisted until the supremacy of the Romans; for the Lacedaemonians held the Helots as state-slaves in a way, having assigned to them certain settlements to live in and special services to perform.
5 Concerning the government of the Laconians and the changes that took place among them, one might omit most things as well known, but there are certain things which it is perhaps worthwhile to mention. For instance, they say that the Achaeans of Phthiotis came down with Pelops into the Peloponnesus, took up their abode in Laconia, and so far excelled in bravery that the Peloponnesus, which now for many ages had been called Argos, came to be called Achaean Argos, and the name was applied not only in a general way to the Peloponnesus, but also in a specific way to Laconia; at any rate, the words of the poet, "Where was Menelaüs?" or was he not in Achaean Argos?" are interpreted by some thus: "or was he not in Laconia?" And at the time of the return of the Heracleidae, when Philonomus betrayed the country to the Dorians, the Achaeans emigrated from Laconia to the country of the Ionians, the country that still to‑day is called Achaea. But I shall speak of them in my description of Achaea. Now the new possessors of Laconia restrained themselves at first, but after they turned over the government to Lycurgus they so far surpassed the rest that they alone of the Greeks ruled over both land and sea, and they continued ruling the Greeks until they were deprived of their hegemony, first by the Thebans, and immediately after them by the Macedonians. However, they did not wholly yield even to the Macedonians, but, preserving their autonomy, always kept up a struggle for the primacy both with the rest of the Greeks and with the kings of the Macedonians. And when the Macedonians had been overthrown by the Romans, the Lacedaemonians committed some slight offences against the praetors who were sent by the Romans, because at that time they were under the rule of tyrants and had a wretched government; but when they had recovered themselves, they were held in particular honour, and remained free, contributing to Rome nothing else but friendly services. But recently Eurycles has stirred up trouble among them, having apparently abused the friendship of Caesar unduly in order to maintain his authority over his subjects; but the trouble quickly came to an end, Eurycles retiring to his fate, and his son being averse to any friendship of this kind. And it also came to pass that the Eleuthero-Lacones got a kind of republican constitution, since the Perioeci and also the Helots, at the time when Sparta was under the rule of tyrants, were the first to attach themselves to the Romans. Now Hellanicus says that Eurysthenes and Procles drew up the constitution; but Ephorus censures Hellanicus, saying that he has nowhere mentioned Lycurgus and that he ascribes the work of Lycurgus to persons who had nothing to do with it. At any rate, Ephorus continues, it is to Lycurgus alone that a temple has been erected and that annual sacrifices are offered, whereas Eurysthenes and Procles, although they were the founders, have not even been accorded the honour of having their respective descendants called Eurysthenidae and Procleidae; instead, the respective descendants are called Agidae, after Agis the son of Eurysthenes, and Eurypontidae, after Eurypon the son of Procles; for Agis and Eurypon reigned in an honourable way, whereas Eurysthenes and Procles welcomed foreigners and through these maintained their overlordship; and hence they were not even honoured with the title of "archegetae," an honour which is always paid to founders; and further, Pausanias, after he was banished because of the hatred of the Eurypontidae, the other royal house, and when he was in exile, prepared a discourse on the laws of Lycurgus, who belonged to the house that banished him, in which he also tells the oracles that were given out to Lycurgus concerning most of the laws.
6 Concerning the nature of the regions, both Laconia and Messenia, one should accept what Euripides says in the following passages: He says that Laconia has "much arable land but is not easy to cultivate, for it is hollow, surrounded by mountains, rugged, and difficult for enemies to invade;" and that Messenia is "a land of fair fruitage and watered by innumerable streams, abounding in pasturage for cattle and sheep, being neither very wintry in the blasts of winter nor yet made too hot by the chariot of Helios;" and a little below, in speaking of the lots which the Heracleidae cast for the country, he says that the first lot conferred "lordships over the land of Laconia, a poor country," and the second over Messenia, "whose fertility is greater than words can express;" and Tyrtaeus speaks of it in the same manner. But one should not admit that the boundary between Laconia and Messenia is formed, as Euripides says, "by the Pamisus, which rushes into the sea," for it flows through the middle of Messenia, nowhere touching the present Laconia. Neither is he right when he says that to mariners Messenia is far away, for Messenia like Laconia lies on the sea; and he does not give the right boundary of Elis either, "and far away, after one crosses the river, lies Elis, the neighbour of Zeus;" for if, on the one hand, he means the present Eleian country, which borders on Messenia, the Pamisus does not touch this country, any more than it does Laconia, for, as I have said, it flows through the middle of Messenia; or if, on the other hand, he means the old Coelê Elis, he deviates much further from the truth; for after one crosses the Pamisus there is still a large part of Messenia to traverse, and then the whole of the territories of the Lepreatae and the Macistii, which they used to call Triphylia; and then come Pisatis and Olympia, and then, three hundred stadia farther on, Elis.
7 Since some critics write Lacedaemon "Ketoessan" and others "Kaietaessan," the question is asked, how should we interpret "Ketoessa," whether as derived from "Ketê," or as meaning "large," which seems to be more plausible. And as for "Kaietaessan," some interpret it as meaning "Kalaminthodê," whereas others say that the clefts caused by earthquakes are called "Kaietoi," and that from "Kaietoi" is derived "Kaietas," the word among the Lacedaemonians for their "prison," which is a sort of cavern. But some prefer to call such cavernous places "Kooi," and whence, they add, comes the expression " 'oreskoioi' monsters." Laconia is subject to earthquakes, and in fact some writers record that certain peaks of Taÿgetus have been broken away. And there are quarries of very costly marble — the old quarries of Taenarian marble on Taenarum; and recently some men have opened a large quarry in Taÿgetus, being supported in their undertaking by the extravagance of the Romans.
8 Homer makes it clear that both the country and the city are called by the same name, Lacedaemon (and when I say "country" I include Messenia with Laconia). For in speaking of the bows, when he says, "beautiful gifts which a friend had given him when he met him in Lacedaemon, even Iphitus the son of Eurytus," and then adds, "these twain met one another in Messenê in the home of Ortilochus," Homer means the country of which Messenia was a part. Accordingly it made no difference to him whether he said "a friend had given him when he met him in Lacedaemon" or "these twain met in Messenê." For, that Pherae is the home of Ortilochus, is clear from this passage: "and they" (Telemachus and Peisistratus) "went to Pherae, the home of Diocles, son of Ortilochus;" and Pherae is in Messenia. But when Homer says that, after Telemachus and his companions set out from Pherae, "they shook the yoke all day long," and then adds, "and the sun set, and they came to Hollow Lacedaemon 'Ketoessan,' and then drove to the palace of Menelaüs," we must interpret him as meaning the city; otherwise it will be obvious that the poet speaks of their arrival at Lacedaemon from Lacedaemon! And, besides, it is not probable that the residence of Menelaüs was not at Sparta, nor yet, if it were not there, that Telemachus would say, "for I would go both to Sparta and to Pylus." But the fact that Homer uses the epithets of the country is in disagreement with this view unless, indeed, one is willing to attribute this to poetic license — as one should do, for it were better for Messenê to be included with Laconia or with the Pylus that was subject to Nestor, and not to be set off by itself in the Catalogue as not even having a part in the expedition. |
|
|
|





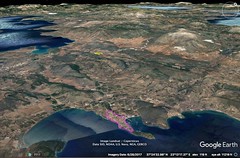

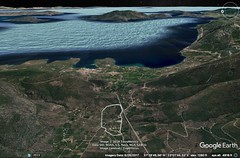

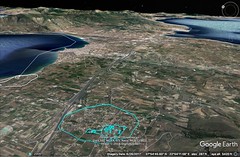

|
8 - 6 Argolis 
1 After Maleae follows the Argolic Gulf, and then the Hermionic Gulf; the former stretches as far as Scyllaeum, facing approximately eastward and towards the Cyclades, while the latter is more to the east than the former and extends as far as Aegina and Epidauria. Now the first places on the Argolic Gulf are occupied by Laconians, and the rest by the Argives. Among the places belonging to the Laconians is Delium, which is sacred to Apollo and bears the same name as the place in Boeotia; and also Minoa, a stronghold, which has the same name as the place in Megaris; and Epidaurus Limera, as Artemidorus says. But Apollodorus observes that this Epidaurus Limera is near Cythera, and that, because it has a good harbour, it was called "Limenera," which was abbreviated and contracted to "Limera," so that its name has been changed. Immediately after sailing from Maleae the Laconian coast is rugged for a considerable distance, but still it affords anchoring places and harbours. The rest of the coast is well provided with harbours; and off the coast lie many small islands, but they are not worth mentioning.
2 But to the Argives belongs Prasiae, and also Temenium, where Temenus was buried, and, still before Temenium, the district through which flows the river Lernê, as it is called, bearing the same name as the marsh in which is laid the scene of the myth of the Hydra. Temenium lies above the sea at a distance of twenty-six stadia from Argos; and from Argos to Heraeum the distance is forty stadia, and thence to Mycenae ten. After Temenium comes Nauplia, the naval station of the Argives: and the name is derived from the fact that the place is accessible to ships. And it is on the basis of this name, it is said, that the myth of Nauplius and his sons has been fabricated by the more recent writers of myth, for Homer would not have failed to mention these, if Palamedes had displayed such wisdom and sagacity, and if he was unjustly and treacherously murdered, and if Nauplius wrought destruction to so many men at Cape Caphereus. But in addition to its fabulous character the genealogy of Nauplius is also wholly incorrect in respect to the times involved; for, granting that he was the son of Poseidon, how could a man who was still alive at the time of the Trojan war have been the son of Amymonê? Next after Nauplia one comes to the caverns and the labyrinths built in them, which are called Cyclopeian.
3 Then come other places, and next after them the Hermionic Gulf; for, since Homer assigns this gulf also to Argeia, it is clear that I too should not overlook this section of the circuit. The gulf begins at the town of Asinê. Then come Hermionê and Troezen; and, as one sails along the coast, one comes also to the island of Calauria, which has a circuit of one hundred and thirty stadia and is separated from the mainland by a strait four stadia wide.
4 Then comes the Saronic Gulf; but some call it a sea and others a strait; and because of this it is also called the Saronic Sea. Saronic Gulf is the name given to the whole of the strait, stretching from the Hermionic Sea and from the sea that is at the Isthmus, that connects with both the Myrtoan and Cretan Seas. To the Saronic Gulf belong both Epidaurus and the island of Aegina that lies off Epidaurus; then Cenchreae, the easterly naval station of the Corinthians; then, after sailing forty-five stadia, one comes to Schoenus, a harbour. From Maleae thither the total distance is about eighteen hundred stadia. Near Schoenus is the "Diolcus," the narrowest part of the Isthmus, where is the temple of the Isthmian Poseidon. However, let us for the present postpone the discussion of these places, for they lie outside of Argeia, and let us resume again our description of those in Argeia.
5 And in the first place let me mention in how many ways the term "Argos" is used by the poet, not only by itself but also with epithets, when he calls Argos "Achaean," or "Iasian," or "hippian," or "Pelasgian," or "horse-pasturing." For, in the first place, the city is called Argos: "Argos and Sparta," "and those who held Argos and Tiryns." And, secondly, the Peloponnesus: "in our home in Argos," for the city of Argos was not his home. And, thirdly, Greece as a whole; at any rate, he calls all Greeks Argives, just as he calls them Danaans and Achaeans. However, he differentiates identical names by epithets, calling Thessaly "Pelasgian Argos": "Now all, moreover, who dwelt in Pelasgian Argos;" and calling the Peloponnesus "Achaean Argos." "And if we should come to Achaean Argos," "Or was he not in Achaean Argos?" And here he signifies that under a different designation the Peloponnesians were also called Achaeans in a special sense. And he calls the Peloponnesus "Iasian Argos": "If all the Achaeans throughout Iasian Argos could see" Penelope, she would have still more wooers; for it is not probable that he meant the Greeks from all Greece, but only those that were near. But the epithets "horse-pasturing" and "hippian" he uses in a general sense.
6 But critics are in dispute in regard to the terms "Hellas," "Hellenes," and "Panhellenes." For Thucydides says that the poet nowhere speaks of barbarians, "because the Hellenes had not as yet been designated by a common distinctive name opposed to that of the barbarians." And Apollodorus says that only the Greeks in Thessaly were called Hellenes: "and were called Myrmidons and Hellenes." He says, however, that Hesiod and Archilochus already knew that all the Greeks were called, not only Hellenes, but also Panhellenes, for Hesiod, in speaking of the daughters of Proteus, says that the Panhellenes wooed them, and Archilochus says that "the woes of the Panhellenes centred upon Thasos." But others oppose this view, saying that the poet also speaks of barbarians, since he speaks of the Carians as men of barbarous speech, and of all the Greeks as Hellenes, "the man whose fame is wide throughout Hellas and mid-Argos," and again, "If thou wishest to journey throughout Hellas and mid-Argos."
7 Now the city of the Argives is for the most part situated in a plain, but it has for a citadel the place called Larisa, a hill that is fairly well fortified and contains a temple of Zeus. And near the city flows the Inachus, a torrential river that has its sources in Lyrceius, the mountain that is near Cynuria in Arcadia. But concerning the sources of which mythology tells us, they are fabrications of poets, as I have already said. And "waterless Argos" is also a fabrication, ("but the gods made Argos well watered"), since the country lies in a hollow, and is traversed by rivers, and contains marshes and lakes, and since the city is well supplied with waters of many wells whose water level reaches the surface. So critics find the cause of the mistake in this verse: "And in utter shame would I return to πολυδίψιον Argos." πολυδίψιον either is used for πολυπόθητον, or, omitting the δ, for πολυΐψιον, in the sense of πολύφθορον, as in the phrase of Sophocles, "and the πολύφθορον home of the Pelopidae there;" for the words προϊάψαι and ἰάψαι and ἴψασθαι signify a kind of destruction or affliction: "Now he is merely making trial, but soon he will afflict the sons of the Achaeans;" "mar her fair flesh;" "untimely sent to Hades." And besides, Homer does not mean the city of Argos (for it was not thither that Agamemnon was about to return), but the Peloponnesus, which certainly is not a "thirsty" land either. Moreover some critics, retaining the δ, interpret the word by the figure hyperbaton and as a case of synaloepha with the connective δέ, so that the verse would read thus: "And in utter shame would I return πολὺ δ’ ἴψιον Ἄργος," that is to say, "would I return πολυίψιον Ἄργοσδε," where Ἄργοσδε stands for εἰς Ἄργος.
8 Now one of the rivers that flows through Argeia is the Inachus, but there is another river in Argeia, the Erasinus. The latter has its source in Stymphalus in Arcadia, that is, in the lake there which is called the Stymphalian Lake, which mythology makes the home of the birds that were driven out by the arrows and drums of Heracles; and the birds themselves are called Stymphalides. And they say that the Erasinus sinks beneath the ground and then issues forth in Argeia and waters the plain. The Erasinus is also called the Arsinus. And another river of the same name flows from Arcadia to the coast near Bura; and there is another Erasinus in the territory of Eretria, and still another in Attica near Brauron. And a spring Amymonê is also pointed out near Lernê. And Lake Lernê, the scene of the story of the Hydra, lies in Argeia and the Mycenaean territory; and on account of the cleansings that take place in it there arose a proverb, "A Lernê of ills." Now writers agree that the county has plenty of water, and that, although the city itself lies in a waterless district, it has an abundance of wells. These wells they ascribe to the daughters of Danaüs, believing that they discovered them; and hence the utterance of this verse, "The daughters of Danaüs rendered Argos, which was waterless, Argos the well watered;" but they add that four of the wells not only were designated as sacred but are especially revered, thus introducing the false notion that there is a lack of water where there is an abundance of it.
9 The acropolis of the Argives is said to have been founded by Danaüs, who is reputed to have surpassed so much those who reigned in this region before him that, according to Euripides, "throughout Greece he laid down a law that all people hitherto named Pelasgians should be called Danaans." Moreover, his tomb is in the centre of the market-place of the Argives; and it is called Palinthus. And I think that it was the fame of this city that prepared the way, not only for the Pelasgians and the Danaans, as well as the Argives, to be named after it, but also for the rest of the Greeks; and so, too, the more recent writers speak of "Iasidae," "Iasian Argos," "Apia," and "Apidones"; but Homer does not mention the "Apidones," though he uses the word "apia," rather of a "distant" land. To prove that by Argos the poet means the Peloponnesus, we can add the following examples: "Argive Helen," and "There is a city Ephyra in the inmost part of Argos," and "mid Argos," and "and that over many islands and all Argos he should be lord." And in the more recent writers the plain, too, is called Argos, but not once in Homer. Yet they think that this is more especially a Macedonian or Thessalian usage.
After the descendants of Danaüs succeeded to the reign in Argos, and the Amythaonides, who were emigrants from Pisatis and Triphylia, became associated with these, one should not be surprised if, being kindred, they at first so divided the country into two kingdoms that the two cities in them which held the hegemony were designated as the capitals, though situated near one another, at a distance of less than fifty stadia, I mean Argos and Mycenae, and that the Heraeum near Mycenae was a temple common to both. In this temple are the images made by Polycleitus, in execution the most beautiful in the world, but in costliness and size inferior to those by Pheidias. Now at the outset Argos was the more powerful, but later Mycenae waxed more powerful on account of the removal thereto of the Pelopidae; for, when everything fell to the sons of Atreus, Agamemnon, being the elder, assumed the supreme power, and by a combination of good fortune and valour acquired much of the country in addition to the possessions he already had; and indeed he also added Laconia to the territory of Mycenae. Now Menelaüs came into possession of Laconia, but Agamemnon received Mycenae and the regions as far as Corinth and Sicyon and the country which at that time was called the country of the Ionians and Aegialians but later the country of the Achaeans. But after the Trojan times, when the empire of Agamemnon had been broken up, it came to pass that Mycenae was reduced, and particularly after the return of the Heracleidae; for when these had taken possession of the Peloponnesus they expelled its former masters, so that those who held Argos also held Mycenae as a component part of one whole. But in later times Mycenae was rased to the ground by the Argives, so that to‑day not even a trace of the city of the Mycenaeans is to be found. And since Mycenae has suffered such a fate, one should not be surprised if also some of the cities which are catalogued as subject to Argos have now disappeared. Now the Catalogue contains the following: "And those who held Argos, and Tiryns of the great walls, and Hermionê and Asinê that occupy a deep gulf, and Troezen and Eiones and vine-clad Epidaurus, and the youths of the Achaeans who held Aegina and Mases." But of the cities just named I have already discussed Argos, and now I must discuss the others.
Now it seems that Tiryns was used as a base of operations by Proetus, and was walled by him through the aid of the Cyclopes, who were seven in number, and were called "Bellyhands" because they got their food from their handicraft, and they came by invitation from Lycia. And perhaps the caverns near Nauplia and the works therein are named after them. The acropolis, Licymna, is named after Licymnius, and it is about twelve stadia distant from Nauplia; but it is deserted, and so is the neighbouring Midea, which is different from the Boeotian Midea; for the former is Mídea, like Prónia, while the latter is Midéa, like Tegéa. And bordering on Midea is Prosymna, . . . this having a temple of Hera. But the Argives laid waste to most of the cities because of their disobedience; and of the inhabitants those from Tiryns migrated to Epidaurus, and those from . . . to Halïeis, as it is called; but those from Asinê (this is a village in Argeia near Nauplia) were transferred by the Lacedaemonians to Messenia, where is a town that bears the same name as the Argolic Asinê; for the Lacedaemonians, says Theopompos, took possession of much territory that belonged to other peoples and settled there all who fled to them and were taken in. And the inhabitants of Nauplia also withdrew to Messenia.
Hermionê is one of the important cities; and its seaboard is held by the Halïeis, as they are called, men who busy themselves on the sea. And it is commonly reported that the descent to Hades in the country of the Hermionians is a short cut; and this is why they do not put passage-money in the mouths of their dead.
It is said that Asinê too was a habitation of the Dryopians — whether, being inhabitants of the regions of the Spercheius, they were settled here by the Arcadian Dryops, as Aristotle has said, or whether they were driven by Heracles out of the part of Doris that is near Parnassus. As for the Scyllaeum in Hermionê, they say that it was named after Scylla, the daughter of Nisus, who, they say, out of love for Minos betrayed Nisaea to him and was drowned in the sea by him, and was here cast ashore by the waves and buried. Eiones was a village, which was depopulated by the Mycenaeans and made into a naval station, but later it disappeared from sight and now is not even a naval station.
Troezen is sacred to Poseidon, after whom it was once called Poseidonia. It is situated fifteen stadia above the sea, and it too is an important city. Off its harbour, Pogon by name, lies Calauria, an isle with a circuit of about one hundred and thirty stadia. Here was an asylum sacred to Poseidon; and they say that this god made an exchange with Leto, giving her Delos for Calauria, and also with Apollo, giving him Pytho for Taenarum. And Ephorus goes on to tell the oracle: "For thee it is the same thing to possess Delos or Calauria, most holy Pytho or windy Taenarum." And there was also a kind of Amphictyonic League connected with this temple, a league of seven cities which shared in the sacrifice; they were Hermion, Epidaurus, Aegina, Athens, Prasïeis, Nauplïeis, and Orchomenus Minyeius; however, the Argives paid dues for the Nauplians, and the Lacedaemonians for the Prasians. The worship of this god was so prevalent among the Greeks that even the Macedonians, whose power already extended as far as the temple, in a way preserved its inviolability, and were afraid to drag away the suppliants who fled for refuge to Calauria; indeed Archias, with soldiers, did not venture to do violence even to Demosthenes, although he had been ordered by Antipater to bring him alive, both him and all the other orators he could find that were under similar charges, but tried to persuade him; he could not persuade him, however, and Demosthenes forestalled him by killing himself with poison. Now Troezen and Pittheus, the sons of Pelops, came originally from Pisatis; and the former left behind him the city which was named after him, and the latter succeeded him and reigned as king. But Anthes, who previously had possession of the place, set sail and founded Halicarnassus; but concerning this I shall speak in my description of Caria and Troy.
Epidaurus used to be called Epicarus, for Aristotle says that Carians took possession of it, as also of Hermionê, but that after the return of the Heracleidae the Ionians who had accompanied the Heracleidae from the Attic Tetrapolis to Argos took up their abode with these Carians. Epidaurus, too, is an important city, and particularly because of the fame of Asclepius, who is believed to cure diseases of every kind and always has his temple full of the sick, and also of the votive tablets on which the treatments are recorded, just as at Cos and Triccê. The city lies in the recess of the Saronic Gulf, has a circular coast of fifteen stadia, and faces the summer risings of the sun. It is enclosed by high mountains which reach as far as the sea, so that on all sides it is naturally fitted for a stronghold. Between Troezen and Epidaurus there was a stronghold called Methana, and also a peninsula of the same name. In some copies of Thucydides the name is spelled "Methonê," the same as the Macedonian city in which Philip, in the siege, had his eye knocked out. And it is on this account, in the opinion of Demetrius of Scepsis, that some writers, being deceived, suppose that it was the Methonê in the territory of Troezen against which the men sent by Agamemnon to collect sailors are said to have uttered the imprecation that its citizens might never cease from their wall-building, since, in his opinion, it was not these citizens that refused, but those of the Macedonian city, as Theopompus says; and it is not likely, he adds, that these citizens who were near to Agamemnon disobeyed him.
Aegina is the name of a place in Epidauria; and it is also the name of an island lying off this part of the mainland — the Aegina of which the poet means to speak in the verses just cited; and it is on this account that some write "the island Aegina" instead of "who held Aegina," thus distinguishing between places of the same name. Now what need have I to say that the island is one of the most famous? for it is said that both Aeacus and his subjects were from there. And this is the island that was once actually mistress of the sea and disputed with the Athenians for the prize of valour in the sea-fight at Salamis at the time of the Persian War. The island is said to be one hundred and eighty stadia in circuit; and it has a city of the same name that faces southwest; and it is surrounded by Attica, Megaris, and the Peloponnesus as far is Epidaurus, being distant about one hundred stadia from each; and its eastern and southern sides are washed by the Myrtoan and Cretan Seas; and around it lie small islands, many of them near the mainland, though Belbina extends to the high sea. The country of Aegina is fertile at a depth below the surface, but rocky on the surface, and particularly the level part; and therefore the whole country is bare, although it is fairly productive of barley. It is said that the Aeginetans were called Myrmidons, — not as the myth has it, because, when a great famine occurred, the ants became human beings in answer to a prayer of Aeacus, but because they excavated the earth after the manner of ants and spread the soil over the rocks, so as to have ground to till, and because they lived in the dugouts, refraining from the use of soil for bricks. Long ago Aegina was called Oenonê, the same name as that of two demes in Attica, one near Eleutherae, "to inhabit the plains that border on Oenonê and Eleutherae;" and another, one of the demes of the Marathonian Tetrapolis, to which is applied the proverb, "To Oenonê — the torrent." Aegina was colonised successively by the Argives, the Cretans, the Epidaurians, and the Dorians; but later the Athenians divided it by lot among settlers of their own; and then the Lacedaemonians took the island away from the Athenians and gave it back to its ancient settlers. And colonists were sent forth by the Aeginetans both to Cydonia in Crete and to the country of the Ombrici. Ephorus says that silver was first coined in Aegina, by Pheidon; for the island, he adds, became a merchant centre, since, on account of the poverty of the soil, the people employed themselves at sea as merchants, and hence, he adds, petty wares were called "Aeginetan merchandise."
The poet mentions some places in the order in which they are actually situated; "and these dwelt in Hyria and Aulis," "and those who held Argos and Tiryns, Hermionê and Asinê, Troezen and Eiones;" but at other times not in their actual order: "Schoenus and Scolus, Thespeia and Graea;" and he mentions the places on the mainland at the same time with the islands: "those who held Ithaca and dwelt in Crocyleia," for Crocyleia is in the country of the Acarnanians. And so, also, he here connects Mases with Aegina, although it is in Argolis on the mainland. Homer does not name Thyreae, although the others often speak of it; and it was concerning Thyreae that a contest arose between the Argives and the Lacedaemonians, three hundred against three hundred; but the Lacedaemonians under the generalship of Othryadasa won the victory. Thucydides says that this place is in Cynuria on the common border of Argeia and Laconia. And there are also Hysiae, a well-known place in Argolis, and Cenchreae, which lies on the road that leads from Tegea to Argos through Mt. Parthenius and Creopolus, but Homer does not know them. Nor yet does he know Lyrceium nor Orneae, which are villages in Argeia, the former bearing the same name as the mountain near it and the latter the same as the Orneae which is situated between Corinth and Sicyon.
So then, of the cities in the Peloponnesus, Argos and Sparta prove to have been, and still are, the most famous; and, since they are much spoken of, there is all the less need for me to describe them at length, for if I did so I should seem to be repeating what has been said by all writers. Now in early times Argos was the more famous, but later and ever afterwards the Lacedaemonians excelled, and persisted in preserving their autonomy, except perhaps when they chanced to make some slight blunder. Now the Argives did not, indeed, admit Pyrrhus into their city (in fact, he fell before the walls, when a certain old woman, as it seems, dropped a tile upon his head), but they became subject to other kings; and after they had joined the Achaean League they came, along with the Achaeans, under the dominion of Rome; and their city persists to this day second in rank after Sparta.
But let me speak next of the places which are named in the Catalogue of Ships as subject to Mycenae and Menelaüs. The words of the poet are as follows: "And those who held Mycenae, well-built fortress, and wealthy Corinth and well-built Cleonae, and dwelt in Orneiae and lovely Araethyreê and Sicyon, wherein Adrastus was king at the first; and those who held Hyperesiê and steep Gonoessa and Pellenê, and dwelt about Aegium and through all the Aegialus and about broad Helicê." Now Mycenae is no longer in existence, but it was founded by Perseus, and Perseus was succeeded by Sthenelus, and Sthenelus by Eurystheus; and the same men ruled over Argos also. Now Eurystheus made an expedition to Marathon against Iolaüs and the sons of Heracles, with the aid of the Athenians, as the story goes, and fell in the battle, and his body was buried at Gargettus, except his head, which was cut off by Iolaüs, and was buried separately at Tricorynthus near the spring Macaria below the wagon road. And the place is called "Eurystheus' Head." Then Mycenae fell to the Pelopidae who had set out from Pisatis, and then to the Heracleidae, who also held Argos. But after the naval battle at Salamis the Argives, along with the Cleonaeans and Tegeatans, came over and utterly destroyed Mycenae, and divided the country among themselves. Because of the nearness of the two cities to one another the writers of tragedy speak of them synonymously as though they were one city; and Euripides, even in the same drama, calls the same city, at one time Mycenae, at another Argos, as, for example, in his Iphigeneia and his Orestes. Cleonae is a town situated by the road that leads from Argos to Corinth, on a hill which is surrounded by dwellings on all sides and is well fortified, so that in my opinion Homer's words, "well-built Cleonae," were appropriate. And here too, between Cleonae and Phlius, are Nemea and the sacred precinct in which the Argives are wont to celebrate the Nemean Games, and the scene of the myth of the Nemean lion, and the village Bembina. Cleonae is one hundred and twenty stadia distant from Argos, and eighty from Corinth. I myself have beheld the settlement from Acrocorinthus.
Corinth is called "wealthy" because of its commerce, since it is situated on the Isthmus and is master of two harbours, of which the one leads straight to Asia, and the other to Italy; and it makes easy the exchange of merchandise from both countries that are so far distant from each other. And just as in early times the Strait of Sicily was not easy to navigate, so also the high seas, and particularly the sea beyond Maleae, were not, on account of the contrary winds; and hence the proverb, "But when you double Maleae, forget your home." At any rate, it was a welcome alternative, for the merchants both from Italy and from Asia, to avoid the voyage to Maleae and to land their cargoes here. And also the duties on what by land was exported from the Peloponnesus and what was imported to it fell to those who held the keys. And to later times this remained ever so. But to the Corinthians of later times still greater advantages were added, for also the Isthmian Games, which were celebrated there, were wont to draw crowds of people. And the Bacchiadae, a rich and numerous and illustrious family, became tyrants of Corinth, and held their empire for nearly two hundred years, and without disturbance reaped the fruits of the commerce; and when Cypselus overthrew these, he himself became tyrant, and his house endured for three generations; and an evidence of the wealth of this house is the offering which Cypselus dedicated at Olympia, a huge statue of beaten gold. Again, Demaratus, one of the men who had been in power at Corinth, fleeing from the seditions there, carried with him so much wealth from his home to Tyrrhenia that not only he himself became the ruler of the city that admitted him, but his son was made king of the Romans. And the temple of Aphroditê was so rich that it owned more than a thousand temple slaves, courtesans, whom both men and women had dedicated to the goddess. And therefore it was also on account of these women that the city was crowded with people and grew rich; for instance, the ship captains freely squandered their money, and hence the proverb, "Not for every man is the voyage to Corinth." Moreover, it is recorded that a certain courtesan said to the woman who reproached her with the charge that she did not like to work or touch wool: "Yet, such as I am, in this short time I have taken down three webs."
The situation of the city, as described by Hieronymus and Eudoxus and others, and from what I myself saw after the recent restoration of the city by the Romans, is about as follows: A lofty mountain with a perpendicular height of three stadia and one half, and an ascent of as much as thirty stadia, ends in a sharp peak; it is called Acrocorinthus, and its northern side is the steepest; and beneath it lies the city in a level, trapezium-shaped place close to the very base of the Acrocorinthus. Now the circuit of the city itself used to be as much as forty stadia, and all of it that was unprotected by the mountain was enclosed by a wall; and even the mountain itself, the Acrocorinthus, used to be comprehended within the circuit of this wall wherever wall-building was possible, and when I went up the mountain the ruins of the encircling wall were plainly visible. And so the whole perimeter amounted to about eighty-five stadia. On its other sides the mountain is less steep, though here too it rises to a considerable height and is conspicuous all round. Now the summit has a small temple of Aphroditê; and below the summit is the spring Peirenê, which, although it has no overflow, is always full of transparent, potable water. And they say that the spring at the base of the mountain is the joint result of pressure from this and other subterranean veins of water — a spring which flows out into the city in such quantity that it affords a fairly large supply of water. And there is a good supply of wells throughout the city, as also, they say, on the Acrocorinthus; but I myself did not see the latter wells. At any rate, when Euripides says, "I am come, having left Acrocorinthus that is washed on all sides, the sacred hill-city of Aphroditê," one should take "washed on all sides" as meaning in the depths of the mountain, since wells and subterranean pools extend through it, or else should assume that in early times Peirenê was wont to rise over the surface and flow down the sides of the mountain. And here, they say, Pegasus, a winged horse which sprang from the neck of the Gorgon Medusa when her head was cut off, was caught while drinking by Bellerophon. And the same horse, it is said, caused Hippu-crenê to spring up on Helicon when he struck with his hoof the rock that lay below that mountain. And at the foot of Peirenê is the Sisypheium, which preserves no inconsiderable ruins of a certain temple, or royal palace, made of white marble. And from the summit, looking towards the north, one can view Parnassus and Helicon — lofty, snow-clad mountains — and the Crisaean Gulf, which lies at the foot of the two mountains and is surrounded by Phocis, Boeotia, and Megaris, and by the parts of Corinthia and Sicyonia which lie across the gulf opposite to Phocis, that is, towards the west. And above all these countries lie the Oneian Mountains, as they are called, which extend as far as Boeotia and Cithaeron from the Sceironian Rocks, that is, from the road that leads along these rocks towards Attica.
The beginning of the seaboard on the two sides is, on the one side, Lechaeum, and, on the other, Cenchreae, a village and a harbour distant about seventy stadia from Corinth. Now this latter they use for the trade from Asia, but Lechaeum for that from Italy. Lechaeum lies beneath the city, and does not contain many residences; but long walls about twelve stadia in length have been built on both sides of the road that leads to Lechaeum. The shore that extends from here to Pagae in Megaris is washed by the Corinthian Gulf; it is concave, and with the shore on the other side, at Schoenus, which is near Cenchreae, it forms the "Diolcus." In the interval between Lechaeum and Pagae there used to be, in early times, the oracle of the Acraean Hera; and here, too, is Olmiae, the promontory that forms the gulf in which are situated Oenoê and Pagae, the latter a stronghold of the Megarians and Oenoê of the Corinthians. From Cenchreae one comes to Schoenus, where is the narrow part of the isthmus, I mean the "Diolcus"; and then one comes to Crommyonia. Off this shore lie the Saronic and Eleusinian Gulfs, which in a way are the same, and border on the Hermionic Gulf. On the Isthmus is also the temple of the Isthmian Poseidon, in the shade of a grove of pine-trees, where the Corinthians used to celebrate the Isthmian Games. Crommyon is a village in Corinthia, though in earlier times it was in Megaris; and in it is laid the scene of the myth of the Crommyonian sow, which, it is said, was the mother of the Caledonian boar; and, according to tradition, the destruction of this sow was one of the labours of Theseus. Tenea, also, is in Corinthia, and in it is a temple of the Teneatan Apollo; and it is said that most of the colonists who accompanied Archias, the leader of the colonists to Syracuse, set out from there, and that afterwards Tenea prospered more than the other settlements, and finally even had a government of its own, and, revolting from the Corinthians, joined the Romans, and endured after the destruction of Corinth. And mention is also made of an oracle that was given to a certain man from Asia, who enquired whether it was better to change his home to Corinth: "Blest is Corinth, but Tenea for me!" But in ignorance some pervert this as follows: "but Tegea for me!" And it is said that Polybus reared Oedipus here. And it seems, also, that there is a kinship between the peoples of Tenedos and Tenea, through Tennes407 the son of Cycnus, as Aristotle says; and the similarity in the worship of Apollo among the two peoples affords strong indications of such kinship.
The Corinthians, when they were subject to Philip, not only sided with him in his quarrel with the Romans, but individually behaved so contemptuously towards the Romans that certain persons ventured to pour down filth upon the Roman ambassadors when passing by their house. For this and other offences, however, they soon paid the penalty, for a considerable army was sent thither, and the city itself was rased to the ground by Leucius Mummius; and the other countries as far as Macedonia became subject to the Romans, different commanders being sent into different countries; but the Sicyonians obtained most of the Corinthian country. Polybius, who speaks in a tone of pity of the events connected with the capture of Corinth, goes on to speak of the disregard shown by the army for the works of art and votive offerings; for he says that he was present and saw paintings that had been flung to the ground and saw the soldiers playing dice on these. Among the paintings he names that of Dionysus by Aristeides, to which, according to some writers, the saying, "Nothing in comparison with the Dionysus," referred; and also the painting of Heracles in torture in the robe of Deianeira. Now I have not seen the latter, but I saw the Dionysus, a most beautiful work, on the walls of the temple of Ceres in Rome; but when recently the temple was burned, the painting perished with it. And I may almost say that the most and best of the other dedicatory offerings at Rome came from there; and the cities in the neighbourhood of Rome also obtained some; for Mummius, being magnanimous rather than fond of art, as they say, readily shared with those who asked. And when Leucullusº built the Temple of Good Fortune and a portico, he asked Mummius for the use of the statues which he had, saying that he would adorn the temple with them until the dedication and then give them back. However, he did not give them back, but dedicated them to the goddess, and then bade Mummius to take them away if he wished. But Mummius took it lightly, for he cared nothing about them, so that he gained more repute than the man who dedicated them. Now after Corinth had remained deserted for a long time, it was restored again, because of its favorable position, by the deified Caesar, who colonised it with people that belonged for the most part to the freedmen class. And when these were removing the ruins and at the same time digging open the graves, they found numbers of terra-cotta reliefs, and also many bronze vessels. And since they admired the workmanship they left no grave unransacked; so that, well supplied with such things and disposing of them at a high price, they filled Rome with Corinthian "mortuaries," for thus they called the things taken from the graves, and in particular the earthenware. Now at the outset the earthenware was very highly prized, like the bronzes of Corinthian workmanship, but later they ceased to care much for them, since the supply of earthen vessels failed and most of them were not even well executed. The city of the Corinthians, then, was always great and wealthy, and it was well equipped with men skilled both in the affairs of state and in the craftsman's arts; for both here and in Sicyon the arts of painting and modelling and all such arts of the craftsman flourished most. The city had territory, however, that was not very fertile, but rifted and rough; and from this fact all have called Corinth "beetling," and use the proverb, "Corinth is both beetle-browed and full of hollows."
Orneae is named after the river that flows past it. It is deserted now, although formerly it was well peopled, and had a temple of Priapus that was held in honour; and it was from Orneae that the Euphronius who composed the Priapeia calls the god "Priapus the Orneatan." Orneae is situated above the plain of the Sicyonians, but the country was possessed by the Argives. Araethyrea is the country which is now called Phliasia; and near the mountain Celossa it had a city of the same name as the country; but the inhabitants later emigrated from here, and at a distance of thirty stadia founded a city which they called Phlius. A part of the mountain Celossa is Mt. Carneates, whence the Asopus takes its beginning — the river that flows past Sicyonia, and forms the Asopian country, which is a part of Sicyonia. There is also an Asopus that flows past Thebes and Plataea and Tanagra, and there is another in the Trachinian Heracleia that flows past a village which they call Parasopii, and there is a fourth in Paros. Phlius is situated in the centre of a circle formed by Sicyonia, Argeia, Cleonae and Stymphalus. In Phlius and Sicyon the temple of Dia is held in honour; and Dia is their name for Hebê.
In earlier times Sicyon was called Meconê, and in still earlier times Aegiali, but Demetrius rebuilt it upon a hill strongly fortified by nature about twenty stadia (others say twelve) from the sea; and the old settlement, which has a harbour, is a naval station. The River Nemea forms the boundary between Sicyonia and Corinthia. Sicyon was ruled by tyrants most of the time, but its tyrants were always reasonable men, among whom the most illustrious was Aratus, who not only set the city free, but also ruled over the Achaeans, who voluntarily gave him the authority, and he increased the league by adding to it both his native Sicyon and the other cities near it. But Hyperesia and the cities that come in their order after it, which the poet mentions, and the Aegialus as far as Dymê and the boundaries of Eleia already belonged to the Achaeans. |
|
|
 |
|
8 - 7 Ionia 
1 In antiquity this country was under the mastery of the Ionians, who were sprung from the Athenians; and in antiquity it was called Aegialeia, and the inhabitants Aegialeians, but later it was called Ionia after the Ionians, just as Attica also was called Ionia after Ion the son of Xuthus. They say that Hellen was the son of Deucalion, and that he was lord of the people between the Peneius and the Asopus in the region of Phthia and gave over his rule to the eldest of his sons, but that he sent the rest of them to different places outside, each to seek a settlement for himself. One of these sons, Dorus, united the Dorians about Parnassus into one state, and at his death left them named after himself; another, Xuthus, who had married the daughter of Erechtheus, founded the Tetrapolis of Attica, consisting of Oenoê, Marathon, Probalinthus, and Tricorynthus. One of the sons of Xuthus, Achaeus, who had committed involuntary manslaughter, fled to Lacedaemon and brought it about that the people there were called Achaeans; and Ion conquered the Thracians under Eumolpus, and thereby gained such high repute that the Athenians turned over their government to him. At first Ion divided the people into four tribes, but later into four occupations: four he designated as farmers, others as artisans, others as sacred officers, and a fourth group as the guards. And he made several regulations of this kind, and at his death left his own name to the country. But the country had then come to be so populous that the Athenians even sent forth a colony of Ionians to the Peloponnesus, and caused the country which they occupied to be called Ionia after themselves instead of Aegialus; and the men were divided into twelve cities and called Ionians instead of Aegialeians. But after the return of the Heracleidae they were driven out by the Achaeans and went back again to Athens; and from there they sent forth with the Codridae the Ionian colony to Asia, and these founded twelve cities on the seaboard of Caria and Lydia, thus dividing themselves into the same number of parts as the cities they had occupied in the Peloponnesus. Now the Achaeans were Phthiotae in race, but they lived in Lacedaemon; and when the Heracleidae prevailed, the Achaeans were won over by Tisamenus, the son of Orestes, as I have said before, attacked the Ionians, and proving themselves more powerful than the Ionians drove them out and took possession of the land themselves; and they kept the division of the country the same as it was when they received it. And they were so powerful that, although the Heracleidae, from whom they had revolted, held the rest of the Peloponnesus, still they held out against one and all, and named the country Achaea. Now from Tisamenus to Ogyges they continued under the rule of kings; then, under a democratic government, they became so famous for their constitutions that the Italiotes, after the uprising against the Pythagoreians, actually borrowed most of their usages from the Achaeans. And after the battle at Leuctra the Thebans turned over to them the arbitration of the disputes which the cities had with one another; and later, when their league was dissolved by the Macedonians, they gradually recovered themselves. When Pyrrhus made his expedition to Italy, four cities came together and began a new league, among which were Patrae and Dymê; and then they began to add some of the twelve cities, except Olenus and Helicê, the former having refused to join and the latter having been wiped out by a wave from the sea.
2 For the sea was raised by an earthquake and it submerged Helicê, and also the temple of the Heliconian Poseidon, whom the Ionians worship even to this day, offering there the Pan-Ionian sacrifices. And, as some suppose, Homer recalls this sacrifice when he says: "but he breathed out his spirit and bellowed, as when a dragged bull bellows round the altar of the Heliconian lord." And they infer that the poet lived after the Ionian colonisation, since he mentions the Pan-Ionian sacrifice, which the Ionians perform in honour of the Heliconian Poseidon in the country of the Prienians; for the Prienians themselves are also said to be from Helicê; and indeed as king for this sacrifice they appoint a Prienian young man to superintend the sacred rites. But still more they base the supposition in question on what the poet says about the bull; for the Ionians believe that they obtain omens in connection with this sacrifice only when the bull bellows while being sacrificed. But the opponents of the supposition apply the above-mentioned inferences concerning the bull and the sacrifice to Helicê, on the ground that these were customary there and that the poet was merely comparing the rites that were celebrated there. Helicê was submerged by the sea two years before the battle at Leuctra. And Eratosthenes says that he himself saw the place, and that the ferrymen say that there was a bronze Poseidon in the strait, standing erect, holding a hippo-campus in his hand, which was perilous for those who fished with nets. And Heracleides says that the submersion took place by night in his time, and, although the city was twelve stadia distant from the sea, this whole district together with the city was hidden from sight; and two thousand men who had been sent by the Achaeans were unable to recover the dead bodies; and they divided the territory of Helicê among the neighbours; and the submersion was the result of the anger of Poseidon, for the Ionians who had been driven out of Helicê sent men to ask the inhabitants of Helicê particularly for the statue of Poseidon, or, if not that, for the model of the temple; and when the inhabitants refused to give either, the Ionians sent word to the general council of the Achaeans; but although the assembly voted favorably, yet even so the inhabitants of Helicê refused to obey; and the submersion resulted the following winter; but the Achaeans later gave the model of the temple to the Ionians. Hesiod mentions still another Helicê, in Thessaly.
3 Now for twenty years the Achaeans continued to have a general secretary and two generals, elected annually; and with them a common council was convened at one place (it was called Amarium), in which these, as did the Ionians before them, dealt with affairs of common interest; then they decided to elect only one general. And when Aratus was general he took the Acrocorinthus away from Antigonus and added the city of Corinth to the Achaean League, just as he had added his native city; and he also took over the Megarians; and breaking up the tyrannies in the several cities he made the peoples who were thus set free members of the Achaean League. And he set the Peloponnesus free from its tyrannies, so that Argos, Hermion, Phlius, and Megalopolis, the largest city in Arcadia, were added to the League; and it was at this time that the League reached the height of its power. It was the time when the Romans, after their expulsion of the Carthaginians from Sicily, made their expedition against the Galatae who lived in the region of the Padus River. But although the Achaean League persisted rather firmly until the time of the generalship of Philopoemen, yet it was gradually dissolved, since by this time the Romans were in possession of the whole of Greece, and they did not deal with the several states in the same way, but wished to preserve some and to destroy others. Then he tells the cause of his enlarging upon the subject of the Achaeans, saying that, although they increased in power to the point of surpassing even the Lacedaemonians, they are not as well known as they deserve to be.
4 The order of the places in which the Achaeans settled, after dividing the country into twelve parts, is as follows: First after Sicyon lies Pellenê; then, second, Aegeira; third, Aegae, which has a temple of Poseidon; fourth, Bura; after Bura, Helicê, whither the Ionians fled for refuge after they were conquered in battle by the Achaeans, and whence at last they were expelled; and, after Helicê, 386Aegium and Rhypes and Patrae and Pharae; then Olenus, past which flows the Peirus, a large river; then Dymê and Tritaea. Now the Ionians lived in villages, but the Achaeans founded cities; and to certain of these they later united others, transferring them from the other divisions, as, for example, Aegae to Aegeira (the inhabitants, however, were called Aegaeans), and Olenus to Dymê. Traces of the old settlement of the Olenians are shown between Patrae and Dymê; and here, too, is the notable temple of Asclepius, which is forty stadia distant from Dymê and eighty from Patrae. Of the same name as this Aegae is the Aegae in Euboea; and of the same name as Olenus is the settlement in Aetolia, this too preserving only traces of its former self. Now the poet does not mention the Olenus in Achaea, just as he does not mention several other inhabited places in the region of the Aegialus, although he speaks of them in a rather general way: "And through all the Aegialus and about broad Helicê." But he mentions the Aetolian Olenus, when he says: "those who dwelt in Pleuron and Olenus." And he speaks of both places called Aegae: the Achaean Aegae, when he says, "yet they bring up gifts for thee into both Helicê and Aegae"; but when he says, "Aegae, where is his famous palace in the deeps of the mere," "where Poseidon halted his horses," it is better to take him as meaning the Aegae in Euboea, from which it is probable that also the Aegean Sea got its name; and here too the poet has placed the activities of Poseidon in connection with the Trojan War. Close to the Achaean Aegae flows the Crathis River, which is increased by the waters of two other rivers; and it gets its name from the fact that it is a mixture, as does also the Crathis in Italy.
5 Each of the twelve divisions consisted of seven or eight communities, so populous was the country. Pellenê is situated sixty stadia above the sea, and it is a strong fortress. But there is also a village Pellenê, from which come the Pellenic cloaks, which they were also wont to set up as prizes at the games; it lies between Aegium and Pellenê. But Pellana is different from these two; it is a Laconian place, and its territory inclines, approximately, towards the territory of Megalopolis. Aegeira is situated on a hill. Bura, which was swallowed up in an earthquake, is situated above the sea at a distance of about forty stadia; and they say that it was from the spring Sybaris in Bura that the river in Italy got its name. Aega (for Aegae is also called thus) is now uninhabited, and the city is in the possession of the people of Aegium. But Aegium has a considerable population. The story is told that Zeus was nursed by a goat there, just as Aratus says: "Sacred goat, which, in story, didst hold thy breast o'er Zeus;" and he goes on to say that "the interpreters call her the Olenian goat of Zeus," thus clearly indicating that the place is near Olenê. Here too is Ceraunia, which is situated on a high rock. These places belong to the people of Aegium, and so does Helicê, and Amarium, precinct of Zeus, where the Achaeans met to deliberate on affairs of common interest. And the Selinus River flows through the territory of Aegium; it bears the same name as the river that flows in Ephesus past the Artemisium, and also the river in the Eleia of to‑day that flows past the plot of land which Xenophon says he bought for Artemis in accordance with an oracle. And there is another Selinus; it flows past the territory of the Hyblaean Megarians, whom the Carthaginians forced to migrate. As for the remaining cities, or divisions, of the Achaeans, one of them, Rhypes, is uninhabited, and the territory called Rhypis was held by the people of Aegium and the people of Pharae. Aeschylus, too, says somewhere: "Sacred Bura and thunder-smitten Rhypes." Myscellus, the founder of Croton, was from Rhypes. And Leuctrum too, a deme of Rhypes, belonged to the district of Rhypis. After Rhypes comes Patrae, a noteworthy city; between the two, however, is Rhium (also Antirrhium), which is forty stadia distant from Patrae. And recently the Romans, after their victory at Actium, settled a considerable part of the army at Patrae; and it is exceptionally populous at present, since it is a Roman colony; and it has a fairly good anchoring-place. Next comes Dymê, a city without a harbour, the farthest of all towards the west, a fact from which it takes its name. But in earlier times it was called Stratos. The boundary between it and the Eleian country, Buprasium, is formed by the Larisus River, which flows from a mountain. Some writers call this mountain Scollis, but Homer calls it the Olenian Rock. When Antimachus calls Dymê "Cauconian," some interpret "Cauconian" as an epithet derived from the Cauconians, since the Cauconians extended as far as Dymê, as I have already said above, but others as derived from a River Caucon, just as Thebes is called "Dircaean" and "Asopian," Argos "Inacheian," and Troy "Simuntian." But shortly before my time Dymê received as colonists a mixed group of people whom Pompey still had left over from the crowd of pirates, after he broke up all piracy and settled some of the pirates at Soli in Cilicia and others in other places — and in particular at Dymê. Phara borders on the territory of Dymê. The people of this Phara are called Phareis, but those of the Messenian city Pharaeatae; and in the territory of Phara is a spring Dircê which bears the same name as the spring at Thebes. But Olenus is deserted; it lies between Patrae and Dymê; and its territory is held by the people of Dymê. Then comes Araxus, the promontory of the Eleian country, one thousand and thirty stadia from the isthmus. |
|
|
|
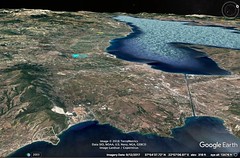




|
8 - 8 Arcadia 
1 Arcadia lies in the middle of the Peloponnesus; and most of the country which it includes is mountainous. The greatest mountain in it is Cyllenê; at any rate some say that its perpendicular height is twenty stadia, though others say about fifteen. The Arcadian tribes — the Azanes, the Parrhasians, and other such peoples — are reputed to be the most ancient tribes of the Greeks. But on account of the complete devastation of the country it would be inappropriate to speak at length about these tribes; for the cities, which in earlier times had become famous, were wiped out by the continuous wars, and the tillers of the soil have been disappearing even since the times when most of the cities were united into what was called the "Great City." But now the Great City itself has suffered the fate described by the comic poet: "The Great City is a great desert." But there are ample pastures for cattle, particularly for horses and asses that are used as stallions. And the Arcadian breed of horses, like the Argolic and the Epidaurian, is most excellent. And the deserted lands of the Aetolians and Acarnanians are also well adapted to horse-raising — no less so than Thessaly.
2 Now Mantineia was made famous by Epameinondas, who conquered the Lacedaemonians in the second battle, in which he himself lost his life. But Mantineia itself, as also Orchomenus, Heraea, Cleitor, Pheneus, Stymphalus, Maenalus, Methydrium, Caphyeis, and Cynaetha, no longer exist; or else traces or signs of them are scarcely to be seen. But Tegea still endures fairly well, and so does the temple of the Alean Athenê; and the temple of Zeus Lycaeus situated near Mt. Lycaeum is also honoured to a slight extent. But three of the cities mentioned by the poet, "Rhipê and Stratiê, and windy Enispê," are not only hard to find, but are of no use to any who find them, because they are deserted.
3 Famous mountains, in addition to Cyllenê, are Pholoê, Lycaeum, Maenalus, and the Parthenium, as it is called, which extends from the territory of Tegea down to the Argive country.
4 I have already mentioned the marvellous circumstances pertaining to the Alpheius and the Eurotas, and also to the Erasinus, which now flows underground from the Stymphalian Lake, and issues forth into the Argive country, although in earlier times it had no outlet, since the "berethra," which the Arcadians call "zerethra," were stopped up and did not admit of the waters being carried off so that the city of the Stymphalians is now fifty stadia distant from the lake, although then it was situated on the lake. But the contrary was the case with the Ladon, since its stream was once checked because of the blocking up of its sources; for the "berethra" near Pheneus, through which it flowed, fell in as the result of an earthquake and checked the stream as far down into the depths of the earth as the veins which supplied its source. Thus some writers tell it. But Eratosthenes says that near Pheneus the river Anias, as it is called, makes a lake of the region in front of the city and flows down into sink-holes, which are called "zerethra"; and when these are stopped up the water sometimes overflows into the plains, and when they are again opened up it rushes out of the plains all at once and empties into the Ladon and the Alpheius, so that even at Olympia the land around the temple was once inundated, while the lake was reduced; and the Erasinus, which flows past Stymphalus, sinks and flows beneath the mountain and reappears in the Argive land; and it was on this account, also, that Iphicrates, when he was besieging Stymphalus and accomplishing nothing, tried to block up the sink with a large quantity of sponges with which he had supplied himself, but desisted when Zeus sent an omen from the sky. And near Pheneus is also the water of the Styx, as it is called — a small stream of deadly water which is held to be sacred. So much may be said concerning Arcadia.
5 Polybius states that the distance from Maleae towards the north as far as the Ister is about ten thousand stadia, but Artemidorus corrects the statement in an appropriate manner by saying that from Maleae to Aegium is a journey of fourteen hundred stadia, and thence to Cyrrha a voyage of two hundred, and thence through Heracleia to Thaumaci a journey of five hundred, and then to Larisa and the Peneius three hundred and forty, and then through Tempê to the outlets of the Peneius two hundred and forty, and then to Thessaloniceia six hundred and sixty, and thence through Eidomenê and Stobi and Dardanii to the Ister three thousand two hundred. According to Artemidorus, therefore, the distance from the Ister to Maleae amounts to six thousand five hundred and forty stadia. The cause of this excess is that he does not give the measurement of the shortest route, but of the chance route which one of the generals took. And it is not out of place, perhaps, to add also the colonisers, mentioned by Ephorus, of the peoples who settled in the Peloponnesus after the return of the Heracleidae: Aletes, the coloniser of Corinth, Phalces of Sicyon, Tisamenus of Achaea, Oxylus of Elis, Cresphontes of Messenê, Eurysthenes and Procles of Lacedaemon, Temenus and Cissus of Argos, and Agaeus and Deïphontes of the region about Actê. |
|
|

|
|
9 Greece 5 103 1:50 
|
9 - 1 Attica 
1 Now that I have completed my circuit of the Peloponnesus, which, as I have said, was the first and the smallest of the peninsulas of which Greece consists, it will be next in order to traverse those that are continuous with it. The second peninsula is the one that adds Megaris to the Peloponnesus, so that Crommyon belongs to the Megarians and not to the Corinthians; the third is the one which, in addition to the second, comprises Attica and Boeotia and a part of Phocis and of the Epicnemidian Locrians. I must therefore describe these two. Eudoxus says that if one should imagine a straight line drawn in an easterly direction from the Ceraunian Mountains to Sunium, the promontory of Attica, it would leave on the right, towards the south, the whole of the Peloponnesus, and on the left, towards the north, the continuous coastline from the Ceraunian Mountains to the Crisaean Gulf and Megaris, and the coastline of all Attica. And he believes that the shore which extends from Sunium to the Isthmus would not be so concave as to have a great bend, if to this shore were not added the districts continuous with the Isthmus which form the Hermionic Gulf and Actê; and, in the same way, he believes that the shore which extends from the Ceraunian Mountains to the Corinthian Gulf would not, viewed by itself alone, have so great a bend as to be concave like a gulf if Rhium and Antirrhium did not draw closely together and afford this appearance; and the same is true of the shores4 that surround the recess of the gulf, where the sea in this region comes to an end.
2 Since this is the description given by Eudoxus, a mathematician and an expert both in geometrical figures and in "climata," and acquainted with these places, one must conceive of this side of Attica together with Megaris — the side extending from Sunium to the Isthmus — as concave, though only slightly so. Now here, at about the centre of the aforesaid line, is the Peiraeus, the seaport of Athens. It is distant from Schoenus, at the Isthmus, about three hundred and fifty stadia, and from p243Sunium three hundred and thirty. The distance from the Peiraeus to Pagae also is nearly the same as to Schoenus, though the former is said to exceed the latter by ten stadia. After doubling Sunium one's voyage is towards the north, but with an inclination towards the west.
3 Actê is washed by two seas; it is narrow at first, and then it widens out into the interior, though none the less it takes a crescent-like bend towards Oropus in Boeotia, with the convex side towards the sea; and this is the second, the eastern side of Attica. Then comes the remaining side, which faces the north and extends from the Oropian country towards the west as far as Megaris — I mean the mountainous part of Attica, which has many names and separates Boeotia from Attica; so that, as I have said before, Boeotia, since it has a sea on either side, becomes an isthmus of the third peninsula above-mentioned, an isthmus comprising within it the parts that lie towards the Peloponnesus, that is, Megaris and Attica. And it is on this account, they say, that the country which is now, by a slight change of letters, called Attica, was in ancient times called Actê and Acticê, because the greatest part of it lies below the mountains, stretches flat along the sea, is narrow, and has considerable length, projecting as far as Sunium. I shall therefore describe these sides, resuming again at that point of the seaboard where I left off.
4 After Crommyon, and situated above Attica, are the Sceironian Rocks. They leave no room for a road along the sea, but the road from the Isthmus to Megara and Attica passes above them. However, the road approaches so close to the rocks that in many places it passes along the edge of precipices, because the mountain situated above them is both lofty and impracticable for roads. Here is the setting of the myth about Sceiron and the Pityocamptes, the robbers who infested the above-mentioned mountainous country and were killed by Theseus. And the Athenians have given the name Sceiron to the Argestes, the violent wind that blows down on the travellers left from the heights of this mountainous country. After the Sceironian Rocks one comes to Cape Minoa, which projects into the sea and forms the harbour at Nisaea. Nisaea is the naval station of the Megarians; it is eighteen stadia distant from the city and is joined to it on both sides by walls. The naval station, too, used to be called Minoa.
5 In early times this country was held by the same Ionians who held Attica. Megara, however, had not yet been founded; and therefore the poet does not specifically mention this region, but when he calls all the people of Attica Athenians he includes these too under the general name, considering them Athenians. Thus, when he says in the Catalogue, "And those who held Athens, well-built city," we must interpret him as meaning the people now called Megarians as well, and assume that these also had a part in the expedition. And the following is proof: In early times Attica was called Ionia and Ias; and when the poet says, "There the Boeotians and the Iaonians," he means the Athenians; and Megaris was a part of this Ionia.
6 Furthermore, since the Peloponnesians and Ionians were having frequent disputes about their boundaries, on which, among other places, Crommyonia was situated, they made an agreement and erected a pillar in the place agreed upon, near the Isthmus itself, with an inscription on the side facing the Peloponnesus reading: "This is Peloponnesus, not Ionia," and on the side facing Megara, "This is not Peloponnesus, but Ionia." And though the writers of the histories of The Land of Atthis are at variance on many things, they all agree on this (at least all writers who are worth mentioning), that Pandion had four sons, Aegeus, Lycus, Pallas, and the fourth, Nisus, and that when Attica was divided into four parts, Nisus obtained Megaris as his portion and founded Nisaea. Now, according to Philochorus, his rule extended from the Isthmus to the Pythium, but according to Andron, only as far as Eleusis and the Thriasian Plain. Although different writers have stated the division into four parts in different ways, it suffices to take the following from Sophocles: Aegeus says that his father ordered him to depart to the shore-lands, assigning to him as the eldest the best portion of this land; then to Lycus "he assigns Euboea's garden that lies side by side therewith; and for Nisus he selects the neighbouring land of Sceiron's shore; and the southerly part of the land fell to this rugged Pallas, breeder of giants." These, then, are the proofs which writers use to show that Megaris was a part of Attica.
7 But after the return of the Heracleidae and the partitioning of the country, it came to pass that many of the former inhabitants were driven out of their homelands into Attica by the Heracleidae and the Dorians who came back with them. Among these was Melanthus, the king of Messenê. And he reigned also over the Athenians, by their consent, after his victory in single combat over Xanthus, the king of the Boeotians. But since Attica was now populous on account of the exiles, the Heracleidae became frightened, and at the instigation chiefly of the people of Corinth and the people of Messenê — of the former because of their proximity and of the latter because Codrus, the son of Melanthus, was at that time king of Attica — they made an expedition against Attica. But being defeated in battle they retired from the whole of the land except the Megarian territory; this they occupied and not only founded the city Megara but also made its population Dorians instead of Ionians. And they also destroyed the pillar which was the boundary between the Ionians and the Peloponnesians.
8 The city of the Megarians has experienced many changes, but nevertheless it has endured until the present time. It once even had schools of philosophers who were called the Megarian sect, these being the successors of Eucleides, the Socratic philosopher, a Megarian by birth, just as the Eleian sect, to which Pyrrhon belonged, were the successors of Phaedon the Eleian, who was also a Socratic philosopher, and just as the Eretrian sect were the successors of Menedemus the Eretrian. The country of the Megarians, like Attica, has rather poor soil, and the greater part of it is occupied by the Oneian Mountains, as they are called — a kind of ridge, which extends from the Sceironian Rocks to Boeotia and Cithaeron, and separates the sea at Nisaea from the Alcyonian Sea, as it is called, at Pagae.
9 On the voyage from Nisaea to Attica one comes to five small islands. Then to Salamis, which is about seventy stadia in length, though some say eighty. It contains a city of the same name; the ancient city, now deserted, faces towards Aegina and the south wind (just as Aeschylus has said, "And Aegina here lies towards the blasts of the south wind"), but the city of to‑day is situated on a gulf, on a peninsula-like place which borders on Attica. In early times it was called by different names, for example, "Sciras" and "Cychreia," after certain heroes. It is from one of these heroes that Athena is called "Sciras," and that a place in Attica is called "Scira," and that a certain sacred rite is performed in honour of "Scirus," and that one of the months is called "Scirophorion." And it is from the other hero that the serpent "Cychreides" took its name — the serpent which, according to Hesiod, was fostered by Cychreus and driven out by Eurylochus because it was damaging the island, and was welcomed to Eleusis by Demeter and made her attendant. And the island was also called Pityussa, from the tree. But the fame of the island is due to the Aiacidae, who ruled over it, and particularly to Aias, the son of Telamon, and also to the fact that near this island Xerxes was defeated by the Greeks in a naval battle and fled to his homeland. And the Aeginetans also shared in the glory of this struggle, since they were neighbours and furnished a considerable fleet. And there is in Salamis a river Bocarus, which is now called Bocalia.
At the present time the island is held by the Athenians, although in early times there was strife between them and the Megarians for its possession. Some say that it was Peisistratus, others Solon, who inserted in the Catalogue of Ships immediately after the verse, "and Aias brought twelve ships from Salamis," the verse, "and, bringing them, halted them where the battalions of the Athenians were stationed,"and then used the poet as a witness that the island had belonged to the Athenians from the beginning. But the critics do not accept this interpretation, because many of the verses bear witness to the contrary. For why is Aias found in the last place in the ship-camp, not with the Athenians, but with the Thessalians under Protesilaüs? "where were the ships of Aias and Protesilaüs." And in the Visitation of the troops, Agamemnon "found Menestheus the charioteer, son of Peteos, standing still; and about him were the Athenians, masters of the battle-cry. And near by stood Odysseus of many wiles, and about him, at his side, the ranks of the Cephallenians." And back again to Aias and the Salaminians, "he came to the Aïantes," and near them, "Idomeneus on the other side," not Menestheus. The Athenians, then, are reputed to have cited alleged testimony of this kind from Homer, and the Megarians to have replied with the following parody: "Aias brought ships from Salamis, from Polichnê, from Aegeirussa, from Nisaea, and from Tripodes"; these four are Megarian places, and, of these, Tripodes is called Tripodiscium, near which the present market-place of the Megarians is situated.
Some say that Salamis is foreign to Attica, citing the fact that the priestess of Athena Polias does not touch the fresh cheese made in Attica, but eats only that which is brought from a foreign country, yet uses, among others, that from Salamis. Wrongly, for she eats cheese brought from the other islands that are admittedly attached to Attica, since those who began this custom considered as "foreign" any cheese that was imported by sea. But it seems that in early times the present Salamis was a separate state, and that Megara was a part of Attica. And it is on the seaboard opposite Salamis that the boundaries between the Megarian country and Atthis are situated — two mountains which are called Cerata.
Then one comes to the city Eleusis, in which is the temple of the Eleusinian Demeter, and the mystic chapel which was built by Ictinus, a chapel which is large enough to admit a crowd of spectators. This Ictinus also built the Parthenon on the Acropolis in honour of Athena, Pericles superintending the work. Eleusis is numbered among the demes.
Then one comes to the Thriasian Plain, and the shore and deme bearing the same name. Then to Cape Amphiale and the quarry that lies above it, and to the passage to Salamis, about two stadia wide, across which Xerxes attempted to build a mole, but was forestalled by the naval battle and the flight of the Persians. Here, too, are the Pharmacussae, two small islands, on the larger of which is to be seen the tomb of Circe.
Above this shore is the mountain called Corydallus, and also the deme Corydalleis. Then one comes to the harbour Phoron, and to Psyttalia, a small, deserted, rocky island, which some have called the eye-sore of the Peiraeus. And near by, too, is Atalanta, which bears the same name as the island near Euboea and the Locrians, and another island similar to Psyttalia. Then one comes to the Peiraeus, which also is classed among the demes, and to Munychia.
Munychia is a hill which forms a peninsula; and it is hollowed out and undermined in many places, partly by nature and partly by the purpose of man, so that it admits of dwellings; and the entrance to it is by means of a narrow opening. And beneath the hill lie three harbours. Now in early times Munychia was walled, and covered with habitations in a manner similar to the city of the Rhodians, including within the circuit of its walls both the Peiraeus and the harbours, which were full of ship-houses, among which was the arsenal, the work of Philon. And the naval station was sufficient for the four hundred ships, for no fewer than this the Athenians were wont to despatch on expeditions. With this wall were connected the "legs" that stretched down from the city; these were the long walls, forty stadia in length, which connected the city with the Peiraeus. But the numerous wars caused the ruin of the wall and of the fortress of Munychia, and reduced the Peiraeus to a small settlement, round the harbours and the temple of Zeus Soter. The small roofed colonnades of the temple have admirable paintings, the works of famous artists; and its open court has statues. The long walls, also, are torn down, having been destroyed at first by the Lacedaemonians, and later by the Romans, when Sulla took both the Peiraeus and the city by siege.
The city itself is a rock situated in a plain and surrounded by dwellings. On the rock is the sacred precinct of Athena, comprising both the old temple of Athena Polias, in which is the lamp that is never quenched, and the Parthenon built by Ictinus, in which is the work in ivory by Pheidias, the Athena. However, if I once began to describe the multitude of things in this city that are lauded and proclaimed far and wide, I fear that I should go too far, and that my work would depart from the purpose I have in view. For the words of Hegesias occur to me: "I see the acropolis, and the mark of the huge trident there. I see Eleusis, and I have become an initiate into its sacred mysteries; yonder is the Leocorium, here is the Theseium; I am unable to point them all out one by one; for Attica is the possession of the gods, who seized it as a sanctuary for themselves, and of the ancestral heroes." So this writer mentioned only one of the significant things on the acropolis; but Polemon the Periegete wrote four books on the dedicatory offerings on the acropolis alone. Hegesias is proportionately brief in referring to the other parts of the city and to the country; and though he mentions Eleusis, one of the one hundred and seventy demes (or one hundred and seventy-four, as the number is given), he names none of the others.
Most of the demes, if not all, have numerous stories of a character both mythical and historical connected with them; Aphidna, for example, has the rape of Helen by Theseus, the sacking of the place by the Dioscuri and their recovery of their sister; Marathon has the Persian battle; Rhamnus has the statue of Nemesis, which by some is called the work of Diodotus and by others of Agoracritus the Parian, a work which both in grandeur and in beauty is a great success and rivals the works of Pheidias; and so with Deceleia, the base of operations of the Peloponnesians in the Deceleian War; and Phyle, whence Thrasybulus brought the popular party back to the Peiraeus and then to the city. And so, also, in the case of several other demes there are many historical incidents to tell; and, further, the Leocorium and the Theseium have myths connected with them, and so has the Lyceium, and the Olympicum (the Olympium is the same thing), which the king who dedicated it left half finished at his death. And in like manner also the Academia, and the gardens of the philosophers, and the Odeium, and the colonnade called "Poecilê," and the temples in the city containing very many marvellous works of different artists.
The account would be much longer if one should pass in review the early founders of the settlement, beginning with Cecrops; for all writers do not agree about them, as is shown even by the names. For instance, Acticê, they say, was derived from Actaeon; and Atthis and Attica from Atthis, the son of Cranaüs, after whom the inhabitants were also called Cranaï; and Mopsopia from Mopsopus; and Ionia from Ion, the son of Xuthus; and Poseidonia and Athens from the gods after whom they were named. As I have already said, the race of the Pelasgi clearly sojourned here too, and on account of their wanderings were called "Pelargi" by the Attic people.
The greater men's fondness for learning about things that are famous and the greater the number of men who have talked about them, the greater the censure, if one is not master of the historical facts. For example, in his Collection of the Rivers, Callimachus says that it makes him laugh if anyone makes bold to write that the Athenian virgins "draw pure liquid from the Eridanus," from which even cattle would hold aloof. Its sources are indeed existent now, with pure and potable water, as they say, outside the Gates of Diochares, as they are called, near the Lyceium; but in earlier times there was also a fountain near by which was constructed by man, with abundant and excellent water; and even if the water is not so now, why should it be a thing to wonder at, if in early times the water was abundant and pure, and therefore also potable, but in later times underwent a change? However, it is not permitted me to linger over details, since they are so numerous, nor yet, on the other hand, to pass by them all in silence without even mentioning one or another of them in a summary way.
It suffices, then, to add thus much: According to Philochorus, when the country was being devastated, both from the sea by the Carians, and from the land by the Boeotians, who were called Aonians, Cecrops first settled the multitude in twelve cities, the names of which were Cecropia, Tetrapolis, Epacria, Deceleia, Eleusis, Aphidna (also called Aphidnae, in the plural), Thoricus, Brauron, Cytherus, Sphettus, Cephisia. And at a later time Theseus is said to have united the twelve into one city, that of to‑day. Now in earlier times the Athenians were ruled by kings; and then they changed to a democracy; but tyrants assailed them, Peisistratus and his sons; and later an oligarchy arose, not only that of the four hundred, but also that of the thirty tyrants, who were set over them by the Lacedaemonians; of these they easily rid themselves, and preserved the democracy until the Roman conquest. 398For even though they were molested for a short time by the Macedonian kings, and were even forced to obey them, they at least kept the general type of their government the same. And some say that they were actually best governed at that time, during the ten years when Cassander reigned over the Macedonians. For although this man is reputed to have been rather tyrannical in his dealings with all others, yet he was kindly disposed towards the Athenians, once he had reduced the city to subjection; for he placed over the citizens Demetrius of Phalerum, one of the disciples of Theophrastus the philosopher, who not only did not destroy the democracy but even improved it, as is made clear in the Memoirs which Demetrius wrote concerning this government. But the envy and hatred felt for oligarchy was so strong that, after the death of Cassander, Demetrius was forced to flee to Egypt; and the statues of him, more than three hundred, were pulled down by the insurgents and melted, and some writers go on to say that they were made into chamber pots. Be that as it may, the Romans, seeing that the Athenians had a democratic government when they took them over, preserved their autonomy and liberty. But when the Mithridatic War came on, tyrants were placed over them, whomever the king wished. The most powerful of these, Aristion, who violently oppressed the city, was punished by Sulla the Roman commander when he took this city by siege, though he pardoned the city itself; and to this day it is free and held in honour among the Romans.
After the Peiraeus comes the deme Phalereis, on the seaboard next to it; then Halimusii, Aexoneis, Alaeeis, Aexonici, and Anagyrasii. Then Thoreis, Lamptreis, Aegilieis, Anaphlystii, Ateneis. These are the demes as far as the cape of Sunium. Between the aforesaid demes is a long cape, the first cape after Aexoneis, Zoster; then another after Thoreis, I mean Astypalaea; off the former of these lies the island Phabra and off the latter the island Eleussa; and also opposite Aexoneisº is Hydrussa. And in the neighbourhood of Anaphlystus is also the shrine of Pan, and the temple of Aphrodite Colias, at which place, they say, were cast forth by the waves the last wreckage of the ships after the Persian naval battle near Salamis, the wreckage concerning which Apollo predicted "the women of Colias will cook food with the oars." Off these places, too, is the island Belbina, at no great distance, and also the palisade of Patroclus. But most of these islands are uninhabited.
On doubling the cape of Sunium one comes to Sunium, a noteworthy deme; then to Thoricus; then to a deme called Potamus, whose inhabitants are called Potamii; then to Prasia, to Steiria, to Brauron, where is the temple of the Artemis Brauronia, to Halae Araphenides, where is the temple of Artemis Tauropolus, to Myrrinus, to Probalinthus, and to Marathon, where Miltiades utterly destroyed the forces under Datis the Persian, without waiting for the Lacedaemonians, who came too late because they wanted the full moon. Here, too, is the scene of the myth of the Marathonian bull, which was slain by Theseus. After Marathon one comes to Tricorynthus; then to Rhamnus, the sanctuary of Nemesis; then to Psaphis, the land of the Oropians. In the neighbourhood of Psaphis is the Amphiaraeium, an oracle once held in honour, where in his flight Amphiaraüs, as Sophocles says, "with four-horse chariot, armour and all, was received by a cleft that was made in the Theban dust." Oropus has often been disputed territory; for it is situated on the common boundary of Attica and Boeotia. Off this coast are islands: off Thoricus and Sunium lies the island Helenê; it is rugged and deserted, and in its length of about sixty stadia extends parallel to the coast. This island, they say, is mentioned by the poet where Alexander says to Helen: "Not even when first I snatched thee from lovely Lacedaemon and sailed with thee on the seafaring ships, and in the island Cranaë joined with thee in love and couch"; for he calls Cranaë the island now called Helenê from the fact that the intercourse took place there. And after Helenê comes Euboea, which lies off the next stretch of coast; it likewise is narrow and long and in length lies parallel to the mainland, like Helenê. The voyage from Sunium to the southerly promontory of Euboea, which is called Leucê Actê, is three hundred stadia. However, I shall discuss Euboea later; but as for the demes in the interior of Attica, it would be tedious to recount them because of their great number.
Of the mountains, those which are most famous are Hymettus, Brilessus, and Lycabettus; and also Parnes and Corydallus. Near the city are most excellent quarries of marble, the Hymettian and Pentelic. Hymettus also produces the best honey. The silver mines in Attica were originally valuable, but now they have failed. Moreover, those who worked them, when the mining yielded only meager returns, melted again the old refuse, or dross, and were still able to extract from it pure silver, since the workmen of earlier times had been unskillful in heating the ore in furnaces. But though the Attic honey is the best in the world, that in the country of the silver mines is said to be much the best of all, the kind which is called acapniston, from the mode of its preparation.
The rivers of Attica are the Cephissus, which has its source in the deme Trinemeis; it flows through the plain (hence the allusions to the "bridge" and the "bridge-railleries") and then through the legs of the walls which extend from the city to the Peiraeus; it empties into the Phaleric Gulf, being a torrential stream most of the time, although in summer it decreases and entirely gives out. And such is still more the case with the Ilissus, which flows from the other part of the city into the same coast, from the region above Agra and the Lyceium, and from the fountain which is lauded by Plato in the Phaedrus. So much for Attica. |
|
|
|



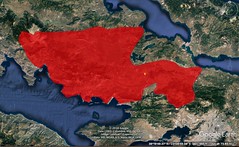

|
9 - 2 Boeotia 
1 Next in order is Boeotia; and when I discuss this country and the tribes that are continuous with it, I must, for the sake of clearness, call to mind what I have said before. As I have said, the seaboard from Sunium to Thessaloniceia extends towards the north, slightly inclining towards the west and keeping the sea on the east; and that the parts above this seaboard lie towards the west — ribbon-like stretches of country extending parallel to one another through the whole country. The first of these parts is Attica together with Megaris — a ribbon-like stretch of country, having as its eastern side the seaboard from Sunium to Oropus and Boeotia, and as its western side the Isthmus and the Alcyonian Sea, which extends from Pagae to the boundaries of Boeotia near Creusa, and as its remaining two sides, the seaboard from Sunium to the Isthmus and the mountainous country approximately parallel thereto which separates Attica from Boeotia. The second of these parts is Boeotia, extending ribbon-like from the east towards the west, from the Euboean Sea to the sea at the Crisaean Gulf; and it is about equal in length to Attica or perhaps less; in the fertility of its soil, however, it is far superior.
2 Ephorus declares that Boeotia is superior to the countries of the bordering tribes, not only in fertility of soil, but also because it alone has three seas and has a greater number of good harbours; in the Crisaean and Corinthian Gulfs it receives the products of Italy and Sicily and Libya, while in the part which faces Euboea, since its seaboard branches off on either side of the Euripus, on one side towards Aulis and the territory of Tanagra and on the other towards Salganeus and Anthedon, the sea stretches unbroken in the one direction towards Egypt and Cyprus and the islands, and in the other direction towards Macedonia and the regions of the Propontis and the Hellespont. And he adds that Euboea has, in a way, been made a part of Boeotia by the Euripus, since the Euripus is so narrow and is spanned by a bridge to Euripus only two plethra long. Now he praises the country on account of these things; and he says that it is naturally well suited to hegemony, but that those who were from time to time its leaders neglected careful training and education, and therefore, although they at times achieved success, they maintained it only for a short time, as is shown in the case of Epameinondas; for after he died the Thebans immediately lost the hegemony, having had only a taste of it; and that the cause of this was the fact that they belittled the value of learning and of intercourse with mankind, and cared for the military virtues alone. Ephorus should have added that these things are particularly useful in dealing with Greeks, although force is stronger than reason in dealing with the barbarians. And the Romans too, in ancient times, when carrying on war with savage tribes, needed no training of this kind, but from the time that they began to have dealings with more civilised tribes and races, they applied themselves to this training also, and so established themselves as lords of all.
3 Be that as it may, Boeotia in earlier times was inhabited by barbarians, the Aones and the Temmices, who wandered thither from Sunium, and by the Leleges and the Hyantes. Then the Phoenicians occupied it, I mean the Phoenicians with Cadmus, the man who fortified the Cadmeia and left the dominion to his descendants. Those Phoenicians founded Thebes in addition to the Cadmeia, and preserved their dominion, commanding most of the Boeotians until the expedition of the Epigoni. On this occasion they left Thebes for a short time, but came back again. And, in the same way, when they were ejected by the Thracians and the Pelasgians, they established their government in Thessaly along with the Arnaei for a long time, so that they were all called Boeotians. Then they returned to the homeland, at the time when the Aeolian fleet, near Aulis in Boeotia, was now ready to set sail, I mean the fleet which the sons of Orestes were despatching to Asia. After adding the Orchomenian country to Boeotia (for in earlier times the Orchomenians were not a part of the Boeotian community, nor did Homer enumerate them with the Boeotians, but as a separate people, for he called them Minyae), they, with the Orchomenians, drove out the Pelasgians to Athens (it was after these that a part of the city was named "Pelasgicon," though they took up their abode below Hymettus), and the Thracians to Parnassus; and the Hyantes founded a city Hyas in Phocis.
4 Ephorus says that the Thracians, after making a treaty with the Boeotians, attacked them by night when they, thinking that peace had been made, were encamping rather carelessly; and when the Boeotians frustrated the Thracians, at the same time making the charge that they were breaking the treaty, the Thracians asserted that they had not broken it, for the treaty said "by day," whereas they had made the attack by night; whence arose the proverb, "Thracian pretense"; and the Pelasgians, when the war was still going on, went to consult the oracle, as did also the Boeotians. Now Ephorus is unable, he says, to tell the oracular response that was given to the Pelasgians, but the prophetess replied to the Boeotians that they would prosper if they committed sacrilege; and the messengers who were sent to consult the oracle, suspecting that the prophetess responded thus out of favour to the Pelasgians, because of her kinship with them (indeed, the temple also was from the beginning Pelasgian), seized the woman and threw her upon a burning pile, for they considered that, whether she had acted falsely or had not, they were right in either case, since, if she uttered a false oracle, she had her punishment, whereas, if she did not act falsely, they had only obeyed the order of the oracle. Now those in charge of the temple, he says, did not approve of putting to death without trial — and that too in the temple — the men who did this, and therefore they brought them to trial, and summoned them before the priestesses, who were also the prophetesses, being the two survivors of the three; but when the Boeotians said that it was nowhere lawful for women to act as judges, they chose an equal number of men in addition to the women. Now the men, he says, voted for acquittal, but the women for conviction, and since the votes cast were equal, those for acquittal prevailed; and in consequence of this prophecies are uttered at Dodona by men to Boeotians only; the prophetesses, however, explain the oracle to mean that the god ordered the Boeotians to steal the tripods and take one of them to Dodona every year; and they actually do this, for they always take down one of the dedicated tripods by night and cover it up with garments, and secretly, as it were, carry it to Dodona.
5 After this the Boeotians cooperated with Penthilus and his followers in forming the Aeolian colony, sending with him most of their own people, so that it was also called a Boeotian colony. A long time afterwards the country was thoroughly devastated by the Persian war that took place near Plataeae. Then they recovered themselves to such an extent that the Thebans, having conquered the Lacedaemonians in two battles, laid claim to supremacy over the Greeks. But Epameinondas fell in the battle, and consequently they were disappointed in this hope; but still they went to war on behalf of the Greeks against the Phocians, who had robbed their common temple. And after suffering loss from this war, as also from the Macedonians when these attacked the Greeks, they lost their city, which was rased to the ground by these same people, and then received it back from them when rebuilt. From that time on the Thebans have fared worse and worse down to our own time, and Thebes to‑day does not preserve the character even of a respectable village; and the like is true of other Boeotian cities, except Tanagra and Thespiae, which, as compared with Thebes, have held out fairly well.
6 Next in order I must make a circuit of the country, beginning at that part of the coastline opposite Euboea which joins Attica. The beginning is Oropus, and the Sacred Harbour, which is called Delphinium, opposite which is the ancient Eretria in Euboea, the distance across being sixty stadia. After Delphinium, at a distance of twenty stadia, is Oropus; and opposite Oropus is the present Eretria, and to it the passage across the strait is forty stadia.
7 Then one comes to Delium, the sanctuary of Apollo, which is a reproduction of that in Delos. It is a small town of the Tanagraeans, thirty stadia distant from Aulis. It was to this place that the Athenians, after their defeat in battle, made their headlong flight; and in the flight Socrates the philosopher, who was serving on foot, since his horse had got away from him, saw Xenophon the son of Gryllus lying on the ground, having fallen from his horse, and took him up on his shoulders and carried him in safety for many stadia, until the flight ceased.
8 Then one comes to a large harbour, which is called Bathys Limen; then to Aulis, a rocky place and a village of the Tanagraeans. Its harbour is large enough for only fifty boats; and therefore it is reasonable to suppose that the naval station of the Greeks was in the large harbour. And near by, also, is the Euripus at Chalcis, to which the distance from Sunium is six hundred and seventy stadia; and over it is a bridge two plethra long, as I have said; and a tower stands on each side, one on the side of Chalcis, and the other on the side of Boeotia; and tube-like passages have been constructed into the towers. Concerning the refluent currents of the Euripus it is enough to say only thus much, that they are said to change seven times each day and night; but the cause of the changes must be investigated elsewhere.
9 Near the Euripus, upon a height, is situated a place called Salganeus. It is named after Salganeus, a Boeotian, who was buried there — the man who guided the Persians when they sailed into this channel from the Maliac Gulf. It is said that he was put to death before they reached the Euripus by Megabates, the commander of the fleet, because he was considered a villain, on the ground that he had deceitfully rushed the fleet into a blind alley of the sea, but that the barbarian, when he perceived that he himself was mistaken, not only repented, but deemed worthy of burial the man who had been put to death without cause.
Near Oropus is a place called Graea, and also the temple of Amphiaraüs, and the monument of Narcissus the Eretrian, which is called "Sigelus's," because people pass it in silence. Some say that Graea is the same as Tanagra. The Poemandrian territory is the same as the Tanagraean; and the Tanagraeans are also called Gephyraeans. The temple of Amphiaraüs was transferred hither in accordance with an oracle from the Theban Cnopia.
Also Mycalessus, a village, is in the Tanagraean territory. It is situated on the road that leads from Thebes to Chalcis; and in the Boeotian dialect it is called Mycalettus. And Harma is likewise in the Tanagraean territory; it is a deserted village near Mycalettus, and received its name from the chariot of Amphiaraüs, and is a different place from the Harma in Attica, which is near Phylë, a deme of Attica bordering on Tanagra. Here originated the proverb, "when the lightning flashes through Harma"; for those who are called the Pythaistae look in the general direction of Harma, in accordance with an oracle, and note any flash of lightning in that direction, and then, when they see the lightning flash, take the offering to Delphi. They would keep watch for three months, for three days and nights each month, from the altar of Zeus Astrapaeus; this altar is within the walls between the Pythium and the Olympium. In regard to the Harma in Boeotia, some say that Amphiaraus fell in the battle out of his chariot near the place where his temple now is, and that the chariot was drawn empty to the place which bears the same name; others say that the chariot of Adrastus, when he was in flight, was smashed to pieces there, but that Adrastus safely escaped on Areion. But Philochorus says that Adrastus was saved by the inhabitants of the village, and that on this account they obtained equal rights of citizenship from the Argives.
To anyone returning from Thebes to Argos, Tanagra is on the left; and . . . is situated on the right. And Hyria, also, belongs to the Tanagraean territory now, though in earlier times it belonged to the Theban territory. Hyria is the scene of the myth of Hyrieus, and of the birth of Orion, of which Pindar speaks in his dithyrambs; it is situated near Aulis. Some say that Hysiae is called Hyria, belonging to the Parasopian country below Cithaeron, near Erythrae, in the interior, and that it is a colony of the Hyrieans and was founded by Nycteus, the father of Antiope. There is also a Hysiae in the Argive territory, a village; and its inhabitants are called Hysiatae. The Erythrae in Ionia is a colony of this Erythrae. And Heleon, also, is a village belonging to Tanagra, having been so named from the "hele."
After Salganeus one comes to Anthedon, a city with a harbour; and it is the last city on that part of the Boeotian seaboard which is opposite to Euboea, as the poet says, "Anthedon at the extremity." As one proceeds a little farther, however, there are still two small towns belonging to the Boeotians: Larymna, near which the Cephissus empties, and, still farther on, Halae, which bears the same name as the Attic demes. Opposite this seaboard is situated, it is said, the Aegae in Euboea, in which is the temple of the Aegaean Poseidon, which I have mentioned before. The distance across the strait from Anthedon to Aegae is one hundred and twenty stadia, but from the other places it is much less. The temple is situated on a high mountain, where there was once a city. And Orobiae also is near Aegae. In the Anthedonian territory is Mount Messapius, named after Messapus, who, when he came into Iapygia, called the country Messapia. Here, too, is the scene of the myth of Glaucus, the Anthedonian, who is said to have changed into a sea-monster.
Near Anthedon, and belonging to Boeotia, is a place that is esteemed sacred, and contains traces of a city, Isus, as it is called, with the first syllable pronounced short. Some, however, think that the verse should be written, "sacred Isus and Anthedon at the extremity," lengthening the first syllable by poetic licence on account of the meter, instead of "sacred Nisa," for Nisa is nowhere to be seen in Boeotia, as Apollodorus says in his work On Ships; so that Nisa could not be the correct reading, unless by "Nisa" the poet means "Isus"; for there was a city Nisa bearing the same name in the territory of Megara, whose inhabitants emigrated to the foothills of Cithaeron, but it has now disappeared. Some, however, think that we should write "sacred Creusa," taking the poet to mean the Creusa of to‑day, the naval station of the Thespians, which is situated in the Crisaean Gulf; but others think that we should read "sacred Pharae." Pharae is one of the "Four United Villages" in the neighbourhood of Tanagra, which are: Heleon, Harma, Mycalessus, and Pharae. And still others write as follows: "sacred Nysa." And Nysa is a village in Helicon. Such, then, is the seaboard facing Euboea.
The plains in the interior, which come next in order, are hollows, and are surrounded everywhere on the remaining sides by mountains; by the mountains of Attica on the south, and on the north by the mountains of Phocis; and, on the west, Cithaeron inclines, obliquely, a little above the Crisaean Sea; it begins contiguous with the mountains of Megara and Attica, and then bends into the plains, terminating in the neighbourhood of Thebes.
Some of these plains are marshy, since rivers spread out over them, though other rivers fall into them and later find a way out; other plains are dried up, and on account of their fertility are tilled in all kinds of ways. But since the depths of the earth are full of caverns and holes, it has often happened that violent earthquakes have blocked up some of the passages, and also opened up others, some up to the surface of the earth and others through underground channels. The result for the waters, therefore, is that some of the streams flow through underground channels, whereas others flow on the surface of the earth, thus forming lakes and rivers. And when the channels in the depths of the earth are stopped up, it comes to pass that the lakes expand as far as the inhabited places, so that they swallow up both cities and districts, and that when the same channels, or others, are opened up, these cities and districts are uncovered; and that the same regions at one time are traversed in boats and at another on foot, and the same cities at one time are situated on the lake and at another far away from it.
One of two things has taken place: either the cities have remained unremoved, when the increase in the waters has been insufficient to overflow the dwellings because of their elevation, or else they have been abandoned and rebuilt elsewhere, when, being oftentimes endangered by their nearness to the lake, they have relieved themselves from fear by changing to districts farther away or higher up. And it follows that the cities thus rebuilt which have kept the same name, though at first called by names truly applying to them, derived from local circumstances, have names which no longer truly apply to them; for instance, it is probable that "Plataeae" was so called from the "blade" of the oars, and "Plataeans" were those who made their living from rowing; but now, since they live far away from the lake, the name can no longer truly apply to them. Helos and Heleon and Heilesium were so called because they were situated near marshes; but now the case is different with these places, since they have been rebuilt elsewhere, or else the lake has been greatly reduced because of outflows that later took place; for this is possible.
This is best shown by the Cephissus, which fills lake Copais; for when the lake had increased so much that Copae was in danger of being swallowed up (Copae is named by the poet, and from it the lake took its name), a rent in the earth, which was formed by the lake near Copae, opened up a subterranean channel about thirty stadia in length and admitted the river; and then the river burst forth to the surface near Larymna in Locris; I mean the Upper Larymna, for there is another Larymna, which I have already mentioned, the Boeotian Larymna on the sea, to which the Romans annexed the Upper Larymna. The place is called Anchoê; and there is also a lake of the same name. And when it leaves this lake the Cephissus at last flows out to the sea. Now at that time, when the flooding of the lake ceased, there was also a cessation of danger to those who lived near it, except in the case of the cities which had already been swallowed up. And though the subterranean channels filled up again, Crates the mining engineer of Chalcis ceased clearing away the obstructions because of party strife among the Boeotians, although, as he himself says in the letter to Alexander, many places had already been drained. Among these places, some writers suppose, was the ancient site of Orchomenus, and others, those of Eleusis and Athens on the Triton River. These cities, it is said, were founded by Cecrops, when he ruled over Boeotia, then called Ogygia, but were later wiped out by inundations. And it is said that a fissure in the earth opened up near Orchomenus, also, and that it admitted the Melas River, which flowed through the territory of Haliartus and formed there the marsh which produces the reed that is used for flutes. But this river has completely disappeared, either because it is dispersed by the fissure into invisible channels or because it is used up beforehand by the marshes and lakes in the neighbourhood of Haliartus, from which the poet calls the place "grassy," when he says, "and grassy Haliartus."
Now these rivers flow down from the Phocian mountains, and among them the Cephissus, which takes its beginning at Lilaea, a Phocian city, as Homer says: "And those who held Lilaea, at the sources of Cephissus." And flowing through Elateia, the largest of the cities of Phocis, and through Parapotamii and Phanoteus, which are likewise Phocian towns, it goes on into Chaeroneia in Boeotia, and then through the territories of Orchomenus and Coroneia, and discharges into Lake Copais. And also the Permessus and the Olmeius, flowing from Helicon, meet one another and fall into the same p309Lake Copais near Haliartus; and also other streams empty into it. Now it is a large lake, having a circuit of three hundred and eighty stadia, but its outlets are nowhere to be seen, except for the fissure which admits the Cephissus, and for the marshes.
Among the neighbouring lakes are Lake Trephia and the Cephissian Lake, which is also mentioned by the poet: "Who dwelt in Hylê, strongly intent upon wealth, on the shore of the Cephissian Lake." For he does not mean Lake Copais, as some think, but lake Hylicê (accented on the last syllable like lyricé), which is named after the village near by that is called Hylê (accented like lýra and thýra), not Hydê, as some write, "who dwelt in Hydê." For Hydê is in Lydia, "below snowy Tmolus in the fertile land of Hydê," whereas Hylê is in Boeotia; at any rate, the poet appends to the words, "on the shore of the Cephissian Lake," the words, "and near him dwelt the rest of the Boeotians." For Lake Copais is large, and not in the territory of Thebes; whereas the other is small, and is filled from lake Copais through subterranean channels; and it is situated between Thebes and Anthedon. Homer, however, uses the word in the singular number, at one time making the first syllable long, as in the Catalogue, "and Hȳlê and Peteôn, by poetic licence, and at another making it short, "who dwelt in Hy̆lê," and "Tychius . . . , by far the best of leatherworkers, who had his home in Hylê." And certain critics are not correct in writing Hydê here, either; for Aias was not sending to fetch his shield from Lydia.
These lakes suggest the order of the places that come next after them, so that nominally their positions are clearly determined, because the poet observes no order in naming the places, whether those that are worthy of mention or those that are not. But it is difficult, in naming so many places, most of them insignificant and situated in the interior, to avoid error in every case in the matter of their order. The seaboard, however, has a certain advantage with regard to this: the places there are better known; and, too, the sea more readily suggests the order of places. Therefore I, too, shall try to take my beginnings from the seaboard, although at present I shall disregard this intention, and following the poet shall make my enumeration of the places, adding everything taken from other writers, but omitted by him, that may be useful to us. He begins at Hyria and Aulis, concerning which I have already spoken.
Schoenus is a district of the Theban territory on the road that leads from Thebes to Anthedon, and is about fifty stadia distant from Thebes; and there is also a river Schoenus which flows through it.
Scolus is a village in the Parasopian country at the foot of Mount Cithaeron, a place that is rugged and hardly habitable; whence the proverb, "neither go to Scolus thyself nor follow another thither." And this is also said to be the place from which Pentheus was brought when he was torn to pieces. And there was another Scolus among the cities in the neighbourhood of Olynthus bearing the same name as this village. And, as I have already said, there is also in the Trachinian Heracleia a village called Parasopii, past which flows a River Asopus; and in Sicyonia there is another Asopus River, and also the country Asopia, through which that Asopus flows; and there are also other rivers which bear this name.
The name "Eteonus" was changed to "Scarphê," and Scarphê too is in Parasopia; for the Asopus and the Ismenus flow through the plain which is in front of Thebes. And there is the spring called Dircê; and also Potniae, where is the scene of the myth of Glaucus of Potniae, who was torn to pieces by the Potnian mares near the city. Cithaeron, also, ends not far from Thebes. The Asopus flows past it, washing its foothills and causing the division of the Parasopii into several settlements; and all the settlements are subject to Thebes, though another set of writers say that Scolus, Eteonus, and Erythrae are in the territory of the Plataeans, for the river flows past Plataea, also, and empties near Tanagra. And in the territory of Thebes are also Therapnae and Teumessus, which latter Antimachus has adorned with praise in many verses, although he enumerates goodly attributes which do not belong to it, as, for instance, "there is a windy little hill"; but the verses are well known.
The "Thespiae" of to‑day is by Antimachus spelled "Thespeia"; for there are many names of places which are used in both ways, both in the singular and in the plural, just as there are many which are used both in the masculine and in the feminine, whereas there are others which are used in either one or the other number only. Thespiae is a city near Mt. Helicon, lying somewhat to the south of it; and both it and Helicon are situated on the Crisaean Gulf. It has a seaport Creusa, also called Creusis. In the Thespian territory, in the part lying towards Helicon, is Ascrê, the native city of Hesiod; it is situated on the right of Helicon, on a high and rugged place, and is about forty stadia distant from Thespiae. This city Hesiod himself has satirised in verses which allude to his father, because at an earlier time his father changed his abode to this place from the Aeolian Cymê, saying: "And he settled near Helicon in a wretched village, Ascrê, which is bad in winter, oppressive in summer, and pleasant at no time." Helicon is contiguous to Phocis in its northerly parts, and to a slight extent also in its westerly parts, in the region of the last harbour belonging to Phocis, the harbour which, from the fact in the case, is called Mychus; for, speaking generally, it is above this harbour of the Crisaean Gulf that Helicon and Ascrê, and also Thespiae and its seaport Creusa, are situated. This is also considered the deepest recess of the Crisaean Gulf, and in general of the Corinthian Gulf. The length of the coast-line from the harbour Mychus to Creusa is ninety stadia; and the length from Creusa as far as the promontory called Holmiae is one hundred and twenty; and hence Pagae and Oenoê, of which I have already spoken, are situated in the deepest recess of the gulf. Now Helicon, not far distant from Parnassus, rivals it both in height and in circuit; for both are rocky and covered with snow, and their circuit comprises no large extent of territory. Here are the temple of the Muses and Hippu-crenê and the cave of the nymphs called the Leibethrides; and from this fact one might infer that those who consecrated Helicon to the Muses were Thracians, the same who dedicated Pieris and Leibethrum and Pimpleia to the same goddesses. The Thracians used to be called Pieres, but, now that they have disappeared, the Macedonians hold these places. It has been said that Thracians once settled in this part of Boeotia, having overpowered the Boeotians, as did also Pelasgians and other barbarians. Now in earlier times Thespiae was well known because of the Eros of Praxiteles, which was sculptured by him and dedicated by Glycera the courtesan (she had received it as a gift from the artist) to the Thespians, since she was a native of the place. Now in earlier times travellers would go up to Thespeia, a city otherwise not worth seeing, to see the Eros; and at present it and Tanagra are the only Boeotian cities that still endure; but of all the rest only ruins and names are left.
After Thespiae Homer names Graea and Mycalessus, concerning which I have already spoken. He likewise says concerning the rest: "And those who lived about Harma and Eilesium and Erythrae, and those who held Eleon and Hylê and Peteon." Peteon is a village in the Theban territory near the road to Anthedon. Ocaleê is midway between Haliartus and Alalcomenium, thirty stadia distant from each; and a river bearing the same name flows past it. The Phocian Medeon is on the Crisaean Gulf, at a distance of one hundred and sixty stadia from Boeotia, whereas the Boeotian Medeon, which was named after it, is near Onchestus at the base of the mountain Phoenicius; and from this fact its name has been changed to Phoenicis. This mountain is also called a part of the Theban territory; but by some both Medeon and Ocalea are called a part of the territory of Haliartus.
Homer then goes on to say: "Copae, and Eutresis, and Thisbê abounding in doves." Concerning Copae I have already spoken. It lies towards the north on Lake Copais; and the others around the lake are these: Acraephiae, Phoenicis, Onchestus, Haliartus, Ocalea, Alalcomenae, Tilphusium, Coroneia. In early times, at least, the lake had no common name, but was called by different names corresponding to the several settlements lying on it, as, for instance, Copais from Copae, Haliartis from Haliartus, and so in the case of the rest of the settlements; but later the whole lake was called Copais, this name prevailing over all others; for the region of Copae forms the deepest recess of the lake. Pindar calls this lake Cephissis; at any rate, he places near it the spring Tilphossa, which flows at the foot of Mount Tilphossius near Haliartus and Alalcomenae, near which latter is the tomb of Teiresias; and here, too, is the temple of the Tilphossian Apollo.
Next in order after Copae Homer names Eutresis, a small village of the Thespians, where Zethus and Amphion are said to have lived before they reigned over Thebes. Thisbê is now called Thisbae; the place is inhabited and is situated slightly above the sea, bordering on the territory of the Thespians and on that of Coroneia; and it, too, lies at the foot of Helicon on the south; and it has a seaport situated on a rocky place, which abounds in doves, in reference to which the poet says, "Thisbê abounding in doves." From here to Sicyon is a voyage of one hundred and sixty stadia.
Next Homer names Coroneia, Haliartus, Plataeae, and Glissas. Now Coroneia is situated on a height near Helicon. The Boeotians took possession of it on their return from the Thessalian Arnê after the Trojan War, at which time they also occupied Orchomenus. And when they got the mastery of Coroneia, they built in the plain before the city the temple of the Itonian Athena, bearing the same name as the Thessalian temple; and they called the river which flowed past it Cuarius, giving it the same name as the Thessalian river. But Alcaeus calls it Coralius, when he says, "Athena, warrior queen, who dost keep watch o'er the corn-fieldsº of Coroneia before thy temple on the banks of the Coralius River." Here, too, the Pamboeotian Festival used to be celebrated. And for some mystic reason, as they say, a statue of Hades was dedicated along with that of Athena. Now the people in Coroneia are called Coronii, whereas those in the Messenian Coroneia are called Coronaeis.
Haliartus is no longer in existence, having been rased to the ground in the war against Perseus; and the country is held by the Athenians, a gift from the Romans. It was situated in a narrow place, between the mountain situated above it and Lake Copais, near the Permessus and Olmeius Rivers and the marsh that produces the flute reed.
Plataeae, which Homer speaks of in the singular number, is at the foot of Cithaeron, between it and Thebes, along the road that leads to Athens and Megara, on the confines of Attica and Megaris; for Eleutherae is near by, which some say belongs to Attica, others to Boeotia. I have already said that the Asopus flows past Plataeae. Here it was that the forces of the Greeks completely wiped out Mardonius and his three hundred thousand Persians; and they built a temple of Zeus Eleutherius, and instituted the athletic games in which the victor received a crown, calling them the Eleutheria. And tombs of those who died in the battle, erected at public expense, are still to be seen. In Sicyonia, also, there is a deme called Plataeae, the home of Mnasalces the poet: "The tomb of Mnasalces the Plataean." Homer speaks of Glissas, a settlement in the mountain Hypatus, which is in the Theban country near Teumessus and Cadmeia. The hillocks below which lies the Aonian Plain, as it is called, which extends from the Hypatus mountain to Thebes, are called "Dria."
In these words of the poet, "and those who held Hypothebes," some take him to mean some little city called Hypothebes, others Potniae; for Thebes, the latter say, was deserted because of the expedition of the Epigoni and had no part in the Trojan War. The former, however, say that the Thebans indeed had a part in the war, but that they were living in the level districts below Cadmeia at that time, since they were unable to rebuild Cadmeia; and since Cadmeia was called Thebes, they add, the poet called the Thebans of that time "Hypothebans" instead of "people who live below Cadmeia."
Onchestus is where the Amphictyonic Council used to convene, in the territory of Haliartus near Lake Copais and the Teneric Plain; it is situated on a height, is bare of trees, and has a sacred Precinct of Poseidon, which is also bare of trees. But the poets embellish things, calling all sacred precincts "sacred groves," even if they are bare of trees. Such, also, is the saying of Pindar concerning Apollo: "stirred, he traversed both land and sea, and halted on great lookouts above mountains, and whirled great stones, laying foundations of sacred groves." But Alcaeus is wrong, for just as he perverted the name of the River Cuarius, so he falsified the position of Onchestus, placing it near the extremities of Helicon, although it is at quite a distance from this mountain.
The Teneric Plain is named after Tenerus. In myth he was the son of Apollo by Melia, and was a prophet of the oracle on the Ptoüs Mountain, which the same poet calls three-peaked: "and once he took possession of the three-peaked hollow of Ptoüs." And he calls Tenerus "temple-minister, prophet, called by the same name as the plains." The Ptoüs lies above the Teneric Plain and Lake Copais near Acraephium. Both the oracle and the mountain belonged to the Thebans. And Acraephium itself also lies on a height. They say that this is called Arnê by the poet, the same name as the Thessalian city.
Some say that Arnê too was swallowed up by the lake, as well as Mideia. Zenodotus, who writes "and those who possessed Ascrê rich in vineyards," seems not to have read the statements of Hesiod concerning his native land, nor those of Eudoxus, who says much worse things concerning Ascrê. For how could anyone believe that such a place was called "rich in vineyards" by the poet? Wrong, also, are those who write "Tarnê" instead of "Arnê"; for not a single place named Tarnê is pointed out among the Boeotians, though there is one among the Lydians, and this the poet mentions: "Idomeneus then slew Phaestus, son of Borus the Maeonian, who came from fertile Tarnê." The remaining Boeotian cities concerning which it is worthwhile to make mention are: of those situated round the lake, Alalcomenae and Tilphossium, and, of the rest, Chaeroneia, Lebadeia, and Leuctra.
Now as for Alalcomenae, the poet mentions it, but not in the Catalogue: "Argive Hera and Alalcomenian Athena." It has an ancient temple of Athena which is held in great honour; and they say, at least, that the goddess was born there, just as Hera was born in Argos, and that it was because of this that the poet named them both in this way, as natives of these places. And it was because of this, perhaps, that he did not mention in the Catalogue the men of Alalcomenae, since, being sacred, they were excused from the expedition. And in fact the city always continued unravaged, although it was neither large nor situated in a secure position, but in a plain. But all peoples, since they revered the goddess, held aloof from any violence towards the inhabitants, so that when the Thebans, at the time of the expedition of the Epigonoi, left their city, they are said to have fled for refuge to Alalcomenae, and to Tilphossius, the mountain, a natural stronghold that lies above it; and at the base of this mountain is a spring called Tilphossa, and the monument of Teiresias, who died there at the time of the flight.
Chaeroneia is near Orchomenus. It was here that Philip the son of Amyntas conquered the Athenians, Boeotians, and Corinthians in a great battle, and set himself up as lord of Greece. And here, too, are to be seen tombs of those who fell in the battle, tombs erected at public expense. And it was in the same region that the Romans so completely defeated the forces of Mithridates, many tens of thousands in number, that only a few escaped in safety to the sea and fled in their ships, whereas the rest either perished or were taken captive.
At Lebadeia is situated an oracle of Trophonian Zeus. The oracle has a descent into the earth consisting of an underground chasm; and the person who consults the oracle descends into it himself. It is situated between Mt. Helicon and Chaeroneia, near Coroneia.
Leuctra is the place where Epameinondas defeated the Lacedaemonians in a great battle and found a beginning of his overthrow of them; for after that time they were never again able to regain the hegemony of the Greeks which they formerly held, and especially because they also fared badly in the second clash near Mantineia. However, although they had suffered such reverses, they continued to avoid being subject to others until the Roman conquest. And among the Romans, also, they have continued to be held in honour because of the excellence of their government. This place is to be seen on the road that leads from Plataeae to Thespiae.
Next the poet gives the catalogue of the Orchomenians, whom he separates from the Boeotian tribe. He calls Orchomenus "Minyeian," after the tribe of the Minyae. They say that some of the Minyae emigrated from there to Iolcus, and that from this fact the Argonauts were called Minyae. Clearly it was in early times both a rich and very powerful city. Now to its wealth Homer also is a witness, for when enumerating the places that abounded in wealth he says: "Nor yet all that comes to Orchomenus nor all that comes to Egyptian Thebes." And of its power there is this proof, that the Thebans were wont to pay tribute to the Orchomenians and to Erginus their tyrant, who is said to have been put to death by Heracles. Eteocles, one of those who reigned as king at Orchomenus, who founded a temple of the Graces, was the first to display both wealth and power; for he honoured these goddesses either because he was successful in receiving graces, or in giving them, or both. For necessarily, when he had become naturally inclined to kindly deeds, he began doing honour to these goddesses; and therefore he already possessed this power; but in addition he also had to have money, for neither could anyone give much if he did not have much, nor could anyone have much if he did not receive much. But if he has both together, he has the reciprocal giving and receiving; for the vessel that is at the same time being emptied and filled is always full for use; but he who gives and does not receive could not succeed in either, for he will stop giving because his treasury fails; also the givers will stop giving to him who receives only and grants no favours; and therefore he could not succeed in either way. And like things might be said concerning power. Apart from the common saying, "money is the most valuable thing to men, and it has the most power of all things among men," we should look into the subject in detail. We say that kings have the greatest power; and on this account we call them potentates. They are potent in leading the multitudes whither they wish, through persuasion or force. Generally they persuade through kindness, for persuasion through words is not kingly; indeed, this belongs to the orator, whereas we call it kingly persuasion when kings win and attract men whither they wish by kindly deeds. They persuade men, it is true, through kindly deeds, but they force them by means of arms. Both these things may be bought with money; for he has the largest army who is able to support the largest, and he who possesses the most means is also able to show the most kindness.
They say that the place now occupied by Lake Copais was formerly dry ground, and that it was tilled in all kinds of ways when it was subject to the Orchomenians, who lived near it. And this fact, accordingly, is adduced as an evidence of their wealth.
Aspledon was by some called Spledon, without the first syllable. Then the name, both of it and of the country, was changed to Eudeielos, perhaps because, from its "evening" inclination, it offered a special advantage peculiar to its inhabitants, especially the mildness of its winters; for the two ends of the day are coldest; and of these the evening is colder than the morning, for as night approaches the cold is more intense, and as night retires it abates. But the sun is a means of mitigating the cold. The place, therefore, that is warmed most by the sun at the coldest time is mildest in winter. Eudeielos is twenty stadia distant from Orchomenus. And the River Melas is between them.
Above the Orchomenian territory lies Panopeus, a Phocian city, and also Hyampolis. And bordering on these is Opus, the metropolis of the Epicnemidian Locrians. Now in earlier times Orchomenus was situated on a plain, they say, but when the waters overflowed, the inhabitants migrated up to the mountain Acontius, which extends for a distance of sixty stadia to Parapotamii in Phocis. And they relate that the Achaeans in Pontus, as they are called, are a colony of Orchomenians who wandered there with Ialmenus after the capture of Troy. There was also an Orchomenus in the neighbourhood of Carystus. Those who have written concerning the Ships have supplied us well with such materials, and are the writers we follow when they say things appropriate to the purpose of our work. |
|
|
|






|
9 - 3 Phocis 
1 After Boeotia and Orchomenus one comes to Phocis; it stretches towards the north alongside Boeotia, nearly from sea to sea; it did so in early times, at least, for in those times Daphnus belonged to Phocis, splitting Locris into two parts and being placed by geographers midway between the Opuntian Gulf and the coast of the Epicnemidians. The country now belongs to the Locrians (the town has been rased to the ground), so that even here Phocis no longer extends as far as the Euboean Sea, though it does border on the Crisaean Gulf. For Crisa itself belongs to Phocis, being situated by the sea itself, and so do Cirrha and Anticyra and the places which lie in the interior and contiguous to them near Parnassus — I mean Delphi, Cirphis, and Daulis — and Parnassus itself which belongs to Phocis and forms its boundary on its western side. In the same way as Phocis lies alongside Boeotia, so also Locris lies alongside Phocis on either side; for Locris is double, being divided into two parts by Parnassus, the part on the western side lying alongside Parnassus and occupying a part of it, and extending to the Crisaean Gulf, whereas the part on the side towards the east ends at the Euboean Sea. The Westerners are called Locrians and Ozolae; and they have the star Hesperus engraved on their public seal. The other division of inhabitants is itself also divided, in a way, into two parts: the Opuntians, named after their metropolis, whose territory borders on Phocis and Boeotia, and the Epicnemidians, named after a mountain called Cnemis, who are next to the Oetaeans and Malians. In the middle between both, I mean the Westerners and the other division, is Parnassus, extending lengthwise into the northerly part of the country, from the region of Delphi as far as the junction of the Oetaean and the Aetolian mountains, and the country of the Dorians which lies in the middle between them. For again, just as Locris, being double, lies alongside Phocis, so also the country of the Oetaeans together with Aetolia and with certain places of the Dorian Tetrapolis, which lie in the middle between them, lie alongside either part of Locris and alongside Parnassus and the country of the Dorians. Immediately above these are the Thessalians, the northerly Aetolians, the Acarnanians, and some of the Epeirote and Macedonian tribes. As I was saying before, one should think of the aforementioned countries as ribbon-like stretches, so to speak, extending parallel to one another from the west towards the east. The whole of Parnassus is esteemed as sacred, since it has caves and other places that are held in honour and deemed holy. Of these the best known and most beautiful is Corycium, a cave of the nymphs bearing the same name as that in Cilicia. Of the sides of Parnassus, the western is occupied by the Ozolian Locrians and by some of the Dorians and by the Aetolians who live near the Aetolian mountain called Corax; whereas the other side is occupied by Phocians and by the majority of the Dorians, who occupy the Tetrapolis, which in a general way lies round Parnassus, but widens out in its parts that face the east. Now the long sides of each of the aforementioned countries and ribbon-like stretches are all parallel, one side being towards the north and the other towards the south; but as for the remaining sides, the western are not parallel to the eastern; neither are the two coastlines, where the countries of these tribes end, I mean that of the Crisaean Gulf as far as Actium and that facing Euboea as far as Thessaloniceia, parallel to one another. But one should conceive of the geometrical figures of these regions as though several lines were drawn in a triangle parallel to the base, for the figures thus marked off will be parallel to one another, and they will have their opposite long sides parallel, but as for the short sides this is no longer the case. This, then, is my rough sketch of the country that remains to be traversed and is next in order. Let me now describe each separate part in order, beginning with Phocis.
2 Of Phocis two cities are the most famous, Delphi and Elateia. Delphi, because of the temple of the Pythian Apollo, and because of the oracle, which is ancient, since Agamemnon is said by the poet to have had an oracle given him from there; for the minstrel is introduced as singing "the quarrel of Odysseus and Achilles, son of Peleus, how once they strove . . . , and Agamemnon, lord of men, rejoiced at heart . . . , for thus Phoebus Apollo, in giving response to him at Pytho, had told him that it should be." Delphi, I say, is famous because of these things, but Elateia, because it is the largest of all the cities there, and has the most advantageous position, because it is situated in the narrow passes and because he who holds this city holds the passes leading into Phocis and Boeotia. For, first, there are the Oetaean Mountains; and then those of the Locrians and Phocians, which are not everywhere passable to invaders from Thessaly, but have passes, both narrow and separated from one another, which are guarded by the adjacent cities; and the result is, that when these cities are captured, their captors master the passes also. But since the fame of the temple at Delphi has the priority of age, and since at the same time the position of its places suggests a natural beginning (for these are the most westerly parts of Phocis), I should begin my description there.
3 As I have already said, Parnassus is situated on the western boundaries of Phocis. Of this mountain, then, the side towards the west is occupied by the Ozolian Locrians, whereas the southern is occupied by Delphi, a rocky place, theatre-like, having the oracle and the city on its summit, and filling a circuit of sixteen stadia. Situated above Delphi is Lycoreia, on which place, above the temple, the Delphians were established in earlier times. But now they live close to the temple, round the Castalian fountain. Situated in front of the city, toward the south, is Cirphis, a precipitous mountain, which leaves in the intervening space a ravine, through which flows the Pleistus River. Below Cirphis lies Cirrha, an ancient city, situated by the sea; and from it there is an ascent to Delphi of about eighty stadia. It is situated opposite Sicyon. In front of Cirrha lies the fertile Crisaean Plain; for again one comes next in order to another city, Crisa, from which the Crisaean Gulf is named. Then to Anticyra, bearing the same name as the city on the Maliac Gulf near Oeta. And, in truth, they say that it is in the latter region that the hellebore of fine quality is produced, though that produced in the former is better prepared, and on this account many people resort thither to be purged and cured; for in the Phocian Anticyra, they add, grows a sesame-like medicinal plant with which the Oetaean hellebore is prepared.
4 Now Anticyra still endures, but Cirrha and Crisa have been destroyed, the former earlier, by the Crisaeans, and Crisa itself later, by Eurylochus the Thessalian, at the time of the Crisaean War. For the Crisaeans, already prosperous because of the duties levied on importations from Sicily and Italy, proceeded to impose harsh taxes on those who came to visit the temple, even contrary to the decrees of the Amphictyons. And the same thing also happened in the case of the Amphissians, who belonged to the Ozolian Locrians. For these too, coming over, not only restored Crisa and proceeded to put under cultivation again the plain which had been consecrated by the Amphictyons, but were worse in their dealings with foreigners than the Crisaeans of old had been. Accordingly, the Amphictyons punished these too, and gave the territory back to the god. The temple, too, has been much neglected, though in earlier times it was held in exceedingly great honour. Clear proofs of this are the treasure-houses, built both by peoples and by potentates, in which they deposited not only money which they had dedicated to the god, but also works of the best artists; and also the Pythian Games, and the great number of the recorded oracles.
5 They say that the seat of the oracle is a cave that is hollowed out deep down in the earth, with a rather narrow mouth, from which arises breath that inspires a divine frenzy; and that over the mouth is placed a high tripod, mounting which the Pythian priestess receives the breath and then utters oracles in both verse and prose, though the latter too are put into verse by poets who are in the service of the temple. They say that the first to become Pythian priestess was Phemonoê; and that both the prophetess and the city were so called from the word pythésthai," though the first syllable was lengthened, as in āthanatos, ākamatos, and diākonos. Now the following is the idea which leads to the founding of cities and to the holding of common sanctuaries in high esteem: men came together by cities and by tribes, because they naturally tend to hold things in common, and at the same time because of their need of one another; and they met at the sacred places that were common to them for the same reasons, holding festivals and general assemblies; for everything of this kind tends to friendship, beginning with eating at the same table, drinking libations together, and lodging under the same roof; and the greater the number of the sojourners and the greater the number of the places whence they came, the greater was thought to be the use of their coming together.
6 Now although the greatest share of honour was paid to this temple because of its oracle, since of all oracles in the world it had the repute of being the most truthful, yet the position of the place added something. For it is almost in the centre of Greece taken as a whole, between the country inside the Isthmus and that outside it; and it was also believed to be in the centre of the inhabited world, and people called it the navel of the earth, in addition fabricating a myth, which is told by Pindar, that the two eagles (some say crows) which had been set free by Zeus met there, one coming from the west and the other from the east. There is also a kind of navel to be seen in the temple; it is draped with fillets, and on it are the two likenesses of the birds of the myth.
7 Such being the advantages of the site of Delphi, the people easily came together there, and especially those who lived near it. And indeed the Amphictyonic League was organised from the latter, both to deliberate concerning common affairs and to keep the superintendence of the temple more in common, because much money and many votive offerings were deposited there, requiring great vigilance and holiness. Now the facts of olden times are unknown, but among the names recorded Acrisius is reputed to have been the first to administer the Amphictyony and to determine the cities that were to have a part in the council and to give a vote to each city, to one city separately or to another jointly with a second or with several, and also to proclaim the Amphictyonic Rights — all the rights that cities have in their dealings with cities. Later there were several other administrations, until this organisation, like that of the Achaeans, was dissolved. Now the first cities which came together are said to have been twelve, and each sent a Pylagoras, the assembly convening twice a year, in spring and in late autumn; but later still more cities were added. They called the assembly Pylaea, both that of spring and that of late autumn, since they convened at Pylae, which is also called Thermopylae; and the Pylagorae sacrificed to Demeter. Now although at the outset only the people who lived near by had a share both in these things and in the oracle, later the people living at a distance also came and consulted the oracle and sent gifts and built treasure-houses, as, for instance, Croesus, and his father Alyattes, and some of the Italiotes, and the Sicilians.
8 But wealth inspires envy, and is therefore difficult to guard, even if it is sacred. At present, certainly, the temple at Delphi is very poor, at least so far as money is concerned; but as for the votive offerings, although some of them have been carried off, most of them still remain. In earlier times the temple was very wealthy, as Homer states: "nor yet all the things which the stone threshold of the archer Phoebus Apollo enclosed in rocky Pytho." The treasure-houses clearly indicate its wealth, and also the plundering done by the Phocians, which kindled the Phocian War, or Sacred War, as it is called. Now this plundering took place in the time of Philip, the son of Amyntas, although writers have a notion of another and earlier plundering, in ancient times, in which the wealth mentioned by Homer was carried out of the temple. For, they add, not so much as a trace of it was saved down to those later times in which Onomarchus and his army, and Phaÿllus and his army, robbed the temple; but the wealth then carried away was more recent than that mentioned by Homer; for there were deposited in treasure-houses offerings dedicated from spoils of war, preserving inscriptions on which were included the names of those who dedicated them; for instance, Gyges, Croesus, the Sybarites, and the Spinetae who lived near the Adriatic, and so with the rest. And it would not be reasonable to suppose that the treasures of olden times were mixed up with these, as indeed is clearly indicated by other places that were ransacked by these men. Some, however, taking "aphetor" to mean "treasure-house," and "threshold of the aphetor" to mean "underground repository of the treasure-house," say that that wealth was buried in the temple, and that Onomarchus and his army attempted to dig it up by night, but since great earthquakes took place they fled outside the temple and stopped their digging, and that their experience inspired all others with fear of making a similar attempt.
9 Of the temples, the one "with wings" must be placed among the myths; the second is said to be the work of Trophonius and Agamedes; and the present temple was built by the Amphictyons. In the sacred precinct is to be seen the tomb of Neoptolemus, which was made in accordance with an oracle, Machaereus, a Delphian, having slain him because, according to the myth, he was asking the god for redress for the murder of his father; but according to all probability it was because he had attacked the temple. Branchus, who presided over the temple at Didyma, is called a descendant of Machaereus.
As for the contests at Delphi, there was one in early times between citharoedes, who sang a paean in honour of the god; it was instituted by the Delphians. But after the Crisaean war, in the time of Eurylochus, the Amphictyons instituted equestrian and gymnastic contests in which the prize was a crown, and called them Pythian Games. And to the citharoedes they added both flute-players and citharists who played without singing, who were to render a certain melody which is called the Pythian Nome. There are five parts of it: angkrousis, ampeira, katakeleusmos, iambi and dactyli, and syringes. Now the melody was composed by Timosthenes, the admiral of the second Ptolemy, who also compiled The Harbours, a work in ten books; and through this melody he means to celebrate the contest between Apollo and the dragon, setting forth the prelude as anakrousis, the first onset of the contest as ampeira, the contest itself as katakeleusmos, the triumph following the victory as iambus and dactylus, the rhythms being in two measures, one of which, the dactyl, is appropriate to hymns of praise, whereas the other, the iamb, is suited to reproaches (compare the word "iambize"), and the expiration of the dragon as syringes, since with syringes players imitated the dragon as breathing its last in hissings.
Ephorus, whom I am using more than any other authority because, as Polybius, a noteworthy writer, testifies, he exercises great care in such matters, seems to me sometimes to do the opposite of what he intended, and at the outset promised, to do. At any rate, after censuring those who love to insert myths in the text of their histories, and after praising the truth, he adds to his account of this oracle a kind of solemn promise, saying that he regards the truth as best in all cases, but particularly on this subject; for it is absurd, he says, if we always follow such a method in dealing with every other subject, and yet, when speaking of the oracle which is the most truthful of all, go on to use the accounts that are so untrustworthy and false. Yet, though he says this, he adds forthwith that historians take it for granted that Apollo, with Themis, devised the oracle because he wished to help our race; and then, speaking of the helpfulness of it, he says that Apollo challenged men to gentleness and inculcated self control by giving out oracles to some, commanding them to do certain things and forbidding them to do other things, and by absolutely refusing admittance to other consultants. Men believe that Apollo directs all this, he says, some believing that the god himself assumes a bodily form, others that he transmits to human beings a knowledge of his own will.
A little further on, when discussing who the Delphians were, he says that in olden times certain Parnassians who were called indigenous inhabited Parnassus; and that at this time Apollo, visiting the land, civilised the people by introducing cultivated fruits and cultured modes of life; and that when he set out from Athens to Delphi he went by the road which the Athenians now take when they conduct the Pythias; and that when he arrived at the land of the Panopaeans he destroyed Tityus, a violent and lawless man who ruled there; and that the Parnassians joined him and informed him of another cruel man named Python and known as the Dragon, and that when Apollo shot at him with his arrows the Parnassians shouted "Hie Paean" to encourage him (the origin, Ephorus adds, of the singing of the Paean which has been handed down as a custom for armies just before the clash of battle); and that the tent of Python was burnt by the Delphians at that time, just as they still burn it to this day in remembrance of what took place at that time. But what could be more mythical than Apollo shooting with arrows and punishing Tityuses and Pythons, and travelling from Athens to Delphi and visiting the whole earth? But if Ephorus did not take these stories for myths, by what right did he call the mythological Themis a woman, and the mythological Dragon a human being — unless he wished to confound the two types, history and myth? Similar to these statements are also those concerning the Aetolians; for after saying that from all time their country had been unravaged, he at one time says that Aeolians took up their abode there, having ejected the barbarians who were in possession of it, and at another time that Aetolus together with the Epeii from Elis took up their abode there, but that these were destroyed by the Aeolians, and that these latter were destroyed by Alcmaeon and Diomedes. But I return to the Phocians.
On the sea-coast after Anticyra, one comes first to a town called Opisthomarathus; then to a cape called Pharygium, where there is an anchoring-place; then to the harbour that is last, which, from the fact in the case, is called Mychus; and it lies below Helicon and Ascrê. And the oracle of Abae is not far from this region, nor Ambrysus, nor Medeon, which bears the same name as the Boeotian Medeon. Still farther in the interior, after Delphi, approximately towards the east, is a town Daulis, where Tereus the Thracian is said to have held sway (the scene of the mythical story of Philomela and Procnê is laid there, though Thucydides says at Megara). The place got its name from the thickets, for they call thickets "dauli." Now Homer called it Daulis, but later writers call it Daulia. And "Cyparissus," in the words "held Cyparissus," is interpreted by writers in two ways, by some as bearing the same name as the tree, and by others, by a slight change in the spelling, as a village below Lycoreia.
Panopeus, the Phanoteus of to‑day, borders on the region of Lebadeia, and is the native land of Epeius. And the scene of the myth of Tityus is laid here. Homer says that the Phaeacians "led" Rhadamanthys into Euboea "to see Tityus, son of the Earth." And a cave called Elarium is to be seen in the island, named after Elara the mother of Tityus; and also a hero-temple of Tityus, and certain honours which are paid to him. Near Lebadeia, also, is Trachin, a Phocian town, which bears the same name as the Oetaean city; and its inhabitants are called Trachinians.
Anemoreia has been named from a circumstance connected with it: squalls of wind sweep down upon it from Catopterius, as it is called, a beetling cliff extending from Parnassus. This place was a boundary between Delphi and the Phocians when the Lacedaemonians caused the Delphians to revolt from the common organisation of the Phocians, and permitted them to form a separate State of their own. Some, however, call the place Anemoleia. And then one comes to Hyampolis (later called Hya by some), to which, as I have said, the Hyantes were banished from Boeotia. This city is very far inland, near Parapotamii, and is not the same as Hyampeia on Parnassus; also far inland is Elateia, the largest city of the Phocians, which is unknown by Homer, for it is more recent than the Homeric age, and it is advantageously situated in that it commands the passes from Thessaly. Demosthenes clearly indicates the natural advantage of its position when he speaks of the commotion that suddenly took place at Athens when a messenger came to the Prytanes with the report that Elateia had been captured.
Parapotamii is a settlement on the Cephissus River near Phanoteus and Chaeroneia and Elateia. Theopompus says that this place is distant from Chaeroneia about forty stadia and marks the boundary of the territories of the Ambryseans, the Panopeans and the Daulians; and that it lies on a moderately high hill at the pass which leads from Boeotia into Phocis, between the mountains Parnassus and Hadylius, between which is left a tract of about five stadia divided by the Cephissus River, which affords a narrow pass on each side. The river, he continues, has its beginnings in the Phocian city Lilaea (just as Homer says, "and those who held Lilaea, at the fountains of Cephissus") and empties into Lake Copais; and the mountain Hadylius extends over a distance of sixty stadia as far as the mountain Acontius, where Orchomenus is situated. And Hesiod, too, describes at considerable length the river and the course of its flow, saying that it flows through the whole of Phocis in a winding and serpentine course; "like a dragon it goes in tortuous courses out past Panopeus and through strong Glechon and through Orchomenus." The narrow pass in the neighbourhood of Parapotamii, or Parapotamia (for the name is spelled both ways), was an object of contention in the Phocian war, since the enemy had here their only entrance into Phocis. There are, besides the Phocian Cephissus, the one at Athens, the one in Salamis, a fourth and a fifth in Sicyon and in Scyros, and a sixth in Argos, which has its sources in Mt. Lyrceius; and at Apollonia near Epidamnus there is a fountain near the gymnasium which is called Cephissus.
Daphnus is now rased to the ground. It was at one time a city of Phocis, bordering on the Euboean Sea; it divided the Epicnemidian Locrians into two parts, one part in the direction of Boeotia, and the other facing Phocis, which at that time reached from sea to sea. And evidence of this is the Schedieium in Daphnus, which, they say, is the tomb of Schedius; but as I have said, Daphnus "split" Locris on either side, so that the Epicnemidian and Opuntian Locrians nowhere bordered on one another; but in later times the place was included within the boundaries of the Opuntians. Concerning Phocis, however, I have said enough. |
|
|
|
|
9 - 4 Locris 
1 Locris comes next in order, and therefore I must describe this country. It is divided into two parts: one part is that which is inhabited by the Locrians and faces Euboea; and, as I was saying, it was once split into two parts, one on either side of Daphnus. The Opuntians were named after their metropolis, and the Epicnemidians after a mountain called Cnemis. The rest of Locris is inhabited by the Western Locrians, who are also called Ozolian Locrians. They are separated from the Opuntians and the Epicnemidians by Parnassus, which is situated between them, and by the Tetrapolis of the Dorians. But I must begin with the Opuntians.
2 Next, then, after Halae, where that part of the Boeotian coast which faces Euboea terminates, lies the Opuntian Gulf. Opus is the metropolis, as is clearly indicated by the inscription on the first of the five pillars in the neighbourhood of Thermopylae, near the Polyandrium: "Opoëis,º metropolis of the Locrians of righteous laws, mourns for these who perished in defence of Greece against the Medes." It is about fifteen stadia distant from the sea, and sixty from the sea-port. Cynus is the sea-port, a cape which forms the end of the Opuntian Gulf, the gulf being about forty stadia in extent. Between Opus and Cynus is a fertile plain; and Cynus lies opposite Aedepsus in Euboea, where are the hot waters of Heracles, and is separated from it by a strait one hundred and sixty stadia wide. Deucalion is said to have lived in Cynus; and the grave of Pyrrha is to be seen there, though that of Deucalion is to be seen at Athens. Cynus is about fifty stadia distant from Mount Cnemis. The island Atalanta is also situated opposite Opus, and bears the same name as the island in front of Attica. It is said that a certain people in Eleia are also called Opuntians, but it is not worth while to mention them, except to say that they are reviving a kinship which exists between them and the Opuntians. Now Homer says that Patroclus was from Opus, and that after committing an involuntary murder he fled to Peleus, but that his father Menoetius remained in his native land; for thither Achilles says that he promised Menoetius to bring back Patroclus when Patroclus should return from the expedition. However, Menoetius was not king of the Opuntians, but Aias the Locrian, whose native land, as they say, was Narycus. They call the man who was slain by Patroclus "Aeanes"; and both a sacred precinct, the Aeaneium, and a spring, Aeanis, named after him, are to be seen.
3 Next after Cynus, one comes to Alopê and to Daphnus, which latter, as I said, is rased to the ground; and here there is a harbour which is about ninety stadia distant from Cynus, and one hundred and twenty stadia from Elateia, for one going on foot into the interior. We have now reached the Maliac Gulf, which is continuous with the Opuntian Gulf.
4 After Daphnus one comes to Cnemides, a natural stronghold, about twenty stadia by sea; and opposite it, in Euboea, lies Cenaeum, a cape facing the west and the Maliac Gulf, and separated from it by a strait about twenty stadia in width. At this point we have now reached the territory of the Epicnemidian Locrians. Here, too, lying off the coast, are the three Lichades Islands, as they are called, named after Lichas; and there are also other islands along the coast, but I am purposely omitting them. After twenty stadia from Cnemides one comes to a harbour, above which, at an equal distance in the interior, lies Thronium. Then one comes to the Boagrius River, which flows past Thronium and empties into the sea. They also call it Manes. It is a winter stream, so that at times one can cross it dry-shod, though at other times it has a breadth of •two plethra. After this one comes to Scarpheia, which is situated ten stadia above the sea, thirty stadia distant from Thronium, and slightly less from the harbour itself. Then one comes to Nicaea and Thermopylae.
5 As for the remaining cities, it is not worthwhile to mention any of them except those which are mentioned by Homer. Calliarus is no longer inhabited, but is now a beautifully-tilled plain, and they so call it from what is the fact in the case. Bessa, too, does not exist; it is a wooded place. Neither does Augeiae, whose territory is held by the Scarphians. Now this Bessa should be written with a double s (for it is named from its being a wooded place, being spelled the same way — like Napê in the plain of Methymnê, which Hellanicus ignorantly names Lapê), whereas the deme in Attica, whose inhabitants are accordingly called Besaeeis, should be written with one s.
6 Tarphê is situated on a height, at a distance of twenty stadia from Thronium; its territory is both fruitful and well-wooded, for already this place had been named from its being thickly wooded. But it is now called Pharygae; and here is situated a temple of Pharygaean Hera, so called from the Hera in the Argive Pharygae; and, indeed, they say that they are colonists of the Argives.
7 However, Homer does not mention the Western Locrians, or at least not in express words, but only in that he seems by contrast to distinguish these from those other Locrians of whom I have already spoken, when he says, "of the Locrians who dwell opposite sacred Euboea," implying that there was a different set of Locrians. But they have not been much talked about by many others either. The cities they held were Amphissa and Naupactus; of these, Naupactus survives, near Antirrhium, and it was named from the shipbuilding that was once carried on there, whether it was because the Heracleidae built their fleet there, or (as Ephorus says) because the Locrians had built ships there even before that time. It now belongs to the Aetolians, having been adjudged to them by Philip.
8 Here, also, is Chalcis, which the poet mentions in the Aetolian Catalogue; it is below Calydon. Here, also, is the hill Taphiassus, on which are the tombs of Nessus and the other Centaurs, from whose putrefied bodies, they say, flows forth at the base of the hill the water which is malodorous and clotted; and it is on this account, they add, that the tribe is also called Ozolian. Molycreia, an Aetolian town, is also near Antirrhium. The site of Amphissa is on the edge of the Crisaean Plain; it was rased to the ground by the Amphictyons, as I have said. And both Oeantheia and Eupalium belong to the Locrians. The whole voyage along the Locrian coast slightly exceeds two hundred stadia in length.
9 There is a place named Alopê, not only here and among the Epicnemidian Locrians, but also in Phthiotis. Now these are colonists of the Epicnemidian Locrians, but the Epizephyrian Locrians are colonists of these.
The Aetolians border on the western Locrians; and the Aenianians who inhabit Mount Oeta border on the Epicnemidian Locrians; and in the middle between them are Dorians. Now these Dorians are the people who inhabited the Tetrapolis, which, they say, was the metropolis of all the Dorians; and the cities they held were Erineus, Boeum, Pindus and Cytinium. Pindus is situated above Erineus; and a river bearing the same name flows past it, emptying into the Cephissus not very far from Lilaea. By some, however, Pindus is called Acyphas. The king of these Dorians was Aegimius, who was driven from his throne, but was brought back again, as the story goes, by Heracles; accordingly, Aegimius requited the favour to Heracles after the latter's death on Oeta; for he adopted Hyllus, the eldest of the sons of Heracles; and Hyllus and his descendants became his successors on the throne. From here it was that the Heracleidae set out on their return to the Peloponnesus.
Now for a time the cities in question were held in respect, although they were small and had poor soil, but afterwards they were lightly esteemed. During the Phocian War and the domination of the p389Macedonians, Aetolians, and Athamanians — it is marvellous that even a trace of them passed to the Romans. And the Aenianians had the same experience, for they too were destroyed by the Aetolians and the Athamanians: by the Aetolians, when they waged war in conjunction with the Acarnanians, and were very powerful, and by the Athamanians, when they attained to distinction (the last of the Epeirotes to do so, the other peoples having by this time been worn out) and under their king Amynander had acquired power. These Athamanians kept possession of Oeta.
This mountain extends from Thermopylae in the east to the Ambracian Gulf in the west; and, in a way, it cuts at right angles the mountainous country which extends from Parnassus to Pindus and to the barbarians who are situated beyond Pindus. Of this mountain, the part which verges towards Thermopylae is called Oeta; its length is two hundred stadia, and it is rugged and high; but it is highest at Thermopylae, for there it rises into a peak, and ends at the sea in sharp and abrupt precipices, though it leaves a narrow pass for invasions from Thessaly into the country of the Locrians.
Now the pass is called not only "Pylae" and "Narrows," but also "Thermopylae," for there are hot waters near it that are held in honour as sacred to Heracles; and the mountain that lies above it is called Callidromus, but by some the remaining part of the mountain, which extends through Aetolia and Acarnania to the Ambracian Gulf, is also called Callidromus. Near Thermopylae, inside the narrows, are forts — Nicaea, towards the sea of the Locrians, and above it, Teichius and Heracleia, the latter in earlier times having been called Trachin, a settlement of Lacedaemonians. Heracleia is about six stadia distant from the old Trachin. Next one comes to Rhoduntia, a natural stronghold.
These places are rendered difficult of access both by the ruggedness of the country and by the number of streams of water which here form ravines through which they flow. For besides the Spercheius, which flows past Anticyra, there is the Dyras River, which, they say, tried to quench the funeral pyre of Heracles, and also another Melas, which is five stadia distant from Trachin. To the south of Trachin, according to Herodotus, there is a deep gorge through which the Asopus, bearing the same name as the aforesaid Asopus Rivers, empties into the sea outside Pylae after receiving the Phoenix River, which meets it from the south and bears the name of the hero Phoenix, whose tomb is to be seen near it. The distance from the Asopus to Thermopylae is fifteen stadia.
Now at that time these places were at the height of their fame when they held the mastery over the keys of the Narrows, and when there were struggles for the primacy between the peoples outside the Narrows and those inside them; for instance, Philip used to call Chalcis and Corinth "the fetters of Greece," having Macedonia in view as his base of operations; and the men of later times called, not only these, but also the city Demetrias "shackles," for Demetrias commanded the passes round Tempê, since it held both Pelion and Ossa. But later, now that all peoples have been brought into subjection to a single power, everything is free from toll and open to all mankind.
It was at these Narrows that Leonidas and his men, with a few who came from the neighbourhood thereof, held out against all those forces of the Persians, until the barbarians, coming around the mountains through by-paths, cut them down. And to‑day their Polyandrium is to be seen, and pillars, and the oft-quoted inscription on the pillar of the Lacedaemonians, which is as follows: "Stranger, report to the Lacedaemonians that we lie here in obedience to their laws."
There is also a large harbour here, and a temple of Demeter, in which at the time of every Pylaean assembly the Amphictyons performed sacrificial rites. From the harbour to Heracleian Trachin the distance on foot is forty stadia, and by boat to Cenaeum seventy stadia. The Spercheius empties immediately outside Pylae. The distance to Pylae from the Euripus is five hundred and thirty stadia. And whereas Locris ends at Pylae, the parts outside Pylae towards the east and the Maliac Gulf belong to the Thessalians, and the parts towards the west belong to the Aetolians and the Acarnanians. As for the Athamanians, they are now extinct.
Now the largest and most ancient composite part of the Greeks is that of the Thessalians, who have been described partly by Homer and partly by several others. The Aetolians Homer always speaks of under one name, classing cities, not tribes, under them, except the Curetes, who in part should be classified as Aetolians. But I must begin with Thessaly, omitting such things as are very old and mythical and for the most part not agreed upon, as I have already done in all other cases, and telling such things as seem to me appropriate to my purpose. |
|
|
|
|
9 - 5 Thessaly 
1 Thessaly comprises, first, on the sea, the coast which extends from Thermopylae to the outlet of the Peneius River and the extremities of Pelion, and faces the east and the northern extremities of Euboea. The parts that are near Euboea and Thermopylae are held by the Malians and the Achaean Phthiotae, and the parts near Pelion by the Magnetans. Let this side of Thessaly, then, be called the eastern or coastal side. As for the two sides of Thessaly: on one side, beginning at Pelion and the Peneius, Macedonia stretches towards the interior as far as Paeonia and the Epeirote tribes, and on the other side, beginning at Thermopylae, the Oetaean and Aetolian mountains lie parallel to Macedonia, bordering on the country of the Dorians and on Parnassus. Let the former side, which borders on Macedonia, be called the northern side, and the latter the southern side. There remains the western side, which is surrounded by the Aetolians and Acarnanians and Amphilochians, and, of the Epeirotes, the Athamanians and Molossians and what was once called the land of the Aethices, or, in a word, the land about Pindus. The land of Thessaly, as a whole, is a plain, except Pelion and Ossa. These mountains rise to a considerable height; they do not, however, enclose much territory in their circuits, but end in the plains.
2 These plains are the middle parts of Thessaly, a country most blest, except so much of it as is subject to inundations by rivers. For the Peneius, which flows through the middle of it and receives many rivers, often overflows; and in olden times the plain formed a lake, according to report, being hemmed in by mountains on all sides except in the region of the sea-coast; and there too the region was more elevated than the plains. But when a cleft was made by earthquakes at Tempê, as it is now called, and split off Ossa from Olympus, the Peneius poured out through it towards the sea and drained the country in question. But there remains, nevertheless, Lake Nessonis, which is a large lake, and Lake Boebeïs, which is smaller than the former and nearer to the sea-coast.
3 Such being its nature, Thessaly was divided into four parts. One part was called Phthiotis, another Hestiaeotis, another Thessaliotis, and another Pelasgiotis. Phthiotis occupies the southern parts which extend alongside Oeta from the Maliac, or Pylaïc, Gulf as far as Dolopia and Pindus, and widen out as far as Pharsalus and the Thessalian plains. Hestiaeotis occupies the western parts and the parts between Pindus and Upper Macedonia. The remaining parts of Thessaly are held, first, by the people who live in the plains below Hestiaeotis (they are called Pelasgiotae and their country borders on Lower Macedonia), and, secondly, by the Thessaliotae next in order, who fill out the districts extending as far as the Magnetan sea-coast. Here, too, there will be an enumeration of famous names of cities, and especially because of the poetry of Homer; only a few of the cities preserve their ancient dignity, but Larisa most of all.
4 The poet, after dividing into ten parts, or dynasties, the whole of the country which we now call Thessaly, and after adding certain parts both of the Oetaean and the Locrian countries, and likewise certain parts of the country now classed under Macedonia, intimates a fact which is common to, and true of, all countries, that whole regions and their several parts undergo changes in proportion to the power of those who hold sway.
5 Now the first peoples he names in the Catalogue are those under Achilles, who occupied the southern side and were situated alongside Oeta and the Epicnemidian Locrians, "all who dwelt in the Pelasgian Argos and those who inhabited Alus and Alopê and Trachin, and those who held Phthia and also Hellas the land of fair women, and were called Myrmidons and Hellenes and Achaeans." With these he joins also the subjects of Phoenix, and makes the expedition common to both leaders. It is true that the poet nowhere mentions the Dolopian army in connection with the battles round Ilium, for he does not represent their leader Phoenix as going forth into the perils of battle either, any more than he does Nestor; yet others so state, as Pindar, for instance, who mentions Phoenix and then says, "who held a throng of Dolopians, bold in the use of the sling and bringing aid to the missiles of the Danaans, tamers of horses." This, in fact, is the interpretation which we must give to the Homeric passage according to the principle of silence, as the grammarians are wont to call it, for it would be ridiculous if the king Phoenix shared in the expedition ("I dwelt in the farthermost part of Phthia, being lord over the Dolopians") without his subjects being present; for if they were not present, he would not have been regarded as sharing in the expedition with Achilles, but only as following him in the capacity of a chief over a few men and as a speaker, perhaps as a counsellor. Homer's verses on this subject mean also to make this clear, for such is the import of the words, "to be a speaker of words and a doer of deeds." Clearly, therefore, he means, as I have already said, that the forces under Achilles and Phoenix are the same. But the aforesaid statements concerning the places subject to Achilles are themselves under controversy. Some take the Pelasgian Argos as a Thessalian city once situated in the neighbourhood of Larisa but now no longer existent; but others take it, not as a city, but as the plain of the Thessalians, which is referred to by this name because Abas, who brought a colony there from Argos, so named it.
6 As for Phthia, some say that it is the same as Hellas and Achaea, and that these constitute the other, the southern, of the two parts into which Thessaly as a whole was divided; but others distinguish between Hellas and Achaea. The poet seems to make Phthia and Hellas two different things when he says, "and those who held Phthia and Hellas," as though there were two, and when he says, "And then (I fled) far away through spacious Hellas, and I came to Phthia," and, "There are many Achaean women throughout Hellas and Phthia." So the poet makes them two, but he does not make it plain whether they are cities or countries. As for later authorities, some, speaking of Hellas as a country, say that it stretches from Palaepharsalus to Phthiotic Thebes. In this country also is the Thetideium, near both Pharsaluses, both the old and the new; and they infer from the Thetideium that this country too is a part of that which was subject to Achilles. As for those, however, who speak of Hellas as a city, the Pharsalians point out at a distance of sixty stadia from their own city a city in ruins which they believe to be Hellas, and also two springs near it, Messeïs and Hypereia, whereas the Melitaeans say that Hellas was situated about ten stadia distant from themselves on the other side of the Enipeus, at the time when their own city was named Pyrrha, and that it was from Hellas, which was situated in a low-lying district, that the Hellenes migrated to their own city; and they cite as bearing witness to this the tomb of Hellen, son of Deucalion and Pyrrha, situated in their market-place. For it is related that Deucalion ruled over Phthia, and, in a word, over ThessaIy. The Enipeus, flowing from Othrys past Pharsalus, turns aside into the Apidanus, and the latter into the Peneius. Thus much, then, concerning the Hellenes.
7 "Phthians" is the name given to those who were subject to Achilles and Protesilaüs and Philoctetes. And the poet is witness to this, for after mentioning in the Catalogue those who were subject to Achilles "and those who held Phthia," he represents these, in the battle at the ships, as staying behind with Achilles in their ships and as being inactive, but those who were subject to Philoctetes as taking part in the battle, having Medon as "marshal," and those who were subject to Protesilaüs as "marshalled by Podarces." Concerning these, speaking in a general way, he says, "And there the Boeotians and Ionians with trailing tunics, the Locrians and Phthians and illustrious Epeians;" and, in a specific way, "and in front of the Phthians was Medon, and also Podarces steadfast in war. These in their armour, in front of the great-hearted Phthians, were fighting along with the Boeotians in defence of the ships." Perhaps the men with Eurypylus also were called Phthians, since their country indeed bordered on Phthia. Now, however, historians regard as belonging to Magnesia, not only the region round Ormenium, which belonged to the country that was subject to Eurypylus, but also the whole of the country that was subject to Philoctetes; but they regard the country that was subject to Protesilaüs as a part of Phthia, extending from Dolopia and Pindus as far as the Magnetan Sea; whereas the land subject to Peleus and Achilles, beginning at the Trachinian and Oetaean countries, is defined as extending in breadth as far as Antron, the city subject to Protesilaüs, the name of which is now spelled in the plural number. And the Maliac Gulf has about the same length.
8 But as regards Halus and Alopê, historians are thoroughly in doubt, suspecting that the poet does not mean the places so named which now are classed in the Phthiotic domain, but those among the Locrians, since the dominion of Achilles extended thus far, just as it also extended as far as Trachin and the Oetaean country; for there is both a Halus and a Halius on the seaboard of the Locrians, just as there is also an Alopê. Some substitute Halius for Alopê and write as follows: "and those who dwelt in Halus and in Halius and in Trachin." The Phthiotic Halus is situated below the end of Othrys, a mountain situated to the north of Phthiotis, bordering on Mount Typhrestus and the country of the Dolopians, and extending from there to the region of the Maliac Gulf. Halus (either feminine or masculine, for the name is used in both genders) is about sixty stadia distant from Itonus. It was Athamas who founded Halus, but in later times, after it had been wiped out, the Pharsalians colonised the place. It is situated above the Crocian Plain; and the Amphrysus River flows close to its walls. Below the Crocian Plain lies Phthiotic Thebes. Halus is called both Phthiotic and Achaean Halus, and it borders on the country of the Malians, as do also the spurs of Othrys Mountain. And just as the Phylacê, which was subject to Protesilaüs, is in that part of Phthiotis which lies next to the country of the Malians, so also is Halus; it is about one hundred stadia distant from Thebes, and it is midway between Pharsalus and the Phthiotae. However, Philip took it away from the Phthiotae and assigned it to the Pharsalians. And so it comes to pass, as I have said before, that the boundaries and the political organizations of tribes and places are always undergoing changes. So, also, Sophocles speaks of Trachinia as belonging to Phthiotis. And Artemidorus places Halus on the seaboard, as situated outside the Maliac Gulf, indeed, but as belonging to Phthiotis; for proceeding thence in the direction of the Peneius, he places Pteleum after Antron, and then Halus at a distance of one hundred and ten stadia from Pteleum. As for Trachin, I have already described it, and the poet mentions it by name.
9 Since the poet often mentions the Spercheius as a river of this country, and since it has its sources in Typhrestus, the Dryopian mountain which in earlier times was called . . . , and empties near Thermopylae and between it and Lamia, he plainly indicates that both the region inside the Gates, I mean in so far as it belonged to the Maliac Gulf, and the region outside the Gates, were subject to Achilles. The Spercheius is about thirty stadia distant from Lamia, which is situated above a certain plain that extends down to the Maliac Gulf. And he plainly indicates that the Spercheius was a river of this country, not only by the assertion of Achilles that he "fostered the growth of his hair as an offering to Spercheius," but also by the fact that Menesthius, one of his commanders, was called the son of Spercheius and the sister of Achilles. And it is reasonable to suppose that all the people, the subjects of Achilles and Patroclus, who had accompanied Peleus in his flight from Aegina, were called Myrmidons. And all the Phthiotae were called Achaeans.
Historians enumerate the settlements in the Phthiotic domain that was subject to Achilles, and they begin with the Malians. They name several, and among them Phthiotic Thebes, Echinus, Lamia (near which the Lamian War arose between the Macedonians, under Antipater, and the Athenians, and in this war Leosthenes, a general of the Athenians, fell, and also Leonnatus, the comrade of king Alexander), and also Narthacium, Erineus, Coroneia (bearing the same name as the Boeotian city), Melitaea, Thaumaci, Proerna, Pharsalus, Eretria (bearing the same name as the Euboean city), and Paracheloïtae (this, too, bearing the same name as the Aetolian city), for here too, near Lamia, is a river Acheloüs, on whose banks live the Paracheloïtae. This country bordered, in its stretch towards the north, on the country of the most westerly of the Asclepiadae, and on the country of Eurypylus, and also on that of Protesilaüs, these countries inclining towards the east; and in its stretch towards the south, on the Oetaean country, which was divided into fourteen demes, and also Heracleia and Dryopis, Dryopis having at one time been a tetrapolis, like Doris, and regarded as the metropolis of the Dryopians who lived in the Peloponnesus. To the Oetaean country belong also Acyphas, Parasopias, Oeneiadae, and Anticyra, which bears the same name as the city among the Western Locrians. But I am speaking of these divisions of the country, not as having always remained the same, but as having undergone various changes. However, only the most significant divisions are particularly worthy of mention.
As for the Dolopians, the poet himself says clearly enough that they were situated in the farthermost parts of Phthia, and that both these and the Phthiotae were under the same leader, Peleus; for "I dwelt," he says, "in the farthermost part of Phthia, being lord over the Dolopians, whom Peleus gave me." The country borders on Pindus, and on the region round Pindus, most of which belongs to the Thessalians. For both on account of the fame and of the predominance of the Thessalians and the Macedonians, the countries of those Epeirotes who were their nearest neighbours were made, some willingly and the others unwillingly, parts of Thessaly or Macedonia; for instance, the Athamanes, the Aethices, and the Talares were made parts of Thessaly, and the Orestae, the Pelagonians, and the Elimiotae of Macedonia.
The Pindus Mountain is large, having the country of the Macedonians on the north, the Perrhaebian immigrants on the west, the Dolopians on the south, and Hestiaeotis on the east; and this last is a part of Thessaly. The Talares, a Molossian tribe, a branch of those who lived in the neighbourhood of Mount Tomarus, lived on Mount Pindus itself, as did also the Aethices, amongst whom, the poet says, the Centaurs were driven by Peirithoüs; but history now tells us that they are "extinct." The term "extinct" is to be taken in one of two meanings; either the people vanished and their country has become utterly deserted, or else merely their ethnic name no longer exists and their political organization no longer remains what it was. When, therefore, any present political organization that survives from an earlier time is utterly insignificant, I hold that it is not worth mentioning, either itself or the new name it has taken; but when it affords a fair pretext for being mentioned, I must needs give an account of the change.
It remains for me to tell the order of the places on the coast that were subject to Achilles, beginning at Thermopylae; for I have already spoken of the Locrian and the Oetaean countries. Thermopylae, then, is separated from Cenaeum by a strait seventy stadia wide; but, to one sailing along the coast beyond Pylae, it is about ten stadia from the Spercheius; and thence to Phalara twenty stadia; and above Phalara, fifty stadia from the sea, is situated the city of the Lamians; and then next, after sailing a hundred stadia along the coast, one comes to Echinus, which is situated above the sea; and in the interior from the next stretch of coast, twenty stadia distant from it, is Larisa Cremastê (it is also called Larisa Pelasgia).
Then one comes to Myonnesus, a small island; and then to Antron, which was subject to Protesilaüs. So much, then, for the portion that was subject to Achilles. But since the poet, through naming both the leaders and the cities subject to them, has divided Thessaly into numerous well-known parts and arranged in order the whole circuit of it, I, following him again, as above, shall go on to complete the remainder of my geographical description of the country. Now he enumerates next in order after those who were subject to Achilles those who were subject to Protesilaüs; and these are also the people who come next in order after the stretch of coast which was subject to Achilles as far as Antron. Therefore, the territory that was subject to Protesilaüs is in the boundaries of the country that comes next in order, that is, it lies outside the Maliac Gulf, but still inside Phthiotis, though not inside the part of Phthiotis that was subject to Achilles. Now Phylacê is near Phthiotic Thebes, which itself is subject to Protesilaüs. And Halus, also, and Larisa Cremastê, and Demetrium, are subject to him, all being situated to the east of the Othrys Mountain. Demetrium he speaks of as "sacred precinct of Demeter," and calls it "Pyrasus." Pyrasus was a city with a good harbor; at a distance of two stadia it had a sacred precinct and a holy temple, and was twenty stadia distant from Thebes. Thebes is situated above Pyrasus, but the Crocian Plain is situated in the interior back of Thebes near the end of Othrys; and it is through this plain that the Amphrysus flows. Above this river are the Itonus, where is the temple of the Itonian, after which the temple in Boeotia is named, and the Cuarius Rivers. But I have already spoken of this river and of Arnê in my description of Boeotia. These places are in Thessaliotis, one of the four portions of all Thessaly, in which were not only the regions that were subject to Eurypylus, but also Phyllus, where is the temple of Phyllian Apollo, and Ichnae, where the Ichnaean Themis is held in honour. Cierus, also, was tributary to it, and so was the rest of that region as far as Athamania. Near Antron, in the Euboean strait, is a submarine reef called "Ass of Antron"; and then one comes to Pteleum and Halus; and then to the temple of Demeter; and to Pyrasus, which has been rased to the ground; and, above it, to Thebes; and then to Cape Pyrrha, and to two isles near it, one of which is called Pyrrha and the other Deucalion. And it is somewhere here that Phthiotis ends.
Next the poet enumerates the peoples that were subject to Eumelus, that is, the adjacent sea-coast, which from this point on belongs to Magnesia and the land of Pelasgiotis. Now Pherae is at the end of the Pelasgian plains on the side towards Magnesia; and these plains extend as far as Pelion, one hundred and sixty stadia. The seaport of Pherae is Pagasae, which is ninety stadia distant from Pherae and twenty from Iolcus. Iolcus has indeed been rased to the ground from early times, but it was from there that Pelias despatched Jason and the Argo. It was from the construction here of the ship Argo, according to mythology, that the place was called Pagasae, though some believe, more plausibly, that this name was given the place from its fountains, which are both numerous and of abundant flow. Nearby is Aphetae also, so named as being the "apheterium" of the Argonauts. Iolcus is situated above the sea seven stadia from Demetrias. Demetrias, which is on the sea between Nelia and Pagasae, was founded by Demetrius Poliorcetes, who named it after himself, settling in it the inhabitants of the nearby towns, Nelia and Pagasae and Ormenium, and also Rhizus, Sepias, Olizon, Boebê, and Iolcus, which are now villages belonging to Demetrias. Furthermore, for a long time this was both a naval station and a royal residence for the kings of the Macedonians; and it held the mastery over both Tempê and the two mountains, Pelion and Ossa, as I have already said. At present it is reduced in power, but still it surpasses all the cities in Magnesia. Lake Boebeïs is near Pherae, and also borders on the foothills of Pelion and the frontiers of Magnesia; and Boebê is a place situated on the lake. Just as seditions and tyrannies destroyed Iolcus after its power had been greatly increased, so they reduced Pherae also, which had once been raised to greatness by its tyrants and was then destroyed along with them. Near Demetrias flows the Anaurus River; and the adjoining shore is also called Iolcus. Here, too, they used to hold the Pylaic Festal Assembly. Artemidorus places the Pagasitic Gulf in the region subject to Philoctetes, farther away from Demetrias; and he says that the island Cicynethos and a town bearing the same name are in the gulf.
The poet next enumerates the cities subject to Philoctetes. Now Mēthonē is different from the Thracian Mĕthonē, which was rased to the ground by Philip. I have mentioned heretofore the change of the names of these places, and of certain places in the Peloponnesus. And the other places enumerated by the poet are Thaumacia and Olizon and Meliboea, which are on the next stretch of sea-coast. Off the country of the Magnetans lie numerous islands, but the only notable ones are Sciathos, Peparethos, and Icos, and also Halonnesos and Scyros, all having cities of the same name. But Scyros is the most notable, because of the family relation between Lycomedes and Achilles, and of the birth and nurture there of Neoptolemus the son of Achilles. In later times, when Philip had waxed powerful and saw that the Athenians dominated the sea and ruled over the islands, both these and the rest, he caused the islands that were near him to be most famous; for, since he was fighting for the hegemony, he always attacked those places which were close to him, and, just as he added to Macedonia most parts of the Magnetan country and of Thrace and of the rest of the land all round, so he also seized the islands off Magnesia and made those which were previously well-known to nobody objects of contention and hence well-known. Now Scyros is chiefly commended by the place it occupies in the ancient legends, but there are other things which cause it to be widely mentioned, as, for instance, the excellence of the Scyrian goats, and the quarries of the Scyrian variegated marble, which is comparable to the Carystian marble, and to the Docimaean or Synnadic, and to the Hierapolitic. For at Rome are to be seen monolithic columns and great slabs of the variegated marble; and with this marble the city is being adorned both at public and at private expense; and it has caused the quarries of white marble to be of little worth.
However, the poet, after proceeding thus far on the Magnetan sea-coast, returns to Upper Thessaly; for, beginning at Dolopia and Pindus, he recounts the parts that stretch alongside Phthiotis, as far as Lower Thessaly: "And those who held Triccê and rocky Ithomê." These places belong in fact to Histiaeotis, though in earlier times Histiaeotis was called Doris, as they say; but when the Perrhaebians took possession of it, who had already subdued Histiaeotis in Euboea and had forced its inhabitants to migrate to the mainland, they called the country Histiaeotis after these Histiaeans, because of the large number of these people who settled there. They call Histiaeotis and Dolopia Upper Thessaly, which is in a straight line with Upper Macedonia, as is Lower Thessaly with Lower Macedonia. Now Triccê, where is the earliest and most famous temple of Asclepius, borders on the country of the Dolopians and the regions round Pindus. Ithomê, which is called by the same name as the Messenian city, ought not, they say, to be pronounced in this way, but without the first syllable; for thus, they add, it was called in earlier times, though now its name has been changed to Ithomê. It is a stronghold and is in reality a heap of stones; and it is situated between four strongholds, which lie in a square, as it were: Triccê, Metropolis, Pelinnaeum, and Gomphi. But Ithomê belongs to the territory of the Metropolitans. Metropolis in earlier times was a joint settlement composed of three insignificant towns; but later several others were added to it, among which was Ithomê. Now Callimachus, in his Iambics, says that, "of all the Aphroditês (for there was not merely one goddess of this name), Aphroditê Castnietis surpasses all in wisdom, since she alone accepts the sacrifice of swine." And surely he was very learned, if any other man was, and all his life, as he himself states, wished to recount these things. But the writers of later times have discovered that not merely one Aphroditê, but several, have accepted this rite; and that among these was the Aphroditê at Metropolis, and that one of the cities included in the settlement transmitted to it the Onthurian rite. Pharcadon, also, is in Histiaeotis; and the Peneius and the Curalius flow through its territory. Of these rivers, the Curalius flows past the temple of the Itonian Athena and empties into the Peneius; but the Peneius itself rises in Pindus, as I have already said, and after leaving Triccê and Pelinnaeum and Pharcadon on the left flows past both Atrax and Larisa, and after receiving the rivers in Thessaliotis flows on through Tempê to its outlet. Historians place the Oechalia which is called the "city of Eurytus"2not only in this region, but also in Euboea and in Arcadia; and they give its name in different ways, as I have already said in my description of the Peloponnesus. They inquire concerning these, and particularly in regard to what Oechalia it was that was captured by Heracles, and concerning what Oechalia was meant by the poet who wrote The Capture of Oechalia These places, then, were classed by Homer as subject to the Asclepiadae.
Next he speaks of the country subject to Eurypylus: "and those who held the fountain Hypereia, and those who held Asterium and the white summits of Titanus." Now at the present time Ormenium is called Orminium; it is a village situated at the foot of Pelion near the Pagasitic Gulf, one of the cities included in the settlement of Demetrias, as I have said. And Lake Boebeïs, also, must be near, since Boebê, as well as Ormenium itself, was one of the dependencies of Demetrias. Now Ormenium is distant by land twenty-seven stadia from Demetrias, whereas the site of Iolcus, which is situated on the road, is distant seven stadia from Demetrias and the remaining twenty stadia from Ormenium. The Scepsian says that Phoenix was from Ormenium, and that he fled thence from his father Amyntor the son of Ormenus into Phthia to Peleus the king; for this place, he adds, was founded by Ormenus the son of Cercaphus the son of Aeolus; and he says that both Amyntor and Euaemon were sons of Ormenus, and that Phoenix was son of the former and Eurypylus of the latter, but that the succession to the throne, to which both had equal right, was kept for Eurypylus, inasmuch as Phoenix had gone away from his homeland. Furthermore, the Scepsian writes thus, "as when first I left Ormenium rich in flocks," instead of "I left Hellas, land of fair women." But Crates makes Phoenix a Phocian, judging this from the helmet of Meges, which Odysseus used at the time of his night spying, concerning which the poet says, "Autolycus filched it from Eleon, from Amyntor the son of Ormenus, having broken into his close-built home." For Eleon, he says, is a town of Parnassus; and Amyntor, son of Ormenus, means no other than the father of Phoenix; and Autolycus, who lived on Parnassus, must have broken into the house of a neighbour (as is the way of any housebreaker), and not into that of people far away. But the Scepsian says that there is no place called Eleon to be seen on Parnassus, though there is a place called Neon, founded in fact after the Trojan War, and also that housebreakings are not confined to neighbours only. And there are other arguments which one might give, but I hesitate to spend further time on this subject. Others write "from Heleon," but Heleon is a place in Tanagria, and this reading would increase the absurdity of the statement, "Then I fled afar off through Hellas and came to Phthia." The fountain Hypereia is in the middle of the city of the Pheraeans, which belonged to Eumelus. It is absurd, therefore, to assign the fountain to Eurypylus. Titanus was named from the fact in the case there; for the region near Arnê and Aphetae has white soil. Asterium, also, is not far from these.
Continuous with this portion of Thessaly is the country of those who are called the subjects of Polypoetes: "And those who held Argissa and dwelt in Gyrtonê, Orthê, and Elonê and the white city Oloosson." In earlier times the Perrhaebians inhabited this country, dwelling in the part near the sea and near the Peneius, extending as far as its outlet and Gyrton, a Perrhaebian city. Then the Lapiths humbled the Perrhaebians and thrust them back into the river-country in the interior, and seized their country — I mean the Lapiths Ixion and his son Peirithoüs, the latter of whom also took possession of Pelion, forcing out the Centaurs, a wild folk, who had seized it. Now these "he thrust from Pelion and made them draw near to the Aethices," and he gave over the plains to the Lapiths, though the Perrhaebians kept possession of some of them, those near Olympus, and also in some places lived completely intermingled with the Lapiths. Now Argissa, the present Argura, is situated on the Peneius; and forty stadia above it lies Atrax, which also is close to the river; and the Perrhaebians held the river country between the two places. Some have called Orthê the acropolis of the Phalannaeans; and Phalanna is a Perrhaebian city close to the Peneius near Tempê. Now the Perrhaebians, being overpowered by the Lapiths, for the most part emigrated to the mountainous country about Pindus and to the countries of the Athamanians and Dolopians, but their country and all Perrhaebians who were left behind there were seized by the Larisaeans, who lived near the Peneius and were their neighbours and dwelt in the most fertile parts of the plains, though not in the very low region near the lake called Nessonis, into which the river, when it overflowed, would carry away a portion of the arable soil belonging to the Larisaeans. Later, however, they corrected this by means of embankments. The Larisaeans, then, kept possession of Perrhaebia and exacted tribute until Philip established himself as lord over the region. Larisa is also the name of a place on Ossa; another is Larisa Cremastê, by some called Pelasgia; and in Crete is a city Larisa, now joined to Hierapytna, whence the plain that lies below is now called Larisian Plain; and, in the Peloponnesus both Larisa, the citadel of the Argives, and the Larisus River, which is the boundary between the Eleian country and Dymê. Theopompus speaks of another city Larisa situated on the same common boundary; and in Asia is a Larisa Phryconis near Cymê; and also the Larisa near Hamaxitis in the Troad; and there is the Ephesian Larisa, and the Larisa in Syria; and there are Larisaean Rocks fifty stadia from Mitylene on the road to Methymnê; and there is a Larisa in Attica; and a village Larisa thirty stadia distant from Tralleis, above the city, on the road which runs through Mesogis towards the Caÿster Plain near the temple of the Isodromian Mother, which in its topographical position and its goodly attributes is like Larisa Cremastê, for it has an abundance of water and of vineyards; and perhaps the Larisaean Zeus received his epithet from this place; and also on the left of the Pontus is a village called Larisa, between Naulochus and . . . , near the end of Mount Haemus. And Oloosson, called "white" from the fact that its soil is a white clay, and Elonê, and Gonnus are Perrhaebian cities. But Elonê changed its name to Leimonê, and is now in ruins. Both are situated below Olympus, not very far from the Europus River, which the poet calls the Titaresius.
The poet next mentions both Titaresius and the Perrhaebians, when he says, "And Guneus led from Cyphus twenty-two ships. And there followed him the Enienians, and the Perrhaebians steadfast in war, who had established their homes round wintry Dodona, and dwelt in the fields about lovely Titaresius." Now he speaks of these places as belonging to the Perrhaebians, places which fell into their possession as a part of Hestiaeotis. And also the cities subject to Polypoetes were in part Perrhaebian. However, he assigned them to the Lapiths because the two peoples lived intermingled with one another, and also because, although the Lapiths held possession of the plains and the Perrhaebian element there were for the most part subject to the Lapiths, the Perrhaebians held possession of the more mountainous parts near Olympus and Tempê, as, for example, Cyphus, and Dodona, and the region about the Titaresius; this river rises in the Titarius Mountain, which connects with Olympus, and flows into the territory of Perrhaebia which is near Tempê, and somewhere in that neighbourhood unites with the Peneius. Now the water of the Peneius is pure, but that of the Titaresius is oily, because of some substance or other, so that it does not mingle with that of the Peneius, "but runs over it on the top like oil." Because of the fact that the two peoples lived intermingled, Simonides uses the terms Perrhaebians and Lapiths of all the Pelasgiotes who occupy the region about Gyrton and the outlets of the Peneius and Mount Ossa and Mount Pelion, and the region about Demetrias, and the region in the plain, I mean Larisa, Crannon, Scotussa, Mopsium, Atrax, and the region about Lake Nessonis and Lake Boebeïs. Of these places the poet mentions only a few, because the rest of them had not yet been settled, or else were only wretched settlements, on account of the inundations which took place at various times. Indeed, he does not mention Lake Nessonis either, but Lake Boebeïs only (though it is much smaller), because the latter alone persisted, whereas the former, in all probability, was at times filled at irregular intervals and at times gave out altogether. Scotussa I have already mentioned in my account of Dodona and of the oracle in Thessaly, saying that originally it was near this place. In the territory of Scotussa there is a place called Cynoscephalae, near which Titus Quintius and the Romans, along with the Aetolians, in a great battle conquered Philip the son of Demetrius, king of the Macedonians.
Magnetis, also, has been treated by Homer in about the same way. For although he has already enumerated many of the places in Magnetis, none of these are called Magnetan by him except those two places, and even these are designated by him in a dim and indistinct way: "who dwelt about Peneius and Pelion with its shaking foliage." Assuredly, however, about the Peneius and Pelion lived those who held Gyrton, whom he had already named, as also those who held Ormenium, and several other Perrhaebian peoples; and yet farther away from Pelion there were still Magnetans, beginning with those subject to Eumelus, at least according to the writers of later times. These writers, however, on account of the continual migrations, changes of political administrations, and intermixture of tribes, seem to have confused both the names and the tribes, so that they sometimes present difficult questions for the writers of to‑day. For example, this has proved true, in the first place, in the case of Crannon and Gyrton; for in earlier times the Gyrtonians were called "Phlegyae," from Phlegyas, the brother of Ixion, and the Crannonians "Ephyri," so that it is a difficult question who can be meant by the poet when he says, "Verily these twain, going forth from Thrace, arm themselves to pursue the Ephyri, or to pursue the great-hearted Phlegyae."
Again, the same thing is true in the case of the Perrhaebians and Aenianians. For Homer connected the two, as living near one another; and in fact we are told by the writers of later times that for a long time the habitation of the Aenianians was in the Dotian Plain. This plain is near the Perrhaebia just mentioned above, and Ossa and Lake Boebeïs; and while it is situated in the middle of Thessaly, yet it is enclosed all round by hills of its own. Concerning this plain Hesiod has spoken thus: "Or as the unwedded virgin who, dwelling on the holy Didyman Hills, in the Dotian Plain, in front of Amyrus, bathed her foot in Lake Boebeïs." Now as for the Aenianians, most of them were driven into Oeta by the Lapiths; and there too they became predominant, having taken away certain parts of the country from the Dorians and the Malians as far as Heracleia and Echinus, although some remained in the neighbourhood of Cyphus, a Perrhaebian mountain which had a settlement of the same name. As for the Perrhaebians, some of them drew together round the western parts of Olympus and stayed there, being neighbours to the Macedonians, but the greater part of them were driven out of their country into the mountains round Athamania and Pindus. But to‑day little or no trace of them is preserved. At any rate, the Magnetans mentioned last by the poet in the Thessalian Catalogue should be regarded as those inside Tempê, extending from the Peneius and Ossa as far as Pelion, and bordering on the Pieriotae in Macedonia, who held the country on the far side of the Peneius as far as the sea. Now Homolium, or Homolê (for it is spelled both ways), should be p451assigned to the Magnetans; as I have said in my description of Macedonia, it is close to Ossa, situated where the Peneius begins to discharge its waters through Tempê. And if one were to proceed as far as the sea-coast nearest to Homolium, there is reason for assigning to them Rhizus and Erymnae, which were situated on that part of the sea-coast which was subject to Philoctetes and on that which was subject to Eumelus. However, let this question remain undecided. And also the order of the places next thereafter as far as the Peneius is not plainly told by the poet; but since these places are without repute, neither should I myself regard the matter as of great importance. Cape Sepias, however, was afterwards celebrated both in tragedies and in hymns on account of the total destruction there of the Persian fleet. Sepias itself is a rocky cape, but between it and Casthanaea, a village situated at the foot of Pelion, is a beach where the fleet of Xerxes was lying in wait when, a violent east wind bursting forth, some of the ships were immediately driven high and dry on the beach and broken to pieces on the spot, and the others were carried along the coast to Ipni, one of the rugged places in the region of Pelion, or to Meliboea, or to Casthanaea, and destroyed. The whole voyage along the coast of Pelion is rough, a distance of about eighty stadia; and that along the coast of Ossa is equally long and rough. Between the two mountains is a gulf more than two hundred stadia in circuit, on which is Meliboea. The whole voyage along the coast from Demetrias to the Peneius, following the sinuosities of the gulfs, is more than one thousand stadia in length, and from the Sperchius eight hundred more, and from the Euripus two thousand three hundred and fifty. Hieronymus declares that the plain country of Thessaly and Magnetis is three thousand stadia in circuit, and that it was inhabited by Pelasgians, and that these were driven out of their country by the Lapiths, and that the present Pelasgian Plain, as it is called, is that in which are situated Larisa, Gyrtonê, Pherae, Mopsium, Boebeïs, Ossa, Homolê, Pelion, and Magnetis. Mopsium is named, not after Mopsus, the son of Manto the daughter of Teiresias, but after Mopsus the Lapith who sailed with the Argonauts. But Mopsopus, after whom the Attic Mopsopia is named, is a different person.
So much, then, for the several parts of Thessaly. But speaking of it as a whole, I may say that in earlier times it was called Pyrrhaea, after Pyrrha the wife of Deucalion, and Haemonia after Haemon, and Thessaly after Thessalus the son of Haemon. But some writers, dividing it into two parts, say that Deucalion obtained the portion towards the south and called it Pandora after his mother, and that the other part fell to Haemon, after whom it was called Haemonia, but that the former name was changed to Hellas, after Hellen the son of Deucalion, and the latter to Thessaly, after the son of Haemon. Some, however, say that descendants of Antiphus and Pheidippus, the sons of Thessalus the son of Heracles, invaded the country from Thesprotian Ephyra and named it after Thessalus, their own ancestor. And it has been said that the country too was once named Nessonis, like the lake, after Nesson the son of Thessalus. |
|
|
|
|
10 Greek Islands 5 86 1:50 
|
10 - 1 Euboea 
1 Since Euboea lies parallel to the whole of the coast from Sunium to Thessaly, with the exception of the ends on either side,1 it would be appropriate to connect my description of the island with that of the parts already described before passing on to Aetolia and Acarnania, which are the remaining parts of Europe to be described.
2 In its length, then, the island extends parallel to the coast for a distance of about one thousand two hundred stadia from Cenaeum to Geraestus, but its breadth is irregular and generally only about one hundred and fifty stadia. Now Cenaeum lies opposite to Thermopylae and, to a slight extent, to the region outside Thermopylae, whereas Geraestus and Petalia lie towards Sunium. Accordingly, the island lies across the strait and opposite Attica, Boeotia, Locris, and the Malians. Because of its narrowness and of the above-mentioned length, it was named Macris by the ancients. It approaches closest to the mainland at Chalcis, where it juts out in a convex curve towards the region of Aulis in Boeotia and forms the Euripus. Concerning the Euripus I have already spoken rather at length, as also to a certain extent concerning the places which lie opposite one another across the strait, both on the mainland and on the island, on either side of the Euripus, that is, the regions both inside and outside the Euripus. But if anything has been left out, I shall now explain more fully. And first, let me explain that the parts between Aulis and the region of Geraestus are called the Hollows of Euboea; for the coast bends inwards, but when it approaches Chalcis it forms a convex curve again towards the mainland.
3 The island was called, not only Macris, but also Abantis; at any rate, the poet, although he names Euboea, never names its inhabitants "Euboeans," but always "Abantes": "And those who held Euboea, the courage-breathing Abantes . . . . And with him followed the Abantes." Aristotle says that Thracians, setting out from the Phocian Aba, recolonised the island and renamed those who held it "Abantes." Others derive the name from a hero, just as they derive "Euboea" from a heroine. But it may be, just as a certain cave on the coast which fronts the Aegaean, where Io is said to have given birth to Epaphus, is called Boösº Aulê, that the island got the name Euboea from the same cause. The island was also called Ochê; and the largest of its mountains bears the same name. And it was also named Ellopia, after Ellops the son of Ion. Some say that he was the brother of Aïclus and Cothus; and he is also said to have founded Ellopia, a place in Oria, as it is called, in Histiaeotis near the mountain Telethrius, and to have added to his dominions Histiaea, Perias, Cerinthus, Aedepsus, and Orobia; in this last place was an oracle most averse to falsehood (it was an oracle of Apollo Selinuntius). The Ellopians migrated to Histiaea and enlarged the city, being forced to do so by Philistides the tyrant, after the battle of Leuctra. Demosthenes says that Philistides was set up by Philip as tyrant of the Oreitae too; for thus in later times the Histiaeans were named, and the city was named Oreus instead of Histiaea. But according to some writers, Histiaea was colonised by Athenians from the deme of the Histiaeans, as Eretria was colonised from that of the Eretrians. Theopompus says that when Pericles overpowered Euboea the Histiaeans by agreement migrated to Macedonia, and that two thousand Athenians who formerly composed the deme of the Histiaeans came and took up their abode in Oreus.
4 Oreus is situated at the foot of the mountain Telethrius in the Drymus, as it is called, on the River Callas, upon a high rock; and hence, perhaps, it was because the Ellopians who formerly inhabited it were mountaineers that the name Oreus was assigned to the city. It is also thought that Orion was so named because he was reared there. Some writers say that the Oreitae had a city of their own, but because the Ellopians were making war on them they migrated and took up their abode with the Histiaeans; and that, although they became one city, they used both names, just as the same city is called both Lacedaemon and Sparta. As I have already said, Histiaeotis in Thessaly was also named after the Histiaeans who were carried off from here into the mainland by the Perrhaebians.
5 Since Ellopia induced me to begin my description with Histiaea and Oreus, let me speak of the parts which border on these places. In the territory of this Oreus lies, not only Cenaeum, near Oreus, but also, near Cenaeum, Dium and Athenae Diades, the latter founded by the Athenians and lying above that part of the strait where passage is taken across to Cynus; and Canae in Aeolis was colonised from Dium. Now these places are in the neighbourhood of Histiaea; and so is Cerinthus, a small city by the sea; and near it is the Budorus River, which bears the same name as the mountain in Salamis which is close to Attica.
6 Carystus is at the foot of the mountain Oche; and near it are Styra and Marmarium, in which latter are the quarry of the Carystian columns and a temple of Apollo Marmarinus; and from here there is a passage across the strait to Halae Araphenides. In Carystus is produced also the stone which is combed and woven, so that the woven material is made into towels, and, when these are soiled, they are thrown into fire and cleansed, just as linens are cleansed by washing. These places are said to have been settled by colonists from the Marathonian Tetrapolis and by Steirians. Styra was destroyed in the Malian war by Phaedrus, the general of the Athenians; but the country is held by the Eretrians. There is also a Carystus in the Laconian country, a place belonging to Aegys, towards Arcadia; whence the Carystian wine of which Alcman speaks.
7 Geraestus is not named in the Catalogue of Ships, but still the poet mentions it elsewhere: "and at night they landed at Geraestus." And he plainly indicates that the place is conveniently situated for those who are sailing across from Asia to Attica, since it comes near to Sunium. It has a temple of Poseidon, the most notable of those in that part of the world, and also a noteworthy settlement.
8 After Geraestus one comes to Eretria, the greatest city in Euboea except Chalcis; and then to Chalcis, which in a way is the metropolis of the island, being situated on the Euripus itself. Both are said to have been founded by the Athenians before the Trojan War. And after the Trojan War, Aïclus and Cothus, setting out from Athens, settled inhabitants in them, the former in Eretria and the latter in Chalcis. There were also some Aeolians from the army of Penthilus who remained in the island, and, in ancient times, some Arabians who had crossed over with Cadmus. Be this as it may, these cities grew exceptionally strong and even sent forth noteworthy colonies into Macedonia; for Eretria colonised the cities situated round Pallenê and Athos, and Chalcis colonised the cities that were subject to Olynthus, which later were treated outrageously by Philip. And many places in Italy and Sicily are also Chalcidian. These colonies were sent out, as Aristotle states, when the government of the Hippobotae, as it is called, was in power; for at the head of it were men chosen according to the value of their property, who ruled in an aristocratic manner. At the time of Alexander's passage across, the Chalcidians enlarged the circuit of the walls of their city, taking inside them both Canethus and the Euripus, and fortifying the bridge with towers and gates and a wall.
9 Above the city of the Chalcidians lies the so‑called Lelantine Plain. In this plain are fountains of hot water suited to the cure of diseases, which were used by Cornelius Sulla, the Roman commander. And in this plain was also a remarkable mine which contained copper and iron together, a thing which is not reported as occurring elsewhere; now, however, both metals have given out, as in the case of the silver mines at Athens. The whole of Euboea is much subject to earthquakes, but particularly the part near the strait, which is also subject to blasts through subterranean passages, as are Boeotia and other places which I have already described rather at length. And it is said that the city which bore the same name as the island was swallowed up by reason of a disturbance of this kind. This city is also mentioned by Aeschylus in his Glaucus Pontius: "Euboïs, about the bending shore of Zeus Cenaeus, near the very tomb of wretched Lichas." In Aetolia, also, there is a place called by the same name Chalcis: "and Chalcis near the sea, and rocky Calydon," and in the present Eleian country: "and they went past Cruni and rocky Chalcis," that is, Telemachus and his companions, when they were on their way back from Nestor's to their homeland.
As for Eretria, some say that it was colonised from Triphylian Macistus by Eretrieus, but others say from the Eretria at Athens, which now is a market-place. There is also an Eretria near Pharsalus. In the Eretrian territory there was a city Tamynae, sacred to Apollo; and the temple, which is near the strait, is said to have been founded by Admetus, at whose house the god served as an hireling for a year. In earlier times Eretria was called Melaneïs and Arotria. The village Amarynthus, which is seven stadia distant from the walls, belongs to this city. Now the old city was rased to the ground by the Persians, who "netted" the people, as Herodotus says, by means of their great numbers, the barbarians being spread about the walls (the foundations are still to be seen, and the place is called Old Eretria); but the Eretria of to‑day was founded on it. As for the power the Eretrians once had, this is evidenced by the pillar which they once set up in the temple of Artemis Amarynthia. It was inscribed thereon that they made their festal procession with three thousand heavy-armed soldiers, six hundred horsemen, and sixty chariots. And they ruled over the peoples of Andros, Teos, Ceos, and other islands. They received new settlers from Elis; hence, since they frequently used the letter r, not only at the end of words, but also in the middle, they have been ridiculed by comic writers. There is also a village Oechalia in the Eretrian territory, the remains of the city which was destroyed by Heracles; it bears the same name as the Trachinian Oechalia and that near Triccê, and the Arcadian Oechalia, which the people of later times called Andania, and that in Aetolia in the neighbourhood of the Eurytanians.
Now at the present time Chalcis by common consent holds the leading position and is called the metropolis of the Euboeans; and Eretria is second. Yet even in earlier times these cities were held in great esteem, not only in war, but also in peace; indeed, they afforded philosophers a pleasant and undisturbed place of abode. This is evidenced by the school of the Eretrian philosophers, Menedemus and his disciples, which was established in Eretria, and also, still earlier, by the sojourn of Aristotle in Chalcis, where he also ended his days.
Now in general these cities were in accord with one another, and when differences arose concerning the Lelantine Plain they did not so completely break off relations as to wage their wars in all respects according to the will of each, but they came to an agreement as to the conditions under which they were to conduct the fight. This fact, among others, is disclosed by a certain pillar in the Amarynthium, which forbids the use of long distance missiles. In fact among all the customs of warfare and of the use of arms there neither is, nor has been, any single custom; for some use long distance missiles, as, for example, bowmen and slingers and javelin-throwers, whereas others use close-fighting arms, as, for example, those who use sword, or outstretched spear; for the spear is used in two ways, one in hand-to‑hand combat and the other for hurling like a javelin; just as the pike serves both purposes, for it can be used both in close combat and as a missile for hurling, which is also true of the sarissa and the hyssus.
The Euboeans excelled in "standing" combat, which is also called "close" and "hand-to‑hand" combat; and they used their spears outstretched, as the poet says: "spearmen eager with outstretched ashen spears to shatter corselets." Perhaps the javelins were of a different kind, such as probably was the "Pelian ashen spear," which, as the poet says, "Achilles alone knew how to hurl;" and he who said, "And the spear I hurl farther than any other man can shoot an arrow," means the javelin-spear. And those who fight in single combat are first introduced as using javelin-spears, and then as resorting to swords. And close-fighters are not those who use the sword alone, but also the spear hand-to‑hand, as the poet says: "he pierced him with bronze-tipped polished spear, and loosed his limbs." Now he introduces the Euboeans as using this mode of fighting, but he says the contrary of the Locrians, that "they cared not for the tolls of close combat, . . . but relying on bows and well-twisted slings of sheep's wool they followed with him to Ilium." There is current, also, an oracle which was given out to the people of Aegium, "Thessalian horse, Lacedemonian woman, and men who drink the water of sacred Arethusa," meaning that the Chalcidians are best of all, for Arethusa is in their territory.
There are now two rivers in Euboea, the Cereus and the Neleus; and the sheep which drink from one of them turn white, and from the other black. A similar thing takes place in connection with the Crathis River, as I have said before.
When the Euboeans were returning from Troy, some of them, after being driven out of their course to Illyria, set out for home through Macedonia, but remained in the neighbourhood of Edessa, after aiding in war those who had received them hospitably; and they founded a city Euboea. There was also a Euboea in Sicily, which was founded by the Chalcidians of Sicily, but they were driven out of it by Gelon; and it became a stronghold of the Syracusans. In Corcyra, also, and in Lemnos, there were places called Euboea; and in the Argive country a hill of that name.
Since the Aetolians, Acarnanians, and Athamanians (if these too are to be called Greeks) live to the west of the Thessalians and the Oetaeans, it remains for me to describe these three, in order that I may complete the circuit of Greece; I must also add the islands which lie nearest to Greece and are inhabited by the Greeks, so far as I have not already included them in my description. |
|
|

|
|
10 - 2 Acarnania 
1 Now the Aetolians and the Acarnanians border on one another, having between them the Acheloüs River, which flows from the north and from Pindus on the south through the country of the Agraeans, an Aetolian tribe, and through that of the Amphilochians, the Acarnanians holding the western side of the river as far as that part of the Ambracian Gulf which is near Amphilochi and the temple of the Actian Apollo, but the Aetolians the eastern side as far as the Ozalian Locrians and Parnassus and the Oetaeans. Above the Acarnanians, in the interior and the parts towards the north, are situated the Amphilochians, and above these the Dolopians and Pindus, and above the Aetolians are the Perrhaebians and Athamanians and a part of the Aenianians who hold Oeta. The southern side, of Acarnania and Aetolia alike, is washed by the sea which forms the Corinthian Gulf, into which empties the Acheloüs River, which forms the boundary between the coast of the Aetolians and that of Acarnania. In earlier times the Acheloüs was called Thoas. The river which flows past Dymê bears the same name as this, as I have already said,1 and also the river near Lamia. I have already stated, also, that the Corinthian Gulf is said to begin at the mouth of this river.
2 As for cities, those of the Acarnanians are Anactorium, which is situated on a peninsula near Actium and is a trading-centre of the Nicopolis of to‑day, which was founded in our times; Stratus, where one may sail up the Acheloüs River more than two hundred stadia; and Oeneiadae, which is also on the river — the old city, which is equidistant from the sea and from Stratus, being uninhabited, whereas that of to‑day lies at a distance of about seventy stadia above the outlet of the river. There are also other cities, Palaerus, Alyzia, Leucas, Argos Amphilochicum, and Ambracia, most of which, or rather all, have become dependencies of Nicopolis. Stratus is situated about midway of the road between Alyzia and Anactorium.
3 The cities of the Aetolians are Calydon and Pleuron, which are now indeed reduced, though in early times these settlements were an ornament to Greece. Further, Aetolia has come to be divided into two parts, one part being called Old Aetolia and the other Aetolia Epictetus. The Old Aetolia was the seacoast extending from the Acheloüs to Calydon, reaching for a considerable distance into the interior, which is fertile and level; here in the interior lie Stratus and Trichonium, the latter having excellent soil. Aetolia Epictetus is the part which borders on the country of the Locrians in the direction of Naupactus and Eupalium, being a rather rugged and sterile country, and extends to the Oetaean country and to that of the Athamanians and to the mountains and tribes which are situated next beyond these towards the north.
4 Aetolia also has a very large mountain, Corax, which borders on Oeta; and it has among the rest of its mountains, and more in the middle of the country than Corax, Aracynthus, near which New Pleuron was founded by the inhabitants of the Old, who abandoned their city, which had been situated near Calydon in a district both fertile and level, at the time when Demetrius, surnamed Aetolicus, laid waste the country; above Molycreia are Taphiassus and Chalcis, rather high mountains, on which were situated the small cities Macynia and Chalcis, the latter bearing the same name as the mountain, though it is also called Hypochalcis. Near Old Pleuron is the mountain Curium, after which, as some have supposed, the Pleuronian Curetes were named.
5 The Evenus River begins in the territory of those Bomians who live in the country of the Ophians, the Ophians being an Aetolian tribe (like the Eurytanians and Agraeans and Curetes and others), and flows at first, not through the Curetan country, which is the same as the Pleuronian, but through the more easterly country, past Chalcis and Calydon; and then, bending back towards the plains of Old Pleuron and changing its course to the west, it turns towards its outlets and the south. In earlier times it was called Lycornas. And there Nessus, it is said, who had been appointed ferryman, was killed by Heracles because he tried to violate Deïaneira when he was ferrying her across the river.
6 The poet also names Olenus and Pylenê as Aetolian cities. Of these, the former, which bears the same name as the Achaean city, was rased to the ground by the Aeolians; it was near New Pleuron, but the Acarnanians claimed possession of the territory. The other, Pylenê, the Aeolians moved to higher ground, and also changed its name, calling it Proschium. Hellanicus does not know the history of these cities either, but mentions them as though they too were still in their early status; and seeming the early cities he names Macynia and Molycreia, which were founded even later than the return of the Heracleidae, almost everywhere in his writings displaying a most convenient carelessness.
7 Upon the whole, then, this is what I have to say concerning the country of the Acarnanians and the Aetolians, but the following is also to be added concerning the seacoast and the islands which lie off it: Beginning at the mouth of the Ambracian Gulf, the first place which belongs to the Acarnanians is Actium. The temple of the Actian Apollo bears the same name, as also the cape which forms the mouth of the Gulf and has a harbour on the outer side. Anactorium, which is situated on the gulf, is forty stadia distant from the temple, whereas Leucas is two hundred and forty.
8 In early times Leucas was a peninsula of Acarnania, but the poet calls it "shore of the mainland," using the term "mainland" for the country which is situated across from Ithaca and Cephallenia; and this country is Acarnania. And therefore, when he says, "shore of the mainland," one should take it to mean "shore of Acarnania." And to Leucas also belonged, not only Nericus, which Laertes says he took ("verily I took Nericus, well-built citadel, shore of the mainland, when I was lord over the Cephallenians"), but also the cities which Homer names in the Catalogue ("and dwelt in Crocyleia and rugged Aegilips"). But Corinthians sent by Cypselus and Gorgus took possession of this shore and also advanced as far as the Ambracian Gulf; and both Ambracia and Anactorium were colonised at this time; and the Corinthians dug a canal through the isthmus of the peninsula and made Leucas an island; and they transferred Nericus to the place which, though once an isthmus, is now a strait spanned by a bridge, and they changed its name to Leucas, which was named, as I think, after Leucatas; for Leucatas is a rock of white colour jutting out from Leucas into the sea and towards Cephallenia, and therefore it took its name from its colour.
9 It contains the temple of Apollo Leucatas, and also the "Leap," which was believed to put an end to the longings of love. "Where Sappho is said to have been the first," as Menander says, "when through frantic longing she was chasing the haughty Phaon, to fling herself with a leap from the far‑seen rock, calling upon thee in prayer, O lord and master." Now although Menander says that Sappho was the first to take the leap, yet those who are better versed than he in antiquities say that it was Cephalus, who was in love with Pterelas the son of Deïoneus. It was an ancestral custom among the Leucadians, every year at the sacrifice performed in honour of Apollo, for some criminal to be flung from this rocky look‑out for the sake of averting evil, wings and birds of all kinds being fastened to him, since by their fluttering they could lighten the leap, and also for a number of men, stationed all round below the rock in small fishing-boats, to take the victim in, and, when he had been taken on board, to do all in their power to get him safely outside their borders. The author of the Alcmaeonis says that Icarius, the father of Penelope, had two sons, Alyzeus and Leucadius, and that these two reigned over Acarnania with their father; accordingly, Ephorus thinks that the cities were named after these.
But though at the present time only the people of the island Cephallenia are called Cephallenians, Homer so calls all who were subject to Odysseus, among whom are also the Acarnanians. For after saying, "but Odysseus led the Cephallenians, who held Ithaca and Neritum with quivering foliage" (Neritum being the famous mountain on the island, as always when he says, "and those from Dulichium and the sacred Echinades," Dulichium itself being one of the Echinades; and "those who dwelt in Buprasium and Elis," Buprasium being in Elis; and "those who held Euboea and Chalcis and Eiretria," meaning that these cities were in Euboea; and "Trojans and Lycians and Dardanians," meaning that the Lycians and Dardanians were Trojans) — however, after mentioning "Neritum," he says, "and dwelt in Crocyleia and rugged Aegilips, and those who held Zacynthos and those who dwelt about Samos, and those who held the mainland and dwelt in the parts over against the islands." By "mainland," therefore, he means the parts over against the islands, wishing to include, along with Leucas, the rest of Acarnania as well, concerning which he also speaks in this way, "twelve herd on the mainland, and as many flocks of sheep," perhaps because Epeirotis extended thus far in early times and was called by the general name "mainland." But by "Samos" he means the Cephallenia of to‑day, as, when he says, "in the strait between Ithaca and rugged Samos"; for by the epithet he differentiates between the objects bearing the same name, thus making the name apply, not to the city, but to the island. For the island was a Tetrapolis, and one of its four cities was the city called indifferently either Samos or Samê, bearing the same name as the island. And when the poet says, "for all the nobles who hold sway over the islands, Dulichium and Samê and woody Zacynthos," he is evidently making an enumeration of the islands and calling "Samê" that island which he had formerly called Samos. But Apollodorus, when he says in one passage that ambiguity is removed by the epithet when the poet says "and rugged Samos," showing that he meant the island, and then, in another passage, says that one should copy the reading, "Dulichium and Samos," instead of "Samê," plainly takes the position that the city was called "Samê" or "Samos" indiscriminately, but the island "Samos" only; for that the city was called Samê is clear, according to Apollodorus, from the fact that, in enumerating the wooers from the several cities, the poet said, "from Samê came four and twenty men," and also from the statement concerning Ktimenê, "they then sent her to Samê to wed." But this is open to argument, for the poet does not express himself distinctly concerning either Cephallenia or Ithaca and the other places near by; and consequently both the commentators and the historians are at variance with one another.
For instance, when Homer says in regard to Ithaca, "those who held Ithaca and Neritum with quivering foliage," he clearly indicates by the epithet that he means the mountain Neritum; and in other passages he expressly calls it a mountain; "but I dwell in sunny Ithaca, wherein is a mountain, Neritum, with quivering leaves and conspicuous from afar." But whether by Ithaca he means the city or the island, is not clear, at least in the following verse, "those who held Ithaca and Neritum"; for if one takes the word in its proper sense, one would interpret it as meaning the city, just as though one should say "Athens and Lycabettus," or "Rhodes and Atabyris," or "Lacedaemon and Taÿgetus"; but if he takes it in a poetical sense the opposite is true. However, in the word, "but I dwelt in sunny Ithaca, wherein is a mountain Neritum," his meaning is clear, for the mountain is in the island, not in the city. But when he says as follows, "we have come from Ithaca below Neïum," it is not clear whether he means that Neïum is the same as Neritum or different, or whether it is a mountain or place. However, the critic who writes Nericum instead of Neritum, or the reverse, is utterly mistaken; for the poet refers to the latter as "quivering with foliage," but to the former as "well-built citadel," and to the latter as "in Ithaca," but to the former as "shore of the mainland."
The following verse also is thought to disclose a sort of contradiction: "Now Ithaca itself lies chthamalê, panypertatê on the sea"; for chthamalê means "low," or "on the ground," whereas panypertatê means "high up," as Homer indicates in several places when he calls Ithaca "rugged." And so when he refers to the road that leads from the harbour as "rugged path up through the wooded place," and when he says "for not one of the islands which lean upon the sea is eudeielos or rich in meadows, and Ithaca surpasses them all." Now although Homer's phraseology presents incongruities of this kind, yet they are not poorly explained; for, in the first place, writers do not interpret chthamalê as meaning "low‑lying" here, but "lying near the mainland," since it is very close to it, and, secondly, they do not interpret panypertatê as meaning "highest," but "highest towards the darkness," that, farthest removed towards the north beyond all the others; for this is what he means by "towards the darkness," but the opposite by "towards the south," as in "but the other islands lie aneuthe towards the dawn and the sun," for the word aneuthe is "at a distance," or "apart," implying that the other islands lie towards the south and farther away from the mainland, whereas Ithaca lies near the mainland and towards the north. That Homer refers in this way to the southerly region is clear also from these words, "whether they go to the right, towards the dawn and the sun, or yet to the left towards the misty darkness," and still more clear from these words, "my friends, lo, now we know not where is the place of darkness, nor of dawn, nor where the sun, that gives light to men, goes beneath the earth, nor where he rises." For it is indeed possible to interpret this as meaning the four "climata," if we interpret "the dawn" as meaning the southerly region (and this has some plausibility), but it is better to conceive of the region which is along the path of the sun as set opposite to the northerly region, for the poetic words are intended to signify a considerable change in the celestial phenomena, not merely a temporary concealment of the "climata," for necessarily concealment ensues every time the sky is clouded, whether by day or by night; but the celestial phenomena change to a greater extent as we travel farther and farther towards the south or in the opposite direction. Yet this travel causes a hiding, not of the western or eastern sky, but only of the southern or northern, and in fact this hiding takes place when the sky is clear; for the pole is the most northerly point of the sky, but since the pole moves and is sometimes at our zenith and sometimes below the earth, the arctic circles also change with it and in the course of such travels sometimes vanish with it, so that you cannot know where the northern "clima" is, or even where it begins. And if this is true, neither can you know the opposite "clima." The circuit of Ithaca is about eighty stadia. So much for Ithaca.
As for Cephallenia, which is a Tetrapolis, the poet mentions by its present name neither it nor any of its cities except one, Samê or Samos, which now no longer exists, though traces of it are to be seen midway of the passage to Ithaca; and its people are called Samaeans. The other three, however, survive even to this day in the little cities Paleis, Pronesus, and Cranii. And in our time Gaius Antonius, the uncle of Marcus Antonius, founded still another city, when, after his consulship, which he held with Cicero the orator, he went into exile, sojourned in Cephallenia, and held the whole island in subjection as though it were his private estate. However, before he could complete the settlement he obtained permission to return home, and ended his days amid other affairs of greater importance.
Some, however, have not hesitated to identify Cephallenia with Dulichium, and others with Taphos, calling the Cephallenians Taphians, and likewise Teleboans, and to say that Amphitryon made an expedition thither with Cephalus, the son of Deïoneus, whom, an exile from Athens, he had taken along with him, and that when Amphitryon seized the island he gave it over to Cephalus, and that the island was named after Cephalus and the cities after his children. But this is not in accordance with Homer; for the Cephallenians were subject to Odysseus and Laertes, whereas Taphos was subject to Mentes: "I declare that I am Mentes the son of wise Anchialus, and I am lord over the oar‑loving Taphians." Taphos is now called Taphius. Neither is Hellanicus in accordance with Homer when he identifies Cephallenia with Dulichium, for him makes Dulichium and the remainder of the Echinades subject to Meges; and their inhabitants were Epeians, who had come there from Elis; and it is on this account that he calls Otus the Cyllenian "comrade of Phyleides and ruler of the high-hearted Epeians"; "but Odysseus led the high-hearted Cephallenians." According to Homer, therefore, neither is Cephallenia Dulichium nor is Dulichium a part of Cephallenia, as Andron says; for the Epeians held possession of Dulichium, whereas the Cephallenians held possession of the whole of Cephallenia and were subject to Odysseus, whereas the Epeians were subject to Meges. Neither is Paleis called Dulichium by the poet, as Pherecydes writes. But that writer is most in opposition to Homer who identifies Cephallenia with Dulichium, if it be true that "fifty‑two" of the suitors were "from Dulichium" and "twenty-four from Samê"; for in that case would not Homer say that fifty‑two came from the island as a whole and a half of that number less two from a single one of its four cities? However, if one grants this, I shall ask what Homer can mean by "Samê" in the passage, "Dulichium and Samê and woody Zacynthos."
Cephallenia lies opposite Acarnania, at a distance of about fifty stadia from Leucatas (some say forty), and about one hundred and eighty from Chelonatas. It has a perimeter of about three hundred stadia, is long, extending towards Eurus, and is mountainous. The largest mountain upon it is Aenus, whereon is the temple of Zeus Aenesius; and where the island is narrowest it forms an isthmus so low‑lying that it is often submerged from sea to sea. Both Paleis and Cranii are on the gulf near the narrows.
Between Ithaca and Cephallenia is the small island Asteria (the poet calls it Asteris), which the Scepsian says no longer remains such as the poet describes it, "but in it are harbours safe for anchorage with entrances on either side"; Apollodorus, however, says that it still remains so to this day, and mentions a town Alalcomenae upon it, situated on the isthmus itself.
The poet also uses the name "Samos" for that Thrace which we now call Samothrace. And it is reasonable to suppose that he knows the Ionian Samos, for he also appears to know of the Ionian migration; otherwise he would not have differentiated between the places of the same name when referring to Samothrace, which he designates at one time by the epithet, "high on the topmost summit of woody Samos, the Thracian," and at another time by connecting it with the islands near it, "unto Samos and Imbros and inhospitable Lemnos." And again, "between Samos and rugged Imbros." He therefore knew the Ionian island, although he did not name it; in fact it was not called by the same name in earlier times, but Melamphylus, then Anthemis, then Parthenia, from the River Parthenius, the name of which was changed to Imbrasus. Since, then, both Cephallenia and Samothrace were called Samos at the time of the Trojan War (for of which Hecabe would not be introduced as saying that he was for selling her children whom he might take captive "unto Samos and unto Imbros"), and since the Ionian Samos had not yet been colonised, it plainly got its name from one of the islands which earlier bore the same name. Whence that other fact is also clear, that those writers contradict ancient history who say that colonists came from Samos after the Ionian migration and the arrival of Tembrion and named Samothrace Samos, since this story was fabricated by the Samians to enhance the glory of their island. Those writers are more plausible who say that the island came upon this name from the fact that lofty places are called "samoi," "for thence all Ida was plain to see, and plain to see were the city of Priam and the ships of the Achaeans." But some say that the island was called Samos after the Saïi, the Thracians who inhabited it in earlier times, who also held the adjacent mainland, whether these Saïi were the same people as the Sapaeï or Sinti (the poet calls them Sinties) or a different tribe. The Saïi are mentioned by Archilochus: "One of the Saïi robbed me of my shield, which, a blameless weapon, I left behind me beside a bush, against my will."
Of the islands classified as subject to Odysseus, Zacynthos remains to be described. It leans slightly more to the west of the Peloponnesus than Cephallenia and lies closer to the latter. The circuit of Zacynthos is one hundred and sixty stadia. It is about sixty stadia distant from Cephallenia. It is indeed a woody island, but it is fertile; and its city, which bears the same name, is worthy of note. The distance thence to the Libyan Hesperides is three thousand three hundred stadia.
To the east of Zacynthos and Cephallenia are situated the Echinades Islands, among which is Dulichium, now called Dolicha, and also what are called the Oxeiae, which the poet called Thoae. Dolicha lies opposite Oeneiadae and the outlet of the Acheloüs, at a distance of one hundred stadia from Araxus, the promontory of the Eleians; the rest of the Echinades (they are several in number, all poor-soiled and rugged) lie off the outlet of the Acheloüs, the farthermost being fifteen stadia distant and the nearest five. In earlier times they lay out in the high sea, but the silt brought down by the Acheloüs has already joined some of them to the mainland and will do the same to others. It was this silt which in early times caused the country called Paracheloïtis, which the river overflows, to be a subject of dispute, since it was always confusing the designated boundaries between the Acarnanians and the Aetolians; for they would decide the dispute by arms, since they had no arbitrators, and the more powerful of the two would win the victory; and this is the cause of the fabrication of a certain myth, telling how Heracles defeated Acheloüs and, as the prize of his victory, won the hand of Deïaneira, the daughter of Oeneus, whom Sophocles represents as speaking as follows: "For my suitor was a river‑god, I mean Acheloüs, who would demand me of my father in three shapes, coming now as a bull in bodily form, now as a gleaming serpent in coils, now with trunk of man and front of ox." Some writers add to the myth, saying that this was the horn of Amaltheia, which Heracles broke off from Acheloüs and gave to Oeneus as a wedding gift. Others, conjecturing the truth from the myths, say that the Acheloüs, like the other rivers, was called "like a bull" from the roaring of its waters, and also from the bendings of its streams, which were called Horns, and "like a serpent" because of its length and windings, and "with front of ox" for the same reason that he was called "bull-faced"; and that Heracles, who in general was inclined to deeds of kindness, but especially for Oeneus, since he was to ally himself to him by marriage, regulated the irregular flow of the river by means of embankments and channels, and thus rendered a considerable part of Paracheloïtis dry, all to please Oeneus; and that this was the horn of Amaltheia. Now, as for the Echinades, or the Oxeiae, Homer says that they were ruled over in the time of Trojan War by Meges, "who was begotten by the knightly Phyleus, dear to Zeus, who once changed his abode to Dulichium because he was wroth with his father." His father was Augeas, the ruler of the Eleian country and the Epeians; and therefore the Epeians who set out for Dulichium with Phyleus held these islands.
The islands of the Taphians, or, in earlier times, of the Teleboans, among which was Taphos, now called Taphius, were distinct from the Echinades; not in the matter of distances (for they lie near them), but in that they are classified as under different commanders, Taphians and Teleboans. Now in earlier times Amphitryon made an expedition against them with Cephalus the son of Deïoneus, an exile from Athens, and gave over their government to him, but the poet says that they were marshalled under Mentes, calling them pirates, as indeed all the Teleboans are said to be pirates. So much, then, for the islands lying off Acarnania.
Between Leucas and the Ambracian Gulf is a salt-lake, called Myrtuntium. Next after Leucas one comes to Palaerus and Alyzia, cities of Acarnania; of these, Alyzia is fifteen stadia distant from the sea, where is a harbour sacred to Heracles and a sacred precinct. It is from this precinct that one of the commanders carried to Rome the "Labours of Heracles," works of Lysippus, which were lying out of place where they were, because it was a deserted region. Then one comes to Cape Crithotê, and the Echinades, and the city Astacus, which bears the same name as the city near Nicomedeia and Gulf Astacenus, the name being used in the feminine gender. Crithotê also bears the same name as one of the little cities in the Thracian Chersonesus. All parts of the coast between these places have good harbours. Then one comes to Oeniadae and the Acheloüs; then to a lake of the Oeniadae, called Melitê, which is thirty stadia in length and twenty in breadth; and to another lake, Cynia, which is twice the size of Melitê, both in length and in breadth; and to a third, Uria, which is smaller than those. Now Cynia empties into the sea, but the others lie about half a stadium above it. Then one comes to the Evenus, to which the distance from Actium is six hundred and seventy stadia. After the Evenus one comes to the mountain Chalcis, which Artemidorus has called Chalcia; then to Pleuron; then to the village Halicyrna, above which, thirty stadia in the interior, lies Calydon; and near Calydon is the temple of the Laphrian Apollo. Then one comes to the mountain Taphiassus; then to the city Macynia; then to Molycreia and, near by, to Antirrhium, the boundary between Aetolia and Locris, to which the distance from the Evenus is about one hundred and twenty stadia. Artemidorus, indeed, does not give this account of the mountain, whether we call it Chalcis or Chalcia, since he places it between the Acheloüs and Pleuron, but Apollodorus, as I have said before, places both Chalcis and Taphiassus above Molycreia, and he also says that Calydon is situated between Pleuron and Chalcis. Perhaps, however, we should postulate two mountains, one near Pleuron called Chalcis, and the other near Molycreia called Chalcis. Near Calydon, also, is a lake, which is large and well supplied with fish; it is held by the Romans who live in Patrae.
Apollodorus says that in the interior of Acarnania there is a people called Erysichaeans, who are mentioned by Alcman: "nor yet an Erysichaean nor shepherd, but from the heights of Sardeis." But Olenus, which Homer mentions in the Aetolian catalogue, was in Aetolia, though only traces of it are left, near Pleuron at the foot of Aracynthus. Near it, also, was Lysimachia; this, too, has disappeared; it was situated by the lake now called Lysimachia, in earlier times Hydra, between Pleuron and the city Arsinoê. In early times Arsinoê was only a village, and was called Conopa, but it was first founded as a city by Arsinoê, who was both wife and sister of Ptolemy the Second; it was rather happily situated at the ford across the Acheloüs. Pylenê has also suffered a fate similar to that of Olenus. When the poet calls Calydon both "steep" and "rocky," one should interpret him as referring to the country; for, as I have said, they divided the country into two parts and assigned the mountainous part, or Epictetus, to Calydon and the level country to Pleuron.
At the present time both the Acarnanians and the Aetolians, like many of the other tribes, have been exhausted and reduced to impotence by their continual wars. However, for a very long time the Aetolians, together with the Acarnanians, stood firm, not only against the Macedonians and the other Greeks, but also finally against the Romans, when fighting for autonomy. But since they are often mentioned by Homer, as also both by the other poets and by historians, sometimes in words that are easy to interpret and about which there is no disagreement, and sometimes in words that are less intelligible (this has been shown in what I have already said about them), I should also add some of those older accounts which afford us a basis of fact to begin with, or are matters of doubt.
For instance, in the case of Acarnania, Laertes and the Cephallenians acquired possession of it, as I have said; but as to what people held it before that time, many writers have indeed given an opinion, but since they do not agree in their statements, which have, however, a wide currency, there is left for me a word of arbitration concerning them. They say that the people who were called both Taphians and Teleboans lived in Acarnania in earlier times, and that their leader Cephalus, who had been set up by Amphitryon as master over the islands about Taphos, gained the mastery over this country too. And from this fact they go on to add the myth that Cephalus was the first to take the leap from Leucatas which became the custom, as I have said before. But the poet does not say that the Taphians were ruling the Acarnanians before the Cephallenians and Laertes came over, but only that they were friends to the Ithacans, and therefore, according to the poet, they either had not ruled over the region at all, or had yielded Acarnania to the Ithacans voluntarily, or had become joint-occupants with them. It appears that also a colony from Lacedaemon settled in Acarnania, I mean Icarius, father of Penelope, and his followers; for in the Odyssey the poet represents both Icarius and the brothers of Penelope as living: "who shrink from going to the house of her father, Icarius, that he himself may exact the bride-gifts for his daughter," and, concerning her brothers, "for already her father and her brothers bid her marry Eurymachus"; for, in the first place, it is improbable that they were living in Lacedaemon, since in that case Telemachus would not have lodged at the home of Menelaüs when he went to Lacedaemon, and, secondly, we have no tradition of their having lived elsewhere. But they say that Tyndareus and his brother Icarius, after being banished by Hippocoön from their home-land, went to Thestius, the ruler of the Pleuronians, and helped him to acquire possession of much of the country on the far side of the Acheloüs on condition that they should receive a share of it; that Tyndareus, however, went back home, having married Leda, the daughter of Thestius, whereas Icarius stayed on, keeping a portion of Acarnania, and by Polycastê, the daughter of Lygaeus, begot both Penelope and her brothers. Now I have already set forth that the Acarnanians were enumerated in the Catalogue of Ships, that they took part in the expedition to Ilium, and that among these were named "those who lived on the 'shore,' " and also "those who held the mainland and dwelt in parts opposite." But as yet neither had the mainland been named "Acarnania" nor the shore "Leucas."
Ephorus denies that they joined the Trojan expedition, for he says that Alcmaeon, the son of Amphiaraüs, made an expedition with Diomedes and the other Epigoni, and had brought to a successful issue the war against the Thebans, and then joined Diomedes and with him took vengeance upon the enemies of Oeneus, after which he himself, first giving over Aetolia to them, passed into Acarnania and subdued it; and meanwhile Agamemnon attacked the Argives and easily prevailed over them, since the most of them had accompanied the army of Diomedes; but a little later, when the expedition against Ilium confronted him, he conceived the fear that, when he was absent on the expedition, Diomedes and his army might come back home (and in fact it was reported that a great army had gathered round him) and seize the empire to which they had the best right, for one was the heir of Adrastus and the other of his father; and accordingly, after thinking this all over, Agamemnon invited them both to resume possession of Argos and to take part in the war; and although Diomedes was persuaded to take part in the expedition, Alcmaeon was vexed and refused to heed the invitation; and for this reason the Acarnanians alone refused to share in the expedition with the Greeks. And it was probably by following this account that the Acarnanians tricked the Romans, as they are said to have done, and obtained from them their autonomy, urging that they alone had had no part in the expedition against the ancestors of the Romans, for they were named neither in the Aetolian catalogue nor separately, and in fact their name was not mentioned in the Epic poems at all.
Ephorus, then, makes Acarnania subject to Alcmaeon even before the Trojan War; and he not only declares that the Amphilochian Argos was not founded by him, but also says that Acarnania was named after Alcmaeon's son Acarnan, and the Amphilochians after Alcmaeon's brother Amphilochus; therefore his account is to be cast out amongst those contrary to Homeric history. But Thucydides and others say that Amphilochus, on his return from the Trojan expedition, was displeased with the state of affairs at Argos, and took up his abode in this country, some saying that he came by right of succession to the domain of his brother, others giving a different account. So much may be said of the Acarnanians specifically; I shall now speak of their history in a general way, in so far as their history is interwoven with that of the Aetolians, relating next in order the history of the Aetolians, in so far as I have thought best to add to my previous narrative. |
|
|
|
|
10 - 3 Aetolia 
1 As for the Curetes, some assign them to the Acarnanians, others to the Aetolians; and some assert that the tribe originated in Crete, but others in Euboea; but since Homer mentions them, I should first investigate his account. It is thought that he means that they were Aetolians rather than Acarnanians, if indeed the sons of Porthaon were "Agrius and Melas, and, the third, Oeneus the knight";1 "and they lived in Pleuron and steep Calydon." These are both Aetolian cities, and are referred to in the Aetolian catalogue; and therefore, since, even according to the poet, the Curetes obviously lived in Pleuron, they would be Aetolians. Those writers who oppose this view misled by Homer's mode of expression when he says, "the Curetes were fighting, and the Aetolians steadfast in battle, about the city of Calydon"; for, they add, neither would he have spoken appropriately if he had said, "the Boeotians and the Thebans were fighting against one another"; or "the Argives and the Peloponnesians." But, as I have shown heretofore,4 this habit of expression not only is Homeric, but is much used by the other poets also. This interpretation, then, is easy to defend; but let those writers explain how the poet could catalogue the Pleuronians among the Aetolians if they were not Aetolians or at least of the same race.
2 Ephorus, after saying that the Aetolians were a race which had never become subject to any other people, but throughout all time of which there is any record had remained undevastated, both because of the ruggedness of their country and because of their training in warfare, says at the outset that the Curetes held possession of the whole country, but when Aetolus, the son of Endymion, arrived from Elis and overpowered them in war, the Curetes withdrew to what is now called Acarnania, whereas the Aetolians came back with Epeians and founded the earliest of the cities of Aetolia, and in the tenth generation after that Elis was settled by Oxylus the son of Haemon, who had crossed over from Aetolia. And he cites as evidence of all this two inscriptions, the one at Therma in Aetolia (where it is the ancestral custom to hold their elections of magistrates), engraved on the based of the statue of Aetolus: "Founder of the country, once reared beside the eddies of the Alpheius, neighbour of the race-courses of Olympia, son of Endymion, this Aetolus has been set up by the Aetolians as a memorial of his valour to behold"; and the other inscription in the market-place of the Eleians on the statue of Oxylus: "Aetolus once left this autochthonous people, and through many a toil with the spear took possession of the land of Curetis; but the tenth scion of the same stock, Oxylus, the son of Haemon, founded this city in early times."
3 Now through these inscriptions Ephorus correctly signifies the kinship of the Eleians and Aetolians with one another, since both inscriptions agree, not merely as to the kinship of the two peoples, but also that each people was the founder of the other, through which he successfully convicts of falsehood those who assert that, while the Eleians were indeed colonists of the Aetolians, the Aetolians were not colonists of the Eleians. But here, too, Ephorus manifestly displays the same inconsistency in his writing and his pronouncements as in the case of the oracle at Delphi, which I have already set forth;8 for, after saying that Aetolia has been undevastated throughout all times of which there is any record, and after saying also that in the beginning the Curetes held possession of this country, he should have added as a corollary to what he had already said that the Curetes continued to hold possession of the Aetolian land down to his own time, for only thus could it have been rightly said that the land had been undevastated and that it had never come under the power of others; and yet, utterly forgetting his promise,9 he does not add this, but the contrary, that when Aetolus arrived from Elis and overpowered the Curetes in war, they withdrew into Acarnania. What else, pray, is specifically characteristic of a devastation than being overpowered in war and abandoning the country? And this is evidenced also by the inscription among the Eleians, for Aetolus, there is says, "through many a toil with the spear took possession of the land of Curetis."
4 Perhaps, however, one might say that Ephorus means that Aetolia was undevastated from the time when it got this name, that is, after Aetolus arrived there; but Ephorus has deprived himself of the argument in support of this idea by saying in his next words that this, meaning the tribe of the Epeians, constituted the greatest part of the people who stayed on among the Aetolians, but that later, when Aetolians, who at the same time with Boeotians had been compelled to migrate from Thessaly, were intermingled with them, they in common with these held possession of the country. Is it credible, pray, that without war they invaded the country of a different people and divided it up with its possessors, when the latter had no need of such a partnership? Or, since this is not credible, is it credible that those who were overpowered by arms came out on an equality with the victors? What else, pray, is devastation than being overpowered by arms? Apollodorus, also, says that, according to history, the Hyantes left Boeotia and settled among the Aetolians. But Ephorus, as though he had achieved success in his argument, adds: "It is my wont to examine such matters as these with precision, whenever any matter is either altogether doubtful or falsely interpreted."
5 But though Ephorus is such, still he is better than others. And Polybius himself, who praises him so earnestly, and says concerning the Greek histories that Eudoxus indeed gave a good account, but Ephorus gave the best account of the foundings of cities, kinships, migrations, and original founders, "but I," he says, "shall show the facts as they now are, as regards both the position of places and the distances between them; for this is the most appropriate function of Chorography." But assuredly you, Polybius, who introduce "popular notions" concerning distances, not only in dealing with places outside of Greece, but also when treating Greece itself, must also submit to an accounting, not only to Poseidonius, and to Apollodorus, but to several others as well. One should therefore pardon me as well, and not be vexed, if I make any mistakes when I borrow from such writers most of my historical material, but should rather be content if in the majority of cases I improve upon the accounts given by others, or if I add such facts as have elsewhere, owing to lack of knowledge, been left untold.
6 Concerning the Curetes still further accounts, to the following effect, are given, some of them being more closely related to the history of the Aetolians and the Acarnanians, others more remotely. More closely related are such accounts as I have given before — that the Curetes were living in the country which is now called Aetolia, and that the Aetolians came with Aetolus and drove them into Acarnania; and also accounts of this kind, that, when Pleuronia was inhabited by the Curetes and was called Curetis, Aeolians made an invasion and took it away from them, and drove out its occupants. Archemachus the Euboean says that the Curetes settled at Chalcis, but since they were continually at war for the Lelantine Plain and the enemy would catch them by the front hair and drag them down, he says, they let their hair grow long behind but cut short the part in front, and because of this they were called "Curetes," from the cut of their hair, and they then migrated to Aetolia, and, after taking possession of the region round Pleuron, called the people who lived on the far side of the Acheloüs "Acarnanians," because they kept their heads "unshorn." But some say that each of the two tribes got its name from a hero; others, that the Curetes were named after the mountain Curium, which is situated about Pleuron, and also that this is an Aetolian tribe, like the Ophians and the Agraeans and the Eurytanians and several others. But, as I have already stated, when Aetolia was divided into two parts, the region round Calydon, they say, was in the possession of Oeneus, whereas a certain part of Pleuronia was in the possession of the sons of Porthaon, that is, Agrius and his followers, if it be true that "they lived in Pleuron and steep Calydon"; the mastery over Pleuronia, however, was held by Thestius (the father-in‑law of Oeneus and father of Althaea), who was leader of the Curetes; but when war broke out between the sons of Thestius, on the one hand, and Oeneus and Meleager, on the other ("about the hog's head and skin," as the poet says, following the mythical story of the boar,but in all probability about the possession of a part of the territory), according to the words of the poet, "the Curetes were fighting, as also the Aetolians steadfast in battle." So much for the accounts which are more closely related.
7 The accounts which are more remotely related, however, to the present subject, but are wrongly, on account of the identity of the names, brought into the same connection by the historians — I mean those accounts which, although they are called "Curetan History" and "History of the Curetes," just as if they were the history of those Curetes who lived in Aetolia and Acarnania, not only are different from that history, but are more like the accounts of the Satyri, Sileni, Bacchae, and Tityri; for the Curetes, like these, are called genii or ministers of gods by those who have handed down to us the Cretan and Phrygian traditions, which are interwoven with certain sacred rites, some mystical, the others connected in part with the rearing of the child Zeus in Crete and in part with the orgies in honour of the mother of the gods which are celebrated in Phrygia and in the region of the Trojan Ida. But the variation in these accounts is so small that, whereas some represent the Corybantes, the Cabeiri, the Idaean Dactyli, and the Telchines as identical with the Curetes, others represent them as all kinsmen of one another and differentiate only certain small matters in which they differ in respect to one another; but, roughly speaking and in general, they represent them, one and all, as a kind of inspired people and as subject to Bacchic frenzy, and, in the guise of ministers, as inspiring terror at the celebration of the sacred rites by means of war‑dances, accompanied by uproar and noise and cymbals and drums and arms, and also by flute and outcry; and consequently these rites are in a way regarded as having a common relationship, I mean these and those of the Samothracians and those in Lemnos and in several other places, because the divine ministers are called the same. However, every investigation of this kind pertains to theology, and is not foreign to the speculation of the philosopher.
8 But since also the historians, because of the identity of name of the Curetes, have classed together things that are unlike, neither should I myself shrink from discussing them at greater length, by way of digression, adding such account of their physical habits as is appropriate to history. And yet some historians even wish to assimilate their physical habits with those others, and perhaps there is something plausible in their undertaking. For instance, they say that the Curetes of Aetolia got this name because, like "girls," they wore women's clothes, for, they add, there was a fashion of this kind among the Greeks, and the Ionians were called "tunic-trailing," and the soldiers of Leonidas were "dressing their hair" when they were to go forth to battle, so that the Persians, it is said, conceived a contempt for them, though in the battle they marvelled at them. Speaking generally, the art of caring for the hair consists both in its nurture and in the way it is cut, and both are given special attention by "girls" and "youths"; so that there are several ways in which it is easy to derive an etymology of the word "Curetes." It is reasonable to suppose, also, that the war‑dance was first introduced by persons who were trained in this particular way in the matter of hair and dress, these being called Curetes, and that this dance afforded a pretext to those also who were more warlike than the rest and spent their life under arms, so that they too came to be called by the same name, "Curetes" — I mean the Curetes in Euboea, Aetolia, and Acarnania. And indeed him applied this name to young soldiers, "choose thou the noblest young men from all the Achaeans, and bring the gifts from the swift ship, all that we promised yesterday to Achilles"; and again, "the young men of the Achaeans brought the gifts. So much for the etymology of the word "Curetes." The war‑dance was a soldier's dance and this is plainly indicated both by the "Pyrrhic dance," and by "Pyrrichus," who is said to be the founder of this kind of training for young men, as also by the treatises on military affairs.
9 But I must now investigate how it comes about that so many names have been used of one and the same thing, and the theological element contained in their history. Now this is common both to the Greeks and to the barbarians, to perform their sacred rites in connection with the relaxation of a festival, these rites being performed sometimes with religious frenzy, sometimes without it; sometimes with music, sometimes not; and sometimes in secret, sometimes openly. And it is in accordance with the dictates of nature that this should be so, for, in the first place, the relaxation draws the mind away from human occupations and turns the real mind towards that which is divine; and, secondly, the religious frenzy seems to afford a kind of divine inspiration and to be very like that of the soothsayer; and, thirdly, the secrecy with which the sacred rites are concealed induces reverence for the divine, which is to avoid being perceived by our human senses; and, fourthly, music, which includes dancing as well as rhythm and melody, at the same time, by the delight it affords and by its artistic beauty, brings us in touch with the divine, and this for the following reason; for although it has been well said that human beings then act most like the gods when they are doing good to others, yet one might better say, when they are happy; and such happiness consists of rejoicing, celebrating festivals, pursuing philosophy, and engaging in music; for, if music is perverted when musicians turn their arts to sensual delights at symposiums and in orchestric and scenic performances and the like, we should not lay the blame upon music itself, but should rather examine the nature of our system of education, since this is based on music.
And on this account Plato, and even before his time the Pythagoreians, called philosophy music; and they say that the universe is constituted in accordance with harmony, assuming that every form of music is the work of the gods. And in this sense, also, the Muses are goddesses, and Apollo is leader of the Muses, and poetry as a whole is laudatory of the gods. And by the same course of reasoning they also attribute to music the upbuilding of morals, believing that everything which tends to correct the mind is close to the gods. Now most of the Greeks assigned to Dionysus, Apollo, Hecatê, the Muses, and above all to Demeter, everything of an orgiastic or Bacchic or choral nature; and they give the name "Iacchus" not only to Dionysus but also to the leader-in‑chief of the mysteries, who is the genius of Demeter. And branch-bearing, choral dancing, and initiations are common elements in the worship of these gods. As for the Muses and Apollo, the Muses preside over the choruses, whereas Apollo presides both over these and the rites of divination. But all educated men, and especially the musicians, are ministers of the Muses; and both these and those who have to do with divination are ministers of Apollo; and the initiated and torch-bearers and hierophants, of Demeter; and the Sileni and Satyri and Bacchae, and also the Lenae and Thyiae and Mimallones and Naïdes and Nymphae and the beings called Tityri, of Dionysus.
In Crete, not only these rites, but in particular those sacred to Zeus, were performed along with orgiastic worship and with the kind of ministers who were in the service of Dionysus, I mean the Satyri. These ministers they called "Curetes," young men who executed movements in armour, accompanied by dancing, as they set forth the mythical story of the birth of Zeus; in this they introduced Cronus as accustomed to swallow his children immediately after their birth, and Rhea as trying to keep her travail secret and, when the child was born, to get it out of the way and save its life by every means in her power; and to accomplish this it is said that she took as helpers the Curetes, who, by surrounding the goddess with tambourines and similar noisy instruments and with war‑dance and uproar, were supposed to strike terror into Cronus and without his knowledge to steal his child away; and that, according to tradition, Zeus was actually reared by them with the same diligence; consequently the Curetes, either because, being young, that is "youths," they performed this service, or because they "reared" Zeus "in his youth" (for both explanations are given), were accorded this appellation, as if they were Satyrs, so to speak, in the service of Zeus. Such, then, were the Greeks in the matter of orgiastic worship.
But as for the Berecyntes, a tribe of Phrygians, and the Phrygians in general, and those of the Trojans who live round Ida, they too hold Rhea in honour and worship her with orgies, calling her Mother of the gods and Agdistis and Phrygia the Great Goddess, and also, from the places where she is worshipped, Idaea and Dindymenê and Sipylenê and Pessinuntis and Cybelê and Cybebê. The Greeks use the same name "Curetes" for the ministers of this goddess, not taking the name, however, from the same mythical story, but regarding them as a different set of "Curetes," helpers as it were, analogous to the Satyri; and the same they also call Corybantes.
The poets bear witness to such views as I have suggested. For instance, when Pindar, in the dithyramb which begins with these words, "In earlier times there marchedthe lay of the dithyrambs long drawn out," mentions the hymns sung in honour of Dionysus, both the ancient and the later ones, and then, passing on from these, says, "To perform the prelude in thy honour, great Mother, the whirling of cymbals is at hand, and among them, also, the clanging of castanets, and the torch that blazeth beneath the tawny pine-trees," he bears witness to the common relationship between the rites exhibited in the worship of Dionysus among the Greeks and those in the worship of the Mother of the gods among the Phrygians, for he makes these rites closely akin to one another. And Euripides does likewise, in his Bacchae, citing the Lydian usages at the same time with those of Phrygia, because of their similarity: "But ye who left Mt. Tmolus, fortress of Lydia, revel-band of mine, women whom I brought from the land of barbarians as my assistants and travelling companions, uplift the tambourines native to Phrygian cities, inventions of mine and mother Rhea." And again, "happy he who, blest man, initiated in the mystic rites, is pure in his life, . . . who, preserving the righteous orgies of the great mother Cybelê, and brandishing the •thyrsus on high, and wreathed with ivy, doth worship Dionysus. Come, ye Bacchae, come, ye Bacchae, bringing down Bromius, god the child of god; Dionysus, out of the Phrygian mountains into the broad highways of Greece." And again, in the following verses he connects the Cretan usages also with the Phrygian: "O thou hiding-bower of the Curetes, and sacred haunts of Crete that gave birth to Zeus, where for me the triple-crested Corybantesin their caverns invented this hide-stretched circlet, and blent its Bacchic revelry with the high-pitched, sweet-sounding breath of Phrygian flutes, and in Rhea's hands placed its resounding noise, to accompany the shouts of the Bacchae, and from Mother Rhea frenzied Satyrs obtained it and joined it to the choral dances of the Trieterides, in whom Dionysus takes delight." And in the Palamedes the Chorus says, "Thysa, daughter of Dionysus, who on Ida rejoices with his dear mother in the Iacchic revels of tambourines."
And when they bring Seilenus and Marsyas and Olympus into one and the same connection, and make them the historical inventors of flutes, they again, a second time, connect the Dionysiac and the Phrygian rites; and they often in a confused manner drum on Ida and Olympus as the same mountain. Now there are four peaks of Ida called Olympus, near Antandria; and there is also the Mysian Olympus, which indeed borders on Ida, but is not the same. At any rate, Sophocles, in his Polyxena, representing Menelaüs as in haste to set sail from Troy, but Agamemnon as wishing to remain behind for a short time for the sake of propitiating Athena, introduces Menelaüs as saying, "But do thou, here remaining, somewhere in the Idaean land collect flocks of Olympus and offer them in sacrifice."
They invented names appropriate to the flute, and to the noises made by castanets, cymbals, and drums, and to their acclamations and shouts of "ev‑ah," and stampings of the feet; and they also invented some of the names by which to designate the ministers, choral dancers, and attendants upon the sacred rites, I mean "Cabeiri" and "Corybantes" and "Pans" and "Satyri" and "Tityri," and they called the god "Bacchus," and Rhea "Cybelê" or "Cybebê" or "Dindymenê" according to the places where she was worshipped. Sabazius also belongs to the Phrygian group and in a way is the child of the Mother, since he too transmitted the rites of Dionysus.
Also resembling these rites are the Cotytian and the Bendidaean rites practised among the Thracians, among whom the Orphic rites had their beginning. Now the Cotys who is worshipped among the Edonians, and also the instruments used in her rites, are mentioned by Aeschylus; for he says, "O adorable Cotys among the Edonians, and ye who hold mountain-ranging instruments"; and he mentions immediately afterwards the attendants of Dionysus: "one, holding in his hands the bombyces, toilsome work of the turner's chisel, fills full the fingered melody, the call that brings on frenzy, while another causes to resound the bronze-bound cotylae"; and again, "stringed instruments raise their shill cry, and frightful mimickers from some place unseen bellow like bulls, and the semblance of drums, as of subterranean thunder, rolls along, a terrifying sound"; for these rites resemble the Phrygian rites, and it is at least not unlikely that, just as the Phrygians themselves were colonists from Thrace, so also their sacred rites were borrowed from there. Also when they identify Dionysus and the Edonian Lycurgus, they hint at the homogeneity of their sacred rites.
From its melody and rhythm and instruments, all Thracian music has been considered to be Asiatic. And this is clear, first, from the places where the Muses have been worshipped, for Pieria and Olympus and Pimpla and Leibethrum were in ancient times Thracian places and mountains, though they are now held by the Macedonians; and again, Helicon was consecrated to the Muses by the Thracians who settled in Boeotia, the same who consecrated the cave of the nymphs called Leibethrides. And again, those who devoted their attention to the music of early times are called Thracians, I mean Orpheus, Musaeus, and Thamyris; and Eumolpus, too, got his name from there. And those writers who have consecrated the whole of Asia, as far as India, to Dionysus, derive the greater part of music from there. And one writer says, "striking the Asiatic cithara"; another calls flutes "Berecyntian" and "Phrygian"; and some of the instruments have been called by barbarian names, "nablas," "sambycê," "barbitos," "magadis," and several others.
Just as in all other respects the Athenians continue to be hospitable to things foreign, so also in their worship of the gods; for they welcomed so many of the foreign rites that they were ridiculed therefor by the comic writers; and among these were the Thracian and Phrygian rites. For instance, the Bendideian rites are mentioned by Plato, and the Phrygian by Demosthenes, when he casts the reproach upon Aeschines' mother and Aeschines himself that he was with her when she conducted initiations, that he joined her in leading the Dionysiac march, and that many a time he cried out "êvoe saboe," and "hyês attês, attês hyês"; for these words are in the ritual of Sabazius and the Mother.
Further, one might also find, in addition to these facts concerning these genii and their various names, that they were called, not only ministers of gods, but also gods themselves. For instance, Hesiod says that five daughters were born to Hecaterus and the daughter of Phoroneus, "from whom sprang the mountain-ranging nymphs, goddesses, and the breed of Satyrs, creatures worthless and unfit for work, and also the Curetes, sportive gods, dancers." And the author of Phoronis speaks of the Curetes as "flute-players" and "Phrygians"; and others as "earth-born" and "wearing brazen shields." Some call the Corybantes, and not the Curetes, "Phrygians," but the Curetes "Cretes," and say that the Cretes were the first people to don brazen armour in Euboea, and that on this account they were also called "Chalcidians"; still others say that the Corybantes, who came from Bactriana (some say from among the Colchians), were given as armed ministers to Rhea by the Titans. But in the Cretan accounts the Curetes are called "rearers of Zeus," and "protectors of Zeus," having been summoned for Phrygia to Crete by Rhea. Some say that, of the nine Telchines who lived in Rhodes, those who accompanied Rhea to Crete and "reared" Zeus "in his youth" were named "Curetes"; and that Cyrbas, a comrade of these, who was the founder of Hierapytna, afforded a pretext to the Prasians for saying among the Rhodians that the Corybantes were certain genii, sons of Athena and Helius. Further, some call the Corybantes sons of Cronus, but others say that the Corybantes were sons of Zeus and Calliopê and were identical with the Cabeiri, and that these went off to Samothrace, which in earlier times was called Melitê, and that their rites were mystical.
But though the Scepsian, who compiled these myths, does not accept the last statement, on the ground that no mystic story of the Cabeiri is told in Samothrace, still he cites also the opinion of Stesimbrotus the Thasian that the sacred rites in Samothrace were performed in honour of the Cabeiri: and the Scepsian says that they were called Cabeiri after the mountain Cabeirus in Berecyntia. Some, however, believe that the Curetes were the same as the Corybantes and were ministers of Hecatê. But the Scepsian again states, in opposition to the words of Euripides, that the rites of Rhea were not sanctioned or in vogue in Crete, but only in Phrygia and the Troad, and that those who say otherwise are dealing in myths rather than in history, though perhaps the identity of the place-names contributed to their making this mistake. For instance, Ida is not only a Trojan, but also a Cretan, mountain; and Dictê is a place in Scepsia and also a mountain in Crete; and Pytna, after which the city Hierapytna was named, is a peak of Ida. And there is a Hippocorona in the territory of Adramyttium and a Hippocoronium in Crete. And Samonium is the eastern promontory of the island and a plain in the territory of Neandria and in that of the Alexandreians.
Acusilaüs, the Argive, calls Cadmilus the son of Cabeiro and Hephaestus, and Cadmilus the father of three Cabeiri, and these the fathers of the nymphs called Cabeirides. Pherecydes says that nine Cyrbantes were sprung from Apollo and Rhetia, and that they took up their abode in Samothrace; and that three Cabeiri and three nymphs called Cabeirides were the children of Cabeiro, the daughter of Proteus, and Hephaestus, and that sacred rites were instituted in honour of each triad. Now it has so happened that the Cabeiri are most honoured in Imbros and Lemnos, but they are also honoured in separate cities of the Troad; their names, however, are kept secret. Herodotus says that there were temples of the Cabeiri in Memphis, as also of Hephaestus, but that Cambyses destroyed them. The places where these deities were worshipped are uninhabited, both the Corybanteium in Hamaxitia in the territory now belonging to the Alexandreians near Sminthium, and Corybissa in Scepsia in the neighbourhood of the river Eurëeis and of the village which bears the same name and also of the winter-torrent Aethalöeis. The Scepsian says that it is probable that the Curetes and the Corybantes were the same, being those who had been accepted as young men, or "youths," for the war‑dance in connection with the holy rites of the Mother of the gods, and also as "corybantes" from the fact that they "walked with a butting of their heads" in a dancing way. These are called by the poet "betarmones": "Come now, all ye that are the best 'betarmones' of the Phaeacians." And because the Corybantes are inclined to dancing and to religious frenzy, we say of those who stirred with frenzy that they are "corybantising."
Some writers say that the name "Idaean Dactyli" was given to the first settlers of the lower slopes of Mt. Ida, for the lower slopes of mountains are called "feet," and the summits "heads"; accordingly, the several extremities of Ida (all of which are sacred to the Mother of the gods) were called Dactyli. Sophocles thinks that the first male Dactyli were five in number, who were the first to discover and to work iron, as well as many other things which are useful for the purposes of life, and that their sisters were five in number, and that they were called Dactyli from their number. But different writers tell the myth in different ways, joining difficulty to difficulty; and both the names and numbers they use are different; and they name one of them "Celmis" and others "Damnameneus" and "Heracles" and "Acmon." Some call them natives of Ida, others settlers; but all agree that iron was first worked by these on Ida; and all have assumed that they were wizards and attendants of the Mother of the gods, and that they lived in Phrygia about Ida; and they use the term Phrygia for the Troad because, after Troy was sacked, the Phrygians, whose territory bordered on the Troad, got the mastery over it. And they suspect that both the Curetes and the Corybantes were offspring of the Idaean Dactyli; at any rate, the first hundred men born in Crete were called Idaean Dactyli, they say, and as offspring of these were born nine Curetes, and each of these begot ten children who were called Idaean Dactyli.
I have been led on to discuss these people rather at length, although I am not in the least fond of myths, because the facts in their case border on the province of theology. And theology as a whole must examine early opinions and myths, since the ancients expressed enigmatically the physical notions which they entertained concerning the facts and always added the mythical element to their accounts. Now it is not easy to solve with accuracy all the enigmas, but if the multitude of myths be set before us, some agreeing and others contradicting one another, one might be able more readily to conjecture out of them what the truth is. For instance, men probably speak in their myths about the "mountain-roaming" of religious zealots and of gods themselves, and about their "religious frenzies," for the same reason that they are prompted to believe that the gods dwell in the skies and show forethought, among their other interests, for prognostication by signs. Now seeking for metals, and hunting, and searching for the things that are useful for the purposes of life, are manifestly closely related to mountain-roaming, whereas juggling and magic are closely related to religious frenzies, worship, and divination. And such also is devotion to the arts, in particular to the Dionysiac and Orphic arts. But enough on this subject. |
|
|
|
|
10 - 4 Crete 
1 Since I have already described the islands of the Peloponnesus in detail, not only the others, but also those in the Corinthian Gulf and those in front of it, I must next discuss Crete (for it, too, belongs to the Peloponnesus) and any islands that are in the neighbourhood of Crete. Among these the Cyclades and the Sporades, some worthy of mention, others of less significance.
2 But at present let me first discuss Crete. Now although Eudoxus says that it is situated in the Aegaean Sea, one should not so state, but rather that it lies between Cyrenea and that part of Greece which extends from Sunium to Laconia, stretching lengthwise parallel with these countries from west to east, and that it is washed on the north by the Aegaean and the Cretan Seas, and on the south by the Libyan Sea, which borders on the Aegyptian. As for its two extremities, the western is in the neighbourhood of Phalasarna; it has a breadth of about two hundred stadia and is divided into two promontories (of these the southern is called Criumetopon, the northern Cimarus), whereas the eastern is Samonium, which falls toward the east not much farther than Sunium.
3 As for its size, Sosicrates, whose account of the island, according to Apollodorus, is exact, defines it as follows: In length, more than two thousand three hundred stadia, and in breadth, . . . , so that its circuit, according to him, would amount to more than five thousand stadia; but Artemidorus says it is four thousand one hundred. Hieronymus says that its length is two thousand stadia and its breadth irregular, and therefore might mean that the circuit is greater than Artemidorus says. For about a third of its length . . .; and then comes an isthmus of about one hundred stadia, which, on the northern sea, has a settlement called Amphimalla, and, on the southern, Phoenix, belonging to the Lampians. The island is broadest near the middle. And from here the shores again converge to an isthmus narrower than the former, about sixty stadia in width, which extends from Minoa, city of the Lyctians, to Hierapytna and the Libyan Sea; the city is situated on the gulf. Then the island projects into a sharp promontory, Samonium, which slopes in the direction of Aegypt and the islands of the Rhodians.
4 The island is mountainous and thickly wooded, but it has fruitful glens. Of the mountains, those towards the west are called Leuca;6 they do not fall short of Taÿgetus in height, extend in length about three hundred stadia, and form a ridge which terminates approximately at the narrows. In the middle, in the most spacious part of the island, is Mount Ida, loftiest of the mountains of Crete and circular in shape, with a circuit of six hundred stadia; and around it are the best cities. There are other mountains in Crete that are about as high as the Leuca, some terminating towards the south and others towards the east.
5 The voyage from Cyrenaea to Criumetopon takes two days and nights, and the distance from Cimarus to Taenarum is seven hundred stadia, Cythera lying between them; and the voyage from Samonium to Aegypt takes four days and nights, though some say three. Some state that this is a voyage of five thousand stadia, but others still less. Eratosthenes says that the distance from Cyrenaea to Criumetopon is two thousand, and from there to the Peloponnesus less . . .
6 "But one tongue with others is mixed," the poet says; "there dwell Achaeans, there Eteo-Cretans proud of heart, there Cydonians and Dorians, too, of waving plumes, and goodly Pelasgians." Of these peoples, according to Staphylus, the Dorians occupy the part towards the east, the Cydonians the western part, the Eteo-Cretans the southern; and to these last belongs the town Prasus, where is the temple of the Dictaean Zeus; whereas the other peoples, since they were more powerful, dwelt in the plains. Now it is reasonable to suppose that the Eteo-Cretans and the Cydonians were autochthonous, and that the others were foreigners, who, according to Andron, came from Thessaly, from the country which in earlier times was called Doris, but is now called Hestiaeotis; it was from this country that the Dorians who lived in the neighbourhood of Parnassus set out, as he says, and founded Erineüs, Boeüm, and Cytinium, and hence by Homer are called "trichaïces." However, writers do not accept the account of Andron at all, since he represents the Tetrapolis Doris as being a Tripolis, and the metropolis of the Dorians as a mere colony of Thessalians; and they derive the meaning of "trichaïces" either from the "trilophia," or from the fact that the crests were "trichini."
7 There are several cities in Crete, but the greatest and most famous are three: Cnossus, Gortyna and Cydonia. The praises of Cnossus are hymned above the rest both by Homer, who calls it "great" and "the kingdom of Minos," and by the later poets. Furthermore, it continued for a long time to win the first honours; then it was humbled and deprived of many of its prerogatives, and its superior rank passed over to Gortyna and Lyctus; but later it again recovered its olden dignity as the metropolis. Cnossus is situated in a plain, its original circuit being thirty stadia, between the Lyctian and Gortynian territories, being two hundred stadia distant from Gortyna, and a hundred and twenty from Lyttus, which the poet named Lyctus. Cnossus is twenty-five stadia from the northern sea, Gortyna is ninety from the Libyan Sea, and Lyctus itself is eighty from the Libyan. And Cnossus has Heracleium as its seaport.
8 But Minos is said to have used as seaport Amnisus, where is the temple of Eileithuia. In earlier times Cnossus was called Caeratus, bearing the same name as the river which flows past it. According to history, Minos was an excellent law‑giver, and also the first to gain the mastery of the sea; and he divided the island into three parts and founded a city in each part, Cnossus in the . . . opposite the Peloponnesus. And it, too, lies to the north. As Ephorus states, Minos was an emulator of a certain Rhadamanthys of early times, a man most just and bearing the same name as Minos's brother, who is reputed to have been the first to civilise the island by establishing laws and by uniting cities under one city as metropolis by setting up constitutions, alleging that he brought from Zeus the several decrees which he promulgated. So, in imitation of Rhadamanthys, Minos would go up every nine years, as it appears, to the cave of Zeus, tarry there, and come back with commandments drawn up in writing, which he alleged were ordinances of Zeus; and it was for this reason that the poet says, "there Minos reigned as king, who held converse with great Zeus every ninth year." Such is the statement of Ephorus; but again the early writers have given a different account of Minos, which is contrary to that of Ephorus, saying that he was tyrannical, harsh, and an exactor of tribute, representing in tragedy the story of the Minotaur and the Labyrinth, and the adventures of Theseus and Daedalus.
9 Now, as for these two accounts, it is hard to say which is true; and there is another subject that is not agreed upon by all, some saying that Minos was a foreigner, but others that he was a native of the island. The poet, however, seems rather to advocate the second view when he says, "Zeus first begot Minos, guardian o'er Crete." In regard to Crete, writers agree that in ancient times it had good laws, and rendered the best of the Greeks its emulators, and in particular the Lacedaemonians, as is shown, for instance, by Plato in his Laws, and also by Ephorus, who in his Europe has described its constitution. But later it changed very much for the worse; for after the Tyrrhenians, who more than any other people ravaged Our Sea, the Cretans succeeded to the business of piracy; their piracy was later destroyed by the Cilicians; but all piracy was broken up by the Romans, who reduced Crete by war and also the piratical strongholds of the Cilicians. And at the present time Cnossus has even a colony of Romans.
So much for Cnossus, a city to which I myself am not alien, although, on account of man's fortune and of the changes and issues therein, the bonds which at first connected me with the city have disappeared: Dorylaüs was a military expert and one of the friends of Mithridates Euergetes. He, because of his experience in military affairs, was appointed to enlist mercenaries, and often visited not only Greece and Thrace, but also the mercenaries of Crete, that is, before the Romans were yet in possession of the island and while the number of mercenary soldiers in the island, from whom the piratical bands were also wont to be recruited, was large. Now when Dorylaüs was sojourning there war happened to break out between the Cnossians and the Gortynians, and he was appointed general, finished the war successfully, and speedily won the greatest honours. But when, a little later, he learned that Euergetes, as the result of a plot, had been treacherously slain in Sinopê by his closest associates, and heard that the succession had passed to his wife and young children, he despaired of the situation there and stayed on at Cnossus. There, by a Macetan woman, Steropê by name, he begot two sons, Lagetas and Stratarchas (the latter of whom I myself saw when he was an extremely old man), and also one daughter. Now Euergetes had two sons, one of whom, Mithridates, surnamed Eupator, succeeded to the rule when he was eleven years old. Dorylaüs, the son of Philetaerus, was his foster brother; and Philetaerus was a brother of Dorylaüs the military expert. And when the king Mithridates reached manhood, he was so infatuated with the companionship of his foster brother Dorylaüs that he not only conferred upon him the greatest honours, but also cared for his kinsmen and summoned those who lived at Cnossus. These were the household of Lagetas and his brother, their father having already died, and they themselves having reached manhood; and they quit Cnossus and went home. My mother's mother was the sister of Lagetas. Now when Lagetas prospered, these others shared in his prosperity, but when he was ruined (for he was caught in the act of trying to cause the kingdom to revolt to the Romans, on the understanding that he was to be established at the head of the government), their fortunes were also ruined at the same time, and they were reduced to humility; and the bonds which connected them with the Cnossians, who themselves had undergone countless changes, fell into neglect. But enough for my account of Cnossus.
After Cnossus, the city of the Gortynians seems to have ranked second in power; for when these two co‑operated they held in subjection all the rest of the inhabitants, and when they had a quarrel there was dissension throughout the island. But Cydonia was the greatest addition to whichever side it attached itself. The city of the Gortynians also lies in a plain; and in ancient times, perhaps, it was walled, as Homer states, "and well-walled Gortyn," but later it lost its walls from their very foundations, and has remained unwalled ever since; for although Ptolemy Philopator began to build a wall, he proceeded with it only about eighty stadia; at any rate, it is worth mentioning that the settlement once filled out a circuit of about fifty stadia. It is ninety stadia distant from the Libyan Sea at Leben, which is its trading-centre; it also has another seaport, Matalum, from which it is a hundred and thirty stadia distant. The Lethaeus River flows through the whole of its territory.
From Leben came Leucocomas and his lover Euxynthetus, the story of whom is told by Theophrastus in his treatise On Love. Of the tasks which Leucocomas assigned to Euxynthetus, one, he says, was this — to bring back his dog from Prasus. The country of the Prasians borders on that of the Lebenians, being seventy stadia distant from the sea and a hundred and eighty from Gortyn. As I have said, Prasus belonged to the Eteo-Cretans; and the temple of the Dictaean Zeus was there; for Dictê is near it, not "close to the Idaean Mountain," as Aratus says, for Dictê is a thousand stadia distant from Ida, being situated at that distance from it towards the rising sun, and a hundred from Samonium. Prasus was situated between Samonium and the Cherronesus, sixty stadia above the sea; it was rased to the ground by the Hierapytnians. And neither is Callimachus right, they say, when he says that Britomartis, in her flight from the violence of Minos, leaped from Dictê into fishermen's "nets," and that because of this she herself was called Dictynna by the Cydoniatae, and the mountain Dictê; for Cydonia is not in the neighbourhood of these places at all, but lies near the western limits of the island. However, there is a mountain called Tityrus in Cydonia, on which is a temple, not the "Dictaean" temple, but the "Dictynnaean."
Cydonia is situated on the sea, facing Laconia, and is equidistant, about eight hundred stadia, from the two cities Cnossus and Gortyn, and is eighty stadia distant from Aptera, and forty from the sea in that region. The seaport of Aptera is Cisamus. The territory of the Polyrrhenians borders on that of the Cydoniatae towards the west, and the temple of Dictynna is in their territory. They are about thirty stadia distant from the sea, and sixty from Phalasarna. They lived in villages in earlier times; and then Achaeans and Laconians made a common settlement, building a wall round a place that was naturally strong and faced towards the south.
Of the three cities that were united under one metropolis by Minos, the third, which was Phaestus, was rased to the ground by the Gortynians; it is sixty stadia distant from Gortyn, twenty from the sea, and forty from the seaport Matalum; and the country is held by those who rased it. Rhytium, also, together with Phaestus, belongs to the Gortynians: "and Phaestus and Rhytium." Epimenides, who performed the purifications by means of his verses, is said to have been from Phaestus. And Lissen also is in the Phaestian territory. Of Lyctus, which I have mentioned before, the seaport is Chersonesus, as it is called, where is the temple of Britomartis. But the cities Miletus and Lycastus, which are catalogued along with Lyctus, no longer exist; and as for their territory, the Lyctians took one portion of it and the Cnossians the other, after they had rased the city to the ground.
Since the poet speaks of Crete at one time as "possessing a hundred cities," and also at another as "possessing ninety cities," Ephorus says that the ten were founded later than the others, after the Trojan War, by the Dorians who accompanied Althaemenes the Argive; he adds that it was Odysseus, however, who called it "Crete of the ninety cities." Now this statement is plausible, but others say that the ten cities were rased to the ground by the enemies of Idomeneus. However, in the first place, the poet does not say that Crete had one hundred cities at the time of the Trojan War, but rather in his own time (for he is speaking in his own person, although, if the statement was made by some person who was living at the time of the Trojan War, as is the case in the Odyssey, when Odysseus says "of the ninety cities," then it would be well to interpret it accordingly). In the second place, if we should concede this, the next statement could not be maintained; for it is not likely that these cities were wiped out by the enemies of Idomeneus either during the expedition or after his return from Troy; for when the poet said, "and all his companions Idomeneus brought to Crete, all who escaped from the war, and the sea robbed him of none," he would also have mentioned this disaster; for of course Odysseus could not have known of the obliteration of the cities, since he came in contact with no Greeks either during his wanderings or later. And he who accompanied Idomeneus on the expedition to Troy and returned safely at home at the same time could not have known what occurred in the homeland of Idomeneus either during the expedition or the return from Troy, nor yet even after the return; for if Idomeneus escaped with all his companions, he returned home strong, and therefore his enemies were not likely to be strong enough to take ten cities away from him. Such, then, is my description of the country of the Cretans.
As for their constitution, which is described by Ephorus, it might suffice to tell in a cursory way its most important provisions. The lawgiver, he says, seems to take it from granted that liberty is a state's greatest good, for this alone makes property belong specifically to those who have acquired it, whereas in a condition of slavery everything belongs to the rulers and not to the ruled; but those who have liberty must guard it; now harmony ensues when dissension, which is the result of greed and luxury, is removed; for when all citizens live a self-restrained and simple life there arises neither envy nor arrogance nor hatred towards those who are like them; and this is why the lawgiver commanded the boys to attend the "Troops," as they are called, and the full-grown men to eat together at the public mess which they call the "Andreia," so that the poorer, being fed at public expense, might be on an equality with the well-to‑do; and in order that courage, and not cowardice, might prevail, he commanded that from boyhood they should grow up accustomed to arms and toils, so as to scorn heat, cold, marches over rugged and steep roads, and blows received in gymnasiums or regular battles; and that they should practise, not only archery, but also the war‑dance, which was invented and made known by the Curetes at first, and later, also, by the man who arranged the dance that was named after him, I mean the Pyrrhic dance, so that not even their sports were without a share in activities that were useful for warfare; and likewise that they should use in their songs the Cretic rhythms, which were very high-pitched, and were invented by Thales, to whom they ascribe, not only their Paeans and other local songs, but also many of their institutions; and that they should use military dress and shoes; and that arms should be to them the most valuable of gifts.
It is said by some writers, Ephorus continues, that most of the Cretan institutions are Laconian, but the truth is that they were invented by the Cretans and only perfected by the Spartans; and the Cretans, when their cities, and particularly that of the Cnossians, were devastated, neglected military affairs; but some of the institutions continued in use among the Lyctians, Gortynians, and certain other small cities to a greater extent than among the Cnossians; in fact, the institutions of the Lyctians are cited as evidence by those who represent the Laconian as older; for, they argue, being colonists, they preserve the customs of the mother-city, whence even on general grounds it is absurd to represent those who are better organised and governed as emulators of their inferiors; but this is not correct, Ephorus says, for, in the first place, one should not draw evidence as to antiquity from the present state of things, for both peoples have undergone a complete reversal; for instance, the Cretans in earlier times were masters of the sea, and hence the proverb, "The Cretan does not know the sea," is applied to those who pretend not to know what they do know, although now the Cretans have lost their fleet; and, in the second place, it does not follow that, because some of the cities in Crete were Spartan colonies, they were under compulsion to keep to the Spartan institutions; at any rate, many colonial cities do not observe their ancestral customs, and many, also, of those in Crete that are not colonial have the same customs as the colonists.
Lycurgus the Spartan law‑giver, Ephorus continues, was five generations later than the Althaemenes who conducted the colony to Crete; for historians say that Althaemenes was son of the Cissus who founded Argos about the same time when Procles was establishing Sparta as metropolis; and Lycurgus, as agreed by all, was sixth in descent from Procles; and copies are not earlier than their models, nor more recent things earlier than older things; not only the dancing which is customary among the Lacedaemonians, but also the rhythms and paeans that are sung according to the law, and many other Spartan institutions, are called "Cretan" among the Lacedaemonians, as though they originated in Crete; and some of the public offices are not only administered in the same way as in Crete, but also have the same names, as, for instance, the office of the "Gerontes," and that of the "Hippeis" (except that the "Hippeis" in Crete actually possessed horses, and from this fact it is inferred that the office of the "Hippeis" in Crete is older, for they preserve the true meaning of the appellation, whereas the Lacedaemonian "Hippeis" do not keep horses); but though the Ephors have the same functions as the Cretan Cosmi, they have been named differently; and the public messes are, even to‑day, still called "Andreia" among the Cretans, but among the Spartans they ceased to be called by the same name as in earlier times;at any rate, the following is found in Alcman: "In feasts and festive gatherings, amongst the guests who partake of the Andreia, 'tis meet to begin the paean."
It is said by the Cretans, Ephorus continues, that Lycurgus came to them for the following reason: Polydectes was the elder brother of Lycurgus; when he died he left his wife pregnant; now for a time Lycurgus reigned in his brother's place, but when a child was born he became the child's guardian, since the office of king descended to the child, but some man, railing at Lycurgus, said that he knew for sure that Lycurgus would be king; and Lycurgus, suspecting that in consequence of such talk he himself might be falsely accused of plotting against the child, and fearing that, if by any chance the child should die, he himself might be blamed for it by his enemies, sailed away to Crete; this, then, is said to be the cause of his sojourn in Crete; and when he arrived he associated with Thales, a melic poet and an expert in lawgiving; and after learning from him the manner in which both Rhadamanthys in earlier times and Minos in later times published their laws to men as from Zeus, and after sojourning in Egypt also and learning among other things their institutions, and, according to some writers, after meeting Homer, who was living in Chios, he sailed back to his homeland, and found his brother's son, Charilaüs the son of Polydectes, reigning as king; and then he set out to frame the laws, making visits to the god at Delphi, and bringing thence the god's decrees, just as Minos and his house had brought their ordinances from the cave of Zeus, most of his being similar to theirs.
The following are the most important provisions in the Cretan institutions as stated by Ephorus. In Crete all those who are selected out of the "Troop" of boys at the same time are forced to marry at the same time, although they do not take the girls whom they have married to their own homes immediately, but as soon as the girls are qualified to manage the affairs of the house. A girl's dower, if she has brothers, is half of the brother's portion. The children must learn, not only their letters, but also the songs prescribed in the laws and certain forms of music. Now those who are still younger are taken to the public messes, the "Andreia"; and they sit together on the ground as they eat their food, clad in shabby garments, the same both winter and summer, and they also wait on the men as well as themselves. And those who eat together at the same mess join battle both with one another and with those from different messes. A boy‑director presides over each mess. But the older boys are taken to the "Troops"; and the most conspicuous and influential of the boys assemble the "Troops," each collecting as many boys as he possibly can; the leader of each "Troop" is generally the father of the assembler, and he has authority to lead them forth to hunt and to run races, and to punish anyone who is disobedient; and they are fed at public expense; and on certain appointed days "Troop" contends with "Troop," marching rhythmically into battle, to the tune of flute and lyre, as is their custom in actual war; and they actually bear marks of the blows received, some inflicted by the hand, others by iron weapons.
They have a peculiar custom in regard to love affairs, for they win the objects of their love, not by persuasion, but by abduction; the lover tells the friends of the boy three or four days beforehand that he is going to make the abduction; but for the friends to conceal the boy, or not to let him go forth by the appointed road, is indeed a most disgraceful thing, a confession, as it were, that the boy is unworthy to obtain such a lover; and when they meet, if the abductor is the boy's equal or superior in rank or other respects, the friends pursue him and lay hold of him, though only in a very gentle way, thus satisfying the custom; and after that they cheerfully turn the boy over to him to lead away; if, however, the abductor is unworthy, they take the boy away from him. And the pursuit does not end until the boy is taken to the "Andreium" of his abductor. They regard as a worthy object of love, but the boy who is exceptionally handsome, but the boy who is exceptionally manly and decorous. After giving the boy presents, the abductor takes him away to any place in the country he wishes; and those who were present at the abduction follow after them, and after feasting and hunting with them for two months (for it is not permitted to detain the boy for a longer time), they return to the city. The boy is released after receiving as presents a military habit, an ox, and a drinking‑cup (these are the gifts required by law), and other things so numerous and costly that the friends, on account of the number of the expenses, make contributions thereto. Now the boy sacrifices the ox to Zeus and feasts those who returned with him; and then he makes known the facts about his intimacy with his lover, whether, perchance, it has pleased him or not, the law allowing him this privilege in order that, 4if any force was applied to him at the time of the abduction, he might be able at this feast to avenge himself and be rid of the lover. It is disgraceful for those who are handsome in appearance or descendants of illustrious ancestors to fail to obtain lovers, the presumption being that their character is responsible for such a fate. But the parastathentes (for thus they call those who have been abducted) receive honours; for in both the dances and the races they have the positions of highest honour, and are allowed to dress in better clothes than the rest, that is, in the habit given them by their lovers; and not then only, but even after they have grown to manhood, they wear a distinctive dress, which is intended to make known the fact that each wearer has become "kleinos," for they call the loved one "kleinos" and the lover "philetor." So much for their customs in regard to love affairs.
The Cretans choose ten Archons. Concerning the matters of greatest importance they use as counsellors the "Gerontes," as they are called. Those who have been thought worthy to hold the office of the "Cosmi" and are otherwise adjudged men of approved worth are appointed members of this Council. I have assumed that the constitution of the Cretans is worthy of description both on account of its peculiar character and on account of its fame. Not many, however, of these institutions endure, but the administration of affairs is carried on mostly by means of the decrees of the Romans, as is also the case in the other provinces. |
|
|







|
|
10 - 5 Greek islands (Sporades and Cyclades) 
1 The islands near Crete are Thera, the metropolis of the Cyrenaeans, a colony of the Lacedaemonians, and, near Thera, Anaphê, where is the temple of the Aegletan Apollo. Callimachus speaks in one place as follows, "Aegletan Anaphê, neighbour to Laconian Thera," and in another, mentioning only Thera, "mother of my fatherland, famed for its horses." Thera is a long island, being two hundred stadia in perimeter; it lies opposite Dia, an island near the Cnossian Heracleium, but it is seven hundred stadia distant from Crete. Near it are both Anaphê and Therasia. One hundred stadia distant from the latter is the little island Ios, where, according to some writers, the poet Homer was buried. From Ios towards the west one comes of Sicinos and Lagusa and Pholegandros, which last Aratus calls "Iron" Island, because of its ruggedness. Near these is Cimolos, whence comes the Cimolian earth. From Cimolos Siphnos is visible, in reference to which island, because of its worthlessness, people say "Siphnian knuckle-bone." And still nearer both to Cimolos and to Crete is Melos, which is more notable than these and is seven hundred stadia from the Hermionic promontory, the Scyllaeum, and almost the same distance from the Dictynnaeum. The Athenians once sent an expedition to Melos and slaughtered most of the inhabitants from youth upwards. Now these islands are indeed in the Cretan Sea, but Delos itself and the Cyclades in its neighbourhood and the Sporades which lie close to these, to which belong the aforesaid islands in the neighbourhood of Crete, are rather in the Aegaean Sea.
2 Now the city which belongs to Delos, as also the temple of Apollo, and the Letöum, are situated in a plain; and above the city lies Cynthus, a bare and rugged mountain; and a river named Inopus flows through the island — not a large river, for the island itself is small. From olden times, beginning with the times of the heroes, Delos has been revered because of its gods, for the myth is told that there Leto was delivered of her travail by the birth of Apollo and Artemis: "for aforetime," says Pindar, "it was tossed by the billows, by the blasts of all manner of winds, but when the daughter of Coeüs in the frenzied pangs of childbirth set foot upon it, then did four pillars, resting on adamant, rise perpendicular from the roots of the earth, and on their capitals sustain the rock. And there she gave birth to, and beheld, her blessed offspring." The neighbouring islands, called the Cyclades, made it famous, since in its honour they would send at public expense sacred envoys, sacrifices, and choruses composed of virgins, and would celebrate great general festivals there.
3 Now at first the Cyclades are said to have been only twelve in number, but later several others were added. At any rate, Artemidorus enumerates fifteen, after saying of Helena that it stretches parallel to the coast from Thoricus to Sunium and is a long island, about sixty stadia in length; for it is from Helena, he says, that the Cyclades, as they are called, begin; and he names Ceos, the island nearest to Helena, and, after this island, Cythnos and Seriphos and Melos and Siphnos and Cimolos and Prepesinthos and Oliaros, and, in addition to these, Paros, Naxos, Syros, Myconos, Tenos, Andros, and Gyaros. Now I consider all of these among the twelve except Prepesinthos, Oliaros, and Gyaros. When our ship anchored at one of these, Gyaros, I saw a small village that was settled by fishermen; and when we sailed away we took on board one of the fishermen, who had been chosen to go from there to Caesar as ambassador (Caesar was at Corinth, on his way to celebrate the Triumph after the victory at Actium). While on the voyage he told enquirers that he had been sent as ambassador to request a reduction in their tribute; for, he said, they were paying one hundred and fifty drachmas 4when they could only with difficulty pay one hundred. Aratus also points out the poverty of the island in his Catalepton: "O Leto, shortly thou wilt pass by me, who am like either iron Pholegandros or worthless Gyaros."
4 Now although Delos had become so famous, yet the rasing of Corinth to the ground by the Romans increased its fame still more; for the importers changed their business to Delos because they were attracted both by the immunity which the temple enjoyed and by the convenient situation of the harbour; for it is happily situated for those who are sailing from Italy and Greece to Asia. The general festival is a kind of commercial affair, and it was frequented by Romans more than by any other people, even when Corinth was still in existence. And when the Athenians took the island they at the same time took good care of the importers as well as of the religious rites. But when the generals of Mithridates, and the tyrant who caused it to revolt, visited Delos, they completely ruined it, and when the Romans again got the island, after the king withdrew to his homeland, it was desolate; and it has remained in an impoverished condition until the present time. It is now held by the Athenians.
5 Rheneia is a desert isle within four stadia from Delos, and there the Delians bury their dead; for it is unlawful to bury, or even burn, a corpse in Delos itself, and it is unlawful even to keep a dog there. In earlier times it was called Ortygia.
6 Ceos was at first a Tetrapolis, but only two cities are left, Iulis and Carthaea, into which the remaining two were incorporated, Poeëessa into Carthaea and Coressia into Iulis. Both Simonides the melic poet and his nephew Bacchylides were natives of Iulis, and also after their time Erasistratus the physician, and Ariston the peripatetic philosopher and emulator of Bion the Borysthenite. It is reputed that there was once a law among these people (it is mentioned by Menander, "Phanias, the law of the Ceians is good, that he who is unable to live well should not live wretchedly"), which appears to have ordered those who were over sixty years of age to drink hemlock, in order that the food might be sufficient for the rest. And it is said that once, when they were being besieged by the Athenians, they voted, setting a definite age, that the oldest among them should be put to death, but the Athenians raised the siege. The city lies on a mountain, about twenty-five stadia distant from the sea; and its seaport is the place on which Coressia was situated, which has not as great a population as even a village. Near Coressia, and also near Poeëessa, is a temple of Sminthian Apollo; and between the temple and the ruins of Poeëessa is the temple of Nedusian Athena, founded by Nestor when he was on his return from Troy. There is also a River Elixus in the neighbourhood of Coressia.
7 After Ceos one comes to Naxos and Andros, notable islands, and to Paros. Archilochus the poet was a native of Paros. Thasos was founded by the Parians, as also Parium, a city on the Propontis. Now the altar in this city is said to be a spectacle worth seeing, its sides being a stadium in length; and so is the Parian stone, as it is called, in Paros, the best for sculpture in marble.
8 And there is Syros (the first syllable is pronounced long), where Pherecydes the son of Babys was born. The Athenian Pherecydes is later than he. The poet seems to mention this island, though he calls it Syria: "There is an island called Syria, above Ortygia."
9 And there is Myconos, beneath which, according to the myth, lie the last of the giants that were destroyed by Heracles. Whence the proverb, "all beneath Myconos alone," applied to those who bring under one title even those things which are by nature separate. And further, some call bald men Myconians, from the fact that baldness is prevalent in the island.
And there is Seriphos, the scene of the mythical story of Dictys, who with his net drew to land the chest in which were enclosed Perseus and his mother Danaê, who had been sunk in the sea by Acrisius the father of Danaê; for Perseus was reared there, it is said, and when he brought the Gorgon's head there, he showed it to the Seriphians and turned them all into stone. This he did to avenge his mother, because Polydectes the king, with their co‑operation, intended to marry his mother against her will. The island is so rocky that comedians say that it was made thus by the Gorgon.
Tenos has no large city, but it has the temple of Poseidon, a great temple in a sacred precinct outside the city, a spectacle worth seeing. In it have been built great banquet-halls — an indication of the multitude of neighbours who congregate there and take part with the inhabitants of Tenos in celebrating the Poseidonian festival.
And there is Amorgos, one of the Sporades, the home of Simonides the iambic poet; and also Lebinthos, and Leros: "And thus saith Phocylides, 'the Lerians are bad, not one, but every one, all except Procles; and Procles is a Lerian.' " For the natives of the island were reproached with being unprincipled.
Near by are both Patmos and the Corassiae; these are situated to the west of Icaria, and Icaria to the west of Samos. Now Icaria is deserted, though it has pastures, which are used by the Samians. But although it is such an isle as it is, still it is famous, and after it is named the sea that lies in front of it, in which are itself and Samos and Cos and the islands just mentioned — the Corassiae and Patmos and Leros. Famous, also, is the mountain in it, Cerceteus, more famous than the Ampelus,which is situated about the city of Samians. The Icarian Sea connects with the Carpathian Sea on the south, and the Carpathian with the Aegyptian, and on the west with the Cretan and the Libyan.
In the Carpathian Sea, also, are many of the Sporades, and in particular between Cos and Rhodes and Crete. Among these are Astypalaea, Telos, Chalcia, and those which Homer names in the Catalogue: "And those who held the islands Nisyros and Crapathos and Casos and Cos, the city of Eurypylus, and the Calydnian Islands"; for, excepting Cos and Rhodes, which I shall discuss later, I place them all among the Sporades, and in fact, even though they are near Asia and not Europe, I make mention of them here because my argument has somehow impelled me to include the Sporades with Crete and the Cyclades. But in my geographical description of Asia I shall add a description of such islands that lie close to it as are worthy of note, Cyprus, Rhodes, Cos, and those that lie on the seaboard next thereafter, Samos, Chios, Lesbos, and Tenedos. But now I shall traverse the remainder of the Sporades that are worth mentioning.
Now Astypalaea lies far out in the high sea, and has a city. Telos extends alongside Cnidia, is long, high, narrow, has a perimeter of about one hundred and forty stadia, and has an anchoring-place. Chalcia is eighty stadia distant from Telos, four hundred from Carpathos, about twice as far from Astypalaea, and has also a settlement of the same name and a temple of Apollo and a harbour.
Nisyros lies to the north of Telos, and is about sixty stadia distant both from it and from Cos. It is round and high and rocky, the rock being that of which millstones are made; at any rate, the neighbouring peoples well supplied with millstones from there. It has also a city of the same name and a harbour and hot springs and a temple of Poseidon. Its perimeter is eighty stadia. Close to it are also isles called Isles of the Nisyrians. They say that Nisyros is a fragment of Cos, and they add the myth that Poseidon, when he was pursuing one of the giants, Polybotes, broke off a fragment of Cos with his trident and hurled it upon him, and the missile became an island, Nisyros, with the giant lying beneath it. But some say that he lies beneath Cos.
Carpathos, which the poet calls Crapathos, is high, and has a circuit of two hundred stadia. At first it was a Tetrapolis, and it had a renown which is worth noting; and it was from this fact that the sea got the name Carpathian. One of the cities was called Nisyros, the same name as that of the island of the Nisyrians. It lies opposite Leucê Actê in Libya, which is about one thousand stadia distant from Alexandreia and about four thousand from Carpathos.
Casos is seventy stadia from Carpathos, and two hundred and fifty from Cape Samonium in Crete. It has a circuit of eighty stadia. In it there is also a city of the same name, and round it are several islands called Islands of the Casians.
They say that the poet calls the Sporades "Calydnian Islands," one of which, they say, is Calymna. But it is reasonable to suppose that, as the islands which are near, and subject to, Nisyros and Casos are called "Islands of the Nisyrians" and "Islands of the Casians," so also those which lie round Calymna were called "Islands of the Calymnians" — Calymna at that time, perhaps, being called Calydna. But some say that there are only two Calydnian islands, Leros and Calymna, the two mentioned by the poet. The Scepsian says that the name of the island was used in the plural, "Calymnae," like "Athenae" and "Thebae"; but, he adds, the words of the poet should be interpreted as a case of hyperbaton, for he does not say, "Calydnian Islands," but "those who held the islands Nisyros and Crapathos and Casos and Cos, the city of Eurypylus, and Calydnae." Now all the honey produced in the islands is, for the most part, good, and rivals that of Attica, but the honey produced in the islands in question is exceptionally good, and in particular the Calymnian. |
|
|
|
|
11 West Asia 1 11 83 1:50 
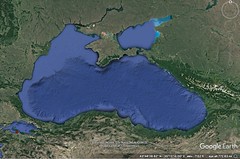
|
11 - 1 Preliminary remarks about Asia 
1 Asia is adjacent to Europe, bordering thereon along the Tanaïs River. I must therefore describe this country next, first dividing it, for the sake of clearness, by means of certain natural boundaries. That is, I must do for Asia precisely what Eratosthenes did for the inhabited world as a whole.
2 The Taurus forms a partition approximately through the middle of this continent, extending from the west towards the east, leaving one portion of it on the north and the other on the south. Of these portions, the Greeks call the one the "Cis‑Tauran" Asia and the other "Trans-Tauran." I have said this before, but let me repeat it by way of reminder.
3 Now the mountain has in many places as great a breadth as three thousand stadia, and a length as great as that of Asia itself, that is, about forty-five thousand stadia, reckoning from the coast opposite Rhodes to the eastern extremities of India and Scythia.
4 It has been divided into many parts with many names, determined by boundaries that circumscribe areas both large and small. But since certain tribes are comprised within the vast width of the mountain, some rather insignificant, but others extremely well known (as, for instance, the Parthians, the Medes, the Armenians, a part of the Cappadocians, the Cilicians, and the Pisidians), those which lie for the most part in its northerly parts must be assigned there, and those in its southern parts to the southern, while those which are situated in the middle of the mountains should, because of the likeness of their climate, be assigned to the north, for the climate in the middle is cold, whereas that in the south is hot. Further, almost all the rivers that rise in the Taurus flow in contrary directions, that is, some into the northern region and others into the southern (they do so at first, at least, although later some of them bend towards the east or west), and they therefore are naturally helpful in our use of these mountains as boundaries in the two‑fold division of Asia — just as the sea inside the Pillars, which for the most part is approximately in a straight line with these mountains, has proved convenient in the forming of two continents, Europe and Libya, it being the noteworthy boundary between the two.
5 As we pass from Europe to Asia in our geography, the northern division is the first of the two divisions to which we come; and therefore we must begin with this. Of this division the first portion is that in the region of the Tanaïs River, which I have taken as the boundary between Europe and Asia. This portion forms, in a way, a peninsula, for it is surrounded on the west by the Tanaïs River and Lake Maeotis as far as the Bosporus and that part of the coast of the Euxine Sea which terminates at Colchis; and then on the north by the Ocean as far as the mouth of the Caspian Sea; and then on the east by this same sea as far as the boundary between Albania and Armenia, where empty the rivers Cyrus and Araxes, the Araxes flowing through Armenia and the Cyrus through Iberia and Albania; and lastly, on the south by the tract of country which extends from the outlet of the Cyrus River to Colchis, which is about three thousand stadia from sea to sea, across the territory of the Albanians and the Iberians, and therefore is described as an isthmus. But those writers who have reduced the width of the isthmus as much as Cleitarchus has, who says that it is subject to inundation from either sea, should not be considered even worthy of mention. Poseidonius states that the isthmus is fifteen hundred stadia across, as wide as the isthmus from Pelusium to the Red Sea. "And in my opinion," he says, "the isthmus from Lake Maeotis to the Ocean does not differ much therefrom."
6 But I do not know how anyone can trust him concerning things that are uncertain if he has nothing plausible to say about them, when he reasons so illogically about things that are obvious; and this too, although he was a friend of Pompey, who made an expedition against the Iberians and the Albanians, from sea to sea on either side, both the Caspian and the Colchian Seas. At any rate, it is said that Pompey, upon arriving at Rhodes on his expedition against the pirates (immediately thereafter he was to set out against both Mithridates and the tribes which extended as far as the Caspian Sea), happened to attend one of the lectures of Poseidonius, and that when he went out he asked Poseidonius whether he had any orders to give, and that Poseidonius replied: "Ever bravest be, and pre‑eminent o'er others." Add to this that among other works he wrote also the history of Pompey. So for this reason he should have been more regardful of the truth.
7 The second portion would be that beyond the Hyrcanian Sea, which we call the Caspian Sea, as far as the Scythians near India. The third portion would consist of the part which is adjacent to the isthmus above mentioned and of those parts of the region inside Taurus and nearest Europe which come next after this isthmus and the Caspian Gates, I mean Media and Armenia and Cappadocia and the intervening regions. The fourth portion is the land inside the Halys River, and all the region in the Taurus itself and outside thereof which falls within the limits of the peninsula which is formed by the isthmus that separates the Pontic and the Cilician Seas. As for the other countries, I mean the Trans-Tauran, I place among them not only India, but also Ariana as far as the tribes that extend to the Persian Sea and the Arabian Gulf and the Nile and the Egyptian and Issic Seas. |
|
|

|

|
11 - 2 Shore of the Black Sea from the Maeotian Lake to Colchis 
1 Of the portions thus divided, the first is inhabited, in the region toward the north and the Ocean, by Scythian nomads and waggon-dwellers, and south of these, by Sarmatians, these too being Scythians, and by Aorsi and Siraci,1 who extend towards the south as far as the Caucasian Mountains, some being nomads and others tent-dwellers and farmers. About Lake Maeotis live the Maeotae. And on the sea lies the Asiatic side of the Bosporus, or the Sindic territory. After this latter, one comes to the Achaei and the Zygi and the Heniochi, and also the Cercetae and the Macropogones. And above these are situated the narrow passes of the Phtheirophagi;3 and after the Heniochi the Colchian country, which lies at the foot of the Caucasian, or Moschian, Mountains. But since I have taken the Tanaïs River as the boundary between Europe and Asia, I shall begin my detailed description therewith.
2 Now the Tanaïs flows from the northerly region, — not, however, as most people think, in a course diametrically opposite to that of the Nile, but more to the east than the Nile — and like the Nile its sources are unknown. Yet a considerable part of the Nile is well known, since it traverses a country which is everywhere easily accessible and since it is navigable for a great distance inland. But as for the Tanaïs, although we know its outlets (they are two in number and are in the most northerly region of Lake Maeotis, being sixty stadia distant from one another), yet but little of the part that is beyond its outlets is known to us, because of the coldness and the poverty of the country. This poverty can indeed be endured by the indigenous peoples, who, in nomadic fashion, live on flesh and milk, but people from other tribes cannot stand it. And besides, the nomads, being disinclined to intercourse with any other people and being superior both in numbers and in might, have blocked off whatever parts of the country are passable, or whatever parts of the river happen to be navigable. This is what has caused some to assume that the Tanaïs has its sources in the Caucasian Mountains, flows in great volume towards the north, and then, making a bend, empties into Lake Maeotis (Theophanes of Mitylenê has the same opinion as these), and others to assume that it flows from the upper region of the Ister, although they produce no evidence of its flowing from so great a distance or from other "climata," as though it were impossible for the river to flow both from a near‑by source and from the north.
3 On the river and the lake is an inhabited city bearing the same name, Tanaïs; it was founded by the Greeks who held the Bosporus. Recently, however, it was sacked by King Polemon because it would not obey him. It was a common emporium, partly of the Asiatic and the European nomads, and partly of those who navigated the lake from the Bosporus, the former bringing slaves, hides, and such other things as nomads possess, and the latter giving in exchange clothing, wine, and the other things that belong to civilised life. At a distance of one hundred stadia off the emporium lies an island called Alopecia, a settlement of promiscuous people. There are also other small islands near by in the lake. The Tanaïs is two thousand two hundred stadia distant from the mouth of Lake Maeotis by a direct voyage towards the north; but it is not much farther by a voyage along the coast.
4 In the voyage along the coast, one comes first, at a distance of eight hundred stadia from the Tanaïs, to the Greater Rhombites River, as it is called, where are made the greatest catches of the fish that are suitable for salting. Then, at a distance of eight hundred more, to the Lesser Rhombites and a cape, which latter also has fisheries, although they are smaller. The people who live about the Greater Rhombites have small islands as bases for their fishing; but the people who carry on the business at the Lesser Rhombites are the Maeotae themselves, for the Maeotae live along the whole of this coast; and though farmers, they are no less warlike than the nomads. They are divided into several tribes, those who live near the Tanaïs being rather ferocious, but those whose territory borders on the Bosporus being more tractable. It is six hundred stadia from the Lesser Rhombites to Tyrambê and the Anticeites River; then a hundred and twenty to the Cimmerian village, which is a place of departure for those who navigate the lake; and on this coast are said to be some look‑out places belonging to the Clazomenians.
5 Cimmericum was in earlier times a city situated on a peninsula, and it closed the isthmus by means of a trench and a mound. The Cimmerians once possessed great power in the Bosporus, and this is why it was named Cimmerian Bosporus. These are the people who overran the country of those who lived in the interior on the right side of the Pontus as far as Ionia. However, these were driven out of the region by the Scythians; and then the Scythians were driven out by the Greeks who founded Panticapaeum and the other cities on the Bosporus.
6 Then, twenty stadia distant, one comes to the village Achilleium, where is the temple of Achilles. Here is the narrowest passage across the mouth of Lake Maeotis, about twenty stadia or more; and on the opposite shore is a village, Myrmecium; and near by are Heracleium and Parthenium.
7 Thence ninety stadia to the monument of Satyrus, which consists of a mound thrown up on a certain cape in memory of one of the illustrious potentates of the Bosporus.
8 Near by is a village, Patraeus, from which the distance to a village Corocondamê is one hundred and thirty stadia; and this village constitutes the limit of the Cimmerian Bosporus, as it is called. The Narrows at the mouth of the Maeotis are so called from the narrow passage at Achilleium and Myrmecium; they extend as far as Corocondamê and the small village named Acra, which lies opposite to it in the land of the Panticapaeans, this village being separated from it by a strait seventy stadia wide; for the ice, also, extends as far as this, the Maeotis being so frozen at the time of frosts that it can be crossed on foot. And these Narrows have good harbours everywhere.
9 Above Corocondamê lies a lake of considerable size, which derives its name, Corocondamitis, from that of the village. It empties into the sea at a distance of ten stadia from the village. A branch of the Anticeites empties into the lake and forms a kind of island which is surrounded by this lake and the Maeotis and the river. Some apply the name Hypanis to this river, just as they do to the river near the Borysthenes.
Sailing into Lake Corocondamitis one comes to Phanagoreia, a noteworthy city, and to Cepi, and to Hermonassa, and to Apaturum, the sanctuary of Aphroditê. Of these, Phanagoreia and Cepi are situated on the island above-mentioned, on the left as one sails in, but the other cities are on the right, across the Hypanis, in the Sindic territory. There is also a place called Gorgipia in the Sindic territory, the royal residence of the Sindi, near the sea; and also a place called Aboracê. All the people who are subject to the potentates of the Bosporus are called Bosporians; and Panticapaeum is the metropolis of the European Bosporians, while Phanagoreium (for the name of the city is also spelled thus) is the metropolis of the Asiatic Bosporians. Phanagoreia is reputed to be the emporium for the commodities that are brought down from the Maeotis and the barbarian country that lies above it, and Panticapaeum for those which are carried up thither from the sea. There is also in Phanagoreia a notable temple of Aphroditê Apaturus. Critics derive the etymology of the epithet of the goddess by adducing a certain myth, according to which the Giants attacked the goddess there; but she called upon Heracles for help and hid him in a cave, and then, admitting the Giants one by one, gave them over to Heracles to be murdered through "treachery."
Among the Maeotae are the Sindi themselves, Dandarii, Toreatae, Agri, and Arrechi, and also the Tarpetes, Obidiaceni, Sittaceni, Dosci, and several others. Among these belong also the Aspurgiani, who live between Phanagoreia and Gorgipia, within a stretch of five hundred stadia; these were attacked by King Polemon under a pretence of friendship, but they discovered his pretence, outgeneralled him, and taking him alive killed him. As for the Asiatic Maeotae in general, some of them were subjects of those who possessed the emporium on the Tanaïs, and the others of the Bosporians; but in those days different peoples at different times were wont to revolt. And often the rulers of the Bosporians held possession of the region as far as the Tanaïs, and particularly the latest rulers, Pharnaces, Asander, and Polemon. Pharnaces is said at one time actually to have conducted the Hypanis River over the country of the Dandarii through an old canal which he cleared out, and to have inundated the country.
After the Sindic territory and Gorgipia, on the sea, one comes to the coast of the Achaei and the Zygi and the Heniochi, which for the most part is harbourless and mountainous, being a part of the Caucasus. These peoples live by robberies at sea. Their boats are slender, narrow, and light, holding only about twenty-five people, though in rare cases they can hold thirty in all; the Greeks call them "camarae." They say that the Phthiotic Achaei in Jason's crew settled in this Achaea, but the Laconians in Heniochia, the leaders of the latter being Rhecas and Amphistratus, the "heniochi" of the Dioscuri, and that in all probability the Heniochi were named after these. At any rate, by equipping fleets of "camarae" and sailing sometimes against merchant-vessels and sometimes against a country or even a city, they hold the mastery of the sea. And they are sometimes assisted even by those who hold the Bosporus, the latter supplying them with mooring-places, with market-place, and with means of disposing of their booty. And since, when they return to their own land, they have no anchorage, they put the "camarae" on their shoulders and carry them to the forests where they live and where they till a poor soil. And they bring the "camarae" down to the shore again when the time for navigation comes. And they do the same thing in the countries of others, for they are well acquainted with wooded places; and in these they first hide their "camarae" and then themselves wander on foot night and day for the sake of kidnapping people. But they readily offer to release their captives for ransom, informing their relatives after they have put out to sea. Now in those places which are ruled by local chieftains the rulers go to the aid of those who are wronged, often attacking and bringing back the "camarae," men and all. But the territory that is subject to the Romans affords but little aid, because of the negligence of the governors who are sent there.
Such is the life of these people. They are governed by the chieftains called "sceptuchi," but the "sceptuchi" themselves are subject to tyrants or kings. For instance, the Heniochi had four kings at the time when Mithridates Eupator, in flight from the country of his ancestors to the Bosporus, passed through their country; and while he found this country passable, yet he despaired of going through that of the Zygi, both because of the ruggedness of it and because of the ferocity of the inhabitants; and only with difficulty could he go along the coast, most of the way marching on the edge of the sea, until he arrived at the country of the Achaei; and, welcomed by these, he completed his journey from Phasis, a journey not far short of four thousand stadia.
Now the voyage from Corocondamê is straight towards the east; and at a distance of one hundred and eighty stadia is the Sindic harbour and city; and then, at a distance of four hundred stadia, one comes to Bata, as it is called, a village and harbour, at which place Sinopê on the south is thought to lie almost directly opposite this coast, just as Carambis has been referred to as opposite Criumetopon. After Bata Artemidorus mentions the coast of the Cercetae, with its mooring-places and villages, extending thence about eight hundred and fifty stadia; and then the coast of the Achaei, five hundred stadia; and then that of the Heniochi, one thousand; and then Greater Pityus, extending three hundred and sixty stadia to Dioscurias. The more trustworthy historians of the Mithridatic wars name the Achaei first, then the Zygi, then the Heniochi, and then the Cercetae and Moschi and Colchi, and the Phtheirophagi who live above these three peoples and the Soanes, and other small tribes that live in the neighbourhood of the Caucasus. Now at first the coast, as I have said, stretches towards the east and faces the south, but from Bata it gradually takes a turn, and then faces the west and ends at Pityus and Dioscurias; for these places border on the above-mentioned coast of Colchis. After Dioscurias comes the remaining coast of Colchis and the adjacent coast of Trapezus, which makes a considerable bend, and then, extending approximately in a straight line, forms the right-hand side of the Pontus, which faces the north. The whole of the coast of the Achaei and of the other peoples as far as Dioscurias and of the places that lie in a straight line towards the south in the interior lie at the foot of the Caucasus.
This mountain lies above both seas, both the Pontic and the Caspian, and forms a wall across the isthmus that separates the two seas. It marks the boundary, on the south, of Albania and Iberia, and, on the north, of the plains of the Sarmatae. It is well wooded with all kinds of timber, and especially the kind suitable for ship-building. According to Eratosthenes, the Caucasus is called "Caspius" by the natives, the name being derived perhaps from the "Caspii." Branches of it project towards the south; and these not only comprise the middle of Albania but also join the mountains of Armenia and the Moschian Mountains, as they are called, and also the Scydises and the Paryadres Mountains. All these are parts of the Taurus, which forms the southern side of Armenia, — parts broken off, as it were, from that mountain on the north and projecting as far as the Caucasus and that part of the coast of the Euxine which stretches from Colchis to Themiscyra.
Be this as it may, since Dioscurias is situated in such a gulf and occupies the most easterly point of the whole sea, it is called not only the recess of the Euxine, but also the "farthermost" voyage. And the proverbial verse, "To Phasis, where for ships is the farthermost run," must be interpreted thus, not as though the author of the iambic verse meant the river, much less the city of the same name situated on the river, but as meaning by a part of Colchis the whole of it, since from the river and the city of that name there is left a straight voyage into the recess of not less than six hundred stadia. The same Dioscurias is the beginning of the isthmus between the Caspian Sea and the Euxine, and also the common emporium of the tribes who are situated above it and in its vicinity; at any rate, seventy tribes come together in it, though others, who care nothing for the facts, actually say three hundred. All speak different languages because of the fact that, by reason of their obstinacy and ferocity, they live in scattered groups and without intercourse with one another. The greater part of them the Sarmatae, but they are all Caucasii. So much, then, for the region of Dioscurias.
Further, the greater part of the remainder of Colchis is on the sea. Through it flows the Phasis, a large river having its sources in Armenia and receiving the waters of the Glaucus and the Hippus, which issue from the neighbouring mountains. It is navigated as far as Sarapana, a fortress capable of admitting the population even of a city. From here people go by land to the Cyrus in four days by a wagon-road. On the Phasis is situated a city bearing the same name, an emporium of the Colchi, which is protected on one side by the river, on another by a lake, and on another by the sea. Thence people go to Amisus and Sinopê by sea (a voyage of two or three days), because the shores are soft and because of the outlets of the rivers. The country is excellent both in respect to its produce — except its honey, which is generally bitter — and in respect to everything that pertains to ship-building; for it not only produces quantities of timber but also brings it down on rivers. And the people make linen in quantities, and hemp, wax, and pitch. Their linen industry has been famed far and wide; for they used to export linen to outside places; and some writers, wishing to show forth a kinship between the Colchians and the Egyptians, confirm their belief by this. Above the aforesaid rivers in the Moschian country lies the temple of Leucothea, founded by Phrixus, and the oracle of Phrixus, where a ram is never sacrificed; it was once rich, but it was robbed in our time by Pharnaces, and a little later by Mithridates of Pergamum. For when a country is devastated, "things divine are in sickly plight and wont not even to be respected," says Euripides.
The great fame this country had in early times is disclosed by the myths, which refer in an obscure way to the expedition of Jason as having proceeded as far even as Media, and also, before that time, to that of Phrixus. After this, when kings succeeded to power, the country being divided into "sceptuchies," they were only moderately prosperous; but when Mithridates Eupator grew powerful, the country fell into his hands; and he would always send one of his friends as sub‑governor or administrator of the country. Among these was Moaphernes, my mother's uncle on her father's side. And it was from this country that the king received most aid in the equipment of his naval forces. But when the power of Mithridates had been broken up, all the territory subject to him was also broken up and distributed among many persons. At last Polemon got Colchis; and since his death his wife Pythodoris has been in power, being queen, not only of the Colchians, but also of Trapezus and Pharnacia and of the barbarians who live above these places, concerning whom I shall speak later on.Now the Moschian country, in which is situated the temple, is divided into three parts: one part is held by the Colchians, another by the Iberians, and another by the Armenians. There is also a small city in Iberia, the city of Phrixus, the present Ideëssa, well fortified, on the confines of Colchis. And near Dioscurias flows the Chares River.
Among the tribes which come together at Dioscurias are the Phtheirophagi, who have received their name from their squalor and their filthiness. Near them are the Soanes, who are no less filthy, but superior to them in power, — indeed, one might almost say that they are foremost in courage and in power. At any rate, they are masters of the peoples around them, and hold possession of the heights of the Caucasus above Dioscurias. They have a king and a council of three hundred men; and they assemble, according to report, an army of two hundred thousand; for the whole of the people are a fighting force, though unorganised. It is said that in their country gold is carried down by the mountain-torrents, and that the barbarians obtain it by means of perforated troughs and fleecy skins, and that this is the origin of the myth of the golden fleece — unless they call them Iberians, by the same name as the western Iberians, from the gold mines in both countries. The Soanes use remarkable poisons for the points of their missiles; and even people who are not wounded by the poisoned missiles suffer from their odour. Now in general the tribes in the neighbourhood of the Caucasus occupy barren and cramped territories, but the tribes of the Albanians and the Iberians, which occupy nearly all the isthmus above-mentioned, might also be called Caucasian tribes; and they possess territory that is fertile and capable of affording an exceedingly good livelihood. |
|
|
|
|
11 - 3 Asian Iberia 
1 Furthermore, the greater part of Iberia is so well built up in respect to cities and farmsteads that their roofs are tiled, and their houses as well as their market-places and other public buildings are constructed with architectural skill.
2 Parts of the country are surrounded by the Caucasian Mountains; for branches of these mountains, as I said before, project towards the south; they are fruitful, comprise the whole of Iberia, and border on both Armenia and Colchis. In the middle is a plain intersected by rivers, the largest being the Cyrus. This river has its beginning in Armenia, flows immediately into the plain above-mentioned, receives both the Aragus, which flows from the Caucasus, and other streams, and empties through a narrow valley into Albania; and between the valley and Armenia it flows in great volume through plains that have exceedingly good pasture, receives still more rivers, among which are the Alazonius, Sandobanes, Rhoetaces, and Chanes, all navigable, and empties into the Caspian Sea. It was formerly called Corus.
3 Now the plain of the Iberians is inhabited by people who are rather inclined to farming and to peace, and they dress after both the Armenian and the Median fashion; but the major, or warlike, portion, occupy the mountainous territory, living like the Scythians and the Sarmatians, of whom they are both neighbours and kinsmen; however, they engage also in farming. And they assemble many tens of thousands, both from their own people and from the Scythians and Sarmatians, whenever anything alarming occurs.
4 There are four passes leading into their country; one through Sarapana, a Colchian stronghold, and through the narrow defiles there. Through these defiles the Phasis, which has been made passable by one hundred and twenty bridges because of the windings of its course, flows down into Colchis with rough and violent stream, the region being cut into ravines by many torrents at the time of the heavy rains. The Phasis rises in the mountains that lie above it, where it is supplied by many springs; and in the plains it receives still other rivers, among which are the Glaucus and the Hippus. Thus filled and having by now become navigable, it issues forth into the Pontus; and it has on its banks a city bearing the same name; and near it is a lake. Such, then, is the pass that leads from Colchis into Iberia, being shut in by rocks, by strongholds, and by rivers that run through ravines.
5 From the country of the nomads on the north there is a difficult ascent into Iberia requiring three days' travel; and after this ascent comes a narrow valley on the Aragus River, with a single-file road requiring a four days' journey. The end of the road is guarded by a fortress which is hard to capture. The pass leading from Albania into Iberia is at first hewn through rock, and then leads through a marsh formed by the River Alazonius, which falls from the Caucasus. The passes from Armenia into Iberia are the defiles on the Cyrus and those on the Aragus. For, before the two rivers meet, they have on their banks fortified cities that are situated upon rocks, these being about sixteen stadia distant from each other — I mean Harmozicê on the Cyrus and Seusamora on the other river. These passes were used first by Pompey when he set out from the country of the Armenians, and afterwards by Canidius.
6 There are also four castes among the inhabitants of Iberia. One, and the first of all, is that from which they appoint their kings, the appointee being both the nearest of kin to his predecessor and the eldest, whereas the second in line administers justice and commands the army. The second caste is that of the priests, who among other things attend to all matters of controversy with the neighbouring peoples. The third is that of the soldiers and the farmers. And the fourth is that of the common people, who are slaves of the king and perform all the services that pertain to human livelihood. Their possessions are held in common by them according to families, although the eldest is ruler and steward of each estate. Such are the Iberians and their country. |
|
|
|
|
11 - 4 (Asian) Albania 
1 The Albanians are more inclined to the shepherd's life than the Iberians and closer akin to the nomadic people, except that they are not ferocious; and for this reason they are only moderately warlike. They live between the Iberians and the Caspian Sea, their country bordering on the sea towards the east and on the country of the Iberians towards the west. Of the remaining sides the northern is protected by the Caucasian Mountains (for these mountains lie above the plains, though their parts next to the sea are generally called Ceraunian), whereas the southern side is formed by Armenia, which stretches alongside it; and much of Armenia consists of plains, though much of it is mountainous, like Cambysenê, where the Armenians border on both the Iberians and the Albanians.
2 The Cyrus, which flows through Albania, and the other rivers by which it is supplied, contribute to the excellent qualities of the land; and yet they thrust back the sea, for the silt, being carried forward in great quantities, fills the channel, and consequently even the adjacent isles are joined to the mainland and form shoals that are uneven and difficult to avoid; and their unevenness is made worse by the back-wash of the flood-tides. Moreover, they say that the outlet of the river is divided into twelve mouths, of which some are choked with silt, while the others are altogether shallow and leave not even a mooring-place. At any rate, they add, although the shore is washed on all sides by the sea and the rivers for a distance of more than sixty stadia, every part of it is inaccessible; and the silt extends even as far as five hundred stadia, making the shore sandy. Near by is also the mouth of the Araxes, a turbulent stream that flows down from Armenia. But the silt which this river pushes before it, thus making the channel passable for its stream, is compensated for by the Cyrus.
3 Now perhaps a people of this kind have no need of a sea; indeed, they do not make appropriate use of their land either, which produces, not only every kind of fruit, even the most highly cultivated kind, but also every plant, for it bears even the evergreens. It receives not even slight attention, yet the good things all "spring up for them without sowing and ploughing," according to those who have made expeditions there, who describe the mode of life there as "Cyclopeian."a In many places, at any rate, they say, the land when sown only once produces two crops or even three, the first a crop of even fifty-fold, and that too without being ploughed between crops; and even when it is ploughed, it is not ploughed with an iron share, but with a wooden plough shaped by nature. The plain as a whole is better watered by its rivers and other waters than the Babylonian and the Egyptian plains; consequently it always keeps a grassy appearance, and therefore is also good for pasturage. In addition to this, the climate here is better than there. And the people never dig about the vines, although they prune them every fifth year; the new vines begin to produce fruit the second year, and when mature they yield so much that the people leave a large part of the fruit on the branches. Also the cattle in their country thrive, both the tame and the wild.
4 The inhabitants of this country are unusually handsome and large. And they are frank in their dealings, and not mercenary; for they do not in general use coined money, nor do they know any number greater than one hundred, but carry on business by means of barter, and otherwise live an easy-going life. They are also unacquainted with accurate measures and weights, and they take no forethought for war or government or farming. But still they fight both on foot and on horseback, both in light armour and in full armour, like the Armenians.
5 They send forth a greater army than that of the Iberians; for they equip sixty thousand infantry and twenty‑two thousand horsemen, the number with which they risked their all against Pompey. Against outsiders the nomads join with the Albanians in war, just as they do with the Iberians, and for the same reasons; and besides, they often attack the people, and consequently prevent them from farming. The Albanians use javelins and bows; and they wear breastplates and large oblong shields, and helmets made of the skins of wild animals, similar to those worn by the Iberians. To the country of the Albanians belongs also the territory called Caspianê, which was named after the Caspian tribe, as was also the sea; but the tribe has now disappeared. The pass from Iberia into Albania leads through Cambysenê, a waterless and rugged country, to the Alazonius River. Both the people and their dogs are surpassingly fond of hunting, engaging in it not so much because of their skill in it as because of their love for it.
Their kings, also, are excellent. At the present time, indeed, one king rules all the tribes, but formerly the several tribes were ruled separately by kings of their own according to their several languages. They have twenty‑six languages, because of the fact that they have no easy means of intercourse with one another. The country produces also certain of the deadly reptiles, and scorpions and phalangia. Some of the phalangia cause people to die laughing, while others cause people to die weeping over the loss of their deceased kindred.
7 As for gods, they honour Helius, Zeus, and Selenê, but especially Selenê; her temple is near Iberia. The office of priest is held by the man who, after the king, is held in highest honour; he has charge of the sacred land, which is extensive and well-populated, and also of the temple slaves, many of whom are subject to religious frenzy and utter prophecies. And any one of those who, becoming violently possessed, wanders alone in the forests, is by the priest arrested, bound with sacred fetters, and sumptuously maintained during that year, and then led forth to the sacrifice that is performed in honour of the goddess, and, being anointed, is sacrificed along with other victims. The sacrifice is performed as follows: Some person holding a sacred lance, with which it is the custom to sacrifice human victims, comes forward out of the crowd and strikes the victim through the side into the heart, he being not without experience in such a task; and when the victim falls, they draw auguries from his fall and declare them before the public; and when the body is carried to a certain place, they all trample upon it, thus using it as a means of purification.
8 The Albanians are surpassingly respectful to old age, not merely to their parents, but to all other old people. And when people die it is impious to be concerned about them or even to mention them. Indeed, they bury their money with them, and therefore live in poverty, having no patrimony. So much for the Albanians. It is said that Jason, together with Armenus the Thessalian, on his voyage to the country of the Colchians, pressed on from there as far as the Caspian Sea, and visited, not only Iberia and Albania, but also many parts of Armenia and Media, as both the Jasonia and several other memorials testify. And it is said that Armenus was a native of Armenium, one of the cities on Lake Boebeïs between Pherae and Larisa, and that he and his followers took up their abode in Acilisenê and Syspiritis, occupying the country as far as Calachanê and Adiabenê; and indeed that he left Armenia named after himself. |
|
|
|
|
11 - 5 Caucasus and the country of the Amazons 
The Amazons, too, are said to live in the mountains above Albania. Now Theophanes, who made the expedition with Pompey and was in the country of the Albanians, says that the Gelae and the Legae, Scythian people, live between the Amazons and the Albanians, and that the Mermadalis River flows there, midway between these people and the Amazons. But others, among whom are Metrodorus of Scepsis and Hypsicrates, who themselves, likewise, were not unacquainted with the region in question, say that the Amazons live on the borders of the Gargarians, in the northerly foothills of those parts of the Caucasian Mountains which are called Ceraunian; that the Amazons spend the rest of their time off to themselves, performing their several individual tasks, such as ploughing, planting, pasturing cattle, and particularly in training horses, though the bravest engage mostly in hunting on horseback and practise warlike exercises; that the right breasts of all are seared when they are infants, so that they can easily use their right arm for every needed purpose, and especially that of throwing the javelin; that they also use bow and sagaris and light shield, and make the skins of wild animals serve as helmets, clothing, and girdles; but that they have two special months in the spring in which they go up into the neighbouring mountain which separates them and the Gargarians. The Gargarians also, in accordance with an ancient custom, go up thither to offer sacrifice with the Amazons and also to have intercourse with them for the sake of begetting children, doing this in secrecy and darkness, any Gargarian at random with any Amazon; and after making them pregnant they send them away; and the females are born are retained by the Amazons themselves, but the males are taken to the Gargarians to be brought up; and each Gargarian to whom a child is brought adopts the child as his own, regarding the child as his son because of his uncertainty.
2 The Mermodas dashes down from the mountains through the country of the Amazons and through Siracenê and the intervening desert and then empties into Lake Maeotis. It is said that the Gargarians went up from Themiscyra into this region with the Amazons, then revolted from them and in company with some Thracians and Euboeans who had wandered thus far carried on war against them, and that they later ended the war against them and made a compact on the conditions above-mentioned, that is, that they should have dealings with one another only in the matter of children, and that each people should live independent of the other.
3 A peculiar thing has happened in the case of the account we have of the Amazons; for our accounts of other peoples keep a distinction between the mythical and the historical elements; for the things that are ancient and false and monstrous are called myths, but history wishes for the truth, whether ancient or recent, and contains no monstrous element, or else only rarely. But as regards the Amazons, the same stories are told now as in early times, though they are marvellous and beyond belief. For instance, who could believe that an army of women, or a city, or a tribe, could ever be organised without men, and not only be organised, but even make inroads upon the territory of other people, and not only overpower the peoples near them to the extent of advancing as far as what is now Ionia, but even send an expedition across the sea as far as Attica? For this is the same as saying that the men of those times were women and that the women were men. Nevertheless, even at the present time these very stories are told about the Amazons, and they intensify the peculiarity above-mentioned and our belief in the ancient accounts rather than those of the present time.
4 At any rate, the founding of cities and the giving of names to them are ascribed to the Amazons, as, for instance, Ephesus and Smyrna and Cymê and Myrinê; and so are tombs and other monuments; and Themiscyra and the plains about Thermodon and the mountains that lie above them are by all writers mentioned as having belonged to the Amazons; but they say that the Amazons were driven out of these places. Only a few writers make assertions as to where they are at the present time, but their assertions are without proof and beyond belief, as in the case of Thalestria, queen of the Amazons, with whom, they say, Alexander associated in Hyrcania and had intercourse for the sake of offspring; for this assertion is not generally accepted.a Indeed, of the numerous historians, those who care most for the truth do not make the assertion, nor do those who are most trustworthy mention any such thing, nor do those who tell the story agree in their statements. Cleitarchus says that Thalestria set out from the Caspian Gates and Thermodon and visited Alexander; but the distance from the Caspian country to Thermodon is more than six thousand stadia.
5 The story that have been spread far and wide with a view to glorifying Alexander are not accepted by all; and their fabricators were men who cared for flattery rather than truth. For instance: they transferred the Caucasus into the region of the Indian mountains and of the eastern sea which lies near those mountains from the mountains which lie above Colchis and the Euxine; for these are the mountains which the Greeks named Caucasus, which is more thirty thousand stadia distant from India; and here it was that they laid the scene of the story of Prometheus and of his being put in bonds; for these were the farthermost mountains towards the east that were known to writers of that time. And the expedition of Dionysus and Heracles to the country of the Indians look like a mythical story of later date, because Heracles is said to have released Prometheus one thousand years later. And although it was a more glorious thing for Alexander to subdue Asia as far as the Indian mountains than merely to the recess of the Euxine and to the Caucasus, yet the glory of the mountain, and its name, and the belief that Jason and his followers had accomplished the longest of all expeditions, reaching as far as the neighbourhood of the Caucasus, and the tradition that Prometheus was bound at the ends of the earth on the Caucasus, led writers to suppose that they would be doing the king a favour if they transferred the name Caucasus to India.
6 Now the highest parts of the real Caucasus are the most southerly — those next to Albania, Iberia, and the Colchians, and the Heniochians. They are inhabited by the peoples who, as I have said, assemble at Dioscurias; and they assemble there mostly in order to get salt. Of these tribes, some occupy the ridges of the mountains, while the others have their abodes in glens and live mostly on the flesh of wild animals, and on wild fruits and milk. The summits of the mountains are impassable in winter, but the people ascend them in summer by fastening to their feet broad shoes made of raw ox‑hide, like drums, and furnished with spikes, on account of the snow and the ice. They descend with their loads by sliding down seated upon skins, as is the custom in Atropatian Media and on Mount Masius in Armenia; there, however, the people also fasten wooden discs furnished with spikes to the soles of their shoes. Such, then, are the heights of the Caucasus.
7 As one descends into the foothills, the country inclines more towards the north, but its climate is milder, for there it borders on the plains of the Siraces. And here are also some Troglodytae, who, on account of the cold, live in caves; but even in their country there is plenty of barley. After the Troglodytae one comes to certain Chamaecoetae9 and Polyphagi, as they are called, and to the villages of the Eisadici, who are able to farm because they are not altogether exposed to the north.
8 The next peoples to which one comes between Lake Maeotis and the Caspian Sea are nomads, the Nabiani and the Panxani, and then next the tribes of the Siraces and the Aorsi. The Aorsi and the Siraces are thought to be fugitives from the upper tribes of those namesand the Aorsi are more to the north than the Siraces. Now Abeacus, king of the Siraces, sent forth twenty thousand horsemen at the time when Pharnaces held the Bosporus; and Spadines, king of the Aorsi, two hundred thousand; but the upper Aorsi sent a still larger number, for they held dominion over more land, and, one may almost say, ruled over most of the Caspian coast; and consequently they could import on camels the Indian and Babylonian merchandise, receiving it in their turn from the Armenians and the Medes, and also, owing to their wealth, could wear golden ornaments. Now the Aorsi live along the Tanaïs, but the Siraces live along the Achardeüs, which flows from the Caucasus and empties into Lake Maeotis. |
|
|
|
|
11 - 6 Western approaches to the Caspian Sea 
1 The second portion begins at the Caspian Sea, at which the first portion ends. The same sea is also called Hyrcanian. But I must first describe this sea and the tribes which live about it.
This sea is the gulf which extends from the ocean towards the south; it is rather narrow at its entrance, but it widens out as it advances inland, and especially in the region of its recess, where its width is approximately five thousand stadia. The length of the voyage for its entrance to its recess might be slightly more than that, since its entrance is approximately on the borders of the uninhabited world. Eratosthenes says that the circuit of this sea was known to the Greeks; that the part along the coast of the Albanians and the Cadusians is five thousand four hundred stadia; and that the part along the coast of the Anariaci and Mardi and Hyrcani to the mouth of the Oxus River is four thousand eight hundred, and thence to the Iaxartes, two thousand four hundred. But we must understand in a more general sense the accounts of this portion and the regions that lie so far removed, particularly in the matter of distances.
2 On the right, as one sails into the Caspian Sea, are those Scythians, or Sarmatians, who live in the country contiguous to Europe between the Tanaïs River and this sea; the greater part of them are nomads, of whom I have already spoken. On the left are the eastern Scythians, also nomads, who extend as far as the Eastern Sea and India. Now all the peoples towards the north were by the ancient Greek historians given the general name "Scythians" or "Celtoscythians"; but the writers of still earlier times, making distinctions between them, called those who lived above the Euxine and the Ister and the Adriatic "Hyperboreans," "Sauromatians," and "Arimaspians," and they called those who lived across the Caspian Sea in part "Sacians" and in part "Massagetans," but they were unable to give any accurate account of them, although they reported a war between Cyrus5 and the Massagetans. However, neither have the historians given an accurate and truthful account of these peoples, nor has much credit been given to the ancient history of the Persians or Medes or Syrians, on account of the credulity of the historians and their fondness for myths.
3 For, seeing that those who were professedly writers of myths enjoyed repute, they thought that they too would make their writings pleasing if they told in the guise of history what they had never seen, nor even heard — or at least not from persons who knew the facts — with this object alone in view, to tell what afforded their hearers pleasure and amazement. One could more easily believe Hesiod and Homer in the stories of the heroes, or the tragic poets, than Ctesias, Herodotus, Hellanicus, and other writers of this kind.
4 Neither is it easy to believe most of those who have written the history of Alexander; for these toy with facts, both because of the glory of Alexander and because his expedition reached the ends of Asia, far away from us; and statements about things that are far away are hard to refute. But the supremacy of the Romans and that of the Parthians has disclosed considerably more knowledge than that which had previously come down to us by tradition; for those who write about those distant regions tell a more trustworthy story than their predecessors, both of the places and of the tribes among which the activities took place, for they have looked into the matter more closely. |
|
|
|
|
11 - 7 Hyrcania 
1 Those nomads, however, who live along the coast on the left as one sails into the Caspian Sea are by the writers of to‑day called Däae, I mean, those who are surnamed Aparni; then, in front of them, intervenes a desert country; and next comes Hyrcania, where the Caspian resembles an open sea to the point where it borders on the Median and Armenian mountains. The shape of these mountains is crescent-like along the foot-hills, which end at the sea and form the recess of the gulf. This side of the mountains, beginning at the sea, is inhabited as far as their heights for a short stretch by a part of the Albanians and the Armenians, but for the most part by Gelae, Cadusii, Amardi, Vitii, and Anariacae. They say that some of the Parrhasii took up their abode with the Anariacae, who, they say, are now called Parsii; and that the Aenianes built a walled city in the Vitian territory, which, they say, is called Aeniana; and that Greek armour, brazen vessels, and burial-places are to be seen there; and that there is also a city Anariacê there, in which, they say, is to be seen an oracle for sleepers, and some other tribes that are more inclined to brigandage and war than to farming; but this is due to the ruggedness of the region. However, the greater part of the seaboard round the mountainous country is occupied by Cadusii, for a stretch of almost five thousand stadia, according to Patrocles, who considers this sea almost equal to the Pontic Sea. Now these regions have poor soil.
2 But Hyrcania is exceedingly fertile, extensive, and in general level; it is distinguished by notable cities, among which are Talabrocê, Samarianê, Carta, and the royal residence Tapê, which, they say, is situated slightly above the sea and at a distance of one thousand four hundred stadia from the Caspian Gates. And because of its particular kind of prosperity writers go on to relate evidences thereof: the vine produces one metretes of wine, and the fig‑tree sixty medimni; the grain grows up from the seed that falls from the stalk; bees have their hives in the trees, and honey drips from the leaves; and this is also the case in Matianê in Media, and in Sacasenê and Araxenê in Armenia.6 However, neither the country itself nor the sea that is named after it has received proper attention, the sea being both without vessels and unused. There are islands in this sea which could afford a livelihood, and, according to some writers, contain gold ore. The cause of this lack of attention was the fact that the first governors of the Hyrcanians, I mean the Medes and Persians, as also the last, I mean the Parthians, who were inferior to the former, were barbarians, and also the fact that the whole of the neighbouring country was full of brigands and nomads and deserted regions. The Macedonians did indeed rule over the country for a short time, but they were so occupied with wars that they could not attend to their remote possessions. According to Aristobulus, Hyrcania, which is a wooded country, has the oak, but does not produce the torch-pine7 or fir8 or stone-pine, though India abounds in these trees. Nesaea, also, belongs to Hyrcania, though some writers set it down as an independent district.
3 Hyrcania is traversed by the rivers Ochus and Oxus to their outlets into the sea; and of these, the Ochus flows also through Nesaea, but some say that the Ochus empties into the Oxus. Aristobulus declares that the Oxus is the largest of the rivers he has seen in Asia, except those in India. And he further says that it is navigable (both he and Eratosthenes taking this statement from Patrocles) and that large quantities of Indian wares are brought down on it to the Hyrcanian Sea, and thence on that sea are transported to Albania and brought down on the Cyrus River and through the region that comes next after it to the Euxine. The Ochus is not mentioned at all by the ancient writers. Apollodorus, however, who wrote the Parthica, names it continually, implying that it flows very close to the country of the Parthians.
4 Many false notions were also added to the account of this sea because of Alexander's love of glory; for, since it was agreed by all that the Tanaïs separated Asia from Europe, and that the region between the sea and the Tanaïs, being a considerable part of Asia, had not fallen under the power of the Macedonians, it was resolved to manipulate the account of Alexander's expedition so that in fame at least he might be credited with having conquered those parts of Asia too. They therefore united Lake Maeotis, which receives the Tanaïs, with the Caspian Sea, calling this too a lake and asserting that both were connected with one another by an underground passage and that each was a part of the other. Polycleitus goes on to adduce proofs in connection with his belief that the sea is a lake (for instance, he says that it produces serpents, and that its water is sweetish); and that it is no other than Maeotis he judges from the fact that the Tanaïs empties into it. From the same Indian mountains, where the Ochus and the Oxus and several other rivers rise, flows also the Iaxartes, which, like those rivers, empties into the Caspian Sea and is the most northerly of them all. This river, accordingly, they named Tanaïs; and in addition to so naming it they gave as proof that it was the Tanaïs mentioned by Polycleitus that the country on the far side of this river produces the fir‑tree and that the Scythians in that region use arrows made of fir‑wood; and they say that this is also evidence that the country on the far side belongs to Europe and not to Asia, for, they add, Upper and Eastern Asia does not produce the fir‑tree. But Eratosthenes says that the fir‑tree grows also in India and that Alexander built his fleet out of fir‑wood from there. Eratosthenes tries to reconcile many other differences of this kind, but as for me, let what I have said about them suffice.
5 This too, among the marvellous things recorded of Hyrcania, is related by Eudoxus and others: that there are some cliffs facing the sea with caverns underneath, and between these and the sea, below the cliffs, is a low‑lying shore; and that rivers flowing from the precipices above rush forward with so great force that when they reach the cliffs they hurl their waters out into the sea without wetting the shore, so that even armies can pass underneath sheltered by the stream above; and the natives often come down to the place for the sake of feasting and sacrifice, and sometimes they recline in the caverns down below and sometimes they enjoy themselves basking in the sunlight beneath the stream itself, different people enjoying themselves in different ways, having in sight at the same time on either side both the sea and the shore, which latter, because of the moisture, is grassy and abloom with flowers. |
|
|
|
|
11 - 8 East of the Caspian Sea: the Sacae and the Massagetae 
As one proceeds from the Hyrcanian Sea towards the east, one sees on the right the mountains that extend as far as the Indian Sea, which by the Greeks are named the Taurus. Beginning at Pamphylia and Cilicia they extend thus far in a continuous line from the west and bear various different names. In the northerly parts of the range dwell first the Gelae and Cadusii and Amardi, as I have said,1 and certain of the Hyrcanians, and after them the tribe of the Parthians and that of the Margianians and the Arians; and then comes the desert which is separated from Hyrcania by the Sarnius River as one goes eastwards and towards the Ochus River. The mountain which extends from Armenia to this point, or a little short of it, is called Parachoathras. The distance from the Hyrcanian Sea to the country of the Arians is about six thousand stadia. Then comes Bactriana, and Sogdiana, and finally the Scythian nomads. Now the Macedonians gave the name Caucasus to all the mountains which follow in order after the country of the Arians; but among the barbarians the extremities on the north were given the separate names "Paropamisus" and "Emoda" and "Imaus"; and other such names were applied to separate parts.
2 On the left and opposite these people are situated the Scythian or nomadic tribes, which cover the whole of the northern side. Now the greater part of the Scythians, beginning at the Caspian Sea, are called Däae, but those who are situated more to the east than these are named Massagetae and Sacae, whereas all the rest given the general name of Scythians, though each people is given a separate name of its own. They all for the most part nomads. But the best known of the nomads are those who took away Bactriana from the Greeks, I mean the Asii, Pasiani, Tochari, and Sacarauli, who originally came from the country on the other side of the Iaxartes River that adjoins that of the Sacae and the Sogdiani and was occupied by the Sacae. And as for the Däae, some of them are called Aparni, some Xanthii, and some Pissuri. Now of these the Aparni are situated closest to Hyrcania and the part of the sea that borders on it, but the remainder extend even as far as the country that stretches parallel to Aria.
3 Between them and Hyrcania and Parthia and extending as far as the Arians is a great waterless desert, which they traversed by long marches and then overran Hyrcania, Nesaea, and the plains of the Parthians. And these people agreed to pay tribute, and the tribute was to allow the invaders at certain appointed times to overrun the country and carry off booty. but when the invaders overran their country more than the agreement allowed, war ensued, and in turn their quarrels were composed and new wars were begun. Such is the life of the other nomads also, who are always attacking their neighbours and then in turn settling their differences.
4 The Sacae, however, made raids like those of Cimmerians and Treres, some into regions close to their own country, others into regions farther away. For instance, they occupied Bactriana, and acquired possession of the best land in Armenia, which they left named after themselves, Sacasenê; and they advanced as far as the country of the Cappadocians, particularly those situated close to the Euxine, who are now called the Pontici. But when they were holding a general festival and enjoying their booty, they were attacked by night by the Persian generals who were then in that region and utterly wiped out. And these generals, heaping up a mound of earth over a certain rock in the plain, completed it in the form of a hill, and erected on it a wall, and established the temple of Anaïtis and the gods who share her altar — Omanus and Anadatus, Persian deities; and they instituted an annual sacred festival, the Sacaea, which the inhabitants of Zela (for thus the place is called) continue to celebrate to the present day. It is a small city belonging for the most part to the temple-slaves. But Pompey added considerable territory to it, settled the inhabitants thereof within the walls, and made it one of the cities which he organised after his overthrow of Mithridates.
5 Now this is the account which some writers give of the Sacae. Others say that Cyrus made an expedition against the Sacae, was defeated in the battle, and fled; but that he encamped in the place where he had left behind his supplies, which consisted of an abundance of everything and especially of wine, rested his army a short time, and set out at nightfall, as though he were in flight, leaving the tents full of supplies; and that he proceeded as far as he thought best and halted; and that the Sacae pursued, found the camp empty of men but full of things conducive to enjoyment, and filled themselves to the full; and that Cyrus turned back, and found them drunk and crazed, so that some were slain while lying stupefied and asleep, whereas others fell victims to the arms of the enemy while dancing and revelling naked, and almost all perished; and Cyrus, regarding the happy issue as of divine origin, consecrated that day to the goddess of his fathers and called it Sacaea; and that wherever there is a temple of this goddess, there the festival of the Sacaea, a kind of Bacchic festival, is the custom, at which men, dressed in the Scythian garb, pass day and night drinking and playing wantonly with one another, and also with the women who drink with them.
6 The Massagetae disclosed their valour in their war with Cyrus, to which many writers refer again and again; and it is from these that we must get our information. Statements to the following effect are made concerning the Massagetae: that some of them inhabit mountains, some plains, others marshes which formed by the rivers, and others the islands in the marshes. But the country is inundated most of all, they say, by the Araxes River, which splits into numerous branches and empties by its other mouths into the other sea on the north, though by one single mouth it reaches the Hyrcanian Gulf. They regard Helius alone as god, and to him they sacrifice horses. Each man marries only one wife, but they use also the wives of one another; not in secret, however, for the man who is to have intercourse with the wife of another hangs up his quiver on the wagon and has intercourse with her openly. And they consider it the best kind of death when they are old to be chopped up with the flesh of cattle and eaten mixed up with that flesh. But those who die of disease are cast out as impious and worthy only to be eaten by wild beasts. They are good horsemen and foot-soldiers; they use bows, short swords, breastplates, and sagares made of brass; and in their battles they wear head-bands and belts made of gold. And their horses have bits and girths made of gold. Silver is not found in their country, and only a little iron, but brass and gold in abundance.
7 Now those who live in the islands, since they have no grain to sow, use roots and wild fruits as food, and they clothe themselves with the bark of trees (for they have no cattle either), and they drink the juice squeezed out of the fruit of the trees. Those who live in the marshes eat fish, and clothe themselves in the skins of the seals that run up thither from the sea. The mountaineers themselves also live on wild fruits; but they have sheep also, though only a few, and therefore they do not butcher them, sparing them for their wool and milk; and they variegate the colour of their clothing by staining it with dyes whose colours do not easily fade. The inhabitants of the plains, although they possess land, do not till it, but in the nomadic or Scythian fashion live on sheep and fish. Indeed, there not only is a certain mode of life common to all such peoples, of which I often speak, but their burials, customs, and their way of living as a whole, are alike, that is, they are self-assertive, uncouth, wild, and warlike, but, in their business dealings, straightforward and not given to deceit.
8 Belonging to the tribe of the Massagetae and the Sacae are also the Attasii and the Chorasmii, to whom Spitamenes fled from the country of the Bactriani and the Sogdiani. He was one of the Persians who escaped from Alexander, as did also Bessus; and later Arsaces, when he fled from Seleucus Callinicus, withdrew into the country of the Apasiacae. Eratosthenes says that the Arachoti and Massagetae situated alongside the Bactrians towards the west along the Oxus River, and that the Sacae and the Sogdiani, with the whole of their lands, are situated opposite India, but the Bactriani only for a slight distance; for, he says, they are situated for the most part alongside the Paropamisus, and the Sacae and the Sogdiani are separated from one another by the Iaxartes River, and the Sogdiani and the Bactriani by the Oxus River; and the Tapyri live between the Hyrcanians and the Arians; and in a circuit round the sea after the Hyrcanians one comes to the Amardi, Anariacae, Cadusii, Albani, Caspii, Vitii, and perhaps also other peoples, until one reaches the Scythians; and on the other side of the Hyrcanians are Derbices; and the Cadusii border on the Medi and Matiani below the Parachoathras.
9 Eratosthenes gives the distances as follows: From Mt. Caspius to the Cyrus River, about one thousand eight hundred stadia; thence to the Caspian Gates, five thousand six hundred; then to Alexandreia in the country of the Arians, six thousand four hundred; then to the city Bactra, also called Zariaspa, three thousand eight hundred and seventy; then to the Iaxartes River, to which Alexander came, about five thousand; a distance all told of twenty‑two thousand six hundred and seventy stadia. He gives also the distance from the Caspian Gates to India as follows: To Hecatompylus, they say one thousand nine hundred and sixty stadia; to Alexandreia in the country of the Arians, four thousand five hundred and thirty; then to Prophthasia in Drangê, one thousand six hundred (others say one thousand five hundred); then to the city Arachoti, four thousand one hundred and twenty; then to Ortospana, to the junction of the three roads leading from Bactra, two thousand; then to the borders of India, one thousand; a distance all told of fifteen thousand three hundred stadia. We must conceive of the length of India, reckoned from the Indus River to the eastern sea, as continuous with this distance in a straight line. So much for the Sacae. |
|
|
|
|
11 - 9 Parthia proper 
1 As for the Parthian country, it is not large; at any rate, it paid its tribute along with the Hyrcanians in the Persian times, and also after this, when for a long time the Macedonians held the mastery. And, in addition to its smallness, it is thickly wooded and mountainous, and also poverty-stricken, so that on this account the kings send their own throngs through it in great haste, since the country is unable to support them even for a short time. At present, however, it has increased in extent. Parts of the Parthian country are Comisenê and Chorenê, and, one may almost say, the whole region that extends as far as the Caspian Gates and Rhagae and the Tapyri, which formerly belonged to Media. And in the neighbourhood of Rhagae are the cities Apameia and Heracleia. The distance from the Caspian Gates to Rhagae is five hundred stadia, as Apollodorus says, and to Hecatompylus, the royal seat of the Parthians, one thousand two hundred and sixty. Rhagae is said to have got its name from the earthquakes that took place in that country, by which numerous cities and two thousand villages, as Poseidonius says, were destroyed. The Tapyri are said to live between the Derbices and the Hyrcanians. It is reported of the Tapyri that it was a custom of theirs to give their wives in marriage to other husbands as soon as they had had two or three children by them; just as in our times, in accordance with an ancient custom of the Romans, Cato gave Marcia in marriage to Hortensius at the request of the later.
2 But when revolutions were attempted by the countries outside the Taurus, because of the fact that the kings of Syria and Media, who were in possession also of these countries, were busily engaged with others, those who had been entrusted with their government first caused the revolt of Bactriana and of all the country near it, I mean Euthydemus and his followers; and then Arsaces, a Scythian, with some of the Däae (I mean the Aparnians, as they were called, nomads who lived along the Ochus), invaded Parthia and conquered it. Now at the outset Arsaces was weak, being continually at war with those who had been deprived by him of their territory, both he himself and his successors, but later they grew so strong, always taking the neighbouring territory, through successes in warfare, that finally they established themselves as lords of the whole country inside the Euphrates. And they also took a part of Bactriana, having forced the Scythians, and still earlier Eucratides and his followers, to yield to them; and at the present time they rule over so much land and so many tribes that in the size of their empire they have become, in a way, rivals of the Romans. The cause of this is their mode of life, and also their customs, which contain much that is barbarian and Scythian in character, though more that is conducive to hegemony and success in war.
3 They say that the Aparnian Däae were emigrants from the Däae above Lake Maeotis, who are called Xandii or Parii. But the view is not altogether accepted that the Däae are a part of the Scythians who live about Maeotis. At any rate, some say that Arsaces derives his origin from the Scythians, whereas others say that he was a Bactrian, and that when in flight from the enlarged power of Diodotus and his followers he caused Parthia to revolt. But since I have said much about the Parthian usages in the sixth book of my Historical Sketches and in the second book of my History of events after Polybius,1 I shall omit discussion of that subject here, lest I may seem to be repeating what I have already said, though I shall mention this alone, that the Council of the Parthians, according to Poseidonius, consists of two groups, one that of kinsmen, and the other that of wise men and Magi, from both of which groups the kings were appointed. |
|
|
|
|
11 - 10 Aria and Margiana 
1 Aria and Margiana are the most powerful districts in this part of Asia, these districts in part being enclosed by the mountains and in part having their habitations in the plains. Now the mountains are occupied by Tent-dwellers, and the plains are intersected by rivers that irrigate them, partly by the Arius and partly by the Margus. Aria borders on Margiana and . . . Bactria; it is about six thousand stadia distant from Hyrcania. And Drangiana, as far as Carmania, was joined with Aria in the payment of tribute — Drangiana, for the most part, lying below the southern parts of the mountains, though some parts of it approach the northern region opposite Aria. But Arachosia, also, is not far away, this country too lying below the southern parts of the mountains and extending as far as the Indus River, being a part of Ariana. The length of Aria is about two thousand stadia, and the breadth of the plain about three hundred. Its cities are Artacaëna and Alexandreia, and Achaïa, all named after their founders. The land is exceedingly productive of wine, which keeps good for three generations in vessels not smeared with pitch.
2 Margiana is similar to this country, although its plain is surrounded by deserts. Admiring its fertility, Antiochus Soter enclosed a circuit of fifteen hundred stadia with a wall and founded a city Antiocheia. The soil of the country is well suited to the vine; at any rate, they say that a stock of the vine is often found which would require two men to girth it, and that the bunches of grapes are two cubits. |
|
|
|
|
11 - 11 Bactria 
1 As for Bactria, a part of it lies alongside Aria towards the north, though most of it lies above Aria and to the east of it. And much of it produces everything except oil. The Greeks who caused Bactria to revolt grew so powerful on account of the fertility of the country that they became masters, not only of Ariana, but also of India, as Apollodorus of Artemita says: and more tribes were subdued by them than by Alexander — by Menander in particular (at least if he actually crossed the Hypanis towards the east and advanced as far as the Imaüs), for some were subdued by him personally and others by Demetrius, the son of Euthydemus the king of the Bactrians; and they took possession, not only of Patalena, but also, on the rest of the coast, of what is called the kingdom of Saraostus and Sigerdis. In short, Apollodorus says that Bactriana is the ornament of Ariana as a whole; and, more than that, they extended their empire even as far as the Seres and the Phryni.
2 Their cities were Bactra (also called Zariaspa, through which flows a river bearing the same name and emptying into the Oxus), and Darapsa, and several others. Among these was Eucratidia, which was named after its ruler. The Greeks took possession of it and divided it into satrapies, of which the satrapy Turiva and that of Aspionus were taken away from Eucratides by the Parthians. And they also held Sogdiana, situated above Bactriana towards the east between the Oxus River, which forms the boundary between the Bactrians and the Sogdians, and the Iaxartes River. And the Iaxartes forms also the boundary between the Sogdians and the nomads.
3 Now in early times the Sogdians and Bactrians did not differ much from the nomads in their modes of life and customs, although the Bactrians were a little more civilised; however, of these, as of the others, Onesicritus1 does not report their best traits, saying, for instance, that those who have become helpless because of old age or sickness are thrown out alive as prey to dogs kept expressly for this purpose, which in their native tongue are called "undertakers," and that while the land outside the walls of the metropolis of the Bactrians looks clean, yet most of the land inside the walls is full of human bones; but that Alexander broke up the custom. And the reports about the Caspians are similar, for instance, that when parents live beyond seventy years they are shut in and starved to death. Now this latter custom is more tolerable; and it is similar to that of the Ceians,2 although it is of Scythian origin; that of the Bactrians, however, is much more like that of the Scythians. And so, if it was proper to be in doubt as to the facts at the time when Alexander was finding such customs there, what should one say as to what sort of customs were probably in vogue among them in the time of the earliest Persian rulers and the still earlier rulers?
4 Be this as it may, they say that Alexander founded eight cities in Bactriana and Sogdiana, and that he rased certain cities to the ground, among which was Cariatae in Bactriana, in which Callisthenes was seized and imprisoned, and Maracanda and Cyra in Sogdiana, Cyra being the last city founded by Cyrus and being situated on the Iaxartes River, which was the boundary of the Persian empire; and that although this settlement was fond of Cyrus, he rased it to the ground because of its frequent revolts; and that through a betrayal he took also two strongly fortified rocks, one in Bactrians, that of Sisimithres, where Oxyartes kept his daughter Rhoxana, and the other in Sogdiana, that of Oxus, though some call it the rock of Ariamazes. Now writers report that that of Sisimithres is fifteen stadia in height and eighty in circuit, and that on top it is level and has a fertile soil which can support five hundred men, and that here Alexander met with sumptuous hospitality and married Rhoxana, the daughter of Oxyartes; but the rock in Sogdiana, they say, is twice as high as that in Bactriana. And near these places, they say, Alexander destroyed also the city of the Branchidae, whom Xerxes had settled there — people who voluntarily accompanied him from their home-land — because of the fact that they had betrayed to him the riches and treasures of the god at Didyma. Alexander destroyed the city, they add, because he abominated the sacrilege and the betrayal.
5 Aristobulus calls the river which flows through Sogdiana Polytimetus, a name imposed by the Macedonians (just as they imposed names on many other places, giving new names to some and slightly altering the spelling of the names of others); and watering the country it empties into a desert and sandy land, and is absorbed in the sand, like the Arius which flows through the country of the Arians. It is said that people digging near the Ochus River found a spring of oil. It is reasonable to suppose that, just as nitrous5 and astringent and bituminous and sulphurous liquids flow through the earth, so also oily liquids are found; but the rarity causes surprise. According to some, the Ochus flows through Bactriana; according to others, alongside it. And according to some, it is a different river from the Oxus as far as its mouths, being more to the south than the Oxus, although they both have their outlets into the Caspian Sea in Hyrcania, whereas others say that it is different at first, but unites with the Oxus, being in many places as much as six or seven stadia wide. The Iaxartes, however, from beginning to end, is a different river from the Oxus, and although it ends in the same area, the mouths of the two, according to Patrocles, are about eighty parasangs distant from one another. The Persian parasang, according to some, is sixty stadia, but according to others thirty or forty. When I was sailing up the Nile, they used different measures when they named the distance in "schoeni" from city to city, so that in some places the same number of "schoeni" meant a longer voyage and in others a shorter; and thus the variations have been preserved to this day as handed down from the beginning.
6 Now the tribes one encounters in going from Hyrcania towards the rising sun as far as Sogdiana became known at first to the Persians — I mean the tribes inside Taurus — and afterwards to the Macedonians and to the Parthians; and the tribes situated on the far side of those tribes and in a straight line with them are supposed, from their identity in kind, to be Scythian, although no expeditions have been made against them that I know of, any more than against the most northerly of the nomads. Now Alexander did attempt to lead an expedition against these when he was in pursuit of Bessus9 and Spitamenes, but when Bessus was captured alive and brought back, and Spitamenes was slain by the barbarians, he desisted from his undertaking. It is not generally agreed that persons have sailed around from India to Hyrcania, but Patrocles states that it is possible.
It is said that the last part of the Taurus, which is called Imaïus and borders on the Indian Sea, neither extends eastwards farther than India nor into it; but that, as one passes to the northern side, the sea gradually reduces the length and breadth of the country, and therefore causes to taper towards the east the portion of Asia now being sketched, which is comprehended between the Taurus and the ocean that fills the Caspian Sea. The maximum length of this portion from the Hyrcanian Sea to the ocean that is opposite the Imaïus is about thirty thousand stadia, the route being along the mountainous tract of the Taurus, and the breadth less than ten thousand; for, as has been said, the distance from the Gulf of Issus to the eastern sea at India is about forty thousand stadia, and to Issus from the western extremity at the Pillars of Heracles thirty thousand more. The recess of the Gulf of Issus is only slightly, if at all, farther east than Amisus, and the distance from Amisus to the Hyrcanian land is about ten thousand stadia, being parallel to that of the above-mentioned distance from issu to India. Accordingly, there remain thirty thousand stadia as the above-mentioned length towards the east of the portion now described. Again, since the maximum breadth of the inhabited world, which is chlamys-shaped, is about thirty thousand stadia, this distance would be measured near the meridian line drawn through the Hyrcanian and Persian Seas, if it be true that the length of the inhabited world is seventy thousand stadia. Accordingly, if the distance from Hyrcania to Artemita in Babylonia is eight thousand stadia, as is stated by Apollodorus of Artemita, and the distance from there to the mouth of the Persian Sea another eight thousand, and again eight thousand, or a little less, to the places that lie on the same parallel as the extremities of Ethiopia, there would remain of the above-mentioned breadth of the inhabited world the distance which I have already given, from the recess of the Hyrcanian Sea to the mouth of that sea. Since this segment of the earth tapers towards the eastern parts, its shape would be like a cook's knife, the mountain being in a straight line and conceived of as corresponding to the edge of the knife, and the coast from the mouth of the Hyrcanian Sea to Tamarum as corresponding to the other side of the knife, which ends in a line that curves sharply to the point.
8 I must also mention some strange customs, everywhere talked about, of the utterly barbarous tribes; for instance, the tribes round the Caucasus and the mountainous country in general. What Euripides refers to is said to be a custom among some of them, "to lament the new‑born babe, in view of all the sorrows it will meet in life, but on the other hand to carry forth from their homes with joy and benedictions those who are dead and at rest from their troubles"; and it is said to be a custom among others to put to death none of the greatest criminals, but only to cast them and their children out of their borders — a custom contrary to that of the Derbices, for these slaughter people even for slight offences. The Derbices worship Mother Earth; and they do not sacrifice, or eat, anything that is female; and when men become over seventy years of age they are slaughtered, and their flesh is consumed by their nearest of kin; but their old women are strangled and then buried. However, the men who die under seventy years of age are not eaten, but only buried. The Siginni imitate the Persians in all their customs, except that they use ponies that are small and shaggy, which, though unable to carry a horseman, are yoked together in a four-horse team and are driven by women trained thereto from childhood; and the woman who drives best cohabits with whomever she wishes. Others are said to practise making their heads appear as long as possible and making their foreheads project beyond their chins. It is a custom of the Tapyri for the men to dress in black and wear their hair long, and for the women to dress in white and wear their hair short. They live between the Derbices and the Hyrcanians. And he who is adjudged the bravest marries whomever he wishes. The Caspians starve to death those who are over seventy years of age and place their bodies out in the desert; and then they keep watch from a distance, and if they see them dragged from their biers by birds, they consider them fortunate, and if by wild beasts or dogs, less so, but if by nothing, they consider them cursed by fortune. |
|
|
|
|
11 - 12 Cis-Tauran Asia and the Taurus 
1 Since the northern parts of Asia are formed by the Taurus, — I mean the parts which are also called "Cis‑Tauran" Asia, I have chosen to describe these first. These include all or most of the regions in the mountains themselves. All that lie farther east than the Caspian Gates admit of a simpler description because of the wildness of their inhabitants; and it would not make much difference whether they were named as belonging to this "clima" or that, whereas all that lie to the west afford abundant matter for description, and therefore I must proceed to the parts which are adjacent to the Caspian Gates. Adjacent to the Caspian Gates on the west is Media, a country at one time both extensive and powerful, and situated in the midst of the Taurus, which is split into many parts in the region of Media and contains many valleys, as is also the case in Armenia.
2 For this mountain has its beginning in Caria and Lycia; there, indeed, it has neither any considerable breadth nor height, but it first rises to a considerable height opposite the Chelidoniae, which are islands at the beginning of the coast of Pamphylia, and then stretching towards the east encloses long valleys, those in Cilicia, and then on one side the Amanus Mountain splits off it and on the other the Antitaurus Mountain, in which latter is situated Comana, in Upper Cappadocia, as it is called. Now the Antitaurus ends in Cataonia, whereas the mountain Amanus extends to the Euphrates River and Melitenê, where Commagenê lies adjacent to Cappadocia. And it is succeeded in turn by the mountains on the far side of the Euphrates, which are continuous with those aforementioned, except that they are cleft by the river that flows through the midst of them. Here its height and breadth greatly increase and its branches are more numerous. At all events, the most southerly part is the Taurus proper, which separates Armenia from Mesopotamia.
3 Thence flow both rivers, I mean the Euphrates and the Tigris, which encircle Mesopotamia and closely approach each other in Babylonia and then empty into the Persian Sea. The Euphrates is not only the larger of the two rivers, but also, with its winding stream, traverses more country, having its sources in the northerly region of the Taurus, and flowing towards the west through Greater Armenia, as it is called, to Lesser Armenia, having the latter on its right and Acilisenê on the left. It then bends towards the south, and at its bend joins the boundaries of Cappadocia; and leaving these and the region of Commagenê on the right, and Acilisenê and Sophenê in Greater Armenia on the left, it runs on to Syria and again makes another bend into Babylonia and the Persian Gulf. The Tigris, running from the southerly part of the same mountain to Seleuceia, approaches close to the Euphrates and with it forms Mesopotamia, and then flows into the same gulf as the Euphrates. The sources of the Euphrates and the Tigris are about two thousand five hundred stadia distant from each other.
4 Now the Taurus has numerous branches towards the north, one of which is that of the Antitaurus, as it is called, for there too the mountain which encloses Sophenê in a valley situated between itself and the Taurus was so named. On the far side of the Euphrates, near Lesser Armenia and next to the Antitaurus towards the north, there stretches a large mountain with many branches, one of which is called Paryadres, another the Moschian Mountains, and another which is called by various names; and these comprehend the whole of Armenia as far as Iberia and Albania. Then other mountains rise towards the east, I mean those which lie above the Caspian Sea, extending as far as Media, not only the Atropatian Media but also the Greater Media. Not only all these parts of the mountains are called Parachoathras, but also those which extend to the Caspian Gates and those which extend still farther towards the east, I mean those which border on Aria. The mountains on the north, then, bear these names, whereas those on the south, on the far side of the Euphrates, in their extent towards the east from Cappadocia and Commagenê, are, at their beginning, called Taurus proper, which separates Sophenê and the rest of Armenia from Mesopotamia; by some, however, these are called the Gordyaean Mountains, and among these belongs also Masius, the mountain which is situated above Nisibis and Tigranocerta. Then the Taurus rises higher and bears the name Niphates; and somewhere here are the sources of the Tigris, on the southern side of the mountainous country. Then from the Niphates the mountain-chain extends still farther and farther and forms the mountain Zagrus which separates Media and Babylonia. After the Zagrus there follows, above Babylonia, the mountainous country of the Elymaei and that of the Paraetaceni, and also, above Media, that of the Cossaei. In the middle are Media and Armenia, which comprise many mountains, many plateaus, and likewise many low plains and large valleys, and also numerous tribes that live round among the mountains and are small in numbers and range the mountains and for the most part are given to brigandage. Thus, then, I am placing inside the Taurus both Media, to which the Caspian Gates belong, and Armenia.
5 According to the way in which I place them, then, these tribes would be towards the north, since they are inside the Taurus, but Eratosthenes, who is the author of the division of Asia into "Southern Asia" and "Northern Asia" and into "Sphragides," as he calls them, calling some of the "sphragides" "northern" and others "southern," represents the Caspian Gates as a boundary between the two "climata"; reasonably, therefore he might represent as "southern" the parts that are more southerly, stretching towards the east, than the Caspian Gates, among which are Media and Armenia, and the more northerly as "northern," since this is the case no matter what distribution into parts is otherwise made of the country. But perhaps it did not strike Eratosthenes that no part either of Armenia or of Media lay outside the Taurus. |
|
|
|
|
11 - 13 Media 
1 Media is divided into two parts. One part of it is called Greater Media, of which the metropolis is Ecbatana, a large city containing the royal residence of the Median empire (the Parthians continue to use this as a royal residence even now, and their kings spend at least their summers there, for Media is a cold country; but their winter residence is at Seleuceia, on the Tigris near Babylon). The other part is Atropatian Media, which got its name from the commander1 Atropates, who prevented also this country, which was a part of greater Media, from becoming subject to the Macedonians. Furthermore, after he was proclaimed king, he organised this country into a separate state by itself, and his succession of descendants is preserved to this day, and his successors have contracted marriages with the kings of the Armenians and Syrians and, in later times, with the kings of the Parthians.
2 This country lies east of Armenia and Matianê, west of Greater Media, and north of both; and it lies adjacent to the region round the recess of the Hyrcanian Sea and to Matianê on the south. It is no small country, considering its power, as Apollonides says, since it can furnish as many as ten thousand horsemen and forty thousand foot-soldiers. It has a harbour, Capauta, in which salts effloresce and solidify. These salts cause itching and are painful, but this effect is relieved by olive‑oil; and the water restores weathered garments, if perchance through ignorance one should dip them in it to wash them. They have powerful neighbours in the Armenians and the Parthians, by whom they are often plundered. But still they hold out against them and get back what has been taken away from them, as, for example, they got back Symbacê from the Armenians when the latter became subject to the Romans; and they themselves have attained to friendship with Caesar. But they are also paying court to the Parthians at the same time.
3 Their royal summer palace is situated in a plain at Gazaca, and their winter palace in a fortress called Vera, which was besieged by Antony on his expedition against the Parthians. This fortress is distant from the Araxes, which forms the boundary between Armenia and Atropatenê, two thousand four hundred stadia, according to Dellius, the friend of Antony, who wrote an account of Antony's expedition against the Parthians, on which he accompanied Antony and was himself a commander. All regions of this country are fertile except the part towards the north, which is mountainous and rugged and cold, the abode of the mountaineers called Cadusii, Amardi, Tapyri, Cyrtii and other such peoples, who are migrants and predatory; for the Zagrus and Niphates mountains keep these tribes scattered; and the Cyrtii in Persis, and the Mardi (for the Amardi are also thus called), and those in Armenia who to this day are called by the same name, are of the same character.
4 The Cadusii, however, are but little short of the Ariani in the number of their foot-soldiers; and their javelin-throwers are excellent; and in rugged places foot-soldiers instead of horsemen do the fighting. It was not the nature of the country that made the expedition difficult for Antony, but his guide Artavasdes, the king of the Armenians, whom, though plotting against him, Antony rashly made his counsellor and master of decisions respecting the war. Antony indeed punished him, but too late, when the latter had been proved guilty of numerous wrongs against the Romans, not only he himself, but also that other guide, who made the journey from the Zeugma on the Euphrates to the borders of Atropatenê eight thousand stadia long, more than twice the direct journey, guiding the army over mountains and roadless regions and circuitous routes.
5 In ancient times Greater Armenia ruled the whole of Asia, after it broke up the empire of the Syrians, but later, in the time of Astyages, it was deprived of that great authority by Cyrus and the Persians, although it continued to preserve much of its ancient dignity; and Ecbatana was winter residence for the Persian kings, and likewise for the Macedonians who, after overthrowing the Persians, occupied Syria; and still to‑day it affords the kings of the Parthians the same advantages and security.
6 Greater Media is bounded on the east by Parthia and the mountains of the Cossaei, a predatory people, who once supplied the Elymaei, with whom they were allies in the war against the Susians and Babylonians, with thirteen thousand bowmen. Nearchus says that there were four predatory tribes and that of these the Mardi were situated next to the Persians; the Uxii and Elymaei next to the Mardi and the Susians; and the Cossaei next to the Medians; and that whereas all four exacted tribute from the kings, the Cossaei also received gifts at the times when the king, after spending the summer in Ecbatana, went down into Babylonia; but that Alexander put an end to their great audacity when he attacked them in the winter time. So then, Greater Media is bounded on the east by these tribes, and also by the Paraetaceni, who border on the Persians and are themselves likewise mountaineers and predatory; on the north by the Cadusii who live above the Hyrcanian Sea, and by the other tribes which I have just described; on the south by Apolloniatis, which the ancients called Sitacenê, and by the mountain Zagrus, at the place where Massabaticê is situated, which belongs to Media, though some say that it belongs to Elymaea; and on the west by the Atropatii and certain of the Armenians. There are also some Greek cities in Media, founded by the Macedonians, among which are Laodicea, Apameia and the city near Rhagae, and Rhaga itself, which was founded by Nicator. By him it was named Europus, but by the Parthians Arsacia; it lies about five hundred stadia to the south of the Caspian Gates, according to Apollodorus of Artemita.
7 Now most of the country is high and cold; and such, also, are the mountains which lie above Ecbatana and those in the neighbourhood of Rhagae and the Caspian Gates, and in general the northerly regions extending thence to Matianê and Armenia; but the region below the Caspian Gates, consisting of low‑lying lands and hollows, is very fertile and productive of everything but the olive; and even if the olive is produced anyway, it is dry and yields no oil. This, as well as Armenia, is an exceptionally good "horse-pasturing" country; and a certain meadow there is called "Horse-pasturing," and those who travel from Persis and Babylon to the Caspian Gates pass through it; and in the time of the Persians it is said that fifty thousand mares were pastured in it and that these herds belonged to the kings. As for the Nesaean horses, which the kings used because they were the best and the largest, some writers say that the breed came from here, while others say from Armenia. They are characteristically different in form, as are also the Parthian horses, as they are now called, as compared with the Helladic and the other horses in our country. Further, we call the grass that makes the best food for horses by the special name "Medic," from the fact that it abounds there. The country also produces silphium; whence the "Medic" juice, as it is called, which in general is inferior to the "Cyrenaic" juice, but sometimes is even superior to it, either owing to regional differences, or because of a variation in the species of the plant, or even owing to the people who extract and prepare the juice in such a way as to conserve its strength for storage and for use.
8 Such is the nature of the country. As for its size, its length and breadth are approximately equal. The greatest breadth of Media seems to be that from the pass that leads over the Zagrus, which is called Medic Gate, to the Caspian Gates through Sigrianê, four thousand one hundred stadia. The reports on the tributes paid agree with the size and the power of the country; for Cappadocia paid the Persians yearly, in addition to the silver tax, fifteen hundred horses, two thousand mules, and fifty thousand sheep, whereas Media paid almost twice as much as this.
9 As for customs, most of theirs and of those of the Armenians are the same, because their countries are similar. The Medes, however, are said to have been the originators of customs for the Armenians, and also, still earlier, for the Persians, who were their masters and their successors in the supreme authority over Asia. For example, their "Persian" stolê, as it is now called, and the court they pay to their kings, and their ornaments, and the divine reverence paid by subjects to kings, came to the Persians from the Medes. And that this is true is particularly clear from their dress; for tiara, citaris, pilus, tunics with sleeves reaching to the hands, and trousers, are indeed suitable things to wear in cold and northerly regions, such as the Medes wear, but by no means in southerly regions; and most of the settlements possessed by the Persians were on the Red Sea, farther south than the country of the Babylonians and the Susians. But after the overthrow of the Medes the Persians acquired in addition certain parts of the country that reached to Media. However, the customs even of the conquered looked to the conquerors so august and appropriate to royal pomp that they submitted to wear feminine robes instead of going naked or lightly clad, and to cover their bodies all over with clothes.
Some say that Medeia introduced this kind of dress when she, along with Jason, held dominion in this region, even concealing her face whenever she went out in public in place of the king; and that the Jasonian hero‑chapels, which are much revered by the barbarians, are memorials of Jason (and above the Caspian Gates on the left is a large mountain called Jasonium), whereas the dress and the name of the country are memorials of Medeia. It is said also that Medus her son succeeded to the empire and left his own name to the country. In agreement with this are the Jasonia of Armenia and the name of that country and several other things which I shall discuss.
This, too, is a Medic support — to choose the bravest man as king; not, however, among all Medes, but only among the mountaineers. More general is the custom for the kings to have many wives; this is the custom of the mountaineers of the Medes, and all Medes, and they are not permitted to have less than five; likewise, the women are said to account it an honourable thing to have as many husbands as possible and to consider less than five a calamity. But though the rest of Media is extremely fertile, the northerly mountainous part has poor soil; at any rate, the people live on the fruits of trees, making cakes out of apples that are sliced and dried, and bread from roasted almonds; and they squeeze out a wine from certain roots; and they use the meat of wild animals, but do not breed tame animals. Thus much I add concerning the Medes. As for the institutions in common use throughout the whole of Media, since they prove to have been the same as those of the Persians because of the conquest of the Persians, I shall discuss them in my account of the latter. |
|
|
|
|
11 - 14 Armenia 
1 As for Armenia, the southern parts of it have the Taurus situated in front of them, which separates it from the whole of the country between the Euphrates and the Tigris, the country called Mesopotamia; and the eastern parts border on Greater Armenia and Atropatenê; and on the north the mountains of Parachoathras that lie above the Caspian Sea, and Albania, and Iberia, and the Caucasus, which last encircles these nations and borders on Armenia, and borders also on the Moschian and Colchian mountains as far as the Tibarani, as they are called; and on the west are these nations and the mountains Paryadres and Scydises in their extent to Lesser Armenia and the river-land of the Euphrates, which latter separates Armenia from Cappadocia and Commagenê.
2 For the Euphrates, having its beginnings on the northern side of the Taurus, flows at first towards the west through Armenia, and then bends towards the south and cuts through the Taurus between Armenia, Cappadocia, and Commagenê, and then, after falling outside the Taurus and reaching the borders of Syria, it bends towards the winter-sunrise as far as Babylon, and with the Tigris forms Mesopotamia; and both rivers end in the Persian Gulf. Such, then, is our circuit of Armenia, almost all parts being mountainous and rugged, except the few which verge toward Media. But since the above-mentioned Taurus3 takes a new beginning on the far side of the Euphrates opposite Commagenê and Melitenê, countries formed by that river, Mt. Masius is the mountain which lies above the Mygdonians of Mesopotamia on the south, in whose country is Nisibis, whereas Sophenê is situated in the northern parts, between Masius and Antitaurus. The Antitaurus takes its beginning at the Euphrates nd the Taurus and ends towards the eastern parts of Armenia, thus on one side4 enclosing the middle of Sophenê, and having on its other side Acilisenê, which is situated between the Antitaurus6 and the river-land of the Euphrates, before that river bends towards the south. The royal city of Sophenê is Carcathiocerta. Above Mt. Masius, far towards the east opposite Gordyenê, lies Mt. Niphates; and then comes Mt. Abus, whence flow both the Euphrates and the Araxes, the former towards the west and the latter towards the east; and then Mt. Nibarus, which stretches as far as Media.
3 I have already described the course of the Euphrates. As for the Araxes, it first flows towards the east as far as Atropatenê, and then bends towards the west and towards the north and flows first past Azara and then past Artaxata, Armenian cities, and then, passing through the Araxene Plain, empties into the Caspian Sea.
In Armenia itself there are many mountains and many plateaus, in which not even the vine can easily grow; and also many valleys, some only moderately fertile, others very fertile, for instance, the Araxene Plain, through which the Araxes River flows to the extremities of Albania and then empties into the Caspian Sea. After these come Sacasenê, this too bordering on Albania and the Cyrus River; and then comes Gogarenê. Indeed, the whole of this country abounds in fruits and cultivated trees and evergreens, and even bears the olive. There is also Phauenê, a province of Armenia, and Comisenê, and Orchistenê, which last furnishes the most cavalry. Chorzenê and Cambysenê are the most northerly and the most subject to snows, bordering on the Caucasian mountains and Iberia and Colchis. It is said that here, on the passes over the mountains, whole caravans are often swallowed up in the snow when unusually violent snowstorms take place, and that to meet such dangers people carry staves, which they raise to the surface of the snow in order to get air to breathe and to signify their plight to people who come along, so as to obtain assistance, be dug out, and safely escape. It is said that hollow masses of ice form in the snow which contain good water, in a coat of ice as it were; and also that living creatures breed in the snow (Apollonides calls these creatures "scoleces"and Theophanes "thripes"); and that good water is enclosed in these hollow masses which people obtain for drinking by slitting open the coats of ice; and the genesis of these creatures is supposed to be like that of the gnats which spring from the flames and sparks at mines.
5 According to a report, Armenia, though a small country in earlier times, was enlarged by Artaxias and Zariadris, who formerly were generals of Antiochus the Great, but later, after his defeat, reigned as kings (the former as king of Sophenê, Acisenê, Odomantis, and certain other countries, and the latter as king of the country round Artaxata), and jointly enlarged their kingdoms by cutting off for themselves parts of the surrounding nations, — I mean by cutting off Caspianê and Phaunitis and Basoropeda from the country of the Medes; and the country along the side of Mt Paryadres and Chorzenê and Gogarenê, which last is on the far side of the Cyrus River, from that of the Iberians; and Carenitis and Xerxenê, which border on Lesser Armenia or else parts of it, from that of the Chalybians and the Mosynoeci; and Acilisenê and the country round the Antitaurus from that of the Cataonians; and Taronitis from that of the Syrians; and therefore they all speak the same language, as we are told.
6 The cities of Armenia are Artaxata, also called Artaxiasata, which was founded by Hannibal for Artaxias the king, and Arxata, both on the Araxes River, Arxata being near the borders of Atropatia, whereas Artaxata is near the Araxene plain, being a beautiful settlement and the royal residence of the country. It is situated on a peninsula-like elbow of land and its walls have the river as protection all round them, except at the isthmus, which is enclosed by a trench and a palisade. Not far from the city the treasuries of Tigranes and Artavasdes, the strong fortresses Babyrsa and Olanê. And there were other fortresses on the Euphrates. Of these, Artageras was caused to revolt by Ador, its commandant, but Caesar's generals sacked it after a long siege and destroyed its walls.
7 There are several rivers in the country, but the best known are the Phasis and the Lycus, which empty into the Pontic Sea (Eratosthenes wrongly writes "Thermodon" instead of "Lycus"), whereas the Cyrus and the Araxes empty into the Caspian Sea, and the Euphrates and the Tigris into the Red Sea.
8 There are also large lakes in Armenia; one the Mantianê, which being translated means "Blue"; it is the largest salt-water lake after Lake Maeotis, as they say, extending as far as Atropatia; and it also has salt-works. Another is Arsenê, also called Thopitis. It contains soda, and it cleanses and restores clothes; but because of this ingredient the water is also unfit for drinking. The Tigris flows through this lake after issuing from the mountainous country near the Niphates; and because of its swiftness it keeps its current unmixed with the lake; whence the name Tigris, since the Median word for "arrow" is "tigris." And while the river has fish of many kinds, the fish in the lake are of one kind only. Near the recess of the lake the river falls into a pit, and after flowing underground for a considerable distance rises near Chalonitis. Thence the river begins to flow down towards Opis and the wall of Semiramis, as it is called, leaving the Gordiaeans and the whole of Mesopotamia on the right, while the Euphrates, on the contrary, has the same country on the left. Having approached one another and formed Mesopotamia, the former flows through Seleuceia to the Persian Gulf and the latter through Babylon, as I have already said somewhere in my arguments against Eratosthenes and Hipparchus.
9 There are gold mines in Syspiritis and Caballa, to which Menon was sent by Alexander with soldiers, and he was led up to them by the natives. There are also other mines, in particular those of sandyx, as it is called, which is also called "Armenian" colour, like chalcê. The country is so very good for "horse-pasturing," not even inferior to Media, that the Nesaean horses, which were used by the Persian kings, are also bred there. The satrap of Armenia used to send to the Persian king twenty thousand foals every year at the time of the Mithracina. Artavasdes, at the time when he invaded Media with Antony, showed him, apart from the rest of the cavalry, six thousand horses drawn up in battle array in full armour. Not only the Medes and the Armenians pride themselves upon this kind of cavalry, but also the Albanians, for they too use horses in full armour.
As for the wealth and power of the country, the following is no small sign of it, that when Pompey imposed upon Tigranes, the father of Artavasdes, a payment of six thousand talents of silver, he forthwith distributed to the Roman forces as follows: to each soldier fifty drachmas, to each centurion a thousand drachmas, and to each hipparch and chiliarch a talent.
The size of the country is given by Theophanes: the breadth one hundred "schoeni," and the length twice as much, putting the "schoenus" at forty stadia; but his estimate is too high; it is nearer the truth to put down as length what he gives as breadth, and as breadth the half, or a little more, of what he gives as breadth. Such, then, is the nature and power of Armenia.
There is an ancient story of the Armenian race to this effect: that Armenus of Armenium, a Thessalian city, which lies between Pherae and Larisa on Lake Boebe, as I have already said, accompanied Jason into Armenia; and Cyrsilus the Pharsalian and Medius the Larisaean, who accompanied Alexander, say that Armenia was named after him, and that, of the followers of Armenus, some took up their abode in Acilisenê, which in earlier times was subject to the Sopheni, whereas others took up their abode in Syspiritis, as far as Calachenê and Adiabenê, outside the Armenian mountains. They also say that the clothing of the Armenians is Thessalian, for example, the long tunics, which in tragedies are called Thessalian and are girded round the breast; and also the cloaks that are fastened on with clasps, another way in which the tragedians imitated the Thessalians, for the tragedian had to have some alien decoration of this kind; and since the Thessalians in particular wore long robes, probably because they of all the Greeks lived in the most northerly and coldest region, they were the most suitable objects of imitation for actors in their theatrical make‑ups. And they say that their style of horsemanship is Thessalian, both theirs and alike that of the Medes. To this the expedition of Jason and the Jasonian monuments bear witness, some of which were built by the sovereigns of the country, just as the temple of Jason at Abdera was built by Parmenion.
It is thought that the Araxes was given the same name as the Peneius by Armenus and his followers because of its similar to that river, for that river, too, they say, was called Araxes because of the fact that it "cleft" Ossa from Olympus, the cleft called Tempê. And it is said that in ancient times the Araxes in Armenia, after descending from the mountains, spread out and formed a sea in the plains below, since it had anoint outlet, but that Jason, to make it like Tempê, made the cleft through which the water now precipitates itself into the Caspian Sea, and that in consequence of this the Araxene Plain, through which the river flows to its precipitate descent, was relieved of the sea. Now this account of the Araxes contains some plausibility, but that of Herodotus not at all; for he says that after flowing out of the country of the Matieni it splits into forty rivers and separates the Scythians from the Bactrians. Callisthenes, also, follows Herodotus.
It is also said of certain of the Aenianes that some of them took up their abode in Vitia and others above the Armenians beyond the Abus and the Nibarus. These two mountains are parts of the Taurus, and of these the Abus is near the road that leads into Ecbatana past the temple of Baris. It is also said that certain of the Thracians, those called "Saraparae," that is "Decapitators," took up their abode beyond Armenia near the Guranii and the Medes, a fierce and intractable people, mountaineers, scalpers, and beheaders, for this last is the meaning of "Saraparae." I have already discussed Medeia in my account of the Medes; and therefore, from all this, it is supposed that both the Medes and the Armenians are in a way kinsmen to the Thessalians and the descendants of Jason and medeia.
This, then, is the ancient account; but the more recent account, and that which begins with Persian times and extends continuously to our own, might appropriately be stated in brief as follows: The Persians and Macedonians were in possession of Armenia; after this, those who held Syria and Media; and the last was Orontes, the descendant of Hydarnes, one of the seven Persians; and then the country was divided into two parts by Artaxias and Zariadris, the generals of Antiochus the Great, who made war against the Romans; and these generals ruled the country, since it was turned over to them by the king; but when the king was defeated, they joined the Romans and were ranked as autonomous, with the title of king. Now Tigranes was a descendant of Artaxias and held what is properly called Armenia, which lay adjacent to Media and Albania and Iberia, extending as far as Colchis and Cappadocia on the Euxine, whereas the Sophenian Artanes, who held the southern parts and those that lay more to the west than these, was a descendant of Zariadris. But he was overcome by Tigranes, who established himself as lord of all. The changes of fortune experienced by Tigranes were varied, for at first he was a hostage among the Parthians; and then through them he obtained the privilege of returning home, they receiving as reward therefor seventy valleys in Armenia; but when he had grown in power, he not only took these places back but also devastated their country, both that about Ninus and that about Arbela; and he subjugated to himself the rulers of Atropatenê and Gordyaea, and along with these the rest of Mesopotamia, and also crossed the Euphrates and by main strength took Syria itself and Phoenicia; and, exalted to this height, he also founded a city near Iberia, between this place and the Zeugma on the Euphrates; and, having gathered peoples thither from twelve Greek cities which had laid waste, he named it Tigranocerta; but Leucullus, who had waged war against Mithridates, arrived before Tigranes finished his undertaking and not only dismissed the inhabitants to their several home-lands but also attacked and pulled down the city, which was still only half finished, and left it a small village; and he drove Tigranes out of both Syria and Phoenicia. His successor Artavasdes was indeed prosperous for a time, while he was a friend to the Romans, but when he betrayed Antony to the Parthians in his war against them he paid the penalty for it, for he was carried off prisoner to Alexandreia by Antony and was paraded in chains through the city; and for a time he was kept in prison, but was afterwards slain, when the Actian war broke out. After him several kings reigned, these being subject to Caesar and the Romans; and still to‑day the country is governed in the same way.
Now the sacred rites of the Persians, one and all, are held in honour by both the Medes and the Armenians; but those of Anaïtis are held in exceptional honour by the Armenians, who have built temples in her honour in different places, and especially in Acilisenê. Here they dedicate to her service male and female slaves. This, indeed, is not a remarkable thing; but the most illustrious men of the tribe actually consecrate to her their daughters while maidens; and it is the custom for these first to be prostituted in the temple of the goddess for a long time and after this to be given in marriage; and no one disdains to live in wedlock with such a woman. Something of this kind is told also by Herodotus in his account of the Lydian women, who, one and all, he says, prostitute themselves. And they are so kindly disposed to their paramours that they not only entertain them hospitably but also exchange presents with them, often giving more than they receive, inasmuch as the girls from wealthy homes are supplied with means. However, they do not admit any man that comes along, but probably those of equal rank with themselves. |
|
|
|
|
12 West Asia 2 8 92 1:50 
|
12 - 1 Cappadocia 
1 Cappadocia, also, is a country of many parts and has undergone numerous changes. However, the inhabitants who speak the same language are, generally speaking, those who are bounded on the south by the "Cilician" Taurus, as it is called, and on the east by Armenia and Colchis and by the intervening peoples who speak a different group of languages, and on the north by Euxine as far as the outlets of the Halys River, and on the west both by the tribe of the Paphlagonians and by those Galatae who settled in Phrygia and extended as far as the Lycaonians and those Cilicians who occupy Cilicia Tracheia.
2 Now as for the tribes themselves which speak the same language, the ancients set one of them, the Cataonians, by themselves, contradistinguishing them from the Cappadocians, regarding the latter as a different tribe; and in their enumeration of the tribes they placed Cataonia after Cappadocia, and then placed the Euphrates and the tribes beyond it so as to include in Cataonia Melitenê, which lies between Cataonia and the Euphrates, borders on Commagenê, and, according to the division of Cappadocia into ten prefectures, is a tenth portion of the country. Indeed, it was in this way that the kings in my time who preceded Archelaüs held their several prefectures over Cappadocia. And Cataonia, also, is a tenth portion of Cappadocia. In my time each of the two countries had its own prefect; but since, as compared with the other Cappadocians, there is no difference to be seen either in the language or in any other usages of the Cataonians, it is remarkable how utterly all signs of their being a different tribe have disappeared. At any rate, they were once a distinct tribe, but they were annexed by Ariarathes, the first man to be called king of the Cappadocians.
3 Cappadocia constitutes the isthmus, as it were, of a large peninsula bounded by two seas, by that of the Issian Gulf as far as Cilicia Tracheia and by that of the Euxine as far as Sinopê and the coast of the Tibareni. I mean by "peninsula" all the country which is west of Cappadocia this side the isthmus, which by Herodotus is called "the country this side the Halys River"; for this is the country which in its entirety was ruled by Croesus, whom Herodotus calls the tyrant of the tribes this side the Halys River. However, the writers of to‑day give the name of Asia to the country this side the Taurus, applying to this country the same name as to the whole continent of Asia. This Asia comprises the first nations on the east, the Paphlagonians and Phrygians and Lycaonians, and then the Bithynians and Mysians and the Epictetus, and, besides these, the Troad and Hellespontia, and after these, on the sea, the Aeolians and Ionians, who are Greeks, and, among the rest, the Carians and Lycians, and, in the interior, the Lydians. As for the other tribes, I shall speak of them later.
4 Cappadocia was divided into two satrapies by the Persians at the time when it was taken over by the Macedonians; the Macedonians willingly allowed one part of the country, but unwillingly the other, to change to kingdoms instead of satrapies; and one of these kingdoms they named "Cappadocia Proper" and "Cappadocia near Taurus," and even "Greater Cappadocia," and the other they named "Pontus," though others named it Cappadocia Pontica. As for Greater Cappadocia, we at present do not yet know its administrative divisions, for after the death of king Archelaüs Caesar6 and the senate decreed that it was a Roman province. But when, in the reign of Archelaüs and of the kings who preceded him, the country was divided into ten prefectures, those near the Taurus were reckoned as five in number, I mean Melitenê, Cataonia, Cilicia, Tyanitis, and Garsauritis; and Laviansenê, Sargarausenê, Saravenê, Chamanenê, and Morimenê as the remaining five. The Romans later assigned to the predecessors of Archelaüs an eleventh prefecture, taken from Cilicia, I mean the country round Castabala and Cybistra, extending to Derbê, which last had belonged to Antipater the pirate; and to Archelaüs they further assigned the part of Cilicia Tracheia round Elaeussa, and also all the country that had organised the business of piracy. |
|
|
|
|
12 - 2 Cataonia and Melitene 
1 Melitenê is similar to Commagenê, for the whole of it is planted with fruit-trees, the only country in all Cappadocia of which this is true, so that it produces, not only the olive, but also the Monarite wine, which rivals the Greek wines. It is situated opposite to Sophenê; and the Euphrates River flows between it and Commagenê, which latter borders on it. On the far side of the river is a noteworthy fortress belonging to the Cappadocians, Tomisa by name. This was sold to the ruler of Sophenê for one hundred talents, but later was presented by Leucullus as a meed of valour to the ruler of Cappadocia who took the field with him in the war against Mithridates.
2 Cataonia is a broad hollow plain, and produces everything except evergreen-trees. It is surrounded on its southern side by mountains, among others by the Amanus, which is a branch of the Cilician Taurus, and by the Antitaurus, which branches off in the opposite direction; for the Amanus extends from Cataonia to Cilicia and the Syrian Sea towards the west and south, and in this intervening space it surrounds the whole of the Gulf of Issus and the intervening plains of the Cilicians which lie towards the Taurus. But the Antitaurus inclines to the north and takes a slightly easterly direction, and then terminates in the interior of the country.
3 In this Antitaurus are deep and narrow valleys, in which are situated Comana and the temple of Enyo,1 whom the people there call "Ma." It is a considerable city; its inhabitants, however, consist mostly of the divinely inspired people and the temple-servants who live in it. Its inhabitants are Cataonians, who, though in a general way classed as subject to the king, are in most respects subject to the priest. The priest is master of the temple, and also of the temple-servants, who on my sojourn there were more than six thousand in number, men and women together. Also, considerable territory belongs to the temple, and the revenue is enjoyed by the priest. He is second in rank in Cappadocia after the king; and in general the priests belonged to the same family as the kings. It is thought that Orestes, with his sister Iphigeneia, brought these sacred rites here from the Tauric Scythia, the rite in honour of Artemis Tauropolus, and that here they also deposited the hair of mourning; whence the city's name. Now the Sarus River flows through this city and passes out through the gorges of the Taurus to the plains of the Cilicians and to the sea that lies below them.
4 But the Pyramus, a navigable river with its sources in the middle of the plain, flows through Cataonia. There is a notable pit in the earth through which one can see the water as it runs into a long hidden passage undoing and then rises to the surface. If one lets down a javelin from above into the pit, the force of the water resists so strongly that the javelin can hardly be immersed in it. But although it flows in great volume because of its immense depth and breadth, yet, when it reaches the Taurus, it undergoes a remarkable contraction; and remarkable also is the cleft of the mountain through which the stream is carried; for, as in the case of rocks which have been broken and split into two parts, the projections on either side correspond so exactly to the cavities on the other that they could be fitted together, so it was in the case of the rocks I saw there, which, lying above the river on either side and reaching almost to the summit of the mountain at a distance of two or three plethra from each other, had cavities corresponding with the opposite projections. The whole intervening bed is rock, and it has a cleft through the middle which is deep and so extremely narrow that a dog or hare could leap across it. This cleft is the channel of the river, is full to the brim, and in breadth resembles a canal; but on account of the crookedness of its course and its great contraction in width and the depth of the gorge, a noise like thunder strikes the ears of travellers long before they reach it. In passing out through the mountains it brings down so much silt to the sea, partly from Cataonia and partly from the Cilician plains, that even an oracle is reported as having been given out in reference to it, as follows: "Men that are yet to be shall experience this at the time when the Pyramus of the silver eddies shall silt up its sacred sea‑beach and come to Cyprus." Indeed, something similar to this takes place also in Egypt, since the Nile is always turning the sea into dry land by throwing out silt. Accordingly, Herodotus calls Egypt "the gift of the Nile," while Homer speaks of Pharos as "being out in the open sea," since in earlier times it was not, as now, connected with the mainland of Egypt.7
7 The third in rank is the priesthood of Zeus Daciëus,9 which, though inferior to that of Enyo, is noteworthy. At this place there is a reservoir of salt water which has the circumference of a considerable lake; it is shut in by brows of hills so high and steep that people go down to it by ladder-like steps. The water, they say, neither increases nor anywhere has a visible outflow.
6 Neither the plain of the Cataonians nor the country Melitenê has a city, but they have strongholds on the mountains, I mean Azamora and Dastarcum; and round the latter flows the Carmalas River. It contains also a temple, that of the Cataonian Apollo, which is held in honour throughout the whole of Cappadocia, the Cappadocians having made it the model of temples of their own. Neither do the other prefectures, except two, contain cities; and of the remaining prefectures, Sargarausenê contains a small town Herpa, and also the Carmalas River, this too emptying into the Cilician Sea. In the other prefectures are Argos, a lofty stronghold near the Taurus, and Nora, now called Neroassus, in which Eumenes held out against a siege for a long time. In my time it served as the treasury of Sisines, who made an attack upon the empire of the Cappadocians. To him also belonged Cadena, which had the royal palace and had the aspect of a city. Situated on the borders of Lycaonia is also a town called Garsauira. This too is said once to have been the metropolis of the country. In Morimenê, at Venasa, is the temple of the Venasian Zeus, which has a settlement of almost three thousand temple-servants and also a sacred territory that is very productive, affording the priest a yearly revenue of fifteen talents. He, too, is priest for life, as is the priest at Comana, and is second in rank after him.
7 Only two prefectures have cities, Tyanitis the city Tyana, which lies below the Taurus at the Cilician Gates, where for all is the easiest and most commonly used pass into Cilicia and Syria. It is called "Eusebeia near the Taurus"; and its territory is for the most part fertile and level. Tyana is situated upon a mound of Semiramis, which is beautifully fortified. Not far from this city are Castabala and Cybistra, towns still nearer to the mountain. At Castabala is the temple of the Perasian Artemis, where the priestesses, it is said, walk with naked feet over hot embers without pain. And here, too, some tell us over and over the same story of Orestes and Tauropolus, asserting that she was called "Perasian" because she was brought "from the other side." So then, in the prefecture Tyanitis, one of the ten above mentioned is Tyana (I am not enumerating along with these prefectures those that were acquired later, I mean Castabala and Cybistra and the places in Cilicia Tracheia, where is Elaeussa, a very fertile island, which was settled in a noteworthy manner by Archelaüs, who spent the greater part of his time there), whereas Mazaca, the metropolis of the tribe, is in the Cilician prefecture, as it is called. This city, too, is called "Eusebeia," with the additional words "near the Argaeus," for it is situated below the Argaeus, the highest mountain of all, whose summit never fails to have snow upon it; and those who ascend it (those are few) say that in clear weather both seas, both the Pontus and the Issian Sea, are visible from it. Now in general Mazaca is not naturally a suitable place for the founding of a city, for it is without water and unfortified by nature; and, because of the neglect of the prefects, it is also without walls (perhaps intentionally so, in order that people inhabiting a plain, with hills above it that were advantageous and beyond range of missiles, might not, through too much reliance on the wall as a fortification, engage in plundering). Further, the districts all round are utterly barren and untilled, although they are level; but they are sandy and are rocky underneath. And, proceeding a little farther on, one comes to plains extending over many stadia that are volcanic and full of fire-pits; and therefore the necessaries of life must be brought from a distance. And further, that which seems to be an advantage is attended with peril, for although almost the whole of Cappadocia is without timber, the Argaeus has forests all round it, and therefore the working of timber is close at hand; but the region which lies below the forests also contains fires in many places and at the same time has an underground supply of cold water, although neither the fire nor the water emerges to the surface; and therefore most of the country is covered with grass. In some places, also, the ground is marshy, and at night flames rise therefrom. Now those who are acquainted with the country can work the timber, since they are on their guard, but the country is perilous for most people, and especially for cattle, since they fall into the hidden fire-pits.
8 There is also a river in the plain before the city; it is called Melas, is about forty stadia distant from the city, and has its sources in a district that is below the level of the city. For this reason, therefore, it is useless to the inhabitants, since its stream is not in a favourable position higher up, but spreads abroad into marshes and lakes, and in the summer-time vitiates the air round the city, and also makes the stone-quarry hard to work, though otherwise easy to work; for there are ledges of flat stones from which the Mazaceni obtain an abundant supply of stone for their buildings, but when the slabs are concealed by the waters they are hard to obtain. And these marshes, also, are everywhere volcanic. Ariarathes the king, since the Melas had an outlet into the Euphrates by a certain narrow defile, dammed this and converted the neighbouring plain into a sea‑like lake, and there, shutting off certain isles — like the Cyclades — from the outside world, passed his time there in boyish diversions. But the barrier broke all at once, the water streamed out again, and the Euphrates,thus filled, swept away much of the soil of Cappadocia, and obliterated numerous settlements and plantations, and also damaged no little of the country of the Galatians who held Phrygia. In return for the damage the inhabitants, who gave over the decision of the matter to the Romans, exacted of him a fine of three hundred talents. The same was the case also in regard to Herpa; for there too he dammed the stream of the Carmalas River; and then, the mouth having broken open and the water having ruined certain districts in Cilicia in the neighbourhood of Mallus, he paid damages to those who had been wronged.
9 However, although the district of the Mazaceni is in many respects not naturally suitable for habitation, the kings seem to have preferred it, because of all places in the country this was nearest to the centre of the region which contained timber and stone for buildings, and at the same time provender, of which, being cattle-breeders, they needed a very large quantity, for in a way the city was for them a camp. And as for their security in general, both that of themselves and of their slaves, they got it from the defences in their strongholds, of which there are many, some belonging to the king and others to their friends. Mazaca is distant from Pontus about eight hundred stadia to the south, from the Euphrates slightly less than double that distance, and from the Cilician Gates and the camp of Cyrus a journey of six days by way of Tyana. Tyana is situated at the middle of the journey and is three hundred stadia distant from Cybistra. The Mazaceni use the laws of Charondas, choosing also a Nomodus, who, like the jurisconsults among the Romans, is the expounder of the laws. But Tigranes, the Armenian, put the people in bad plight when he overran Cappadocia, for he forced them, one and all, to migrate into Mesopotamia; and it was mostly with these that he settled Tigranocerta. But later, after the capture of Tigranocerta, those who could returned home.
The size of the country is as follows: In breadth, from Pontus to the Taurus, about one thousand eight hundred stadia, and in length, from Lycaonia and Phrygia to the Euphrates towards the east and Armenia, about three thousand. It is an excellent country, not only in respect to fruits, but particularly in respect to grain and all kinds of cattle. Although it lies farther south than Pontus, it is colder. Bagadania, though level and farthest south of all (for it lies at the foot of the Taurus), produces hardly any fruit-bearing trees, although it is grazed by wild asses, both it and the greater part of the rest of the country, and particularly that round Garsauira and Lycaonia and Morimenê. In Cappadocia is produced also the ruddle called "Sinopean," the best in the world, although the Iberian rivals it. It was named "Sinopean" because the merchants were wont to bring it down thence to Sinope before the traffic of the Ephesians had penetrated as far as the people of Cappadocia. It is said that also slabs of crystal and of onyx stone were found by the miners of Archelaüs near the country of the Galatians. There was a certain place, also, which had white stone that was like ivory in colour and yielded pieces of the size of small whetstones; and from these pieces they made handles for their small swords. And there was another place which yielded such large lumps of transparent stone that they were exported. The boundary of Pontus and Cappadocia is a mountain tract parallel to the Taurus, which has its beginning at the western extremities of Chammanenê, where is situated Dasmenda, a stronghold with sheer ascent, and extends to the eastern extremities of Laviansenê. Both Chammanenê and Laviansenê are prefectures in Cappadocia.
It came to pass, as soon as the Romans, after conquering Antiochus, began to administer the affairs of Asia and were forming friendships and alliances both with the tribes and with the kings, that in all other cases they gave this honour to the kings individually, but gave it to the king of Cappadocia and the tribe jointly. And when the royal family died out, the Romans, in accordance with their compact of friendship and alliance with the tribe, conceded to them the right to live under their own laws; but those who came on the embassy not only begged off from the freedom (for they said that they were unable to bear it), but requested that a king be appointed for them. The Romans, amazed that any people should be so tired of freedom, — at any rate, they permitted them to choose by vote from their own number whomever they wished. And they chose Ariobarzanes; but in the course of the third generation his family died out; and Archelaüs was appointed king, though not related to the people, being appointed by Antony. So much for Greater Cappadocia. As for Cilicia Tracheia, which was added to Greater Cappadocia, it is better for me to describe it in my account of the whole of Cilicia. |
|
|
|
|
12 - 3 Pontus, Paphlagonia, Lesser Armenia 
1 As for Pontus, Mithridates Eupator established himself as king of it; and he held the country bounded by the Halys River as far as the Tibarani and Armenia, and held also, of the country this side the Halys, the region extending to Amastris and to certain parts of Paphlagonia. And he acquired, not only the sea‑coast towards the west as far as Heracleia, the native land of Heracleides the Platonic philosopher, but also, in the opposite direction, the sea‑coast extending to Colchis and Lesser Armenia; and this, as we know, he added to Pontus. And in fact this country was comprised within these boundaries when Pompey took it over, upon his overthrow of Mithridates. The parts towards Armenia and those round Colchis he distributed to the potentates who had fought on his side, but the remaining parts he divided into eleven states and added them to Bithynia, so that out of both there was formed a single province. And he gave over to the descendants of Pylaemenes the office of king over certain of the Paphlagonians situated in the interior between them, just as he gave over the Galatians to the hereditary tetrarchs. But later the Roman prefects made different divisions from time to time, not only establishing kings and potentates, but also, in the case of cities, liberating some and putting others in the hands of potentates and leaving others subject to the Roman people. As I proceed I must speak of things in detail as they now are, but I shall touch slightly upon things as they were in earlier times whenever this is useful. I shall begin at Heracleia, which is the most westerly place in this region.
2 Now as one sails into the Euxine Sea from the Propontis, one has on his left the parts which adjoin Byzantium (these belong to the Thracians, and are called "the Left-hand Parts" of the Pontus), and on his right the parts which adjoin Chalcedon. The first of these latter belong to the Bithynians, the next to the Mariandyni (by some also called Caucones), the next to the Paphlagonians as far as the Halys River, and the next to the Pontic Cappadocians and to the people next in order after them as far as Colchis. All these are called the "Right-hand Parts" of the Pontus. Now Eupator reigned over the whole of this sea‑coast, beginning at Colchis and extending as far as Heracleia, but the parts farther on, extending as far as the mouth of the Pontus and Chalcedon, remained under the rule of the king of Bithynia. But when the kings had been overthrown, the Romans preserved the same boundaries, so that Heracleia was added to Pontus and the parts farther on went to the Bithynians.
3 Now as for the Bithynians, it is agreed by most writers that, though formerly Mysians, they received this new name from the Thracians — the Thracian Bithynians and Thynians — who settled the country in question, and they put down as evidences of the tribe of the Bithynians that in Thrace certain people are to this day called Bithynians, and of that of the Thynians, that the coast near Apollonia and Salmydessus is called Thynias. And the Bebryces, who took up their abode in Mysia before these people, were also Thracians, as I suppose. It is stated that even the Mysians themselves are colonists of those Thracians who are now called Moesians. Such is the account given of these people.
4 But all do not give the same account of the Mariandyni and the Caucones; for Heracleia, they say, is situated in the country of the Mariandyni, and was founded by the Milesians; but nothing has been said as to who they are or whence they came, nor yet do the people appear characterised by any ethnic difference, either in dialect or otherwise, although they are similar to the Bithynians. Accordingly, it is reasonable to suppose that this tribe also was at first Thracian. Theopompus says that Mariandynus ruled over a part of Paphlagonia, which was under the rule of many potentates, and then invaded and took possession of the country of the Bebryces, but left the country which he had abandoned named after himself. This, too, has been said, that the Milesians who were first to found Heracleia forced the Mariandyni, who held the place before them, to serve as Helots, so that they sold them, but not beyond the boundaries of their country (for the two peoples came to an agreement on this), just as the Mnoan class, as it is called, were serfs of the Cretans and the Penestae of the Thessalians.
5 As for the Cauconians, who, according to report, took up their abode on the sea‑coast next to the Mariandyni and extended as far as the Parthenius River, with Tieium as their city, some say that they were Scythians, others that they were a certain people of the Macedonians, and others that they were a certain people of the Pelasgians. But I have already spoken of these people in another place. Callisthenes in his treatise on The Marshalling of the Ships was for inserting after the words "Cromna, Aegialus, and lofty Erythini" the words "the Cauconians were led by the noble son of Polycles — they who lived in glorious dwellings in the neighbourhood of the Parthenius River," for, he adds, the Cauconians extended from Heracleia and the Mariandyni to the White Syrians, whom we call Cappadocians, and the tribe of the Cauconians round Tieium extended to the Parthenius River, whereas that of the Heneti, who held Cytorum, were situated next to them after the Parthenius River, and still to‑day certain "Cauconitae" live in the neighbourhood of the Parthenius River.
6 Now Heracleia is a city that has good harbours and is otherwise worthy of note, since, among other things, it has also sent forth colonies; for both Chersonesus and Callatis are colonies from it. It was at first an autonomous city, and then for some time was ruled by tyrants, and then recovered its freedom, but later was ruled by kings, when it became subject to the Romans. The people received a colony of Romans, sharing with them a part of their city and territory. But Adiatorix, the son of Domnecleius, tetrarch of the Galatians, received from Antony that part of the city which was occupied by the Heracleiotae; and a little before the Battle of Actium he attacked the Romans by night and slaughtered them, by permission of Antony, as he alleged. But after the victory at Actium he was led in triumph and slain together with his son. The city belongs to the Pontic Province which was united with Bithynia.
7 Between Chalcedon and Heracleia flow several rivers, among which are the Psillis and the Calpas and the Sangarius, which last is mentioned by the poet. The Sangarius has its sources near the village Sangia, about one hundred and fifty stadia from Pessinus. It flows through the greater part of Phrygia Epictetus, and also through a part of Bithynia, so that it is distant from Nicomedeia a little more than three hundred stadia, reckoning from the place where it is joined by the Gallus River, which has its beginnings at Modra in Phrygia on the Hellespont. This is the same country as Phrygia Epictetus, and it was formerly occupied by the Bithynians. Thus increased, and now having become navigable, though of old not navigable, the river forms a boundary of Bithynia at its outlets. Off this coast lies also the island Thynia. The plant called aconite grows in the territory of Heracleia. This city is about one thousand five hundred stadia from the Chalcedonian temple and five hundred from the Sangarius River.
8 Tieium is a town that has nothing worthy of mention except that Philetaerus, the founder of the family of Attalic Kings, was from there. Then comes the Parthenius River, which flows through flowery districts and on this account came by its name; it has its sources in Paphlagonia itself. And then comes Paphlagonia and the Eneti. Writers question whom the poet means by "the Eneti," when he says, "And the rugged heart of Pylaemenes led the Paphlagonians, from the land of the Eneti, whence the breed of wild mules"; for at the present time, they say, there are no Eneti to be seen in Paphlagonia, though some say that there is a village on the Aegialus ten schoeni distant from Amastris. But Zenodotus writes "from Enetê," and says that Homer clearly indicates the Amisus of to‑day. And others say that a tribe called Eneti, bordering on the Cappadocians, made an expedition with the Cimmerians and then were driven out to the Adriatic Sea. But the thing upon which there is general agreement is, that the Eneti, to whom Pylaemenes belonged, were the most notable tribe of the Paphlagonians, and that, furthermore, these made the expedition with him in very great numbers, but, losing their leader, crossed over to Thrace after the capture of Troy, and on their wanderings went to the Enetian country, as it is now called. According to some writers, Antenor and his children took part in this expedition and settled at the recess of the Adriatic, as mentioned by me in my account of Italy. It is therefore reasonable to suppose that it was on this account that the Eneti disappeared and are not to be seen in Paphlagonia.
9 As for the Paphlagonians, they are bounded on the east by the Halys River, "which," according to Herodotus, "flows from the south between the Syrians and the Paphlagonians and empties into the Euxine Sea, as it is called"; by "Syrians," however, he means the "Cappadocians," and in fact they are still to‑day called "White Syrians," while those outside the Taurus are called "Syrians." As compared with those this side the Taurus, those outside have a tanned complexion, while those this side do not, and for this reason received the appellation "white." And Pindar says that the Amazons "swayed a 'Syrian' army that reached afar with their spears," thus clearly indicating that their abode was in Themiscyra. Themiscyra is in the territory of the Amiseni; and this territory belongs to the White Syrians, who live in the country next after the Halys River. On the east, then, the Paphlagonians are bounded by the Halys River; on the south by Phrygians and the Galatians who settled among them; on the west by the Bithynians and the Mariandyni (for the race of the Cauconians has p385everywhere been destroyed) and on the north by the Euxine. Now this country was divided into two parts, the interior and the part on the sea, each stretching from the Halys River to Bithynia; and Eupator not only held the coast as far as Heracleia, but also took the nearest part of the interior,certain portions of which extended across the Halys (and the boundary of the Pontic Province has been marked off by the Romans as far as this). The remaining parts of the interior, however, were subject to potentates, even after the overthrow of Mithridates. Now as for the Paphlagonians in the interior, I mean those not subject to Mithridates, I shall discuss them later, but at present I propose to describe the country which was subject to him, called the Pontus.
After the Parthenius River, then, one comes to Amastris, a city bearing the same name as the woman who founded it. It is situated on a peninsula and has harbours on either side of the isthmus. Amastris was the wife of Dionysius the tyrant of Heracleia and the daughter of Oxyathres, the brother of the Dareius whom Alexander fought. Now she formed the city out of four settlements, Sesamus and Cytorum and Cromna (which Homer mentions in his marshalling of the Paphlagonian ships) and, fourth, Tieium. This last, however, soon revolted from the united city, but the other three remained together; and, of these three, Sesamus is called the acropolis of Amastris. Cytorum was once the emporium of the Sinopeans; it was named after Cytorus, the son of Phryxus, as Ephorus says. The most and the best box‑wood grows in the territory of Amastris, and particularly round Cytorum. The Aegialus is a long shore of more than a hundred stadia, and it has also a village bearing the same name, which the poet mentions when he says, "Cromna and Aegialus and the lofty Erythini," though some write, "Cromna and Cobialus." They say that the Erythrini of to‑day, from their colour, used to be called Erythini; they are two lofty rocks. After Aegialus one comes to Carambis, a great cape extending towards the north and the Scythian Chersonese. I have often mentioned it, as also Criumetopon which lies opposite it, by which the Euxine Pontus is divided into two seas. After Carambis one comes to Cinolis, and to Anticinolis, and to Abonuteichus, a small town, and to Armenê, to which pertains the proverb, "whoever had no work to do walled Armenê." It is a village of the Sinopeans and has a harbour.
Then one comes to Sinopê itself, which is fifty stadia distant from Armenê; it is the most noteworthy of the cities in that part of the world. This city was founded by the Milesians; and, having built a naval station, it reigned over the sea inside the Cyaneae, and shared with the Greeks in many struggles even outside the Cyaneae; and, although it was independent for a long time, it could not eventually preserve its freedom, but was captured by siege, and was first enslaved by Pharnaces and afterwards by his successors down to Eupator and to the Romans who overthrew Eupator. Eupator was both born and reared at Sinopê; and he accorded it special honour and treated it as the metropolis of his kingdom. Sinopê is beautifully equipped both by nature and by human foresight, for it is situated on the neck of a peninsula, and has on either side of the isthmus harbours and roadsteads and wonderful pelamydes-fisheries, of which I have already made mention, saying that the Sinopeans get the second catch and the Byzantians the third. Furthermore, the peninsula is protected all round by ridgy shores, which have hollowed‑out places in them, rock-cavities, as it were, which the people call "choenicides"; these are filled with water when the sea rises, and therefore the place is hard to approach, not only because of this, but also because the whole surface of the rock is prickly and impassable for bare feet. Higher up, however, and above the city, the ground is fertile and adorned with diversified market-gardens; and especially the suburbs of the city. The city itself is beautifully walled, and is also splendidly adorned with gymnasium and market-place and colonnades. But although it was such a city, still it was twice captured, first by Pharnaces, who unexpectedly attacked it all of a sudden, and later by Leucullus and by the tyrant who was garrisoned within it, being besieged both inside and outside at the same time; for, since Bacchides, who had been set up by the king as commander of the garrison, was always suspecting treason from the people inside, and was causing many outrages and murders, he made the people, who were unable either nobly to defend themselves or to submit by compromise, lose all heart for either course. At any rate, the city was captured; and though Leucullus kept intact the rest of the city's adornments, he took away the globe of Billarus and the work of Sthenis, the statue of Autolycus, whom they regarded as founder of their city and honoured as god. The city had also an oracle of Autolycus. He is thought to have been one of those who went on the voyage with Jason and to have taken possession of the place. Then later the Milesians, seeing the natural advantages of the place and the weakness of its inhabitants, appropriated it to themselves and sent forth colonists to it. But at present it has received also a colony of Romans; and a part of the city and the territory belong to these. It is three thousand five hundred stadia distant from the Hieron, two thousand from Heracleia, and seven hundred from Carambis. It has produced excellent men: among the philosophers, Diogenes the Cynic and Timotheus Patrion; among the poets, Diphilus the comic poet; and, among the historians, Baton, who wrote the work entitled The Persian.
Thence, next, one comes to the outlet of the Halys River. It was named from the "halae," past which it flows. It has its sources in Greater Cappadocia in Camisenê near the Pontic country; and, flowing in great volume towards the west, and then turning towards the north through Galatia and Paphlagonia, it forms the boundary between these two countries and the country of the White Syrians. Both Sinopitis and all the mountainous country extending as far as Bithynia and lying above the aforesaid seaboard have shipbuilding timber that is excellent and easy to transport. Sinopitis produces also the maple and the mountain‑nut, the trees from which they cut the wood used for tables. And the whole of the tilled country situated a little above the sea is planted with olive trees.
After the outlet of the Halys comes Gazelonitis, which extends to Saramenê; it is a fertile country and is everywhere level and productive of everything. It has also a sheep-industry, that of raising flocks clothed in skins and yielding soft wool, of which there is a very great scarcity throughout the whole of Cappadocia and Pontus. The country also produces gazelles, of which there is a scarcity elsewhere. One part of this country is occupied by the Amiseni, but the other was given to Deïotarus by Pompey, as also the regions of Pharnacia and Trapezusia as far as Colchis and Lesser Armenia. Pompey appointed him king of all these, when he was already in possession of his ancestral Galatian tetrarchy,the country of the Tolistobogii. But since his death there have been many successors to his territories.
After Gazelon one comes to Saramenê, and to a notable city, Amisus, which is about nine hundred stadia from Sinopê. Theopompus says that it was first founded by the Milesians, . . . by a leader of the Cappadocians, and thirdly was colonised by Athenocles and Athenians and changed its name to Peiraeus. The kings also took possession of this city; and Eupator adorned it with temples and founded an addition to it. This city too was besieged by Leucullus, and then by Pharnaces, when he crossed over from the Bosporus. After it had been set free by the deified Caesar, it was given over to kings by Antony. Then Straton the tyrant put it in bad plight. And then, after the Battle of Actium, it was again set free by Caesar Augustus; and at the present time it is well organised. Besides the rest of its beautiful country, it possesses also Themiscyra, the abode of the Amazons, and Sidenê.
Themiscyra is a plain; on one side it is washed by the sea and is about sixty stadia distant from the city, and on the other side it lies at the foot of the mountainous country, which is well-wooded and coursed by streams that have their sources therein. So one river, called the Thermodon, being supplied by all these streams, flows out through the plain; and another river similar to this, which flows out of Phanaroea, as it is called, flows out through the same plain, and is called the Iris. It has its sources in Pontus itself, and, after flowing through the middle of the city Comana in Pontus and through Dazimonitis, a fertile plain, towards the west, then turns towards the north past Gaziura itself, an ancient royal residence, though now deserted, and then bends back again towards the east, after receiving the waters of the Scylax and other rivers, and after flowing past the very wall of Amaseia, my fatherland, a very strongly fortified city, flows on into Phanaroea. Here the Lycus River, which has its beginnings in Armenia, joins it, and itself also becomes the Iris. Then the stream is received by Themiscyra and by the Pontic Sea. On this account the plain in question is always moist and covered with grass and can support herds of cattle and horses alike and admits of the sowing of millet-seeds and sorghum-seeds in very great, or rather unlimited, quantities. Indeed, their plenty of water offsets any drought, so that no famine comes down on these people, never once; and the country along the mountain yields so much fruit, self-grown and wild, I mean grapes and pears and apples and nuts, that those who go out to the forest at any time in the year get an abundant supply — the fruits at one time still hanging on the trees and at another lying on the fallen leaves or beneath them, which are shed deep and in great quantities. And numerous, also, are the catches of all kinds of wild animals, because of the good yield of food.
After Themiscyra one comes to Sidenê, which is a fertile plain, though it is not well-watered like Themiscyra. It has strongholds on the seaboard: Sidê, after which Sidenê was named, and Chabaca and Phabda. Now the territory of Amisus extends to this point; and the city has produced men noteworthy for their learning, Demetrius, the son of Rhathenus, and Dionysodorus, the mathematicians, the latter bearing the same name as the Melian geometer, and Tyrannion the grammarian, of whom I was a pupil.
After Sidenê one comes to Pharnacia, a fortified town; and afterwards to Trapezus, a Greek city, to which the voyage from Amisus is about two thousand two hundred stadia. Then from here the voyage to Phasis is approximately one thousand four hundred stadia, so that the distance from Hieron to Phasis is, all told, about eight thousand stadia, or slightly more or less. As one sails along this seaboard from Amisus, one comes first to the Heracleian Cape, and then to another cape called Jasonium, and to Genetes, and then to a town called Cytorus, from the inhabitants of which Pharnacia was settled, and then to Ischopolis, now in ruins, and then to a gulf, on which are both Cerasus and Hermonassa, moderate-sized settlements, and then, near Hermonassa, to Trapezus, and then to Colchis. Somewhere in this neighbourhood is also a settlement called Zygopolis. Now I have already described Colchis and the coast which lies above it.
Above Trapezus and Pharnacia are situated the Tibarani and Chaldaei and Sanni, in early times called Macrones, and Lesser Armenia; and the Appaïtae, in earlier times called the Cercitae, are fairly close to these regions. Two mountains cross the country of these people, not only the Scydises, a very rugged mountain, which joins the Moschian Mountains above Colchis (its heights are occupied by the Heptacometae), but also the Paryadres, which extends from the region of Sidenê and Themiscyra to Lesser Armenia and forms the eastern side of Pontus. Now all these peoples who live in the mountains are utterly savage, but the Heptacometae are worse than the rest. Some also live in trees or turrets; and it was on this account that the ancients called them "Mosynoeci," the turrets being called "mosyni." They live on the flesh of wild animals and on nuts; and they also attack wayfarers, leaping down upon them from their scaffolds. The Heptacometae cut down three maniples of Pompey's army when they were passing through the mountainous country; for they mixed bowls of the crazing honey which is yielded by the tree-twigs, and placed them in the roads, and then, when the soldiers drank the mixture and lost their senses, they attacked them and easily disposed of them. Some of these barbarians were also called Byzeres.
The Chaldaei of to‑day were in ancient times named Chalybes; and it is just opposite their territory that Pharnacia is situated, which, on the sea, has the natural advantages of pelamydes-fishing (for it is here that this fish is first caught) and, on the land, has the mines, only iron-mines at the present time, though in earlier times it also had silver-mines. Upon the whole, the seaboard in this region is extremely narrow, for the mountains, full of mines and forests, are situated directly above it, and not much of it is tilled. But there remains for the miners their livelihood from the mines, and for those who busy themselves on the sea their livelihood from their fishing, and especially from their catches of pelamydes and dolphins; for the dolphins pursue the schools of fish — the cordylê and the tunny-fish and the pelamydes themselves; and they not only grow fat on them, but also become easy to catch because they are rather eager to approach the land. These are the only people who cut up the dolphins, which are caught with bait, and use their abundance of fat for all purposes.
So it is these people, I think, that the poet calls Halizoni, mentioning them next after the Paphlagonians in his Catalogue. "But the Halizones were led by Odius and Epistrophus, from Alybê far away, where is the birth-place of silver," since the text has been changed from "Chalybê far away" or else the people were in earlier times called "Alybes" instead of "Chalybes"; for at the present time it proves impossible that they should have been called "Chaldaei," deriving their name from "Chalybê," if in earlier times they could not have been called "Chalybes" instead of "Alybes," and that too when names undergo many changes, particularly among the barbarians; for instance, certain of the Thracians were called Sinties, then Sinti and then Saïi, in whose country Archilochus says he flung away his shield: "One of the Saïi robbed me of my shield, which, a blameless weapon, I left behind me beside a bush, against my will." These same people are now named Sapaei; for all these have their abode round Abdera and the islands round Lemnos. Likewise the Brygi and Bryges and Phryges are the same people; and the Mysi and Maeones and Meïones are the same; but there is no use of enlarging on the subject. The Scepsian doubts the alteration of the name from "Alybes" to "Chalybes"; and, failing to note what follows and what accords with it, and especially why the poet calls the Chalybians Halizoni, he rejects this opinion. As for me, let me place his assumption and those of the other critics side by side with my own and consider them.
Some change the text and make it read "Alazones," others "Amazones," and for the words "from Alybê" they read "from Alopê," or "from Alobê," calling the Scythians beyond the Borysthenes River "Alazones," and also "Callipidae" and other names — names which Hellanicus and Herodotus and Eudoxus have foisted on us — and placing the Amazons between Mysia and Caria and Lydia near Cymê, which is the opinion also of Ephorus, who was a native of Cymê. And this opinion might perhaps not be unreasonable, for he may mean the country which was later settled by the Aeolians and the Ionians, but earlier by the Amazons. And there are certain cities, it is said, which got their names from the Amazons, I mean Ephesus, Smyrna, Cymê, and Myrina. But how could Alybê, or, as some call it, "Alopê" or "Alobê," be found in this region, and how about "far away," and how about "the birth-place of silver"?
These objections Ephorus solves by his change of the text, for he writes thus: "But the Amazons were led by Odius and Epistrophus, from Alopê far away, where is the race of Amazons." But in solving these objections he has fallen into another fiction; for Alopê is nowhere to be found in this region; and, further, his change of the text, with innovations so contrary to the evidence of the early manuscripts, looks like rashness. But the Scepsian apparently accepts neither the opinion of Ephorus nor of those who suppose them to be the Halizoni near Pallenê, whom I have mentioned in my description of Macedonia. He is also at a loss to understand how anyone could think that an allied force came to help the Trojans from the nomads beyond the Borysthenes River; and he especially approves of the opinions of Hecataeus of Miletus, and of Menecrates of Elaea, one of the disciples of Xenocrates, and all of that of Palaephatus. The first of these says in his Circuit of the Earth: "Near the city Alazia is the River Odrysses, which flows out of Lake Dascylitis from the west through the plain of Mygdonia and empties into the Rhyndacus." But he goes on to say that Alazia is now deserted, and that many villages of the Alazones, through whose country the Odrysses flows, are inhabited, and that in these villages Apollo is accorded exceptional honour, and particularly on the confines of the Cyziceni. Menecrates in his work entitled The Circuit of the Hellespont says that above the region of Myrleia there is an adjacent mountainous tract which is occupied by the tribe of the Halizones. One should spell the name with two l's, he says, but on account of the metre the poet spells it with only one. But Palaephatus says that it was from the Amazons who then lived in Alopê, but now in Zeleia, that Odius and Epistrophus made their expedition. How, then, can the opinions of these men deserve approval? For, apart from the fact that these men also disturb the early text, they neither show us the silver-mines, nor where in the territory of Myrleia Alopê is, nor how those who went from there to Ilium were "from far away," even if one should grant that there actually was an Alopê or Alazia; for these, of course, are much nearer the Troad than the places round Ephesus. But still those who speak of the Amazons as living in the neighbourhood of Pygela between Ephesus and Magnesia and Prienê talk nonsense, Demetrius says, for, he adds, "far away" cannot apply to that region. How much more inapplicable, then, is it to the region of Mysia and Teuthrania?
Yes, by Zeus, but he goes on to say that some things are arbitrarily inserted in the text, for example, "from Ascania far away," and "Arnaeus was his name, for his revered mother had given him this name at his birth," and "Penelope took the bent key in her strong hand." Now let this be granted, but those other things are not to be granted to which Demetrius assents without even making a plausible reply to those who have assumed that we ought to read "from Chalybê far away"; for although he concedes that, even if the silver-mines are not now in the country of the Chalybians, they could have been there in earlier times, he does not concede that other point, that they were both famous and worthy of note, like the iron-mines. But, one might ask, what is there to prevent them from being famous like the iron-mines? Or can an abundance of iron make a place famous but an abundance of silver not do so? And if the silver-mines had reached fame, not in the time of the heroes, but in the time of Homer, could any person find fault with the assertion of the poet? How, pray, could the fame of the copper-mine at Temesa in Italy have reached him? How the fame of the wealth of Thebes in Egypt, although he was about twice as far from Thebes as from the Chaldaeans? But Demetrius is not even in agreement with those for whose opinions he pleads; for in fixing the sites round Scepsis, his birth-place, he speaks of Nea, a village, and of Argyria and Alazonia as near Scepsis and the Aesepus River. These places, then, if they really exist, would be near the sources of the Aesepus; but Hecataeus speaks of them as beyond the outlets of it; and Palaephatus, although he says that they formerly lived in Alopê, but now in Zeleia, says nothing like what these men say. But if Menecrates does so, not even he tells us what kind of a place "Alopê" is or "Alobê," or however they wish to write the name, and neither does Demetrius himself.
As regards Apollodorus, who discusses the same subject in his Marshalling of the Trojan Forces, I have already said much in answer to him, but I must now speak again; for he does not think that we should take the Halizoni as living outside the Halys River; for, he says, no allied force came to the Trojans from beyond the Halys. First, therefore, we shall ask of him who are the Halizoni this side the Halys and "from Alybê far away, where is the birth-place of silver." For he will be unable to tell us. And we shall next ask him the reason why he does not concede that an allied force came also from the country on the far side of the river; for, if it is the case that all the rest of the allied forces except the Thracians lived this side the river, there was nothing to prevent this one allied force from coming from the far side of the Halys, from the country beyond the White Syrians. Or was it possible for peoples who fought the Trojans to cross over from these regions and from the regions beyond, as he says the Amazons and Treres and Cimmerians did, and yet impossible for people who fought as allies with them to do so? Now the Amazons would not fight on Priam's side because of the fact that he had fought against them as an ally of the Phrygians, against the "Amazons, peers of men, who came at that time," as Priam says, "for I too, being their ally, was numbered among them"; but since the peoples whose countries bordered on that of the Amazons were not even far enough away to make difficult the Trojan summons for help from their countries, and since, too, there was no underlying cause for hatred, there was nothing to prevent them, I think, from being allies of the Trojans.
Neither can Apollodorus impute such an opinion to the early writers, as though they, one and all, voiced the opinion that no peoples from the far side of the Halys River took part in the Trojan war. One might rather find evidence to the contrary; at any rate, Maeandrius says that the Eneti first set forth from the country of the White Syrians and allied themselves with the Trojans, and that they sailed away from Troy with the Thracians and took up their abode round the recess of the Adrias, but that the Eneti who did not have a part in the expedition had become Cappadocians. The following might seem to agree with this account, I mean the fact that the whole of that part of Cappadocia near the Halys River which extends along Paphlagonia uses two languages which abound in Paphlagonian names, as "Bagas," "Biasas," "Aeniates," "Rhatotes," "Zardoces," "Tibius," "Gasys," "Oligasys," and "Manes," for these names are prevalent in Bamonitis, Pimolitis, Gazelonitis, Gazacenê and most of the other districts. Apollodorus himself quotes the Homeric verse as written by Zenodotus, stating that he writes it as follows: "from Enetê, whence the breed of the wild mules"; and he says that Hecataeus of Miletus takes Enetê to be Amisus. But, as I have already stated, Amisus belongs to the White Syrians and is outside the Halys River.
Apollodorus somewhere states, also, that the poet got an account of those Paphlagonians who lived in the interior from men who had passed through the country on foot, but that he was ignorant of the Paphlagonian coast, just as he was ignorant of the rest of the Pontic coast; for otherwise he would have named them. On the contrary, one can retort and say, on the basis of the description which I have now given, that Homer traverses the whole of the coast and omits nothing of the things that were then worth recording, and that it is not at all remarkable if he does not mention Heracleia and Amastris and Sinopê, cities which had not yet been founded, and that it is not at all strange if he has mentioned no part of the interior. And further, the fact that Homer does not name many of the known places is no sign of ignorance, as I have already demonstrated in the foregoing part of my work; for he says that Homer was ignorant of many of the famous things round the Pontus, for example, rivers and tribes, for otherwise, he says, Homer would have named them. This one might grant in the case of certain very significant things, for example, the Scythians and Lake Maeotis and the Ister River, for otherwise Homer would not have described the nomads by significant characteristics as "Galactophagi" and "Abii" and as "men most just," and also as "proud Hippemolgi," and yet fail to call the Scythians either Sauromatae or Sarmatae, if indeed they were so named by the Greeks, nor yet, when he mentions the Rhodians and Mysians near the Ister, pass by the Ister in silence, greatest of the rivers, and especially when he is inclined to mark the boundaries of places by rivers, nor yet, when he mentions the Cimmerians, omit any mention of the Bosporus or Lake Maeotis.
But in the case of things not so significant, either not at that time or for the purposes of his work, how could anyone find fault with Homer for omitting them? For example, for omitting the Tanaïs River, which is well known for no other reason than that it is the boundary between Asia and Europe. But the people of that time were not yet using either the name "Asia" or "Europe," nor yet had the inhabited world been divided into three continents as now, for otherwise he would have named them somewhere because of their very great significance, just as he mentions Libya and also the Lips, the wind that blows from the west parts of Libya. But since the cliffs had not yet been distinguished, there was no need of mentioning the Tanaïs either. Many things were indeed worthy of mention, but they did not occur to him; for of course adventitiousness is much in evidence both in one's discourse and in one's actions. From all these facts it is clear that every man who judges from the poet's failure to mention anything that he is ignorant of that thing uses faulty evidence. And it is necessary to set forth several examples to prove that it is faulty, for many use such evidence to a great extent. We must therefore rebuke them when they bring forward such evidences, even though in so doing I shall be repeating previous argument. For example, in the case of rivers, if anyone should say that the poet is ignorant of some river because he does not name it, I shall say that his argument is silly, because the poet does not even name the Meles River, which flows past Smyrna, the city which by most writers is called his birth-place, although he names the Hermus and Hyllus Rivers; neither does he name the Pactolus River, which flows into the same channel as these two rivers and rises in Tmolus, a mountain which he mentions; neither does he mention Smyrna itself, nor the rest of the Ionian cities; nor the most of the Aeolian cities, though he mentions Miletus and Samos and Lesbos and Tenedos; nor yet the Lethaeus River, which flows past Magnesia, nor the Marsyas River, which rivers empty into the Maeander, which last he mentions by name, as also "the Rhesus and Heptaporus and Caresus and Rhodius," and the rest, most of which are no more than small streams. And when he names both many countries and cities, he sometimes names with them the rivers and mountains, but sometimes he does not. At any rate, he does not mention the rivers in Aetolia or Attica, nor in several other countries. Besides, if he mentions rivers far away and yet does not mention those that are very near, it is surely not because he was ignorant of them, since they were known to all others. Nor yet, surely, was he ignorant of peoples that were equally near, some of which he names and some not; for example he names the Lycians and the Solymi, but not the Milyae; nor yet the Pamphylians or Pisidians; and though he names the Paphlagonians, Phrygians, and Mysians, he does not name Mariandynians or Thynians or Bithynians or Bebryces; and he mentions the Amazons, but not the White Syrians or Syrians, or Cappadocians, or Lycaonians, though he repeatedly mentions the Phoenicians and the Egyptians and the Ethiopians. And although he mentions the Aleïan plain and the Arimi, he is silent as to the tribe to which both belong. Such a test of the poet, therefore, is false; but the test is true only when it is shown that some false statement is made by him. But Apollodorus has not been proved correct in this case either, I mean when he was bold enough to say that the "proud Hippemolgi" and "Galactophagi" were fabrications of the poet. So much for Apollodorus. I now return to the part of my description that comes next in order.
Above the region of Pharnacia and Trapezus are the Tibareni and the Chaldaei, whose country extends to Lesser Armenia. This country is fairly fertile. Lesser Armenia, like Sophenê, was always in the possession of potentates, who at times were friendly to the other Armenians and at times minded their own affairs. They held as subjects the Chaldaei and the Tibareni, and therefore their empire extended to Trapezus and Pharnacia. But when Mithridates Eupator had increased in power, he established himself as master, not only of Colchis, but also of all these places, these having been ceded to him by Antipater, the son of Sisis. And he cared so much for these places that he built seventy-five strongholds in them and therein deposited most of his treasures. The most notable of these strongholds were these: Hydara and Basgoedariza and Sinoria; Sinoria was close to the borders of Greater Armenia, and this is why Theophanes changed its spelling to Sinoria. For as a whole the mountainous range of the Paryadres has numerous suitable places for such strongholds, since it is well-watered and woody, and is in many places marked by sheer ravines and cliffs; at any rate, it was here that most of his fortified treasuries were built; and at last, in fact, Mithridates fled for refuge into these farthermost parts of the kingdom of Pontus, when Pompey invaded the country, and having seized a well-watered mountain near Dasteira in Acilisenê (near by, also, was the Euphrates, which separates Acilisenê from Lesser Armenia), he stayed there until he was besieged and forced to flee across the mountains into Colchis and from there to the Bosporus. Near this place, in Lesser Armenia, Pompey built a city, Nicopolis,which endures even to this day and is well peopled.
Now as for Lesser Armenia, it was ruled by different persons at different times, according to the will of the Romans, and finally by Archelaüs. But the Tibareni and Chaldaei, extending as far as Colchis, and Pharnacia and Trapezus are ruled by Pythodoris, a woman who is wise and qualified to preside over affairs of state. She is the daughter of Pythodorus of Tralles. She became the wife of Polemon and reigned along with him for a time, and then, when he died in the country of the Aspurgiani, as they are called, one of the barbarian tribes round Sindicê, she succeeded to the rulership. She had two sons and a daughter by Polemon. Her daughter was married to Cotys the Sapaean, but he was treacherously slain, and she lived in widowhood, because she had children by him; and the eldest of these is now in power. As for the sons of Pythodoris, one of them as a private citizen is assisting his mother in the administration of her empire, whereas the other has recently been established as king of Greater Armenia. She herself married Archelaüs and remained with him to the end;but she is living in widowhood now, and is in possession not only of the places above mentioned, but also of others still more charming, which I shall describe next.
Sidenê and Themiscyra are contiguous to Pharnacia. And above these lies Phanaroea, which has the best portion of Pontus, for it is planted with olive trees, abounds in wine, and has all the other goodly attributes a country can have. On its eastern side it is protected by the Paryadres Mountain, in its length lying parallel to that mountain; and on its western side by the Lithrus and Ophlimus Mountains. It forms a valley of considerable breadth as well as length; and it is traversed by the Lycus River, which flows from Armenia, and by the Iris, which flows from the narrow passes near Amaseia. The two rivers met at about the middle of the valley; and at their junction is situated a city which the first man who subjugated it called Eupatoria after his own name, but Pompey found it only half-finished and added to it territory and settlers, and called it Magnopolis. Now this city is situated in the middle of the plain, but Cabeira is situated close to the very foothills of the Paryadres Mountains about one hundred and fifty stadia farther south than Magnopolis, the same distance that Amaseia is farther west than Magnopolis. It was at Cabeira that the palace of Mithridates was built, and also the water-mills; and here were the zoological gardens, and, near by, the hunting grounds, and the mines.
Here, also, is Kainon Chorion, as it is called, a rock that is sheer and fortified by nature, being less than two hundred stadia distant from Cabeira. It has on its summit a spring that sends forth much water, and at its foot a river and a deep ravine. The height of the rock above the neck is immense, so that it is impregnable; and it is enclosed by remarkable walls, except the part where they have been pulled down by the Romans. And the whole country around is so overgrown with forests, and so mountainous and waterless, that it is impossible for an enemy to encamp within one hundred and twenty stadia. Here it was that the most precious of the treasures of Mithridates were kept, which are now stored in the Capitolium, where they were dedicated by Pompey. Pythodoris possesses the whole of this country, which is adjacent to the barbarian country occupied by her, and also Zelitis and Megalopolitis. As for Cabeira, which by Pompey had been built into a city and called Diospolis, Pythodoris further adorned it and changed its name to Sebastê; and she uses the city as a royal residence. It has also the temple of Mên of Pharnaces, as it is called, — the village-city Ameria, which has many temple-servants, and also a sacred territory, the fruit of which is always reaped by the ordained priest. And the kings revered this temple so exceedingly that they proclaimed the "royal" oath as follows: "By the Fortune of the king and by Mên of Pharnaces." And this is also the temple of Selenê, like that among the Albanians and those in Phrygia, I mean that of Mên in the place of the same name and that of Mên Ascaeus near the Antiocheia that is near Pisidia and that of Mên in the country of the Antiocheians.
Above Phanaroea is the Pontic Comana, which bears the same name as the city in Greater Cappadocia, having been consecrated to the same goddess and copied after that city; and I might almost say that the courses which they have followed in their sacrifices, in their divine obsessions, and in their reverence for their priests, are about the same, and particularly in the times of the kings who reigned before this, I mean in the times when twice a year, during the "exoduses" of the goddess, as they are called, the priest wore a diadem and ranked second in honour after the king.
Heretofore I have mentioned Dorylaüs the tactician, who was my mother's grandfather, and also a second Dorylaüs, who was the nephew of the former and the son of Philetaerus, saying that, although he had received all the greatest honours from Eupator and in particular the priesthood of Comana, he was caught trying to cause the kingdom to revolt to the Romans; and when he was overthrown, the family was cast into disrepute along with him. But long afterwards Moaphernes, my mother's uncle, came into distinction just before the dissolution of the kingdom, and again they were unfortunate along with the king, both Moaphernes and his relatives, except some who revolted from the king beforehand, as did my maternal grandfather, who, seeing that the cause of the king was going badly in the war with Leucullus, and at the same time being alienated from him out of wrath at his recently having put to death his cousin Tibius and Tibius' son Theophilus, set out to avenge both them and himself; and, taking pledges from Leucullus, he caused fifteen garrisons to revolt to him; and although great promises were made in return for these services, yet, when Pompey, who succeeded Leucullus in the conduct of the war, went over, he took for enemies all who had in any way favoured Leucullus, because of the hatred which had arisen between himself and Leucullus; and when he finished the war and returned home, he won so completely that the Senate would not ratify those honours which Leucullus had promised to certain of the people of Pontus, for, he said, it was unjust, when one man had brought the war to a successful issue, that the prizes and the distribution of the rewards should be placed in the hands of another man.
Now in the times of the kings the affairs of Comana were administered in the manner already described, but when Pompey took over the authority, he appointed Archelaüs priest and included within his boundaries, in addition to the sacred land, a territory of two schoeni (that is, sixty stadia) in circuit and ordered the inhabitants to obey his rule. Now he was governor of these, and also master of the temple-servants who lived in the city, except that he was not empowered to sell them. And even here the temple servants were no fewer in number than six thousand. This Archelaüs was the son of the Archelaüs who was honoured by Sulla and the Senate, and was also a friend of Gabinius, a man of consular rank. When Gabinius was sent into Syria, Archelaüs himself also went there in the hope of sharing with him in his preparations for the Parthian War, but since the Senate would not permit him, he dismissed that hope and found another of greater importance. For it happened at that time that Ptolemaeus, the father of Cleopatra, had been banished by the Egyptians, and his daughter, elder sister of Cleopatra, was in possession of the kingdom; and since a husband of royal family was being sought for her, Archelaüs proffered himself to her agents, pretending that he was the son of Mithridates Eupator; and he was accepted, but he reigned only six months. Now this Archelaüs was slain by Gabinius in a pitched battle, when the latter was restoring Ptolemaeus to his kingdom.
But his son succeeded to the priesthood; and then later, Lycomedes, to whom was assigned an additional territory of four hundred schoeni; but now that he has been deposed, the office is held by Dyteutus, son of Adiatorix, who is thought to have obtained the honour from Caesar Augustus because of his excellent qualities; for Caesar, after leading Adiatorix in triumph together with his wife and children, resolved to put him to death together with the eldest of his sons (for Dyteutus was the eldest), but when the second of the brothers told the soldiers who were leading them away to execution that he was the eldest, there was a contest between the two for a long time, until the parents persuaded Dyteutus to yield the victory to the younger, for he, they said, being more advanced in age, would be a more suitable guardian for his mother and for the remaining brother. And thus, they say, the younger was put to death with his father, whereas the elder was saved and obtained the honour of the priesthood. For learning about this, as it seems, after the men had already been put to death, Caesar was grieved, and he regarded the survivors as worthy of his favour and care, giving them the honour in question.
Now Comana is a populous city and is a notable emporium for the people from Armenia; and at the times of the "exoduses" of the goddess people assemble there from everywhere, from both the cities and the country, men together with women, to attend the festival. And there are certain others, also, who in accordance with a vow are always residing there, performing sacrifices in honour of the goddess. And the inhabitants live in luxury, and all their property is planted with vines; and there is a multitude of women who make gain from their persons, most of whom are dedicated to the goddess, for in a way the city is a lesser Corinth, for there too, on account of the multitude of courtesans, who were sacred to Aphroditê, outsiders resorted in great numbers and kept holiday. And the merchants and soldiers who went there squandered all their money, so that the following proverb arose in reference to them: "Not for every man is the voyage to Corinth." Such, then, is my account of Comana.
The whole of the country around is held by Pythodoris, to whom belong, not only Phanaroea, but also Zelitis and Megalopolitis. Concerning Phanaroea I have already spoken. As for Zelitis, it has a city Zela, fortified on a mound of Semiramis, with the temple of Anaïtis, who is also revered by the Armenians. Now the sacred rites performed here are characterised by greater sanctity; and it is here that all the people of Pontus make their oaths concerning their matters of greatest importance. The large number of temple-servants and the honours of the priests were, in the time of the kings, of the same type as I have stated before, but at the present time everything is in the power of Pythodoris. Many persons had abused and reduced both the multitude of temple-servants and the rest of the resources of the temple. The adjacent territory, also, was reduced, having been divided into several domains — I mean Zelitis, as it is called (which has the city Zela on a mound); for in early times the kings governed Zela, not as a city, but as a sacred precinct of the Persian gods, and the priest was the master of the whole thing. It was inhabited by the multitude of temple-servants, and by the priest, who had an abundance of resources; and the sacred territory as well as that of the priest was subject to him and his numerous attendants. Pompey added many provinces to the boundaries of Zelitis, and named Zela, as he did Megalopolis, a city, and he united the latter and Culupenê and Camisenê into one state; the latter two border on both Lesser Armenia and Laviansenê, and they contain rock-salt, and also an ancient fortress called Camisa, now in ruins. The later Roman prefects assigned a portion of these two governments to the priests of Comana, a portion to the priest of Zela, and a portion to Ateporix, a dynast of the family of tetrarchs of Galatia; but now that Ateporix has died, this portion, which is not large, is subject to the Romans, being called a province (and this little state is a political organisation of itself, the people having incorporated Carana into it, from which fact its country is called Caranitis), whereas the rest is held by Pythodoris and Dyteutus.
There remain to be described the parts of the Pontus which lie between this country and the countries of the Amisenians and Sinopeans, which latter extend towards Cappadocia and Galatia and Paphlagonia. Now after the territory of the Amisenians, and extending to the Halys River, is Phazemonitis, which Pompey named Neapolitis, proclaiming the settlement at the village Phazemon a city and calling it Neapolis. The northern side of this country is bounded by Gazelonitis and the country of the Amisenians; the western by the Halys River; the eastern by Phanaroea; and the remaining side by my country, that of the Amaseians, which is by far the largest and best of all. Now the part of Phazemonitis towards Phanaroea is covered by a lake which is like a sea in size, is called Stephanê, abounds in fish, and has all round it abundant pastures of all kinds. On its shores lies a strong fortress, Icizari, now deserted; and, near by, a royal palace, now in ruins. The remainder of the country is in general bare of trees and productive of grain. Above the country of the Amaseians are situated the hot springs of the Phazemonitae, which are extremely good for the health, and also Sagylium, with a stronghold situated on a high steep mountain that runs up into a sharp peak. Sagylium also has an abundant reservoir of water, which is now in neglect, although it was useful to the kings for many purposes. Here Arsaces, one the sons of King Pharnaces, who was playing the dynast and attempting a revolution without permission from any of the prefects, was captured and slain. He was captured, however, not by force, although the stronghold was taken by Polemon and Lycomedes, both of them kings, but by starvation, for he fled up into the mountain without provisions, being shut out from the plains, and he also found the wells of the reservoir choked up by huge rocks; for this had been done by order of Pompey, who ordered that the garrisons be pulled down and not be left useful to those who wished to flee up to them for the sake of robberies. Now it was in this way that Pompey arranged Phazemonitis for administrative purposes, but the later rulers distributed also this country among kings.
My city is situated in a large deep valley, through which flows the Iris River. Both by human foresight and by nature it is an admirably devised city, since it can at the same time afford the advantage of both a city and a fortress; for it is a high and precipitous rock, which descends abruptly to the river, and has on one side the wall on the edge of the river where the city is settled and on the other the wall that runs up on either side to the peaks. These peaks are two in number, are united with one another by nature, and are magnificently towered. Within this circuit are both the palaces and monuments of the kings. The peaks are connected by a neck which is altogether narrow, and is five or six stadia in height on either side as one goes up from the river-banks and the suburbs; and from the neck to the peaks there remains another ascent of one stadium, which is sharp and superior to any kind of force. The rock also has reservoirs of water inside it, a water-supply of which the city cannot be deprived, since two tube-like channels have been hewn out, one towards the river and the other towards the neck. And two bridges have been built over the river, one from the city to the suburbs and the other from the suburbs to the outside territory; for it is at this bridge that the mountain which lies above the rock terminates. And there is a valley extending from the river which at first is not altogether wide, but it later widens out and forms the plain called Chiliocomum; and then comes the Diacopene and Pimolisene country, all of which is fertile, extending to the Halys River. These are the northern parts of the country of the Amaseians, and are about five hundred stadia in length. Then in order comes the remainder of their country, which is much longer than this, extending to Babanomus and Ximenê, which latter itself extends as far as the Halys River. This, then, is the length of their country, whereas the breadth from the north to the south extends, not only to Zelitis, but also to Greater Cappadocia, as far as the Trocmi. In Ximenê there are "halae" of rock salt, after which the river is supposed to have been called "Halys." There are several demolished strongholds in my country, and also much deserted land, because of the Mithridatic War. However, it is all well supplied with trees; a part of it affords pasturage for horses and is adapted to the raising of the other animals; and the whole of it is beautifully adapted to habitation. Amaseia was also given to kings, though it is now a province.
There remains that part of the Pontic province which lies outside the Halys River, I mean the country round Mt. Olgassys, contiguous to Sinopis. Mt. Olgassys is extremely high and hard to travel. And temples that had been established everywhere on this mountain are held by the Paphlagonians. And round it lies fairly good territory, both Blaënê and Domanitis, through which latter flows the Amnias River. Here Mithridates Eupator utterly wiped out the forces of Nicomedes the Bithynian — not in person, however, since it happened that he was not even present, but through his generals. And while Nicomedes, fleeing with a few others, safely escaped to his home-land and from there sailed to Italy, Mithridates followed him and not only took Bithynia at the first assault but also took possession of Asia as far as Caria and Lycia. And here, too, a place was proclaimed a city, I mean Pompeiupolis; and in this city is Mt. Sandaracurgium, not far away from Pimolisa, a royal fortress now in ruins, after which the country on either side of the river is called Pimolisenê. Mt. Sandaracurgium is hollowed out in consequence of the mining done there, since the workmen have excavated great cavities beneath it. The mine used to be worked by publicans, who used as miners the slaves sold in the market because of their crimes; for, in addition to the painfulness of the work, they say that the air in the mines is both deadly and hard to endure on account of the grievous odour of the ore, so that the workmen are doomed to a quick death. What is more, the mine is often left idle because of the unprofitableness of it, since the workmen are not only more than two hundred in number, but are continually spent by disease and death. So much be said concerning Pontus.
After Pompeiupolis comes the remainder of the interior of Paphlagonia, extending westwards as far as Bithynia. This country, small though it is, was governed by several rulers a little before my time, but, the family of kings having died out, it is now in possession of the Romans. At any rate, they give to the country that borders on Bithynia the names "Timonitis," "the country of Gezatorix," and also "Marmolitis," "Sanisenê," and "Potamia." There was also a Cimiatenê, in which was Cimiata, a strong fortress situated at the foot of the mountainous country of the Olgassys. This was used by Mithridates, surnamed Ctistes, as a base of operations when he established himself as lord of Pontus; and his descendants preserved the succession down to Eupator. The last to reign over Paphlagonia was Deïotarus, the son of Castor, surnamed Philadelphus, who possessed Gangra, the royal residence of Morzeüs, which was at the same time a small town and a fortress.
Eudoxus mentions fish that are "dug up" in Paphlagonia "in dry places," but he does not distinguish the place; and he says that they are dug up "in moist places round the Ascanian Lake below Cius," without saying anything clear on the subject. Since I am describing the part of Paphlagonia which borders on Pontus and since the Bithynians border on the Paphlagonians towards the west, I shall try to go over this region also; and then, taking a new beginning from the countries of these people and the Paphlagonians, I shall interweave my description of their regions with that of the regions which follow these in order towards the south as far as the Taurus — the regions that run parallel to Pontus and Paphlagonia; for some such order and division is suggested by the nature of the regions. |
|
|
|
|
12 - 4 Bithynia 
1 Bithynia is bounded on the east by the Paphlagonians and Mariandyni and some of the Epicteti; on the north by the Pontic Sea, from the outlets of the Sangarius River to the mouth of the sea at Byzantium and Chalcedon; on the west by the Propontis; and towards the south by Mysia and by Phrygia "Epictetus," as it is called, though the same is also called "Hellespontiac" Phrygia.
2 In this last country, at the mouth of the Pontus, are situated Chalcedon, founded by the Megarians, and Chrysopolis, a village, and the Chalcedonian temple; and slightly above the sea the country has a spring called Azaritia, which breeds little crocodiles. Then the Chalcedonian shore is followed by the Astacene Gulf, as it is called, a part of the Propontis; and it was on this gulf that Nicomedeia was founded, being named after one of the Bithynian kings, who founded it. But many kings, for example the Ptolemies, were, on account of the fame of the first, given the same name. And on the gulf itself there was also a city Astacus, founded by the Megarians and Athenians and afterwards by Doedalsus; and it was after the city Astacus that the gulf was named. It was rased to the ground by Lysimachus, and its inhabitants were transferred to Nicomedeia by the friend of the latter.
3 Continuous with the Astacene Gulf is another gulf, which runs more nearly towards the rising sun than the former does; and on this gulf is Prusias, formerly called Cius. Cius was rased to the ground by Philip, the son of Demetrius and father of Perseus, and given by him to Prusias the son of Zelas, who had helped him rase both this city and Myrleia, which latter is a neighbouring city and also is near Prusa. And Prusias restored them from their ruins and named the city Cius "Prusias" after himself and Myrleia "Apameia" after his wife. This is the Prusias who welcomed Hannibal, when the latter withdrew thither after the defeat of Antiochus, and who retired from Phrygia on the Hellespont in accordance with an agreement made with the Attalici. This country was in earlier times called Lesser Phrygia, but the Attalici called it Phrygia Epictetus. Above Prusias lies a mountain called Arganthonium. And here is the scene of the myth of Hylas, one of the companions of Herakles who sailed with him on the Argo, and who, when he was going out to get water, was carried off by the nymphs. And when Cius, who was also a companion of Herakles and with him on the voyage, returned from Colchis, he stayed here and founded the city which was named after him. And still to this day a kind of festival is celebrated among the Prusians, a mountain-ranging festival, in which they march in procession and call Hylas, as though making their exodus to the forests in quest of him. And having shown a friendly disposition towards the Romans in the conduct of their government, the Prusians obtained freedom. Prusa is situated on the Mysian Olympus; it is a well-governed city, borders on the Phrygians and the Mysians, and was founded by the Prusias who made war against Croesus.
4 It is difficult to mark the boundaries between the Bithynians and the Phrygians and Mysians, or even those between the Doliones around Cyzicus and the Mygdonians and the Trojans. And it is agreed that each tribe is "apart" from the others (in the case of the Phrygians and Mysians, at least, there is a proverb, "Apart are the boundaries of the Mysians and Phrygians"), but that it is difficult to mark the boundaries between them. The cause of this is that the foreigners who went there, being barbarians and soldiers, did not hold the conquered territory firmly, but for the most part were wanderers, driving people out and being driven out. One might conjecture that all these tribes were Thracian because the Thracians occupy the other side and because the people on either side do not differ much from one another.
5 But still, as far as one is able to conjecture, one might put down Mysia as situated between Bithynia and the outlet of the Aesepus River, as touching upon the sea, and as extending as far as Olympus, along almost the whole of it; and Epictetus as lying in the interior round Mysia, but nowhere touching upon the sea, and as extending to the eastern parts of the Ascanian Lake and territory; for the territory was called by the same name as lake. And a part of this territory was Phrygian and a part Mysian, but the Phrygian part was farther away from Troy. And in fact one should thus interpret the words of the poet when he says, "And Phorcys and godlike Ascanius led the Phrygians from afar, from Ascania," that is, the Phrygian Ascania, since his words imply that another Ascania, the Mysian, near the present Nicaea, is nearer Troy, that is, the Ascania to which the poet refers when he says, "and Palmys, and Ascanius, and Morys, son of Hippotion (Morys being leader of the Mysians, hand-to‑hand fighters), who had come from deep-soiled Ascania to relieve their fellows." And it is not remarkable if he speaks of one Ascanius as a leader of the Phrygians and as having come from Ascania and also of another Ascanius as a leader of the Mysians and as having come from Ascania, for in Homer identity of names is of frequent occurrence, as also the surnaming of people after rivers and lakes and places.
6 And the poet himself gives the Aesepus as a boundary of the Mysians, for after naming the foothills of Troy above Ilium that were subject to Aeneas, which he calls Dardania, he puts down Lycia as next towards the north, the country that was subject to Pandarus, in which Zeleia was situated; and he says, "and they dwelt in Zeleia 'neath the nethermost foot of Mt. Ida, wealthy men, Trojans, who drink the dark water of the Aesepus." Below Zeleia, near the sea, and on this side of the Aesepus, are the plain of Adrasteia, Mt. Tereia, and Pitya (that is, speaking generally, the present Cyzicenê near Priapus), which the poet names next after Zeleia; and then he returns to the parts towards the east and those on the far side of the Aesepus, by which he indicates that he regards the country as far as the Aesepus as the northerly and easterly limit of the road. Assuredly, however, Mysia and Olympus come after the Troad. Now ancient tradition suggests some such position of the tribes as this, but the present differences are the result of numerous changes, since different rulers have been in control at different times, and have confounded together some tribes and sundered others. For both the Phrygians and the Mysians had the mastery after the capture of Troy; and then later the Lydians; and with them the Aeolians and the Ionians; and then the Persians and the Macedonians; and lastly the Romans, under whose reign most of the peoples have already lost both their dialects and their names, since a different partition of the country has been made. But it is better for me to consider this matter when I describe the conditions as they now are, at the same time giving proper attention to conditions as they were in antiquity.
7 In the interior of Bithynia are, not only Bithynium, which is situated above Tieium and holds the territory round Salon, where is the best pasturage for cattle and whence comes the Salonian cheese, but also Nicaea, the metropolis of Bithynia, situated on the Ascanian Lake, which is surrounded by a plain that is large and very fertile but not at all healthful in summer. Nicaea was first founded by Antigonus the son of Philip, who called it Antigonia, and then by Lysimachus, who changed its name to that of Nicaea his wife. She was the daughter of Antipater. The city is sixteen stadia in circuit and is quadrangular in shape; it is situated in a plain, and has four gates; and its streets are cut at right angles, so that the four gates can be seen from one stone which is set up in the middle of the gymnasium. Slightly above the Ascanian Lake is the town Otroea, situated just on the borders of Bithynia towards the east. It is surmised that Otroea was so named after Otroeus.
8 That Bithynia was a settlement of the Mysians will first be testified by Scylax the Caryandian, who says that Phrygians and Mysians lived round the Ascanian Lake; and next by the Dionysius who wrote on "The Foundings" of cities, who says that the strait at Chalcedon and Byzantium, now called the Thracian Bosporus, was in earlier times called the Mysian Bosporus. And this might also be set down as an evidence that the Mysians were Thracians. Further, when Euphorion says, "besides the waters of the Mysian Ascanius," and when Alexander the Aetolian says, "who have their homes on the Ascanian streams, on the lips of the Ascanian Lake, where dwelt Dolion the son of Silenus and Melia," they bear witness to the same thing, since the Ascanian Lake is nowhere to be found but here alone.
9 Bithynia has produced men notable for their learning: Xenocrates the philosopher, Dionysius the dialectician, Hippocrates, Theodosius and his sons the mathematicians, and also Cleochares the rhetorician of Myrleia, and Asclepiades the physician of Prusa.
To the south of the Bithynians are the Mysians round Olympus (who by some are called the Olympeni and by others the Hellespontii) and the Hellespontian Phrygia; and to the south of the Paphlagonians are the Galatae; and still to the south of these two is Greater Phrygia, as also Lycaonia, extending as far as the Cilician and the Pisidian Taurus. But since the region continuous with Paphlagonia is adjacent to Pontus and Cappadocia and the tribes which I have already described, it might be appropriate for me first to give an account of the parts in the neighbourhood of these and then set forth a description of the places that come next thereafter. |
|
|
|
|
12 - 5 Galatia 
1 The Galatians, then, are to the south of the Paphlagonians. And of these there are three tribes; two of them, the Trocmi and the Tolistobogii, are named after their leaders, whereas the third, the Tectosages, is named after the tribe in Celtica. This country was occupied by the Galatae after they had wandered about for a long time, and after they had overrun the country that was subject to the Attalic and Bithynian kings, until by voluntary cession they received the present Galatia, or Gallo-Graecia, as it is called. Leonnorius is generally reputed to have been the chief leader of their expedition across to Asia. The three tribes spoke the same language and differed from each other in no respect; and each was divided into four portions which were called tetrarchies, each tetrarchy having its own tetrarch, and also one judge and one military commander, both subject to the tetrarch, and two subordinate commanders. The Council of the twelve tetrarchs consisted of three hundred men, who assembled at Drynemetum, as it was called. Now the Council passed judgment upon murder cases, but the tetrarchs and the judges upon all others. Such, then, was the organisation of Galatia long ago, but in my time the power has passed to three rulers, then to two, and then to one, Deïotarus, and then to Amyntas, who succeeded him. But at the present time the Romans possess both this country and the whole of the country that became subject to Amyntas, having united them into one province.
2 The Trocmi possess the parts near Pontus and Cappadocia. These are the most powerful of the parts occupied by the Galatians. They have these walled garrisons: Tavium, the emporium of the people in that part of the country, where are the colossal statue of Zeus in bronze and his sacred precinct, a place of refuge; and Mithridatium, which Pompey gave to Bogodiatarus, having separated it from the kingdom of Pontus; and third, Danala, where Pompey and Leucullus had their conference, Pompey coming there as successor of Leucullus in command of the war, and Leucullus giving over to Pompey his authority and leaving the country to celebrate his triumph. The Trocmi, then, possess these parts, but the Tectosages the parts near Greater Phrygia in the neighbourhood of Pessinus and Orcaorci. To the Tectosages belonged the fortress Ancyra, which bore the same name as the Phrygian town situated toward Lydia in the neighbourhood of Blaudus. And the Tolistobogii border on the Bithynians and Phrygia "Epictetus," as it is called. Their fortresses are Blucium and Peïum, the former of which was the royal residence of Deïotarus and the latter the place where he kept his treasures.
3 Pessinus is the greatest of the emporiums of that part of the world, containing a temple of the Mother of the gods, which is an object of great veneration. They call her Agdistis. The priests were in ancient times potentates, I might call them, who reaped the fruits of a great priesthood, but at present the prerogatives of these have been much reduced, although the emporium still endures. The sacred precinct has been built up by the Attalic kings in a manner befitting a holy place, with a sanctuary and also with porticoes of white marble. The Romans made the temple famous when, in accordance with oracles of the Sibyl, they sent for the statue of the goddess there, just as they did in the case of that of Asclepius at Epidaurus. There is also a mountain situated above the city, Dindymum, after which the country Dindymenê was named, just as Cybelê was named after Cybela. Near by, also, flows the Sangarius River; and on this river are the ancient habitations of the Phrygians, of Midas, and of Gordius, who lived even before his time, and of certain others, — habitations which preserve not even traces of cities, but are only villages slightly larger than the others, for instance, Gordium and Gorbeus, the royal residence of Castor the son of Saocondarius, where Deïotarus, Castor's father-in‑law, slew him and his own daughter. And he pulled down the fortress and ruined most of the settlement.
4 After Galatia towards the south are situated Lake Tatta, which lies alongside Greater Cappadocia near Morimenê but is a part of Greater Phrygia, and the country continuous with this lake and extending as far as the Taurus, most of which was held by Amyntas. Now Lake Tatta is a natural salt‑pan; and the water so easily congeals round everything that is immersed in it, that when people let down into it rings made of rope they draw up wreaths of salt, and that, on account of the congealing of the salt, the birds which touch the water with their wings fall on the spot and are thus caught. |
|
|
|
|
12 - 6 Lycaonia 
1 Such, then, is Tatta. And the regions round Orcaorci and Pitnissus, as also the plateaus of the Lycaonians, are cold, bare of trees, and grazed by wild asses, though there is a great scarcity of water; and even where it is possible to find water, the wells are the deepest in the world, just as in Soatra, where the water is actually sold (this is a village-city near Garsaüra). But still, although the country is unwatered, it is remarkably productive of sheep; but the wool is coarse, and yet some persons have acquired very great wealth from this alone. Amyntas had over three hundred flocks in this region. There are also two lakes in this region, the larger being Lake Coralis and the smaller Lake Trogitis. In this neighbourhood is also Iconium, a town that is well settled and has a more prosperous territory than the above-mentioned ass‑grazing country. This place was held by Polemon. Here the region in question is near the Taurus, which separates Cappadocia and Lycaonia from Cilicia Tracheia, which last lies above that region. The boundary between the Lycaonians and the Cappadocians lies between Coropassus, a village of the Lycaonians, and Garsaüra, a town of the Cappadocians. The distance between these strongholds is about one hundred and twenty stadia.
2 To Lycaonia belongs also Isauricê, near the Taurus itself, which has the two Isauras, villages bearing the same name, one of which is called Old Isaura, and the other New Isaura, which is well-fortified. Numerous other villages were subject to these, and they were all settlements of robbers. They were a source of much trouble to the Romans and in particular to Publius Servilius, surnamed Isauricus, with whom I was acquainted; he subjected these places to the Romans and also destroyed most of the strongholds of the pirates that were situated on the sea.
3 On the side of Isauricê lies Derbê, which lies closer to Cappadocia than to any other country and was the royal seat of the tyrant Antipater Derbetes. He also possessed Laranda. But in my time Derbê and also the two Isauras have been held by Amyntas, who attacked and killed Derbetes, although he received Isaura from the Romans. And, indeed, after destroying the Old Isaura, he built for himself a royal residence there. And though he was building a new wall in the same place, he did not live to complete it, but was killed by the Cilicians, when he was invading the country of the Homonadeis and was captured by ambuscade.
4 For, being in possession of the Antiocheia near Pisidia and of the country as far as the Apollonias near Apameia Cibotus and of certain parts of the country alongside the mountain, and of Lycaonia, he was trying to exterminate the Cilicians and the Pisidians, who from the Taurus were overrunning this country, which belonged to the Phrygians and the Cilicians; and he captured many places which previously had been impregnable, among which was Cremna. However, he did not even try to win Sandalium by force, which is situated between Cremna and Sagalassus.
5 Now Cremna is occupied by Roman colonists: and Sagalassus is subject to the same Roman governor to whom the whole kingdom of Amyntas was subject. It is a day's journey distant from Apameia, having a descent of about thirty stadia from the fortress. It is also called Selgessus; this city was also captured by Alexander. Now Amyntas captured Cremna, and, passing into the country of the Homonadeis, who were considered too strong to capture, and having now established himself as master of most of the places, having even slain their tyrant, was caught by treachery through the artifice of the tyrant's wife. And he was put to death by those people, but Cyrinius5 overthrew the inhabitants by starving them, and captured alive four thousand men and settled them in the neighbouring cities, leaving the country destitute of all its men who were in the prime of life. In the midst of the heights of the Taurus, which are very steep and for the most part impassable, there is a hollow and fertile plain which is divided into several valleys. But though the people tilled this plain, they lived on the overhanging brows of the mountains or in caves. They were armed for the most part and were wont to overrun the country of others, having mountains that served as walls about their country. |
|
|
|
|
12 - 7 Pisidia 
1 Contiguous to these are the Pisidians, and in particular the Selgeis, who are the most notable of the Pisidians. Now the greater part of them occupy the summits of the Taurus, but some, situated above Sidê and Aspendus, Pamphylian cities, occupy hilly places, everywhere planted with olive-trees; the region above this (we are now in the mountains) is occupied by the Catenneis, whose country borders on that of the Selgeis and the Homonadeis; but the Sagalasseis occupy the region this side the Taurus that faces Milyas.
2 Artemidorus says that the cities of the Pisidians are Selgê, Sagalassus, Petnelissus, Adada, Tymbriada, Cremna, Pityassus, Amblada, Anabura, Sinda, Aarassus, Tarbassus, and Termessus. Of these, some are entirely in the mountains, while others extend even as far as the foot-hills on either side, to both Pamphylia and Milyas, and border on the Phrygians and the Lydians and the Carians, which are all peaceable tribes, although they are situated towards the north. But the Pamphylians, who share much in the traits of the Cilician stock of people, do not wholly abstain from the business of piracy, nor yet do they allow the peoples on their borders to live in peace, although they occupy the southern parts of the foot-hills of the Taurus. And on the borders of the Phrygians and Caria are situated Tabae and Sinda, and also Amblada, whence is exported the Ambladian wine, which is suitable for use in medicinal diets.
3 Now all the rest of the above-mentioned Pisidians who live in the mountains are divided into separate tribes governed by tyrants, like the Cilicians, and are trained in piracy. It is said that in ancient times certain Leleges, a wandering people, intermingled with them and on account of similarity of character stayed there. Selgê was founded at first by the Lacedaemonians as a city, and still earlier by Calchas; but later it remained an independent city, having waxed so powerful on account of the law‑abiding manner in which its government was conducted that it once contained twenty thousand men. And the nature of the region is wonderful, for among the summits of the Taurus there is a country which can support tens of thousands of inhabitants and is so very fertile that it is planted with the olive in many places, and with fine vineyards, and produces abundant pasture for cattle of all kinds; and above this country, all round it, lie forests of various kinds of timber. But it is the styrax-tree that is produced in greatest abundance there, a tree which is not large but grows straight up, the tree from which the styracine javelins are made, similar to those made of cornel-wood. And a species of wood-eating worm is bred in the trunk which eats through the wood of the tree to the surface, and at first pours out raspings like bran or saw‑dust, which are piled up at the root of the tree; and then a liquid substance exudes which readily hardens into a substance like gum. But a part of this liquid flows down upon the raspings at the root of the tree and mixes with both them and the soil, except so much of it as condenses on the surface of the raspings and remains pure, and except the part which hardens on the surface of the trunk down which it flows, this too being pure. And the people make a kind of substance mixed with wood and earth from that which is not pure, this being more fragrant than the pure substance but otherwise inferior in strength to it (a fact unnoticed by most people), which is used in large quantities as frankincense by the worshippers of the gods. And p485people praise also the Selgic iris and the ointment made from it. The region round the city and the territory of the Selgians has only a few approaches, since their territory is mountainous and full of precipices and ravines, which are formed, among other rivers, by the Eurymedon and the Cestrus, which flow from the Selgic mountains and empty into the Pamphylian Sea. But they have bridges on their roads. Because of their natural fortifications, however, the Selgians have never even once, either in earlier or later times, become subject to others, but unmolested have reaped the fruit of the whole country except the part situated below them in Pamphylia and inside the Taurus, for which they were always at war with the kings; but in their relations with the Romans, they occupied the part in question on certain stipulated conditions. They sent an embassy to Alexander and offered to receive his commands as a friendly country, but at the present time they have become wholly subject to the Romans and are included in the territory that was formerly subject to Amyntas. |
|
|
|
|
12 - 8 Arcadia 
1 Bordering on the Bithynians towards the south, as I have said,1 are the Mysians and Phrygians who live round the Mysian Olympus, as it is called. And each of these tribes is divided into two parts. For one part of Phrygia is called Greater Phrygia, the part over which Midas reigned, a part of which was occupied by the Galatians, whereas the other is called Lesser Phrygia, that on the Hellespont and round Olympus, I mean Phrygia Epictetus, as it is called. Mysia is likewise divided into two parts, I mean Olympenê, which is continuous with Bithynia and Phrygia Epictetus, which, according to Artemidorus, was colonised by the Mysians who lived on the far side of the Ister, and secondly, the country in the neighbourhood of the Caïcus River and Pergamenê, extending as far as Teuthrania and the outlets of the river.
2 But the boundaries of these parts have been so confused with one another, as I have often said, that it is uncertain even as to the country round Mt. Sipylus, which the ancients called Phrygia, whether it was a part of Greater Phrygia or of Lesser Phrygia, where lived, they say, the "Phrygian" Tantalus and Pelops and Niobê. But no matter which of the two opinions is correct, the confusion of the boundaries is obvious; for Pergamenê and Elaïtis, where the Caïcus empties into the sea, and Teuthrania, situated between these two countries, where Teuthras lived and were Telephus was reared, lie between the Hellespont on the one side and the country round Sipylus and Magnesia, which lies at the foot of Sipylus, on the other; and therefore, as I have said before, it is a task to determine the boundaries ("Apart are the boundaries of the Mysians and Phrygians").
3 And the Lydians and the Maeonians, whom Homer called the Meïones, are in some way confused both with these peoples and with one another, because some say that they are the same and others that they are different; and they are confused with these people because some say that the Mysians were Thracians but others that they were Lydians, thus concurring with an ancient explanation given by Xanthus the Lydian and Menecrates of Elaea, who explain the origin of the name of the Mysians by saying that the oxya-tree is so named by the Lydians. And the oxya-tree abounds in the neighbourhood of Mt. Olympus, where they say that the decimated persons were put out and that their descendants were the Mysians of later times, so named after the oxya-tree, and that their language bears witness to this; for, they add, their language is, in a way, a mixture of the Lydian and the Phrygian languages, for the reason that, although they lived round Mt. Olympus for a time, yet when the Phrygians crossed over from Thrace and slew a ruler of Troy and of the country near it, those people took up their abode there, whereas the Mysians took up their abode above the sources of the Caïcus near Lydia.
4 Contributing to the creation of myths of this kind are the confusion of the tribes there and the fertility of the country this side the Halys River, particularly that of the seaboard, on account of which attacks were made against it from numerous places and continually by peoples from the opposite mainland, or else the people near by would attack one another. Now it was particularly in the time of the Trojan War and after that time that invasions and migrations took place, since at the same time both the barbarians and the Greeks felt an impulse to acquire possession of the countries of others; but this was also the case before the Trojan War, for the tribe of the Pelasgians was then in existence, as also that of the Cauconians and Leleges. And, as I have said before, they wandered in ancient times over many regions of Europe. These tribes the poet makes the allies of the Trojans, but not as coming from the opposite mainland. The accounts both of the Phrygians and of the Mysians go back to earlier times than the Trojan War. The existence of two groups of Lycians arouses suspicion that they were of the same tribe, whether it was the Trojan Lycians or those near Caria that colonised the country of the other of the two. And perhaps the same was also true in the case of the Cilicians, for these, too, were two‑fold; however, we are unable to get the same kind of evidence that the present tribe of Cilicians was already in existence before the Trojan War. Telephus might be thought to have come from Arcadia with his mother; and having become related to Teuthras, to whether he was a welcome guest, by the marriage of his mother to that ruler, was regarded as his son and also succeeded to the rulership of the Mysians.
5 Not only the Carians, who in earlier times were islanders, but also the Leleges, as they say, became mainlanders with the aid of the Cretans, who founded, among other places, Miletus, having taken Sarpedon from the Cretan Miletus as founder; and they settled the Termilae in the country which is now called Lycia; and they say that these settlers were brought from Crete by Sarpedon, a brother of Minos and Rhadamanthus, and that he gave the name Termilae to the people who were formerly called Milyae, as Herodotus says, and were in still earlier times called Solymi, but that when Lycus the son of Pandion went over there he named the people Lycians after himself. Now this account represents the Solymi and the Lycians as the same people, but the poet makes a distinction between them. At any rate, Bellerophontes set out from Lycia and "fought with the glorious Solymi." And likewise his son Peisander "was slain when fighting the Solymi" by Ares, as he says. And he also speaks of Sarpedon as a native of Lycia.
6 But the fact that the fertility of the country of which I am speaking was set before the powerful as a common prize of war is confirmed by many things which have taken place even subsequent to the Trojan War, since even the Amazons took courage to attack it, against whom not only Priam, but also Bellerophontes, are said to have made expeditions; and the naming of ancient cities after the Amazons attests this fact. And in the Trojan Plain there is a hill "which by men is called 'Batieia,' but by the immortals 'the tomb of the much-bounding Myrina,' " who, historians say, was one of the Amazons, inferring this from the epithet "much-bounding"; for they say that horses are called "well-bounding" because of their speed, and that Myrina, therefore, was called "much-bounding" p495because of the speed with which she drove her chariot. Myrina, therefore, is named after this Amazon. And the neighbouring islands had the same experience because of their fertility; and Homer clearly testifies that, among these, Rhodes and Cos were already inhabited by Greeks before the Trojan War.
7 After the Trojan War the migrations of the Greeks and the Trerans, and the onsets of the Cimmerians and of the Lydians, and, after this, of the Persians and the Macedonians, and, at last, of the Galatians, disturbed and confused everything. But the obscurity has arisen, not on account of the changes only, but also on account of the disagreements of the historians, who do not say the same things about the same subjects, calling the Trojans Phrygians, as do the tragic poets, and the Lycians Carians; and so in the case of other peoples. But the Trojans, having waxed so strong from a small beginning that they became kings of kings, afforded both the poet and his expounders grounds for enquiring what should be called Troy; for in a general way he calls "Trojans" the peoples, one and all, who fought on the Trojan side, just as he called their opponents both "Danaans" and "Achaeans"; and yet, of course, we shall surely not speak of Paphlagonia as a part of Troy, nor yet Caria, nor the country that borders on Caria, I mean Lycia. I mean when the poet says, "the Trojans advanced with clamour and with a cry like birds," and when he says of their opponents, "but the Achaeans advanced in silence, breathing rage." And in many ways he uses terms differently. But still, although such is the case, I must try to arbitrate the several details to the best of my ability. However, if anything in ancient history escapes me, I must leave it unmentioned, for the task of the geographer does not lie in that field, and I must speak of things as they now are.
8 Above the Propontis, then, there are two mountains, the Mysian Olympus and Mt. Ida. Now the region of the Bithynians lies at the foot of Olympus, whereas Troy is situated between Mt. Ida and the sea and borders on the mountain. As for Troy, I shall describe it and the parts adjacent to it towards the south later on,but at present let me describe the country of Mt. Olympus and the parts which come next in order thereafter, extending as far as the Taurus and lying parallel to the parts which I have previously traversed. Mt. Olympus, then, is not only well settled all round but also has on its heights immense forests and places so well-fortified by nature that they can support bands of robbers; and among these bands there often arise tyrants who are able to maintain their power for a long time; for example, Cleon, who in my time was chieftain of the bands of robbers.
9 Cleon was from the village Gordium, which he later enlarged, making it a city and calling it Juliopolis; but from the beginning he used the strongest of the strongholds, Callydium by name, as retreat and base of operations for the robbers. And he indeed proved useful to Antony, since he made an attack upon those who were levying money for Labienus at the time when the latter held possession of Asia, and he hindered his preparations, but in the course of the Actian War, having revolted from Antony, he joined the generals of Caesar and was honoured more than he deserved, since he also received, in addition to what Antony had given him, what Caesar gave to him, so that he was invested with the guise of dynast, from being a robber, that is, he was priest of Zeus Abrettenus, a Mysian god, and held subject a part of Morenê, which, like Abrettenê, is also Mysian, and received at last the priesthood of Comana in Pontus, although he died within a month's time after he went down to Comana. He was carried off by an acute disease, which either attacked him in consequence of excessive repletion or else, as the people round the temple said, was inflicted upon him because of the anger of the goddess; for the dwelling of both the priest and the priestess is within the circuit of the sacred precinct, and the sacred precinct, apart from its sanctity in other respects, is most conspicuously free from the impurity of eating swine's flesh; in fact, the city as a whole is free from it; and swine cannot even be brought into the city. Cleon, however, among the first things he did when he arrived, displayed the character of the robber by transgressing this custom, as though he had come, not as priest, but as corrupter of all that was sacred.
Such, then, is Mt. Olympus; and towards the north it is inhabited all round by the Bithynians and Mygdonians and Doliones, whereas the rest of it is occupied by Mysians and Epicteti. Now the peoples round Cyzicus, from the Aesepus River to the Rhyndacus River and Lake Dascylitis, are for the most part called Doliones, whereas the peoples who live next after these as far as the country of the Myrleians are called Mygdonians. Above Lake Dascylitis lies two other lakes, large ones, I mean Lake Apolloniatis and Lake Miletopolitis. Near Lake Dascylitis is the city Dascylium, and near Lake Miletopolitis Miletopolis, and near the third lake "Apollonia on Rhyndacus," as it is called. But at the present time most of these places belong to the Cyziceni.
Cyzicus is an island in the Propontis, being connected with the mainland by two bridges; and it is not only most excellent in the fertility of its soil, but in size has a perimeter of about five hundred stadia. It has a city of the same name near the bridges themselves, and two harbours that can be closed, and more than two hundred ship-sheds. One part of the city is on level ground and the other is near a mountain called "Arcton-oros." About this mountain lies another mountain, Dindymus; it rise into a single peak, and it has a temple of Dindymenê, mother of the gods, which was founded by the Argonauts. This city rivals the foremost of the cities of Asia in size, in beauty, and in its excellent administration of affairs both in peace and in war. And its adornment appears to be of a type similar to that of Rhodes and Massalia and ancient Carthage. Now I am omitting most details, but I may say that there are three directors who take care of the public buildings and the engines of war, and three who have charge of the treasure-houses, one of which contains arms and another engines of war and another grain. They prevent the grain from spoiling by mixing Chalcidic earth with it. They showed in the Mithridatic war the advantage resulting from this preparation of theirs; for when the king unexpectedly came over against them with one hundred and fifty thousand men and with a large cavalry, and took possession of the mountain opposite the city, the mountain called Adrasteia, and of the suburb, and then, when he transferred his army to the neck of land above the city and was fighting them, not only on land, but also by sea with four hundred ships, the Cyziceni held out against all attacks, and, by digging a counter-tunnel, all but captured the king alive in his own tunnel; but he forestalled this by taking precautions and by withdrawing outside his tunnel. Leucullus, the Roman general, was able, though late, to send an auxiliary force to the city by night; and, too, as an aid to the Cyziceni, famine fell upon that multitudinous army, a thing which the king did not foresee, because he suffered a great loss of men before he left the island. But the Romans honoured the city; and it is free to this day, and holds a large territory, not only that which it has held from ancient times, but also other territory presented to it by the Romans; for, of the Troad, they possess the parts round Zeleia on the far side of the Aesepus, as also the plain of Adrasteia, and, of Lake Dascylitis, they possess some parts, while the Byzantians possess the others. And in addition to Dolionis and Mygdonia they occupy a considerable territory extending as far as Lake Miletopolitis and Lake Apolloniatis itself. It is through this region that the Rhyndacus River flows; this river has its sources in Azanitis, and then, receiving from Mysia Abrettenê, among other rivers, the Macestus, which flows from Ancyra in Abaëitis, empties into the Propontis opposite the island Besbicos. In this island of the Cyziceni is a well-wooded mountain called Artacê; and in front of this mountain lies an isle bearing the same name; and near by is a promontory called Melanus, which one passes on a coasting-voyage from Cyzicus to Priapus.
To Phrygia Epictetus belong the cities Azani, Nacolia, Cotiaëium, Midaëium, and Dorylaeum, and also Cadi, which, according to some writers, belongs to Mysia. Mysia extends in the interior from Olympenê to Pergamenê, and to the plain of Caïcus, as it is called; and therefore it lies between Mt. Ida and Catacecaumenê, which latter is by some called Mysian and by others Maeonian.
Above Phrygia Epictetus towards the south is Greater Phrygia, which leaves on the left Pessinus and the region of Orcaorci and Lycaonia, and on the right the Maeonians and Lydians and Carians. In Epictetus are Phrygia "Paroreia," as it is called, and the part of Phrygia that lies towards Pisidia, and the parts round Amorium and Eumeneia and Synnada, and then Apameia Cibotus, as it is called, and Laodiceia, which two are the largest of the Phrygian cities. And in the neighbourhood of these are situated towns, and . . . . ., Aphrodisias, Colossae, Themisonium, Sanaüs, Metropolis, and Apollonias; but still farther away than these are Peltae, Tabae, Eucarpia, and Lysias.
Now Phrygia Paroreia has a kind of mountainous ridge extending from the east towards the west; and below it on either side lies a large plain. And there are cities near it: towards the north, Philomelium, and, on the other side, the Antiocheia near Pisidia, as it is called, the former lying wholly in a plain, whereas the latter is on a hill and has a colony of Romans. The latter was settled by Magnetans who lived near the Maeander River. The Romans set them free from their kings at the time when they gave over to Eumenes the rest of Asia this side the Taurus. Here there was also a priesthood of Mên Arcaeus, which had a number of temple-slaves and sacred places, but the priesthood was destroyed after the death of Amyntas by those who were sent thither as his inheritors. Synnada is not a large city; but there lies in front of it a plain planted with olives, about sixty stadia in circuit. And beyond it is Docimaea, a village, and also the quarry of "Synnadic" marble (so the Romans call it, though the natives call it "Docimite" or "Docimaean"). At first this quarry yielded only stones of small size, but on account of the present extravagance of the Romans great monolithic pillars are taken from it, which in their variety of colours are nearly like the alabastrite marble; so that, although the transportation of such heavy burdens to the sea is difficult, still, both pillars and slabs, remarkable for their size and beauty, are conveyed to Rome.
Apameia is a great emporium of Asia, I mean Asia in the special sense of that term, and ranks second only to Ephesus; for it is a common entrepôt for the merchandise from both Italy and Greece. Apameia is situated near the outlets of the Marsyas River, which flows through the middle of the city and has its sources in the city; it flows down to the suburbs, and then with violent and precipitate current joins the Maeander. The latter receives also another river, the Orgas, and traverses a level country with an easy-going and sluggish stream; and then, having by now become a large river, the Maeander flows for a time through Phrygia and then forms the boundary between Caria and Lydia at the Plain of Maeander, as it is called, where its course is so exceedingly winding that everything winding is called "meandering." And at last it flows through Caria itself, which is now occupied by the Ionians, and then empties between Miletus and Prienê. It rises in a hill called Celaenae, on which there is a city which bears the same name as the hill; and it was from Celaenae that Antiochus Soter made the inhabitants move to the present Apameia, the city which he named after his mother Apama, who was the daughter of Artabazus and was given in marriage to Seleucus Nicator. And here is laid the scene of the myth of Olympus and of Marsyas and of the contest between Marsyas and Apollo. Above is situated a lake which produces the reed that is suitable for the mouth-pieces of pipes; and it is from this lake that pour the sources of both the Marsyas and the Maeander.
Laodiceia, though formerly small, grew large in our time and in that of our fathers, even though it had been damaged by siege in the time of Mithridates Eupator. However, it was the fertility of its territory and the prosperity of certain of its citizens that made it great: at first Hieron, who left to the people an inheritance of more than two thousand talents and adorned the city with many dedicated offerings, and later Zeno the rhetorician and his son Polemon, the latter of whom, because of his bravery and honesty, was thought worthy even of a kingdom, at first by Antony and later by Augustus. The country round Laodiceia produces sheep that are excellent, not only for the softness of their wool, in which they surpass even the Milesian wool, but also for its raven-black colour, so that the Laodiceians derive splendid revenue from it, as do also the neighbouring Colosseni from the colour which bears the same name. And here the Caprus River joins the Maeander, as does also the Lycus, a river of good size, after which the city is called the "Laodiceia near Lycus." Above the city lies Mt. Cadmus, whence the Lycus flows, as does also another river of the same name as the mountain. But the Lycus flows under ground for the most part, and then, after emerging to the surface, unites with the other rivers, thus indicating that the country is full of holes and subject to earthquakes; for if any other country is subject to earthquakes, Laodiceia is, and so is Carura in the neighbouring country.
Carura forms a boundary between Phrygia and Caria. It is a village; and it has inns, and also fountains of boiling‑hot waters, some in the Maeander River and some above its banks. Moreover, it is said that once, when a brothel-keeper had taken lodging in the inns along with a large number of women, an earthquake took place by night, and that he, together with all the women, disappeared from sight. And I might almost say that the whole of the territory in the neighbourhood of the Maeander is subject to earthquakes and is undermined with both fire and water as far as the interior; for, beginning at the plains, all these conditions extend through that country to the Charonia, I mean the Charonium at Hierapolis and that at Acharaca in Nysaïs and that near Magnesia and Myus. In fact, the soil is not only friable and crumbly but is also full of salts and easy to burn out. And perhaps the Maeander is winding for this reason, because the stream often changes its course and, carrying down much silt, adds the silt at different times to different parts of the shore; however, it forcibly thrusts a part of the silt out to the high sea. And, in fact, by its deposits of silt, extending forty stadia, it has made Prienê, which in earlier times was on the sea, an inland city.
Phrygia "Catacecaumenê," which is occupied by Lydians and Mysians, received its appellation for some such reason as follows: In Philadelphia, the city near it, not even the walls are safe, but in a sense are shaken and caused to crack every day. And the inhabitants are continually attentive to the disturbances in the earth and plan all structures with a view to their occurrence. And, among the other cities, Apameia was often shaken by earthquakes before the expedition of King Mithridates, who, when he went over to that country and saw that the city was in ruins, gave a hundred talents for its restoration; and it is said that the same thing took place in the time of Alexander. And this, in all probability, is why Poseidon is worshipped in their country, even though it is in the interior, and why the city was called Celaenae, that is, after Celaenus, the son of Poseidon by Celaeno, one of the daughters of Danaüs, or else because of the "blackness" of the stone, which resulted from the burn-outs. And the story of Mt. Sipylus and its ruin should not be put down as mythical, for in our own times Magnesia, which lies at the foot of it, was laid low by earthquakes, at the time when not only Sardeis, but also the most famous of the other cities, were in many places seriously damaged. But the emperor restored them by contributing money; just as his father in earlier times, when the inhabitants of Tralleis suffered their misfortune (when the gymnasium and other parts of the city collapsed), restored their city, as he also restored the city of the Laodiceians.
One should also hear the words of the ancient historians, as, for example, those of Xanthus, who wrote the history of Lydia, when he relates the strange changes that this country often underwent, to which I have already referred somewhere in a former part of my work. And in fact they make this the setting of the mythical story of the Arimi and of the throes of Typhon, calling it the Catacecaumenê country. Also, they do not hesitate to suspect that the parts of the country between the Maeander River and the Lydians are all of this nature, as well on account of the number of the lakes and rivers as on account of the numerous hollows in the earth. And the lake between Laodiceia and Apameia, although like a sea, emits an effluvium that is filthy and of subterranean origin. And they say that lawsuits are brought against the god Maeander for altering the boundaries of the countries on his banks, that is, when the projecting elbows of land are swept away by him; and that when he is convicted the fines are paid from the tolls collected at the ferries.
Between Laodiceia and Carura is a temple of Mên Carus, as it is called, which is held in remarkable veneration. In my own time a great Herophileian school of medicine has been established by Zeuxis, and afterwards carried on by Alexander Philalethes, just as in the time of our fathers the Erasistrateian school was established by Hicesius, although at the present time the case is not at all the same as it used to be.
Writers mention certain Phrygian tribes that are no longer to be seen; for example, the Berecyntes. And Alcman says, "On the pipe he played the Cerbesian, a Phrygian melody." And a certain pit that emits deadly effluvia is spoken of as Cerbesian. This, indeed, is to be seen, but the people are no longer called Cerbesians. Aeschylus, in his Niobê, confounds things that are different; for example, Niobê says that she will be mindful of the house of Tantalus, "those who have an altar of their paternal Zeus on the Idaean hill"; and again, "Sipylus in the Idaean land"; and Tantalus says, "I sow furrows that extend a ten days' journey, Berecyntian land, where is the site of Adrasteia, and where both Mt. Ida and the whole of the Erechtheian plain resound with the bleatings and bellowings of flocks." |
|
|
|
|
13 West Asia 3 4 71 1:50 
|
13 - 1 Troad and Ilium 
1 Let this, then, mark the boundary of Phrygia. I shall now return again to the Propontis and the coast that comes next after the Aesepus River, and follow the same order of description as before. The first country on this seaboard is the Troad, the fame of which, although it is left in ruins and in desolation, nevertheless prompts in writers no ordinary prolixity. With this fact in view, I should ask the pardon of my readers and appeal to them not to fasten the blame for the length of my discussion upon me rather than upon those who strongly yearn for knowledge of the things that are famous and ancient. And my discussion is further prolonged by the number of the peoples who have colonised the country, both Greeks and barbarians, and by the historians, who do not write the same things on the same subjects, nor always clearly either; among the first of these is Homer, who leaves us to guess about most things. And it is necessary for me to arbitrate between his statements and those of the others, after I shall first have described in a summary way the nature of the region in question.
2 The seaboard of the Propontis, then, extends from Cyzicenê and the region of the Aesepus and Granicus Rivers as far as Abydus and Sestus, whereas the parts round Ilium and Tenedos and the Trojan Alexandreia extend from Abydus to Lectum. Accordingly, Mt. Ida, which extends down to Lectum, lies above all these places. From Lectum to the Caïcus River, and to Canae, as it is called, are the parts round Assus and Adramyttium and Atarneus and Pitanê and the Elaïtic Gulf; and the island of the Lesbians extends alongside, and opposite, all these places. Then come next the parts round Cymê, extending to the Hermus and Phocaea, which latter constitutes the beginning of Ionia and the end of Aeolis. Such being the position of the places, the poet indicates in a general way that the Trojans held sway from the region of the Aesepus River and that of the present Cyzicenê to the Caïcus River, their country being divided by dynasties into eight, or nine, portions, whereas the mass of their auxiliary forces are enumerated among the allies.
3 But the later authors do not give the same boundaries, and they use their terms differently, thus allowing us several choices. The main cause of this difference has been the colonisations of the Greeks; less so, indeed, the Ionian colonisation, for it was farther distant from the Troad; but most of p7all that of the Aeolians, for their colonies were scattered throughout the whole of the country from Cyzicenê to the Caïcus River, and they went on still farther to occupy the country between the Caïcus and Hermus Rivers. In fact, the Aeolian colonisation, they say, preceded the Ionian colonisation by four generations, but suffered delays and took a longer time; for Orestes, they say, was the first leader of the expedition, but he died in Arcadia, and his son Penthilus succeeded him and advanced as far as Thrace sixty years after the Trojan War, about the time of the return of the Heracleideae to the Peloponnesus; and then Archelaüs the son of Penthilus led the Aeolian expedition across to the present Cyzicenê near Dascylium; and Gras, the youngest son of Archelaüs, advanced to the Granicus River, and, being better equipped, led the greater part of his army across to Lesbos and occupied it. And they add that Cleues, son of Dorus, and Malaüs, also descendants of Agamemnon, had collected their army at about the same time as Penthilus, but that, whereas the fleet of Penthilus had already crossed over from Thrace to Asia, Cleues and Malaüs tarried a long time round Locris and Mt. Phricius, and only later crossed over and founded the Phryconian Cymê, so named after the Locrian mountain.
4 The Aeolians, then, were scattered throughout the whole of that country which, as I have said, the poet called Trojan. As for later authorities, some apply the name to all Aeolis, but others to only a part of it; and some to the whole of Troy, but others to only a part of it, not wholly agreeing with one another about anything. For instance, in reference to the places on the Propontis, Homer makes the Troad begin at the Aesepus River, whereas Eudoxus makes it begin at Priapus and Artacê, the place on the island of the Cyziceni that lies opposite Priapus, and thus contracts the limits; but Damastes contracts the country still more, making it begin at Parium; and, in fact, Damastes prolongs the Troad to Lectum, whereas other writers prolong it differently. Charon of Lampsacus diminishes its extent by three hundred stadia more, making it begin at Practius, for that is the distance from Parium to Practius; however, he prolongs it to Adramyttium. Scylax of Caryanda makes it begin at Abydus; and similarly Ephorus says that Aeolis extends from Abydus to Cymê, while others define its extent differently.
5 But the topography of Troy, in the proper sense of the term, is best marked by the position of Mt. Ida, a lofty mountain which faces the west and the western sea but makes a slight bend also towards the north and the northern seaboard. This latter is the seaboard of the Propontis, extending from the strait in the neighbourhood of Abydus to the Aesepus River and Cyzicenê, whereas the western sea consists of the outer Hellespont and the Aegaean Sea. Mt. Ida has many foot-hills, is like p11the scolopendra in shape, and is defined by its two extreme limits: by the promontory in the neighbourhood of Zeleia and by the promontory called Lectum, the former terminating in the interior slightly above Cyzicenê (in fact, Zeleia now belongs to the Cyziceni), whereas Lectum extends to the Aegaean Sea, being situated on the coasting-voyage between Tenedos and Lesbos. When the poet says that Hypnos and Hera "came to many-fountained Ida, mother of wild beasts, to Lectum, where first the two left the sea," he describes Lectum in accordance with the facts; for he rightly states that Lectum is a part of Mt. Ida, and also that the mountain is "many-fountained," for there in particular the mountain is abundantly watered, as is shown by the large number of rivers there, "all the rivers that flow forth from the Idaean mountains to the sea, Rhesus and Heptaporus" and the following, all of which are named by the poet and are now to be seen by us. Now while Homer thus describes Lectum and Zeleia as the outermost foot-hills of Mt. Ida in either direction, he also appropriately distinguishes Gargarus from them as a summit, calling it "topmost." And indeed at present time people point out in the upper parts of Ida a place called Gargarum, after which the present Gargara, an Aeolian city, is named. Now between Zeleia and Lectum, beginning from the Propontis, are situated first the parts extending to the straits at Abydus, and then, outside the Propontis, the parts extending to Lectum.
On doubling Lectum one encounters a large wide-open gulf, which is formed by Mt. Ida as it recedes from Lectum to the mainland, and by Canae, the promontory opposite Lectum on the other side. Some call it the Idaean Gulf, others the Adramyttene. On this gulf are the cities of the Aeolians, extending to the outlets of the Hermus River, as I have already said. I have stated in the earlier parts of my work that, as one sails from Byzantium towards the south, the route lies in a straight line, first to Sestus and Abydus through the middle of the Propontis, and then along the coast of Asia as far as Caria. It behooves one, then, to keep this supposition in mind as one listens to the following; and, if I speak of certain gulfs on the coast, one must think of the promontories which form them as lying in the same line, a meridian line, as it were.
7 Now as for Homer's statements, those who have studied the subject more carefully conjecture from them that the whole of this coast became subject to the Trojans, and, though divided into nine dynasties, was under the sway of Priam at the time of the Trojan War and was called Troy. And this is clear from his detailed statements. For instance, Achilles and his army, seeing at the outset that the inhabitants of Ilium were enclosed by walls, tried to carry on the war outside and, by making raids all round, to take away from them all the surrounding places: "Twelve cities of men I have laid waste with my ships, and eleven, I declare, by land throughout the fertile land of Troy." For by "Troy" he means the part of the mainland that was sacked by him; and, along with other places, Achilles also sacked the country opposite Lesbos in the neighbourhood of Thebê and Lyrnessus and Pedasus, which last belonged to the Leleges, and also the country of Eurypylus the son of Telephus. "But what a man was that son of Telephus who was slain by him with the bronze," there is, the hero Eurypylus, slain by Neoptolemus. Now the poet says that these places were sacked, including Lesbos itself: "when he himself took well-built Lesbos"; and "he sacked Lyrnessus and Pedasus"; and "when he laid waste Lyrnessus and the walls of Thebê." It was at Lyrnessus that Briseïs was taken captive, "whom he carried away from Lyrnessus"; and it was at her capture, according to the poet, that Mynes and Epistrophus fell, as is shown by the lament of Briseïs over Patroclus: "thou wouldst not even, not even, let me weep when swift Achilles slew my husband and sacked the city of divine Mynes"; for in calling Lyrnessus "the city of divine Mynes" the poet indicates that Mynes was dynast over it and that he fell in battle there. But it was at Thebê that Chryseïs was taken captive: "We went into Thebê, the sacred city of Eëtion"; and the poet says that Chryseïs was part of the spoil brought from that place. Thence, too, came Andromachê: "Andromachê, daughter of great-hearted Eëtion; Eëtion who dwelt 'neath wooded Placus in Thebê Hypoplacia, and was lord over the men of Cilicia." This is the second Trojan dynasty after that of Mynes. And consistently with these facts writers think that the following statement of Andromachê, "Hector, woe is me! surely to one doom we were born, both of us — thou in Troy in the house of Priam, but I at Thebae," should not be interpreted strictly, I mean the words "thou in Troy, but I at Thebae" (or Thebê), but as a case of hyperbaton, meaning "both of us in Troy — thou in the house of Priam, but I at Thebae." The third dynasty was that of the Leleges, which was also Trojan: "Of Altes, who is lord over the war‑loving Leleges," by whose daughter Priam begot Lycaon and Polydorus. And indeed those who are placed under Hector in the Catalogue are called Trojans: "The Trojans were led by great Hector of the flashing helmet." And then come those under Aeneias: "The Dardanians in turn were commanded by the valiant son of Anchises"; and these, too, were Trojans; at any rate, the poet says, "Aeneias, counsellor of the Trojans." And then come the Lycians under Pandarus, and these also he calls Trojans: "And those who dwelt in Zeleia beneath the nethermost foot of Ida, Aphneiï, who drink the dark water of the Aesepus, Trojans; these in turn were commanded by Pandarus, the glorious son of Lycaon." And this was the sixth dynasty. And indeed those who lived between the Aesepus River and Abydus were Trojans; for not only were the parts round Abydus subject to Asius, "and they who dwelt about Percotê and Practius and held Sestus and Abydus and goodly Arisbê — these in turn were commanded by Asius the son of Hyrtacus," but a son of Priam lived at Abydus, pasturing mares, clearly his father's: "But he smote Democoön, the bastard son of Priam, for Priam had come from Abydus from his swift mares"; while in Percotê a son of Hicetaon was pasturing kine, he likewise pasturing kine that belonged to no other: "And first he rebuked mighty Melanippus the son of Hicetaon, who until this time had been wont to feed the kine of shambling gait in Percotê"; so that this country would be a part of the Troad, as also the next country after it as far as Adrasteia, for the leaders of the latter were "the two sons of Merops of Percotê." Accordingly, the people from Abydus to Adrasteia were all Trojans, although they were divided into two groups, one under Asius and the other under the sons of Merops, just as Cilicia also was divided into two parts, the Theban Cilicia and the Lyrnessian; but one might include in the Lyrnessian Cilicia the territory subject to Eurypylus, which lay next to the Lyrnessian Cilicia. But that Priam was ruler of these countries, one and all, is clearly indicated by Achilles' words to Priam: "And of thee, old sire, we hear that formerly thou wast blest; how of all that is enclosed by Lesbos, out at sea, city of Macar, and by Phrygia in the upland, and by the boundless Hellespont."
8 Now such were the conditions at the time of the Trojan War, but all kinds of changes followed later; for the parts round Cyzicus as far as the Practius were colonised by Phrygians, and those round Abydus by Thracians; and still before these two by Bebryces and Dryopes. And the country that lies next was colonised by the Treres, themselves also Thracians; and the Plain of Thebê by Lydians, then called Maeonians, and by the survivors of the Mysians who had formerly been subject to Telephus and Teuthras. So then, since the poet combines Aeolis and Troy, and since the Aeolians held possession of all the country from the Hermus River to the seaboard at Cyzicus, and founded their cities there, I too might not be guilty of describing them wrongly if I combined Aeolis, now properly so called, extending from the Hermus River to Lectum, and the country next after it, extending to the Aesepus River; for in my detailed treatment of the two, I shall distinguish them again, setting forth, along with the facts as they now are, the statements of Homer and of others.
9 According to Homer, then, the Troad begins after the city of the Cyziceni and the Aesepus River. And he so speaks of it: "And those who dwelt in Zeleia beneath the nethermost foot of Ida, Aphneii, who drink the dark water of the Aesepus, Trojans; these in turn were commanded by Pandarus the glorious son of Lycaon." These he also calls Lycians. And they are thought to have been called "Aphneii" after Lake "Aphnitis," for Lake Dascylitis is also called by that name.
Now Zeleia is situated on the farthermost foot-hill of Mt. Ida, being one hundred and ninety stadia distant from Cyzicus and about eighty stadia from the nearest part of the sea, where the Aesepus empties. And the poet mentions severally, in continuous order, the places that lie along the coast after the Aesepus River: "And they who held Adrasteia and the land of Apaesus, and held Pityeia and the steep mountain of Tereia — these were led by Adrastus and Amphius of the linen corslet, the two sons of Merops of Percotê." These places lie below Zeleia, but they are occupied by Cyziceni and Priapeni even as far as the coast. Now near Zeleia is the Tarsius River, which is crossed twenty times by the same road, like the Heptaporus River, which is mentioned by the poet. And the river that flows from Nicomedeia into Nicaea is crossed twenty-four times, and the river that flows from Pholoê into the Eleian country is crossed many times . . . Scarthon twenty-five times, and the river that flows from the country of the Coscinii into Alabanda is crossed many times, and the river that flows from Tyana into Soli through the Taurus is crossed seventy-five times.
About . . . stadia above the outlet of the Aesepus River is a hill, where is shown the tomb of Memnon, son of Tithonus; and near by is the village of Memnon. The Granicus River flows between the Aesepus River and Priapus, mostly through the plain of Adrasteia, where Alexander utterly defeated the satraps of Dareius in battle, and gained the whole of the country inside the Taurus and the Euphrates River. And on the Granicus was situated the city Sidenê, with a large territory of the same name; but it is now in ruins. On the boundary between the territory of Cyzicus and that of Priapus is a place called Harpagia, from which, according to some writers of myths, Ganymede was snatched, though others say that he was snatched in the neighbourhood of the Dardanian Promontory, near Dardanus.
Priapus is a city on the sea, and also a harbour. Some say that it was founded by Milesians, who at the same time also colonised Abydus and Proconnesus, whereas others say that it was founded by Cyziceni. It was named after Priapus, who was worshipped there; then his worship was transferred thither from Orneae near Corinth, or else the inhabitants felt an impulse to worship the god because he was called the son of Dionysus and a nymph; for their country is abundantly supplied with the vine, both theirs and the countries which border next upon it, I mean those of the Pariani and the Lampsaceni. At any rate, Xerxes gave Lampsacus to Themistocles to supply him with wine. But it was by people of later times that Priapus was declared a god, for even Hesiod does not know of him; and he resembles the Attic deities Orthanê, Conisalus, Tychon, and others like them.
This country was called "Adrasteia" and "Plain of Adrasteia," in accordance with a custom whereby people gave two names to the same place, as "Thebê" and "Plain of Thebê," and "Mygdonia" and "Plain of Mygdonia." According to Callisthenes, among others, Adrasteia was named after King Adrastus, who was the first to found a temple of Nemesis. Now the city is situated between Priapus and Parium; and it has below it a plain that is named after it, in which there was an oracle of Apollo Actaeus and Artemis. . . . But when the temple was torn down, the whole of its furnishings and stone-work were transported to Parium, where was built an altar, the work of Hermocreon, very remarkable for its size and beauty; but the oracle was abolished like that at Zeleia. Here, however, there is no temple of Adrasteia, nor yet of Nemesis, to be seen, although there is a temple of Adrasteia near Cyzicus. Antimachus says as follows: "There is a great goddess Nemesis, who has obtained as her portion all these things from the Blessed. Adrestus was the first to build an altar to her beside the stream of the Aesepus River, where she is worshipped under the name of Adresteia."
The city Parium is situated on the sea; it has a larger harbour than Priapus, and its territory has been increased at the expense of Priapus; for the Parians curried favour with the Attalic kings, to whom the territory of Priapus was subject, and by their permission cut off for themselves a large part of that territory. Here is told the mythical stories that the Ophiogeneis are akin to the serpent tribe; and they say that the males of the Ophiogeneis cure snake-bitten people by continuous stroking, after the manner of enchanters, first transferring the livid colour to their own bodies and then stopping both the inflammation and the pain. According to the myth, the original founder of the tribe, a certain hero, changed from a serpent into a man. Perhaps he was one of the Libyan Psylli, whose power persisted in his tribe for a certain time. Parium was founded by Milesians and Erythraeans and Parians.
Pitya is in Pityus in the territory of Parium, lying below a pine-covered mountain; and it lies between Parium and Priapus in the direction of Linum, a place on the seashore, where are caught the Linusian snails, the best in the world.
On the coasting-voyage from Parium to Priapus lie both the old Proconnesus and the present Proconnesus, the latter having a city and also a great quarry of white marble that is very highly commended; at any rate, the most beautiful works of art in the cities of that part of the world, and especially those in Cyzicus, are made of this marble. Aristeas was a Proconnesian — the author of the Arimaspian epic, as it is called — a charlatan if ever there was one.
As for "the mountain of Tereia," some say that it is the range of mountains in Peirossus which are occupied by the Cyziceni and are adjacent to Zeleia, where a royal hunting-ground was arranged by the Lydians, and later by the Persians; but others point out a hill forty stadia from Lampsacus, on which there is a temple sacred to the mother of the gods, entitled "Tereia's" temple.
Lampsacus, also, is a city on the sea, a notable city with a good harbour, and still flourishing, like Abydus. It is about one hundred and seventy stadia distant from Abydus; and it was formerly called Pityussa, as also, it is said, was Chios. On the opposite shore of the Chersonesus is Callipolis, a small town. It is on the headland and runs far out towards Asia in the direction of the city of the Lampsaceni, so that the passage across to Asia from it is no more than forty stadia.
In the interval between Lampsacus and Parium lay a city and river called Paesus; but the city is in ruins. The Paeseni changed their abode to Lampsacus, they too being colonists from the Milesians, like the Lampsaceni. But the poet refers to the place in two ways, at one time adding the first syllable, "and the land of Apaesus," and at another omitting it, "a man of many possessions, who dwelt in Paesus." And the river is now spelled in the latter way. Colonae, which lies above Lampsacus in the interior of Lampsacenê, is also a colony of the Milesians; and there is another Colonae on the outer Hellespontine sea, which is one hundred and forty stadia distant from Ilium and is said to be the birthplace of Cycnus. Anaximenes says that there are also places in the Erythraean territory and in Phocis and in Thessaly that are called Colonae. And there is an Iliocolonê in the territory of Parium. In the territory of Lampsacus is a place called Gergithium which is rich in vines; and there was also a city called Gergitha from Gergithes in the territory of Cymê, for here too there was a city called Gergithes, in the feminine plural, the birthplace of Cephalon the Gergithian. And still to‑day a place called Gergithium is pointed out in the territory of Cymê near Larissa. Now Neoptolemus, called the Glossographer, a notable man, was from Parium; and Charon the historian and Adeimantus and Anaximenes the rhetorician and Metrodorus the comrade of Epicurus were from Lampsacus; and Epicurus himself was in a sense a Lampsacenian, having lived in Lampsacus and having been on intimate terms with the ablest men of that city, Idomeneus and Leonteus and their followers. It was from here that Agrippa transported the Fallen Lion, a work of Lysippus; and he dedicated it in the sacred precinct between the Lake and the Euripus.
After Lampsacus come Abydus and the intervening places of which the poet, who comprises with them the territory of Lampsacus and part of the territory of Parium (for these two cities were not yet in existence in the Trojan times), speaks as follows: "And those who dwelt about Percotê and Practius, and held Sestus and Abydus and goodly Arisbê — these in turn were led by Asius, the son of Hyrtacus, . . . who was brought by his large sorrel horses from Arisbê, from the River Sellëeis." In speaking thus, the poet seems to set forth Arisbê, whence he says Asius came, as the royal residence of Asius: "who was brought by his horses from Arisbê, from the River Sellëeis." But these places are so obscure that even investigators do not agree about them, except that they are in the neighbourhood of Abydus and Lampsacus and Parium, and that the old Percotê, the site, underwent a change of name.
Of the rivers, the Sellëeis flows near Arisbê, as the poet says, if it be true that Asius came both from Arisbê and from the Sellëeis River. The River Practius is indeed in existence, but no city of that name is to be found, as some have wrongly thought. This river also flows between Abydus and Lampsacus. Accordingly, the words, "and dwelt about Practius," should be interpreted as applying to a river, as should also those other words, "and those who dwelt beside the goodly Cephisus River," "those who had their famed estates about the Parthenius River." There was also a city Arisba in Lesbos, whose territory is occupied by the Methymnaeans. And there is an Arisbus River in Thrace, as I have said before, near which are situated the Thracian Cebrenians. There are many names common to the Thracians and the Trojans; for example, there are Thracians called Scaeans, and a river Scaeus, and a Scaean Wall, and at Troy the Scaean Gates. And there are Thracian Xanthians, and in Troy-land a river Xanthus. And in Troy-land there is a river Arisbus which empties into the Hebrus, as also a city Arisbê. And there was a river Rhesus in Troy-land; and there was a Rhesus who was the king of the Thracians. And there is also, of the same name as this Asius, another Asius in Homer, "who was maternal uncle to horse-taming Hector, and own brother to Hecabê, but son of Dymas, who dwelt in Phrygia by the streams of the Sangarius."
Abydus was founded by Milesians, being founded by permission of Gyges, king of the Lydians; for this district and the whole of the Troad were under his sway; and there is a promontory named Gygas near Dardanus. Abydus lies at the mouth of the Propontis and the Hellespont; and it is equidistant from Lampsacus and Ilium, about one hundred and seventy stadia. Here, separating Europe and Asia, is the Heptastadium, which was bridged by Xerxes. The European promontory that forms the narrows at the place of the bridge is called the Chersonesus because of its shape. And the place of the bridge lies opposite Abydus. Sestus is the best of the cities in the Chersonesus; and, on account of its proximity to Abydus, it was assigned to the same governor as p43Abydus in the times when governorships had not yet been delimited by continents. Now although Abydus and Sestus are about thirty stadia distant from one another from harbour to harbour, yet the line of the bridge across the strait is short, being drawn at an angle to that between the two cities, that is, from a point nearer than Abydus to the Propontis on the Abydus side to a point farther away from the Propontis on the Sestus side. Near Sestus is a place named Apobathra, where the pontoon-bridge was attached to the shore. Sestus lies farther in towards the Propontis, farther up the stream that flows out of the Propontis. It is therefore easier to cross over from Sestus, first coasting a short distance to the Tower of Hero and then letting the ships make the passage across by the help of the current. But those who cross over from Abydus must first follow the coast in the opposite direction about eight stadia to a tower opposite Sestus, and then sail across obliquely and thus not have to meet the full force of the current. After the Trojan War Abydus was the home of Thracians, and then of Milesians. But when the cities were burned by Dareius, father of Xerxes, I mean the cities on the Propontis, Abydus shared in the same misfortune. He burned them because he had learned after his return from his attack upon the Scythians that the nomads were making preparations to cross the strait and attack him to avenge their sufferings, and was afraid that the cities would provide means for the passage of their army. And this too, in addition to the other changes and to the lapse of time, is a cause of the confusion into which the topography of the country has fallen. As for Sestus and the Chersonesus in general, I have already spoken of them in my description of the region of Thrace. Theopompus says that Sestus is small but well fortified, and that it is connected with its harbour by a double wall of two plethra, and that for this reason, as also on account of the current, it is mistress of the passage.
Above the territory of the Abydeni, in the Troad, lies Astyra. This city, which is in ruins, now belongs to the Abydeni, but in earlier times it was independent and had gold mines. These mines are now scant, being used up, like those on Mt. Tmolus in the neighbourhood of the Pactolus River.a From Abydus to the Aesepus the distance is said to be about seven hundred stadia, but less by straight sailing.
Outside Abydus lies the territory of Ilium — the parts on the shore extending to Lectum, and the places in the Trojan Plain, and the parts on the side of Mt. Ida that were subject to Aeneias. The poet names these last parts in two ways, at one time saying as follows: "The Dardanii in turn were led by the valiant son of Anchises," calling the inhabitants "Dardanii"; and at another time, "Dardani": "The Trojans and Lycians and Dardani that fight in close combat." And it is reasonable to suppose that this was in ancient times the site of the Dardania mentioned by the poet when he says, "At first Dardanus was begotten by Zeus the cloud-gatherer, and he founded Dardania"; for at the present time there is not so much as a trace of a city preserved in that territory.
Plato conjectures, however, that after the time of the floods three kinds of civilisation were formed: the first, that on the mountain-tops, which was simple and wild, when men were in fear of the waters which still deeply covered the plains; the second, that on the foot-hills, when men were now gradually taking courage because the plains were beginning to be relieved of the waters; and the third, that in the plains. One might speak equally of a fourth and fifth, or even more, but last of all that on the sea‑coast and in the islands, when men had been finally released from all such fear; for the greater or less courage they took in approaching the sea would indicate several different stages of civilisation and manners, first as in the case of the qualities of goodness and wildness, which in some way further served as a foundation for the milder qualities in the second stage. But in the second stage also there is a difference to be noted, I mean between the rustic and semi-rustic and civilised qualities; and, beginning with these last qualities, the gradual assumption of new names ended in the polite and highest culture, in accordance with the change of manners for the better along with the changes in places of abode and in modes of life. Now these differences, according to Plato, are suggested by the poet, who sets forth as an example of the first stage of civilisation the life of the Cyclopes, who lived on uncultivated fruits and occupied the mountain-tops, living in caves: "but all these things," he says, "grow unsown and unploughed" for them. . . . "And they have no assemblies for council, nor appointed laws, but they dwell on the tops of high mountains in hollow caves, and each is lawgiver to his children and his wives." And as an example of the second stage, the life in the time of Dardanus, who "founded Dardania; for not yet had sacred Ilios been builded to be a city of mortal men, but they were living on the foot-hills of many-fountained Ida." And of the third stage, the life in the plains in the time of Ilus; for he is the traditional founder of Ilium, and it was from him that the city took its name. And it is reasonable to suppose, also, that he was buried in the middle of the plain for this reason — that he was the first to dare to settle in the plains: "And they sped past the tomb of ancient Ilus, son of Dardanus, through the middle of the plain past the wild fig tree." Yet even Ilus did not have full courage, for he did not found the city at the place where it now is, but about thirty stadia higher up towards the east, and towards Mt. Ida and Dardania, at the place now called "Village of the Ilians." But the people of the present Ilium, being fond of glory and wishing to show that their Ilium was the ancient city, have offered a troublesome argument to those who base their evidence on the poetry of Homer, for their Ilium does not appear to have been the Homeric city. Other inquirers also find that the city changed its site several times, but at last settled permanently where it now is at about this time of Croesus. I take for granted, then, that such removals into the parts lower down, which took place in those times, indicate different stages in modes of life and civilisation; but this must be further investigated at another time.
It is said that the city of the present Ilians was for a time a mere village, having its temple of Athena, a small and cheap temple, but that when Alexander went up there after his victory at the Granicus River he adorned the temple with votive offerings, gave the village the title of city, and ordered those in charge to improve it with buildings, and that he adjudged free and exempt from tribute; and that later, after the overthrow of the Persians, he sent down a kindly letter to the place, promising to make a great city of it, and to build a magnificent sanctuary, and to proclaim sacred games. But after his death Lysimachus devoted special attention to the city, and built a temple there and surrounded the city with a wall about forty stadia in circuit, and also incorporated into it the surrounding cities, which were now old and in bad plight. At that time he had already devoted attention to Alexandreia, which had indeed already been founded by Antigonus and called Antigonia, but had changed its name, for it was thought to be a pious thing for the successors of Alexander to found cities bearing his name before they founded cities bearing their own. And indeed the city endured and grew, and at present it not only has received a colony of Romans but is one of the notable cities of the world.
Also the Ilium of to‑day was a kind of village-city when the Romans first set foot on Asia and expelled Antiochus the Great from the country this side of Taurus. At any rate, Demetrius of Scepsis says that, when as a lad he visited the city about that time, he found the settlement so neglected that the buildings did not so much as have tiled roofs. And Hegesianax says that when the Galatae crossed over from Europe they needed a stronghold and went up into the city for that reason, but left it at once because of its lack of walls. But later it was greatly improved. And then it was ruined again by the Romans under Fimbria, who took it by siege in the course of the Mithridatic war. Fimbria had been sent as quaestor with Valerius Flaccus the consul when the latter was appointed to the command against Mithridates; but Fimbria raised a mutiny and slew the consul in the neighbourhood of Bithynia, and was himself set up as lord of the army; and when he advanced to Ilium, the Ilians would not admit him, as being a brigand, and therefore he applied force and captured the place on the eleventh day. And when he boasted that he himself had overpowered on the eleventh day the city which Agamemnon had only with difficulty captured in the tenth year, although the latter had with him on his expedition the fleet of a thousand vessels and the whole of Greece, one of the Ilians said: "Yes, for the city's champion was no Hector." Now Sulla came over and overthrew Fimbria, and on terms of agreement sent Mithridates away to his homeland, but he also consoled the Ilians by numerous improvements. In my time, however, the deified Caesar was far more thoughtful of them, at the same time also emulating the example of Alexander; for Alexander set out to provide for them on the basis of a renewal of ancient kinship, and also because at the same time he was fond of Homer; at any rate, we are told of a recension of the poetry of Homer, the Recension of the Casket, as it is called, which Alexander, along with Callisthenes and Anaxarchus, perused and to a certain extent annotated, and then deposited in a richly wrought casket which he had found amongst the Persian treasures. Accordingly, it was due both to his zeal for the poet and to his descent from the Aeacidae who reigned as kings of the Molossians — where, as we are also told, Andromachê, who had been the wife of Hector, reigned as queen — that Alexander was kindly disposed towards the Ilians. But Caesar, not only being fond of Alexander, but also having better known evidences of kinship with the Ilians, felt encouraged to bestow kindness up them with all the zest of youth: better known evidences, first, because he was a Roman, and because the Romans believe Aeneias to have been their original founder; and secondly, because the name Iulius was derived from that of a certain Iulus who was one of his ancestors, and this Iulus got his appellation from the Iulus who was one of the descendants of Aeneas. Caesar therefore allotted territory to them and also helped them to preserve their freedom and their immunity from taxation; and to this day they remain in possession of these favours. But that this is not the site of the ancient Ilium, if one considers the matter in accordance with Homer's account, is inferred from the following considerations. But first I must give a general description of the region in question, beginning at that point on the coast where I left off.
(59After Abydus, then, comes the Dardanian Promontory, which I mentioned a little while ago,1 and also the city Dardanus, which is seventy stadia distant from Abydus. Between the two places empties the Rhodius River, opposite which, in the Chersonesus, is Cynos-Sema,2 which is said to be the tomb of Hecabê. But some say that the Rhodius empties into the Aesepus. This too is one of the rivers mentioned by the poet: "Rhesus, Heptaporus, Caresus, and Rhodius."3 Dardanus was an ancient settlement, but it was held in such contempt that it was oftentimes transplanted by some of the kings to Abydus and then resettled again by others on the ancient site. It was here that Cornelius Sulla, the Roman commander, and Mithridates surnamed Eupator met and arranged the terms for the conclusion of the war.
Near by is Ophrynium, near which, in a conspicuous place, is the sacred precinct of Hector. And next comes the Lake of Pteleos.
Then come Rhoeteium, a city situated on a hill, and, adjacent to Rhoeteium, a low‑lying shore, on which are a tomb and temple of Aias, and also a statue of him, which was taken up by Antony and carried off to Aegypt; but Augustus Caesar gave it back again to the Rhoeteians, just as he gave p61back other statues to their owners. For Antony took away the finest dedications from the most famous temples, to gratify the Egyptian woman, but Augustus gave them back to the gods.
After Rhoeteium come Sigeium, a destroyed city, and the Naval Station and the Harbour of the Achaeans and the Achaean Camp and Stomalimnê, as it is called, and the outlets of the Scamander; for after the Simoeis and the Scamander meet in the plain, they carry down great quantities of alluvium, silt up the coast, and form a blind mouth, lagoons, and marshes. Opposite the Sigeian Promontory on the Chersonesus are Eleussa and the temple of Protesilaüs, both of which I have mentioned in my description of Thrace.
The length of this coast, I mean on a straight voyage from Rhoeteium to Sigeium, and the monument of Achilles, is sixty stadia; and the whole of it lies below Ilium, not only the present Ilium, from which, at the Harbour of the Achaeans, it is about twelve stadia distant, but also the earlier Ilium, which lies thirty stadia farther inland in the direction of Mt. Ida. Now there are a temple and a monument of Achilles near Sigeium, as also monuments of Patroclus and Antilochus; and the Ilians offer sacrifices to all four heroes, both to these and to Aias. But they do not honour Heracles, giving as their reason his sacking of the city. But one might say that, although Heracles did sack it, yet he sacked it in such a way as still to leave it a city, even though damaged, for those who were later to sack it utterly; and for this reason the poet states it thus: "He sacked the city of Ilios and widowed her streets"; for "widowed" means a loss of the male population, not a complete annihilation. But the others, whom they think fit to worship with sacrifices and to honour as gods, completely annihilated the city. Perhaps they might give as their reason for this that these waged a just war, whereas Heracles waged an unjust one "on account of the horses of Laomedon." But writers set over against this reason the myth that it was not on account of the horses but of the reward offered for Hesionê and the sea‑monster. But let us disregard these reasons, for they end merely in controversies about myths. And perhaps we fail to notice certain more credible reasons why it occurred to the Ilians to honour some and not others. And it appears that the poet, in what he says about Heracles, represents the city as small, if it be true that "with only six ships and fewer men he sacked the city of Ilium." And it is clearly shown by this statement that Priam became great and king of kings from a small beginning, as I have said before. Advancing a little farther along this shore, one comes to the Achaeïum, where begins the part of the mainland that belongs to Tenedos.
Such are the places on the sea. Above these lies the Trojan Plain, which extends inland for many stadia in the direction of the east as far as Mt. Ida. The part of this plain alongside the mountain is narrow, extending on one side towards the south as far as the region of Scepsis, and on the other towards the north as far as the Lycians of Zeleia. This is the country which the poet makes subject to Aeneias and the sons of Antenor, calling it Dardania; and below this is Cebrenia, which is level for the most part and lies approximately parallel to Dardania; and in it there was once a city called Cebrenê. Demetrius suspects that the territory of Ilium subject to Hector extended inland from the naval station as far as Cebrenia, for he says that the tomb of Alexander is pointed out there, as also that of Oenonê, who, according to historians, had been the wife of Alexander before he carried off Helen. And, he continues, the poet mentions "Cebriones, bastard son of glorious Priam," after whom, as one may suppose, the country was named — or the city too, which is more plausible; and Cebrenia extends as far as the territory of Scepsis; and the Scamander, which flows between, is the boundary; and the Cebreni and Scepsians were always hostile to one another and at war until Antigonus settled both peoples together in Antigonia, as it was then called, or Alexandreia, as it is now called; now the Cebreni, he adds, remained with the rest in Alexandreia, but the Scepsians, by permission of Lysimachus, went back to their homeland.
From the mountain range of Ida in this region, according to Demetrius, two spurs extend to the sea, one straight to Rhoeteium and the other straight to Sigeium, forming together a semicircular line, and they end in the plain at the same distance from the sea as the present Ilium; this Ilium, accordingly, lies between the ends of the two spurs mentioned, whereas the old settlement lies between their beginnings; and, he adds, the spurs include both the Simoeisian Plain, through which the Simoeis runs, and the Scamandrian Plain, through which the Scamander flows. This is called the Trojan Plain in the special sense of the term; and here it is that the poet represents most of the fights as taking place, for it is wider; and here it is that we see pointed out the places named by the poet — Erineus, the tomb of Aesyetes, Batieia, and the monument of Ilus. The Scamander and Simoeis Rivers, after running near to Sigeium and Rhoeteium respectively, meet a little in front of the present Ilium, and then issue towards Sigeium and form Stomalimnê, as it is called. The two plains above mentioned are separated from each other by a great neck of land which runs in a straight line between the aforesaid spurs, starting from the present Ilium, with which it is connected, and stretches as far as Cebrenia and, along with the spurs on either side, forms a complete letter ϵ.
A little above this is the Village of the Ilians, where the ancient Ilium is thought to have been situated in earlier times, at a distance of thirty stadia from the present city. And ten stadia above the Village of the Ilians is Callicolonê, a hill, past which, at a distance of five stadia, flows the Simoeis.It therefore becomes easy to understand, first, the reference to Ares: "And over against her leaped Ares, like unto a dreadful whirlwind, in shrill tones cheering the Trojans from the topmost part of the city, and now again as he sped alongside Simoeis o'er Callicolonê"; for if the battle was fought on the Scamandrian Plain, it is plausible that Ares should at one time shout his cheers from the acropolis and at another from the region near the Simoeis and Callicolonê, up to which, in all probability, the battle would have extended. But since Callicolonê is forty stadia distant from the present Ilium, for what useful purpose would the poet have taken in places so far away that the line of battle could not reached them? Again, the words, "And towards Thymbra fell the lot of the Lycians," are more suitable to the ancient settlement, for the plain of Thymbra is near it, as also the Thymbrius River, which flows through the plain and empties into the Scamander at the temple of the Thymbraean Apollo, but Thymbra is actually fifty stadia distant from the present Ilium. And again, Erineus, a place that is rugged and full of wild fig trees, lies at the foot of the ancient site, so that Andromachê might appropriately say, "Stay thy host beside Erineus, where best the city can be approached and the wall scaled," but Erineus stands at a considerable distance from the present Ilium. Further, a little below Erineus is Phegus, in reference to which Achilles says, "But so long as I was carrying on war amid the Achaeans, Hector was unwilling to rouse battle away from the wall, but would come only as far as the Scaean Gates and Phegus."
However, the Naval Station, still now so called, is so near the present Ilium that one might reasonably wonder at the witlessness of the Greeks and the faint-heartedness of the Trojans; witlessness, if the Greeks kept the Naval Station unwalled for so long a time, when they were near to the city and to so great a multitude, both that in the city and that of the allies; for Homer says that the wall had only recently been built (or else it was not built at all, but fabricated and then abolished by the poet, as Aristotle says); and faint-heartedness, if the Trojans, when the wall was built, could besiege it and break into the Naval Station itself and attack the ships, yet did not have the courage to march up and besiege the station when it was still unwalled and only a slight distance away; for it is near Sigeium, and the Scamander empties near it, at a distance of only twenty stadia from Ilium. But if one shall say that the Harbour of Achaeans, as it is now called, is the Naval Station, he will be speaking of a place that is still closer, only about twelve stadia from the city, even if one includes the plain by the sea, because the whole of this plain is a deposit of the rivers — I mean the plain by the sea in front of the city; so that, if the distance between the sea and the city is now twelve stadia, it must have been no more than half as great at that time. Further, the feigned story told by Odysseus to Eumaeus clearly indicates that the distance from the Naval Station to the city is great, for after saying, "as when we led our ambush beneath the walls of Troy," he adds a little below, "for we went very far from the ships." And spies are sent forth to find whether the Trojans will stay by the ships "far away," far separated from their own walls, "or will withdraw again to the city." And Polydamas says, "on both sides, friends, bethink ye well, for I, on my own part, bid you now to go to the city; afar from the walls are we." Demetrius cites also Hestiaea of Alexandreia as a witness, a woman who wrote a work on Homer's Iliad and inquired whether the war took place round the present Ilium and the Trojan Plain, which latter the poet places between the city and the sea; for, she said, the plain now to be seen in front of the present Ilium is a later deposit of the rivers.
Again, Polites, "who was wont to sit as a sentinel of the Trojans, trusting in his fleetness of foot, on the topmost part of the barrow of aged Aesyetes," was doing a foolish thing, for even though he sat on the topmost part of it, still he might have kept watch from the much greater height of the acropolis, at approximately the same distance, with no need of fleetness of foot for safety; for the barrow of Aesyetes now pointed out is five stadia distant on the road to Alexandreia. Neither is the "clear running space" of Hector round the city easy to understand, for the present Ilium has no "clear running space," on account of the ridge that joins it. The ancient city, however, has a "clear running space" round it.
But no trace of the ancient city survives; and naturally so, for while the cities all round it were sacked, but not completely destroyed, yet that city was so utterly demolished that all the stones were taken from it to rebuild the others. At any rate, Archaeanax of Mitylenê is said to have built a wall round Sigeium with stones taken from there. Sigeium was seized by Athenians under Phrynon the Olympian victor, although the Lesbians laid claim to almost the whole of the Troad. Most of the settlements in the Troad belong, in fact, to the Lesbians, and some endure to this day, while others have disappeared. Pittacus of Mitylenê, one of the Seven Wise Men, as they are called, sailed against Phrynon the general and for a time carried on the war, but with poor management and ill consequences. It was at this time that the poet Alcaeus says that he himself, being sorely pressed in a certain battle, threw away his arms and fled. He addresses his story to a certain herald, whom he had bidden to report to the people at home that "Alcaeus is safe, but his arms have been hung up as an offering to Ares by the Attic army in the temple of Athena Glaucopis." But later, on being challenged to single combat by Phrynon, he took up his fishing tackle, ran to meet him, entangled him in his fishing net, and stabbed and slew him with trident and dagger. But since the war still went on, Periander was chosen by both sides as arbiter and ended it.
Demetrius says that Timaeus falsifies when he informs us that Periander fortified Achilleium against the Athenians with stones from Ilium, to help the army of Pittacus; for this place, he says, was indeed fortified by the Mitylenaeans against Sigeium, though not with such stones as those, nor yet by Periander. For how could the opponent of the Athenians have been chosen as arbiter? Achilleium is the place where stands the monument of Achilles and is only a small settlement. Sigeium, also, has been rased to the ground by the Ilians, because of its disobedience; for the whole of the coast as far as Dardanus was later subject to the Ilians and is now subject to them. In ancient times the most of it was subject to the Aeolians, so that Ephorus does not hesitate to apply the name Aeolis to the whole of the coast from Abydus to Cymê. Thucydides says that Troy was taken away from the Mitylenaeans by the Athenians in the Pachetian part of the Peloponnesian War.
The present Ilians further tell us that the city was, in fact, not completely wiped out at its capture by the Achaeans and that it was never even deserted. At any rate the Locrian maidens, beginning a little later, were sent every year. But this too is non‑Homeric, for Homer knows not of the violation of Cassandra, but he says that she was a maiden at about that time, "for he slew Othryoneus, a sojourner in Troy from Cabesus, who had but recently come, following after the rumour of war, and he was asking Cassandra in marriage, the comeliest of the daughters of Priam, without gifts of wooing," and yet he does not so much as mention any violation of her or say that the destruction of Aias in the shipwreck took place because of the wrath of Athena or any such cause; instead, he speaks of Aias as "hated by Athena," in accordance with her general hatred (for since they one and all committed sacrilege against her temple, she was angry at them all), but says that he was destroyed by Poseidon because of his boastful speech. But the fact is that the Locrian maidens were first sent when the Persians were already in power.
So the Ilians tell us, but Homer expressly states that the city was wiped out: "This day shall come when sacred Ilios shall perish"; and "surely we have utterly destroyed the steep city of Priam," "by means of counsels and persuasiveness"; "and in the tenth year the city of Priam was destroyed." And other such evidences of the same thing are set forth; for example, that the wooden image of Athena now to be seen stands upright, whereas Homer clearly indicates that it was sitting, for orders are given to "put" the robe "upon Athena's knees" (compare "that never should there sit upon his knees a dear child"). For it is better to interpret it in this way than, as some do, to interpret it as meaning "to put the robe 'beside' her knees," comparing the words "and she sits upon the hearth in the light of the fire," which they take to mean "beside" the hearth. For how could one conceive of the dedication of a robe "beside" the knees? Moreover, others, changing the accent on γούνασιν, accenting it γουνάσιν, like θυιάσιν (in whichever of two ways they interpret it), talk on endlessly. . . . There are to be seen many of the ancient wooden images of Athena in a sitting posture, as, for example, in Phocaea, Massalia, Rome, Chios, and several other places. Also the more recent writers agree that the city was wiped out, among whom is the orator Lycurgus, who, in mentioning the city of the Ilians, says: "Who has not heard that once for all it was rased to the ground by the Greeks, and is uninhabited?"
It is surmised that those who later thought of refounding the city regarded that site as ill‑omened, either on account of its misfortune or also because, in accordance with an ancient custom, a curse had been laid upon it by Agamemnon, just as Croesus, after he destroyed Sidenê, whither the tyrant Glaucias had fled for refuge, put a curse on any persons who should re‑fortify the site; and that they therefore avoided that place and fortified another. Now the Astypalaeans who held possession of Rhoeteium were the first to settle Polium, now called Polisma, on the Simoeis River, but not on a well-protected site; and therefore it was soon demolished. It was in the time of the Lydians that the present settlement was founded, as also the temple. It was not a city, however, and it was only after many ages, and gradually, as I have said, that it increased. But Hellanicus, to gratify the Ilians, "such is the spirit of that man," agrees with them that the present Ilium is the same as the ancient. When the city was wiped out, its territory was divided up between the inhabitants of Sigeium and Rhoeteium and several other neighbouring peoples, but the territory was given back when the place was refounded.
The epithet "many-fountained" is thought to be especially applied to Mt. Ida because of the great number of rivers that flow from it, particularly in those parts below it where lie the territory of Dardanus — even as far as Scepsis — and the region of Ilium. Demetrius, who as a native was acquainted with the topography of the country, says in one place as follows: There is a hill of Ida called Cotylus; and this hill lies about one hundred and twenty stadia above Scepsis; and from it flow the Scamander, the Granicus, and the Aesepus, the two latter flowing towards the north and the Propontis and constituting a collection of streams from several sources, while the Scamander flows towards the west from only one source; and all the sources lie close together, being comprised within a distance of twenty stadia; but the end of the Aesepus stands farthest away from its beginning, approximately five hundred stadia. But it is a matter of argument what the poet means when he says: "And they came to the two far‑flowing streams, where well up the two springs of eddying Scamander; for the one flows with soft water" (that is, with "hot water"), and the poet adds, "and round about a smoke arises from it as if from a blazing fire, whereas the other even in summer flows forth cold as hail or chill snow." But, in the first place, no hot waters are now to be found at the site, and, secondly, the source of the Scamander is not to be found there, but in the mountain; and it has only one source, not two. It is reasonable to suppose, therefore, that the hot spring has given out, and that the cold one is evacuated from the Scamander through an underground passage and rises to the surface here, or else that because of the nearness of the Scamander this water is called a source of the Scamander; for people are wont to ascribe several sources to one and the same river in this way.
The Scamander is joined by the Andirus, which flows from Caresenê, a mountainous country settled with many villages and beautifully cultivated; it extends alongside Dardania as far as the regions of Zeleia and Pityeia. It is said that the country was named after the Caresus River, which is named by the poet, "Rhesus, Heptaporus, Caresus, and Rhodius," and that the city of the same name as the river was torn down. Again, Demetrius says as follows: "The Rhesus River is now called Rhoeites, unless it be that the river which empties into the Granicus is the Rhesus. The Heptaporus, also called Polyporus, is crossed seven times by one travelling from the region of the Beautiful Pine to the village called Melaenae and the Asclepieium that was founded by Lysimachus. Concerning the Beautiful Pine, King Attalus the First writes as follows: "Its circumference is twenty-four feet; and its trunk rises to a height of sixty-seven feet from the root and then splits into three forks equidistant from one another, and then contracts again into one head, thus completing a total height of two plethra and fifteen cubits." It is one hundred and eighty stadia distant from Adramyttium, to the north of it. The Caresus flows from Malus, a place situated between Palaescepsis and the Achaeïum, the part of the mainland that belongs to the Tenedians; and it empties into the Aesepus. The Rhodius flows from Cleandria and Gordus, which are sixty stadia distant from the Beautiful Pine; and it empties into the Aenius.
In the dale of the Aesepus, on the left of the stream, one comes first to Polichna, a place enclosed by walls; and then to Palaescepsis; and then to Alizonium (this last name having been fabricatedto support the hypothesis about the Halizones, whom I have already discussed); and then to Caresus, which is deserted, and Caresenê, and the river of the same name, which also forms a notable dale, though smaller than that of the Aesepus; and next follow the plains and plateaux of Zeleia, which are beautifully cultivated. On the right of the Aesepus, between Polichna and Palaescepsis, one comes to Nea Comê and Argyria, and this again is a name fabricated to support the same hypothesis, in order to save the words, "where is the birthplace of silver." Now where is Alybê, or Alopê, or however they wish to alter the spelling of the name? For having once made their bold venture, they should have rubbed their faces and fabricated this name too, instead of leaving it lame and readily subject to detection. Now these things are open to objections of this kind, but, in the case of the others, or at least most of them, I take it for granted that we must give heed to him as a man who was acquainted with the region and a native of it, who gave enough thought to this subject to write thirty books of commentary on a little more than sixty lines of Homer, that is, on the Catalogue of the Trojans. He says, at any rate, that Palaescepsis is fifty stadia distant from Aenea and thirty from the Aesepus River, and that from this Palaescepsis the same name was extended to several other sites. But I shall return to the coast at the point where I left off. |
|
|
|
|
13 - 2 Lesbos and its minor islands 
Since Lesbos, an island worthy of a full account, lies alongside and opposite the coast which extends from Lectum to Canae, and also has small islands lying round it, some others it and some between it and the mainland, it is now time to describe these; for these are Aeolian, and I might almost say that Lesbos is the metropolis of the Aeolian cities. But I must begin at the point whence I began to traverse the coast that lies opposite the island.
2 Now as one sails from Lectum to Assus, the Lesbian country begins at Sigrium, its promontory on the north. In this general neighbourhood is also Methymna, a city of the Lesbians, sixty stadia distant from the coast that stretches from Polymedium to Assus. But while the perimeter which is filled out by the island as a whole is eleven hundred stadia, the several distances are as follows: From Methymna to Malia, the southernmost promontory to one keeping the island on the right, I mean at the point where Canae lies most directly opposite the island and precisely corresponds with it, the distance is three hundred and forty stadia; thence to Sigrium, which is the length of the island, five hundred and sixty; and then to Methymna, two hundred and ten. Mitylene, the largest city, lies between Methymna and Malia, being seventy stadia distant from Malia, one hundred and twenty from Canae, and the same distance from the Arginussae, which are three small islands lying near the mainland along Canae. In the interval between Mitylene and Methymna, in the neighbourhood of a village called Aegeirus in the Methymnaean territory, the island is narrowest, with a passage of only twenty stadia over to the Euripus of the Pyrrhaeans. Pyrrha is situated on the western side of Lesbos at a distance of one hundred stadia from Malia. Mitylene has two harbours, of which the southern can be closed and holds only fifty triremes, but the northern is large and deep, and is sheltered by a mole. Off both lies a small island, which contains a part of the city that is settled there. And the city is well equipped with everything.
3 Mitylene has produced famous men: in early times, Pittacus, one of the Seven Wise Men; and the poet Alcaeus, and his brother Antimenidas, who, according to Alcaeus, won a great struggle when fighting on the side of the Babylonians, and rescued them from their toils by killing "a warrior, the royal wrestler" (as he says), "who was but one short of five cubits in height." And along with these flourished also Sappho, a marvellous woman; for in all the time of which we have record I do not know of the appearance of any woman who could rival Sappho, even in a slight degree, in the matter of poetry. The city was in those times ruled over by several tyrants because of the dissensions among the inhabitants; and these dissensions are the subject of the Stasiotic poems, as they are called, of Alcaeus. And also Pittacus6 was one of the tyrants. Now Alcaeus would rail alike at both Pittacus and the rest, Myrsilus and Melanchrus and the Cleanactidae and certain others, though even he himself was not innocent of revolutionary attempts; but even Pittacus himself used monarchy for the overthrow of the oligarchs, and then, after overthrowing them, restored to the city its independence. Diophanes the rhetorician was born much later; but Potamon, Lesbocles, Crinagoras, and Theophanes the historian in my time. Theophanes was also a statesman; and he became a friend to Pompey the Great, mostly through his very ability, and helped him to succeed in all his achievements; whence he not only adorned his native land, partly through Pompey and partly through himself, but also rendered himself the most illustrious of all the Greeks. He left a son, Marcus Pompey, whom Augustus Caesar once set up as Procurator of Asia, and who is now counted among the first of the friends of Tiberius. The Athenians were in danger of suffering an irreparable disgrace when they voted that all Mitylenaeans from youth upwards should be slain, but they changed their minds and their counter-decree reached the generals only one day before the order was to be executed.
4 Pyrrha has been rased to the ground, but its suburb is inhabited and has a harbour, whence there is a passage of eighty stadia over hills to Mitylene. Then, after Pyrrha, one comes to Eressus; it is situated on a hill and extends down to the sea. Then to Sigrium, twenty-eight stadia from Eressus. Both Theophrastus and Phanias, the peripatetic philosophers, disciples of Aristotle, were from Eressus. Theophrastus was at first called Tyrtamus, but Aristotle changed his name to Theophrastus, at the same time avoiding the cacophony of his former name and signifying the fervour of his speech; for Aristotle made all his pupils eloquent, but Theophrastus most eloquent of all. Antissa, a city with a harbour, comes next in order after Sigrium. And then Methymna, whence came Arion, who, according to a myth told by Herodotus and his followers, safely escaped on a dolphin to Taenarum after being thrown into the sea by the pirates. Now Arion played, and sang to, the cithara; and Terpander, also, is said to have been an artist in the same music and to have been born in the same island, having been the first person to use the seven-stringed instead of the four-stringed lyre, as we are told in the verses attributed to him: "For thee I, having dismissed four-toned song, shall sing new hymns to the tune of a seven-stringed cithara." Also Hellanicus the historian, and Callias, who interpreted Sappho and Alcaeus, were Lesbians.
5 In the strait between Asia and Lesbos there are about twenty small islands, but according to Timosthenes, forty. They are called Hecatonnesi, a compound name like Peloponnesus, the second letter n being customarily redundant in such compounds, as in the names Myonnesus, Proconnesus, and Halonnesus; and consequently we have Hecatonnesi, which means Apollonnesi, for Apollo is called Hecatus; for along the whole of this coast, as far as Tenedos, Apollo is highly honoured, being called Sminthian or Grynian or some other appellation. Near these islands is Pordoselenê, which contains a city of the same name, 6and also, in front of this city, another island, larger and of the same name, which is uninhabited and has a temple sacred to Apollo.
6 Some writers, to avoid the indecency of the names, say that in this place we should read "Poroselenê," and that we should call Aspordenum, the rocky and barren mountain round Pergamum, "Asporenum," and the temple of the Mother of the gods there the temple of the "Asporene" mother. What, then, shall we say of Pordalis and Saperdes and Perdiccas, and of the phrase of Simonides, "banished, 'pordacian' clothes and all," instead of "wet" clothes, and, somewhere in the early comedy, "the place is 'pordacian,' " that is, the place that is "marshy"? Lesbos is equidistant from Tenedos and Lemnos and Chios, one might say rather less than five hundred stadia. |
|
|
|
|
13 - 3 Aeolian cities 
1 Since the Leleges and the Cilicians were so closely related to the Trojans, people inquire for the reason why they are not included with the Trojans in the Catalogue. But it is reasonable to suppose that because of the loss of their leaders and the sacking of their cities the few Cilicians that were left were placed under the command of Hector, for both Eëtion and his sons are said to have been slain before the Catalogue:1 "Verily my father was slain by the goodly Achilles, who utterly sacked the city of Cilicians, Thebê of the lofty gates. And the seven brothers of mine in our halls, all these on the same day went inside the home of Hades, for all were slain by swift-footed, goodly Achilles." And so, in the same way, those subject to Mynes lost both their leaders and their city: "And he laid low Mynes and Epistrophus, and sacked the city of godlike Mynes." But he makes the Leleges present at the battles when he says as follows: "Towards the sea are situated the Carians and the Paeonians, with curved bows, and the Leleges and Caucones." And again, "he pierced with his spear Satnius, son of Oenops, whom a noble Naiad nymph bore to Oenops, as he tended his herds besides the banks of the Satnioeis"; for they had not so completely disappeared that they did not have a separate organisation of their own, since their king still survived, "of Altes, who is lord over the war‑loving Leleges," and since their city had not been utterly wiped out, for the poet adds, "who holds steep Pedasus on the Satnioeis." However, the poet has omitted them in the Catalogue, not considering their organisation sufficient to have a place in it, or else including them under the command of Hector because they were so closely related; for Lycaon, who was a brother of Hector, says, "to a short span of life my mother, daughter of the old man Altes, bore me — Altes who is lord over the war‑loving Leleges." Such, then, are the probabilities in this matter.
2 And it is also a matter of reasoning from probabilities if one inquires as to the exact bounds to which the poet means that the Cilicians extended, and the Pelasgians, and also the Ceteians, as they are called, under the command of Eurypylus, who lived between these two peoples. Now as for the Cilicians and the peoples under the command of Eurypylus, all has been said about them that can be said, and that their country is in a general way bounded by the region of the Caïcus River. As for the Pelasgians, it is reasonable, both from the words of Homer and from history in general, to place them next in order after these peoples; for Homer says as follows: "And Hippothoüs led the tribes of the Pelasgians that rage with the spear, them that dwelt in fertile Larisa; these were ruled by Hippothoüs and Pylaeus, scion of Ares, the two sons of Pelasgian Lethus, son of Teutamus." By these words he clearly indicates that the number of Pelasgians was considerable, for he says "tribes," not "tribe"; and he also specifies their abode as "in Larisa." Now there are many Larisas, but we must interpret him as meaning one of those that were near; and best of all one might rightly assume the one in the neighbourhood of Cymê; for of the three Larisas the one near Hamaxitus was in plain sight of Ilium and very near it, within a distance of two hundred stadia, and therefore it could not be said with plausibility that Hippothoüs fell in the fight over Patroclus "far away from" this "Larisa," but rather from the Larisa near Cymê, for the distance between the two is about a thousand stadia. The third Larisa is a village in the territory of Ephesus in the Caÿster Plain; it is said to have been a city in earlier times, containing a temple of Larisaean Apollo and being situated closer to Mt. Tmolus than to Ephesus. It is one hundred and eighty stadia distant from Ephesus, and might therefore be placed under the Maeonians. But the Ephesians, having grown in power, later cut off for themselves much of the territory of the Maeonians, whom we now call Lydians, so that this could not be the Larisa of the Pelasgians either, but rather the one near Cymê. In fact we have no strong evidence that the Larisa in the Caÿster Plain was already in existence at that time, for we have no such evidence as to Ephesus either; but all Aeolian history, which arose but shortly after the Trojan times, bears testimony to the existence of the Larisa near Cymê.
3 For it is said that the people who set out from Phricium, the Locrian mountain above Thermopylae, put in at the place where Cymê now is, and finding the Pelasgians in bad plight because of the Trojan War, though still in possession of Larisa, which was about seventy stadia distant from Cymê, built on their frontier what is still called Neon Teichos, thirty stadia from Larisa, and that, having captured Larisa, they founded Cymê and settled there the survivors. And Cymê is called Cymê Phriconis after the Locrian mountain; and likewise Larisa is called Larisa Phriconis; but Larisa is now deserted. That the Pelasgians were a great tribe is said also to be the testimony of history in general; Menecrates of Elaea, at any rate, in his work On the Founding of Cities, says that the whole of what is now the Ionian coast, beginning at Mycalê, as also the neighbouring islands, were in earlier times inhabited by Pelasgians. But the Lesbians say that their people were placed under the command of Pylaeus, the man whom the poet calls the ruler of the Pelasgians, and that it is from him that the mountain in their country is still called Pylaeus. The Chians, also, say that the Pelasgians from Thessaly were their founders. But the Pelasgian race, ever wandering and quick to migrate, greatly increased and then rapidly disappeared, particularly at the time of the migration of the Aeolians and Ionians to Asia.
4 A peculiar thing happened in the case of the Larisaeans, I mean the Caÿstrian and the Phryconian Larisaeans and, third, those in Thessaly: they all held land that was deposited by rivers, by the Caÿster and by the Hermus and by the Peneius. It is at the Phryconian Larisa at the Piasus is said to have been honoured, who, they say, was ruler of the Pelasgians and fell in love with his daughter Larisa, and, having violated her, paid the penalty for the outrage; for, observing him leaning over a cask of wine, they say, she seized him by the legs, raised him, and plunged him into the cask. Such are the ancient accounts.
5 To the present Aeolian cities we must add Aegae, and also Temnus, the birthplace of Hermagoras, who wrote The Art of Rhetoric. These cities are situated in the mountainous country that lies above the territory of Cymê and that of the Phocians and that of the Smyrnaeans, along which flows the Hermus. Neither is Magnesia, which is situated below Mt. Sipylus and has been adjudged a free city by the Romans, far from these cities. This city too has been damaged by the recent earthquakes. To the opposite parts, which incline towards the Caïcus, from Larisa across the Hermus to Cymê, the distance is seventy stadia; thence to Myrina, forty stadia; thence to Grynium, the same; and from there to Elaea. But, according to Artemidorus, one goes from Cymê to Adae, and then, forty stadia distant, to a promontory called Hydra, which with the opposite promontory Harmatus forms the Elaïtic Gulf. Now the width of the mouth of this gulf is about eighty stadia, but, including the sinuosities of the gulf, Myrina, an Aeolian city with a harbour, is at a distance of sixty stadia; and then one comes to the Harbour of the Achaeans, where are the altars of the twelve gods; and then to a town Grynium and an altar of Apollo and an ancient oracle and a costly shrine of white marble, to which the distance is forty stadia; and then seventy stadia to Elaea, with harbour and naval station belonging to the Attalic kings, which was founded by Menestheus and the Athenians who took the expedition with him to Ilium. I have already spoken of the places that come next, those about Pitanê and Atarneus and the others in that region.
6 The largest and best of the Aeolian cities is Cymê; and this with Lesbos might be called the metropolis of the rest of the cities, about thirty in number, of which not a few have disappeared. Cymê is ridiculed for its stupidity, owing to the repute, as some say, that not until three hundred years after the founding of the city did they sell the tolls of the harbour, and that before this time the people did not reap this revenue. They got the reputation, therefore, of being a people who learned late that they were living in a city by the sea. There is also another report of them, that, having borrowed money in the name of the state, they pledged their porticoes as security, and then, failing to pay the money on the appointed day, were prohibited from walking in them; when it rained, however, their creditors, through a kind of shame, would bid them through a herald to go under the porticoes; so the herald would cry out the words, "Go under the porticoes," but the report went abroad that the Cymaeans did not understand that they were to go under the porticoes when it rained unless they were given notice by the herald. Ephorus, a man indisputably noteworthy, a disciple of Isocrates the orator, and the author of the History and of the work on Inventions, was from this city; and so was Hesiod the poet, still earlier than Ephorus, for Hesiod himself states that his father Dius left Aeolian Cymê and migrated to Boeotia: "And he settled near Helicon in a wretched village, Ascrê, which is bad in winter, oppressive in summer, and pleasant at no time." But it is not agreed that Homer was from Cymê, for many peoples lay claim to him. It is agreed, however, that the name of the city was derived from an Amazon, as was Myrina from the Amazon who lies in the Trojan plain below Batieia, "which verily men call Batieia, but the immortals the tomb of much-bounding Myrina." Ephorus, too, is ridiculed because, though unable to tell of deeds of his native land in his enumeration of the other achievements in history, and yet unwilling that it should be unmentioned, he exclaims as follows: "At about the same time the Cymaeans were at peace."
Since I have traversed at the same time the Trojan and Aeolian coasts, it would be next in order to treat cursorily the interior as far as the Taurus, observing the same order of approach. |
|
|
|
|
13 - 4 Pergamum, Sardis, Catacecaumene, Hierapolis 
A kind of hegemony is held over these places by Pergamum, which is a famous city and for a long time prospered along with the Attalic kings; indeed I must begin my next description here, and first I must show briefly the origin of the kings and the end to which they came. Now Pergamum was a treasure-hold of Lysimachus, the son of Agathocles, who was one of the successors of Alexander, and its people are settled on the very summit of the mountain; the mountain is cone-like and ends in a sharp peak. The custody of this stronghold and the treasure, which amounted to nine thousand talents, was entrusted to Philetaerus of Tieium, who was a eunuch from boyhood; for it came to pass at a certain burial, when a spectacle was being given at which many people were present, that the nurse who was carrying Philetaerus, still an infant, was caught in the crowd and pressed so hard that the child was incapacitated. He was a eunuch, therefore, but he was well trained and proved worthy of this trust. Now for a time he continued loyal to Lysimachus, but he had differences with Arsinoê, the wife of Lysimachus, who slandered him, and so he caused Pergamum to revolt, and governed it to suit the occasion, since he saw that it was ripe for a change; for Lysimachus, beset with domestic troubles, was forced to slay his son Agathocles, and Seleucus Nicator invaded his country and overthrew him, and then he himself was overthrown and treacherously murdered by Ptolemy Ceraunus. During these disorders the eunuch continued to be in charge of the fortress and to manage things through promises and courtesies in general, always catering to any man who was powerful or near at hand. At any rate, he continued lord of the stronghold and the treasure for twenty years.
He had two brothers, the elder of whom was Eumenes, the younger Attalus. Eumenes had a son of the same name, who succeeded to the rule of Pergamum, and was by this time sovereign of the places round about, so that he even joined battle with Antiochus the son of Seleucus near Sardeis and conquered him. He died after a reign of twenty‑two years. Attalus, the son of Attalus and Antiochis, daughter of Achaeus, succeeded to the throne and was the first to be proclaimed king, after conquering the Galatians in a great battle. Attalus not only became a friend of the Romans but also fought on their side against Philip along with the fleet of the Rhodians. He died in old age, having reigned as king forty-three years; and he left four sons by Apollonis, a woman from Cyzicus, Eumenes, Attalus, Philetaerus, and Athenaeus. Now the two younger sons remained private citizens, but Eumenes, the elder of the other two, reigned as king. Eumenes fought on the side of the Romans against Antiochus the Great and against Perseus, and he received from the Romans all the country this side the Taurus that had been subject to Antiochus. But before that time the territory of Pergamum did not include many places that extended as far as the sea at the Elaïtic and Adramyttene Gulfs. He built up the city and planted Nicephorium with a grove, and the other elder brother, from love of splendour, added sacred buildings and libraries and raised the settlement of Pergamum to what it now is. After a reign of forty-nine years Eumenes left his empire to Attalus, his son by Stratonicê, the daughter of Ariathres, king of the Cappadocians. He appointed his brother Attalus as guardian both of his son, who was extremely young, and of the empire. After a reign of twenty‑one years,6 his brother died an old man, having won success in many undertakings; for example, he helped Alexander, the son of Antiochus, to defeat in war Demetrius, the son of Seleucus, and he fought on the side of the Romans against the Pseudo-Philip, and in an expedition against Thrace he defeated Diegylis the king of the Caeni, and he slew Prusias, having incited his son Nicomedes against him, and he left his empire, under a guardian, to Attalus. Attalus, surnamed Philometor, reigned five years, died of disease, and left the Romans his heirs. The Romans proclaimed the country a province, calling it Asia, by the same name as the continent. The Caïcus flows past Pergamum, through the Caïcus Plain, as it is called, traversing land that is very fertile and about the best in Mysia.
Pergamenians have become famous in my time: Mithridates the son of Menodotus and of Adobogion. Menodotus was of the family of the tetrarchs of the Galatians, and Adobogion, it is said, was also the concubine of King Mithridates, and for this reason her relatives gave to the child the name of Mithridates, pretending that he was the son of the king. At any rate, he became a friend to the deified Caesar and reached so great preferment with him that he was appointed tetrarch from his mother's family and king both of the Bosporus and other territories. He was overthrown by Asander, who not only slew King Pharnaces but also took possession of the Bosporus. Mithridates, then, has been thought worthy of a great name, as has also Apollodorus the rhetorician, who wrote the work on Rhetoric and was the leader of the Apollodoreian sect, whatever in the world it is; for numerous philosophies were prevalent, but to pass judgment upon them is beyond my power, and among these are the sects of Apollodorus and Theodorus. But the friendship of Caesar Augustus has most of all exalted Apollodorus, who was his teacher in the art of speech. And Apollodorus had a notable pupil in Dionysius, surnamed Atticus, his fellow-citizen, for he was an able sophist and historian and speech-writer.
4 As one proceeds from the plain and the city towards the east, one comes to a city called Apollonia, which lies on an elevated site, and also, towards the south, to a mountain range, and also, towards the south, to a mountain range, on crossing which, on the road to Sardeis, one comes to Thyateira, on the left-hand side, a settlement of the Macedonians, which by some is called the farthermost city of the Mysians. On the right is Apollonis, which is three hundred stadia distant from Pergamum, and the same distance from Sardeis, and it is named after the Cyzicene Apollonis. Next one comes to the plain of Hermus and to Sardeis. The country to the north of Pergamum is held for the most part by the Mysians, I mean the country on the right of the Abaeïtae, as they are called, on the borders of which is the Epictetus as far as Bithynia.
5 Sardeis is a great city, and, though of later date than the Trojan times, is nevertheless old, and has a strong citadel. It was the royal city of the Lydians, whom the poet calls Meïonians; and later writers call them Maeonians, some identifying them with the Lydians, and others representing them as different, but it is better to call them the same people. Above Sardeis is situated Mt. Tmolus, a blest mountain, with a look‑out on its summit, an arcade of white marble, a work of the Persians, whence there is a view of the plains below all round, particularly the Caÿster Plain. And round it dwell Lydians and Mysians and Macedonians. The Pactolus River flows from Mt. Tmolus; in early times a large quantity of gold-dust was brought down in it, whence, it is said, arose the fame of the riches of Croesus and his forefathers. But the gold-dust has given out. The Pactolus runs down into the Hermus, into which also the Hyllus, now called the Phrygius, empties. These three, and other less significant rivers with them, meet and empty into the sea near Phocaea, as Herodotus says. The Hermus rises in Mysia, in the sacred mountain Dindymenê, and flows through the Catacecaumene country into the territory of Sardeis and the contiguous plains, as I have already said, to the sea. Below the city lie the plain of Sardeis and that of the Cyrus and that of the Hermus and that of the Caÿster, which are contiguous to one another and are the best of all plains. Within forty stadia from the city one comes to Gygaea, which is mentioned by the poet, the name of which was later changed to Coloê, where is the temple of Coloënian Artemis, which is characterised by great holiness. They say that at the festivals here the baskets dance, though I do not know why in the world they talk marvels rather than tell the truth.
6 The verses of Homer are about as follows: "Mnesthles and Antiphus, the two sons of Talaemenes, whose mother was Lake Gygaea, who led also the Meïonians, who were born at the foot of Tmolus"; but some add the following fourth verse: "At the foot of snowy Tmolus, in the first land of Hydê." But there is no Hydê to be found in the country of the Lydians.a Some also put Tychius there, of whom the poet says, "far the best of workers in hide, who lived in Hydê." And they add that the place is woody and subject to strokes of lightning, and that the Arimi live there, for after Homer's verse, "in the land of the Arimi where men say is the couch of Typhon," they insert the words, "in a wooded place, in the fertile land of Hydê." But others lay the scene of this myth in Cilicia, and some lay it in Syria, and still others in the Pithecussae Islands, who say that among the Tyrrhenians "pitheci" are called "arimi." Some call Sardeis Hydê, while others call its acropolis Hydê. But the Scepsian thinks that those writers are most plausible who place the Arimi in the Catacecaumene country in Mysia. But Pindar associates the Pithecussae which lie off the Cymaean territory, as also the territory in Sicily, with the territory in Cilicia, for he says that Typhon lies beneath Aetna: "Once he dwelt in a far‑famed Cilician cavern; now, however, his shaggy breast is o'er‑pressed by the sea‑girt shores above Cymae and by Sicily." And again, "round about him lies Aetna with her haughty fetters," and again, "but it was father Zeus that once amongst the Arimi, by necessity, alone of the gods, smote monstrous Typhon of the fifty heads." But some understand that the Syrians are Arimi, who are now called the Arimaeans, and that the Cilicians in Troy, forced to migrate, settled again in Syria and cut off for themselves from Syria what is now called Cilicia. Callisthenes says that the Arimi, after whom the neighbouring mountains are called Arima, are situated near Mt. Calycadnus and the promontory of Sarpedon near the Corycian cave itself.
7 Near Lake Coloê are the monuments of the kings. At Sardeis is the great mound, on a lofty base, of Alyattes, built, as Herodotus says, by the common people of the city, most of the work on which was done by prostitutes; and he says that all women of that country prostituted themselves; and some call the tomb of Alyattes a monument of prostitution. Some report that Lake Coloê is an artificial lake, made to receive the overflows which take place when the rivers are full. Hypaepa is a city which one comes to on the descent from Mt. Tmolus to the Caÿster Plain.
8 Callisthenes says that Sardeis was captured first by the Cimmerians, and then by the Treres and the Lycians, as is set forth by Callinus the elegiac poet, and lastly in the time of Cyrus and Croesus. But when Callinus says that the incursion of the Cimmerians was against the Esioneis, at the time of which Sardeis was captured, the Scepsian and his followers surmise that the Asioneis were by Callinus called the Esioneis, in the Ionic dialect; for perhaps Meïonia, he says, was called Asia, and accordingly him likewise says, "on the Asian mead about the streams of the Caÿster." The city was later restored in a notable way because of the fertility of its territory, and was inferior to none of its neighbours, though recently it has lost many of its buildings through earthquakes. However, the forethought of Tiberius, our present ruler, has, by his beneficence, restored not only this city but many others — I mean all the cities that shared in the same misfortune at about the same time.
9 Notable men of the same family were born at Sardeis: the two Diodoruses, the orators, of whom the elder was called Zonas, a man who many times pleaded the cause of Asia; and at the time of the attack of King Mithridates, he was accused of trying to cause the cities to revolt from him, but in his defence he acquitted himself of the slander. The younger Diodorus, who was a friend of mine, is the author, not only of historical treatises, but also of melic and other poems, which display full well the ancient style of writing. Xanthus, the ancient historian, is indeed called a Lydian, but whether or not he was from Sardeis I do not know.
After the Lydians come the Mysians; and the city Philadelphia, ever subject to earthquakes. Incessantly the walls of the houses are cracked, different parts of the city being thus affected at different times. For this reason few people live in the city, and most of them spend their lives as farmers in the country, since they have a fertile soil. Yet one may be surprised at the few, that they are so fond of the place when their dwellings so insecure; and one might marvel still more at those who founded the city.
After this region one comes to the Catacecaumene country, as it is called, which has a length of five hundred stadia and a breadth of four hundred, whether it should be called Mysia or Meïonia (for both names are used); the whole of it is without trees except the vine that produces the Catacecaumenite wine, which in quality is inferior to none of the notable wines. The surface of the plains are covered with ashes, and the mountainous and rocky country is black, as though from conflagration. Now some conjecture that this resulted from thunderbolts and from fiery subterranean outbursts, and they do not hesitate to lay there the scene of the mythical story of Typhon; and Xanthus adds that a certain Arimus was king of this region; but it is not reasonable to suppose that all that country was burnt all at once by reason of such disturbances, but rather by reason of an earth-born fire, the sources of which have now been exhausted. Three pits are to be seen there, which are called "bellows," and they are about forty stadia distant from each other. About them lie rugged hills, which are reasonably supposed to have been heaped up by the hot masses blown forth from the earth. That such soil should be well adapted to the vine one might assume from the land of Catana, which was heaped with ashes and now produces excellent wine in great plenty. Some writers, judging from places like this, wittily remark that there is good reason for calling Dionysus "Pyrigenes."
The parts situated next to this region towards the south as far as the Taurus are so inwoven with one another that the Phrygian and the Carian and the Lydian parts, as also those of the Mysians, since they merge into one another, are hard to distinguish. To this confusion no little has been contributed by the fact that the Romans did not divide them according to tribes, but in another way organised their jurisdictions, within which they hold their popular assemblies and their courts. Mt. Tmolus is a quite contracted mass of mountain and has only a moderate circumference, its limits lying within the territory of the Lydians themselves; but the Mesogis extends in the opposite direction as far as Mycalê, beginning at Celaenae, according to Theopompus. And therefore some parts of it are occupied by the Phrygians, I mean the parts near Celaenae and Apameia, and other parts by Mysians and Lydians, and other parts by Carians and Ionians. So, also, the rivers, particularly the Maeander, form the boundary between some of the tribes, but in cases where they flow through the middle of countries they make accurate distinction difficult. And the same is to be said of the plains that are situated on either side of the mountainous territory and of the river-land. Neither should I, perhaps, attend to such matters as closely as a surveyor must, but sketch them only so far as they have been transmitted by my predecessors.
Contiguous on the east to the Caÿster Plain, which lies between the Mesogis and the Tmolus, is the Cilbian Plain. It is extensive and well settled and has a fertile soil. Then comes the Hyrcanian Plain, a name given it by the Persians, who brought Hyrcanian colonists there (the Plain of Cyrus, likewise, was given its name by the Persians). Then come the Peltine Plain (we are now in Phrygian territory) and the Cillanian and the Tabene Plains, which have towns with a mixed population of Phrygians, these towns also containing a Pisidian element; and it is after these that the plains themselves were named.
When one crosses over the Mesogis, between the Carians and the territory of Nysa, which latter is a country on the far side of the Maeander extending to Cibyratis and Cabalis, one comes to certain cities. First, near the Mesogis, opposite Laodiceia, to Hierapolis, where are the hot springs and the Plutonium, both of which have something marvellous about them; for the water of the springs so easily congeals and changes into stone that people conduct streams of it through ditches and thus make stone fencesconsisting of single stones, while the Plutonium, below a small brow of the mountainous country that lies above it, is an opening of only moderate size, large enough to admit a man, but it reaches a considerable depth, and it is enclosed by a quadrilateral handrail, about half a plethrum in circumference, and this space is full of a vapour so misty and dense that one can scarcely see the ground. Now to those who approach the handrail anywhere round the enclosure the air is harmless, since the outside is free from that vapour in calm weather, but any animal that passes inside meets instant death. At any rate, bulls that are led into it fall and are dragged out dead; and I threw in sparrows and they immediately breathed their last and fell. But the Galli, who are eunuchs, pass inside with such impunity that that they even approach the opening, bend over it, and descend into it to a certain depth, though they hold their breath as much as they can (for I could see in their countenances an indication of a kind of suffocating attack, as it were), — whether this immunity belongs to all who are maimed in this way or only to those round the temple, or whether it is because of divine providence, as would be likely in the case of divine obsessions, or whether it is the result of certain physical powers that are antidotes against the vapour. The changing of water into stone is said also to be the case with the rivers in Laodiceia, although their water is potable. The water at Hierapolis is remarkably adapted also to the dyeing of wool, so that wool dyed with the roots rivals that dyed with the coccus or with the marine purple. And the supply of water is so abundant that the city is full of natural baths.
After Hierapolis one comes to the parts on the far side of the Maeander; I have already described those round Laodiceia and Aphrodisias and those extending as far as Carura. The next thereafter are the parts towards the west, I mean the city of the Antiocheians on the Maeander, where one finds himself already in Caria, and also the parts towards the south, I mean Greater Cibyra and Sinda and Cabalis, extending as far as the Taurus and Lycia. Now Antiocheia is a city of moderate size, and is situated on the Maeander itself in the region that lies near Phrygia, and there is a bridge over the river. Antiocheia has considerable territory on each side of the river, which is everywhere fertile, and it produces in greatest quantities the "Antiocheian" fig, as it is called, though they also name the same fig "three-leaved." This region, too, is much subject to earthquakes. Among these people arose a famous sophist, Diotrephes, whose complete course was taken by Hybreas,b who became the greatest orator of my time.
The Cabaleis are said to be the Solymi; at any rate, the hill that lies above the fortress of the Termessians is called Solymus, and the Termessians themselves are called Solymi. Near by is the Palisade of Bellerophon, and also the tomb of his son Peisander, who fell in the battle against the Solymi. This account agrees also with the words of the poet, for he says of Bellerophon, "next he fought with the glorious Solymi," and of his son, "and Peisander his son was slain by Ares, insatiate of war, when he was fighting with the Solymi." Termessus is a Pisidian city, which lies directly above Cibyra and very near it.
It is said that the Cibyratae are descendants of the Lydians who took possession of Cabalis, and later of the neighbouring Pisidians, who settled there and transferred the city to another site, a site very strongly fortified and about one hundred stadia in circuit. It grew strong through its good laws; and its villages extended alongside it from Pisidia and the neighbouring Milyas as far as Lycia and the Peraea of the Rhodians. Three bordering cities were added to it, Bubon, Balbura, and Oenoanda, and the union was called Tetrapolis, each of the three having one vote, but Cibyra two; for Cibyra could send forth thirty thousand foot-soldiers and two thousand horse. It was always ruled by tyrants; but still they ruled it with moderation. However, the tyranny ended in the time of Moagetes, when Murena overthrew it and included Balbura and Bubon within the territory of the Lycians. But none the less the jurisdiction of Cibyra is rated among the greatest in Asia. The Cibyratae used four languages, the Pisidian, that of the Solymi, Greek, and that of the Lydians; but there is not even a trace of the language of the Lydians in Lydia. The easy embossing of iron is a peculiar thing at Cibyra. Milya is the mountain-range extending from the narrows at Termessus and from the pass that leads over through them to the region inside the Taurus towards Isinda, as far as Sagalassus and the country of the Apameians. |
|
|
|
|
14 Islands. 6 101 1:23 
|
14 - 1 Ionia 
It remains for me to speak of the Ionians and the Carians and the seaboard outside the Taurus, which last is occupied by Lycians, Pamphylians, and Cilicians; for in this way I can finish my entire description of the peninsula, the isthmus of which, as I was saying, is the road which leads over from the Pontic Sea to the Issic Sea.
2 The coasting voyage round Ionia is about three thousand four hundred and thirty stadia, this distance being so great because of the gulfs and the fact that the country forms a peninsula of unusual extent; but the distance in a straight line across the isthmus is not great. For instance, merely the distance from Ephesus to Smyrna is a journey, in a straight line, of three hundred and twenty stadia, for the distance to Metropolis is one hundred and twenty stadia and the remainder to Smyrna, whereas the coasting voyage is but slightly short of two thousand two hundred. Be that as it may, the bounds of the Ionian coast extend from the Poseidium of the Milesians, and from the Carian frontiers, as far as Phocaea and the Hermus River, which latter is the limit of the Ionian seaboard.
Pherecydes says concerning this seaboard that Miletus and Myus and the parts round Mycalê and Ephesus were in earlier time occupied by Carians, and that the coast next thereafter, as far as Phocaea and Chios and Samos, which were ruled by Ancaeus, was occupied by Leleges, but that both were driven out by the Ionians and took refuge in the remaining parts of Caria. He says that Androclus, legitimate son of Codrus the king of Athens, was the leader of the Ionian colonisation, which was later than the Aeolian, and that he became the founder of Ephesus; and for this reason, it is said, the royal seat of the Ionians was established there. And still now the descendants of his family are called kings; and they have certain honours, I mean the privilege of front seats at the games and of wearing purple robes as insignia of royal descent, and staff instead of sceptre, and of the superintendence of the sacrifices in honour of the Eleusinian Demeter. Miletus was founded by Neleus, a Pylian by birth. The Messenians and the Pylians pretend a kind of kinship with one another, according to which the more recent poets call Nestor a Messenian; and they say that many of the Pylians accompanied Melanthus, father of Codrus, and his followers to Athens, and that, accordingly, all this people sent forth the colonising expedition in common with the Ionians. There is an altar, erected by Neleus, to be seen on the Poseidium. Myus was founded by Cydrelus, bastard son of Codrus; Lebedus by Andropompus, who seized a place called Artis; Colophon by Andraemon a Pylian, according to Mimnermus in his Nanno; Prienê by Aepytus the son of Neleus, and then later by Philotas, who brought a colony from Thebes; Teos, at first by Athamas, for which reason it is by Anacreon called Athamantis, and at the time of the Ionian colonisation by Nauclus, bastard son of Codrus, and after him by Apoecus and Damasus, who were Athenians, and Geres, a Boeotian; Erythrae by Cnopus, he too a bastard son of Codrus; Phocaea by the Athenians under Philogenes; Clazomenae by Paralus; Chios by Egertius, who brought with him a mixed crowd; Samos by Tembrion, and then later by Procles.
4 These are the twelve Ionian cities, but at a later time Smyrna was added, being induced by the Ephesians to join the Ionian League; for the Ephesians were fellow-inhabitants of the Smyrnaeans in ancient times, when Ephesus was also called Smyrna. And Callinus somewhere so names it, when he calls the Ephesians Smyrnaeans in the prayer to Zeus, "and pity the Smyrnaeans"; and again, "remember, if ever the Smyrnaeans burnt up beautiful thighs of oxen in sacrifice to thee." Smyrna was an Amazon who took possession of Ephesus; and hence the name both of the inhabitants and of the city, just as certain of the Ephesians were called Sisyrbitae after Sisyrbê. Also a certain place belonging to Ephesus was called Smyrna, as Hipponax plainly indicates: "He lived behind the city in Smyrna between Tracheia and Lepra Actê"; for the name Lepra Actê was given to Mt. Prion, which lies above the present city and has on it a part of the city's wall. At any rate, the possessions behind Prion are still now referred to as in the "opistholeprian" territory, and the country alongside the mountain round Coressus was called "Tracheia." The city was in ancient times round the Athenaeum, which is now outside the city near the Hypelaeus, as it is called; so that Smyrna was near the present gymnasium, behind the present city, but between Tracheia and Lepra Actê. On departing from the Ephesians, the Smyrnaeans marched to the place where Smyrna now is, which was in the possession of the Leleges, and, having driven them out, they founded the ancient Smyrna, which is about twenty stadia distant from the present Smyrna. But later, being driven out by the Aeolians, they fled for refuge to Colophon, and then with the Colophonians returned to their own land and took it back, as Mimnermus tells us in his Nanno, after recalling that Smyrna was always an object of contention: "After we left Pylus, the steep city of Neleus, we came by ship to lovely Asia, and with our overweening might settled in beloved Colophon, taking the initiative in grievous insolence. And from there, setting out from the Astëeis River, by the will of the gods we took Aeolian Smyrna." So much, then, on this subject. But I must again go over the several parts in detail, beginning with the principal places, those where the foundings first took place, I mean those round Miletus and Ephesus; for these are the best and most famous cities.
5 Next after the Poseidium of the Milesians, eighteen stadia inland, is the oracle of Apollo Didymeus among the Branchidae. It was set on fire by Xerxes, as were also the other temples, except that at Ephesus. The Branchidae gave over the treasures of the god to the Persian king, and accompanied him in his flight in order to escape punishment for the robbing and the betrayal of the temple. But later the Milesians erected the largest temple in the world, though on account of its size it remained without a roof. At any rate, the circuit of the sacred enclosure holds a village settlement; and there is a magnificent sacred grove both inside and outside the enclosure; and other sacred enclosures contain the oracle and the shrines. Here is laid the scene of the myth of Branchus and the love of Apollo. The temple is adorned with costliest offerings consisting of early works of art. Thence to the city is no long journey, by land or by sea.
6 Ephorus says: Miletus was first founded and fortified above the sea by the Cretans, where the Miletus of olden times is now situated, being settled in Sarpedon, who brought colonists from the Cretan Miletus and named the city after that Miletus, the place formerly being in the possession of the Leleges; but later Neleus and his followers fortified the present city. The present city has four harbours, one of which is large enough for a fleet. Many are the achievements of this city, but the greatest is the number of its colonisations; for the Euxine Pontus has been colonised everywhere by these people, as also the Propontis and several other regions. At any rate, Anaximenes of Lampsacus says that the Milesians colonised the islands Icaros and Leros; and, near the Hellespont, Limnae in the Chersonesus, as also Abydus and Arisba and Paesus in Asia; and Artacê and Cyzicus in the island of the Cyziceni; and Scepsis in the interior of the Troad. I, however, in my detailed description speak of the other cities, which have been omitted by him. Both Milesians and Delians invoke an Apollo "Ulius," that is, as god of "health and healing," for the verb "ulein" means "to be healthy"; whence the noun "ulê" and the salutation, "Both health and great joy to thee"; for Apollo is the god of healing. And Artemis has her name from the fact that she makes people "Artemeas." And both Helius and Selenê are closely associated with these, since they are the causes of the temperature of the air. And both pestilential diseases and sudden deaths are imputed to these gods.
7 Notable men were born at Miletus: Thales, one of the Seven Wise Men, the first to begin the science of natural philosophy and mathematics among the Greeks, and his pupil Anaximander, and again the pupil of the latter, Anaximenes, and also Hecataeus, the author of the History, and, in my time, Aeschines the orator, who remained in exile to the end, since he spoke freely, beyond moderation, before Pompey the Great. But the city was unfortunate, since it shut its gates against Alexander and was taken by force, as was also the case with Halicarnassus; and also, before that time, it was taken by the Persians. And Callisthenes says that Phrynichus the tragic poet was fined a thousand drachmas by the Athenians because he wrote a play entitled The Capture of Miletus by Dareius. The island Ladê lies close in front of Miletus, as do also the isles in the neighbourhood of the Tragaeae, which afford anchorage for pirates.
8 Next comes the Latmian Gulf, on which is situated "Heracleia below Latmus," as it is called, a small town that has an anchoring-place. It was at first called Latmus, the same name as the mountain that lies above it, which Hecataeus indicates, in his opinion, to be the same as that which by the poet is called "the mountain of the Phtheires" (for he says that the mountain of the Phtheires lies above Latmus), though some say that it is Mt. Grium, which is approximately parallel to Latmus and extends inland from Milesia towards the east through Caria to Euromus and Chalcetores. This mountain lies above Heracleia, and at a high elevation. At a slight distance away from it, after one has crossed a little river near Latmus, there is to be seen the sepulchre of Endymion, in a cave. Then from Heracleia to Pyrrha, a small town, there is a voyage of about one hundred stadia.
9 But the voyage from Miletus to Heracleia, including the sinuosities of the gulfs, is a little more and one hundred stadia, though that from Miletus to Pyrrha, in a straight course, is only thirty — so much longer is the journey along the coast. But in the case of famous places my reader must needs endure the dry part of such geography as this.
The voyage from Pyrrha to the outlet of the Maeander River is fifty stadia, a place which consists of shallows and marshes; and, going inland in rowboats thirty stadia, one comes to the city Myus, one of the twelve Ionian cities, which, on account of its sparse population, has now been incorporated into Miletus. Xerxes is said to have given this city to Themistocles to supply him with fish, Magnesia to supply him with bread, and Lampsacus with wine.
Thence, within four stadia, one comes to a village, the Carian Thymbria, near which is Aornum, a sacred cave, which is called Charonium, since it emits deadly vapours. Above it lies Magnesia on the Maeander, a colony of the Magnesians of Thessaly and the Cretans, of which I shall soon speak.
After the outlets of the Maeander comes the shore of Prienê, above which lies Prienê, and also the mountain Mycalê, which is well supplied with wild animals and with trees. This mountain lies above the Samian territory and forms with it, on the far side of the promontory called Trogilian, a strait about seven stadia in width. Prienê is by some writers called Cadmê, since Philotas, who founded it, was a Boeotian. Bias, one of the Seven Wise Men, was a native of Prienê, of whom Hipponax says "stronger in the pleading of his cases than Bias of Prienê."
Off the Trogilian promontory lies an isle of the same name. Thence the nearest passage across to Sunium is one thousand six hundred stadia; on the voyage one has at first Samos and Icaria and Corsia on the right, and the Melantian rocks on the left; and the remainder of the voyage is through the midst of the Cyclades islands. The Trogilian promontory itself is a kind of spur of Mt. Mycalê. Close to Mycalê lies another mountain, in the Ephesian territory, I mean Mt. Pactyes, in which the Mesogis terminates.
The distance from the Trogilian promontory to Samos is forty stadia. Samos faces the south, both it and its harbour, which latter has a naval station. The greater part of it is on level ground, being washed by the sea, but a part of it reaches up into the mountain that lies above it. Now on the right, as one sails towards the city, is the Poseidium, a promontory which with Mt. Mycalê forms the seven-stadia strait; and it has a temple of Poseidon; and in front of it lies an isle called Narthecis; and on the left is the suburb near the Heraeum, which consists of an ancient temple and a great shrine, which latter is now a repository of tablets. Apart from the number of the tablets placed there, there are other repositories of votive tablets and some small chapels full of ancient works of art. And the temple, which is open to the sky, is likewise full of most excellent statues. Of these, three of colossal size, the work of Myron, stood upon one base; Antony took these statues away, but Augustus Caesar restored two of them, those of Athena and Heracles, to the same base, although he transferred the Zeus to the Capitolium, having erected there a small chapel for that statue.
The voyage round the island of the Samians is six hundred stadia. In earlier times, when it was inhabited by Carians, it was called Parthenia, then Anthemus, then Melamphyllus, and then Samos, whether after some native hero or after someone who colonised it from Ithaca and Cephallenia. Now in Samos there is a promontory approximately facing Drepanum in Icaria which is called Ampelus, but the entire mountain which makes the whole of the island mountainous is called by the same name. The island does not produce good wine,a although good wine is produced by the islands all round, and although most of the whole of the adjacent mainland produces the best of wine, for example, Chios and Lesbos and Cos. And indeed the Ephesian and Metropolitan wines are good; and Mt. Mesogis and Mt. Tmolus and the Catacecaumene country and Cnidos and Smyrna and other less significant places produce exceptionally good wine, whether for enjoyment or medicinal purposes. Now Samos is not altogether fortunate in regard to wines, but in all other respects it is a blest country, as is clear from the fact that it became an object of contention in war, and also from the fact that those who praise it do not hesitate to apply to it the proverb, that "it produces even birds' milk," as Menander somewhere says. This was also the cause of the establishment of the tyrannies there, and of their enmity against the Athenians.
Now the tyrannies reached their greatest height in the time of Polycrates and his brother Syloson. Polycrates was such a brilliant man, both in his good fortune and in his natural ability, that he gained supremacy over the sea; and it is set down, as a sign of his good fortune, that he purposely flung into the sea his ring, a ring of very costly stone and engraving, and that a little later one of the fishermen brought him the very fish that swallowed it; and that when the fish was cut open the ring was found; and that on learning this the king of the Egyptians, it is said, declared in a kind of prophetic way that any man who had been exalted so highly in welfare would shortly come to no happy end of life; and indeed this is what happened, for he was captured by treachery by the satrap of the Persians and hanged. Anacreon the melic poet lived in companionship with Polycrates; and indeed the whole of his poetry is full of his praises. It was in his time, as we are told, that Pythagoras, seeing that the tyranny was growing in power, left the city and went off to Egypt and Babylon, to satisfy his fondness for learning; but when he came back and saw that the tyranny still endured, he set sail for Italy and lied there to the end of his life. So much for Polycrates.
Syloson was left a private citizen by his brother, but to gratify Dareius, the son of Hystaspes, he gave him a robe which Dareius desired when he saw him wearing it; and Dareius at that time was not yet king, but when Dareius became king, Syloson received as a return-gift the tyranny of Samos. But he ruled so harshly that the city became depopulated; and thence arose the proverb, "by the will of Syloson there is plenty of room."
The Athenians at first sent Pericles as general and with him Sophocles the poet, who by a siege put the disobedient Samians in bad plight; but later they sent two thousand allottees from their own people, among whom was Neocles, the father of Epicurus the philosopher, a schoolmaster as they call him. And indeed it is said that Epicurus grew up here and in Teos, and that he became an ephebus at Athens, and that Menander the comic poet became an ephebus at the same time. Creophylus, also, was a Samian, who, it is said, once entertained Homer and received as a gift from him the inscription of the poem called The Capture of Oechalia. But Callimachus clearly indicates the contrary in an epigram of his, meaning that Creophylus composed the poem, but that it was ascribed to Homer because of the story of the hospitality shown him: "I am the toil of the Samian, who once entertained in his house the divine Homer. I bemoan Eurytus, for all that he suffered, and golden-haired Ioleia. I am called Homer's writing. For Creophylus, dear Zeus, this is a great achievement." Some call Creophylus Homer's teacher, while others say that it was not Creophylus, but Aristeas the Proconnesian, who was his teacher.
Alongside Samos lies the island Icaria, whence was derived the name of the Icarian Sea. This island is named after Icarus the son of Daedalus, who, it is said, having joined his father in flight, both being furnished with wings, flew away from Crete and fell here, having lost control of their course; for, they add, on rising too close to the sun, his wings slipped off, since the wax melted. The whole island is three hundred stadia in perimeter; it has no harbours, but only places of anchorage, the best of which is called Histi. It has a promontory which extends towards the west. There is also on the island a temple of Artemis, called Tauropolium; and a small town Oenoê; and another small town Dracanum, bearing the same name as the promontory on which it is situated and having near by a place of anchorage. The promontory is eighty stadia distant from the promontory of the Samians called Cantharius, which is the shortest distance between the two. At the present time, however, it has but few inhabitants left, and is used by Samians mostly for the grazing of cattle.
After the Samian strait, near Mt. Mycalê, as one sails to Ephesus, one comes, on the right, to the seaboard of the Ephesians; and a part of this seaboard is held by the Samians. First on the seaboard is Panionium, lying three stadia about the sea where the Pan‑Ionia, a common festival of the Ionians, are held, and where sacrifices are performed in honour of the Heliconian Poseidon; and Prienians serve as priests at this sacrifice, but I have spoken of them in my account of the Peloponnesus. Then comes Neapolis, which in earlier times belonged to the Ephesians, but now belongs to the Samians, who gave in exchange for it Marathesium, the more distant for the nearer place. Then comes Pygela, a small town, with a temple of Artemis Munychia, founded by Agamemnon and inhabited by a part of his troops; for it is said that some of his soldiers became afflicted with a disease of the buttocks and were called diseased-buttocks," and that, being afflicted with this disease, they stayed there, and that the place thus received this appropriate name. Then comes the harbour called Panormus, with a temple of the Ephesian Artemis; and then the city Ephesus. On the same coast, slightly above the sea, is also Ortygia, which is a magnificent grove of all kinds of trees, of the cypress most of all. It is traversed by the Cenchrus River, where Leto is said to have bathed herself after her travail. For here is the mythical scene of the birth, and of the nurse Ortygia, and of the holy place where the birth took place, and of the olive tree near by, where the goddess is said first to have taken a rest after she was relieved from her travail. Above the grove lies Mt. Solmissus, where, it is said, the Curetes stationed themselves, and with the din of their arms frightened Hera out of her wits when she was jealously spying on Leto, and when they helped Leto to conceal from Hera the birth of her children. There are several temples in the place, some ancient and others built in later times; and in the ancient temples are many ancient wooden images, but in those of later times there are works of Scopas; for example, Leto holding a sceptre and Ortygia standing beside her with a child in each arm. A general festival is held there annually; and by a certain custom the youths vie for honour, particularly in the splendour of their banquets there. At that time, also, a special college of the Curetes holds symposiums and performs certain mystic sacrifices.
The city of Ephesus was inhabited both by Carians and by Leleges, but Androclus drove them out and settled the most of those who had come with him round the Athenaeum and the Hypelaeus, though he also included a part of the country situated on the slopes of Mt. Coressus. Now Ephesus was thus inhabited until the time of Croesus, but later the people came down from the mountainside and abode round the present temple until the time of Alexander. Lysimachus built a wall round the present city, but the people were not agreeably disposed to change their abodes to it; and therefore he waited for a downpour of rain and himself took advantage of it and blocked the sewers so as to inundate the city; and the inhabitants were then glad to make the change. He named the city after his wife Arsinoê; the old name, however, prevailed. There was a senate, which was conscripted; and with these were associated the Epicteti, as they were called, who administered all the affairs of the city.
As for the temple of Artemis, its first architect was Chersiphron; and then another man made it larger. But when it was set on fire by a certain Herostratus, the citizens erected another and better one, having collected the ornaments of the women and their own individual belongings, and having sold also the pillars of the former temple. Testimony is borne to these facts by the decrees that were made at that time. Artemidorus says: Timaeus of Tauromenium, being ignorant of these decrees and being anyway an envious and slanderous fellow (for which reason he was also called Epitimaeus), says that they exacted means for the restoration of the temple from the treasures deposited in their care by the Persians; but there were no treasures on deposit in their care at that time, and, even if there had been, they would have been burned along with the temple; and after the fire, when the roof was destroyed, who could have wished to keep deposits of treasure lying in a sacred enclosure that was open to the sky? Now Alexander, Artemidorus adds, promised the Ephesians to pay all expenses, both past and future, on condition that he should have the credit therefor on the inscription, but they were unwilling, just as they would have been far more unwilling to acquire glory by sacrilege and a spoliation of the temple. And Artemidorus praises the Ephesian who said to the king that it was inappropriate for a god to dedicate offerings to gods.
After the completion of the temple, which, he says, was the work of Cheirocrates (the same man who built Alexandreia and the same man who proposed to Alexander to fashion Mt. Athos into his likeness, representing him as pouring a libation from a kind of ewer into a broad bowl, and to make two cities, one on the right of the mountain and the other on the left, and a river flowing from one to the other) — after the completion of the temple, he says, the great number of dedications in general were secured by means of the high honour they paid their artists, but the whole of the altar was filled, one might say, with the works of Praxiteles. They showed me also some of the works of Thrason, who made the chapel of Hecatê, the waxen image of Penelopê, and the old woman Eurycleia. They had eunuchs as priests, whom they called Megabyzi. And they were always in quest of persons from other places who were worthy of this preferment, and they held them in great honour. And it was obligatory for maidens to serve as colleagues with them in their priestly office. But though at the present time some of their usages are being preserved, yet others are not; but the temple remains a place of refuge, the same as in earlier times, although the limits of the refuge have often been changed; for example, when Alexander extended them for a stadium, and when Mithridates shot an arrow from the corner of the roof and thought it went a little farther than a stadium, and when Antony doubled this distance and included within the refuge a part of the city. But this extension of the refuge proved harmful, and put the city in the power of criminals; and it was therefore nullified by Augustus Caesar.
The city has both an arsenal and a harbour. The mouth of the harbour was made narrower by the engineers, but they, along with the king who ordered it, were deceived as to the result, I mean Attalus Philadelphus; for he thought that the entrance would be deep enough for large merchant vessels — as also the harbour itself, which formerly had shallow places because of the silt deposited by the Caÿster River — if a mole were thrown up at the mouth, which was very wide, and therefore ordered that the mole should be built. But the result was the opposite, for the silt, thus hemmed in, made the whole of the harbour, as far as the mouth, more shallow. Before this time the ebb and flow of the tides would carry away the silt and draw it to the sea outside. Such, then, is the harbour; and the city, because of its advantageous situation in other respects, grows daily, and is the largest emporium in Asia this side the Taurus.
Notable men have been born in this city: in ancient times, Heracleitus the Obscure, as he is called; and Hermodorus, concerning whom Heracleitus himself says: "It were right for the Ephesians from youth upwards to be hanged, who banished their most useful man, saying: 'Let no man of us be most useful; otherwise, let him be elsewhere and with other people.' " Hermodorus is reputed to have written certain laws for the Romans. And Hipponax the poet was from Ephesus; and so were Parrhasius the painter and Apelles, and more recently Alexander the orator, surnamed Lychnus, who was a statesman, and wrote history, and left behind him poems in which he describes the position of the heavenly bodies and gives a geographic description of the continents, each forming the subject of a poem.
After the outlet of the Caÿster River comes a lake that runs inland from the sea, called Selinusia; and next comes another lake that is confluent with it, both affording great revenues. Of these revenues, though sacred, the kings deprived the goddess, but the Romans gave them back; and again the tax‑gatherers forcibly converted the tolls to their own use; but when Artemidorus was sent on an embassy, as he says, he got the lakes back for the goddess, and he also won the decision over Heracleotis, which was in revolt, his case being decided at Rome; and in return for this the city erected in the temple a golden image of him. In the innermost recess of the lake there is a temple of a king, which is said to have been built by Agamemnon.
Then one comes to the mountain Gallesius, and to Colophon, an Ionian city, and to the sacred precinct of Apollo Clarius, where there was once an ancient oracle. The story is told that Calchas the prophet, with Amphilochus the son of Amphiaraüs, went there on foot on his return from Troy, and that having met near Clarus a prophet superior to himself, Mopsus, the son of Manto, the daughter of Teiresias, he died of grief. Now Hesiod revises the myth as follows, making Calchas propound to Mopsus this question: "I am amazed in my heart at all these figs on this wild fig tree, small though it is; can you tell me the number?" And he makes Mopsus reply: "They are ten thousand in number, and their measure is a medimnus; but there is one over, which you cannot put in the measure." "Thus he spake," Hesiod adds, "and the number the measure could hold proved true. And then the eyes of Calchas were closed by the sleep of death." But Pherecydes says that the question propounded by Calchas was in regard to a pregnant sow, how many pigs she carried, and that Mopsus said, "three, one of which is a female," and that when Mopsus proved to have spoken the truth, Calchas died of grief. Some say that Calchas propounded the question in regard to the sow, but that Mopsus propounded the question in regard to the wild fig tree, and that the latter spoke the truth but that the former did not, and died of grief, and in accordance with a certain oracle. Sophocles tells the oracle in his Reclaiming of Helen, that Calchas was destined to die when he met a prophet superior to himself, but he transfers the scene of the rivalry and of the death of Calchas to Cilicia. Such are the ancient stories.
The Colophonians once possessed notable naval and cavalry forces, in which latter they were so far superior to the others that wherever in wars that were hard to bring to an end, the cavalry of the Colophonians served as ally, the war came to an end; whence arose the proverb, "he put Colophon to it," which is quoted when a sure end is put to any affair.b Native Colophonians, among those of whom we have record, were: Mimnermus, who was both a flute-player and elegiac poet; Xenophanes, the natural philosopher, who composed the "Silli" in verse; and Pindar speaks also of a certain Polymnastus as one of the famous musicians: "Thou knowest the voice, common to all, of Polymnastus the Colophonian." And some say that Homer was from there. On a straight voyage it is seventy stadia from Ephesus, but if one includes the sinuosities of the gulfs it is one hundred and twenty.
After Colophon one comes to the mountain Coracius and to an isle sacred to Artemis, whither deer, it has been believed, swim across and give birth to their young. Then comes Lebedus, which is one hundred and twenty stadia distant from Colophon. This is the meeting-place and settlement of all the Dionysiac artists in Ionia as far as the Hellespont; and this is the place where both games and a general festal assembly are held every year in honour of Dionysus. They formerly lived in Teos, the city of the Ionians that comes next after Colophon, but when the sedition broke out they fled for refuge to Ephesus. And when Attalus settled them in Myonnesus between Teos and Lebedus the Tëians sent an embassy to beg of the Romans not to permit Myonnesus to be fortified against them; and they migrated to Lebedus, whose inhabitants gladly received them because of the dearth of population by which they were then afflicted. Teos, also, is one hundred and twenty stadia distant from Lebedus; and in the intervening distance there is an island Aspis, by some called Arconnesus. And Myonnesus is settled on a height that forms a peninsula.
Teos also is situated on a peninsula; and it has a harbour. Anacreon the melic poet was from Teos; in whose time the Tëians abandoned their city and migrated to Abdera, a Thracian city, being unable to bear the insolence of the Persians; and hence the verse in reference to Abdera. "Abdera, beautiful colony of the Tëians." But some of them returned again in later times. As I have already said, Apellicon also was a Tëian; and Hecataeus the historian was from the same city. And there is also another harbour to the north, thirty stadia distant from the city, called Gerrhaeïdae.
Then one comes to Chalcideis, and to the isthmus of the Chersonesus, belonging to the Tëians and Erythraeans. Now the latter people live this side the isthmus, but the Tëians and Clazomenians live on the isthmus itself; for the southern side of the isthmus, I mean the Chalcideis, is occupied by Tëians, but the northern by Clazomenians, where their territory joins the Erythraean. At the beginning of the isthmus lies the place called Hypocremnus, which lies between the Erythraean territory this side the isthmus and that of the Clazomenians on the other side. Above the Chalcideis is situated a sacred precinct consecrated to Alexander the son of Philip; and games, called the Alexandreia, are proclaimed by the general assembly of the Ionians and are celebrated there. The passage across the isthmus from the sacred precinct of Alexander and from the Chalcideis to Hypocremnus is fifty stadia, but the voyage round by sea is more than one thousand. Somewhere about the middle of the circuit is Erythrae, an Ionian city, which has a harbour, and also four isles lying off it, called Hippi.
Before coming to Erythrae, one comes first to a small town Erae belonging to the Tëians; and then to Corycus, a high mountain, and to a harbour at the foot of it, Casystes, and to another harbour called Erythras, and to several others in order thereafter. The waters along the coast of Mt. Corycus, they say, were everywhere the haunt of pirates, the Corycaeans, as they are called, who had found a new way of attacking vessels; for, they say, the Corycaeans would scatter themselves among the harbours, follow up the merchants whose vessels lay at anchor in them, and overhear what cargoes they had aboard and whither they were bound, and then come together and attack the merchants after they had put to sea and plunder their vessels; and hence it is that we call every person who is a busybody and tries to overhear private and secret conversations a Corycaean; and that we say in a proverb: "Well then, the Corycaean was listening to this," when one thinks that he is doing or saying something in secret, but fails to keep it hidden because of persons who spy on him and are eager to learn what does not concern them.
After Mt. Corycus one comes to Halonnesos, a small island. Then to Argennum, a promontory of the Erythraean territory; it is very close to the Poseidium of the Chians, which latter forms a strait about sixty stadia in width. Between Erythrae and Hypocremnus lies Mimas, a lofty mountain, which is well supplied with game and well wooded. Then one comes to a village Cybelia, and to a promontory Melaena, as it is called, which has a millstone quarry.
Erythrae was the native city of Sibylla, a woman who was divinely inspired and had the gift of prophecy, one of the ancients. And in the time of Alexander there was another woman who likewise had the gift of prophecy; she was called Athenaïs, and was a native of the same city. And, in my time, Heracleides the Herophileian physician, fellow-pupil of Apollonius Mys, was born there.
As for Chios, the voyage round it along the coast is nine hundred stadia; and it has a city with a good port and with a naval station for eighty ships. On making the voyage round it from the city, with the island on the right, one comes first to the Poseidium. Then to Phanae, a deep harbour, and to a temple of Apollo and a grove of palm trees. Then to Notium, a shore suited to the anchoring of vessels. Then to Laïus, this too a shore suited to the anchoring of vessels: whence to the city there is an isthmus of sixty stadia, but the voyage round, which I have just now described, is three hundred and sixty stadia. Then to Melaena, a promontory, opposite to which lies Psyra, an island fifty stadia distant from the promontory, lofty, and having a city of the same name. The circuit of the island is forty stadia. Then one comes to Ariusia, a rugged and harbourless country, about thirty stadia in extent, which produces the best of the Grecian wines. Then to Pelinaeus, the highest mountain in the island. And the island also has a marble quarry. Famous natives of Chios are: Ion the tragic poet, and Theopompus the historian, and Theocritus the sophist. The two latter were political opponents of one another. The Chians also claim Homer, setting forth as strong testimony that the men called Homeridae were descendants of Homer's family; these are mentioned by Pindar: "Whence also the Homeridae, singers of deftly woven lays, most often . . . ." The Chians at one time possessed also a fleet, and attained to liberty and to maritime empire. The distance from Chios to Lesbos, sailing southwards, is about four hundred stadia.
After Hypocremnus one comes to Chytrium, the site on which Clazomenae was situated in earlier times. Then to the present Clazomenae, with eight small islands lying off it that are under cultivation. Anaxagoras, the natural philosopher, an illustrious man and associate of Anaximenes the Milesian, was a Clazomenian. And Archelaüs the natural philosopher and Euripides the poet took his entire course. Then to a temple of Apollo and to hot springs, and to the gulf and the city of the Smyrnaeans.
Next one comes to another gulf, on which is the old Smyrna, twenty stadia distant from the present Smyrna. After Smyrna had been rased by the Lydians, its inhabitants continued for about four hundred years to live in villages. Then they were reassembled into a city by Antigonus, and afterwards by Lysimachus, and their city is now the most beautiful of all; a part of it is on a mountain and walled, but the greater part of it is in the plain near the harbour and near the Metroüm and near the gymnasium. The civilian into streets is exceptionally good, in straight lines as far as possible; and the streets are paved with stone; and there are large quadrangular porticoes, with both lower and upper stories. There is also a library; and the Homereium, a quadrangular portico containing a shrine and wooden statue of Homer; for the Smyrnaeans also lay especial claim to the poet; and indeed a bronze coin of theirs is called Homereium. The River Meles flows near the walls; and, in addition to the rest of the city's equipment, there is also a harbour that can be closed. But there is one error, not a small one, in the work of the engineers, that when they paved the streets they did not give them underground drainage; instead, filth covers the surface, and particularly during rains, when the cast‑off filth is discharged upon the streets. It was here that Dolabella captured by siege, and slew, Trebonius, one of the men who treacherously murdered the deified Caesar; and he set free many parts of the city.
After Smyrna one comes to Leucae, a small town, which after the death of Attalus Philometor was caused to revolt by Aristonicus, who was reputed to belong to the royal family and intended to usurp the kingdom. Now he was banished from Smyrna, after being defeated in a naval battle near the Cymaean territory by the Ephesians, but he went up into the interior and quickly assembled a large number of resourceless people, and also of slaves, invited with a promise of freedom, whom he called Heliopolitae. Now he first fell upon Thyateira unexpectedly, and then got possession of Apollonis, and then set his efforts against other fortresses. But he did not last long; the cities immediately sent a large number of troops against him, and they were assisted by Nicomedes the Bithynian and by the kings of the Cappadocians. Then came five Roman ambassadors, and after that an army under Publius Crassus the consul, and after that Marcus Perpernas,º who brought the war to an end, having captured Aristonicus alive and sent him to Rome. Now Aristonicus ended his life in prison; Perpernas died of disease; and Crassus, attacked by certain people in the neighbourhood of Leucae, fell in battle. And Manius Aquillius came over as consul with ten lieutenants and organised the province into the form of government that still now endures. After Leucae one comes to Phocaea, on a gulf, concerning which I have already spoken in my account of Massalia.c Then to the boundaries of the Ionians and the Aeolians; but I have already spoken of these. In the interior above the Ionian seaboard there remain to be described the places in the neighbourhood of the road that leads from Ephesus to Antiocheia and the Maeander River. These places are occupied by Lydians and Carians mixed with Greeks.
The first city one comes to after Ephesus is Magnesia, which is an Aeolian city and is called "Magnesia on the Maeander," for it is situated near that river. But it is much nearer the Lethaeus River, which empties into the Maeander and has its beginning in Mt. Pactyes, the mountain in the territory of the Ephesians. There is another Lethaeus in Gortyna, and another near Triccê, where Asclepius is said to have been born, and still another in the country of the Western Libyans. And the city lies in the plain near the mountain called Thorax, on which Daphitas the grammarian is said to have been crucified, because he reviled the kings in a distich: "Purpled with stripes, mere filings of the treasure of Lysimachus, ye rule the Lydians and Phrygia." It is said that an oracle was given out that Daphitas should be on his guard against Thorax.
The Magnetans are thought to be descendants of Delphians who settled in the Didyman hills, in Thessaly, concerning whom Hesiod says: "Or as the unwedded virgin who, dwelling on the holy Didyman hills, in the Dotian Plain, in front of Amyrus, bathed her foot in Lake Boebeïs." Here was also the temple of Dindymenê, Mother of the gods. According to tradition, the wife of Themistocles, some say his daughter, served as a priestess here. But the temple is not now in existence, because the city has been transferred to another site. In the present city is the temple of Artemis Leucophryenê, which in the size of its shrine and in the number of its votive offerings is inferior to the temple at Ephesus, but in the harmony and skill shown in the structure of the sacred enclosure is far superior to it. And in size it surpasses all the sacred enclosures in Asia except two, that at Ephesus and that at Didymi. In ancient times, also, it came to pass that the Magnetans were utterly destroyed by the Treres, a Cimmerian tribe, although they had for a long time been a prosperous people, but the Milesians took possession of the place in the following year. Now Callinus mentions the Magnetans as still being a prosperous people and as being successful in their war against the Ephesians, but Archilochus is obviously already aware of the misfortune that befell them: "to bewail the woes of the Thasians, not those of the Magnetans"; whence one may judge that he was more recent than Callinus. And Callinus recalls another, and earlier, invasion of the Cimmerians when he says: "And now the army of the Cimmerians, mighty in deeds, advanceth," in which he plainly indicates the capture of Sardeis.
Well-known natives of Magnesia are: Hegesias the orator, who, more than any other, initiated the Asiatic style, as it is called, whereby he corrupted the established Attic custom; and Simus the melic poet, he too a man who corrupted the style handed down by the earlier melic poets and introduced the Simoedia, just as that style was corrupted still more by the Lysioedi and the Magoedi, and by Cleomachus the pugilist, who, having fallen in love with a certain cinaedus and with a young female slave who was kept as a prostitute by the cinaedus, imitated the style of dialects and mannerisms that was in vogue among the cinaedi. Sotades was the first man to write the talk of the cinaedi; and then Alexander the Aetolian. But though these two men imitated that talk in mere speech, Lysis accompanied it with song; and so did Simus, who was still earlier than he. As for Anaxenor, the citharoede, the theatres exalted him, but Antony exalted him all he possibly could, since he even appointed him exactor of tribute from four cities, giving him a body-guard of soldiers. Further, his native land greatly increased his honours, having clad him in purple as consecrated to Zeus Sosipolis, as is plainly indicated in his painted image in the market-place. And there is also a bronze statue of him in the theatre, with the inscription, "Surely this is a beautiful thing, to listen to a singer such as this man is, like unto the gods in voice." But the engraver, missing his guess, left out the last letter of the second verse, the base of the statue not being wide enough for its inclusion; so that he laid the city open to the charge of ignorance, because of the ambiguity of the writing, as to whether the last word should be taken in the nominative case or in the dative; for many write the dative case without the iota, and even reject the ordinary usage as being without natural cause.
After Magnesia comes the road to Tralleis, with Mt. Mesogis on the left, and, at the road itself and on the right, the plain of the Maeander River, which is occupied by Lydians and Carians, and by Ionians, both Milesians and Myesians, and also by the Aeolians of Magnesia. And the same kind of topographical account applies as far as Nysa and Antiocheia. The city of the Tralleians is situated upon a trapezium-shaped site, with a height fortified by nature; and the places all round are well defended. And it is as well peopled as any other city in Asia by people of means; and always some of its men hold the chief places in the province, being called Asiarchs. Among these was Pythodorus, originally a native of Nysa, but he changed his abode to Tralleis because of its celebrity; and with only a few others he stood out conspicuously as a friend of Pompey. And he came into possession of the wealth of a king, worth more than two thousand talents, which, though sold by the deified Caesar, was redeemed by him through his friendship with Pompey and was left by him unimpaired to his children. He was the father of Pythodoris, the present queen in Pontus, of whom I have already spoken. Pythodorus, then, flourished in my time, as also Menodorus, a man of learning, and otherwise august and grave, who held the priesthood of Zeus Larisaeus. But he was overthrown by a counter-party friendly to Dometiusº Ahenobarbus; and Dometius, relying on his informers, slew him, as guilty of causing the fleet to revolt. Here were born famous orators: Dionysocles and afterwards Damasus Scombrus. Tralleis is said to have been founded by Argives and by certain Tralleian Thracians, and hence the name. And the city was ruled for a short time by tyrants, the sons of Cratippus, at the time of the Mithridatic war.
Nysa is situated near Mt. Mesogis, for the most part lying upon its slopes; and it is a double city, so to speak, for it is divided by a torrential stream that forms a gorge, which at one place has a bridge over it, joining the two cities, and at another is adorned with an amphitheatre, with a hidden underground passage for the torrential waters. Near the theatre are two heights, below one of which is the gymnasium of youths; and below the other is the market-place and the gymnasium for older persons. The plain lies to the south of the city, as it does to the south of Tralleis.
On the road between the Tralleis and Nysa is a village of the Nysaeans, not far from the city, Acharaca, where is the Plutonium, with a costly sacred precinct and a shrine of Pluto and Corê, and also the Charonium, a cave that lies but also the sacred precinct, by nature wonderful; for they say that those who are diseased and give heed to the cures prescribed by the god resort thither and live in the village near the cave among experienced priests, who on their behalf sleep in the cave and through dreams prescribe the cures. These are also the men who invoke the healing power of the gods. And they often bring the sick into the cave and leave them there, to remain in quiet, like animals in their lurking-holes, without food for many days. And sometimes the sick give heed also to their own dreams, but still they use those other men, as priests, to initiate them into the mysteries and to counsel them. To all others the place is forbidden and deadly. A festival is celebrated every year at Acharaca; and at that time in particular those who celebrate the festival can see and hear concerning all these things; and at the festival, too, about noon, the boys and young men of the gymnasium, nude and anointed with oil, take up a bull and with haste carry him up into the cave; and, when let loose, the bull goes forward a short distance, falls, and breathes out his life.
Thirty stadia from Nysa, after one crosses over Mt. Tmolus and the mountain called Mesogis, towards the region to the south of the Mesogis, there is a place called Leimon, whither the Nysaeans and all the people about go to celebrate their festivals. And not far from Leimon is an entrance into the earth sacred to the same gods, which is said to extend down as far as Acharaca. The poet is said to name this meadow when he says, "On the Asian meadow"; and they point out a hero-temple of Caÿster and a certain Asius, and the Caÿster River that streams forth near by.
The story is told that three brothers, Athymbrus and Athymbradus and Hydrelus, who came from Lacedaemon, founded the three cities which were named after them, but that the cities later became scantily populated, and that the city Nysa was founded by their inhabitants; but that Athymbrus is now regarded by Nysaeans as their original founder.
Near Nysa, on the far side of the Maeander River, are situated noteworthy settlements; I mean Coscinia and Orthosia; and this side the river, Briula, Mastaura, and Acharaca, and above the city, on the mountain, Aroma (in which the letter rho is short), whence comes the best Mesogitan wine, I mean the Aromian.
Famous men born at Nysa are: Apollonius the Stoic philosopher, best of the disciples of Panaetius; and Menecrates, pupil of Aristarchus; and Aristodemus, his son, whose entire course, in his extreme old age, I in my youth took at Nysa; and Sostratus, the brother of Aristodemus, and another Aristodemus, his cousin, who trained Pompey the Great, proved themselves notable grammarians. But my teacher also taught rhetoric and had two schools, both in Rhodes and in his native land, teaching rhetoric in the morning and grammar in the evening; at Rome, however, when he was in charge of the children of Pompey the Great, he was content with the teaching of grammar. |
|
|
|
|
14 - 2 Caria 
Coming now to the far side of the Maeander, the parts that remain to be described are all Carian, since here the Lydians are no longer intermingled with the Carians, and the latter occupy all the country by themselves, except that a segment of the seaboard is occupied by Milesians and Myesians. Now the beginning of the seaboard is the Peraea of the Rhodians on the sea, and the end of it is the Poseidium of the Milesians; but in the interior are the extremities of the Taurus, extending as far as the Maeander River. For it is said that the mountains situated above the Chelidonian islands, as they are called, which islands lie off the confines of Pamphylia and Lycia, form the beginning of the Taurus, for thence the Taurus rises to a height; but the truth is that the whole of Lycia, towards the parts outside and on its southern side, is separated by a mountainous ridge of the Taurus from the country of the Cibyrans as far as the Peraea of the Rhodians. From here the ridge continues, but is much lower and is no longer regarded as a part of the Taurus; neither are the parts outside the Taurus and this side of it so regarded, because of the fact that the eminences and depressions are scattered equally throughout the breadth and the length of the whole country, and present nothing like a wall of partition. The whole of the voyage round the coast, following the sinuosities of the gulfs, is four thousand nine hundred stadia, and merely that round the Peraea of the Rhodians is close to fifteen hundred.
2 The Peraea of the Rhodians begins with Daedala, a place in the Rhodian territory, but ends with Mt. Phoenix, as it is called, which is also in the Rhodian territory. Off the Peraea lies the island Elaeussa, distant one hundred and twenty stadia from Rhodes. Between the two, as one sails towards the west from Daedala in a straight line with the coast of Cilicia and Pamphylia and Lycia, one comes to a gulf called Glaucus, which has good harbours; then to the Artemisium, a promontory and temple; then to the sacred precinct of Leto, above which, and above the sea, at a distance of sixty stadia, lies Calynda, a city; then to Caunus and to the Calbis, a river near Caunus, which is deep and affords passage for merchant vessels; and between the two lies Pisilis.
3 The city has dockyards, and a harbour that can be closed. Above the city, on a height, lies Imbrus, a stronghold. Although the country is fertile, the city is agreed by all to have foul air in the summer, as also in autumn, because of the heat and the abundance of fruits. And indeed little tales of the following kind are repeated over and over, that Stratonicus the citharist, seeing that the Caunians were pitiably pale, said that this was the thought of the poet in the verse, "even as is the generation of leaves, such is that also of men"; and when people complained that he was jeering at the city as though it were sickly, he replied, "Would I be so bold as to call this city sickly, where even the corpses walk about?" The Caunians once revolted from the Rhodians, but by a judicial decision of the Romans they were restored to them. And there is extant a speech of Molon entitled Against the Caunians. It is said that they speak the same language as the Carians, but that they came from Crete and follow usages of their own.
4 Next one comes to Physcus, a small town, which has a harbour and a sacred precinct of Leto; and then to Loryma, a rugged coast, and to the highest mountain in that part of the country; and on top of the mountain is Phoenix, a stronghold bearing the same name as the mountain; and off the mountain, at a distance of four stadia, lies Elaeussa, an island, which is about eight stadia in circuit.
5 The city of the Rhodians lies on the eastern promontory of Rhodes; and it is so far superior to all others in harbours and roads and walls and improvements in general that I am unable to speak of any other city as equal to it, or even as almost equal to it, much less superior to it. It is remarkable also for its good order, and for its careful attention to the administration of affairs of state in general; and in particular to that of naval affairs, whereby it held the mastery of the sea for a long time and overthrew the business of piracy, and became a friend to the Romans and to all kings who favoured both the Romans and the Greeks. Consequently it not only has remained autonomous but also has been adorned with many votive offerings, which for the most part are to be found in the Dionysium and the gymnasium, but partly in other places. The best of these are, first, the Colossus of Helius,8 of which the author of the iambic verse says, "seven times ten cubits in height, the work of Chares the Lindian"; but it now lies on the ground, having been thrown down by an earthquake and broken at the knees. In accordance with a certain oracle, the people did not raise it again. This, then, is the most excellent of the votive offerings (at any rate, it is by common agreement one of the Seven Wonders); and there are also the paintings of Protogenes, his Ialysus and also his Satyr, the latter standing by a pillar, on top of which stood a male partridge. And at this partridge, as would be natural, the people were so agape when the picture had only recently been set up, that they would behold him with wonder but overlook the Satyr, although the latter was a very great success. But the partridge-breeders were still more amazed, bringing their tame partridges and placing them opposite the painted partridge; for their partridges would make their call to the painting and attract a mob of people. But when Protogenes saw that the main part of the work had become subordinate, he begged those who were in charge of the sacred precinct to permit him to go there and efface the partridge, and so he did. The Rhodians are concerned for the people in general, although their rule is not democratic; still, they wish to take care of their multitude of poor people. Accordingly, the people are supplied with provisions and the needy are supported by the well-to‑do, by a certain ancestral custom; and there were certain liturgies that supply provisions, so that at the same time the poor man receives his sustenance and the city does not run short of useful men, and in particular for the manning of the fleets. As for the roadsteads, some of them were kept hidden and forbidden to the people in general; and death was the penalty for any person who spied on them or passed inside them. And here too, as in Massalia and Cyzicus, everything relating to the architects, the manufacture of instruments of war, and the stores of arms and everything else are objects of exceptional care, and even more so than anywhere else.
6 The Rhodians, like the people of Halicarnassus and Cnidus and Cos, are Dorians; for of the Dorians who founded Megara after the death of Codrus, some remained there, others took part with Althaemenes the Argive in the colonisation of Crete, and others were distributed to Rhodes and to the cities just mentioned. But these events are later than those mentioned by Homer, for Cnidus and Halicarnassus were not yet in existence, although Rhodes and Cos were; but they were inhabited by Heracleidae. Now when Tlepolemus had grown to manhood, "he forthwith slew his own father's dear uncle, Licymnius, who was then growing old; and straightway he built him ships, and when he had gathered together a great host he went in flight." The poet then adds, "he came to Rhodes in his wanderings, where his people settled in three divisions by tribes"; and he names the cities of that time, "Lindus, Ialysus, and Cameirus white with chalk," the city of the Rhodians having not yet been founded. The poet, then, nowhere mentions Dorians by name here, but perhaps indicates Aeolians and Boeotians, if it be true that Heracles and Licymnius settled there. But if, as others say, Tlepolemus set forth from Argos and Tiryns, even so the colonisation could not have taken place before the return of the Heracleidae. And of the Coans, also, Homer says, "these were led by Pheidippus and Antiphus, the two sons of lord Thessalus, son of Heracles"; and these names indicate the Aeolian stock of people rather than the Dorian.
7 In earlier times Rhodes was called Ophiussa and Stadia, and then Telchinis, after the Telchines, who took up their abode in the island. Some say that the Telchines are "maligners" and "sorcerers," who pour the water of the Styx mixed with sulphur upon animals and plants in order to destroy them. But others, on the contrary, say that since they excelled in workmanship they were "maligned" by rival workmen and thus received their bad reputation; and that they first came from Crete to Cypros, and then to Rhodes; and that they were the first to work iron and brass, and in fact fabricated the scythe for Cronus. Now I have already described them before, but the number of the myths about them causes me to resume their description, filling up the gaps, if I have omitted anything.
8 After the Telchines, the Heliadae, according to the mythical story, took possession of the island; and to one of these, Cercaphus, and to his wife Cydippê, were born children who founded the cities that are named after them, "Lindus, Ialysus, and Cameirus white with chalk." But some say that Tlepolemus founded them and gave them the same names as those of certain daughters of Danäus.
9 The present city was founded at the time of the Peloponnesian War by the same architect, as they say, who founded the Peiraeus. But the Peiraeus no longer endures, since it was badly damaged, first by the Lacedaemonians, who tore down the two walls, and later by Sulla, the Roman commander.
It is also related of the Rhodians that they have been prosperous by sea, not merely since the time when they founded the present city, but that even many years before the establishment of the Olympian Games they used to sail far away from their homeland to insure the safety of their people. Since that time, also, they have sailed as far as Iberia; and there they founded Rhodes, of which the Massaliotes later took possession; among the Opici they founded Parthenopê; and among the Daunians they, along with the Coans, founded Elpiae. Some say that the islands called the Gymnesiae were founded by them after their departure from Troy; and the larger of these, according to Timaeus, is the largest of all islands after the seven — Sardinia, Sicily, Cypros, Crete, Euboea, Cyrnos, and Lesbos, but this is untrue, for there are others much larger. It is said that "gymnetes" are called "balearides" by the Phoenicians, and that on this account the Gymnesiae were called Balearides. Some of the Rhodians took up their abode round Sybaris in Chonia. The poet, too, seems to bear witness to the prosperity enjoyed by the Rhodians from ancient times, forthwith from the first founding of the three cities: "and there his people settled in three divisions by tribes, and were loved of Zeus, who is lord over gods and men; and upon them a wondrous wealth was shed by the son of Cronus." Other writers refer these verses to a myth, and say that gold rained on the island at the time when Athena was born from the head of Zeus, as Pindar states. The island has a circuit of nine hundred and twenty stadia.
As one sails from the city, with the island on the right, one comes first to Lindus, a city situated on a mountain and extending far towards the south and approximately towards Alexandria. In Lindus there is a famous temple of Athena Lindia, founded by the daughters of Danäus. Now in earlier times the Lindians were under a separate government of their own, as were also the Cameirians and the Ialysians, but after this they all came together at Rhodes. Cleobulus, one of the Seven Wise Men, was a native of Lindus.
After Lindus one comes to Ixia, a stronghold, and to Mnasyrium; then to Atabyris, the highest of the mountains there, which is sacred to Zeus Atabyrius; then to Cameirus; then to Ialysus, a village, above which there is an acropolis called Ochyroma; then to the city of the Rhodians, at a distance of about eighty stadia. Between these lies Thoantium, a kind of promontory; and it is off Thoantium, generally speaking, that Chalcia and the Sporades in the neighbourhood of Chalcia lie, which I have mentioned before.
Many men worthy of mention were native Rhodians, both commanders and athletes, among whom were the ancestors of Panaetius the philosopher; and, among statesmen and rhetoricians and philosophers, Panaetius himself and Stratocles and Andronicus, one of the Peripatetics, and Leonides the Stoic; and also, before their time, Praxiphanes and Hieronymus and Eudemus. Poseidonius engaged in affairs of state in Rhodes and taught there, although he was a native of Apameia in Syria, as was also the case with Apollonius Malacus and Molon, for they were Alabandians, pupils of Menecles the orator. Apollonius Malacus began his sojourn there earlier than Molon, and when, much later, Molon came, the former said to him, "you are a late 'molon,' " instead of saying, "late 'elthon.' " and Peisander the poet, who wrote the Heracleia, was also a Rhodian; and so was Simmias the grammarian, as also Aristocles of my own time. And Dionysius the Thracian and the Apollonius who wrote the Argonauts, though Alexandrians, were called Rhodians. As for Rhodes, I have said enough about it.
As for the Carian coast that comes after Rhodes, beginning at Eleus and Loryma, it bends sharply back towards the north, and the voyage thereafter runs in a straight line as far as the Propontis, forming, as it were, a meridian line about five thousand stadia long, or slightly short of that distance. Along this line is situated the remainder of Caria, as are also the Ionians and the Aeolians and Troy and the parts round Cyzicus and Byzantium. After Loryma, then, one comes to Cynos-Sema and to Symê, an island.
Then to Cnidus, with two harbours, one of which can be closed, can receive triremes, and is a naval station for twenty ships. Off it lies an island which is approximately seven stadia in circuit, rises high, is theatre-like, is connected by moles with the mainland, and in a way makes Cnidus a double city, for a large part of its people live on the island, which shelters both harbours. Opposite it, in the high sea, is Nisyrus. Notable Cnidians were: first, Eudoxus the mathematician, one of the comrades of Plato; then Agatharchides, one of the Peripatetics, a historian; and, in my own time, Theopompus, the friend of the deified Caesar, being a man of great influence with him, and his son Artemidorus. Thence, also, came Ctesias, who served Artaxerxes as physician and wrote the works entitled Assyrica and Persica. Then, after Cnidus, one comes to Ceramus and Bargasa, small towns situated above the sea.
Then to Halicarnassus, the royal residence of the dynasts of Caria, which was formerly called Zephyra. Here is the tomb of Mausolus, one of the Seven Wonders, a monument erected by Artemisia in honour of her husband; and here is the fountain called Salmacia, which has the slanderous repute, for what reason I do not know, of making effeminate all who drink from it. It seems that the effeminacy of man is laid to the charge of the air or of the water; yet it is not these, but rather riches and wanton living, that are the cause of effeminacy. Halicarnassus has an acropolis; and off the city lies Arconnesus. Its colonisers were, among others, Anthes and a number of Troezenians. Natives of Halicarnassus have been: Herodotus the historian, whom they later called a Thurian, because he took part in the colonisation of the Thurii; and Heracleitus the poet, the comrade of Callimachus; and, in my time, Dionysius the historian.
This city, too, met a reverse when it was forcibly seized by Alexander. For Hecatomnus, the king of the Carians, had three sons, Mausolus and Hidrieus and Pixodarus, and two daughters. Mausolus, the eldest of the brothers, married Artemisia, the elder of the daughters, and Hidrieus, the second son, married Ada, the other sister. Mausolus became king and at last, childless, he left the empire to his wife, by whom the above-mentioned tomb was erected. But she pined away and died through grief for her husband, and Hidrieus then became ruler. He died from a disease and was succeeded by his wife Ada; but she was banished by Pixodarus, the remaining son of Hecatomnos. Having espoused the side of the Persians, he sent for a satrap to share the empire with him; and when he too departed from life, the satrap took possession of Halicarnassus. And when Alexander came over, the satrap sustained a siege. His wife was Ada, who was the daughter of Pixodarus by Aphenis, a Cappadocian woman. But Ada, the daughter of Hecatomnos, whom Pixodarus had banished, entreated Alexander and persuaded him to restore her to the kingdom of which she had been deprived, having promised to co‑operate with him against the parts of the country which were in revolt, for those who held these parts, she said, were her own relations; and she also gave over to him Alinda, where she herself was residing. He assented and appointed her queen; and when the city, except the acropolis (it was a double city), had been captured, he assigned to her the siege of the acropolis. This thorough was captured a little later, the siege having now become a matter of anger and personal enmity.
Next one comes to a promontory, Termerium, belonging to the Myndians, opposite which lies Scandaria, a promontory of Cos, forty stadia distant from the mainland. And there is a place called Termerum above the promontory of Cos.
The city of the Coans was in ancient times called Astypalaea; and its people lived on another site, which was likewise on the sea. And then, on account of a sedition, they changed their abode to the present city, near Scandarium, and changed the name to Cos, the same as that of the island. Now the city is not large, but it is the most beautifully settled of all, and is most pleasing to behold as one sails from the high sea to its shore. The size of the island is about five hundred and fifty stadia. It is everywhere well supplied with fruits, but like Chios and Lesbos it is best in respect to its wine. Towards the south it has a promontory, Laceter, whence the distance to Nisyros is sixty stadia (but near Laceter there is a place called Halisarna), and on the west it has Drecanum and a village called Stomalimnê. Now Drecanum is about two hundred stadia distant from there, but Laceter adds thirty-five stadia to the length of the voyage. In the suburb is the Asclepïeium, a temple exceedingly famous and full of numerous votive offerings, among which is the Antigonus of Apelles. And Aphrodite Anadyomenê used to be there, but it is now dedicated to the deified Caesar in Rome, Augustus having thus dedicated to his father the female founder of his family. It is said that the Coans got a remission of one hundred talents of the appointed tribute in return for the painting. And it is said that the dietetics practised by Hippocrates were derived mostly from the cures recorded on the votive tablets there. He, then, is one of the famous men from Cos; and so is Simus the physician; as also Philetas, at the same time poet and critic; and, in my time, Nicias, who also reigned as tyrant over the Coans; and Ariston, the pupil and heir of the Peripatetic; and Theomnestus, a renowned harper, who was a political opponent of Nicias, was a native of the island.
On the coast of the mainland near the Myndian territory lies Astypalaea, a promontory; and also Zephyrium. Then forthwith one comes to Myndus, which has a harbour; and after Myndus to Bargylia, which is also a city; between the two is Caryanda, a harbour, and also an island bearing the same name, where the Caryandians lived. Here was born Scylax, the ancient historian. Near Bargylia is the temple of Artemis Cindyas, round which the rain is believed to fall without striking it. And there was once a place called Cindyê. From Bargylia there was a man of note, the Epicurean Protarchus, who was the teacher of Demetrius called Lacon.
Then one comes to Iasus, which lies on an island close to the mainland. It has a harbour; and the people gain most of their livelihood from the sea, for the sea here is well supplied with fish, but the soil of the country is rather poor. Indeed, people fabricate stories of this kind in regard to Iasus: When a citharoede was giving a recital, the people all listened for a time, but when the bell that announced the sale of fish rang, they all left him and went away to the fish market, except one man who was hard of hearing. The citharoede, therefore, went up to him and said: "Sir, I am grateful to you for the honour you have done me and for your love of music, for all the others except you went away the moment they heard the sound of the bell." And the man said, "What's that you say? Has the bell already rung?" And when the citharoede said "Yes," the man said, "Fare thee well," and himself arose and went away. Here was born the dialectician Diodorus, nicknamed Cronus, falsely so at the outset, for it was Apollonius his master who was called Cronus, but the nickname was transferred to him because of the true Cronus' lack of repute.
After Iasus one comes to the Poseidium of the Milesians. In the interior are three noteworthy cities: Mylasa, Stratoniceia, and Alabanda. The others are dependencies of these or else of the cities on the coast, among which are Amyzon, Heracleia, Euromus, and Chalcetor. As for these, there is less to be said.
But as for Mylasa: it is situated in an exceedingly fertile plain; and above the plain, towering into a peak, rises a mountain, which has a most excellent quarry of white marble. Now this quarry is of no small advantage, since it has stone in abundance and close at hand, for building purposes and in particular for the building of temples and other public works; accordingly this city, as much as any other, is in every way beautifully adorned with porticoes and temples. But one may well be amazed at those who so absurdly founded the city at the foot of a steep and commanding crag. Accordingly, one of the commanders, amazed at the fact, is said to have said, "If the man who founded this city was not afraid, was he not even ashamed?" The Mylasians have two temples of Zeus, Zeus Osogo, as he is called, and Zeus Labrandenus. The former is in the city, whereas Labranda is a village far from the city, being situated on the mountain near the pass that leads over from Alabanda to Mylasa. At Labranda there is an ancient shrine and statue of Zeus Stratius. It is honoured by the people all about and by the Mylasians; and there is a paved road of almost sixty stadia from the shrine to Mylasa, called the Sacred Way, on which their sacred processions are conducted. The priestly offices are held by the most distinguished of the citizens, always for life. Now these temples belong peculiarly to the city; but there is a third temple, that of the Carian Zeus, which is a common possession of all Carians, and in which, as brothers, both Lydians and Mysians have a share. It is related that Mylasa was a mere village in ancient times, but that it was the native land and royal residence of the Carians of the house of Hecatomnos. The city is nearest to the sea at Physcus; and this is their seaport.
Mylasa has had two notable men in my time, who were at once orators and leaders of the city, Euthydemus and Hybreas. Now Euthydemus, having inherited from his ancestors great wealth and high repute, and having added to these his own cleverness, was not only a great man in his native land, but was also thought worthy of the foremost honour in Asia. As for Hybreas, as he himself used to tell the story in his school and as confirmed by his fellow-citizens, his father left him a mule-driver and a wood-carrying mule. And, being supported by these, he became a pupil of Diotrephes of Antiocheia for a short time, and then came back and "surrendered himself to the office of market-clerk." But when he had been "tossed about" in this office and had made but little money, he began to apply himself to the affairs of state and to follow closely the speakers of the forum. He quickly grew in power, and was already an object of amazement in the lifetime of Euthydemus, but in particular after his death, having become master of the city. So long as Euthydemus lived he strongly prevailed, being at once powerful and useful to the city, so that even if there was something tyrannical about him, it was atoned for by the fact that it was attended by what was good for the city. At any rate, people applaud the following statement of Hybreas, made by him towards the end of a public speech: "Euthydemus: you are an evil necessary to the city, for we can live neither with you nor without you." 6However, although he had grown very strong and had the repute of being both a good citizen and orator, he stumbled in his political opposition to Labienus; for while the others, since they were without arms and inclined to peace, yielded to Labienus when he was coming against them with an army and an allied Parthian force, the Parthians by that time being in possession of Asia, yet Zeno of Laodiceia and Hybreas, both orators, refused to yield and caused to cities to revolt. Hybreas also provoked Labienus, a lada who was irritable and full of folly, by a certain pronouncement; for when Labienus proclaimed himself Parthian Emperor, Hybreas said: "Then I too call myself Carian Emperor." Consequently Labienus set out against the city with cohorts of Roman soldiers in Asia that were already organised. Labienus did not seize Rhodes, but he shamefully maltreated his home, with its costly furnishings, and plundered it. And he likewise damaged the whole of the city. But though Hybreas abandoned Asia, he came back and rehabilitated both himself and the city. So much, then, for Mylasa.
Stratoniceia is a settlement of Macedonians. And this too was adorned with costly improvements by the kings. There are two temples in the country of the Stratoniceians, of which the most famous, that of Hecatê, is at Lagina; and it draws great festal assemblies every year. And near the city is the temple of Zeus Chrysaoreus, the common possession of all Carians, whither they gather both to offer sacrifice and to deliberate on their common interests. Their League, which consists of villages, is called "Chrysaorian." And those who present the most villages have a preference in the vote, like, for example, the people of Ceramus. The Stratoniceians also have a share in the League, although they are not of the Carian stock, but because they have villages belonging to the Chrysaorian League. Here, too, in the time of our fathers, was born a noteworthy man, Menippus, surnamed Catocas, whom Cicero, as he says in one of his writings, applauded above all the Asiatic orators he had heard, comparing him with Xenocles and with the other orators who flourished in the latter's time. But there is also another Stratoniceia, "Stratoniceia under the Taurus," as it is called; it is a small town situated near the mountain.
Alabanda is also situated at the foot of hills, two hills that are joined together in such a way that they present the appearance of an ass laden with panniers. And indeed Apollonius Malacus, in ridiculing the city both in regard to this and in regard to the large number of scorpions there, said that it was an "ass laden with panniers of scorpions." Both this city and Mylasa are full of these creatures, and so is the whole of the mountainous country between them. Alabanda is a city of people who live in luxury and debauchery, containing many girls who play the harp. Alabandians worthy of mention are two orators, brothers, I mean Menecles, whom I mentioned a little above, and Hierocles, and also Apollonius and Molon, who changed their abode to Rhodes.
Of the numerous accounts of the Carians, the one that is generally agreed upon is this, that the Carians were subject to the rule of Minos, being called Leleges at that time, and lived in the islands; then, having migrated to the mainland, they took possession of much of the coast and of the interior, taking it away from its previous possessors, who for the most part were Leleges and Pelasgians. In turn these were deprived of a part of their country by the Greeks, I mean Ionians and Dorians. As evidences of their zeal for military affairs, writers adduce shield-holders, shield-emblems, and crests, for all these are called "Carian." At least Anacreon says, "Come, put thine arm through the shield-holder, work of the Carians." And Alcaeus says, "shaking the Carian crest."
When the poet says, "Masthles in turn led the Carians, of barbarian speech," we have no reason to inquire how it is that, although he knew so many barbarian tribes, he speaks of the Carians alone as "of barbarian speech," but nowhere speaks of "barbarians." Thucydides, therefore, is not correct, for he says that Homer "did not use the term 'barbarians' either, because the Hellenes on their part had not yet been distinguished under one name as opposed to them"; for the poet himself refutes the statement that the Hellenes had not yet been so distinguished when he says, "My husband, whose fame is wide through Hellas and mid‑Argos." And again, "And if thou dost wish to journey through Hellas and mid‑Argos." Further, if they were not called "barbarians," how could they properly be called a people "of barbarian speech"? So neither Thucydides is correct, nor Apollodorus the grammarian, who says that the general term was used by the Hellenes in a peculiar and abusive sense against the Carians, and in particular by the Ionians, who hated them because of their enmity and the continuous military campaigns; for it was right to name them barbarians in this sense. But I raise the question, Why does he call them people "of barbarian speech," but not even once calls them barbarians?" "Because," Apollodorus replies, "the plural does not fall in with the metre; this is why he does not call them barbarians." But though this case does not fall in with metre, the nominative case does not differ metrically from that of "Dardanians": "Trojans and Lycians and Dardanians." So, also, the word "Trojan," in "of what kind the Trojan horses are." Neither is he correct when he says that the language of the Carians is very harsh, for it is not, but even has very many Greek words mixed up with it, according to the Philip who wrote The Carica. I suppose that the word "barbarian" was at first uttered onomatopoetically in reference to people who enunciated words only with difficulty and talked harshly and raucously, like our words "battarizein," "traulizein," and "psellizein"; for we are by nature very much inclined to denote sounds by words that sound like them, on account of their homogeneity. Wherefore onomatopoetic words abound in our language, as, for example, "celaryzein," and also "clangê," "psophos," "boê," and "crotos," most of which are by now used in their proper sense. Accordingly, when all who pronounced words thickly were being called barbarians onomatopoetically, it appeared that the pronunciations of all alien races were likewise thick, I mean of those that were not Greek. Those, therefore, they called barbarians in the special sense of the term, at first derisively, meaning that they pronounced words thickly or harshly; and then we misused the word as a general ethnic term, thus making a logical distinction between the Greeks and all other races. The fact is, however, that through our long acquaintance and intercourse with the barbarians this effect was at last seen to be the result, not of a thick pronunciation or any natural defect in the vocal organs, but of the peculiarities of their several languages. And there appeared another faulty and barbarian-like pronunciation in our language, whenever any person speaking Greek did not pronounce it correctly, but pronounced the words like barbarians who are only beginning to learn Greek and are unable to speak it accurately, as is also the case with us in speaking their languages. This was particularly the case with the Carians, for, although the other peoples were not yet having very much intercourse with the Greeks nor even trying to live in Greek fashion or to learn our language — with the exception, perhaps, of rare persons who by chance, and singly, mingled with a few of the Greeks — yet the Carians roamed throughout the whole of Greece, serving on expeditions for pay. Already, therefore, the barbarous element in their Greek was strong, as a result of their expeditions in Greece; and after this it spread much more, from the time they took up their abode with the Greeks in the islands; and when they were driven thence into Asia, even here they were unable to live apart from the Greeks, I mean when the Ionians and Dorians later crossed over to Asia. The term "barbarise," also, has the same origin; for we are wont to use this too in reference to those who speak Greek badly, not to those who talk Carian. So, therefore, we must interpret the terms "speak barbarously" and "barbarously-speaking" as applying to those who speak Greek badly. And it was from the term "Carise" that the term "barbarise" was used in a different sense in works on the art of speaking Greek; and so was the term "soloecise," whether derived from Soli, or made up in some other way.
Artemidorus says that, as one goes from Physcus, in the Peraea of the Rhodians, to Ephesus, the distance to Lagina is eight hundred and fifty stadia; and thence to Alabanda, two hundred and fifty more; and to Tralleis, one hundred and sixty. But one comes to the road that leads into Tralleis after crossing the Maeander River, at about the middle of the journey, where are the boundaries of Caria. The distance all told from Physcus to the Maeander along the road to Ephesus amounts to one thousand one hundred and eighty stadia. Again, from the Maeander, traversing next in order the length of Ionia along the same road, the distance from the river to Tralleis is eighty stadia; then to Magnesia, one hundred and forty; to Ephesus, one hundred and twenty; to Smyrna, three hundred and twenty; and to Phocaea and the boundaries of Ionia, less than two hundred; so that the length of Ionia in a straight line would be, according to Artemidorus, slightly more than eight hundred stadia. Since there is a kind of common road constantly used by all who travel from Ephesus towards the east, Artemidorus traverses this too: from Ephesus to Carura, a boundary of Caria towards Phrygia, through Magnesia, Tralleis, Nysa, and Antiocheia, is a journey of seven hundred and forty stadia; and, from Carura, the journey in Phrygia, through Laodiceia, Apameia, Metropolis and Chelidonia. Now near the beginning of Paroreius, one comes to Holmi, about nine hundred and twenty stadia from Carura, and, near the end of Paroreius near Lycaonia, through Philomelium, to Tyriaeum, slightly more than five hundred. Then Lycaonia, through Laodiceia Catacecaumenê, as far as Coropassus, eight hundred and forty stadia; from Coropassus in Lycaonia to Garsaura, a small town in Cappadocia, situated on its borders, one hundred and twenty; thence to Mazaca, the metropolis of the Cappadocians, through Soandum and Sadacora, six hundred and eighty; and thence to the Euphrates River, as far as Tomisa, a place in Sophenê, through Herphae, a small town, one thousand four hundred and forty. The places on a straight line with these as far as India are the same in Artemidorus as they are in Eratosthenes. But Polybiusb says that we should rely most on Artemidorus in regard to the places here. He begins with Samosata in Commagenê, which lies at the river-crossing and at Zeugma, and states that the distance to Samosata, across the Taurus, from the boundaries of Cappadocia round Tomisa is four hundred and fifty stadia. |
|
|
|
|
14 - 3 Lycia 
After the Peraea of the Rhodians, of which Daedala is a boundary, sailing next in order towards the rising sun, one comes to Lycia, which extends as far as Pamphylia; then to Pamphylia, extending as far as the Tracheian Cilicians; and then to the country of these, extending as far as the other Cilicians living round the Gulf of Issus. These are parts of the peninsula, the isthmus of which, as I was saying, is the road from Issus to Amisus, or, according to some, Sinopê, but they lie outside the Taurus on the narrow coast which extends from Lycia as far as the region of Soli, the present Pompeïopolis. Then forthwith the coast that lies on the Issic Gulf, beginning at Soli and Tarsus, spreads out into plains. So then, when I have traversed the coast, my account of the whole peninsula will have been completed. Then I shall pass to the other parts of Asia that are outside the Taurus. And lastly I shall set forth my account of Libya.
2 After Daedala of the Rhodians, then, one comes to a mountain in Lycia which bears the same name as the city, Daedala, whence the whole voyage along the Lycian coast takes its beginning; this coast extends one thousand seven hundred and twenty stadia, and is rugged and hard to travel, but is exceedingly well supplied with harbours and inhabited by decent people. Indeed, the nature of the country, at least, is similar to both that of the Pamphylians and the Tracheian Cilicians, but the former used their places as bases of operation for the business of piracy, when they engaged in piracy themselves or offered them to pirates as markets for the sale of booty and as naval stations. In Sidê, at any rate, a city in Pamphylia, the dockyards stood open to the Cilicians, who would sell their captives at auction there, though admitting that these were freemen. But the Lycians continued living in such a civilised and decent way that, although the Pamphylians through their successes gained the mastery of the sea as far as Italy, still they themselves were stirred by no desire for shameful gain, but remained within the ancestral domain of the Lycian League.
3 There are twenty-three cities that share in the vote. They come together from each city to a general congress, after choosing whatever city they approve of. The largest of the cities control three votes each, the medium-sized two, and the rest one. In the same proportion, also, they make contributions and discharge other liturgies. Artemidorus said that the six largest were Xanthus, Patara, Pinara, Olympus, Myra, and Tlos, the last-named being situated near the pass that leads over into Cibyra. At the congress they first choose a "Lyciarch," and then other officials of the League; and general courts of justice are designated. In earlier times they would deliberate about war and peace and alliances, but now they naturally do not do so, since these matters necessarily lie in the power of the Romans, except, perhaps when the Romans should give them permission or it should be for their benefit. Likewise, judges and magistrates are elected from the several cities in the same proportion. And since they lived under such a good government, they remained ever free under the Romans, thus retaining their ancestral usages; and they saw the pirates utterly wiped out, first by Servilius Isauricus, at the time that he demolished Isaura, and later by Pompey the Great, when he set fire to more than thirteen hundred boats and laid waste their settlements. Of the pirates who survived the fights, he brought some down to Soli, which he named Pompeïopolis, and the others to Dymê, where there was a dearth of population; it is now occupied by a colony of Romans. The poets, however, and especially the tragic poets, confuse the tribes, as, for example, the Trojans and the Mysians and the Lydians, whom they call Phrygians; and likewise the Lycians, whom they call Carians.
4 After Daedala, then, I mean the mountain in Lycia, one comes to a Lycian town near it, Telmessus, and to Telmessis, a promontory with a harbour. Eumenes5 received this place from the Romans in the Antiochian War, but when his kingdom was dissolved the Lycians got it back again.
5 Then, next, one comes to Anticragus, a steep mountain, where is Carmylessus, an inhabited place situated in a ravine; and, after this, to Cragus, which has eight promontories and a city of the same name. The scene of the myth of Chimaera is laid in the neighbourhood of these mountains. Chimaera, a ravine extending up from the shore, is not far from them. At the foot of Cragus, in the interior, lies Pinara, one of the largest cities in Lycia. Here Pandarus is held in honour, who may, perhaps, be identical with the Trojan hero, as when the poet says, "the daughter of Pandareus, the nightingale of the greenwood," for Pandareus is said to have been from Lycia.
6 Then one comes to the Xanthus River, which the people of earlier times called the Sirbis. Sailing up this river by rowboat for ten stadia one comes to the Letoüm; and proceeding sixty stadia beyond the temple one comes to the city of the Xanthians, the largest city in Lycia. After Xanthus, to Patara, which is also a large city, has a harbour, has a temple of Apollo, and was founded by Patarus. When Ptolemy Philadelphus repaired it, he called it Lycian Arsinoê, but the original name prevailed.
7 Then one comes to Myra, at a distance of twenty stadia above the sea, on a lofty hill. Then to the outlet of the Limyrus River, and then, going twenty stadia inland on foot, to Limyra, a small town. In the intervening distance on the coasting voyage there are numerous isles and harbours, among which are the island Megistê, with a city of the same name, and Cisthenê. And in the interior are places called Phellus and Antiphellus and Chimaera, which last I have mentioned above.
8 Then one comes to the promontory Hiera; and to the Chelidoniae, three rugged islands, which are about equal in size and are about five stadia distant from one another. They lie about six stadia off the shore, and one of them has a landing-place for vessels. Here it is, according to the majority of writers, that the Taurus takes its beginning, not only because of the loftiness of the promontory and because it extends down from the Pisidian mountains that lie above Pamphylia, but also because of the islands that lie off it, presenting, as they do, a sort of conspicuous sign in the sea, like outskirts of a mountain. But in truth the mountainous tract is continuous from the Peraea of the Rhodians to the parts near Pisidia; and this tract too is called the Taurus. The Chelidoniae are likewise thought to lie approximately opposite to Canobus; and the passage thence to Canobus is said to be four thousand stadia. From the promontory Hiera to Olbia there remain three hundred and sixty-seven stadia; and on this stretch lie, not only Crambusa, but also Olympus, a large city and a mountain of the same name, which latter is also called Phoenicus. Then one comes to Corycus, a tract of sea‑coast.
9 Then one comes to Phaselis, with three harbours, a city of note, and to a lake. Above it lies Solyma, a mountain, and also Termessus, a Pisidian city situated near the defiles, through which there is a pass over the mountain to Milyas. Alexander destroyed Milyas for the reason that he wished to open the defiles. Near Phaselis, by the sea, there are defiles, through which Alexander led his army. And here there is a mountain called Climax, which lies near the Pamphylian Sea and leaves a narrow pass on the shore; and in calm weather this pass is free from water, so that it is passable for travelers, but when the sea is at flood it is to a considerable extent hidden by the waves. Now the pass that leads over through the mountain is circuitous and steep, but in fair weather people use the pass along the shore. Alexander, meeting with a stormy season, and being a man who in general trusted to luck, set out before the waves had receded; and the result was that all day long his soldiers marched in water submerged to their navels. Now this city too is Lycian, being situated on the borders towards Pamphylia, but it has no part in the common League and is a separate organisation to itself.
Now the poet makes the Solymi different from the Lycians, for when Bellerophon was sent by the king of the Lycians to the second struggle, "he fought with the glorious Solymi." But others, who assert that the Lycians were in earlier times called Solymi, but in later times were called Termilae from the Termilae who came there from Crete with Sarpedon, and after this were called Lycians, from Lycius the son of Pandion, who, after having been banished from his homeland, was admitted by Sarpedon as a partner in his empire, are not in agreement with Homer. Better is the opinion of those who assert that by "Solymi" the poet means the people who are now called the Milyae, of whom I have already spoken. |
|
|
|
|
14 - 4 Pamphylia 
After Phaselis one comes to Olbia, the beginning of Pamphylia, a large fortress; and after this to the Cataractes River, so called, which dashes down from a lofty rock in such volume and so impetuously that the noise can be heard from afar. Then to a city, Attaleia, so named after its founder Attalus Philadelphus, who also sent a colony to Corycus, a small neighbouring town, and surrounded it with a greater circuit-wall. It is said that both Thebê and Lyrnessus are to be seen between Phaselis and Attaleia, a part of the Trojan Cilicians having been driven out of the plain of Thebê into Pamphylia, as Callisthenes states.
2 Then one comes to the Cestrus River; and, sailing sixty stadia up this river, one comes to Pergê, a city; and near Pergê, on a lofty site, to the temple of Artemis Pergaea, where a general festival is celebrated every year. Then, about forty stadia above the sea, one comes to Syllium, a lofty city that is visible from Pergê. Then one comes to a very large lake, Capria; and after this, to the Eurymedon River; and, sailing sixty stadia up this river, to Aspendus, a city with a flourishing population and founded by the Argives. Above Aspendus lies Petnelissus. Then comes another river; and also numerous isles that lie off it. Then Sidê, a colony of the Cymaeans, which has a temple of Athena; and near by is the coast of the Lesser Cibyratae. Then the Melas River and a mooring-place. Then Ptolemaïs, a city. And after this come the boundaries of Pamphylia, and also Coracesium, the beginning of Cilicia Tracheia. The whole of the voyage along the coast of Pamphylia is six hundred and forty stadia.
Herodotus says that the Pamphylians are the descendants of the peoples led by Amphilochus and Calchas, a miscellaneous throng who accompanied them from Troy; and that most of them remained here, but that some of them were scattered to numerous places on earth. Callinus says that Calchas died in Clarus, but that the peoples led by Mopsus passed over the Taurus, and that, though some remained in Pamphylia, the others were dispersed in Cilicia, and also in Syria as far even as Phoenicia. |
|
|
|
|
14 - 5 Cilicia 
1 As for Cilicia outside the Taurus, one part of it is called Tracheia and the other Pedias. As for Tracheia, its coast is narrow and has no level ground, or scarcely any; and, besides that, it lies at the foot of the Taurus, which affords a poor livelihood as far as its northern side in the region of Isaura and of the Homonadeis as far as Pisidia; and the same country is also called Tracheiotis, and its inhabitants Tracheiotae. But Cilicia Pedias extends from Soli and Tarsus as far as Issus, and also to those parts beyond which, on the northern side of the Taurus, Cappadocians are situated; for this country consists for the most part of plains and fertile land. Since some parts of this country are inside the Taurus and others outside it, and since I have already spoken of those inside it, let me now speak of those outside it, beginning with the Tracheiotae.
2 The first place in Cilicia, then, to which one comes, is a stronghold, Coracesium, situated on an abrupt rock, which was used by Diodotus, called Tryphon, as a base of operations at the time when he caused Syria to revolt from the kings and was fighting it out with them, being successful at one time and failing at another. Now Tryphon was hemmed up in a certain place by Antiochus, son of Demetrius, and forced to kill himself; and it was Tryphon, together with the worthlessness of the kings who by succession were then reigning over Syria and at the same time over Cilicia, who caused the Cilicians to organise their gangs of pirates; for on account of his revolutionary attempts others made like attempts at the same time, and thus the dissensions of brethren with one another put the country at the mercy of any who might attack it. The exportation of slaves induced them most of all to engage in their evil business, since it proved most profitable; for not only were they easily captured, but the market, which was large and rich in property, was not extremely far away, I mean Delos, which could both admit and send away ten thousand slaves on the same day; whence arose the proverb, "Merchant, sail in, unload your ship, everything has been sold." The cause of this was the fact that the Romans, having become rich after the destruction of Carthage and Corinth, used many slaves; and the pirates, seeing the easy profit therein, bloomed forth in great numbers, themselves not only going in quest of booty but also trafficking in slaves. The kings both of Cyprus and of Egypt co‑operated with them in this, being enemies to the Syrians. Neither were the Rhodians friendly to the Syrians, and they therefore afforded them no assistance. And at the same time the pirates, pretending to be slave-dealers, carried on their evil business unchecked. Neither were the Romans concerning themselves as yet so much about the peoples outside the Taurus; but they sent Scipio Aemilianus, and again certain others, to inspect the tribes and the cities; and they decided that the above mentioned piracy was due to the incompetence of the rulers, although they were ashamed, since they themselves had ratified the hereditary succession from Seleucus Nicator, to deprive them of it. And this is what made the Parthians masters of the country, who got possession of the region on the far edge of the Euphrates; and at last made also the Armenians masters, who not only seized the country outside the Taurus even as far as Phoenicia, but also, so far as they could, overthrew the kings and the whole royal stock; the sea, however, they gave over to the Cilicians. Then, after these people had grown in power, the Romans were forced to destroy them by war and with an army, although they had not hindered their growing power. Now it is hard to condemn the Romans of negligence, since, being engaged with matters that were nearer and more urgent, they were unable to watch those that were farther away. So much I have decided to say by way of a brief digression from my geographical description.
3 After Coracesium, one comes to Arsinoê, a city; then to Hamaxia, a settlement on a hill, with a harbour, where ship-building timber is brought down. Most of this timber is cedar; and it appears that this region beyond others abounds in cedar-wood for ships; and it was on this account that Antony assigned this region to Cleopatra, since it was suited to the building of her fleets. Then one comes to Laertes, a stronghold on a breast-shaped hill, with a mooring-place. Then to Selinus, a city and river. Then to Cragus, a rock which is precipitous all round and near the sea. Then to Charadrus, a fortress, which also has a mooring-place (above it lies Mt. Andriclus); and the coast alongside it, called Platanistes, is rugged. Then to Anemurium, a promontory, where the mainland approaches closest to Cyprus, in the direction of the promontory of Crommyus, the passage across being three hundred and fifty stadia. Now the coasting-voyage along Cilicia from the borders of Pamphylia to Anemurium is eight hundred and twenty stadia, whereas the rest, as far as Soli, is about five hundred stadia. On this latter one comes to Nagidus, the first city after Anemurium; then to Arsinoê, which has a landing-place; then to a place called Melania, and to Celenderis, a city with a harbour. Some writers, among whom is Artemidorus, make Celenderis, not Coracesium, the beginning of Cilicia. And he says that the distance from the Pelusian mouth to Orthosia is three thousand nine hundred stadia; to the Orontes River, one thousand one hundred and thirty; to the Gates next thereafter, five hundred and twenty-five; and to the borders of the Cilicians, one thousand two hundred and sixty.
4 Then one comes to Holmi, where the present Seleuceians formerly lived; but when Seleuceia on the Calycadnus was founded, they migrated there; for immediately on doubling the shore, which forms a promontory called Sarpedon, one comes to the outlet of the Calycadnus. Near the Calycadnus is also Zephyrium, likewise a promontory. The river affords a voyage inland to Seleuceia, a city which is well-peopled and stands far aloof from the Cilician and Pamphylian usages. Here were born in my time noteworthy men of the Peripatetic sect of philosophers, Athenaeus and Xenarchus. Of these, Athenaeus engaged also in affairs of state and was for a time leader of the people in his native land; and then, having fallen into a friendship with Murena, he was captured along with Murena when in flight with him, after the plot against Augustus Caesar had been detected, but, being clearly proven guiltless, he was released by Caesar. And when, on his return to Rome, the first men who met him were greeting him and questioning him, he repeated the following from Euripides: "I am come, having left the vaults of the dead and the gates of darkness." But he survived his return only a short time, having been killed in the collapse, which took place in the night, of the house in which he lived. Xenarchus, however, of whom I was a pupil, did not tarry long at home, but resided at Alexandria and at Athens and finally at Rome, having chosen the life of a teacher; and having enjoyed the friendship both of Areius and later of Caesar Augustus, he continued to be held in honour down to old age; but shortly before the end he lost his sight, and then died of a disease.
5 After the Calycadnus one comes to the rock Poecilê, as it is called, which has steps hewn in it that lead to Seleuceia; then to Anemurium, a promontory, bearing the same name as the former, and to Crambusa, an island, and to Corycus, a promontory, above which, at a distance of twenty stadia, is the Corycian cave, in which the best crocus grows. It is a great circular hollow, with a rocky brow situated all round it that is everywhere quite high. Going down into it, one comes to a floor that is uneven and mostly rocky, but full of trees of the shrub kind, both the evergreen and those that are cultivated. And among these trees are dispersed also the plots of ground which produce the crocus. There is also a cave here, with a great spring, which sends forth a river of pure and transparent water; the river forthwith empties beneath the earth, and then, after running invisible underground, issues forth into the sea. It is called Picrum Hydor.
6 Then, after Corycus, one comes to Elaeussa, an island lying close to the mainland, which Archelaüs settled, making it a royal residence, after he had received the whole of Cilicia Tracheia except Seleuceia — the same way in which it was obtained formerly by Amyntasand still earlier by Cleopatra; for since the region was naturally well adapted to the business of piracy both by land and by sea — by land, because of the height of the mountains and the large tribes that live beyond them, tribes which have plains and farm-lands that are large and very easily overrun, and by sea, because of the good supply, not only of shipbuilding timber, but also of harbours and fortresses and secret recesses — with all this in view, I say, the Romans thought that it was better for the region to be ruled by kings than to be under the Roman prefects sent to administer justice, who were not likely always to be present or to have armed forces with them. Thus Archelaüs received, in addition to Cappadocia, Cilicia Tracheia; and the boundary of the latter, the river Lamus and the village of the same name, lies between Soli and Elaeussa.
7 Near the mountain ridges of the Taurus lies the piratical stronghold of Zenicetus — I mean Olympus, both mountain and fortress, whence are visible all Lycia and Pamphylia and Pisidia and Milyas; but when the mountain was captured by Isauricus, Zenicetus burnt himself up with his whole house. To him belonged also Corycus and Phaselis and many places in Pamphylia; but all were taken by Isauricus.
8 After Lamus one comes to Soli, a noteworthy city, the beginning of the other Cilicia, that which is round Issus; it was founded by Achaeans and Rhodians from Lindus. Since this city was of scant population, Pompey the Great settled in it those survivors of the pirates whom he judged most worthy of being saved and provided for; and he changed its name to Pompeïopolis. Among the famous natives of Soli were: Chrysippus the Stoic philosopher, whose father had moved there from Tarsus; Philemon, the comic poet; and Aratus, who wrote the work hand entitled The Phaenomena, in verse.
9 Then to Zephyrium, which bears the same name as the place near Calycadnus. Then, a little above the sea, to Anchialê, which, according to Aristobulus, was founded by Sardanapallus. Here, he says, is the tomb of Sardanapallus, and a stone figure which represents the fingers of the right hand as snapping together, and the following inscription in Assyrian letters: "Sardanapallus, the son of Anacyndaraxes, built Anchialê and Tarsus in one day. Eat, drink, be merry, because all things else are not worth this," meaning the snapping of the fingers. Choerilus also mentions this inscription; and indeed the following verses are everywhere known: "Mine are all that I have eaten, and my loose indulgences and the delights of love that I have enjoyed; but those numerous blessings have been left behind."
Above Anchialê lies Cyinda, a fortress, which at one time was used as a treasury by the Macedonians. But the treasures were taken away by Eumenes, when he revolted from Antigonus. And still above this and Soli is a mountainous country, in which is a city Olbê, with a temple of Zeus, founded by Ajax the son of Teucer. The priest of this temple became dynast of Cilicia Tracheia; and then the country was beset by numerous tyrants, and the gangs of pirates were organised. And after the overthrow of these they called this country the domain of Teucer, and called the same also the priesthood of Teucer; and most of the priests were named Teucer or Ajax. But Aba, the daughter of Xenophanes, one of the tyrants, came into this family by marriage and herself took possession of the empire, her father having previously received it in the guise of guardian. But later both Antony and Cleopatra conferred it upon her as a favour, being moved by her courteous entreaties. And then she was overthrown, but the empire remained with her descendants. After Anchialê one comes to the outlets of the Cydnus, near the Rhegma, as it is called. It is a place that forms into a lake, having also ancient arsenals; and into it empties the Cydnus River, which flows through the middle of Tarsus and has its sources in the city Taurus, which lies above Taurus. The lake is also the naval station of Tarsus.
Now thus far the seaboard as a whole, beginning at the Peraea of the Rhodians, extends towards the equinoctial east from the equinoctial west, and then bends in the direction of winter sunrise as far as Issus, and then forthwith takes a bend towards the south as far as Phoenicia; and the remainder extends towards the east as far as the Pillars and there ends. Now the truth is that the actual isthmus of the peninsula which I have described is that which extends from Tarsus and the outlet of the Cydnus to Amisus, for this is the shortest distance from Amisus to the boundaries of Cilicia; and the distance thence to Tarsus is one hundred and twenty stadia, and the distance from there to the outlet of the Cydnus is no more than that. And in fact to Issus, and the sea near it, there is no other road from Amisus which is shorter than that through Tarsus, and Tarsus is not nearer to Issus than to the Cydnus; and therefore it is clear that in reality this would be the isthmus; but still people call that which extends as far as the Gulf of Issus the true isthmus, thus betraying the facts because of the significance of the gulf. And it is because of this very thing that I, without making any accurate distinctions, represent the line from Rhodes, which I have prolonged to the Cydnus, to be the same as the line extending as far as the Issus, and also assert that the Taurus extends in a straight line with that line as far as India.
As for Tarsus, it lies in a plain; and it was founded by the Argives who wandered with Triptolemus in quest of Io; and it is intersected in the middle by the Cydnus River, which flows past the very gymnasium of the young men. Now inasmuch as the source of the river is not very far away and its stream passes through a deep ravine and then empties immediately into the city, its discharge is both cold and swift; and hence it is helpful both to men and to cattle that are suffering from swollen sinews, if they immerse themselves in its waters.
The people at Tarsus have devoted themselves so eagerly, not only to philosophy, but also to the whole round of education in general, that they have surpassed Athens, Alexandria, or any other place that can be named where there have been schools and lectures of philosophers. But it is so different from other cities that there the men who are fond of learning are all natives, and foreigners are not inclined to sojourn there; neither do these natives stay there, but they complete their education abroad; and when they have completed it they are pleased to live abroad, and but few go back home. But the opposite is the case with the other cities which I have just mentioned except Alexandria; for many resort to them and pass time there with pleasure, but you would not see many of the natives either resorting to places outside their country through love of learning or eager about pursuing learning at home. With the Alexandrians, however, both things take place, for they admit many foreigners and also send not a few of their own citizens abroad. Further, the city of Tarsus has all kinds of schools of rhetoric; and in general it not only has a flourishing population but also is most powerful, thus keeping up the reputation of the mother-city.
The following men were natives of Tarsus: among the Stoics, Antipater and Archedemus and Nestor; and also the two Athenodoruses, one of whom, called Cordylion, lived with Marcus Cato and died at his house; and the other, the son of Sandon, called Cananites after some other village, was Caesar's teacher and was greatly honoured by him; and when he returned to his native land, now an old man, he broke up the government there established, which was being badly conducted by Boethus, among others, who was a bad poet and a bad citizen, having prevailed there by currying the favour of the people. He had been raised to prominence by Antony, who at the outset received favourably the poem which he had written upon the victory at Philippi, but still more by that facility prevalent among the Tarsians whereby he could instantly speak offhand and unceasingly on any given subject. Furthermore, Antony promised the Tarsians an office of gymnasiarch, but appointed Boethus instead of a gymnasiarch, and entrusted to him the expenditures. But Boethus was caught secreting, among other things, the olive‑oil; and when he was being proven guilty by his accusers in the presence of Antony he deprecated Antony's wrath, saying, among other things, that "Just as Homer had hymned the praises of Achilles and Agamemnon and Odysseus, so I have hymned thine. It is not right, therefore, that I should be brought before you on such slanderous charges." When, however, the accuser caught the statement, he said, "Yes, but Homer did not steal Agamemnon's oil, nor yet that of Achilles, but you did; and therefore you shall be punished." However, he broke the wrath of Antony by courteous attentions, and no less than before kept on plundering the city until the overthrow of Antony. Finding the city in this plight, Athenodorus for a time tried to induce both Boethus and his partisans to change their course; but since they would abstain from no act of insolence, he used the authority given him by Caesar, condemned them to exile, and expelled them. These at first indicted him with the following inscription on the walls: "Work for young men, counsels for the middle-aged, and flatulence for old men"; and when he, taking the inscription as a joke, ordered the following words to be inscribed beside it, "thunder for old men," someone, contemptuous of all decency and afflicted with looseness of the bowels, profusely bespattered the door and wall of Athenodorus' house as he was passing by it at night. Athenodorus, while bringing accusations in the assembly against the faction, said: "One may see the sickly plight and the disaffection of the city in many ways, and in particular from its excrements." These men were Stoics; but the Nestor of my time, the teacher of Marcellus, son of Octavia the sister of Caesar, was an Academician. He too was at the head of the government of Tarsus, having succeeded Athenodorus; and he continued to be held in honour both by the prefects and in the city.
Among the other philosophers from Tarsus, "whom I could well note and tell their names," are Plutiades and Diogenes, who were among those philosophers that went round from city to city and conducted schools in an able manner. Diogenes also composed poems, as if by inspiration, when a subject was given him — for the most part tragic poems; and as for grammarians whose writings are extant, there are Artemidorus and Diodorus; and the best tragic poet among those enumerated in the "Pleias" was Dionysides. But it is Rome that is best able to tell us the number of learned men from this city; for it is full of Tarsians and Alexandrians. Such is Tarsus.
After the Cydnus River one comes to the Pyramus River, which flows from Cataonia, a river which I have mentioned before. According to Artemidorus, the distance thence to Soli in a straight voyage is five hundred stadia. Near by, also, is Mallus, situated on a height, founded by Amphilochus and Mopsus, the latter the son of Apollo and Manto, concerning whom many myths are told. And indeed I, too, have mentioned them in my account of Calchas and of the quarrel between Calchas and Mopsus about their powers of divination. For some writers transfer this quarrel, Sophocles, for example, to Cilicia, which he, following the custom of tragic poets, calls Pamphylia, just as he calls Lycia "Caria" and Troy and Lydia "Phrygia." And Sophocles, among others, tells us that Calchas died there. But, according to the myth, the contest concerned, not only the power of divination, but also the sovereignty; for they say that Mopsus and Amphilochus went from Troy and founded Mallus, and that Amphilochus then went away to Argos, and, being dissatisfied with affairs there, returned to Mallus, but that, being excluded from a share in the government there, he fought a duel with Mopsus, and that both fell in the duel and were buried in places that were not in sight of one another. And to‑day their tombs are to be seen in the neighbourhood of Magarsa near the Pyramus River. This was the birthplace of Crates the grammarian, of whom Panaetius is said to have been a pupil.
Above this coast lies the Aleïan Plain, through which Philotas led the cavalry for Alexander, when Alexander led his phalanx from Soli along the coast and the territory of Mallus against Issus and the forces of Dareius. It is said that Alexander performed sacrifices to Amphilochus because of his kinship with the Argives. Hesiod says that Amphilochus was slain by Apollo at Soli; but others say that he was slain in the neighbourhood of the Aleïan Plain, and others in Syria, when he was quitting the Aleïan Plain because of the quarrel.
After Mallus one comes to Aegaeae, a small town, with a mooring-place; and then to the Amanides Gates, with a mooring-place, where ends the mountain Amanus, which extends down from the Taurus and lies above Cilicia towards the east. It was always ruled by several powerful tyrants, who possessed strongholds; but in my time a notable man established himself as lord of all, and was named king by the Romans because of his manly virtues — I refer to Tarcondimotus, who bequeathed the succession to his posterity.
After Aegaeae, one comes to Issus, a small town with a mooring-place, and to the Pinarus River. It was here that the struggle between Alexander and Dareius occurred; and the gulf is called the Issic Gulf. On this gulf are situated the city Rhosus, the city Myriandrus, Alexandreia, Nicopolis, Mopsuestia, and Pylae, as it is called, which is the boundary between the Cilicians and the Syrians. In Cilicia is also the temple and oracle of the Sarpedonian Artemis; and the oracles are delivered by persons who are divinely inspired.
After Cilicia the first Syrian city is Seleuceia-in‑Pieria, near which the Orontes River empties. The voyage from Seleuceia to Soli, on a straight course, is but little short of one thousand stadia.
Since the Cilicians in the Troad whom Homer mentions are far distant from the Cilicians outside the Taurus, some represent those in Troy as original colonisers of the latter, and point out certain places of the same name there, as, for example, Thebê and Lyrnessus in Pamphylia, whereas others of contrary opinion point out also an Aleïan Plain in the former.
Now that the part of the aforesaid peninsula outside the Taurus have been described, I must add what follows.
Apollodorus, in his work On the Catalogue of Ships, goes on to say to this effect, that all the allies of the Trojans from Asia were enumerated by the poet as being inhabitants of the peninsula, of which the narrowest isthmus is that between the innermost recess at Sinopê and Issus. And the exterior sides of this peninsula, he says, which is triangular in shape, are unequal in length, one of them extending from Cilicia to the Chelidonian Islands, another from the Chelidonian Islands to the mouth of the Euxine, and the third thence back to Sinopê. Now the assertion that the allies were alone those who lived in the peninsula can be proved wrong by the same arguments by which I have previously shown that the allies were not alone those who lived this side the Halys River. For just as the places round Pharnacia, in which, as I said, the Halizoni lived, are outside the Halys River, so also they are outside the isthmus, if indeed they are outside the narrows between Sinopê and Issus; and not outside these alone, but also outside the true narrows between Amisus and Issus, for he too incorrectly defines the isthmus and its narrows, since he substitutes the former for the latter. But the greatest absurdity is this, that, after calling the peninsula triangular in shape, he represents the "exterior sides" as three in number; for when he speaks of the "exterior sides" he seems privily to exclude the side along the narrows, as though this too were a side, but not "exterior" or on the sea. If, then, these narrows were so shortened that the exterior side ending at Issus and that ending at Sinopê lacked but little of joining one another, one might concede that the peninsula should be called triangular; but, as it is, since the narrows mentioned by him leave a distance of three thousand stadia between Issus and Sinopê, it is ignorance and not knowledge of chorography to call such a four-sided figure triangular. Yet he published in the metre of comedy a work on chorography entitle A Description of the Earth. The same ignorance still remains even though one should reduce the isthmus to the minimum distance, I mean, to one‑half of the whole distance, as given by those who have most belied the facts, among whom is also Artemidorus, that is, fifteen hundred stadia; for even this does not contract the side along the narrows enough to make the peninsula a triangular figure. Neither does Artemidorus correctly distinguish the exterior sides when he speaks of "the side that extends from Issus as far as the Chelidonian Islands," for there still remains to this side the whole of the Lycian coast, which lies in a straight line with the side he mentions, as does also the Peraea of the Rhodians as far as Physcus. And thence the mainland bends and begins to form the second, or westerly, side extending as far as the Propontis and Byzantium.
But though Ephorus said that this peninsula was inhabited by sixteen tribes, of which three were Hellenic and the rest barbarian, except those that were mixed, adding that the Cilicians, Pamphylians, Lycians, Bithynians, Paphlagonians, Mariandynians, Trojans, and Carians lived on the sea, but the Pisidians, Mysians, Chalybians, Phrygians, and Milyans in the interior, Apollodorus, who passes judgment upon this matter, says that the tribe of the Galatians, which is more recent than the time of Ephorus, is a seventeenth, and that, of the aforesaid tribes, the Hellenic had not yet, in the time of the Trojan War, settled there, and that the barbarian tribes are much confused because of the lapse of time; and that the poet names in his Catalogue the tribes of the Trojans and of the Paphlagonians, as they are now named, and of the Mysians and Phrygians and Carians and Lycians, as also the Meïonians, instead of the Lydians, and other unknown peoples, as, for example, the Halizones and Caucones; and, outside the Catalogue, the Ceteians and the Solymi and the Cilicians from the plain of Thebê and the Leleges, but nowhere names the Pamphylians, Bithynians, Mariandynians, Pisidians, Chalybians, Milyans, or Cappadocians — some because they had not yet settled in this region, and others because they were included among other tribes, as, for example, the Hidrieis and the Termilae among the Carians, and the Doliones and Bebryces among the Phrygians.
But obviously Apollodorus does not pass a fair judgment upon the statement of Ephorus, and also confuses and falsifies the words of the poet; for he ought first to have asked Ephorus this question: Why he placed the Chalybians inside the peninsula when they were so far distant towards the east from both Sinopê and Amisus? For those who say that the isthmus of this peninsula is the line from Issus to the Euxine make this line a kind of meridian, which some think should be the line to Sinopê, and others, that to Amisus, but no one that to the land of the Chalybians, which is absolutely oblique; in fact, the meridian through the land of the Chalybians would be drawn through Lesser Armenia and the Euphrates, cutting off on this side of it the whole of Cappadocia, Commagenê, Mt. Amanus, and the Issic Gulf. If, however, we should concede that the oblique line bounds the isthmus, at least most of these places, and Cappadocia in particular, would be cut off on this side, as also the country now called Pontus in the special sense of the term, which is a part of Cappadocia towards the Euxine; so that, if the land of the Chalybians must be set down as a part of the peninsula, much more should Cataonia and both Cappadocias, as also Lycaonia, which is itself omitted by him. Again, why did Ephorus place in the interior the Chalybians, whom the poet called Halizones, as I have already demonstrated? For it would have been better to divide them and set one part of them on the sea and the other in the interior, as should also be done in the case of Cappadocia and Cilicia; but Ephorus does not even name Cappadocia, and speaks only of the Cilicians on the sea. Now as for the people who were subject to Antipater Derbetes, and the Homonadeis and several other peoples who border on the Pisidians, "men who do not know the sea and even do not eat food mingled with salt," where are they to be placed? Neither does he say in regard to the Lydians or Meïones whether they are two peoples or the same, or whether they live separately by themselves or are included within another tribe. For it would be impossible to lose from sight so significant a tribe; and if Ephorus says nothing about it, would he not seem to have omitted something most important?
And who are the "mixed" tribes? For we would be unable to say that, as compared with the aforesaid places, others were either named or omitted by him which we shall assign to the "mixed" tribes; neither can we call "mixed" any of these peoples themselves whom he has mentioned or omitted; for, even if they had become mixed, still the predominant element has made them either Hellenes or barbarians; and I know nothing of a third tribe of people that is "mixed."
And how can there be three Hellenic tribes that live on the peninsula? For if it is because the Athenians and the Ionians were the same people in ancient times, let also the Dorians and the Aeolians be called the same people; and thus there would be only two tribes. But if one should make distinctions in accordance with the customs of later times, as, for example, in accordance with dialects, then the tribes, like the dialects, would be four in number. But this peninsula, particularly in accordance with the division of Ephorus, is inhabited, not only by Ionians, but also by Athenians, as I have shown in my account of the several places. Now although it is worth while to raise such questions as these with reference to Ephorus, yet Apollodorus took no thought for them and also goes on to add to the sixteen tribes a seventeenth, that of the Galatians — in general a useful thing to do, but unnecessary for the passing of judgment upon what is said or omitted by Ephorus. But Apollodorus states the reason himself, that all this is later than the time of Ephorus.
Passing to the poet, Apollodorus rightly says that much confusion of the barbarian tribes has taken place from the Trojan times to the present because of the changes, for some of them have been added to, others have vanished, others have been dispersed, and others have been combined into one tribe. But he incorrectly sets forth as twofold the reason why the poet does not mention some of them; either because a country was not yet inhabited by this or that tribe or because this or that tribe was included within another; for instance, the poet fails to mention Cappadocia, Cataonia, and likewise Lycaonia, but for neither of these reasons, for we have no history of this kind in their case. Further it is ridiculous that Apollodorus should concern himself about the reason why Homer omitted the Cappadocians and Lycaonians and speak in his defence, and yet should himself omit to tell the reason why Ephorus omitted them, and that too when he had cited the statement of the man for the very purpose of examining it and passing judgment upon it; and also to teach us why Homer mentioned Meïonians instead of Lydians, but not to remark that Ephorus mentions neither Lydians nor Meïonians.
After saying that the poet mentions certain unknown tribes, Apollodorus rightly names the Cauconians, the Solymi, the Ceteians, the Leleges, and the Cilicians of the plain of Thebê; but the Halizones are fabrication of his own, or rather of the first men who, not knowing who the Halizones were, wrote the name in several different ways and fabricated the "birthplace of silver" and many other mines, all of which have given out. And in furtherance of their emulous desire they also collected the stories cited by Demetrius of Scepsis from Callisthenes and certain other writers, who were not free from the false notions about the Halizones. Likewise the wealth of Tantalus and the Pelopidae arose from the mines round Phrygia and Sipylus; that of Cadmus from those round Thrace and Mt. Pangaeus; that of Priam from the gold mines at Astyra near Abydus (of which still to‑day there are small remains; here the amount of earth thrown out is considerable, and the excavations are signs of the mining in olden times); and that of Midas from those round Mt. Bermius; and that of Gyges and Alyattes and Croesus from those in Lydia and from the region between Atarneus and Pergamum, where is a small deserted town, whose lands have been exhausted of ore.
Still further one might find fault with Apollodorus, because, when the more recent writers make numerous innovations contrary to the statements of Homer, he is wont frequently to put these innovations to the test, but in the present case he not only has made small account of them, but also, on the contrary, identifies things that are not meant alike; for instance, Xanthus the Lydian says that it was after the Trojan War that the Phrygians came from Europe and the left-hand side of the Pontus, and that Scamandrius led them from the Berecyntes and Ascania, but Apollodorus adds to this the statement that Homer refers to this Ascania that is mentioned by Xanthus: "And Phorcys and godlike Ascanius led the Phrygians from afar, from Ascania." However, if this is so, the migration must have taken place later than the Trojan War, whereas the allied force mentioned by the poet came from the opposite mainland, from the Berecyntes and Ascania. Who, then, were the Phrygians, "who were then encamped along the banks of the Sangarius," when Priam says, "for I too, being an ally, was numbered among these"? And how could Priam have sent for Phrygians from the Berecyntes, with whom he had no compact, and yet leave uninvited those who lived on his borders and to whom he had formerly been ally? And after speaking in this way about the Phrygians he adds also an account of the Mysians that is not in agreement with this; for he says that there is also a village in Mysia which is called Ascania, near a lake of the same name, whence flows the Ascanius River, which is mentioned by Euphorion, "beside the waters to Mysian Ascanius," and by Alexander the Aetolian, "who have their homes on the Ascanian streams, on the lips of the Ascanian Lake, where dwelt Dolion, the son of Silenus and Melia." And he says that the country round Cyzicus, as one goes to Miletupolis, is called Dolionis and Mysia. If this is so, and if witness thereto is borne both by the places now pointed out and by the poets, what could have prevented Homer from mentioning this Ascania, and not the Ascania spoken of by Xanthus? I have discussed this before, in my account of the Mysians and Phrygians; and therefore let this be the end of that subject. |
|
|
|
|
14 - 6 Cyprus 
1 It remains for me to describe the island which lies alongside this peninsula on the south, I mean Cyprus. I have already said that the sea surrounded by Egypt, Phoenicia, Syria, and the rest of the coast as far as Rhodia consists approximately of the Aegyptian and Pamphylian Seas and of the sea at the gulf of Issus. In this last sea lies Cypros; its northern parts closely approach Cilicia Tracheia, where they are closest to the mainland, its eastern parts border on the Issic Gulf, and its western on the Pamphylian Sea, being washed by that sea, and its southern by the Aegyptian Sea. Now the Aegyptian Sea is confluent on the west with the Libyan and Carpathian Seas, but in its southern and eastern parts borders on Aegypt and the coast next thereafter as far as Seleuceia and Issus, and towards the north on Cypros and the Pamphylian Sea; but the Pamphylian Sea is surrounded on the north by the extremities of Cilicia Tracheia, of Pamphylia, and of Lycia, as far as Rhodia, and on the west by the island of the Rhodians, and on the east by the part of Cypros near Paphos and the Acamas, and on the south is confluent with the Aegyptian Sea.
2 The circuit of Cypros is three thousand four hundred and twenty stadia, including the sinuosities of the gulfs. The length from Cleides to the Acamas by land, traveling from east to west, is one thousand four hundred stadia. The Cleides are two isles lying off Cypros opposite the eastern parts of the island, which are seven hundred stadia distant from the Pyramus. The Acamas is a promontory with two breasts and much timber. It is situated at the western part of the island, and extends towards the north; it lies closest to Selinus in Cilicia Tracheia, the passage across being one thousand stadia, whereas the passage across to Sidê in Pamphylia is sixteen hundred and to the Chelidonian islands one thousand nine hundred. The shape of the island as a whole is oblong; and in some places it forms isthmuses on the sides which define its breadth. But the island also has its several parts, which I shall describe briefly, beginning with the point that is nearest to the mainland.
3 I have said somewhere that opposite to Anemurium, a cape of Cilicia Tracheia, is the promontory of the Cyprians, I mean the promontory of Crommyus, at a distance of three hundred and fifty stadia. Thence forthwith, keeping the island on the right and the mainland on the left, the voyage to the Cleides lies in a straight line towards the north-east, a distance of seven hundred stadia. In the interval is the city Lapathus, with a mooring-place and dockyards; it was founded by Laconians and Praxander, and opposite it lies Nagidus. Then one comes to Aphrodisium, where the island is narrow, for the passage across to Salamis is only seventy stadia. Then to the beach of the Achaeans, where Teucer, the founder of Salamis in Cypros, first landed, having been banished, as they say, by his father Telamon. Then to a city Carpasia, with a harbour. It is situated opposite the promontory Sarpedon; and the passage from Carpasia across the isthmus to the Carpasian Islands and the southern sea is thirty stadia. Then to a promontory and mountain. The mountain peak is called Olympus; and it has a temple of Aphroditê Acraea, which cannot be entered or seen by women. Off it, and near it, lie the Cleides, as also several other islands; and then one comes to the Carpasian Islands; and, after these, to Salamis, where Aristus the historian was born. Then to Arsinoê, a city and harbour. Then to another harbour, Leucolla. Then to a promontory, Pedalium, above which lies a hill that is rugged, high, trapezium-shaped, and sacred to Aphroditê, whereto the distance from the Cleides is six hundred and eighty stadia. Then comes the coasting-voyage to Citium, which for the most part is sinuous and rough. Citium has a harbour that can be closed; and here were born both Zeno, the original founder of the Stoic sect, and Apollonius, a physician. The distance thence to Berytus is one thousand five hundred stadia. Then to the city Amathus, and, in the interval, to a small town called Palaea, and to a breast-shaped mountain called Olympus. Then to Curias, which is peninsula-like, whereto the distance from Throni is seven hundred stadia. Then to a city Curium, which has a mooring-place and was founded by the Argives. One may therefore see at once the carelessness of the poet who wrote the elegy that begins, "we hinds, sacred to Phoebus, racing across many billows, came hither in our swift course to escape the arrows of our pursuers," whether the author was Hedylus or someone else; for he says that the hinds set out from the Corycian heights and swam across from the Cilician shore to the beach of Curias, and further says that "it is a matter of untold amazement to men to think how we ran across the impassable stream by the aid of a vernal west wind"; for while there is a voyage round the island from Corycus to the beach Curias, which is made neither by the aid of a west wind nor by keeping the island on the right nor on the left, there is no passage across the sea between the two places. At any rate, Curium is the beginning of the westerly voyage in the direction of Rhodes; and immediately one comes to a promontory, whence are flung those who touch the altar of Apollo. Then to Treta, and to Boosura, and to Palaepaphus, which last is situated at about ten stadia above the sea, has a mooring-place, and an ancient temple of the Paphian Aphroditê. Then to the promontory Zephyria, with a landing-place, and to another Arsinoê, which likewise has a landing-place and a temple and a sacred precinct. And at a little distance from the sea is Hierocepis. Then to Paphus, which was founded by Agapenor and has both a harbour and well-built temples. It is sixty stadia distant from Palaepaphus by land; and on this road men together with women, who also assemble here from the other cities, hold an annual procession to Palaepaphus. Some say that the distance from Paphus to Alexandria is three thousand six hundred stadia. Then, after Paphus, one comes to the Acamas. Then, after the Acamas, towards the east, one sails to a city Arsinoê and the sacred precinct of Zeus. Then to a city Soli, with a harbour and a river and a temple of Aphroditê and Isis. It was founded by Phalerus and Acamas, Athenians; and the inhabitants are called Solians; and here was born Stasanor, one of the comrades of Alexander, who was thought worthy of a chief command; and above it, in the interior, lies a city Limenia. And then to the promontory of Crommyus.
4 But why should one wonder at the poets, and particularly at writers of the kind that are wholly concerned about style, when we compare the statements of Damastes, who gives the length of the island as from north to south, "from Hierocepias," as he says, "to Cleides"? Neither is Eratosthenes correct, for, although he censures Damastes, he says that Hierocepias is not on the north but on the south; for it is not on the south either, but on the west, since it lies on the western side, where are also Paphus and the Acamas. Such is the geographical position of Cypros.
5 In fertility Cyprus is not inferior to any one of the islands, for it produces both good wine and good oil, and also a sufficient supply of grain for its own use. And at Tamassus there are abundant mines of copper, in which is found chalcanthite3 and also the rust of copper, which latter is useful for its medicinal properties. Eratosthenes says that in ancient times the plains were thickly overgrown with forests, and therefore were covered with woods and not cultivated; that the mines helped a little against this, since the people would cut down the trees to burn the copper and the silver, and that the building of the fleets further helped, since the sea was now being navigated safely, that is, with naval forces, but that, because they could not thus prevail over the growth of the timber, they permitted anyone who wished, or was able, to cut out the timber and to keep the land thus cleared as his own property and exempt from taxes.
6 Now in the earlier times the several cities of the Cyprians were under the rule of tyrants, but from the time the Ptolemaïc kings became established as lords of Egypt Cyprus too came into their power, the Romans often co-operating with them. But when the last Ptolemy that reigned, the brother of the father of Cleopatra, the queen in my time, was decreed to be both disagreeable and ungrateful to his benefactors, he was deposed, and the Romans took possession of the island; and it has become a praetorian province by itself. The chief cause of the ruin of the king was Publius Claudius Pulcher; for the latter, having fallen into the hands of the bands of pirates, the Cilicians then being at the height of their power, and, being asked for a ransom, sent a message to the king, begging him to send and rescue him. The king indeed sent a ransom, but so utterly small that the pirates disdained to take it and sent it back again, but released him without ransom. Having safely escaped, he remembered the favour of both; and, when he became tribune of the people, he was so powerful that he had Marcus Cato sent to take Cypros away from its possessor. Now the king killed himself beforehand, but Cato went over and took Cypros 6and disposed of the king's property and carried the money to the Roman treasury. From that time the island became a province, just as it is now — a praetorian province. During a short intervening time Antony gave it over to Cleopatra and her sister Arsinoê, but when he was overthrown his whole organisation was overthrown with him. |
|
|
|
|
15 East Asia.3 90 1:19 
|
15 - 1 India, basic geography, India, animals, people 
1 It remains for me to describe the island which lies alongside this peninsula on the south, I mean Cyprus. I have already said that the sea surrounded by Egypt, Phoenicia, Syria, and the rest of the coast as far as Rhodia1 consists approximately of the Aegyptian and Pamphylian Seas and of the sea at the gulf of Issus. In this last sea lies Cypros; its northern parts closely approach Cilicia Tracheia, where they are closest to the mainland, its eastern parts border on the Issic Gulf, and its western on the Pamphylian Sea, being washed by that sea, and its southern by the Aegyptian Sea. Now the Aegyptian Sea is confluent on the west with the Libyan and Carpathian Seas, but in its southern and eastern parts borders on Aegypt and the coast next thereafter as far as Seleuceia and Issus, and towards the north on Cypros and the Pamphylian Sea; but the Pamphylian Sea is surrounded on the north by the extremities of Cilicia Tracheia, of Pamphylia, and of Lycia, as far as Rhodia, and on the west by the island of the Rhodians, and on the east by the part of Cypros near Paphos and the Acamas, and on the south is confluent with the Aegyptian Sea.
2 The circuit of Cypros is three thousand four hundred and twenty stadia, including the sinuosities of the gulfs. The length from Cleides to the Acamas by land, traveling from east to west, is one thousand four hundred stadia. The Cleides are two isles lying off Cypros opposite the eastern parts of the island, which are seven hundred stadia distant from the Pyramus. The Acamas is a promontory with two breasts and much timber. It is situated at the western part of the island, and extends towards the north; it lies closest to Selinus in Cilicia Tracheia, the passage across being one thousand stadia, whereas the passage across to Sidê in Pamphylia is sixteen hundred and to the Chelidonian islands one thousand nine hundred. The shape of the island as a whole is oblong; and in some places it forms isthmuses on the sides which define its breadth. But the island also has its several parts, which I shall describe briefly, beginning with the point that is nearest to the mainland.
3 I have said somewhere that opposite to Anemurium, a cape of Cilicia Tracheia, is the promontory of the Cyprians, I mean the promontory of Crommyus, at a distance of three hundred and fifty stadia. Thence forthwith, keeping the island on the right and the mainland on the left, the voyage to the Cleides lies in a straight line towards the north-east, a distance of seven hundred stadia. In the interval is the city Lapathus, with a mooring-place and dockyards; it was founded by Laconians and Praxander, and opposite it lies Nagidus. Then one comes to Aphrodisium, where the island is narrow, for the passage across to Salamis is only seventy stadia. Then to the beach of the Achaeans, where Teucer, the founder of Salamis in Cypros, first landed, having been banished, as they say, by his father Telamon. Then to a city Carpasia, with a harbour. It is situated opposite the promontory Sarpedon; and the passage from Carpasia across the isthmus to the Carpasian Islands and the southern sea is thirty stadia. Then to a promontory and mountain. The mountain peak is called Olympus; and it has a temple of Aphroditê Acraea, which cannot be entered or seen by women. Off it, and near it, lie the Cleides, as also several other islands; and then one comes to the Carpasian Islands; and, after these, to Salamis, where Aristus the historian was born. Then to Arsinoê, a city and harbour. Then to another harbour, Leucolla. Then to a promontory, Pedalium, above which lies a hill that is rugged, high, trapezium-shaped, and sacred to Aphroditê, whereto the distance from the Cleides is six hundred and eighty stadia. Then comes the coasting-voyage to Citium, which for the most part is sinuous and rough. Citium has a harbour that can be closed; and here were born both Zeno, the original founder of the Stoic sect, and Apollonius, a physician. The distance thence to Berytus is one thousand five hundred stadia. Then to the city Amathus, and, in the interval, to a small town called Palaea, and to a breast-shaped mountain called Olympus. Then to Curias, which is peninsula-like, whereto the distance from Throni is seven hundred stadia. Then to a city Curium, which has a mooring-place and was founded by the Argives. One may therefore see at once the carelessness of the poet who wrote the elegy that begins, "we hinds, sacred to Phoebus, racing across many billows, came hither in our swift course to escape the arrows of our pursuers," whether the author was Hedylus or someone else; for he says that the hinds set out from the Corycian heights and swam across from the Cilician shore to the beach of Curias, and further says that "it is a matter of untold amazement to men to think how we ran across the impassable stream by the aid of a vernal west wind"; for while there is a voyage round the island from Corycus to the beach Curias, which is made neither by the aid of a west wind nor by keeping the island on the right nor on the left, there is no passage across the sea between the two places. At any rate, Curium is the beginning of the westerly voyage in the direction of Rhodes; and immediately one comes to a promontory, whence are flung those who touch the altar of Apollo. Then to Treta, and to Boosura, and to Palaepaphus, which last is situated at about ten stadia above the sea, has a mooring-place, and an ancient temple of the Paphian Aphroditê. Then to the promontory Zephyria, with a landing-place, and to another Arsinoê, which likewise has a landing-place and a temple and a sacred precinct. And at a little distance from the sea is Hierocepis. Then to Paphus, which was founded by Agapenor and has both a harbour and well-built temples. It is sixty stadia distant from Palaepaphus by land; and on this road men together with women, who also assemble here from the other cities, hold an annual procession to Palaepaphus. Some say that the distance from Paphus to Alexandria is three thousand six hundred stadia. Then, after Paphus, one comes to the Acamas. Then, after the Acamas, towards the east, one sails to a city Arsinoê and the sacred precinct of Zeus. Then to a city Soli, with a harbour and a river and a temple of Aphroditê and Isis. It was founded by Phalerus and Acamas, Athenians; and the inhabitants are called Solians; and here was born Stasanor, one of the comrades of Alexander, who was thought worthy of a chief command; and above it, in the interior, lies a city Limenia. And then to the promontory of Crommyus.
4 But why should one wonder at the poets, and particularly at writers of the kind that are wholly concerned about style, when we compare the statements of Damastes, who gives the length of the island as from north to south, "from Hierocepias," as he says, "to Cleides"? Neither is Eratosthenes correct, for, although he censures Damastes, he says that Hierocepias is not on the north but on the south; for it is not on the south either, but on the west, since it lies on the western side, where are also Paphus and the Acamas. Such is the geographical position of Cypros.
5 In fertility Cyprus is not inferior to any one of the islands, for it produces both good wine and good oil, and also a sufficient supply of grain for its own use. And at Tamassus there are abundant mines of copper, in which is found chalcanthite and also the rust of copper, which latter is useful for its medicinal properties. Eratosthenes says that in ancient times the plains were thickly overgrown with forests, and therefore were covered with woods and not cultivated; that the mines helped a little against this, since the people would cut down the trees to burn the copper and the silver, and that the building of the fleets further helped, since the sea was now being navigated safely, that is, with naval forces, but that, because they could not thus prevail over the growth of the timber, they permitted anyone who wished, or was able, to cut out the timber and to keep the land thus cleared as his own property and exempt from taxes.
6 Now in the earlier times the several cities of the Cyprians were under the rule of tyrants, but from the time the Ptolemaïc kings became established as lords of Egypt Cyprus too came into their power, the Romans often co-operating with them. But when the last Ptolemy that reigned, the brother of the father of Cleopatra, the queen in my time, was decreed to be both disagreeable and ungrateful to his benefactors, he was deposed, and the Romans took possession of the island; and it has become a praetorian province by itself. The chief cause of the ruin of the king was Publius Claudius Pulcher; for the latter, having fallen into the hands of the bands of pirates, the Cilicians then being at the height of their power, and, being asked for a ransom, sent a message to the king, begging him to send and rescue him. The king indeed sent a ransom, but so utterly small that the pirates disdained to take it and sent it back again, but released him without ransom. Having safely escaped, he remembered the favour of both; and, when he became tribune of the people, he was so powerful that he had Marcus Cato sent to take Cypros away from its possessor. Now the king killed himself beforehand, but Cato went over and took Cypros and disposed of the king's property and carried the money to the Roman treasury. From that time the island became a province, just as it is now — a praetorian province. During a short intervening time Antony gave it over to Cleopatra and her sister Arsinoê, but when he was overthrown his whole organisation was overthrown with him.
But I must tell also the several details concerning the rivers, so far as they are useful for the purposes of geography and so far as I have learned their history. For the rivers in particular, being a kind of natural boundary for both the size and the shape of countries, are very convenient for the purposes of the whole of our present subject; but the Nile and the Indian rivers offer a certain advantage as compared with the rest because of the fact that apart from them the countries are uninhabitable, being at the same time navigable and tillable, and that they can neither be travelled over otherwise nor inhabited at all. Now as for the rivers worthy of mention that flow down into the Indus, I shall tell their history, as also that of the countries traversed by them; but as for the rest there is more ignorance than knowledge. For Alexander, who more than any other uncovered these regions, at the outset, when those who had treacherously slain Dareius set out to cause the revolt of Bactriana, resolved that it would be most desirable to pursue and overthrow them. p45He therefore approached India through Ariana, and, leaving India on the right, crossed over Mt. Paropamisus to the northerly parts and Bactriana; and, having subdued everything there that was subject to the Persians and still more, he then forthwith reached out for India too, since many menhad been describing it to him, though not clearly. Accordingly he returned, passing over the same mountains by other and shorter roads, keeping India on the left, and then turned immediately towards India and its western boundaries and the Cophes River and the Choaspes, which latter empties into the Cophes River near a city Plemyrium, after flowing past Gorys, another city, and flowing forth through both Bandobenê and Gandaritis. He learned by inquiry that the mountainous and northerly part was the most habitable and fruitful, but that the southerly part was partly without water and partly washed by rivers and utterly hot, more suitable for wild beasts than for human beings. Accordingly, he set out to acquire first the part that was commended to him, at the same time considering that the rivers which it was necessary to cross, since they flow transversely and cut through the country which he meant to traverse, could more easily be crossed near their sources. At the same time he also heard that several rivers flowed together into one stream, and that this was always still more the case the farther forward they advanced, so that the country was more difficult to cross, especially in the event of lack of boats. Afraid of this, therefore, he crossed the Cophes and began to subdue all the mountainous country that faced towards the east.
After the Cophes he went to the Indus, then to the Hydaspes, then to the Acesines and the Hyarotis, and last to the Hypanis; for he was prevented from advancing farther, partly through observance of certain oracles and partly because he was forced by his army, which had already been worn out by its labours, though they suffered most of all from the waters, being continually drenched with rain. Of the eastern parts of India, then, there have become known to us all those parts which lie this side the Hypanis, and also any parts beyond the Hypanis of which an account has been added by those who, after Alexander, advanced beyond the Hypanis, as far as the Ganges and Palibothra. Now after the Cophes follows the Indus; and the region between these rivers is occupied by Astaceni, Masiani, Nysaei, and Hypasii; and then one comes to the country of Assacanus, where is a city Mesoga, the royal seat of the country; and now near the Indus again, one comes to another city, Peucolaïtis, near which a bridge that had already been built afforded a passage for the army.
Between the Indus and the Hydaspes lies Taxila, a city which is large and has most excellent laws; and the country that lies round it is spacious and very fertile, immediately bordering also on the plains. Both the inhabitants and their king, Taxiles, received Alexander in a kindly way; and they obtained from Alexander more gifts than they themselves presented, so that the Macedonians were envious and said that Alexander did not have anyone, as it seemed, on whom to bestow his benefactions until he crossed the Indus. Some say that this country is larger than Aegypt. Above this country in the mountains lies the country of Abisarus, who, according to the ambassadors that came from him, kept two serpents, one eighty cubits in length and another one hundred and forty, according to Onesicritus, who cannot so properly be called arch-pilot of Alexander as of things that are incredible; for though all the followers of Alexander preferred to accept the marvellous rather than the true, Onesicritus seems to surpass all those followers of his in the telling of prodigies. However, he tells some things that are both plausible and worthy of mention, and therefore they are not passed by in silence even by one who disbelieves them. At any rate, others too speak of the serpents, saying that they are caught in the Emodi mountains and kept in caves.
Between the Hydaspes and the Acesines is, first, the country of Porus, extensive and fertile, containing about three hundred cities; secondly, the forest near the Emodi mountains, from which Alexander cut, and brought down on the Hydaspes, a large quantity of fir, pine, cedar, and other logs of all kinds fit for shipbuilding, from which he built a fleet on the Hydaspes near the cities founded by him on either side of the river where he crossed and conquered Porus. Of these cities, he named one Bucephalia, after Bucephalas, the horse which fell during the battle with Porus (the horse was called Bucephalas from the width of his forehead; he was an excellent war-horse and was always used by Alexander in his fights); and he called the other Nicaea, after his victory. In the forest above-mentioned both the number and the size of the long-tailed apes are alike described as so extraordinary that once the Macedonians, seeing many of these standing as in front-line array on some bare hills (for this animal is very human-like in mentality, no less so than the elephant), got the impression that they were an army of men; and they actually set out to attack them as human enemies, but on learning the truth from Taxiles, who was then with the king, desisted. The capture of the animal is effected in two ways. It is an imitative animal and takes to flight up the trees. Now the hunters, when they see an ape seated on a tree, place in sight a bowl containing water and rub their own eyes with it; and then they put down a bowl of bird-lime instead of the water, go away, and lie in wait at a distance; and when the animal leaps down and besmears itself with the bird-lime, and when, upon winking, its eyelids are shut together, the hunters approach and take it alive. Now this is one way, but there is another. They put on baggy breeches like trousers and then go away, leaving behind them others that are shaggy and smeared inside with bird-lime; and when the animals put these on, they are easily captured.a
Some put both Cathaea and the country of Sopeithes, one of the provincial chiefs, between these two rivers, but others on the far side of the Acesines and the Hyarotis, as bordering on the country of the second Porus, who was a cousin of the Porus captured by Alexander. The country that was subject to him is called Gandaris. As for Cathaea, a most novel regard for beauty there is reported; I mean that it is prized in an exceptional manner, as, for example, for the beauty of its horses and dogs; and, in fact, Onesicritus says that they choose the handsomest person as king, and that a child is judged in public after it is two months old as to whether it has the beauty of form required by law and is worthy to live or not; and that when it is judged by the appointed magistrate it is allowed to live or is put to death; and that the men dye their beards with many most florid colours for the sole reason that they wish to beautify themselves; and that this practice is carefully followed by numerous other Indian peoples also (for the country produces marvellous colours, he says), who dye both their hair and their garments; and that the people, though shabby in every other way, are fond of adornment. The following too is reported as a custom peculiar to the Cathaeans: the groom and bride choose one another themselves, and wives are burned up with their deceased husbands for a reason of this kind — that they sometimes fell in love with young men and deserted their husbands or poisoned them; and therefore the Cathaeans established this as a law, thinking that they would put a stop to the poisoning.b However, the law is not stated in a plausible manner, nor the cause of it either. It is said that in the country of Sopeithes there is a mountain of mineral salt sufficient for the whole of India. And gold and silver mines are reported in other mountains not far away, excellent mines, as has been plainly shown by Gorgus the mining expert. But since the Indians are inexperienced in mining and smelting, they also do not know what their resources are, and handle the business in a rather simple manner.
Writers narrate also the excellent qualities of the dogs in the country of Sopeithes. They say, at any rate, that Alexander received one hundred and fifty dogs from Sopeithes; and that, to prove them, two were let loose to attack a lion, and when they were being overpowered, two others were let loose upon him, and that then, the match having now become equal, Sopeithes bade someone to take one of the dogs by the leg and pull him away, and if the dog did not yield to cut off his leg; and that Alexander would not consent to cutting off the dog's leg at first, wishing to spare the dog, but consented when Sopeithes said that he would give him four instead; and that the dog suffered the cutting off of his leg by slow amputation before he let go his grip.
Now the march to the Hydaspes was for the most part towards the south, but from there to the Hypanis it was more towards the east, and as a whole it kept to the foothills more than to the plains. At all events, Alexander, when he returned from the Hypanis to the Hydaspes and the naval station, proceeded to make ready his fleet and then to set sail on the Hydaspes. All the above-mentioned rivers, last of all the Hypanis, unite in one river, the Indus; and it is said that the Indus is joined by fifteen noteworthy rivers all told, and that after being filled so full by all that it is widened in some places, according to writers who are immoderate, even to the extent of one hundred stadia, but, according to the more moderate, fifty at the most and seven at the least (and there are many tribes and cities all about it), it then empties into the southern sea by two mouths and forms the island called Patalenê. Alexander conceived this purpose after dismissing from his mind the parts towards the east; first, because he had been prevented from crossing the Hypanis, and, secondly, because he had learned by experience the falsity of the report which had preoccupied his mind, that the parts in the plains were burning hot and more habitable for wild beasts than for a human race; and therefore he set out for these parts, dismissing those others, so that the former became better known than those others.
Now the country between the Hypanis and the Hydaspes is said to contain nine tribes, 701 and also cities to the number of five thousand — cities no smaller than Cos Meropis,though the number stated seems to be excessive. And as for the country between the Indus and the Hydaspes, I have stated approximately the peoples worthy of mention by which it is inhabited;and below them, next in order, are the people called Sibae, whom I have mentioned before,and the Malli and the Sydracae, large tribes. It was in the country of the Malli that Alexander was in peril of death, being wounded in the capture of some small city; and as for the Sydracae, I have already spoken of them as mythically akin to Dionysus. Near Patalenê, they say, one comes at once to the country of Musicanus, and to that of Sabus, where is Sindomana, and also to the country of Porticanus and others, who, one and all, were conquered by Alexander, these peoples dwelling along the river-lands of the Indus; but last of all to Patalenê, a country formed by the Indus, which branches into two mouths. Now Aristobulus says that these mouths are one thousand stadia distant from one another, but Nearchus adds eight hundred; and Onesicritus reckons each of the two sides of the included island, which is triangular in shape, at two thousand, and the width of the river, where it branches into the mouths, at about two hundred; and he calls the island Delta, a statement which is not true. For it is said that the Aegyptian Delta has a base of one thousand three hundred stadia, though each of the two sides is shorter than the base. In Patalenê there is a noteworthy city, Patala, after which the island is named.
Onesicritus says that most of the seaboard in this part of the world abounds in shoals, particularly at the mouths of the rivers, on account of the silt and the overflows and also of the fact that no breezes blow from the land, and that this region is subject for the most part to winds that blow from the high sea. He describes also the country of Musicanus, lauding it rather at length for things of which some are reported as common also to other Indians, as, for example, their length of life, thirty years beyond one hundred (and indeed some say that the Seres live still longer than this), and their healthfulness, and simple diet, even though their country has an abundance of everything. Peculiar to them is the fact that they have a kind of Laconian common mess, where they eat in public and use as food the meat of animals taken in the chase; and that they do not use gold or silver, although they have mines; and that instead of slaves they use young men in the vigour of life, as the Cretans use the Aphamiotae and the Laconians the Helots; and that they make no accurate study of the sciences except that of medicine, for they regard too much training in some of them as wickedness; for example, military science and the like; and that they have no process at law except for murder and outrage, for it is not in one's power to avoid suffering these, whereas the content of contracts is in the power of each man himself, so that he is required to endure it if anyone breaks faith with him, and also to consider carefully who should be trusted and not to fill the city with lawsuits. This is the account of those who made the expedition with Alexander.
But there has also been published a letter of Craterus to his mother Aristopatra, which alleges many other strange things and agrees with no one else, particularly in saying that Alexander advanced as far as the Ganges. And he says that he himself saw the river and monsters on its banks, and a magnitude both of width and of depth which is remote from credibility rather than near it. Indeed, it is sufficiently agreed that the Ganges is the largest of known rivers on the three continents, and after it the Indus, and third and fourth the Ister and the Nile; but the several details concerning it are stated differently by different writers, some putting its minimum breadth at thirty stadia and others even at three, whereas Megasthenes says that when its breadth is medium it widens even to one hundred stadia and that its least depth is twenty fathoms.
It is said that Palibothra lies at the confluence of the Ganges and the other river, a city eighty stadia in length and fifteen in breadth, in the shape of a parallelogram, and surrounded by a wooden wall that is perforated so that arrows can be shot through the holes; and that in front of the wall lies a trench used both for defence and as a receptacle of the sewage that flows from the city; and that the tribe of people amongst whom this city is situated is called the Prasii and is far superior to all the rest; and that the reigning king must be surnamed after the city, being called Palibothrus in addition to his own family name, as, for example, King Sandrocottus to whom Megasthenes was sent on an embassy. Such is also the custom among the Parthians; for all are called Arsaces, although personally one king is called Orodes, another Phraates, and another something else.
Writers are agreed that the country as a whole on the far side of the Hypanis is best; but they do not describe it accurately, and because of their ignorance and of its remoteness magnify all things or make them more marvellous. For example, the stories of the ants that mine gold and of other creatures, both beasts and human beings, which are of peculiar form and in respect to certain natural powers have undergone complete changes, as, for example, the Seres, who, they say, are long-lived, and prolong their lives even beyond two hundred years. They tell also of a kind of aristocratic order of government that was composed outright of five thousand counsellors, each of whom furnishes the new commonwealth with an elephant. Megasthenes says that the largest tigers are found among the Prasii, even nearly twice as large as lions, and so powerful that a tame one, though being led by four men, seized a mule by the hind leg and by force drew the mule to itself; and that the long-tailed apes are larger than the largest dogs, are white except for their faces, which are black (the contrary is the case elsewhere), that their tails are more than two cubits long, and that they are very tame and not malicious as regards attacks and thefts; and that stones are dug up the colour of frankincense and sweeter than figs or honey; and that in other places there are reptiles two cubits long with membranous wings like bats, and that they too fly by night, discharging drops of urine, or also of sweat, which putrefy the skin of anyone who is not on his guard; and that there are winged scorpions of surpassing size; and that ebony is also produced; and that there are also brave dogs, which do not let go the object bitten till water is poured down into their nostrils; and that some bite so vehemently that their eyes become distorted and sometimes actually fall out; and that even a lion was held fast by a dog, and also a bull, and that the bull was actually killed, being overpowered through the dog's hold on his nose before he could be released.
Megasthenes goes on to say that in the mountainous country there is a River Silas on which nothing floats; that Democritus, however, disbelieves this, inasmuch as he had wandered over much of Asia. But Aristotle also disbelieves it, although there are atmospheres so thin that no winged creature can fly in them. Besides, certain rising vapours tend to attract to themselves and "gulp down," as it were, whatever flies over them, as amber does with chaff and the magnet with iron; and perhaps there might also be natural powers of this kind in water. Now these things border, in a way, on natural philosophy and on the science of floating bodies, and therefore should be investigated there; but in this treatise I must still add the following, and whatever else is closer to the province of geography.
He says, then, that the population of India is divided into seven castes: the one first in honour, but the fewest in number, consists of the philosophers; and these philosophers are used, each individually, by the people making sacrifice to the gods or making offerings to the dead, but jointly by the kings at the Great Synod, as it is called, at which, at the beginning of the new year, the philosophers, one and all, come together at the gates of the king; and whatever each man has drawn up in writing or observed as useful with reference to the prosperity of either fruits or living beings or concerning the government, he brings forward in public; and he who is thrice found false is required by law to keep silence for life, whereas he who has proved correct is adjudged exempt from tribute and taxes.
The second caste, he says, is that of the farmers, who are not only the most numerous, but also the most highly respected, because of their exemption from military service and right of freedom in their farming; and they do not approach a city, either because of a public disturbance or on any other business; at any rate, he says, it often happens that at the same time and place some are in battle array and are in peril of their lives against the enemy, while the farmers are ploughing or digging without peril, the latter having the former as defenders. The whole of the country is of royal ownership; and the farmers cultivate it for a rental in addition to paying a fourth part of the produce.
The third caste is that of the shepherds and hunters, who alone are permitted to hunt, to breed cattle, and to sell or hire out beasts of burden; and in return for freeing the land from wild beasts and seed-picking birds, they receive proportionate allowances of grain from the king, leading, as they do, a wandering and tent-dwelling life. No private person is permitted to keep a horse or elephant. The possession of either is a royal privilege, and there are men to take care of them.
The chase of the elephant is conducted as follows: they dig a deep ditch round a treeless tract about four or five stadia in circuit and bridge the entrance with a very narrow bridge; and then, letting loose into the enclosure three or four of their tamest females, they themselves lie in wait under cover in hidden huts. Now the wild elephants do not approach by day, but they make the entrance one by one at night; and when they have entered, the men close the entrance secretly; and then, leading the most courageous of their tame combatants into the enclosure, they fight it out with the wild elephants, at the same time wearing them down also by starvation; and, once the animals are worn out, the boldest of the riders secretly dismount and each creeps under the belly of his own riding-elephant, and then, starting from here, creeps under the wild elephant and binds his feet together; and when this is done, they command the tamed elephants to beat those whose feet have been bound until they fall to the ground; and when they fall, the men fasten their necks to those of the tamed elephants with thongs of raw ox-hide; and in order that the wild elephants, when they shake those who are attempting to mount them, may not shake them off, the men make incisions round their necks and put the thongs round at these incisions, so that through pain they yield to their bonds and keep quiet. Of the elephants captured, they reject those that are too old or too young for service and lead away the rest to the stalls; and then, having tied their feet to one another and their necks to a firmly planted pillar, they subdue them by hunger; and then they restore them with green cane and grass. After this the elephants are taught to obey commands, some through words of command and others through being charmed by tunes and drum-beating. Those that are hard to tame are rare; for by nature the elephant is of a mild and gentle disposition, so that it is close to a rational animal; and some elephants have even taken up their riders who had fallen from loss of blood in the fight and carried them safely out of the battle, while others have fought for, and rescued, those who had crept between their fore-legs. And if in anger they have killed one of their feeders or masters, they yearn after him so strongly that through grief they abstain from food and sometimes even starve themselves to death.
They copulate and bear young like horses, mostly in the spring. It is breeding-time for the male when he is seized with frenzy and becomes ferocious; at that time he discharges a kind of fatty matter through the breathing-hole which he has beside his temples. And it is breeding-time for the females when this same passage is open. They are pregnant eighteen months at the most and sixteen at the least; and the mother nurses her young six years. Most of them live as long as very long-lived human beings, and some continue to live even to two hundred years, although they are subject to many diseases and are hard to cure. A remedy for eye diseases is to bathe the eyes with cow's milk; but for most diseases they are given dark wine to drink; and, in the case of wounds, melted butter is applied to them (for it draws out the bits of iron), while ulcers are poulticed with swine's flesh. Onesicritus says that they live as long as three hundred years and in rare cases even as long as five hundred; but that they are most powerful when about two hundred years of age, and that females are pregnant for a period of ten years. And both he and others state that they are larger and strong than the Libyan elephants; at any rate, standing up on their hind feet, they tear down battlements and pull up trees by the roots by means of the proboscis. Nearchus says that in the hunt for them foot-traps also are put at places where tracks meet, and that the wild elephants are driven together into these by the tamed ones, which latter are stronger and guided by riders; and that they are so easy to tame that they learn to throw stones at a mark and to use weapons; and that they are excellent swimmers; and that a chariot drawn by elephants is considered a very great possession, and that they are driven under yoke like camels; and that a woman is highly honoured if she receives an elephant as a gift from a lover. But this statement is not in agreement with that of the man who said that horse and elephant were possessed by kings alone.
Nearchus says that the skins of gold-mining ants are like those of leopards. But Megasthenes speaks of these ants as follows: that among the Derdae, a large tribe of Indians living towards the east and in the mountains, there is a plateau approximately three thousand stadia in circuit, and that below it are gold mines, of which the miners are ants, animals that are no smaller than foxes, are surpassingly swift, and live on the prey they catch. They dig holes in winter and heap up the earth at the mouths of the holes, like moles; and the gold-dust requires but little smelting. The neighbouring peoples go after it on beasts of burden by stealth, for if they go openly the ants fight it out with them and pursue them when they flee, and then, having overtaken them, exterminate both them and their beasts; but to escape being seen by the ants, the people lay out pieces of flesh of wild beasts at different places, and when the ants are drawn away from around the holes, the people take up the gold-dust and, not knowing how to smelt it, dispose of it unwrought to traders at any price it will fetch.
But since, in my account of the hunters and of the wild beasts, I have mentioned what both Megasthenes and others have said, I must go one to add the following. Nearchus wonders at the number of the reptiles and their viciousness, for he says that at the time of the inundations they flee up from the plains into the settlements that escape the inundations, and fill the houses; and that on this account, accordingly, the inhabitants not only make their beds high, but sometimes even move out of their houses when infested by too many of them; and that if the greater part of the multitude of reptiles were not destroyed by the waters, the country would be depopulated; and that the smallness of some of them is troublesome because it is difficult to guard against them, and the huge ones because of their strength, inasmuch as vipers even sixteen cubits long are to be seen; and that charmers go around who are believed to cure the wounds; and that this is almost the only art of medicine, for the people do not have many diseases on account of the simplicity of their diet and their abstinence from wine; but that if diseases arise, they are cured by the Wise Men. But Aristobulus says that he saw none of the animals of the huge size that are everywhere talked about, except a viper nine cubits and one span long. And I myself saw one of about the same size in Aegypt that had been brought from India. He says that you have many much smaller vipers, and asps, and large scorpions, but that none of these is so troublesome as the slender little snakes that are no more than a span long, for they are found hidden in tents, in vessels, and in hedges; and that persons bitten by them bleed from every pore with anguish, and then die unless they receive aid immediately; but that aid is easy because of the virtue of the Indian roots and drugs. He says further that crocodiles, neither numerous nor harmful to man, are to be found in the Indus, and also that most of the other animals are the same as those which are found in the Nile except the hippopotamus. Onesicritus, however, says that this animal too is found in India. And Aristobulus says that on account of the crocodiles no sea-fish swim up into the Nile except the thrissa, the cestreus, and the dolphin, but that there is a p81large number of different fish in the Indus. Of the carides, the small ones swim up the Indus only as far as a mountain, but the large ones as far as the confluence of the Indus and the Acesines. So much, then, is reported about the wild animals. Let me now return to Megasthenes and continue his account from the point where I left off.
After the hunters and the shepherds, he says, follows the fourth caste — the artisans, the tradesmen, and the day-labourers; and of these, some pay tribute to the state, whereas the armour-makers and ship-builders receive wages and provisions, at a published scale, from the king, for they work for him alone; and arms are furnished the soldiers by the commander-in‑chief, whereas the ships are let out for hire to sailors and merchants by the admiral.
The fifth caste is that of the warriors, who, when they are not in service, spend their lives in idleness and at drinking-bouts, being maintained at the expense of the royal treasury; so that they make their expeditions quickly when need arises, since they bring nothing else of their own but their bodies.
The sixth is that of the inspectors, to whom it is given to inspect what is being done and report secretly to the king, using the courtesans as colleagues, the city inspectors using the city courtesans and the camp inspectors the camp courtesans; but the best and most trustworthy men are appointed to this office.
The seventh is that of the advisers and councillors of the king, who hold the chief offices of state, the judgeships, and the administration of everything. It is not legal for a man either to marry a wife from another caste or to change one's pursuit of work from one to another; nor yet for the same man to engage in several, except in case he should be one of the philosophers, for, Megasthenes says, the philosopher is permitted to do so on account of his superiority.
Of the officials, some are market commissioners, others are city commissioners, and others are in charge of the soldiers. Among these, the first keep the rivers improved and the land remeasured, as in Aegypt, and inspect the closed canals from which the water is distributed into the conduits, in order that all may have an equal use of it. The same men also have charge of the hunters and are authorized to reward or punish those who deserve either. They also collect the taxes and superintend the crafts connected with the land — those of wood-cutters, carpenters, workers in brass, and miners. And they make roads, and at every ten stadia place pillars showing the by-roads and the distances.
The city commissioners are divided into six groups of five each. One group looks after the arts of the handicraftsmen. Another group entertains strangers, for they assign them lodgings, follow closely their behaviour, giving them attendants, and either escort them forth or forward the property of those who die; and they take care of them when they are sick and bury them when they die. The third group is that of those who scrutinize births and deaths, when and how they take place, both for the sake of taxes and in order that births and deaths, whether better or worse, may not be unknown. The fourth group is that which has to do with sales and barter; and these look after measures and the fruits of the season, that the latter may be sold by stamp. But the same man cannot barter more than one thing without paying double taxes. The fifth group is that of those who have charge of the works made by artisans and sell these by stamp, the new apart from the old; and the man who mixes them is fined. The sixth and last group is that of those who collect a tenth part of the price of the things sold; and death is the penalty for the man who steals. These are the special duties performed by each group, but they all take care jointly of matters both private and public, and of the repairs of public works, of prices, market-places, harbours, and temples.
After the city commissioners there is a third joint administration, in charge of military affairs, which is also divided into six groups of five each. Of these groups, one is stationed with the admiral; another with the man in charge of the ox-teams, by which are transported instruments of war and food for both man and beast and all other requisites of the army. These also furnish the menials, I mean drum-beaters, gong-carriers, as also grooms and machinists and their assistants; and they send forth the foragers to the sound of bells, and effect speed and safety by means of reward and punishment. The third group consists of those in charge of the infantry; the fourth, of those in charge of the horses; the fifth, of those in charge of the chariots; and the sixth, of those in charge of the elephants. The stalls for both horses and beasts are royal, and the armoury is also royal; for the soldier returns the equipment to the armoury, the horse to the royal horse-stable, and likewise the beast; and they use them without bridles. The chariots are drawn on the march by oxen; but the horses are led by halter, in order that their legs may not be chafed by harness, and also that the spirit they have when drawing chariots may not be dulled. There are two combatants in each chariot in addition to the charioteer; but the elephant carries four persons, the driver and three bowmen, and these three shoot arrows from the elephant's back.
All Indians live a simple life, and especially when they are on expeditions; and neither do they enjoy useless disturbances; and on this account they behave in an orderly manner. But their greatest self-restraint pertains to theft; at any rate, Megasthenes says that when he was in the camp of Sandrocottus, although the number in camp was forty thousand, he on no day saw reports of stolen articles that were worth more than two hundred drachmae; and that too among a people who use unwritten laws only. For, he continues, they have no knowledge of written letters, and regulate every single thing from memory; but still they fare happily, because of their simplicity and their frugality; and indeed they do not drink wine, except at sacrifices, but drink a beverage which they make from rice instead of barley; and also that their food consists for the most part of rice porridge; and their simplicity is also proven in their laws and contracts, which arises from the fact that they are not litigious; for they do not have lawsuits over either pledges or deposits, or have need of witnesses or seals, but trust persons with whom they stake their interests; and further, they generally leave unguarded what they have at their homes. Now these things tend to sobriety; but no man could approve those other habits of theirs — of always eating alone and of not having one common hour for all for dinner and breakfast instead of eating as each one likes; for eating in the other way is more conducive to a social and civic life.
For exercise they approve most of all of rubbing;a and among other ways, they smooth out their bodies through means of smooth sticks of ebony. Their funerals are simple and their mounds small. But, contrary to their simplicity in general, they like to adorn themselves; for they wear apparel embroidered with gold, and use ornaments set with precious stones, and wear gay-coloured linen garments, and are accompanied with sun-shades; for, since they esteem beauty, they practise everything that can beautify their appearance. Further, they respect alike virtue and truth; and therefore they give no precedence even to the age of old men, unless these are also superior in wisdom. They marry many wives, whom they purchase from their parents, and they get them in exchange for a yoke of oxen, marrying some of them for the sake of prompt obedience and the others for the sake of pleasure and numerous offspring; but if the husband does not force them to be chaste, they are permitted to prostitute themselves. No one wears a garland when he makes sacrifice or burns incense or pours out a libation; neither do they cut the throat of the victim, but strangle it, in order that it may be given to the god in its entirety and not mutilated. Anyone caught guilty of false-witness has his hands and feet cut off, and anyone who maims a person not only suffers in return the same thing, but also has his hands cut off; and if he causes the loss of a hand or an eye of a craftsman, he is put to death. But although Megasthenes says that no Indian uses slaves, Onesicritus declares that slavery is peculiar to the Indians in the country of Musicanus, and tells what a success it is there, just as he mentions many other successes of this country, speaking of it as a country excellently governed.
Now the care of the king's person is committed to women, who also are purchased from their fathers; and the body-guards and the rest of the military force are stationed outside the gates. And a woman who kills a king when he is drunk receives as her reward the privilege of consorting with his successor; and their children succeed to the throne. Again, the king does not sleep in daytime; and even at night he is forced to change his bed from time to time because of the plots against him. Among the non-military departures he makes from his palace, one is that to the courts, where he spends the whole day hearing cases to the end, none the less even if the hour comes for the care of his person. This care of his person consists of his being rubbed with sticks of wood, for while he is hearing the cases through, he is also rubbed by four men who stand around him and rub him. A second departure is that to the sacrifices. A third is that to a kind of Bacchic chase wherein he is surrounded by women, and, outside them, by the spear-bearers. The road is lined with ropes; and death is the penalty for anyone who passes inside the ropes to the women; and they are preceded by drum-beaters and gong-carriers. The king hunts in the fenced enclosures, shooting arrows from a platform in his chariot (two or three armed women stand beside him), and also in the unfenced hunting-grounds from an elephant; and the women ride partly in chariots, partly on horses, and partly on elephants, and they are equipped with all kinds of weapons, as they are when they go on military expeditions with the men.
Now these customs are very novel as compared with our own, but the following are still more so. For example, Megasthenes says that the men who inhabit the Caucasus have intercourse with the women in the open and that they eat the bodies of their kinsmen; and that the monkeys are stone-rollers, and, haunting precipices, roll stones down upon their pursuers; and that most of the animals which are tame in our country are wild in theirs. And he mentions horses with one horn and the head of a deer; and reeds, some straight up thirty fathoms in length, and others lying flat on the ground fifty fathoms, and so large that some are three cubits and others six in diameter.
But Megasthenes, going beyond all bounds to the realm of myth, speaks of people five spans long and three spans long, some without nostrils, having instead merely two breathing orifices above their mouths; and he says that it is the people three spans long that carry on war with the cranes (the war to which Homer refers) and with the partridges, which are as large as geese; and that these people pick out and destroy the eggs of the cranes, which, he adds, lay eggs there; and that it is on this account that neither eggs nor, of course, young cranes are anywhere to be found; and that very often a crane escapes from the fights there with a bronze arrow-point in its body. Like this, also, are the stories of the people that sleep in their ears, and the wild people, and other monstrosities. Now the wild people, he continues, could not be brought to Sandrocottus, for they would starve themselves to death; and they have their heels in front, with toes and flat of the foot behind; but certain mouthless people were brought to him, a gentle folk; and they live round the sources of the Ganges; and they sustain themselves by means of vapours from roasted meats and odours from fruits and flowers, since instead of mouths they have only breathing orifices; and they suffer pain when they breathe bad odours, and on this account can hardly survive, particularly in a camp. He says that the other peoples were described to him by the philosophers, who reported the Ocypodes, a people who run away faster than horses; and Enotocoetae, who have ears that extend to their feet, so that they can sleep in them, and are strong enough to pluck up trees and to break bowstrings; and another people, Monommati, with dog's ears, with the eye in the middle of the forehead, with hair standing erect, and with shaggy breasts; and that the Amycteres eat everything, including raw meat, and live but a short time, dying before old age; and the upper lip protrudes much more than the lower. Concerning the Hyperboreans who live a thousand years he says the same things as Simonides and Pindar and other myth-tellers. The statement of Timagenes is also a myth, that brass rained down from the sky in brazen drops and was swept down. But Megasthenes is nearer the truth when he says that the rivers carry down gold-dust and that part of it is paid as a tax to the king; for this is also the case in Iberia.
Speaking of the philosophers, Megasthenes says that those who inhabit the mountains hymn the praises of Dionysus and point out as evidences the wild grape-vine, which grows in their country alone, and the ivy, laurel, myrtle, box-tree, and other evergreens, no one of which is found on the far side of the Euphrates except a few in parks, which can be kept alive only with great care; and that the custom of wearing linen garments, mitres, and gay-coloured garments, and for the king to be attended by gong-carriers and drum-beaters on his departures from the palace, are also Dionysiac; but the philosophers in the plains worship Heracles. Now these statements of Megasthenes are mythical and refuted by many writers, and particularly those about the vine and wine; for much of Armenia, and the whole of Mesopotamia, and the part of Media next thereafter, extending as far as Persis and Carmania, are on the far side of the Euphrates; and a large part of the country of each of these tribes is said to have good vines and good wine.
Megasthenes makes another division in his discussion of the philosophers, asserting that there are two kinds of them, one kind called Brachmanes and the other Garmanes; that the Brachmanes, however, enjoy fairer repute, for they are more in agreement in their dogmas; and that from conception, while in the womb, the children are under the care of learned men, who are reputed to go to the mother and the unborn child, and, ostensibly, to enchant them to a happy birth, but in truth to give prudent suggestions and advice; and that the women who hear them with the greatest pleasure are believed to be the most fortunate in their offspring; and that after the birth of children different persons, one after another, succeed to the care of them, the children always getting more accomplished teachers as they advance in years; and that the philosophers tarry in a grove in front of the city in an enclosure merely commensurate with their needs, leading a frugal life, lying on straw mattresses and skins, abstaining from animal food and the delights of love, and hearkening only to earnest words, and communicating also with anyone who wishes to hear them; and that the hearer is forbidden either to talk or to cough or even to spit; and if he does, he is banished from association with them for that day as a man who has no control over himself; and that, after having lived in this way for thirty-seven years, they retire, each man to his own possessions, where they live more freely and under less restraint, wearing linen garments, ornaments of gold in moderation in their ears and on their hands, and partake of meats of animals that are of no help to man in his work, but abstain from pungent and seasoned food; and that they marry as many wives as possible, in order to have numerous children, for from many wives the number of earnest children would be greater; and, since they have no servants, it is necessary for them to provide for more service from children — the service that is nearest at hand; but that the Brachmanes do not share their philosophy with their wedded wives, for fear, in the first place, that they might tell some forbidden secret to the profane if they become corrupt, and, secondly, that they might desert them if they became earnest, for no person who has contempt for pleasure and toil, and likewise for life and death, is willing to be subject to another; and that the earnest man and the earnest woman are such persons; and that they converse more about death than anything else, for they believe that the life here is, as it were, that of a babe still in the womb, and that death, to those who have devoted themselves to philosophy, is birth into the true life, that is, the happy life; and that they therefore discipline themselves most of all to be ready for death; and that they believe that nothing that happens to mankind is good or bad, for otherwise some would not be grieved and others delighted by the same things, both having dream-like notions, and that the same persons cannot at one time be grieved and then in turn change and be delighted by the same things. As for the opinions of the Brachmanes about the natural world, Megasthenes says that some of their opinions indicate mental simplicity, for the Brachmanes are better in deeds than in words, since they confirm most of their beliefs through the use of myths; and that they are of the same opinion as the Greeks about many things; for example, their opinion that the universe was createdand is destructible, as also the Greeks assert, and that it is spherical in shape,and that the godwho made it and regulates it pervades the whole of it; and that the primal elements of all things else are different, but that water was the primal element of all creation; and that, in addition to the four elements, there is a fifth natural element of which the heavens and the heavenly bodies are composed; and that the earth is situated in the centre of the universe. And writers mention similar opinions of the Brachmanes about the seed and the soul, as also several other opinions of theirs. And they also weave in myths, like Plato, about the immortality of the soul and the judgments in Hades and other things of this kind. So much for his account of the Brachmanes.
As for the Garmanes, he says that the most honourable of them are named Hylobii and that they live in forests, subsisting on leaves and wild fruits, clothed with the bark of trees, and abstaining from wine and the delights of love; and that they communicate with the kings, who through messengers inquire about the causes of things and through the Hylobii worship and supplicate the Divinity; and that, after the Hylobii, the physicians are second in honour, and that they are, as it were, humanitarian philosophers, men who are of frugal habits but do not live out of doors, and subsist upon rice and barley-groats, which are given to them by everyone of whom they beg or who offers them hospitality; and that through sorceryb they can cause people to have numerous offspring, and to have either male or female children; and that they cure diseases mostly through means of cereals, and not through means of medicaments; and that, among their medicaments, their ointments and their poultices are most esteemed, but that the rest of their remedies have much in them that is bad; and that both this class and the other practise such endurance, both in toils and in perseverance, that they stay in one posture all day long without moving; and that there are also diviners and enchanters, who are skilled both in the rites and in the customs pertaining to the deceased, and go about begging alms from village to village and from city to city; and that there are others more accomplished and refined than these, but that even these themselves do not abstain from the common talk about Hades, insofar as it is thought to be conducive to piety and holiness; and that women, as well as men, study philosophy with some of them, and that the women likewise abstain from the delights of love.
Aristobulus says that he saw two of the sophists at Taxila, both Brachmanes; and that the elder had had his head shaved but that the younger had long hair, and that both were followed by disciples; and that when not otherwise engaged they spent their time in the market-place, being honoured as counsellors and being authorized to take as a gift any merchandise they wished; and that anyone whom they accosted poured over them sesame oil, in such profusion that it flowed down over their eyes; and that since quantities of honey and sesame were put out for sale, they made cakes of it and subsisted free of charge; and that they came up to the table of Alexander, ate dinner standing, and taught him a lesson in endurance by retiring to a place near by, where the elder fell to the ground on his back and endured the sun's rays and the rains (for it was now raining, since the spring of the year had begun); and that the younger stood on one leg holding aloft in both hands a log about three cubits in length, and when one leg tired he changed the support to the other and kept this up all day long; and that the younger showed a far greater self-mastery than the elder; for although the younger followed the king a short distance, he soon turned back again towards home, and when the king went after him, the man bade him to come himself if he wanted anything of him; but that the elder accompanied the king to the end, and when he was with him changed his dress and mode of life; and that he said, when reproached by some, that he had completed the forty years of discipline which he had promised to observe; and that Alexander gave his children a present.
Aristobulus mentions some novel and unusual customs at Taxila: those who by reason of poverty are unable to marry off their daughters, lead them forth to the market-place in the flower of their age to the sound of both trumpets and drums (precisely the instruments used to signal the call to battle), thus assembling a crowd; and to any man who comes forward they first expose her rear parts up to the shoulders and then her front parts, and if she pleases him, and at the same time allows herself to be persuaded, on approved terms, he marries her; and the dead are thrown out to be devoured by vultures; and to have several wives is a custom common also to others. And he further says that he heard that among certain tribes wives were glad to be burned up along with their deceased husbands, and that those who would not submit to it were held in disgrace; and this custom is also mentioned by other writers.
Onesicritus says that he himself was sent to converse with these sophists; for Alexander had heard that the people always went naked and devoted themselves to endurance, and that they were held in very great honour, and that they did not visit other people when invited, but bade them to visit them if they wished to participate in anything they did or said; and that therefore, such being the case, since to Alexander it did not seem fitting either to visit them or to force them against their will to do anything contrary to their ancestral customs, he himself was sent; and that he found fifteen men at a distance of twenty stadia from the city, who were in different postures, standing or sitting or lying naked and motionless till evening, and that they then returned to the city; and that it was very hard to endure the sun, which was so hot that at midday no one else could easily endure walking on the ground with bare feet.
Onesicritus says that he conversed with one of these sophists, Calanus, who accompanied the king as far as Persis and died in accordance with the ancestral custom, being placed upon a pyre and burned up. He says that Calanus happened to be lying on stones when he first saw him; that he therefore approached him and greeted him; and told him that he had been sent by the king to learn the wisdom of the sophists and report it to him, and that if there was no objection he was ready to hear his teachings; and that when Calanus saw the mantle and broad-brimmed hat and boots he wore, he laughed at him and said: "In olden times the world was full of barley-meal and wheaten-meal, as now of dust; and fountains then flowed, some with water, others with milk and likewise with honey, and others with wine, and some with olive oil; but, by reason of his gluttony and luxury, man fell into arrogance beyond bounds. But Zeus, hating this state of things, destroyed everything and appointed for man a life of toil. And when self-control and the other virtues in general reappeared, there came again an abundance of blessings. But the condition of man is already close to satiety and arrogance, and there is danger of destruction of everything in existence." And Onesicritus adds that Calanus, after saying this, bade him, if he wished to learn, to take off his clothes, to lie down naked on the same stones, and thus to hear his teachings; and that while he was hesitating what to do, Mandanis, who was the oldest and wisest of the sophists, rebuked Calanus as a man of arrogance, and that too after censuring arrogance himself; and that Mandanis called him and said that he commended the king because, although busied with the government of so great an empire, he was desirous of wisdom; for the king was the only philosopher in arms that he ever saw, and that it was the most useful thing in the world if those men were wise who have the power of persuading the willing, and forcing the unwilling, to learn self-control; but that he might be pardoned if, conversing through three interpreters, who, with the exception of language, knew no more than the masses, he should be unable to set forth anything in his philosophy that would be useful; for that, he added, would be like expecting water to flow pure through mud!c
At all events, all he said, according to Onesicritus, tended to this, that the best teaching is that which removes pleasure and pain from the soul; and that pain and toil differ, for the former is inimical to man and the latter friendly, since man trains the body for toil in order that his opinions may be strengthened, whereby he may put a stop to dissensions and be ready to give good advice to all, both in public and in private; and that, furthermore, he had now advised Taxiles to receive Alexander, for if he received a man better than himself he would be well treated, but if inferior, he would improve him. Onesicritus says that, after saying this, Mandanis inquired whether such doctrines were taught among the Greeks; and that when he answered that Pythagoras taught such doctrines, and also bade people to abstain from meat, as did also Socrates and Diogenes, and that he himself had been a pupil of Diogenes, Mandanis replied that he regarded the Greeks as sound-minded if, but that they were wrong in one respect, in that they preferred custom to nature; for otherwise, Mandanis said, they would not be ashamed to go naked, like himself, and live on frugal fare; for, he added, the best house is that which requires the least repairs. And Onesicritus goes on to say that they inquire into numerous natural phenomena, including prognostics, rains, droughts, and diseases; and that when they depart for the city they scatter to the different market-places; and whatever they chance upon anyone carrying figs or bunches of grapes, they get fruit from that person as a free offering; but that if it is oil, it is poured down over them and they are anointed with it; and that the whole of a wealthy home is open to them, even to the women's apartments, and that they enter and share in meals and conversation; and that they regard disease of the body as a most disgraceful thing; and that he who suspects disease in his own body commits suicide through means of fire, piling a funeral pyre; and that he anoints himself, sits down on the pyre, orders it to be lighted, and burns without a motion.
Nearchus speaks of the sophists as follows: That the Brachmanes engaged in affairs of state and attend the kings as counsellors; but that the other sophists investigate natural phenomena; and that Calanus is one of these; and that their wives join them in the study of philosophy; and that the modes of life of all are severe. As for the customs of the rest of the Indians, he declares as follows: That their laws, some public and some private, are unwritten, and that they contain customs that are strange as compared with those of the other tribes; for example, among some tribes the virgins are set before all as a prize for the man who wins the victory in a fist-fight, so that they may marry the victor without dowry; and among other tribes different groups cultivate the crops in common on the basis of kinship, and, when they collect the produce, they each carry off a load sufficient for sustenance during the year, but burn the remainder in order to have work to do thereafter and not be idle. Their weapons, he says, consist of bow and arrows, the latter three cubits long, or a javelin, and a small shield and a broad sword three cubits long; and instead of bridles they use nose-bands, which differ but slightly from a muzzle; and the lips of their horses have holes pierced through them by spikes.
Nearchus, in explaining the skill of the Indians in handiwork, says that when they saw sponges in use among the Macedonians they made imitations by sewing tufts of wool through and through with hairs and light cords and threads, and that after compressing them into felt they drew out the inserts and dyed the sponge-like felt with colours; and that makers of strigils and of oil-flasks quickly arose in great numbers; and that they write missives on linen cloth that is very closely woven, though the other writers say that they make no use of written characters; and that they use brass that is cast, and not the kind that is forged; and he does not state the reason, although he mentions the strange result that follows the use of the vessels made of cast brass, that when they fall to the ground they break into pieces like pottery. Among the statements made concerning India is also the following, that it is the custom, instead of making obeisance, to offer prayers to the kings and to all who are in authority and of superior rank. The country also produces precious stones, I mean crystals and anthraces of all kinds, as also pearls.
As an example of the lack of agreement among the historians, let us compare their accounts of Calanus. They all agree that he went with Alexander and that he voluntarily died by fire in Alexander's presence; but their accounts of the manner in which he was burned up are not the same, and neither do they ascribe his act to the same cause. Some state it thus: that he went along as a eulogiser of the king, outside the boundaries of India, contrary to the common custom of the philosophers there, for the philosophers attend the kings in India only, guiding them in their relations with the gods, as the Magi attend the Persian kings; but that at Pasargadae he fell ill, the first illness of his life, and despatched himself during his seventy-third year, paying no attention to the entreaties of the king; and that a pyre was made and a golden couch placed on it, and that he laid himself upon it, covered himself up, and was burned to death. But others state it thus: that a wooden house was built, and that it was filled with leaves and that a pyre was built on its roof, and that, being shut in as he had bidden, after the procession which he had accompanied, flung himself upon the pyre and, like a beam of timber, was burned up along with the house. But Megasthenes says that suicide is not a dogma among the philosophers, and that those who commit suicide are judged guilty of the impetuosity of youth; that some who are by nature hardy rush to meet a blow or over precipices; whereas others, who shrink from suffering, plunge into deep waters; and others, who are much suffering, hang themselves; and others, who have a fiery temperament, fling themselves into fire; and that such was Calanus, a man who was without self-control and a slave to the table of Alexander; and that therefore Calanus is censured, whereas Mandanis is commended; for when Alexander's messengers summoned Mandanis to visit the son of Zeus and promised that he would receive gifts if he obeyed, but punishment if he disobeyed, he replied that, in the first place, Alexander was not the son of Zeus, inasmuch as he was not ruler over even a very small part of the earth, and, secondly, that he had no need of gifts from Alexander, of which there was no satiety, and, thirdly, that he had no fear of threats, since India would supply him with food while he was alive, and when he died he would be released from the flesh wasted by old age and be translated to a better and purer life; and that the result was that Alexander commended him and acquiesced.
The following statements are also made by the historians: that the Indians worship Zeus and the Ganges River and the local deities. And when the king washes his hair, they celebrate a great festival and bring big presents, each man making rivalry in display of his own wealth. And they say that some of the ants that mine gold have wings; and that gold-dust is brought down by the rivers, as by the rivers in Iberia. And in the processions at the time of festivals many elephants are paraded, all adorned with gold and silver, as also many four-horse chariots and ox-teams; and then follows the army, all in military uniform; and then golden vessels consisting of large basins and bowls a fathom in breadth; and tables, high chairs, drinking-cups, and bath-tubs, all of which are made of Indian copper and most of them are set with precious stones — emeralds, beryls, and Indian anthraces; and also variegated garments spangled with gold, and tame bisons, leopards, and lions, and numbers of variegated and sweet-voiced birds. And Cleitarchus speaks of four-wheeled carriages on which large-leaved trees are carried, and of different kinds of tamed birds that cling to these trees, and states that of these birds the orion has the sweetest voice, but that the catreus, as it is called, has the most splendid appearance and the most variegated plumage; for its appearance approaches nearest that of the peacock. But one must get the rest of the description from Cleitarchus.
In classifying the philosophers, writers oppose to the Brachmanes the Pramnae, a contentious and disputatious sect; and they say that the Brachmanes study natural philosophy and astronomy, but that they are derided by the Pramnae as quacks and fools; and that, of these, some are called "Mountain" Pramnae, others "Naked" Pramnae, and others "City" Pramnae or "Neighbouring" Pramnae; and that the "Mountain" Pramnae wear deer-skins, and carry wallets full of roots and drugs, pretending to cure people with these, along with witchery and enchantments and amulets; and that the "Naked" Pramnae, as their name implies, live naked, for the most part in the open air, practising endurance, as I have said before, for thirty-seven years; and that women associate with them but do not have intercourse with them; and that these philosophers are held in exceptional esteem.
They say that the "City" Pramnae wear linen garments and live in the city, or else out in the country, and go clad in the skins of fawns or gazelles; but that, in general, the Indians wear white clothing, white linen or cotton garments, contrary to the accounts of those who say that they wear highly coloured garments; and that they all wear long hair and long beards, and that they braid their hair and surround it with a head-band.
Artemidorus says that the Ganges River flows down from the Emoda mountains towards the south, and that when it arrives at the city Ganges it turns towards the east to Palibothra and its outlet into the sea. And he calls one of its tributaries Oedanes, saying that it breeds both crocodiles and dolphins. And he goes on to mention certain other things, but in such a confused and careless manner that they are not to be considered. But one might add to the accounts here given that of Nicolaüs Damascenus.
He says that at Antioch, near Daphnê, he chanced to meet the Indian ambassadors who had been despatched to Caesar Augustus; that the letter plainly indicated more than three ambassadors, but that only three had survived (whom he says he saw), but the rest, mostly by reason of the long journeys, had died; and that the letter was written in Greek on a skin; and that it plainly showed that Porus was the writer, and that, although he was ruler of six hundred kings, still he was anxious to be a friend to Caesar, and was ready, not only to allow him a passage through his country, wherever he wished to go, but also to co-operate with him in anything that was honourable. Nicolaüs says that this was the content of the letter to Caesar, and that the gifts carried to Caesar were presented by eight naked servants, who were clad only in loin-cloths besprinkled with sweet-smelling odours; and that the gifts consisted of the Hermes, a man who was born without arms, whom I myself have seen, and large vipers, and a serpent of ten cubits in length, and a river tortoise three cubits in length, and a partridge larger than a vulture; and they were accompanied also, according to him, by the man who burned himself up at Athens; and that whereas some commit suicide when they suffer adversity, seeking release from the ills at hand, others do so when their lot is happy, as was the case with that man; for, he adds, although that man had fared as he wished up to that time, he thought it necessary then to depart this life, lest something untoward might happen to him if he tarried here; and that therefore he leaped upon the pyre with a laugh, his naked body anointed, wearing only a loin-cloth; and that the following words were inscribed on his tomb: "Here lies Zarmanochegas, an Indian from Bargosa, who immortalised himself in accordance with the ancestral customs of Indians." |
|
|
|
|
15 - 2 Ariana, Gedrosia, and Carmania 
1 After India one comes to Ariana, the first portion of the country subject to the Persians after the Indus River and of the upper satrapies situated outside the Taurus. Ariana is bounded on the south and on the north by the same sea and the same mountains as India, as also by the same river, the Indus, which flows between itself and India; and from this river it extends towards the west as far as the line drawn from the Caspian Gates to Carmania, so that its shape is quadrilateral. Now the southern side begins at the outlets of the Indus and at Patalenê, and ends at Carmania and the mouth of the Persian Gulf, where it has a promontory that projects considerably towards the south; and then it takes a bend into the gulf in the direction of Persis. Ariana is inhabited first by the Arbies, whose name is like that of the River Arbis, which forms the boundary between them and the next tribe, the Oreitae; and the Arbies have a seaboard about one thousand stadia in length, as Nearchus says; but this too is a portion of India. Then one comes to the Oreitae, an autonomous tribe. The coasting voyage along the country of this tribe is one thousand eight hundred stadia in length, and the next, along that of the Ichthyophagi, seven thousand four hundred, and that along the country of the Carmanians as far as Persis, three thousand seven hundred, so that the total voyage is twelve thousand nine hundred stadia.
2 The country of the Ichthyophagi is on the sea-level; and most of it is without trees, except palms and a kind of thorn and the tamarisk; and there is a scarcity both of water and of foods produced by cultivation; and both the people and their cattle use fish for food and drink waters supplied by rains and wells; and the meat of their cattle smells like fish; and they build their dwellings mostly with the bones of whales and with oyster-shells, using the ribs of whales as beams and supports, and the jawbones as doorposts; and they use the vertebral bones of whales as mortars, in which they pound the fish after roasting them in the sun; and then they make bread of this, mixing a small amount of flour with it, for they have grinding-mills, although they have no iron. And this is indeed not so surprising, for they could import grinding-mills from other places; but how do they cut them anew when worn smooth? Why, with the same stones, they say, with which they sharpen arrows and javelins that have been hardened in fire. As for fish, they bake some in covered earthen vessels, but for the most part eat them raw; and they catch them, among other ways, with nets made of palm-bark.
3 Above the country of the Ichthyophagi is situated Gedrosia, a country less torrid than India, but more torrid than the rest of Asia; and since it is in lack of fruits and water, except in summer, it is not much better than the country of the Ichthyophagi. But it produces spices, in particular nard plants and myrrh trees, so that Alexander's army on their march used these for tent-coverings and bedding, at the same time enjoying thereby sweet odours and a more salubrious atmosphere; and they made their return from India in the summer on purpose, for at that time Gedrosia has rains, and the rivers and the wells are filled, though in winter they fail, and the rains fall in the upper regions towards the north and near the mountains; and when the rivers are filled the plains near the sea are watered and the wells are full. And the king sent persons before him into the desert country to dig wells and to prepare stations for himself and his fleet.
4 For he divided his forces into three parts, and himself set out with one division through Gedrosia. He kept away from the sea no more than five hundred stadia at most, in order that he might at the same time equip the seaboard for the reception of his fleet; and he often closely approached the sea, although its shores were hard to traverse and rugged. The second division he sent forward through the interior under the command of Craterus, who at the same time was to subdue Ariana and also to advance to the same region whither Alexander was directing his march. The fleet he gave over to Nearchus and Onesicritus, the latter his master pilot, giving them orders to take an appropriate position, and to follow, and sail alongside, his line of march.
5 Moreover, Nearchus says that when now the king was completing his journey he himself began the voyage, in the autumn, at the time of the rising of the Pleiad in the west; and that the winds were not yet favourable, and that the barbarians attacked them and tried to drive them out; for, he adds, the barbarians took courage when the king departed and acted like freemen. Craterus set out from the Hydaspes and went through the country of the Arachoti and of the Drangae into Carmania. But Alexander was in great distress throughout the whole journey, since he was marching through a wretched country; and from a distance, likewise, he could procure additional supplies only in small quantities and at rare intervals, so that his army was famished; and the beasts of burden fagged out, and the baggage was left behind on the roads and in the camps; but they were saved by the date palms, eating not only the fruit but also the cabbage at the top. They say that Alexander, although aware of the difficulties, conceived an ambition, in view of the prevailing opinion that Semiramis escaped in flight from India with only about twenty men and Cyrus with seven, to see whether he himself could safely lead that large army of his through the same country and win this victory too.
6 In addition to the resourcelessness of the country, the heat of the sun was grievous, as also the depth and the heat of the sands; and in some places there were sand-hills so high that, in addition to the difficulty of lifting one's legs, as out of a pit, there were also ascents and descents to be made. And it was necessary also, on account of the wells, to make long marches of two hundred or three hundred stadia, and sometimes even six hundred, travelling mostly by night. But they would encamp at a distance from the wells, often at a distance of thirty stadia, in order that the soldiers might not, to satisfy their thirst, drink too much water; for many would plunge into the wells, armour and all, and drink as submerged men would; and then, after expiring, would swell up and float on the surface and corrupt the wells, which were shallow; and others, exhausted by reason of thirst, would lie down in the middle of the road in the open sun, and then trembling, along with a jerking of hands and legs, they would die like persons seized with chills or ague. And in some cases soldiers would turn aside from the main road and fall asleep, being overcome by sleep and fatigue. And some, falling behind the army, perished by wandering from the roads and by reason of heat and lack of everything, though others arrived safely, but only after suffering many hardships; and a torrential stream, coming on by night, overwhelmed both a large number of persons and numerous articles; and much of the royal equipment was also swept away; and when the guides ignorantly turned aside so far into the interior that the sea was no longer visible, the king, perceiving their error, set out at once to seek for the shore; and when he found it, and by digging discovered potable water, he sent for the army, and thereafter kept close to shore for seven days, with a good supply of water; and then he withdrew again into the interior.
7 There was a kind of plant like the laurel which caused any beast of burden which tasted of it to die with epilepsy, along with foaming at the mouth. And there was a prickly plant, the fruit of which strewed the ground, like cucumbers, and was full of juice; and if drops of this juice struck an eye of any creature, they always blinded it. Further, many were choked by eating unripe dates. And there was also danger from the snakes; for herbs grew on the sand-hills, and beneath these herbs the snakes had crept unnoticed; and they killed every person they struck. It was said that among the Oreitae the arrows, which were made of wood and hardened in fire, were besmeared with deadly poisons; and that Ptolemaeus was wounded and in danger of losing his life; and that when Alexander was asleep someone stood beside him and showed him a root, branch and all, which he bade Alexander to crush and apply to the wound; and that when Alexander awoke from his sleep he remembered the vision, sought for, and found, the root, which grew in abundance; and that he made use of it, both he himself and the others; and that when the barbarians saw that the antidote had been discovered they surrendered to the king. But it is reasonable to suppose that someone who knew of the antidote informed the king, and that the fabulous element was added for the sake of flattery. Having arrived at the royal seat of the Gedrosii on the sixtieth day after leaving the Orae, Alexander gave his multitudinous army only a short rest and then set out for Carmania.
8 Such, then, on the southern side of Ariana, is about the geographical position of the seaboard and of the lands of the Gedrosii and Oreitae, which lands are situated next above the seaboard. It is a large country, and even Gedrosia reaches up into the interior as far as the Drangae, the Arachoti, and the Paropamisadae, concerning whom Eratosthenes has spoken as follows (for I am unable to give any better description). He says that Ariana is bounded on the east by the Indus River, on the south by the great sea, on the north by the Paropamisus mountain and the mountains that follow it as far as the Caspian Gates, and that its parts on the west are marked by the same boundaries by which Parthia is separated from Media and Carmania from Paraetacenê and Persis. He says that the breadth of the country is the length of the Indus from the Paropamisus mountain to the outlets, a distance of twelve thousand stadia (though some say thirteen thousand); and that its length from the Caspian Gates, as recorded in the work entitled Asiatic Stathmi, is stated in two ways: that is, as far as Alexandreia in the country of the Arii, from the Caspian Gates through the country of the Parthians, there is one and the same road; and then, from there, one road leads in a straight line through Bactriana and over the mountain pass into Ortospana to the meeting of the three roads from Bactra, which city is in the country of the Paropamisadae; whereas the other turns off slightly from Aria towards the south to Prophthasia in Drangiana, and the remainder of it leads back to the boundaries of India and to the Indus; so that this road which leads through the country of the Drangae and Arachoti is longer, its entire length being fifteen thousand three hundred stadia. But if one should subtract one thousand three hundred, one would have as the remainder the length of the country in a straight line, fourteen thousand stadia; for the length of the seacoast is not much less, although some writers increase the total, putting down, in addition to the ten thousand stadia, Carmania with six thousand more; for they obviously reckon the length either along with the gulfs or along the part of the Carmanian seacoast that is inside the Persian Gulf; and the name of Ariana is further extended to a part of Persia and of Media, as also to the Bactrians and Sogdians on the north; for these speak approximately the same language, with but slight variations.
9 The geographical position of the tribes is as follows: along the Indus are the Paropamisadae, above whom lies the Paropamisus mountain: then, towards the south, the Arachoti: then next, towards the south, the Gedroseni, with the other tribes that occupy the seaboard; and the Indus lies, latitudinally, alongside all these places; and of these places, in part, some that lie along the Indus are held by Indians, although they formerly belonged to the Persians. Alexander took these away from the Arians and established settlements of his own, but Seleucus Nicator gave them to Sandrocottus, upon terms of intermarriage and of receiving in exchange five hundred elephants. Alongside the Paropamisadae,º on the west, are situated the Arii, and alongside the Arochoti and Gedrosii the Drangae; but the Arii are situated alongside the Drangae on the north as well as on the west, almost surrounding a small part of their country. Bactriana lies to the north alongside both Aria and the Paropamisadae, through whose country Alexander passed over the Caucasus on his march to Bactra. Towards the west, next to the Arii, are situated the Parthians and the region round the Caspian Gates; and to the south of these lies the desert of Carmania; and then follows the rest of Carmania and Gedrosia.
One would understand still better the accounts of the aforesaid mountainous country if one inquired further into the route which Alexander took in his pursuit of Bessus from the Parthian territory towards Bactriana; for he came into Ariana, and then amongst the Drangae, where he put to death the son of Parmenio, whom he caught in a plot; and he also sent persons to Ecbatana to put to death the father of Philotas, as an accomplice in the plot. It is said that these persons, riding on dromedaries, completed in eleven days a journey of thirty days, or even forty, and accomplished their undertaking. The Drangae, who otherwise are imitators of the Persians in their mode of life, have only scanty supplies of wine, but they have tin in their country. Then, from the Drangae, Alexander went to the Evergetae, who were so named by Cyrus, to the Arachoti; and then, at the setting of the Pleiad, through the country of the Paropamisadae, a country which is mountainous, and at that time was covered with snow, so that it was hard to travel. However, numerous villages, well supplied with everything except oil, received them and alleviated their troubles; and they had the mountain summits on their left. Now the southern parts of the Paropamisus mountain belong to India and Ariana; but as for the parts on the north, those towards the west belong to the Bactrians, whereas those towards the east belong to the barbarians who border on the Bactrians. He spent the winter here, with India above him to the right, and founded a city, and then passed over the top of the mountain into Bactriana, through roads that were bare of everything except a few terebinth trees of the shrub kind; and was so in lack of food that it was necessary to eat the flesh of the beasts of burden, and, for lack of wood, even to eat it raw. But the silphium, which grew in abundance there, was helpful in the digestion of the raw food. On the fifteenth day after founding the city and leaving his winter quarters, he came to Adrapsa, a city in Bactriana.
Somewhere in the neighbourhood of these parts of the country that borders on India lies Chaarenê; and this, of all the countries subject to the Parthians, lies closest to India. It is distant from Ariana, through the land of the Arachoti and the above-mentioned mountainous country, nineteen thousand stadia. Craterus traversed this country, at the same time subduing all who refused to submit, and went by the quickest route, being eager to join the king; and indeed both forces of infantry gathered together in Carmania at about the same time. And a little later Nearchus sailed with his fleet into the Persian Gulf, having often suffered distress because of his wanderings and hardships and the huge whales.
Now it is reasonable to suppose that those who made the journey by sea have prated in many cases to the point of exaggeration; but nevertheless their statements show indirectly at the same time the trouble with which they were afflicted — that underlying their real hardships there was apprehension rather than peril. But what disturbed them most was the spouting whales, which, by their spoutings, would emit such massive streams of water and mist all at once that the sailors could not see a thing that lay before them. But the pilots of the voyage informed the sailors, who were frightened at this and did not see the cause of it, that it was caused by creatures in the sea, and that one could get rid of them by sounding trumpets and making loud noises; and consequently Nearchus led his fleet towards the tumultuous spoutings of the whales, where they impeded his progress, and at the same time frightened them with trumpets; and the whales first dived, and then showed up at the sterns of the ships, thus affording the spectacle of a naval combat, but immediately made off.
Those who now sail to India, however, also speak of the size of these creatures and of their manner of appearance, but do not speak of them either as appearing in large groups or as often making attacks, though they do speak of them as being scared away and got rid of by shouts and trumpets. They say that these creatures do not approach the land, but that the bones of those that have died, when bared of flesh, are readily thrown ashore by the waves, and supply the Ichthyophagi with the above-mentioned material for the construction of their huts. According to Nearchus, the size of the whales is twenty-three fathoms. Nearchus says that he found to be false a thing confidently believed by the sailors in the fleet — I mean their belief that there was an island in the passage which caused the disappearance of all who moored near it; for he says that, although a certain light boat on a voyage was no longer to be seen after it approached the island, and although certain men sent in quest of the lost people sailed out past the island and would not venture to disembark upon it, but called the people with loud outcry, and, when no one answered their cry, came on back, yet he himself, though one and all charged their disappearance to the island, sailed thither, moored there, disembarked with a part of those who sailed with him, and went all over it; but that he found no trace of the people sought, gave up his search, came on back, and informed his people that the charge against the island was false (for otherwise both he himself and those who disembarked with him would have met with the same destruction), but that the disappearance of the light boat took place in some other way, since countless other ways were possible.
Carmania is last on the seaboard that begins at the Indus, though it is much more to the north than the outlet of the Indus. The first promontory of Carmania, however, extends out towards the south into the great sea; and Carmania, after forming, along with the cape that extends from Arabia Felix, which is in full view, the mouth of the Persian Gulf, bends towards the Persian Gulf until it borders on Persis. Carmania is a large country and, in the interior, extends between Gedrosia and Persis, although it deviates more towards the north than Gedrosia. This is plainly indicated by its fruitfulness; for it produces all manner of fruits, is full of large trees except the olive, and is also watered by rivers. Gedrosia differs but little from the country of the Ichthyophagi, and therefore often suffers crop failures; and on this account they keep the annual crop in storage, dealing it out for several years. Onesicritus speaks of a river in Carmania that brings down gold-dust; and he says that there are also mines of silver and copper and ruddle, and also that there are two mountains, one consisting of arsenic and the other of salt. Carmania also has a desert which borders at once upon Parthia and Paraetecenê. And it has farm crops similar to those of the Persians, the vine among all the rest. It is from this vine that "the Carmanian," as we here call it, originated — a vine which often has clusters of even two cubits, these clusters being thick with large grapes; and it is reasonable to suppose that this vine is more flourishing there than here. Because of scarcity of horses most of the Carmanians use asses, even for war; and they sacrifice an ass to Ares, the only god they worship, and they are a warlike people. No one marries before he has cut off the head of an enemy and brought it to the king; and the king stores the skull in the royal palace; and he then minces the tongue, mixes it with flour, tastes it himself, and gives it to the man who brought it to him, to be eaten by himself and family; and that king is held in the highest repute to whom the most heads have been brought. Nearchus states that the language and most of the customs of the Carmanians are like those of the Medes and Persians. The voyage across the mouth of the Persian Gulf requires no more than one day. |
|
|
|
|
15 - 3 Persia proper 
1 After Carmania one comes to Persis. A large portion of this country lies on the seaboard of the gulf which is named after it, but a much larger portion of it lies in the interior, particularly in the direction of its length, that is, from the south and Carmania towards the north and the tribes of Media. Persis is of a threefold character, both in its nature and in the temperature of its air. For, in the first place, its seaboard is burning hot, sandy, and stinted of fruits except dates (its length is reckoned at about forty-four, or forty-three, hundred stadia, and it terminates at the largest of the rivers in that part of the world, the Oroatis, as it is called); secondly, the portion above the seaboard produces everything, is level, and is excellent for the rearing of cattle, and also abounds with rivers and lakes; the third portion, that on the north, is wintry and mountainous; and it is on the borders of this portion that the camel-breeders live. Now, according to Eratosthenes, the length of the country towards the north and the Caspian Gates is about eight thousand stadia, if reckoned from certain promontories, and the remainder to the Caspian Gates is not more than two thousand stadia; and the breadth, in the interior, from Susa to Persepolis, is four thousand two hundred stadia, and thence to the borders of Carmania sixteen hundred more. The tribes which inhabit the country are the Pateischoreis, as they are called, and the Achaemenidae and the Magi. Now the Magi follow with zeal a kind of august life, whereas the Cyrtii and the Mardi are brigands and others are farmers.
2 I might almost say that Susis also is a part of Persis; it lies between Persis and Babylonia and has a most notable city, Susa. For the Persians and Cyrus, after mastering the Medes, saw that their native land was situated rather on the extremities of their empire, and that Susa was farther in and nearer to Babylonia and the other tribes, and therefore established the royal seat of their empire at Susa. At the same time, also, they were pleased with the high standing of the city and with the fact that its territory bordered on Persis, and, better still, with the fact that it had never of itself achieved anything of importance, but always had been subject to others and accounted merely a part of a larger political organisation, except, perhaps, in ancient times, in the times of the heroes. For Susa too is said to have been founded by Tithonus the father of Memnon, with a circuit of one hundred and twenty stadia, and oblong in shape; and its acropolis was called Memnonium; and the Susians are also called Cissians; and Aeschylus calls the mother of Memnon Cissia. Memnon is said to have been buried in the neighbourhood of Paltus in Syria, by the river Badas, as Simonides states in his dithyramb entitled Memnon, one of his Delian poems. The wall and the temples and the royal palace were built like those of the Babylonians, of baked brick and asphalt, as some writers state. Polycleitus says that the city is two hundred stadia in circuit and that it has no walls.
3 Although they adorned the palace at Susa more than any other, they esteemed no less highly the palaces at Persepolis and Pasargadae; at any rate, the treasure and the riches and the tombs of the Persians were there, since they were on sites that were at the same time hereditary and more strongly fortified by nature. And there were also other palaces — that at Gabae, somewhere in the upper parts of Persis, and that on the coast near Taocê, as it is called. These were the palaces in the time of the empire of the Persians, but the kings of later times used others, naturally less sumptuous, since Persis had been weakened, not only by the Macedonians, but still more so by the Parthians. For although the Persians are still under the rule of a king, having a king of their own, yet they are most deficient in power and are subject to the king of the Parthians.
4 Now Susa is situated in the interior on the Choaspes River at the far end of the bridge, but its territory extends down to the sea; and its seaboard is about three thousand stadia in length, extending from boundaries of the Persian seaboard approximately to the outlets of the Tigris. The Choaspes River flows through Susis, terminating at the same seaboard, and has its sources in the territory of the Uxii; for a kind of mountainous country intrudes between the Susians and Persis; it is rugged and sheer, and has narrow defiles that are hard to pass, and was inhabited by brigands, who would exact payments even from the kings themselves when they passed from Susis into Persis. Polycleitus says that the Choaspes, the Eulaeus, and also the Tigris meet in a kind of lake, and then empty from that lake into the sea; and that there is an emporium near the lake, since, on account of the cataracts, purposely constructed, the rivers cannot receive the merchandise that comes in from the sea nor bring down any either, and that all traffic is carried on by land; for the distance to Susa is said to be eight hundred stadia. Others, however, say that the rivers which flow through Susis meet in one stream, that of the Tigris, oppose the intermediate canals of the Euphrates; and that on this account the Tigris, at its outlets, has the name of Pasitigris.
5 Nearchus says that the coast of Persis is covered with shoal-waters and that it ends at the Euphrates River; and that at the mouth of this river there is an inhabited village which receives the merchandise from Arabia; for the seaboard of the Arabians borders next on the mouth of the Euphrates and the Pasitigris, the whole of the intervening space being occupied by a lake, that is, the lake that receives the Tigris; and that on sailing up the Pasitigris one hundred and fifty stadia one comes to the raft-bridge that leads from Persis to Susa, being sixty stadia distant from Susa; and that the Pasitigris is about two thousand stadia distant from the Oroatis; and that the inland voyage on the lake to the mouth of the Tigris is six hundred stadia; and that near the mouth there is an inhabited Susian village, which is five hundred stadia distant from Susa; and that the voyage inland from the mouth of the Euphrates to Babylon, through a very prosperous land, is more than three thousand stadia. Onesicritus says that all the rivers empty into the lake, both the Euphrates and the Tigris; but that the Euphrates, again issuing from the lake, joins with the sea by its own separate mouth.
6 There are also several other narrow defiles as one passes out through the territory of the Uxii in the neighbourhood of Persis itself; and Alexander forced his way through these passes too, both at the Persian Gates and at other places, when he was passing through the country and was eager to spy out the most important parts of the country, and the treasure-holds, which had become filled with treasures in those long periods of time in which the Persians had collected tribute from Asia; and he crossed several rivers that flowed through the country and down into the Persian Gulf. For after the Choaspes, one comes to the Copratas River and the Pasitigris, which latter also flows from the country of the Uxii. There is also a river Cyrus, which flows through Coelê Persis, as it is called, in the neighbourhood of Pasargadae; and the king assumed the name of this river, changing his name from Agradatus to Cyrus. Alexander crossed the Araxes near Persepolis itself. Persepolis, next to Susa, was the most beautifully constructed city, and the largest, having a palace that was remarkable, particularly in respect to the high value of its treasures. The Araxes flows from the country of the Paraetaci; and this river is joined by the Medus, which has its source in Media. These rivers run through a very productive valley which borders on Carmania and the eastern parts of the country, as does also Persepolis itself. Alexander burnt up the palace at Persepolis, to avenge the Greeks, because the Persians had destroyed both temples and cities of the Greeks by fire and sword.
7 Alexander then went to Pasargadae; and this too was an ancient royal residence. Here he saw also, in a park, the tomb of Cyrus; it was a small tower and was concealed within the dense growth of trees. The tomb was solid below, but had a roof and sepulchre above, which latter had an extremely narrow entrance. Aristobulus says that at the behest of the king he passed through this entrance and decorated the tomb; and that he saw a golden couch, a table with cups, a golden coffin, and numerous garments and ornaments set with precious stones; and that he saw all these things on his first visit, but that on a later visit the place had been robbed and everything had been carried off except the couch and the coffin, which had only been broken to pieces, and that the robbers had removed the corpse to another place, a fact which plainly proved that it was an act of plunderers, not of the satrap, since they left behind only what could not easily be carried off; and that the robbery took place even though the tomb was surrounded by a guard of Magi, who received for their maintenance a sheep every day and a horse every month. But just as the remoteness of the countries to which Alexander's army advanced, Bactra and India, had led to numerous other revolutionary acts, so too this was one of the revolutionary acts. Now Aristobulus so states it, and he goes to record the following inscription on the tomb: "O man, I am Cyrus, who acquired the empire for the Persians and was king of Asia; grudge me not, therefore, my monument." Onesicritus, however, states that the tower had ten stories and that Cyrus lay in the uppermost story, and that there was one inscription in Greek, carved in Persian letters, "Here I lie, Cyrus, king of kings," and another written in the Persian language with the same meaning.
8 Onesicritus records also the following inscription on the tomb of Dareius: "I was friend to my friends; as horseman and bowman I proved myself superior to all others; as hunter I prevailed; I could do everything." Aristus of Salamis is indeed a much later writer than these, but he says that the tower has only two stories and is large; that it was built at the time of the succession of the Persians, and that the tomb was kept under guard; and that there was one inscription written in Greek, that quoted above, and another written in the Persian language with the same meaning. Cyrus held Pasargadae in honour, because he there conquered Astyages the Mede in his last battle, transferred to himself the empire of Asia, founded a city, and constructed a palace as a memorial of his victory.
Alexander carried off with him all the wealth in Persis to Susa, which was also full of treasures and equipment; and neither did he regard Susa as the royal residence, but rather Babylon, which he intend to build up still further; and there too treasures lay stored. They say that, apart from the treasures in Babylon and in the camp, which were not included in the total, the value of those in Susa and Persis alone was reckoned at forty thousand talents, though some say fifty; and others have reported that all treasures from all sources were brought together at Ecbatana and that they were valued at one hundred and eighty thousand talents; and the treasures which were carried along with Dareius in his flight from Media, eight thousand talents in value, were taken as booty by those who slew him.
At all events, Alexander preferred Babylon, since he saw that it far surpassed the others, not only in its size, but also in all other respects. Although Susis is fertile, it has a hot and scorching atmosphere, and particularly in the neighbourhood of the city, according to that writer. At any rate, he says that when the sun is hottest, at noon, the lizards and the snakes could not cross the streets in the city quickly enough to prevent their being burnt to death in the middle of the streets. He says that this is the case nowhere in Persis, although Persis lies more to the south; and that cold water for baths is put out in the sun and immediately heated, and that barley spread out in the sun bounces like parched barley in ovens; and that on this account earth is put on the roofs of the houses to the depth of two cubits, and that by reason of this weight the inhabitants are forced to build their houses both narrow and long; and that, although they are in want of long beams, yet they need large houses on account of the suffocating heat; and that the palm-tree beam has a peculiar property, for, although it is rigid, it does not, when aged, give way downwards, but curves upwards because of the weight and better supports the roof.a It is said that the cause of the heat is the fact that lofty mountains lie above the country on the north and that these mountains intercept all the northern winds. Accordingly, these winds, blowing aloft from the tops of the mountains and high above the plains, do not touch the plains, although they blow on the more southerly parts of Susis. But calm prevails here, particularly at the time when the Etesian winds cool the rest of the land that is scorched by heat.
Susis abounds so exceedingly in grain that both barley and wheat regularly produce one hundred-fold, sometimes even two hundred; on this account, also, the people do not cut the furrows close together, for the crowding of the roots hinders the sprouting. The vine did not grow there until the Macedonians planted it, both there and at Babylon; however, they did not dig trenches, but only thrust into the ground iron-pointed stakes, and then pulled them out and replaced them at once with the plants. Such, then, is the interior; but the seaboard is full of shallows and without harbours. On this account, at any rate, Nearchus goes on to say that he met with no native guides when he was sailing along the coast with his fleet from India to Babylonia; that the coast had no mooring-places, and that he was also unable to find any experienced people to guide him.
Neighbouring Susis is the part of Babylonia which was formerly called Sitacenê, but is now called Apolloniatis. Above both, on the north and towards the east, lie the countries of the Elymaei and the Paraetaceni, who are predatory peoples and rely on the ruggedness of their mountains. But the Paraetaceni are situated closer to the Apolloniatae, and therefore treat them worse. The Elymaei carry on war against both that people and the Susians, whereas the Uxii too carry on war against the Elymaei; but less so at the present time, in all probability, because of the might of the Parthians, to whom all the peoples in that part of the world are subject. Now when the Parthians fare well, all their subjects fare well too, but when there is an insurrection, as is often the case, even indeed in our own times, the results are different at different times and not the same for all; for some have benefited by disturbances, whereas others have been disappointed in their expectations. Such, then, are the countries of Persis and Susis.
But the Persian customs are the same as those of these peoples and the Medes and several other peoples; and while several writers have made statements about all these peoples, I too must tell what is suitable to my purpose. Now the Persians do not erect statues or altars, but offer sacrifice on a high place, regarding the heavens as Zeus; and they also worship Helius, whom they call Mithras, and Selenê and Aphroditê, and fire and earth and winds and water; and with earnest prayer they offer sacrifice in a purified place, presenting the victim crowned; and when the Magus, who directs the sacrifice, has divided the meat the people go away with their shares, without setting apart a portion for the gods, for they say that the god requires only the soul of the victim and nothing else; but still, according to some writers, they place a small portion of the caul upon the fire.
But it is especially to fire and water that they offer sacrifice. To fire they offer sacrifice by adding dry wood without the bark and by placing fat on top of it; and then they pour oil upon it and light it below, not blowing with their breath, but fanning it; and those who blow the fire with their breath or put anything dead or filthy upon it are put to death. And to water they offer sacrifice by going to a lake or river or spring, where, having dug a trench leading thereto, they slaughter a victim, being on their guard lest any of the water near by should be made bloody, believing that the blood would pollute the water; and then, placing pieces of meat on myrtle or laurel branches, the Magi touch them with slender wands and make incantations, pouring oil mixed with both milk and honey, though not into fire or water, but upon the ground; and they carry on their incantations for a long time, holding in their hands a bundle of slender myrtle wands.
In Cappadocia (for there the sect of the Magi, who are also called Pyraethi, is large, and in that country are also many temples of the Persian gods), the people do not sacrifice victims with a sword either, but with a kind of tree-trunk, beating them to death as with a cudgel. They also have Pyraetheia, noteworthy enclosures; and in the midst of these there is an altar, on which there is a large quantity of ashes and where the Magi keep the fire ever burning. And there, entering daily, they make incantations for about an hour, holding before the fire their bundles of rods and wearing round their heads high turbans of felt, which reach down over their cheeks far enough to cover their lips. The same customs are observed in the temples of Anaïtis and Omanus; and these temples also have sacred enclosures; and the people carry in procession a wooden statue of Omanus. Now I have seen this myself; but those other things, as also what follows, are recorded in the histories.
For the Persians neither urinate, nor wash themselves, in a river; nor yet bathe therein nor cast therein anything dead or any other thing that is considered unclean. And to whatever god they offer sacrifice, to him they first offer prayer with fire.
They are governed by hereditary kings. And he who is disobedient has his head and arms cut off and his body cast forth. The men marry many wives, and at the same time maintain several concubines, for the sake of having many children. The kings set forth prizes annually for those who have the most children; but the children are not brought into the presence of their parents until they are four years old. Marriages are consummated at the beginning of the vernal equinox; and the bridegroom passes to the bridal chamber, having first eaten an apple or a camel's marrow, but nothing else during that day.
From five years of age to twenty-four they are trained to use the bow, to throw the javelin, to ride horseback, and to speak the truth; and they use as teachers of science their wisest men, who also interweave their teachings with the mythical element, thus reducing that element to a useful purpose, and rehearse both with song and without song the deeds both of the gods and of the noblest men. And these teachers wake the boys up before dawn by the sound of brazen instruments, and assemble them in one place, as though for arming themselves or for a hunt; and then they divide the boys into companies of fifty, appoint one of the sons of the king or of a satrap as leader of each company, and order them to follow their leader in a race, having marked off a distance of thirty or forty stadia. They require them also to give an account of each lesson, at the same time training them in loud speaking and in breathing, and in the use of their lungs, and also training them to endure heat and cold and rains, and to cross torrential streams in such a way as to keep both armour and clothing dry, and also to tend flocks and live outdoors all night and eat wild fruits, such as pistachio nuts, acorns, and wild pears. These are called Cardaces, since they live on thievery, for "carda" means the manly and warlike spirit. Their daily food after their gymnastic exercises consists of bread, barley-cake, cardamum, grains of salt, and roasted or boiled meat; but their drink is water. They hunt by throwing spears from horseback, and with bows and slings; and late in the afternoon they are trained in the planting of trees and in the cutting and gathering of roots and in making weapons and in the art of making linen cloths and hunters' nets. The boys do not touch the meat of wild animals, though it is the custom to bring them home. Prizes are offered by the king for victory in running and in the four other contests of the pentathla. The boys are adorned with gold, since the people hold in honour the fiery appearance of that metal; and on this account, in honour of its fiery appearance, they do not apply gold, just as they do not apply fire, to a dead body.b
They serve in the army and hold commands from twenty to fifty years of age, both as foot-soldiers and as horsemen; and they do not approach a market-place, for they neither sell nor buy. They arm themselves with a rhomboidal wicker-shield; and besides quivers they have swords and knives; and on their heads they wear a tower-like hat; and their breastplates are made of scales of iron. The garb of the commanders consists of three-ply trousers, and of a double tunic, with sleeves, that reaches to the knees, the under garment being white and the upper vari-coloured. In summer they wear a purple or vari-coloured cloak, in winter a vari-coloured one only; and their turbans are similar to those of the Magi; and they wear a deep double shoe. Most of the people wear a double tunic that reaches to the middle of the shin, and a piece of linen cloth round the head; and each man has a bow and sling. Persians dine in an extravagant manner, serving whole animals in great numbers and of various kinds; and their couches, as also their drinking-cups and everything else, are so brilliantly ornamented that they gleam with gold and silver.
They carry on their most important deliberations when drinking wine; and they regard decisions then made as more lasting than those made when they are sober. When they meet people on the streets, they approach and kiss those with whom they are acquainted and who are of equal rank, and to those of lower rank they offer the cheek and in that way receive the kiss; but those of still lower rank merely make obeisance. They smear the bodies of the dead with wax before they bury them, though they do not bury the Magi but leave their bodies to be eaten by birds; and these Magi, by ancestral custom, consort even with their mothers. Such are the customs of the Persians.
Perhaps also the following, mentioned by Polycritus, is one of their customs. He says that in Susa each one of the kings built for himself on the acropolis a separate habitation, treasure-houses, and storage places for what tributes they each exacted, as memorials of his administration; and that they exacted silver from the people on the seaboard, and from the people in the interior such things as each country produced, so that they also received dyes, drugs, hair, or wool, or something else of the kind, and likewise cattle; and that the king who arranged the separate tributes was Dareius, called the Long-armed, and the most handsome of men, except for the length of his arms, for they reached even to his knees; and that most of the gold and silver is used in articles of equipment, but not much in money; and that they consider those metals as better adapted for presents and for depositing in storehouses; and that so much coined money as suffices their needs is enough; and that they coin only what money is commensurate with their expenditures.
For their customs are in general temperate; but on account of their wealth the kings fell into such luxury that they sent for wheat from Assus in Aeolis, for Chalymonian wine from Syria, and for water from the Euphrates, which is so far the lightest of all waters that an Attic cotyle of it weights a drachm less than other waters.
The Persians, of all the barbarians, became the most famous among the Greeks, because none of the other barbarians who ruled Asia ruled Greeks; neither were these people acquainted with the Greeks nor yet the Greeks with the barbarians, except for a short time by distant hearsay. Homer, at any rate, knows neither of the empire of the Syrians nor of that of the Medes; for otherwise, since he names Aegyptian Thebes and mentions the wealth there and the wealth in Phoenicia, he would not have passed by in silence that in Babylon and Ninus and Ecbatana. The Persians were the first people to rule over Greeks. The Lydians had indeed ruled over Greeks, but not also over the whole of Asia — only over a small part of it, that inside the Halys River, and that too for only a short time, in the time of Croesus and Alyattes. But the Lydians were mastered by the Persians and deprived by them of whatever glory they had. The Persians, as soon as they broke up the power of the Medes, immediately mastered the Lydians and also got as their subjects the Greeks in Asia; and later they even crossed over into Greece; and, though often defeated in many battles, still they continued to hold Asia as far as the places on the sea until they were subdued by the Macedonians.
Now the man who established the Persians in their hegemony was Cyrus. Cyrus was succeeded by his son Cambyses, who was deposed by the Magi. The Magi were slain by the Seven Persians, who then gave over the empire to Dareius, the son of Hystaspes. And then the successors of Dareius came to an end with Arses. Arses was slain by Bagoüs the eunuch, who set up as king another Dareius, who was not of the royal family. Him Alexander deposed, and reigned himself for ten or eleven years. And then the hegemony of Asia was divided amongst his several successors and their descendants, and then dissolved. The hegemony of the Persians over Asia lasted about two hundred and fifty years. But now, though again organised into a state of their own, the Persians have kings that are subject to other kings, formerly to the kings of Macedonia, but now to those of the Parthians. |
|
|
|
|
16 Syria. 4 114 1:35 
|
16 - 1 Leucania 
1 The country of the Assyrians borders on Persis and Susiana. This name is given to Babylonia and to much of the country all round, which latter, in part, is also called Aturia, in which are Ninus, Apolloniatis, the Elymaei, the Paraetacae, the Chalonitis in the neighbourhood of Mt. Zagrus, the plains in the neighbourhood of Ninus, and also Dolomenê and Calachenê and Chazenê and Adiabenê, and the tribes of Mesopotamia in the neighbourhood of the Gordyaeans, and the Mygdonians in the neighbourhood of Nisibis, as far as the Zeugma of the Euphrates, as also much of the country on the far side of the Euphrates, which is occupied by Arabians, and those people who in a special sense of the term are called by the men of to‑day Syrians, who extend as far as the Cilicians and the Phoenicians and the Judaeans and the sea that is opposite the Aegyptian Sea and the Gulf of Issus.
2 It seems that the name of the Syrians extended not only from Babylonia to the Gulf of Issus, but also in ancient times from this gulf to the Euxine. At any rate, both tribes of the Cappadocians, both those near the Taurus and those near the Pontus, have to the present time been called "White Syrians," as though some Syrians were black, these being the Syrians who live outside the Taurus; and when I say "Taurus," I am extending the name as far as the Amanus. When those who have written histories of the Syrian empire say that the Medes were overthrown by the Persians and the Syrians by the Medes, they mean by the Syrians no other people than those who built the royal palaces in Babylon and Ninus; and, of these Syrians, Ninus was the man who founded Ninus in Aturia, and his wife, Semiramis, was the woman who succeeded her husband and founded Babylon. These two gained the mastery of Asia; and as for Semiramis, apart from her works at Babylon, many others are also to be seen throughout almost the whole of that continent, I mean the mounds called the Mounds of Semiramis, and walls, and the construction of fortifications with aqueducts therein, and of reservoirs for drinking-water, and of ladder-like ascents of mountains, and of channels in rivers and lakes, and of roads and bridges. And they left to their successors their empire until the time of the empires of Sardanapalus and Arbaces. But later the empire passed over to the Medes.
3 Now the city Ninus was wiped out immediately after the overthrow of the Syrians. It was much greater than Babylon, and was situated in the plain of Aturia. Aturia borders on the region of Arbela, with the Lycus River lying between them. Now Arbela, which lies opposite to Babylonia, belongs to that country; and in the country on the far side of the Lycus River lie the plains of Aturia, which surround Ninus. In Aturia is a village Gaugamela, where Dareius was conquered and lost his empire. Now this is a famous place, as is also its name, which, being interpreted, means "Camel's House." Dareius, the son of Hystaspes, so named it, having given it as an estate for the maintenance of the camel which helped most on the toilsome journey through the deserts of Scythia with the burdens containing sustenance and support for the king. However, the Macedonians, seeing that this was a cheap village, but that Arbela was a notable settlement (founded, as it is said, by Arbelus, the son of Athmoneus), announced that the battle and victory took place near Arbela and so transmitted their account to the historians.
4 After Arbela and Mt. Nicatorium (a name applied to it by Alexander after his victory in the neighbourhood of Arbela), one comes to the Caprus River, which lies at the same distance from Arbela as the Lycus. The country is called Artacenê. Near Arbela lies the city Demetrias; and then one comes to the fountain of naphtha, and to the fires, and to the temple of Anea, and to Sandracae, and that royal palace of Dareius the son of Hystaspes, and to Cyparisson, and to the crossing of the Caprus River, where, at last, one is close to Seleuceia and Babylon.
5 Babylon, too, lies in a plain; and the circuit of its wall is three hundred and eighty-five stadia. The thickness of its wall is thirty-two feet; the height thereof between the towers is fifty cubits; that of the towers is sixty cubits; and the passage on top of the wall is such that four-horse chariots can easily pass one another; and it is on this account that this and the hanging garden are called one of the Seven Wonders of the World. The garden is quadrangular in shape, and each side is four plethra in length. It consists of arched vaults, which are situated, one after another, on checkered, cube-like foundations. The checkered foundations, which are hollowed out, are covered so deep with earth that they admit of the largest of trees, having been constructed of baked brick and asphalt — the foundations themselves and the vaults and the arches. The ascent to the uppermost terrace-roofs is made by a stairway; and alongside these stairs there were screws, through which the water was continually conducted up into the garden from the Euphrates by those appointed for this purpose. For the river, a stadium in width, flows through the middle of the city; and the garden is on the bank of the river. Here too is the tomb of Belus, now in ruins, having been demolished by Xerxes, as it is said. It was a quadrangular pyramid of baked brick, not only being a stadium in height, but also having sides a stadium in length. Alexander intended to repair this pyramid; but it would have been a large task and would have required a long time (for merely the clearing away of the mound was a task for ten thousand men for two months), so that he could not finish what he had attempted; for immediately the king was overtaken by disease and death. None of his successors cared for this matter; and even what was left of the city was neglected and thrown into ruins, partly by the Persians and partly by time and by the indifference of the Macedonians to things of this kind, and in particular after Seleucus Nicator had fortified Seleuceia on the Tigris near Babylon, at a distance of about three hundred stadia therefrom. For not only he, but also all his successors, were strongly interested in Seleuceia and transferred the royal residence to it. What is more, Seleuceia at the present time has become larger than Babylon, whereas the greater part of Babylon is so deserted that one would not hesitate to say with one of the comic poets said in reference to the Megalopolitans in Arcadia: "The Great City is a great desert." On account of the scarcity of timber their buildings are finished with beams and pillars of palm-wood. They wind ropes of twisted reed round the pillars; and then they plaster them and paint them with colours, though they coat the doors with asphalt. Both these and the private homes are built high, all being vaulted on account of the lack of timber; for, with the exception of the palm tree, most of the country is bare of trees and bears shrubs only. The palm is most abundant in Babylonia, and is found in abundance in Susa and on the coast of Persis and in Carmania. They do not use tiles much on their houses, for they get no rain; and this is likewise the case both in Susa and Sitacenê.
6 In Babylonia a settlement is set apart for the local philosophers, the Chaldaeans, as they are called, who are concerned mostly with astronomy; but some of these, who are not approved of by the others, profess to be genethlialogists. There is also a tribe of the Chaldaeans, and a territory inhabited by them, in the neighbourhood of the Arabians and of the Persian Sea, as it is called. There are also several tribes of the Chaldaean astronomers. For example, some are called Orcheni, others Borsippeni, and several others by different names, as though divided into different sects which hold to various different dogmas about the same subjects. And the mathematicians make mention of some of these men; as, for example, Cidenasa and Naburianus and Sudinus. Seleucus of Seleuceia is also a Chaldaean, as are also several other noteworthy men.
7 Borsippa is a city sacred to Artemis and Apollo; and it manufactures linen in great quantities. It abounds in bats, much larger in size than those in other places; and these bats are caught and salted for food.
8 The country of the Babylonians is surrounded on the east by the Susians and Elymaeans and Paraetacenians, and on the south by the Persian Gulf and the Chaldaeans as far as the Mesenian Arabians, and on the west by the Arabians called Scenitae, as far as Adiabenê and Gordyaea, and on the north by the Armenians and the Medes as far as the Zagrus and the tribes about that river.
9 The country is traversed by several rivers, though the largest are the Euphrates and the Tigris. Next to the Indian rivers these two, among those in the southern parts of Asia, are said to hold the second place. And they are navigable inland: from Tigris to Opis and the present Seleuceia (the village Opis is an emporium of the places situated round it) and the Euphrates to Babylon, a distance of more than three thousand stadia. Now the Persians, wishing on purpose to prevent voyaging up these rivers, for fear of attacks from without, had constructed artificial cataracts, but Alexander, when he went against them, destroyed as many of them as he could, and in particular those to Opis. He also paid careful attention to the canals; for the Euphrates rises to flood-tide at the beginning of summer, beginning first to rise in the spring when the snows in Armenia melt; so that of necessity it forms lakes and deluges the ploughed lands, unless the excess of the stream, or the surface water, is distributed by means of trenches and canals, as is the case with the Nile in Aegypt. Now this is the origin of the canals; but there is need of much labour to keep them up, for the soil is so deep and soft and yielding that it is easily swept out by the streams, and the plains are laid bare, and the canals are easily filled, and their mouths choked, by the silt; and thus it results again that the overflow of the waters, emptying into the plains near the sea, forms lakes and marshes and reed-beds, which last supply reeds from which all kinds of reed-vessels are woven. Some of these vessels, when smeared all over with asphalt, can hold water, whereas the others are used in their bare state. They also make reed-sails, which are similar to rush-mats or wicker-work.
Now it is impossible, perhaps, altogether to prevent overflows of this kind, but it is the part of good rulers to afford all possible aid. The aid required is this: to prevent most of the overflowing by means of dams, and to prevent the filling up effected by the silt, on the contrary, by keeping the canals cleared and the mouths opened up, Now the clearing of the canals is easy, but the building of dams requires the work of many hands; for, since the earth readily gives in and is soft, it does not support the silt that is brought upon it, but yields to the silt, and draws it on, along with itself, and makes the mouth hard to dam. Indeed there is also need of quick work in order to close the canals quickly and to prevent all the water from emptying out of them. For when they dry up in the summer, they dry up the river too; and when the river is lowered it cannot supply the sluices with water at the time needed, since the water is needed most in summer, when the country is fiery hot and scorched; and it makes no difference whether the crops are submerged by the abundance of water, or are destroyed by thirst for water. At the same time, also, the voyages inland, with their many advantages, were always being thwarted by the two above-mentioned causes, and it was impossible to correct the trouble unless the mouths of the canals were quickly opened up and quickly closed, and unless the canals were regulated so that the water in them neither was excessive nor failed.
Aristobulus says that Alexander himself, when he was sailing up the river and piloting the boat, inspected canals and with his multitude of followers cleared them; and that he likewise stopped up some of the mouths and opened others; and when he noticed that one canal, the one which stretched most directly towards the marshes and lakes that lay in front of Arabia, had a mouth most difficult to deal with and could not easily be stopped up because of the yielding and soft nature of the soil, he opened up another mouth, a new one, at a distance of thirty stadia from it, having selected a place with a rocky bottom, and that he diverted the stream to that place; and that in doing this he was taking forethought at the same time that Arabia should not be made utterly difficult to enter by the lakes or even by the marshes, since, on account of the abundance of water, that country was already taking the form of an island. For of course Alexander, he says, intended to acquire possession of that country, and had already prepared fleets and bases of operations, having built some of his boats in Phoenicia and Cypros, boats that were constructed with bolts and could be taken to pieces, which were conveyed by a seven days' journey to Thapsacus and then down the river to Babylon, and having built others in Babylonia, from the cypress trees in the groves and the parks; for there is a scarcity of timber in Babylonia, although there is a moderately good supply of timber in the countries of the Cossaei and certain other tribes. Now Alexander alleged as cause of the war, Aristobulus says, that the Arabians were the only people on earth who did not send ambassadors to him, but in truth was reaching out to be lord of all; and when he learned that they worshipped two gods only, Zeus and Dionysus, the gods who supply the most requisite needs of life, he took it for granted that they would worship him as a third if he mastered them and allowed them to keep the ancestral independence which they had had before. Accordingly, he adds, Alexander busied himself thus with the canals, and also inspected thoroughly the tombs of the kings and potentates, most of which are situated among the lakes.
Eratosthenes, when he mentions the lakes near Arabia, says that when the water is deprived of exits it opens upon underground passages and through these flows underground as far as the country of Coelê-Syria, and that it is pressed up into the region of Rhinocolura and Mt. Casius and forms the lakes and the pits there; but I do not know whether or not his statement is plausible; for the side-outflows of the Euphrates which form the lakes near Arabia and the marshes are near the Persian Sea, but the isthmus which separates them is neither large nor rocky, so that it was more likely that the water forced its way into the sea in this region, whether underground or on the surface, than that it traversed a distance of more than six thousand stadia, through a country so waterless and dry, and that too when mountains intervene, I mean Mt. Libanus and Mt. Antilibanus and Mt. Casius. Such, then, are the accounts of Aristobulus and Eratosthenes.
Polycleitus, however, says that the Euphrates does not overflow; for, he says, it flows through large plains; and as for the mountains, some stand at a distance of two thousand stadia from it, but the Cossaean mountains at a distance of scarcely one thousand, which latter are not very high, are not covered very deeply with snow, and do not cause the snow to melt quickly in great quantities; for, he says, the heights of the mountains lie in the region above Ecbatana towards the north, but, in the region towards the south, they split, broaden out, and become much lower, and at the same time most of their waters are received by the Tigris and thus overflow the plains. Now this last assertion is obviously absurd, for the Tigris flows down into the same plains as the Euphrates, and the above-mentioned heights of the mountains have different altitudes, the northern heights being more elevated in some places, whereas the southern broaden out in some places; but the quantity of snow is not determined merely by the heights, but also by their latitudes; and the same mountain has more snow in its northern parts than in its southern, and the snow continues longer in the former than the latter. Now the Tigris receives from the southernmost parts of Armenia, which are near Babylonia, the water of the melted snows, which is not much, since it comes from the southern side, and this river would therefore be flooded less than the Euphrates; but the Euphrates receives the water from both parts, and not merely from one mountain, but from many, as I made clear in my description of Armenia, where I added the length of that river, giving first the length of its course in Greater Armenia and Lesser Armenia, and secondly its length from Lesser Armenia and Cappadocia through the Taurus as far as Thapsacus, where it forms the boundary between Lower Syria and Mesopotamia, and, thirdly, the rest of its length as far as Babylon and the outlet, a length, all told, of thirty-six thousand stadia. So much, then, for the canals.
The country produces larger crops of barley than any other country (bearing three hundredfold, they say), and its other needs are supplied by the palm tree; for this tree yields bread, wine, vinegar, honey, and meal; and all kinds of woven articles are supplied by that tree; and the bronze-smiths use the stones of the fruit instead of charcoal; and when soaked in water these stones are used as food for oxen and sheep which are being fattened. There is said to be a Persian song wherein are enumerated three hundred and sixty uses of the palm tree; and, as for oil, the people use mostly that of sesame, but this plant is rare in all other places.
Link to a page in English Babylon produces also great quantities of asphalt, concerning which Eratosthenes states that the liquid kind, which is called naphtha, is found in Susis, but the dry kind, which can be solidified, in Babylonia; and that there is a fountain of this latter asphalt near the Euphrates River; and that when this river is at its flood at the time of the melting of the snows, the fountain of asphalt is also filled and overflows into the river; and that there large clods of asphalt are formed which are suitable for buildings constructed of baked bricks. Other writers say that the liquid kind also is found in Babylonia. Now writers state in particular the great usefulness of the dry kind in the construction of buildings, but they say also that boats are woven with reeds and, when plastered with asphalt, are impervious to water. The liquid kind, which they call naphtha, is of a singular nature; for it the naphtha is brought near fire it catches the fire; and if you smear a body with it and bring it near to the fire, the body bursts into flames; and it is impossible to quench these flames with water (for they burn more violently), unless a great amount is used, though they can be smothered and quenched with mud, vinegar, alum, and bird-lime. It is said that Alexander, for an experiment, poured some naphtha on a boy in a bath and brought a lamp near him; and that the boy, enveloped in flames, would have been nearly burned to death if the bystanders had not, by pouring on him a very great quantity of water, prevailed over the fire and saved his life.b Poseidonius says of the springs of naphtha in Babylonia, that some send forth white naphtha and others black; and that some of these, I mean those that send forth white naphtha, consist of liquid sulphur (and it is these that attract the flames), whereas the others send forth black naphtha, liquid asphalt, which is burnt in lamps instead of oil.
And in ancient times Babylon was the metropolis of Assyria; but now Seleuceia is the metropolis, I mean the Seleuceia on the Tigris, as it is called. Near by is situated a village called Ctesiphon, a large village. This village the kings of the Parthians were wont to make their winter residence, thus sparing the Seleuceians, in order that the Seleuceians might not be oppressed by having the Scythian folk or soldiery quartered amongst them. Because of the Parthian power, therefore, Ctesiphon is a city rather than a village; its size is such that it lodges a great number of people, and it has been equipped with buildings by the Parthians themselves; and it has been provided by the Parthians with wares for sale and with the arts that are pleasing to the Parthians; for the Parthian kings are accustomed to spend the winter there because of the salubrity of the air, but the summer at Ecbatana and in Hyrcania because of the prevalence of their ancient renown. And as we call the country Babylonia, so also we call the men from there Babylonians, that is, not after the city, but after the country; but we do not call men after Seleuceia, if they are from there, as for example, Diogenes the Stoic philosopher.
And there is also Artemita, a noteworthy city, which is five hundred stadia distant from Seleuceia, being situated almost directly towards the east, as is also Sitacenê. For Sitacenê too, both extensive and fertile, lies between Babylon and Susis, so that the whole of the journey for people travelling from Babylon to Susa is through Sitacenê towards the east; and the journey for people travelling from Susa into the interior of Persis through Uxia, and for people travelling from Persis into the middle of Carmania, is also towards the east. Now Carmania in encircled on the north by Persis, which is a large country; and bordering on this country are Paraetacenê and Cossaea as far as the Caspian Gates, which is inhabited by mountainous and predatory tribes. And bordering on Susis is Elymaïs, most of which is rugged and inhabited by brigands; and bordering Elymaïs are Media and the region of the Zagrus.
Now the Cossaeans, like the neighbouring mountaineers, are for the most part bowmen, and are always out of foraging expeditions; for they have a country that is small and barren, so that they must needs live at the expense of the other tribes. And they are of necessity a powerful people, for they are all fighters; at any rate, thirteen thousand Cossaeans joined the Elymaeans in battle, when the latter were warring against both the Babylonians and the Susians. But the Paraetaceni are more interested in agriculture than the Cossaeans; but still even they themselves do not abstain from brigandage. The Elymaeans possess a larger and more diversified country than the Paraetaceni. Now all of it that is fertile is inhabited by farmers, whereas the mountainous part of it is a nursery of soldiers, mostly bowmen; and since the latter part is extensive, it can furnish so large a military force that their king, since he possesses great power, refuses to be subject to the king of the Parthians like the other tribes; and their king was likewise disposed towards the Macedonians, who ruled Syria in later times. Now when Antiochus the Great attempted to rob the temple of Belus, the neighbouring barbarians, all by themselves, attacked and slew him. In later times the king of Parthia, though warned by what had happened to Antiochus, hearing that the temples in that country contained great wealth, and seeing that inhabitants were disobedient subjects, made an invasion with a great force, and took both the temple of Athena and that of Artemis, the latter called Azara, and carried off treasures valued at ten thousand talents. And Seleuceia near the Hedyphon River, a large city, was also taken. In earlier times Seleuceia was called Solocê. There are three entrances into the country that have been supplied by nature: one from Media and the region of the Zagrus through Massabaticê; another from Susis through Gabianê (these, both Gabianê and Massabaticê, are provinces of Elymaea), and the third from Persis. And Corbianê is also a province of Elymaïs. And the countries of the Sagapeni and the Silaceni, small domains, border on that of these people. Such is the size and such is the nature of the tribes situated above Babylonia towards the east. But, as I have said, Media and Armenia are situated on the north; and Adiabenê and Mesopotamia are situated on the west.
Now as for Adiabenê, the most of it consists of plains; and though it too is a part of Babylonia, still it has a ruler of its own; and in some places it borders also on Armenia. For the Medes and the Armenians, and third the Babylonians, the three greatest of the tribes in that part of the world, were so constituted from the beginning, and continued to be, that at times opportune for each they would attack one another and in turn become reconciled. And this continued down to the supremacy of the Parthians. Now the Parthians rule over the Medes and the Babylonians, but they have never once ruled over the Armenians; indeed, the Armenians have been attacked many times, but they could not be overcome by force, since Tigranes opposed all attacks mightily, as I have stated in my description of Armenia. Such, then, is Adiabenê; and the Adiabeni are also called Saccopodes; but I shall describe Mesopotamia and the tribes on the south, after briefly going over the accounts given of the customs of Assyria.
Now in general their customs are like those of the Persians, but it is a custom peculiar to them to appoint three wise men as rulers of each tribe, who present in public the marriageable girls, and sell them by auction to the bridegrooms, always selling first those who are the more highly prized. Thus marriages are contracted; and every time they have intercourse with one another, they arise and go out, each apart from the other, to offer incense; and in the morning they bathe themselves before they touch any vessel; for just as ablution is customary after touching a corpse, so also it is customary after intercourse. And in accordance with a certain oracle all the Babylonian women have a custom of having intercourse with a foreigner, the women going to a temple of Aphrodite with a great retinue and crowd; and each woman is wreathed with a cord round her head. The man who approaches a woman takes her far away from the sacred precinct, and then has intercourse with her; and the money is considered sacred to Aphrodite. They have three tribunals: that of those who are already freed from military service, and that of the most famous, and that of the old men, apart from that appointed by the king. It is the duty of this last to give girls in marriage and to pass judgment in cases of adultery; and the duty of another to pass judgment in cases of theft, and of a third to pass judgment in cases of assault. They place the sick where three roads meet and question those who pass by, on the chance that some one has a cure for the malady; and no one of those who pass by is so base as not to suggest some cure when he falls in with them if he has any in mind. Their clothing consists of a linen tunic reaching to the feet, an upper garment made of wool, and a white cloak; and they wear their hair long, and use a shoe that is like a buskin. They wear also a seal, and carry a staff that is not plain but has a design on it, having on top an apple or rose of lily or something of the kind; and they anoint themselves with sesame; and they bewail the dead, like the Egyptians and many other nations; and they bury their dead in honey, first besmearing them in wax. But three of their tribes have no grain; and these live in marshes and are fish-eaters, living a life similar to that of the inhabitants of Gedrosia.
Mesopotamia has its name from what is the fact in the case. As I have said, it lies between the Euphrates and the Tigris; and the Tigris washes its eastern side only, whereas at Euphrates washes its western and southern sides; and on the north is the Taurus, which separates Armenia from Mesopotamia. Now the greatest distance by which the two rivers are separated is that towards the mountains; and this distance might be the same as that stated by Eratosthenes — I mean that from Thapsacus, where was the old bridge of the Euphrates, to the crossing of the Tigris, where Alexander crossed it — two thousand four hundred stadia; but the shortest distance between the two rivers is somewhere in the neighbourhood of Seleuceia and Babylon, slightly more than two hundred stadia. The Tigris flows through the middle of Lake Thopitis, as it is called, in the direction of its breadth; and, after traversing it to the opposite shore, it sinks underground with upward blasts and a loud noise; and having flowed for a considerable distance invisible, it rises again not far away from Gordyaea; and it traverses the lake so impetuously, as Eratosthenes says, that, although the lake elsewhere is briny and without fish, yet in this part it is fresh, runs like a river, and is full of fish.
Mesopotamia contracts in shape, projecting to a considerable length; and the shape of it somewhat resembles that of a boat; and the greatest part of its periphery is formed by the Euphrates. The distance from Thapsacus to Babylon, as Eratosthenes states, is four thousand eight hundred stadia; and that from the Zeugma at Commagenê, where Mesopotamia begins, to Thapsacus, is not less than two thousand stadia.
The country alongside the mountains is quite fertile; the parts of it near the Euphrates and the Zeugma, both the present Zeugma at Commagenê and the old Zeugma at Thapsacus, are occupied by the Mygdones, who were so named by the Macedonians. In their country lies Nisibis, which is also called Mygdonian Antiocheia; it lies at the foot of Mt. Masius, and so do Tigranocerta and the regions of Carrhae and Nicephorium, and Chordiraza and Sinnaca, in which last Crassus was slain, being treacherously captured by Surena, the Parthian general.
Near the Tigris lie the places belonging to the Gordyaeans, whom the ancients called Carduchians; and their cities are named Sareisa and Satalca and Pinaca, a very powerful fortress, with three citadels, each enclosed by a separate fortification of its own, so that they constitute, as it were, a triple city. But still it not only was held in subjection by the king of the Armenians, but the Romans took it by force, although the Gordyaeans had an exceptional repute as master-builders and as experts in the construction of siege engines; and it was for this reason that Tigranes used them in such work. But also the rest of Mesopotamia became subject to the Romans. Pompey assigned to Tigranes most of the places in this country, I mean all that are worth mentioning; for the country is rich in pasturage, and so rich in plants that it also produces the evergreens and a spice-plant called amomum; and it is a feeding-ground for lions; and it also produces naphtha and the stone called gangitis, which is avoided by reptiles.
Gordys, the son of Triptolemus, is said to have taken up his abode in Gordyenê, and later also the Eretrians, who were carried off by the Persians. Of Triptolemus, however, I shall soon give a clear account in my description of the Syrians.
The parts of Mesopotamia which incline towards the south and are farther from the mountains, which are waterless and barren, are occupied by the Arabian Scenitae, a tribe of brigands and shepherds, who readily move from one place to another when pasture and booty fail them. Accordingly, the people who live alongside the mountains are harassed not only by the Scenitae, but also by the Armenians, who are situated above them and, through their might, oppress them; and at last they are subject for the most part to the Armenians or else to the Parthians, for the Parthians too are situated on the sides of the country and possess both Media and Babylonia.
Between the Euphrates and the Tigris there flows another river, called Basileius; and in the neighbourhood of Anthemusia still another, called Aborras. The road for people travelling from Syria to Seleuceia and Babylon runs through the country of the Scenitae, now called Malians by some writers, and through their desert. Such travellers cross the Euphrates near Anthemusia, a place in Mesopotamia; and above the river, at a distance of four schoeni, lies Bambycê, which is also called Edessa and Hierapolis, where the Syrian goddess Atargatis is worshipped; for after they cross the river, the road runs through the desert to Scenae, a noteworthy city situated on a canal towards the borders of Babylonia. The journey from the crossing of the river to Scenae requires twenty-five days. And on that road are camel-drivers who keep halting-places, which sometimes are well supplied with reservoirs, generally cisterns, though sometimes the camel-drivers use waters brought in from other places. The Scenitae are peaceful, and moderate towards travellers in the exaction of tribute, and on this account merchants avoid the land along the river and risk a journey through the desert, leaving the river on the right for approximately a three days' journey. For the chieftains who live along the river on both sides occupy country which, though not rich in resources, is less resourceless than that of others, and are each invested with their own particular domains and exact a tribute of no moderate amount. For it is hard among so many peoples, and that too among peoples that are self-willed, for a common standard of tribute to be set that is advantageous to the merchant. Scenae is eighteen schoeni distant from Seleuceia.
The Euphrates and the land beyond it constitute the boundary of the Parthian empire. But the parts this side the river are held by the Romans and the chieftains of the Arabians as far as Babylonia, some of these chieftains preferring to give ear to the Parthians and others to the Romans, to whom they are neighbours; less so the nomad Scenitae who are near the river, but more so those that are far away and near Arabia Felix. The Parthians were also in former times eager for friendship with the Romans, but they defended themselves against Crassus, who began war with them; and then, having begun the battle themselves, met with equal reverses when they sent Pacorus against Asia. But Antony, using the Armenian as counsellor, was betrayed and fared badly in his war. Phraates, his successor, was so eager for friendship with Caesar Augustus that he even sent him the trophies which the Parthians had set up as memorials of their defeat of the Romans. And, having called Titius to a conference, who was at that time praefect of Syria, he put in his hands as hostages four of his legitimate sons, Seraspadanes and Rhodaspes and Phraates and Bonones, and two wives and four sons of these, for fear of seditions and attempts upon his life; for he knew that no person could prevail against him unless that person supported some member of the house of Arsaces, because of the fact that the Parthians were extremely fond of his house. Accordingly, he got rid of his children, seeking thus to deprive evil-doers of that hope. Now all his surviving children are cared for in royal style, at public expense, in Rome, and the remaining kings have also continued to send ambassadors and to go into conferences. |
|
|
|
|
16 - 2 Syria — Commagene, Syria proper, Seleucia, Coelesyria (Palestine), Phoenicia 
1 Syria is bounded on the north by Cilicia and Mt. Amanus; and the distance from the sea to the bridge of the Euphrates (from the Gulf of Issus to the bridge at Commagenê), which forms the boundary of that side, is not less than fourteen hundred stadia. It is bounded on the east by the Euphrates and by the Arabian Scenitae this side the Euphrates; and on the south by Arabia Felix and Aegypt; and on the west by the Aegyptian and Syrian Seas as far as Issus.
2 We set down as parts of Syria, beginning at Cilicia and Mt. Amanus, both Commagenê and the Seleucis of Syria, as the latter is called; and then Coelê-Syria, and last, on the seaboard, Phoenicia, and in the interior, Judaea. Some writers divide Syria as a whole into Coelo-Syriansº and Syrians and Phoenicians, and say that four other tribes are mixed up with these, namely, Judaeans, Idumaeans, Gazaeans, and Azotians, and that they are partly farmers, as the Syrians and Coelo-Syrians, and partly merchants, as the Phoenicians.
3 So much for Syria in general. But in detail: Commagenê is rather a small country; and it has a city fortified by nature, Samosata, where the royal residence used to be; but it has now become a province; and the city is surrounded by an exceedingly fertile, though small, territory. Here is now the bridge of the Euphrates; and near the bridge is situated Seleuceia, a fortress of Mesopotamia, which was included within the boundaries of Commagenê by Pompey; and it was here that Tigranes slew Selenê, surnamed Cleopatra, after imprisoning her for a time, when she had been banished from Syria.
4 Seleucis is not only the best of the above-mentioned portions of Syria, but also is called, and is, a Tetrapolis, owing to the outstanding cities in it, for it has several. But the largest are four: Antiocheia near Daphnê, Seleuceia in Pieria, and also Apameia and Laodiceia; and these cities, all founded by Seleucus Nicator, used to be called sisters, because of their concord with one another. Now the largest of these cities was named after his father and the one most strongly fortified by nature after himself, and one of the other two, Apameia, after his wife Apama, and the other, Laodiceia, after his mother. Appropriately to the Tetrapolis, Seleucis was also divided into four satrapies, as Poseidonius says, the same number into which Coelê-Syria was divided, though Mesopotamia formed only one satrapy. Antiocheia is likewise a Tetrapolis, since it consisted of four parts; and each of the four settlements is fortified both by a common wall and by a wall of its own. Now Nicator founded the first of the settlements, transferring thither the settlers from Antigonia, which had been built near it a short time before by Antigonus; the second was founded by the multitude of settlers; the third by Seleucus Callinicus; and the fourth by Antiochus Epiphanes.
5 Furthermore, Antiocheia is the metropolis of Syria; and here was established the royal residence for the rulers of the country. And it does not fall much short, either in power or in size, of Seleuceia on the Tigris or Alexandria in Aegypt. Nicator also settled here the descendants of Triptolemus, whom I mentioned a little before. And it is on this account that the Antiocheians worship him as a hero and celebrate a festival in his honour on Mt. Casius in the neighbourhood of Seleuceia. It is said that he was sent by the Argives in search of Io, who disappeared first in Tyre, and that he wandered through Cilicia; and that there some of his Argive companions left him and founded Tarsus, but the others accompanied him into the next stretch of seaboard, gave up the search in despair, and remained with him in the river-country of the Orontes; and that Gordys, the son of Triptolemus, along with some of the peoples who had accompanied his father, emigrated to Gordyaea, whereas the descendants of the rest became fellow-inhabitants with the Antiocheians.
6 Lying above Antiocheia, at a distance of forty stadia, is Daphnê, a settlement of moderate size; and also a large, thickly-shaded grove intersected by fountain-streams, in the midst of which there is an asylum-precinct and a temple of Apollo and Artemis. Here it is the custom for the Antiocheians and the neighbouring peoples to hold a general festival. The grove is eighty stadia in circuit.
7 The Orontes River flows near the city. This river has its sources in Coelê-Syria; and then, after flowing underground, issues forth again; and then, proceeding through the territory of the Apameians into that of Antiocheia, closely approaches the latter city and flows down to the sea near Seleuceia. Though formerly called Typhon, its name was changed to that of Orontes, the man who built a bridge across it. Here, somewhere, is the setting of the mythical story of the Arimi, of whom I have already spoken. They say that Typhon (who, they add, was a dragon), when struck by the bolts of lightning, fled in search of a descent underground; that he not only cut the earth with furrows and formed the bed of the river, but also descended underground and caused the fountain to break forth to the surface; and that the river got its name from this fact. Now on the west, below Antiocheia and Seleuceia, lies the sea; and it is near Seleuceia that the Orontes forms its outlets, this city being forty stadia distant from the outlets, and one hundred and twenty from Antiocheia. Inland voyages from the sea to Antiocheia are made on the same day one starts. To the east of Antiocheia are the Euphrates, as also Bambycê and Beroea and Heracleia, small towns once ruled by the tyrant Dionysius, the son of Heracleon. Heracleia is twenty stadia distant from the temple of Athena Cyrrhestis.
8 Then one comes to Cyrrhesticê, which extends as far as the territory of Antiocheia.a On the north, near it, lie both Mt. Amanus and Commagenê. Cyrrhesticê borders on these, extending as far as that. Here is Gindarus, a city, which is the acropolis of Cyrrhesticê and a natural stronghold for robbers; and near it is a place called Heracleium. It was in the neighbourhood of these places that Pacorus, the eldest of the sons of the Parthian king, was killed by Ventidius, when he made an expedition against Syria. On the borders of Gindarus lies Pagrae, which is in the territory of Antiocheia and is a natural stronghold situated near the top of the pass over Mt. Amanus, which leads from the Gates of Amanus into Syria. Now below Pagrae lies the plain of the Antiocheians, through which flow the Arecuthus and Orontes and Labotas Rivers; and in this plain is the palisade of Meleager,º as also the Oenoparas River, on the banks of which Ptolemy Philometor conquered Alexander Balas but died from a wound. Above these places lies a hill which, from its similarity, is called Trapezon, whereon Ventidius had the fight with Phranicates, the Parthian general. Near the sea in this region lies Seleuceia, and Pieria, a mountain continuous with Mt. Amanus, and Rhosus, which is situated between Issus and Seleuceia. Seleuceia was in earlier times called Hydatos-Potamoi. The city is a notable fortress and is too strong to be taken by force; and for this reason Pompey, after shutting Tigranes off from it, adjudged it a free city. To the south of the Antiocheians is Apameia, which is situated in the interior; and to the south of the Seleuceians are Mts. Casius and Anticasius; and still further after Seleuceia one comes to the outlets of the Orontes; and then to the Nymphaeum, a kind of sacred cave; and then to Casium; and next to Poseidium, a small town, and to Heracleia.
9 Then one comes to Laodiceia, situated on the sea. It is a city most beautifully built, has a good harbour, and has territory which, besides its other good crops, abounds in wine. Now this city furnishes the most of the wine to the Alexandreians, since the whole of the mountain that lies above the city and is possessed by it is covered with vines almost as far as the summits. And while the summits are at a considerable distance from Laodiceia, sloping up gently and gradually from it, they tower above Apameia, extending up to a perpendicular height. Laodiceia was afflicted in no moderate degree by Dolabella, when he fled to it for refuge, was besieged in it by Cassius till death, and destroyed, along with himself, many parts of the city.
Apameia also has a city that is in general well fortified; for it is a beautifully fortified hill in a hollow plain, and this hill is formed into a peninsula by the Orontes and by a large lake which lies near by and spreads into the broad marshes and exceedingly large cattle-pasturing and horse-pasturing meadows. So the city is thus secretly situated; and so, too, it was called Cherronesus, because of the fact in the case; and it is well supplied with a very large and fertile territory, through which the Orontes flows; and in this territory there are numerous dependent towns. Here, too, Seleucus Nicator kept the five hundred elephants and the greater part of the army, as did also the later kings. It was also called Pella at one time, by the first Macedonians, because the majority of the Macedonians who made the expedition took up their abode there, and because Pella, the native city of Philip and Alexander, had become, as it were, the metropolis of the Macedonians. Here, too, were the war-office and the royal stud. The royal stud consisted of more than thirty thousand mares and three hundred stallions. Here, too, were colt-breakers and instructors who were paid to teach the arts of war. The power of this city is clearly shown by the ascendancy of Tryphon, surnamed Diodotus, and by his attack upon the kingdom of the Syrians, when he made this city the base of his operations. For he was born at Casiana, a fortress of the Apameian country, and, having been reared at Apameia and closely associated with the king and the king's court, when he set out to effect a revolution, he got his resources from this city and also from its dependencies, I mean Larisa and Casiana and Megara and Apollonia and other places like them, all of which were tributary to Apameia. So Tryphon was proclaimed king of this country and held out for a long time. Cecilius Bassus, with two cohorts, caused Apameia to revolt and, though besieged by two large Roman armies, strongly resisted them for so long a time that he did not come under their power until he voluntarily put himself in their hands upon his own terms; for the country supplied his army with provisions, and he had plenty of allies, I mean the neighbouring chieftains, who possessed strongholds; and among these places was Lysias, which is situated above the lake that lies near Apameia, as also Arethusa, belonging to Sampsiceramus and his son Iamblichus, chieftains of the tribe of the Emeseni; and at no great distance, also, were Heliupolis and Chalcis, which latter was subject to Ptolemaeus the son of Mennaeus, who possessed Massyas and the mountainous country of the Ituraeans. Among the allies of Bassus was also Alchaedamnus, king of the Rhambaeans, who were nomads this side the Euphrates River; and he was a friend of the Romans, but upon the belief that he was being treated unjustly by the Roman governors he retired to Mesopotamia and then went into the service of Bassus as a mercenary. Poseidonius, the Stoic, the most learned of all philosophers of my time, was a native of Apameia.
Bordering on the country of the Apameians, on the east, is the Paropotamia, as it is called, of the Arabian chieftains, as also Chalcidicê, which extends down from Massyas, and all the country to the south of the Apameians, which belongs for the most part to Scenitae. These Scenitae are similar to the nomads in Mesopotamia. And it is always the case that the peoples are more civilised in proportion to their proximity to the Syrians, and that the Arabians and Scenitae are less so, the former having governments that are better organised, as, for example, that of Arethusa under Sampsiceramus, and that of Gambarus, and that of Themellas, and those of other chieftains like them.
Such is the interior of the territory of Seleuceia. But the remainder of the coast from Laodiceia is as follows: near Laodiceia are three towns, Poseidium and Heracleium and Gabala; and then forthwith one comes to the seaboard of the Aradians, where are Paltus and Balanaea and Carnus, this last being the naval station of Aradus and having a harbour; and then to Enydra and Marathus, the latter an ancient city of the Phoenicians, now in ruins. Aradians divided up this country among themselves, as also Simyra, the place that comes next thereafter; and continuous with these places is Orthosia, as also Eleutherus, the river near by, which some writers make the boundary of the territory of Seleuceia on the side towards Phoenicia and Coelê-Syria.
Aradus lies off a surfy and harbourless seaboard; it lies approximately between its naval station and Marathus, and is twenty stadia distant from the mainland. It consists of a rock washed all round by the sea, is about seven stadia in circuit, and is full of dwellings; and it has had such a large population, even down to the present time, that the people live in houses with many stories. It was founded, as they say, by exiles from Sidon. They get their water-supply partly from the rains and cisterns and partly from their territory on the mainland. In war-times they get water from the channel at a short distance in front of the city. This channel has an abundant spring; and into this spring the people let down from the water-fetching boat an inverted, wide-mouthed funnel made of lead, the upper part of which contracts into a stem with a moderate-sized hole through it; and round this stem they fasten a leathern tube (unless I should call it bellows), which receives the water that is forced up from the spring through the funnel. Now the first water that is forced up is sea-water, but the boatmen wait for the flow of pure and potable water and catch all that is needed in vessels prepared for the purpose and carry it to the city.
Now in ancient times the Aradians were governed independently by kings, as was also the case with each of the other Phoenician cities; but afterwards the Persians, and then the Macedonians, and to‑day the Romans, have reduced them to their present order of government. The Aradians, however, together with the other Phoenicians, subjected themselves to the Syrian kings as friends of theirs; and then, when a quarrel broke out between two brothers, Callinicus Seleucus and Antiochus Hierax, as he was called, the Aradians joined with Callinicus and made an agreement with him whereby they were to be permitted to receive refugees from the kingdom and not to give them up against their will; they were not, however, to permit refugees to sail from the island without permission from the king. From this agreement they got great advantages; for those who fled for refuge to their country were not ordinary people, but men who had held the highest trusts and were in fear of the direst consequences; and, being received as guests, they regarded their hosts as their benefactors and saviours, and requited the favour, in particular when they went back to their homeland; and it is from this fact, therefore, that the Aradians got possession of a considerable territory on the mainland, most of which they hold even at present, and otherwise have prospered. To this good fortune they added both prudence and industry in their maritime affairs; and when they she said that the neighbouring Cilicians were organising piratical adventures they would not even once take part with them in a business of that kind.
After Orthosia and the Eleutherus River one comes to Tripolis, which has taken its name from what is the fact in the case, for it is a foundation consisting of three cities, Tyre and Sidon and Aradus. Contiguous to Tripolis is Theuprosopon, where Mt. Libanus terminates; and between the two lies Trieres, a kind of stronghold.
Here are two mountains, Libanus and Antilibanus, which form Coelê-Syria, as it is called, and are approximately parallel to each other. They both begin slightly above the sea — Libanus above the sea near Tripolis and nearest to Theuprosopon, and Antilibanus above the sea near Sidon; and somewhere in the neighbourhood of the Arabian mountains above Damascenê and the Trachones, as they are called, the two mountains terminate in other mountains that are hilly and fruitful. They leave a hollow plain between them, the breadth of which, near the sea, is two hundred stadia, and the length, from the sea into the interior, is about twice that number. It is intersected by rivers, the Jordan being the largest, which water a country that is fertile and all-productive. It also contains a lake, which produces the aromatic rush and reed; and likewise marshes. The lake is called Gennesaritis. The plain also produces balsam. Among the rivers is the Chrysorrhoas, which begins at the city and country of the Damasceni and is almost wholly used up in the conduits, for it irrigates a large territory that has a very deep soil; but the Lycus and the Jordan are navigated inland with vessels of burden, mostly by the Aradians.
As for the plains, the first, beginning at the sea, is called Macras, or Macra-Plain. Here, as reported by Poseidonius, was seen the fallen dragon, the corpse of which was about a plethrum in length, and so bulky that horsemen standing by it on either side could not see one another; and its jaws were large enough to admit a man on horseback, and each flake of its horny scales exceeded an oblong shield in length.
After Macras one comes to the Massyas Plain, which contains also some mountainous parts, among which is Chalcis, the acropolis, as it were, of the Massyas. The beginning of this plain is the Laodiceia near Libanus. Now all the mountainous parts are held by Ituraeans and Arabians, all of whom are robbers, but the people in the plains are farmers; and when the latter are harassed by the robbers at different times they require different kinds of help. These robbers use strongholds as bases of operation; those, for example, who hold Libanus possess, high up on the mountain, Sinna and Borrama and other fortresses like them, and, down below, Botrys and Gigartus and the caves by the sea and the castle that was erected on Theuprosopon. Pompey destroyed both these places; and from them the robbers overran both Byblus and the city that comes next after Byblus, I mean the city Berytus, which lie between Sidon and Theuprosopon. Now Byblus, the royal residence of Cinyras,b is sacred to Adonis; but Pompey freed it from tyranny by beheading its tyrant with an axe; and it is situated on a height only a slight distance from the sea.
Then, after Byblus, one comes to the Adonis River and to Mt. Climax and to Palaebyblus; and then to the Lycus River and Berytus. But though Berytus was razed to the ground by Tryphon, it has now been restored by the Romans; and it received two legions, which were settled there by Agrippa, who also added to it much of the territory of Massyas, as far as the sources of the Orontes River. These sources are near Mt. Libanus and Paradeisus and the Aegyptian fortress situated in the neighbourhood of the land of the Apameians. So much, then, for the places on the sea.
Above Massyas lies the Royal Valley, as it is called, and also the Damascene country, which is accorded exceptional praise. The city Damascus is also a noteworthy city, having been, I might almost say, even the most famous of the cities in that part of the world in the time of the Persian empire; and above it are situated two Trachones, as they are called. And then, towards the parts inhabited promiscuously by Arabians and Ituraeans, are mountains hard to pass, in which there are deep-mouthed caves, one of which can admit as many as four thousand people in times of incursions, such as are made against the Damasceni from many places. For the most part, indeed, the barbarians have been robbing the merchants from Arabia Felix, but this is less the case now that the band of robbers under Zenodorus has been broken up through the good government established by the Romans and through the security established by the Roman soldiers that are kept in Syria.
Now the whole of the country above the territory of Seleuceia, extending approximately to Aegypt and Arabia, is called Coelê-Syria; but the country marked off by the Libanus and the Antilibanus is called by that name in a special sense. Of the remainder the seaboard from Orthosia to Pelusium is called Phoenicia, which is a narrow country and lies flat along the sea, whereas the interior above Phoenicia, as far as the Arabians, between Gaza and Antilibanus, is called Judaea.
Since, then, I have traversed Coelê-Syria in the special sense of that name, I shall pass on to Phoenicia. Of this country, I have already described the parts extending from Orthosia to Berytus; and after Berytus one comes to Sidon, at a distance of about four hundred stadia; but between the two places are the Tamyras River and the grove of Asclepius and a city of Leones. After Sidon one comes to Tyre, the largest and oldest city of the Phoenicians, which rivals Sidon, not only in size, but also in its fame and antiquity, as handed down to us in numerous myths. Now although the poets have referred more repeatedly to Sidon than to Tyre (Homer does not even mention Tyre), yet the colonies sent into Libya and Iberia, as far even as outside the Pillars, hymn rather the praises of Tyre. At any rate, both cities have been famous and illustrious, both in early times and at the present time; and no matter which of the two one might call the metropolis of the Phoenicians, there is a dispute in both cities. Now Sidon is situated on the mainland near a harbour that is by nature a good one.
But Tyre is wholly an island, being built up nearly in the same way as Aradus; and it is connected with the mainland by a mole, which was constructed by Alexander when he was besieging it;c and it has two harbours, one that can be closed and the other, called "Aegyptian" harbour, open. The houses here, it is said, have many stories, even more than the houses at Rome, and on this account, when an earthquake took place, it lacked but little of utterly wiping out the city. The city was also unfortunate when it was taken by siege by Alexander; but it overcame such misfortunes and restored itself both by means of the seamanship of its people, in which the Phoenicians in general have been superior to all peoples of all times, and by means of their dye-houses for purple; for the Tyrian purple has proved itself by far the most beautiful of all; and the shell-fish are caught near the coast; and the other things requisite for dyeing are easily got; and although the great number of dye-works makes the city unpleasant to live in, yet it makes the city rich through the superior skill of its inhabitants. The Tyrians were adjudged autonomous, not only by the kings, but also, at small expense to them, by the Romans, when the Romans confirmed the decree of the kings. Heracles is paid extravagant honours by them. The number and the size of their colonial cities is an evidence of their power in maritime affairs. Such, then, are the Tyrians.
The Sidonians, according to tradition, are skilled in many beautiful arts, as the poet also points out; and besides this they are philosophers in the sciences of astronomy and arithmetic, having begun their studies with practical calculations and with night-sailings; for each of these branches of knowledge concerns the merchant and the ship-owner; as, for example, geometry was invented, it is said, from the measurement of lands which is made necessary by the Nile when it confounds the boundaries at the time of its overflows. This science, then, is believed to have come to the Greeks from the Aegyptians; astronomy and arithmetic from the Phoenicians; and at present by far the greatest store of knowledge in every other branch of philosophy is to be had from these cities. And if one must believe Poseidonius, the ancient dogma about atoms originated with Mochus, a Sidonian, born before the Trojan times. However, let us dismiss things ancient. In my time there have been famous philosophers from Sidon; Boethus, with whom I studied the Aristotelian philosophy, and his brother Diodotus; and from Tyre, Antipater, and, a little before my time, Apollonius, who published a tabulated account of the philosophers of the school of Zeno and of their books. Tyre is distant from Sidon not more than two hundred stadia; and between them lies a town called City of Ornithes; and then one comes to a river which empties near Tyre, and after Tyre, to Palae-Tyre, at a distance of thirty stadia.
Then one comes to Ptolemaïs, a large city, in earlier times named Acê; this city was used by the Persians as a base of operations against Aegypt. Between Acê and Tyre is a sandy beach, which produces the sand used in making glass. Now the sand, it is said, is not fused here, but is carried to Sidon and there melted and cast. Some say that the Sidonians, among others, have the glass-sand that is adapted to fusing, though others say that any sand anywhere can be used. I heard at Alexandria from the glass-workers that there was in Aegypt a kind of vitreous earth without which many-coloured and costly designs could not be executed, just as elsewhere different countries require different mixtures; and at Rome, also, it is said that many discoveries are made both for producing the colours and for facility in manufacture, as, for example, in the case of glass-ware, where one can buy a glass beaker or drinking-cup for a copper.
A marvellous occurrence of a very rare kind is reported as having taken place on this shore between Tyre and Ptolemaïs: at the time when the Ptolemaeans, after joining battle the Sarpedon the general, were left in this place, after a brilliant rout had taken place, a wave from the sea, like a flood-tide, submerged the fugitives; and some were carried off into the sea and destroyed, whereas others were left dead in the hollow places; and then, succeeding this wave, the ebb uncovered the shore again and disclosed the bodies of men lying promiscuously among dead fish. Like occurrences take place in the neighbourhood of the Mt. Casius situated near Aegypt, where the land undergoes a single quick convulsion, and makes a sudden change to a higher or lower level, the result being that, whereas the elevated part repels the sea and the sunken part receives it, yet, the land makes a reverse change and the site resumes its old position again, a complete interchange of levels sometimes having taken place and sometimes not. Perhaps such disturbances are subject to periodic principles unknown to us, as is also should be the case of the overflows of the Nile, which prove to be variant but follow some unknown order.
After Acê one comes to the Tower of Strato, which has a landing-place for vessels. Between the two places is Mt. Carmel, as also towns of which nothing more than the names remain — I mean Sycaminopolis, Bucolopolis, Crocodeilopolis, and others like them. And then one comes to a large forest.
Then one comes to Iopê, where the seaboard from Aegypt, though at first stretching towards the east, makes a significant bend towards the north. Here it was, according to certain writers of myths, that Andromeda was exposed to the sea-monster; for the place is situated at a rather high elevation — so high, it is said, that Jerusalem, the metropolis of the Judaeans, is visible from it; and indeed the Judaeans have used this place as a seaport when they have gone down as far as the sea; but the seaports of robbers are obviously only robbers' dens. To these people belonged, not only Carmel, but also the forest; and indeed this place was so well supplied with men that it could muster forty thousand men from the neighbouring village Iamneia and the settlements all round. Thence to Mt. Casius near Pelusium the distance is a little more than one thousand stadia; and, three hundred stadia farther, one comes to Pelusium itself.
But in the interval one comes to Gadaris, which the Judaeans appropriated to themselves; and then to Azotus and Ascalon. The distance from Iamneia to Azotus and Ascalon is about two hundred stadia. The country of the Ascalonitae is a good onion-market, though the town is small. Antiochus the philosopher, who was born a little before my time, was a native of this place. Philodemus, the Epicurean, and Meleager and Menippus, the satirist, and Theodorus, the rhetorician of my own time, were natives of Gadaris.
Then, near Ascalon, one comes to the harbour of the Gazaeans. The city of the Gazaeans is situated inland at a distance of seven stadia; it became famous at one time, but was rased to the ground by Alexander and remains uninhabited. Thence there is said to be an overland passage of one thousand two hundred and sixty stadia to Aela, a city situated near the head of the Arabian Gulf. This head consists of two recesses: one extending into the region near Arabia and Gaza, which is called Aelanites, after the city situated on it, and there, extending to the region near Aegypt in the neighbourhood of the City of Heroes, to which the overland passage from Pelusium is shorter; and the overland journeys are made on camels through desert and sandy places; and on these journeys there are also many reptiles to be seen.
After Gaza one comes to Rhaphia, where a battle was fought between Ptolemaeus the Fourth and Antiochus the Great. Then to Rhinocolura, so called from the people with mutilated noses that had been settled there in early times; for some Aethiopian invaded Aegypt and, instead of killing the wrongdoers, cut off their noses and settled them at that place, assuming that on account of their disgraceful faces they would no longer dare to do people wrong.
Now the whole of this country from Gaza is barren and sandy, but still more so is the country that lies next above it, which contains Lake Sirbonis, a lake which lies approximately parallel to the sea and, in the interval, leaves a short passage as far as the Ecregma, as it is called; the lake is about two hundred stadia in length and its maximum breadth is about sixty stadia; but the Ecregma his become filled up with earth. Then follows another continuous tract of this kind as far as Casius; and then one comes to Pelusium.
Casius is a sandy hill without water and forms a promontory; the body of Pompey the Great is buried there; and on it is a temple of Zeus Casius. Near this place Pompey the Great was slain, being treacherously murdered by the Aegyptians. Then comes the road to Pelusium, on which lie Gerrha and the Palisade of Chabrias, as it is called, and the pits near Pelusium. These pits are formed by side-flows from the Nile, the region being by nature hollow and marshy. Such is Phoenicia. Artemidorus says that the distance to Pelusium from Orthosia is three thousand six hundred and fifty stadia, including the sinuosities of the gulfs; and from Melaenae, or Melaniae, in Cilicia, near Celenderis, to the common boundaries of Cilicia and Syria, one thousand nine hundred; and thence to the Orontes River, five hundred and twenty; and then to Orthosia one thousand one hundred and thirty.
As for Judaea, its western extremities towards Casius are occupied by the Idumaeans and by the lake. The Idumaeans are Nabataeans, but owing to a sedition they were banished from there, joined the Judaeans, and shared in the same customs with them. The greater part of the region near the sea is occupied by Lake Sirbonis and by the country continuous with the lake as far as Jerusalem; for this city is also near the sea; for, as I have already said, it is visible from the seaport of Iopê. This region lies towards the north; and it is inhabited in general, as is each place in particular, by mixed stocks of people from Aegyptian and Arabian and Phoenician tribes; for such are those who occupy Galilee and Hiericus and Philadelphia and Samaria, which last Herod surnamed Sebastê. But though the inhabitants are mixed up thus, the most prevalent of the accredited reports in regard to the temple at Jerusalem represents the ancestors of the present Judaeans, as they are called, as Aegyptians.
Moses, namely, was one of the Aegyptian priests, and held a part of Lower Aegypt, as it is called, but he went away from there to Judaea, since he was displeased with the state of affairs there, and was accompanied by many people who worshipped the Divine Being. For he says, and taught, that the Aegyptians were mistaken in representing the Divine Being by the images of beasts and cattle,as were also the Libyans; and that the Greeks were also wrong in modelling gods in human form; for, according to him, God is this one thing alone that encompasses us all and encompasses land and sea — the thing which we call heaven, or universe, or the nature of all that exists. What man, then, if he has sense, could be bold enough to fabricate an image of God resembling any creature amongst us? Nay, people should leave off all image-carving, and, setting apart a sacred precinct and a worthy sanctuary, should worship God without an image; and people who have good dreams should sleep in the sanctuary, not only themselves on their own behalf, but also others for the rest of the people; and those who live self-restrained and righteous lives should always expect some blessing or gift or sign from God, but no other should expect them.
Now Moses, saying things of this kind, persuaded not a few thoughtful men and led them away to this place where the settlement of Jerusalem now is; and he easily took possession of the place, since it was not a place that would be looked on with envy, nor yet one for which anyone would make a serious fight; for it is rocky, and, although it itself is well supplied with water, its surrounding territory is barren and waterless, and the part of the territory within a radius of sixty stadia is also rocky beneath the surface. At the same time Moses, instead of using arms, put forward as defence his sacrifices and his Divine Being, being resolved to seek a seat of worship for Him and promising to deliver to the people a kind of worship and a kind of ritual which would not oppress those who adopted them either with expenses or with divine obsessions or with other absurd troubles. Now Moses enjoyed fair repute with these people, and organised no ordinary kind of government, since the peoples all round, one and all, came over to him, because of his dealings with them and of the prospects he held out to them.
His successors for some time abided by the same course, acting righteously and being truly pious towards God; but afterwards, in the first place, superstitious men were appointed to the priesthood, and then tyrannical people; and from superstition arose abstinence from flesh, from which it is their custom to abstain even to‑day, and circumcisions and excisions and other observances of the kind. And from the tyrannies arose the bands of robbers;for some revolted and harassed the country, both their own country and that of their neighbours, whereas others, co-operating with the rulers, seized the property of others and subdued much of Syria and Phoenicia. But still they had respect for their acropolis, since they did not loathe it as the seat of tyranny, but honoured and revered it as a holy place.
For this is natural; and it is common to the Greeks and to the barbarians; for, being members of states, they live under common mandates; for otherwise it would be impossible for the mass of people in any country to do one and the same thing in harmony with one another, which is precisely what life in a free state means, or in any other way to live a common life. And the mandates are twofold; for they come either from gods or from men; and the ancients, at least, held those from the gods in greater honour and veneration; and on this account men who consulted oracles were much in evidence at that time — men who ran to Dodona "to hear the will of Zeus from the high-tressed oak," thus using Zeus as their counsellor, and also to Delphi, "seeking to learn whether the child which had been exposed to die was no longer alive;" but the child himself "was on his way to the home of Phoebus, wishing to discover his parents." And among the Cretans Minos "reigned as king, who held converse with great Zeus every ninth year," every nine years, as Plato says, when he would go up to the cave of Zeus and receive decrees from him and carry them to the people. And Lycurgus,his emulator, did likewise; for oftentimes, as it appears, he would go abroad to inquire of the Pythian priestess what ordinances it was proper for him to report to the Lacedaemonians.
For these things, whatever truth there may be in them, have at least been believed and sanctioned among men; and for this reason the prophets too were held in so much honour that they were deemed worthy to be kings, on the ground that they promulgated to us ordinances and amendments from the gods, not only when they were alive, but also when they were dead, as, for example, Teiresias, "to whom even in death Persephone granted reason, that he alone should have understanding, whereas the others flit about as shadows." Such, also, were Amphiaraüs, Trophonius, Orpheus, Musaeus, and the god among the Getae, who in ancient times was Zamolxis, a Pythagoreian, and in my time was Decaeneus, the diviner of Byrebistas; and, among the Bosporeni, Achaecarus; and, among the Indians, the Gymnosophists; and, among the Persians, the Magi and the necromancers, as also the dish-diviners and water-diviners, as they are called; and, among the Assyrians, the Chaldaeans; and, among the Romans, the Tyrrhenian nativity-casters. Moses was such a person as these, as also his successors, who, with no bad beginning, turned out for the worse.
At any rate, when now Judaea was under the rule of tyrants, Alexander was first to declare himself king instead of priest; and both Hyrcanus and Aristobulus were sons of his; and when they were at variance about the empire, Pompey went over and overthrew them and rased their fortifications, and in particular took Jerusalem itself by force; for it was a rocky and well-watered fortress; and though well supplied with water inside, its outside territory was wholly without water; and it had a trench cut in rock, sixty feet in depth and two hundred and sixty feet in breadth; and, from the stone that had been hewn out, the wall of the temple was fenced with towers. Pompey seized the city, it is said, after watching for the day of fasting, when the Judaeans were abstaining from all work; he filled up the trench and threw ladders across it; moreover, he gave orders to rase all the walls and, so far as he could, destroyed the haunts of robbers and the treasure-holds of the tyrants. Two of these were situated on the passes leading to Hiericus, I mean Threx and Taurus, and others were Alexandrium and Hyrcanium and Machaerus and Lysias and those in the neighbourhood of Philadelphia and Scythopolis in the neighbourhood of Galilaea.
Hiericus is a plain surrounded by a kind of mountainous country, which, in a way, slopes towards it like a theatre. Here is the Phoenicon, which is mixed also with other kinds of cultivated and fruitful trees, though it consists mostly of palm trees; it is one hundred stadia in length, and is everywhere watered with streams and full of dwellings. Here are also the palace and the balsam park. The balsam is of the shrub kind, resembling cytisus and terminthus, and has a spicy flavour. The people make incisions in the bark and catch the juice in vessels. This juice is a glutinous, milk-white substance; and when it is put up in small quantities it solidifies; and it is remarkable for its cure of headache and of incipient cataracts and of dimness of sight. Accordingly, it is costly; and also for the reason that it is produced nowhere else. Such is also the case with the Phoenicon, which alone has the caryotic palm, excepting the Babylonian and that beyond Babylonia towards the east. Accordingly, the revenue derived from it is great. And they use the xylo-balsam as spice.
Lake Sirbonis is large; in fact some state that it is one thousand stadia in circuit; however, it extends parallel to the coast to a length of slightly more than two hundred stadia, is deep to the very shore, and has water so very heavy that there is no use for divers, and any person who walks into it and proceeds no farther than up to his navel is immediately raised afloat. It is full of asphalt. The asphalt is blown to the surface at irregular intervals from the midst of the deep, and with it rise bubbles, as though the water were boiling; and the surface of the lake, being convex, presents the appearance of a hill. With the asphalt there arises also much soot, which, though smoky, is imperceptible to the eye; and it tarnishes copper and silver and anything that glistens, even gold; and when their vessels are becoming tarnished the people who live round the lake know that the asphalt is beginning to rise; and they prepare to collect it by means of rafts made of reed. The asphalt is a clod of earth, which at first is liquefied by heat, and is blown up to the surface and spreads out; and then again, by reason of the cold water, the kind of water the lake in question has, it changes to a firm, solidified substance, and therefore requires cutting and chopping; and then it floats, because of the nature of the water, owing to which, as I was saying, there is no use for divers; and no person who walks into it can immerse himself either, but is raised afloat. They reach the asphalt on rafts and chop it and carry off as much as they each can.
Such, then, is the fact in the case; but according to Poseidonius the people are sorcerers and pretend to use incantations, as also urine and other malodorous liquids, which they first pour all over the solidified substance, and squeeze out the asphalt and harden it, and then cut it into pieces; unless there is some suitable element of this kind in urine, such, for example, as chrysocolla, which forms in the bladder of people who have bladder-stones and is derived from the urine of children. It is reasonable that this behaviour should occur in the middle of the lake, because the source of the fire and also the greater part of the asphalt is at the middle of it; but the bubbling up is irregular, because the movement of the fire, like that of many other subterranean blasts, follows no order known to us. Such, also, are the phenomena at Apollonia in Epirus.
Many other evidences are produced to show that the country is fiery; for near Moasada are to be seen rugged rocks that have been scorched, as also, in many places, fissures and ashy soil, and drops of pitch that emit foul odours to a great distance, and ruined settlements here and there; and therefore people believe the oft-repeated assertions of the local inhabitants, that there were once thirteen inhabited cities in that region of which Sodom was the metropolis, but that a circuit of about sixty stadia of that city escaped unharmed; and that by reason of earthquakes and of eruptions of fire and of hot waters containing asphalt and sulphur, the lake burst its bounds, and rocks were enveloped with fire; and, as for the cities, some were swallowed up and others were abandoned by such as were able to escape. But Eratosthenes says, on the contrary, that the country was a lake, and that most of it was uncovered by outbreaks, as was the case with the sea.
In Gadaris, also, there is noxious lake water; and when animals taste it they lose hair and hoofs and horns. At the place called Taricheae the lake supplies excellent fish for pickling; and on its banks grow fruit-bearing trees resembling apple trees. The Aegyptians use the asphalt for embalming the bodies of the dead.
Now Pompey clipped off some of the territory that had been forcibly appropriated by the Judaeans, and appointed Herod to the priesthood; but later a certain Herod, a descendant of his and a native of the country, who slinked into the priesthood, was so superior to his predecessors, particularly in his intercourse with the Romans and in his administration of affairs of state, that he received the title of king, being given that authority first by Antony and later by Augustus Caesar. As for his sons, he himself put some of them to death, on the ground that they had plotted against him; and at his death left others as his successors, having assigned to them portions of his kingdom. Caesar also honoured the sons of Herod and his sister Salomê and her daughter Berenicê. However, his sons were not successful, but became involved in accusations; and one of them spent the rest of his life in exile, having taken up his abode among the Allobrogian Gauls, whereas the others, by much obsequiousness, but with difficulty, found leave to return home, with a tetrarchy assigned to each. |
|
|
|
|
16 - 3 Continued 4.3 3:35 
1 Above Judaea and Coelê-Syria, as far as Babylonia and the river-country of the Euphrates towards the south, lies the whole of Arabia, with the exception of the Scenitae in Mesopotamia. Now I have already spoken of Mesopotamia and the tribes that occupy it; but as for the parts on the far side of the Euphrates, those near its outlets are occupied by Babylonians and the tribe of the Chaldaeans, of whom I have already spoken; and of those parts that follow after Mesopotamia as far as Coelê-Syria, the part that lies near the river, as well as Mesopotamia, is occupied by Arabian Scenitae, who are divided off into small sovereignties and live in tracts that are barren for want of water. These people till the land either little or none, but they keep herds of all kinds, particularly of camels. Above these people lies an extensive desert; but the parts lying still farther south than their country are held by the people who inhabit Arabia Felix, as it is called. The northern side of Arabia Felix is formed by the above-mentioned desert, the eastern by the Persian Gulf, the western by the Arabian Gulf, and the southern by the great sea that lies outside both gulfs, which as a whole is called Erythra.
2 Now the Persian Gulf is also called the Persian Sea; and Eratosthenes describes it as follows: its mouth, he says, is so narrow that from Harmozi, the promontory of Carmania, one can see the promontory at Macae in Arabia; and from its mouth the coast on the right, being circular, inclines at first, from Carmania, slightly towards the east, and then towards the north, and, after this, towards the west as far as Teredon and the outlet of the Euphrates; and it comprises the coast of the Carmanians and in part that of the Persians and Susians and Babylonians, a distance of about ten thousand stadia. I have already spoken of these peoples. And thence next to its mouth it extends another ten thousand stadia, as stated, Eratosthenes says, by Androsthenes the Thasian, who made the voyage, not only with Nearchus but also on his own account; so that it is clear from this that this sea is but little short of the Euxine in size; and Eratosthenes says that Androsthenes, who sailed round the gulf with a fleet, states that in making the coasting voyage, with the continent on the right, one sees next after Teredon the island Icarus and a temple sacred to Apollo in it and an oracle of Tauropolus.
3 After sailing along the coast of Arabia for a distance of two thousand four hundred stadia, one comes to Gerrha, a city situated on a deep gulf; it is inhabited by Chaldaeans, exiles from Babylon; the soil contains salt and the people live in houses made of salt; and since flakes of salt continually scale off, owing to the scorching heat of the rays of the sun, and fall away, the people frequently sprinkle the houses with water and thus keep the walls firm. The city is two hundred stadia distant from the sea; and the Gerrhaeans traffic by land, for the most part, in the Arabian merchandise and aromatics, though Aristobulus says, on the contrary, that the Gerrhaeans import most of their cargoes on rafts to Babylonia, and thence sail up the Euphrates with them, and then convey them by land to all parts of the country.
4 On sailing farther, one comes to other islands, I mean Tyre and Aradus, which have temples like those of the Phoenicians. It is asserted, at least by the inhabitants of the islands, that the islands and cities of the Phoenicians which bear the same name are their own colonies. These islands are distant a ten days' sail from Teredon and a one day's sail from the promontory near the mouth of the gulf at Macae.
5 Both Nearchus and Orthagoras state that the island Ogyris lies in the high sea at a distance of two thousand stadia from Carmania, and that on it is to be seen the grave of Erythras, a large mound planted with wild palm trees; and that Erythras reigned as king over that region and left the sea named after himself. Nearchus says that these things were pointed out to them by Mithropastes, the son of Aristes, which latter was satrap of Phrygia; and that the former was banished by Dareius, took up his residence in the island, joined them when they landed in the Persian Gulf, and sought through them to be restored to his homeland.
6 Along the whole of the coast of the Red Sea, down in the deep, grow trees like the laurel and the olive, which at the ebb tides are wholly visible above the water but at the full tides are sometimes wholly covered; and while this is the case, the land that lies above the sea has no trees, and therefore the peculiarity is all the greater. Such are the statements of Eratosthenes concerning the Persian Sea, which, as I was saying, forms the eastern side of Arabia Felix.
7 Nearchus says that they were met by Mithropastes, in company with Mazenes; that Mazenes was ruler of an island in the Persian Gulf; that the island was called Oaracta; that Mithropastes took refuge, and obtained hospitality, in this island upon his departure from Ogyris; that, furthermore, Mithropastes had a conference with Mazenes for the purpose of being recommended by him to the Macedonians in the fleet; and that Mazenes became guide in their voyage. Nearchus goes on to say that there is an island at the beginning of the Persian Gulf where quantities of valuable pearls are to be found; and that in other islands there are pebbles of transparent and brilliant stones; and that in the islands off the mouth of the Euphrates there are trees which smell like frankincense, and that juice flows from their roots when they are broken in pieces. And he speaks of the large size of the crabs and sea-urchins, which is a common thing in the whole of the exterior sea; for, he adds, some are larger than hats and others as large as a vessel holding two cotylae; and he says that he saw a whale stranded on the beach that was fifty cubits in length. |
|
|
|
|
16 - 4 Contintued 52.6 43:50. 
1 Arabia commences on the side of Babylonia with Maecenê. In front of Maecenê, on one side, lies the desert of the Arabians; and on another side lie the marshes opposite the Chaldaeans, which are formed by diversions of water from the Euphrates; and another side lies the Persian Sea. The country has foul air, is misty, and is subject both to rains and to scorching heat; but still its products are excellent. The vine grows in the marshes, as much earth being thrown on hurdles of reeds as the plant may require; so that the vine is often carried away, and then is pushed back again to its proper place by means of poles.
2 But I return to Eratosthenes, who next sets forth his opinions concerning Arabia. He says concerning the northerly, or desert, part of Arabia, which lies between Arabia Felix and Coelê-Syria and Judaea, extending as far as the recess of the Arabian Gulf, that from the City of Heroes, which forms a recess of the Arabian Gulf near the Nile, the distance in the direction of the Petra of the Nabataeans to Babylon is five thousand six hundred stadia, the whole of the journey being in the direction of the summer sunrise and through the adjacent countries of the Arabian tribes, I mean the Nabataeans and the Chaulotaeans and the Agraeans. Above these lies Arabia Felix, which extends for a distance of twelve thousand stadia towards the south, to the Atlantic Sea. The first people who occupy Arabia Felix, after the Syrians and Judaeans, are farmers. After these the soil is sandy and barren, producing a few palm-trees and a thorny tree and the tamarisk, and affording water by digging, as is the case in Gedrosia; and it is occupied by tent-dwellers and camel-herds. The extreme parts towards the south, lying opposite to Aethiopia, are watered by summer rains and are sowed twice, like India; and the rivers there are used up in supplying plains and lakes. The country is in general fertile, and abounds in particular with places for making honey; and, with the exception of horses and mules and hogs, it has an abundance of domesticated animals; and, with the exception of geese and chickens, has all kinds of birds. The extreme part of the country above-mentioned is occupied by the four largest tribes; by the Minaeans, on the side towards the Red Sea, whose largest city is Carna or Carnana; next to these, by the Sabaeans, whose metropolis is Mariaba; third, by Cattabanians, whose territory extends down to the straits and the passage across the Arabian Gulf, and whose royal seat is called Tamna; and, farthest toward the east, the Chatramotitae, whose city is Sabata.
3 All these cities are ruled by monarchs and are prosperous, being beautifully adorned with both temples and royal palaces. And the houses are like those of the Aegyptians in respect to the manner in which the timbers are joined together. The four jurisdictions cover more territory than the Aegyptian Delta; and no son of a king succeeds to the throne of his father, but the son of some notable man who is born first after the appointment of the king; for at the same time that some one is appointed to the throne, they register the pregnant wives of their notable men and place guards over them; and by law the wife's son who is born first is adopted and reared in a royal manner as future successor to the throne.
4 Cattabania produces frankincense, and Chatramotitis produces myrrh; and both these and the other aromatics are bartered to merchants. These arrive there in seventy days from Aelana (Aelana is a city on the other recess of the Arabian Gulf, the recess near Gaza called Aelanites, as I have said before), but the Gerrhaeans arrive at Chatramotitis in forty days. The part of the Arabian Gulf along the side of Arabia, beginning at the Aelanites recess, is, as recorded by Alexander's associates and by Anaxicrates, fourteen thousand stadia, though this figure is excessive; and the part opposite the Troglodytic country (which is on the right side as one sails from the City of Heroes), as far as Ptolemaïs and the country where elephants are captured, extends nine thousand stadia towards the south and slightly in the direction of the east; and thence, as far as the straits, four thousand five hundred stadia, in a direction more towards the east. The straits are formed towards Aethiopia by a promontory called Deirê, and by a town bearing the same name, which is inhabited by the Ichthyophagi. And here, it is said, there is a pillar of Sesostris the Aegyptian, which tells in hieroglyphics of his passage across the gulf; for manifestly he was the first man to subdue the countries of the Aethiopians and the Troglodytes; and he then crossed into Arabia, and thence invaded the whole of Asia; and actually, for this reason, there are in many places palisades of Sesostris, as they are called, and reproductions of temples of Aegyptian gods. The straits at Deirê contract to a width of sixty stadia. However, it is not these that are called straits now, but a place farther along on the voyage, where the voyage across the gulf between the two continents is about two hundred stadia, and where are six islands, which follow one another in close succession, fill up the channel, and leave between them extremely narrow passages; through these merchandise is transported from one continent to the other; and for these the name "straits" is used. After the islands, the next voyage, following the sinuosities of the bays, along the myrrh-bearing country in the direction of south and east as far as the cinnamon-bearing country, is about five thousand stadia; and to the present time, it is said, no one has arrived beyond that country; and though there are not many cities on the coast, there are many in the interior that are beautifully settled. Such, then, is Eratosthenes' account of Arabia; but I must also add the accounts of the other writers.
5 Artemidorus says that the promontory on the Arabian side opposite to Deirê is called Acila; and that the males in the neighbourhood of Deirê have their sexual glands mutilated. As one sails from the City of Heroes along the Troglodytic country, one comes to a city Philotera, which was named after the sister of the second Ptolemy, having been founded by Satyrus, who had been sent for the purpose of investigating the Troglodytic country and the hunting of elephants. Then to another city, Arsinoê. Then to springs of hot water, salty and bitter, which flow down a high rock and empty into the sea. Near by, in a plain, is a mountain that is red as ruddle. Then one comes to Myus Harbour, which is also called Aphrodite's Harbour; it is a large harbour with a winding entrance, off which lie three islands; two of these are densely shaded with olive trees, while the third is less so and is full of guinea-fowls. Then, next, one comes to the Acathartus Gulf, which also, like Myus Harbour, lies opposite Thebaïs, and is really "acathartus,"º for it is roughened by reefs and submarine rocks, and, most of the time, by tempestuous winds. And here, deep inland on the recess of the gulf, lies a city Berenicê.
6 After the gulf, one comes to the island Ophiodes, so called from the fact in the case; but it was freed from the serpents by the king, both because of their destruction of the people who landed there and on account of the topazes found there. Topaz is a transparent stone that sparkles with a golden lustre — so dimly in the day-time, however, that one cannot easily see it (for it is outshone by the rays of the sun), but those who collect it see it at night, place a vessel over it as a sign and dig it up in the day-time. There was an organisation of people who were appointed by the kings of Aegypt to keep guard over this stone and the collecting of it; and this organisation was supplied by them with provisions.
7 After this island one comes to many tribes of Ichthyophagi and Nomads. And then to the Harbour of Soteira, which was so called from the fact in the case by certain commanders who had been saved from great dangers. After this there is a great change in the coast and the gulf; for the coasting voyage is no longer rough, and in a way closely approaches Arabia; and the sea is as low, I might almost say, as two fathoms in depth; and the surface is covered, grass-like, with sea-weeds and rock-weeds that are visible below the surface — a thing still more in evidence at the strait, where, among the plants, even trees grow down below the water; and the strait has also a large number of sea-dogs. Then one comes to the Tauri, two mountains which from a distance present the outlines of the animals. Then to another mountain, which has a temple sacred to Isis, a reproduction built by Sesostris. Then to an island planted with olive trees and subject to inundation; and after this to Ptolemaïs, near the hunting-grounds for elephants, a city founded by Eumedes, who had been sent to the hunting-grounds by Philadelphius; Eumedes secretly enclosed a kind of peninsula with a ditch and wall, and then, by courteous treatment of those who tried to hinder the work, actually won them over as friends instead of foes.
8 In the interval there empties a branch of the Astaboras River, as it is called, which, having its source in a lake, empties a part of its waters, but for the most part joins the Nile. Then one comes to six islands called Latomiae; and then to the Sabaïtic mouth, as it is called, and to a fortress in the interior which was founded by Tosuches. And then to a harbour called Elaea and to the island of Strato. And then to a harbour called Saba and to a hunting-ground for elephants of the same name. The country deep in the interior is called Tenessis; and it is occupied by the Aegyptians who went there as exiles from Psammitichus. They are called Sembritae, as being foreigners. They are governed by a queen, to whom also Meroê, an island in the Nile near that region, is subject; and above this island, at no great distance, is another island in the river, a settlement of these same exiles. The journey from Meroê to this sea, for a well-girded traveller, requires fifteen days. Near Meroê is the confluence of the Astaboras and the Astapus, as also of the Astasobas with the Nile.
9 Along these rivers live the Rhizophagi and the Heleii, who are so called because they cut roots from the adjacent marsh, crush them with stones, form them into cakes, and then heat the cakes in the sun's rays and use them for food. This region is the haunt of lions; and the beasts are driven out of this region by large gnats on the days of the rising of the dog-star. Near by are also the Spermophagi, who, when the seeds fail, live on nuts, preparing them for eating in the same manner as the Rhizophagi prepare roots. After Elaea one comes to the Lookouts of Demetrius and the Altars of Conon; and in the interior grows an abundance of Indian reeds; and the country is called the country of Coracius. Deep in the interior was a place called Endera, a settlement of naked people, who use bows made of reeds and arrows hardened by fire; and generally they shoot wild animals from trees, but sometimes from the ground; and they have in their country a great multitude of wild cattle; and they live on the flesh of these and the other wild animals, but when they take nothing in the chase they bake dried skins on hot coals and are satisfied with such food as that. It is their custom to propose contests in archery for boys who are in their teens. After the Altars of Conon one comes to the Melinus Harbour, above which lie a Fortress of Coraüs, as it is called, and a Hunting-ground of Coraüs and another fortress and several hunting-grounds. And then to the Harbour of Antiphilus, and, above this, to the Creophagi, of whom the males have their sexual glands mutilated and the women are excised in the Jewish fashion.
Also above these, approximately towards the south, are the Cynamolgi, by the natives called Agrii, who have long hair and long beards and raise good-sized dogs. With these dogs they hunt Indian cattle which come in from the neighbouring territory, whether driven thither by wild beasts or by scarcity of pasturage. The time of their incursion is from the summer solstice to mid-winter. Next after the Harbour of Antiphilus one comes to the Grove of the Colobi, and to Berenicê, a Sabaean city, and to Sabae, a good-sized city; and then to the Grove of Eumenes. Above the grove lie a city Daraba and the hunting-ground for elephants called "The one near the well"; they are inhabited by the Elephantophagi, who engage in the chase of elephants. When from trees they first see a herd of elephants moving through the forest they do not then attack them, but stealthily follow the herd and hamstring those that have wandered from the rear of the herd. Some, however, kill them with arrows dipped in the gall of serpents. But the shooting of the bow is performed by three persons; two of these step to the front and hold the bow, and the third draws the string. Others, noting the trees against which the elephants are wont to rest, approach them from the other side and cut the trunks of these trees low down. So when the elephant approaches and leans against it, the tree falls and the elephant falls too; and since the elephant is unable to arise, because its legs have only a continuous and unbending bone, they leap down from the trees and cut the animal to pieces.a The Nomads call the hunters "Acatharti."
Above these is situated a tribe of no large size, that of the Struthophagi, in whose country there are birds of the size of deer, which, though unable to fly, run swiftly, like ostriches. Some hunt them with bows and arrows, whereas others, covered with the skins of birds, conceal the right hand in the neck of the skin and move it in the same way as the birds move their necks, and with the left hand they pour forth seeds from a bag suspended to the side, and with these seeds they bait the creatures and run them together into gullies, where men with cudgels, standing over them, slaughter them. And their skins are used both for clothing and for bed-covers. The Aethiopians called "Simi" carry on war with these people; they use as weapons the horns of gazelles.
Neighbouring this people are the Acridophagi, who are blacker than the rest and shorter in stature and the shortest-lived; for they rarely live beyond forty years, since their flesh is infested with parasites. They live on locusts, which are driven into this region in the spring-time by strong-blowing south-west and western winds. They cast smoking timber in the ravines, lighting it slightly (and thus easily catch the locusts), for when they fly above the smoke they are blinded and fall. The people pound them with salt, make them into cakes, and use them for food. Above these people lies a large uninhabited region, which has pastures in abundance. It was abandoned by reason of the multitude of scorpions and tarantulas, the tetragnathi, as they are called; these once prevailed and caused a complete desertion by the inhabitants.
After the Harbour of Eumenes, as far as Deirê and the straits opposite the six islands, the country is inhabited by the Ichthyophagi and the Creophagi and the Colobi, who extend as far as the interior. In this region are several hunting-grounds for elephants, and insignificant cities, and islands lying off the coast. The greater part of the people are nomads; and those who till the soil are few in number. And in some parts of their country styrax grows in no small quantities. The Ichthyophagi collect the fish at the ebb-tides, throw them upon the rocks, and bake them in the sun; and then, when they have thoroughly baked them, they pile up the bones, tread the flesh with their feet and make it into cakes; and again they bake these cakes and use them for food. But in stormy weather, when they are unable to collect the fish, they pound the bones which they have piled up and mould them into cakes and use them for food; and they suck the bones when fresh. But some, who have shell-fish, fatten them by throwing them down into gullies and pools of sea-water, and then, throwing in minnows as food for them, use them for food when there is a scarcity of fish. They also have all kinds of places for hatching and feeding fish, from which they parcel them out. Some of the people who inhabit the part of the coast that is without water go inland every five days, families and all, with a shouting of paeans, to the water-reservoirs, throw themselves upon the ground face downwards, drink like cattle until their stomachs are filled out as tight as drums, and then return to the sea again. They live in caves, or in pens roofed over with beams and cross-beams, consisting of the bones of whales and small fish, as also with olive branches.
The Chelonophagi live under cover of turtle-shells, which are so large that they are used as boats; but some of these people, since the sea-weed is thrown ashore in great quantities and forms high and hill-like heaps, dig beneath these and dwell under them. They throw out their dead as food for the fish, the bodies being caught up by the flood-tides. Some of the islands, three of them, follow in succession: Tortoise Island, Seal Island, and Hawk Island, as it is called; and the whole of the coast has palm-trees, olive groves, and laurel groves, not only the part inside the straits, but also most of the part outside. And there is also an island called Philip's Island, opposite which, above the coast, lies the hunting-ground for elephants called the Hunting-ground of Pythangelus. Then one comes to Arsinoê, a city and harbour; and, after these, to Deirê; and above these lies a hunting-ground for elephants. The next country after Deirê produces aromatics, the first that produces myrrh (this country belongs to the Ichthyophagi and Creophagi), and it also produces both persea and the Aegyptian sycaminus. Above this country lies a hunting-ground for elephants, called the Hunting-ground of Lichas. In many places there are pools of rain-water; and when these dry up, the elephants, with their trunks and tusks, dig wells and find water. On this coast, extending as far as the promontory of Pytholaüs, there are two lakes of fair size, one of which has salt water and is called a sea, whereas the other has fresh water, supports both hippopotamus and crocodiles, and has papyrus round its edges; and the ibis is also to be seen in the neighbourhood of this place. Beginning with those who live near the promontory of Pytholaüs, the people are wholly free from mutilation of the body. After these, one comes to the country that bears frankincense; and here is a promontory and a temple that has a grove of poplars. In the interior lie the river-land of Isis, as it is called, and another river-land called Neilus, both of which produce both myrrh and frankincense along their banks. Here, too, there is a kind of reservoir which is filled by waters from the mountains; and after this one comes to the Lookout of Leon and the Harbour of Pythangelus; and the next country has, among other things, pseudo-cassia. And one comes to several river-lands in succession that produce frankincense along the rivers, and to rivers that extend as far as the cinnamon-bearing country; and the river which bounds this country produces also the flowering rush in very great quantities. Then to another river and to the Daphnus Harbour and to the River-land of Apollo, as it is called, which produce, in addition to frankincense, both myrrh and cinnamon; but the cinnamon is more abundant in the neighbourhood of the places that are deep in the interior. Then to Elephas, the mountain, which juts out into the sea, and to a trench, and, next thereafter, to the large Harbour of Psygmus, and to a watering-place called the Watering-place of the Cynocephali, and to the last promontory of this coast, Notu-ceras. After rounding this promontory approximately towards the south, we no longer, he says, have any record of harbours or places, because the promontory is not known from here on, and the same is true of the coast next after it.
One comes also to pillars and altars of Pytholaüs and Lichas and Pythangelus and Leon and Charimortus along the known coast, extending from Deirê as far as Notu-ceras, but the distance is unknown. The country abounds in elephants, and also in lions called ants, which have their genital organs reversed, and are golden in colour, but are less hairy than those in Arabia. It also produces fierce leopards and the rhinoceros. The latter, the rhinoceros, is but little short of the elephant in size, not, as Artemidorus says, "in length to the tail" (although he says that he saw the animal at Alexandria), but falls short, I might almost say, only about . . . in height, judging at least from the one I saw; nor does their colour resemble that of box-wood, but rather that of the elephant; and it is of the size of a bull; and its shape is most nearly like that of the wild boar, particularly in its foreparts, except its nose, which has a snub horn harder than any bone; and it uses its horn as a weapon, just as the wild boar uses its tusks; and it also has two hard welts extending round from its chine to its belly, like the coils of serpents, one of which is on its withers and the other on its loins. Now I am giving this description from the one I saw; but Artemidorus goes on to explain that the creature is especially inclined to fight with the elephant for places of pasture, thrusting its forehead under the elephant and ripping up its stomach, unless it is prevented from so doing by the proboscis and tusks of the elephant.
In this region, also, are found camelopards, though they are in no respect like leopards; for the dappled marking of their skin is more like that of a fawnskin, which latter is flecked with spots, and their hinder parts are so much lower than their front parts that they appear to be seated on their tail-parts, which have the height of an ox, although their forelegs are no shorter than those of camels; and their necks rise high and straight up, their heads reaching much higher up than those of camels. On account of this lack of symmetry the speed of the animal cannot, I think, be so great as stated by Artemidorus, who says that its speed is not to be surpassed. Furthermore, it is not a wild beast, but rather a domesticated animal, for it shows no signs of wildness. And in this country are also found, he says, sphinxes and cynocephali and cebi, which last have the face of a lion, and a body otherwise like that of a panther and with the size of a gazelle. The country also has bulls that are wild, carnivorous, and far surpass those in our part of the world in size and speed; and their colour is red. The crocuttas is a mixed progeny of wolf and dog, as Artemidorus says. But what Metrodorus of Scepsis says in his book on Habits is like a myth and should be disregarded. Artemidorus also speaks of serpents thirty cubits in length which overpower elephants and bulls; and his measurement is moderate, at least for serpents in this part of the world, for the Indian serpents are rather fabulous, as also those in Libya, which are said to grow grass on their backs.
Now the Troglodytes live a nomadic life; and their several tribes are ruled by tyrants; and both wives and children are held in common except those of the tyrants; and the fine for anyone who corrupts the wife of a tyrant consists of a sheep. The women paint their eyelids carefully with stibi; and they wear shells for amulets round their necks. The Troglodytes go to war about pasturage, at first pushing their way through with their hands and then with stones, and also, when a wound is inflicted, with arrows and daggers; but the fighters are reconciled by the women, who advance into the midst of the combatants and ply them with entreaties. Their food consists of flesh and bones which are first chopped up together and wrapped in skins and then baked, or prepared in numerous other ways by the cooks (whom they call "unclean"), so that they not only eat the flesh, but also the bones and the skin; and they also use the blood mixed with milk. As for beverages, most of the people drink a brew of buckthorn, but the tyrants drink a mixture of honey and water, the honey being pressed out of some kind of flower. They have winter when the Etesian winds blow (for they have rains); but the rest of the time is summer. They also go lightly clad, wear skins, and carry clubs; and they not only mutilate their bodies, but some of them are also circumcised, like the Aegyptians. The Aethiopian Megabari have iron knobs on their clubs, and also use spears and shields made of rawhide, but the rest of the Aethiopians use the bow and arrow and lances. Before burying their dead, some of the Troglodytes bind the neck of the corpses to the legs with twigs of the buckthorn, and then immediately, with merriment and laughter, throw stones upon them until the body is hidden from sight; and then they place a ram's horn on the barrow and go away. They travel by night, first fastening bells to the male cattle, so as to drive away the wild beasts with the noise; and they also use torches and bows to repel the wild beasts; and, for the sake of their flocks, they also keep watch during the night, singing a kind of song near the fire.
After saying all this about the Troglodytes and the neighbouring Aethiopians, Artemidorus returns to the Arabians; and first, beginning at Poseidium, he describes Arabians who border on the Arabian Gulf and live opposite the Troglodytes. He says that Poseidium lies farther in than the Aelanites Gulf; and that contiguous to Poseidium there is a grove of palm trees, which is well supplied with water and is highly valued because all the country around is hot and waterless and shadeless; and that here the fertility of the palms is wonderful; and that a man and a woman have charge of the grove, being appointed to that charge through hereditary right. They wear skins, and live on dates from the palm trees; but on account of the number of wild beasts they build huts in trees and sleep there. Then, next, one comes to the Island of Phocae, which was so named from the number of seals there. Near the island is a promontory, which extends to the Rock of the Nabataean Arabians, as they are called, and to the Palaestine country, whither Minaeans and Gerrhaeans and all the neighbouring peoples convey their loads of aromatics. Then one comes to another coast, which was formerly called the coast of the Maranitae, some of whom were farmers and others tent-dwellers, but is now called the coast of the Garindaeans, who destroyed the Maranitae by treachery; for the Garindaeans attacked them while they were celebrating some quadrennial festival, and not only destroyed all the people at the festival but also overran and exterminated the rest of the tribe. Then to the Aelanites Gulf, and to Nabataea, a country with a large population and well supplied with pasturage. They also dwell on islands situated off the coast near by; and these Nabataeans formerly lived a peaceful life, but later, by means of rafts, went to plundering the vessels of people sailing from Aegypt. But they paid the penalty when a fleet went over and sacked their country. One comes next to a plain which is well supplied with trees and water and is full of all kinds of domestic animals — mules among others; and it has a multitude of wild camels, deer, and gazelles, as also numerous lions, leopards, and wolves. Off this plain lies an island called Dia. Then one comes to a gulf about five hundred stadia in extent, which is enclosed all round by mountains and a mouth that is difficult to enter; and round it live men who hunt the land animals. Then to three uninhabited islands, full of olive trees, not the kind in our country, but the indigenous kind, called Aethiopic, the sap of which has medicinal power. Next in order one comes to a stony beach, and after that to a stretch of coast about one thousand stadia in length which is rugged and difficult for vessels to pass, for lack of harbours and anchoring-places, since a rugged and lofty mountain stretches along it. Then one comes to foot-hills, which are rocky and extend to the sea; and these, especially at the time of the Etesian winds and the rains, present to sailors a danger that is beyond all help. Next is a gulf with scattered islands; and continuous with the gulf are three exceedingly high banks of black sand; and after these lies Charmothas Harbour, about one hundred stadia in circuit, with an entrance that is narrow and dangerous for all kinds of boats. A river flows into it; and there is an island in the middle of it which is well supplied with trees and fit for tillage. Then one comes to a rugged stretch of coast; and after that to certain gulfs and to a country of nomads who get their livelihood from camels; for they carry on war from the backs of camels, travel upon them, and subsist upon their milk and flesh. A river flows through their country that brings down gold-dust, but the inhabitants do not know how to work it. They are called Debae; and some of them are nomads, whereas others are also farmers. I am not giving most of the names of the tribes because of their insignificance and at the same time because of the oddity of the pronunciations. Next to the Debae are men more civilised than they; and the country these live in has a more temperate climate; for it is well watered, and well supplied with rains. Gold obtained by digging is found in their country — not gold-dust, but gold nuggets, which do not require much purification; the smallest nuggets have the size of a fruit-stone, the medium that of a medlar, and the largest that of a walnut. They make collars with these nuggets, perforating them and stringing them alternately with transparent stones by means of thread; and they wear them round their necks and wrists. They also sell the gold at a cheap price to their neighbours, giving it in exchange for three times the quantity of brass and double the quantity of silver, because of their lack of experience in working gold and because of the scarcity of the things received in exchange, which are more important for the necessities of life.
Bordering upon these people is the very fertile country of the Sabaeans, a very large tribe, in whose country myrrh and frankincense and cinnamon are produced; and on the coast is found balsam, as also another kind of herb of very fragrant smell, which quickly loses its fragrance. There are also sweet-smelling palms, and reeds; and serpents a span in length, which are dark-red in colour, can leap even as far as a hare, and inflict an incurable bite. On account of the abundance of fruits the people are lazy and easy-going in their modes of life. Most of the populace sleep on the roots of trees which they have cut out of the ground. Those who live close to one another receive in continuous succession the loads of aromatics and deliver them to their next neighbours, as far as Syria and Mesopotamia; and when they are made drowsy by the sweet odours they overcome the drowsiness by inhaling the incense of asphalt and goats' beard. The city of the Sabaeans, Mariaba, is situated upon a well-wooded mountain; and it has a king who is authority in lawsuits and everything else; but it is not lawful for him to leave the palace, or, if he does, the rabble, in accordance with some oracle, stone him to death on the spot. Both he himself and those about him live in effeminate luxury; but the masses engage partly in farming and partly in the traffic in aromatics, both the local kinds and those from Aethiopia; to get the latter they sail across the straits in leathern boats. They have these aromatics in such abundance that they use cinnamon and cassia and the others instead of sticks and firewood. In the country of the Sabaeans is also found larimnum, a most fragrant incense. From their trafficking both the Sabaeans and the Gerrhaeans have become richest of all; and they have a vast equipment of both gold and silver articles, such as couches and tripods and bowls, together with drinking-vessels and very costly houses; for doors and walls and ceilings are variegated with ivory and gold and silver set with precious stones. This is Artemidorus' account of these peoples, but the rest of his statements are partly similar to those of Eratosthenes and partly quoted from the other historians.
For example, he says that some writers call the sea "Erythra" from the colour it presents as the result of reflection, whether from the rays of the sun when it is in the zenith, or from the mountains, which have been reddened by the scorching heat; for, he continues, conjecture runs both ways about the cause; but Ctesias the Cnidian reports a spring, consisting of red and ochre-coloured water, as emptying into the sea; and Agatharchides,º a fellow-citizen of Ctesias, reports from a certain Boxus, of Persian descent, that when a herd of horses had been driven out of the country by a passion-frenzied lioness as far as the sea and from there the herd had crossed over to a certain island, a certain Persian, Erythras by name, built a raft and was the first man to cross to the island; and that when he saw that it was beautifully adapted to habitation, he drove the herd back to Persis, sent forth colonists to that island and to the others and to the coast, and caused the sea to be named after himself; the other writers, he says, declare that Erythras was the son of Perseus, and that he ruled over this region. Some writers say that the distance from the straits of the Arabian Gulf to the extremity of the cinnamon-bearing country is five thousand stadia, without distinguishing clearly whether they mean towards the south or towards the east. It is said also that the emerald and the beryl are found in the gold mines. And there are also fragrant salts in the country of the Arabians, as Poseidonius says.
The first people above Syria who dwell in Arabia Felix are the Nabataeans and the Sabaeans. They overran Syria before they became subject to the Romans; but at present both they and the Syrians are subject to the Romans. The metropolis of the Nabataeans is Petra, as it is called; for it lies on a site which is otherwise smooth and level, but it is fortified all round by a rock, the outside parts of the site being precipitous and sheer, and the inside parts having springs in abundance, both for domestic purposes and for watering gardens. Outside the circuit of the rock most of the territory is desert, in particular towards Judaea. Here, too, is the shortest road to Hiericus, a journey of three or four days, as also to the grove of palm trees, a journey of five days. Petra is also ruled by some king from the royal family; and the king has as Administrator one of his companions, who is called "brother." It is exceedingly well-governed; at any rate, Athenodorus, a philosopher and companion of mine, who had been in the city of the Petraeans, used to describe their government with admiration, for he said that he found both many Romans and many other foreigners sojourning there, and that he saw that the foreigners often engaged in lawsuits, both with one another and with the natives, but that none of the natives prosecuted one another, and that they in every way kept peace with one another.
Many of the special characteristics of Arabia have been disclosed by the recent expedition of the Romans against the Arabians, which was made in my own time under Aelius Gallus as commander. He was sent by Augustus Caesar to explore the tribes and the places, not only in Arabia, but also in Aethiopia, since Caesar saw that the Troglodyte country which adjoins Aegypt neighbours upon Arabia, and also that the Arabian Gulf, which separates the Arabians from the Troglodytes, is extremely narrow. Accordingly he conceived the purpose of winning the Arabians over to himself or of subjugating them. Another consideration was the report, which had prevailed from all time, that they were very wealthy, and that they sold aromatics and the most valuable stones for gold and silver, but never expended with outsiders any part of what they received in exchange; for he expected either to deal with wealthy friends or to master wealthy enemies. He was encouraged also by the expectation of assistance from the Nabataeans, since they were friendly and promised to co-operate with him in every way.
Upon these considerations, therefore, Gallus set out on the expedition; but he was deceived by the Nabataean Administrator, Syllaeus, who, although he had promised to be guide on the march and to supply all needs and to co-operate with him, acted treacherously in all things, and pointed out neither a safe voyage along the coast nor a safe journey by land, misguiding him through places that had no roads and by circuitous routes and through regions destitute of everything, or along rocky shores that had no harbours or through waters that were shallow or full of submarine rocks; and particularly in places of that kind the flood-tides, as also the ebb-tides, caused very great distress. Now this was the first mistake of Gallus, to build long boats, since there was no naval war at hand, or even to be expected; for the Arabians are not very good warriors even on land, rather being hucksters and merchants, to say nothing of fighting at sea. But Gallus built not less than eighty boats, biremes and triremes and light boats, at Cleopatris, which is near the old canal which extends from the Nile. But when he realised that he had been thoroughly deceived, he built one hundred and thirty vessels of burden, on which he set sail with about ten thousand infantry, consisting of Romans in Aegypt, as also of Roman allies, among whom were five hundred Jews and one thousand Nabataeans under Syllaeus. After many experiences and hardships he arrived in fourteen days at Leucê Comê in the land of the Nabataeans, a large emporium, although he had lost many of his boats, some of these being lost, crews and all, on account of difficult sailing, but not on account of any enemy. This was caused by the treachery of Syllaeus, who said that there was no way for an army to go to Leucê Comê by land; and yet camel-traders travel back and forth from Petra to this place in safety and ease, and in such numbers of men and camels that they differ in no respect from an army.
This came to pass because Obodas, the king, did not care much about public affairs, and particularly military affairs (this is a trait common to all the Arabian kings), and because he put everything in the power of Syllaeus; and because Syllaeus treacherously out-generalled Gallus in every way, and sought, as I think, to spy out the country and, along with the Romans, to destroy some of its cities and tribes, and then to establish himself lord of all, after the Romans were wiped out by hunger and fatigue and diseases and any other evils which he had treacherously contrived for them. However, Gallus put in at Leucê Comê, his army now being sorely tried both with scurvy and with lameness in the leg, which are native ailments, the former disclosing a kind of paralysis round the mouth and the latter around the legs, both being the result of the native water and herbs. At all events, he was forced to spend both the summer and the winter there, waiting for the sick to recover. Now the loads of aromatics are conveyed from Leucê Comê to Petra, and thence to Rhinocolura, which is in Phoenicia near Aegypt, and thence to the other peoples; but at the present time they are for the most part transported by the Nile to Alexandria; and they are landed from Arabia and India at Myus Harbour; and then they are conveyed by camels over to Coptus in Thebaïs, which is situated on a canal of the Nile, and then to Alexandria. Again Gallus moved his army from Leucê Comê and marched through regions of such a kind that water had to be carried by camels, because of the baseness of the guides; and therefore it took many days to arrive at the land of Aretas, a kinsman of Obodas. Now Aretas received him in a friendly way and offered him gifts, but the treason of Syllaeus made difficult the journey through that country too; at any rate, it took thirty days to traverse the country, which afforded only zeia, a few palm trees, and butter instead of oil, because they passed through parts that had no roads. The next country which he traversed belonged to nomads and most of it was truly desert; and it was called Ararenê; and its king was Sabos; and in passing through this country, through parts that had no roads, he spent fifty days, arriving at the city of the Negrani and at a country which was both peaceable and fertile. Now the king had fled and the city was seized at the first onset; and from there he arrived at the river in six days. Here the barbarians joined battle with the Romans, and about ten thousand of them fell, but only two Romans; for they used their weapons in an inexperienced manner, being utterly unfit for war, using bows and spears and swords and slings, though most of them used a double-edged axe; and immediately afterwards he took the city called Asca, which had been forsaken by its king; and thence he went to a city called Athrula; and, having mastered it without a struggle, he placed a garrison in it, arranged for supplies of grain and dates for his march, advanced to a city called Marsiaba, which belonged to the tribe of the Rhammanitae, who were subject to Ilasarus. Now he assaulted and besieged this city for six days, but for want of water desisted. He was indeed only a two days' journey from the country that produced aromatics, as informed by his captives, but he had used up six months' time on his marches because of bad guidance, and he realised the fact when he turned back, when at last he had learned the plot against him and had gone back by other roads; for on the ninth day he arrived at Negrana, where the battle had taken place, and thence on the eleventh day at Hepta Phreata, as the place is called, from the fact that it has seven wells; and thence, at last, marching through a peaceable country, he arrived at a village called Chaalla, and again at another village called Malotha, which is situated near a river; and then through a desert country, which had only a few watering-places, as far as a village called Egra. The village is in the territory of Obodas; and it is situated on the sea. On his return he accomplished the whole journey within sixty days, although he had used up six months in his first journey. Thence he carried his army across the Myus Harbour within eleven days, and marched by land over to Coptus, and, with all who had been fortunate enough to survive, landed at Alexandria. The rest he had lost, not in wars, but from sickness and fatigue and hunger and bad roads; for only seven men perished in war. For these reasons, also this expedition did not profit us to a great extent in our knowledge of those regions, but still it made a slight contribution. But the man who was responsible for this failure, I mean Syllaeus, paid the penalty at Rome, since, although he pretend friendship, he was convicted, in addition to his rascality in this matter, of other offences too, and was beheaded.
Now writers divide the country that produces aromatics into four parts, as I have said before; and among the aromatics, they say that frankincense and myrrh are produced from trees and that cassia is produced also from marshes. Some say that most of the latter comes from India and that the best frankincense is produced near Persis. But, according to another division, Arabia Felix is split up into five kingdoms, one of which comprises the warriors, who fight for all; another, the farmers, who supply food to all the rest; another, those who engage in the mechanical arts; another, the myrrh-bearing country, and another the frankincense-bearing country, although the same countries produce cassia, cinnamon, and nard. Occupations are not changed from one class to another, but each and all keep to those of their fathers. The greater part of their wine is made from the palm. Brothers are held in higher honour than children. The descendants of the royal family not only reign as kings, but also hold other offices, in accordance with seniority of birth; and property is held in common by all kinsmen, though the eldest is lord of all. One woman is also wife for all; and he who first enters the house before any other has intercourse with her, having first placed his staff before the door, for by custom each man must carry a staff; but she spends the night with the eldest. And therefore all children are brothers. They also have intercourse with their mothers; and the penalty for an adulterer is death; but only the person from another family is an adulterer. A daughter of one of the kings who was admired for her beauty had fifteen brothers, who were all in love with her, and therefore visited her unceasingly, one after another. At last, being tired out by their visits, she used the following device: she had staves made like theirs, and, when one of them left her, she always put a staff like his in front of the door, a little later another, then another — it being her aim that the one who was likely to visit her next might not have a staff similar to the one in front of the door; and so once, when all the brothers were together at the market-place, one of them, going to her door and seeing the staff in front of it, surmised that someone was with her; and, from the fact that he had left all his brothers in the market-place, he suspected that her visitor was an adulterer; but after running to his father and bringing him into the house, he was proved to have falsely accused his sister.
The Nabataeans are a sensible people, and are so much inclined to acquire possessions that they publicly fine anyone who has diminished his possessions and also confer honours on anyone who has increased them. Since they have but few slaves, they are served by their kinsfolk for the most part, or by one another, or by themselves; so that the custom extends even to their kings. They prepare common meals together in groups of thirteen persons; and they have two girl-singers for each banquet. The king holds many drinking-bouts in magnificent style, but no one drinks more than eleven cupfuls, p369each time using a different golden cup. The king is so democratic that, in addition to serving himself, he sometimes even serves the rest himself in his turn. He often renders an account of his kingship in the popular assembly; and sometimes his mode of life is examined. Their homes, through the use of stone, are costly; but, on account of peace, the cities are not walled. Most of the country is well supplied with fruits except the olive; they use sesame-oil instead. The sheep are white-fleeced and the oxen are large, but the country produces no horses. Camels afford the service they require instead of horses. They go out without tunics, with girdles about their loins, and with slippers on their feet — even the kings, though in their case the colour is purple. Some things are imported wholly from other countries, but others not altogether so, especially in the case of those that are native products, as, for example, gold and silver and most of the aromatics, whereas brass and iron, as also purple garb, styrax, crocus, costaria, embossed works, paintings, and moulded works are not produced in their country. They have the same regard for the dead as for dung, as Heracleitus says: "Dead bodies more fit to be cast out than dung"; and therefore they bury even their kings beside dung-heaps. They worship the sun, building an altar on the top of the house, and pouring libations on it daily and burning frankincense.
When the poet says, "I came to Aethiopians and Sidonians and Erembians," historians are entirely at loss to know, in the first place, in regard to the Sidonians, whether one should call them a certain people who dwelt in the Persian Gulf, from whom the Sidonians in our part of the world were colonists, just as they speak of Tyrians there, islanders, as also of Aradians, from whom they say those in our part of the world were colonists, or whether one should call them the Sidonians themselves; but, secondly, the inquiry about the Erembians is more doubtful, whether one should suspect that the Troglodytes are meant, as do those who force the etymology of "Erembi" from eran embainein, that is, go into the earth, or the Arabians. Now our Zeno alters the text thus: "and to Sidonians and Arabians"; but Poseidonius more plausibly writes, with only a slight alteration of the text, "and Sidonians and Arambians," on the ground that the poet so called the present Arabians, just as they were named by all others in his time. Poseidonius says that the Arabians consist of three tribes, that they are situated in succession, one after another, and that this indicates that they are homogeneous with one another, and that for this reason they were called by similar names — one tribe "Armenians," another "Aramaeans," and another "Arambians." And just as one may suppose that the Arabians were divided into three tribes, according to the differences in the latitudes, which ever vary more and more, so also one may suppose that they used several names instead of one. Neither are those who write "Eremni" plausible; for that name is more peculiarly applicable to the Aethiopians. The poet also mentions "Arimi," by which, according to Poseidonius, we should interpret the poet as meaning, not some place in Syria or in Cilicia or in some other land, but Syria itself; for the people in Syria are Aramaeans, though perhaps the Greeks called them Arimaeans or Arimi. The changes in names, and particularly in those of the barbarians, are numerous: for example, they called Dareius "Darieces," Parysatis "Pharziris," and Athara "Atargatis," though Ctesias calls her "Derceto." As for the blest lot of Arabia, one might make even Alexander a witness thereof, since he intended, as they say, even to make it his royal abode after his return from India. Now all his enterprises were broken up because of his sudden death; but, at any rate, this too was one of his enterprises, to see whether they would receive him voluntarily, and if they did not, to go to war with them; and accordingly, when he saw that they had not sent ambassadors to him, either before or after, he set about making preparations for war, as I have stated heretofore in this work.
For Ptolemy the son of Lagus succeeded Alexander; and he in turn was succeeded by Philadelphius, and he by Euergetes, and then he by Philopator the son of Agathocleia, and then he by Epiphanes, and then he by Philometor, a son always succeeding a father; but Philometor was succeeded by a brother, the second Euergetes, who is also called Physcon, and he by the Ptolemy nicknamed Lathurus, and he by the Auletes of our own time, who was the father of Cleopatra. Now all at kings after the third Ptolemy, being corrupted by luxurious living, have administered the affairs of government badly, but worst of all the fourth, seventh, and the last, Auletes, who, apart from his general licentiousness, practised the accompaniment of choruses with the flute, and upon this he prided himself so much that he would not hesitate to celebrate contests in the royal palace, and at these contests would come forward to vie with the opposing contestants. He, however, was banished by the Alexandrians; and since he had three daughters, of whom one, the eldest, was legitimate, they proclaimed her queen; but his two sons, who were infants, were completely excluded from service at the time. When she had been established on the throne, they sent after a husband for her from Syria, a certain Cybiosactes,who had pretended that he belonged to the family of the Syrian kings. Now the queen had this man strangled to death within a few days, being unable to bear his coarseness and vulgarity; but in his place came a man who likewise had pretended that he was a son of Mithridates Eupator — I mean Archelaüs, who was son of the Archelaüs who carried on war against Sulla and afterwards was honoured by the Romans, and was grandfather of the man who was last to reign as king over the Cappadocians in our time, and was priest of Comana in Pontus. At that time he had been tarrying with Gabinius, in the hope of joining with him on an expedition against the Parthians, but without the knowledge of Gabinius he was brought by certain agents to the queen and proclaimed king. In the meantime Pompeius Magnus, having received Auletes, who had arrived at Rome, recommended him to the Senate and effected, not only his restoration, but also the death of most of the ambassadors, one hundred in number, who had undertaken the embassy against him, and among these was Dion the academic philosopher, who had been made chief ambassador. Accordingly, on being restored by Gabinius, Ptolemy slew both Archelaüs and his own daughter. But before he had added much time to his reign, he died of disease, leaving behind two sons and also two daughters, the eldest daughter being Cleopatra. Now the Alexandrians proclaimed as sovereigns both the elder of the boys and Cleopatra; but the associates of the boy caused an uprising and banished Cleopatra, and she set sail with her sister to Syria. In the meantime Pompeius Magnus had come in flight from Palaepharsalus to Pelusium and Mt. Casius. Now Pompey was treacherously slain by the king's party, but when Caesar arrived he put the lad to death, and, having summoned Cleopatra from exile, established her as queen of Aegypt; and he appointed her remaining brother to reign as king with her, although he was exceedingly young. After the death of Caesar and the battle of Philippi, Antony crossed over to Asia and held Cleopatra in such extraordinary honour that he chose her as wife and had children by her; and he undertook the battle at Actium with her and fled with her; and after this Augustus Caesar pursued them, destroyed both, and put an end to Aegypt's being ruled with drunken violence.
Egypt is now a Province; and it not only pays considerable tribute, but also is governed by prudent men — the praefects who are sent there from time to time. Now he who is sent has the rank of the king; and subordinate to him is the administrator of justice, who has supreme authority over most of the law-suits; and another is the official called Idiologus, who inquires into all properties that are without owners and that ought to fall to Caesar; and these are attended by freedmen of Caesar, as also by stewards, who are entrusted with affairs of more or less importance. There are also three legions of soldiers, one of which is stationed in the city and the others in the country; and apart from these there are nine Roman cohorts, three in the city, three on the borders of Aethiopia in Syenê, as a guard for that region, and three in the rest of the country. And there are also three bodies of cavalry, which likewise are assigned to the various critical points. Of the native officials in the city, one is the Interpreter, who is clad in purple, has hereditary prerogatives, and has charge of the interests of the city; and another the Recorder; and another the Chief Judge;and the fourth the Night Commander. Now these officers existed also in the time of the kings, but, since the kings were carrying on a bad government, the prosperity of the cities was also vanishing on account of the prevailing lawlessness. At any rate, Polybius, who had visited the city, is disgusted with the state of things then existing; and he says that three classes inhabited the city: first, the Aegyptian or native stock of people, who were quick-tempered and not inclined to strife; and, secondly, the mercenary class, who were severe and numerous and intractable (for by an ancient custom they would maintain foreign men-at‑arms, who had been trained to rule rather than to be ruled, on account of the worthlessness of the kings); and, third, the tribe of the Alexandrians, who also were not distinctly inclined to civil life, and for the same reasons, but still they were better than those others, for even though they were a mixed people, still they were Greeks by origin and mindful of the customs common to the Greeks. But after this mass of people had also been blotted out, chiefly by Euergetes Physcon, in whose time Polybius went to Alexandria (for, being opposed by factions, Physcon more often sent the masses against the soldiers and thus caused their destruction) — such being the state of affairs in the city, Polybius says, in very truth there remained for one, in the words of the poet, merely "to go to Aegypt, a long and painful journey."
Such, then, if not worse, was the state of affairs under the later kings also; but the Romans have, to the best of their ability, I might say, set most things right, having organised the city as I have said, and having appointed throughout the country officials called Epistrategi and Nomarchs and Ethnarchs, thought worthy to superintend affairs of no great importance. Among the happy advantages of the city, the greatest is the fact that this is the only place in all Aegypt which is by nature well situated with reference to both things — both to commerce by sea, on account of the good harbours, and to commerce by land, because the river easily conveys and brings together everything into a place so situated — the greatest emporium in the inhabited world.
Now one might call these the excellent attributes of the city; and as for the revenues of Aegypt, Cicero tells about them in a certain speech, saying that a tribute of twelve thousand five hundred talents was paid annually to Auletes, the father of Cleopatra. If, then, the man who administered the kingdom in the worst and most careless way obtained so large a revenue, what should one think of the present revenues, which are managed with so much diligence, and when the commerce with the Indians and the Troglodytes has been increased to so great an extent? In earlier times, at least, not so many as twenty vessels would dare to traverse the Arabian Gulf far enough to get a peep outside the straits, but at the present time even large fleets are despatched as far as India and the extremities of Aethiopia, from which the most valuable cargoes are brought to Aegypt, and thence sent forth again to the other regions; so that double duties are collected, on both imports and exports; and on goods that cost heavily the duty is also heavy. And in fact the country has monopolies also; for Alexandria alone is not only the receptacle of goods of this kind, for the most part, but also the source of supply to the outside world. And, further, one can perceive more clearly these natural advantages if one travels round the country, visiting first of all the part of the coast which begins at Catabathmus — for Aegypt extends as far as that place, though the country next thereafter belongs to the Cyrenaeans and to the neighbouring barbarians, the Marmaridae.
Now the run from Catabathmus to Paraetonium, if one sails in a straight course, is nine hundred stadia. It is a city and large harbour of about forty stadia. Some call the city Paraetonium, but others Ammonia. In the interval, one comes to the village of the Aegyptians, to the promontory Aenesisphyra, and to the Tyndareian Rocks, which latter are four small islands with a harbour; then next to Drepanum, a promontory, and to Aenesippeia, an island with a harbour, and to Apis, a village, from which the distance to Paraetonium is one hundred stadia, and to the temple of Ammon, a five days' journey. The distance from Paraetonium to Alexandria is approximately one thousand three hundred stadia; and in the interval one comes first to a promontory of white earth, Leucê Actê, as it is called, and then to Phoenicus, a harbour, and to Pnigeus, a village, and then of Pedonia, an island with a harbour, and then to Antiphrae, which is at only a little distance from the sea. The whole of this country is without good wine, since the wine-jars receive more sea-water than wine; and this they call "Libyan" wine, which, as also beer, is used by most of the tribe of Alexandrians; but Antiphrae is ridiculed most. Then one comes to the harbour Derrhis, so called because of the black rock near by, which resembles a "derrhis"; and the neighbouring place is also called Zephyrium. Then to another harbour, Leucaspis and several others; and then to Cynos-Sema; and then to Taposeiris, not on the sea, which holds a great public festival. (There is also another Taposeiris on the other side of the city and quite far from it.) And near it there is a rocky place on the sea where likewise crowds of people in the prime of life assemble during every season of the year. And then one comes to Plinthinê and to the village of Nicias, and to Cherronesus, a stronghold, where we are now near Alexandria and Necropolis, a distance of seventy stadia. Lake Mareia, which extends even as far as this, has a breadth of more than one hundred and fifty stadia and a length of less than three hundred. It contains eight islands; and all the shores round it are well inhabited; and the vintages in this region are so good that the Mareotic wine is racked off with a view to ageing it.
The byblus was in the Aegyptian marshes and lakes, as also the Aegyptian cyamus, from which comes the ciborium; you have stalks approximately equal in height, about ten feet. But whereas the byblus is a bare stock with a tuft on top, the cyamus produces leaves and flowers in many parts, and also a fruit like our cyamus, differing only in size and taste. Accordingly, the bean-fields afford a pleasing sight, and also enjoyment to those who wish to hold feasts therein. They hold feasts in cabin-boats, in which they enter the thick of the cyami and the shade of the leaves; for the leaves are so very large that they are used both from drinking-cups and for bowls, for these even have a kind of concavity suited to this purpose; and in fact Alexandria is full of these in the work-shops, where they are used as vessels and the farms have also this as one source of their revenues — I mean the revenue from the leaves. Such, then, is the cyamus. As for the byblus, it does not grow in large quantities here (for it is not cultivated), but it grows in large quantities in the lower parts of the Delta, one kind being inferior, and the other superior, that is, the Hieratica. And here, too, certain of those who wished to enhance the revenues adopted the shrewd practice of the Judaeans, which the latter had invented in the case of the palm tree (particularly the caryotic palm) and the balsam tree; for they do not allow the byblus to grow in many places, and because of the scarcity they set a higher price on it and thus increase the revenues, though they injure the common use of the plant.
On the right of the Canobic Gate, as one goes out, one comes to the canal which is connected with the lake and leads to Canobus; and it is by this canal that one sails, not only to Schedia, that is, to the great river, but also to Canobus, though first to Eleusis. Eleusis is a settlement near both Alexandria and Necropolis, is situated on the Canobic canal itself, and has lodging-places and commanding views for those who wish to engage in revelry, both men and women, and is a beginning, as it were, of the "Canobic" life and the shamelessness there current. On proceeding a slight distance from Eleusis, and on the right, one comes to the canal which leads up the Schedia. Schedia is four schoeni distant from Alexandria; it is a settlement of the city, and contains the station of the cabin-boats on which the praefects sail to Upper Aegypt. And at Schedia is also the station for paying duty on the goods brought down from above it and brought up from below it; and for this purpose, also, a schedia has been laid across the river, from which the place has its name. After the canal which leads to Schedia, one's next voyage, to Canobus, is parallel to that part of the coast-line which extends from Pharos to the Canobic mouth; for a narrow ribbon-like strip of land extends between the sea and the canal, and on this, after Nicopolis, lies the Little Taposeiris, as also the Zephyrium, a promontory which contains a shrine of Aphroditê Arsinoê. In ancient times, it is said, there was also a city called Thonis here, which was named after the king who received Menelaüs and Helen with hospitality. At any rate, the poet speaks of Helen's drugs as follows: "goodly drugs which Polydamna, the wife of Thon, had given her."
Canobus is a city situated at a distance of one hundred and twenty stadia from Alexandria, if one goes on foot, and was named after Canobus, the pilot of Menelaüs, who died there. It contains the temple of Sarapis, which is honoured with great reverence and effects such cures that even the most reputable men believe in it and sleep in it — themselves on their own behalf or others for them. Some writers go on to record the cures, and others the virtues of the oracles there. But to balance all this is the crowd of revellers who go down from Alexandria by the canal to the public festivals; for every day and every night is crowded with people on the boats who play the flute and dance without restraint and with extreme licentiousness, both men and women, and also with the people of Canobus itself, who have resorts situated close to the canal and adapted to relaxation and merry-making of this kind.
After Canobus one comes to the Heracleium, when contains a temple of Heracles; and then to the Canobic mouth and the beginning of the Delta. The parts on the right of the Canobic canal are the Menelaïte Nome, so called from the brother of the first Ptolemy — not, by heaven, from the hero, as some writers say, among whom is also Artemidorus. After the Canobic mouth one comes to the Bolbitine mouth, and then to the Sebennytic, and to the Phatnitic, which is third in size as compared with the first two, which form the boundaries of the Delta; for not far from the vertex of the Delta the Phatnitic splits, sending a branch into the interior of the Delta. Lying close to the Phatnitic mouth is the Mendesian; and then one comes to the Tanitic, and, last of all, to the Pelusiac. There are also others in among these, pseudo-mouths as it were, which are rather insignificant. Their mouths indeed afford entrance to boats, but are adapted, not to large boats, but to tenders only, because the mouths are shallow and marshy. It is chiefly, however, the Canobic mouth that they used as an emporium, since the harbours at Alexandria were kept closed, as I have said before. After the Bolbitine mouth one comes to a low and sandy promontory which projects rather far into the sea; it is called Agnu-Ceras. And then to the Watch-tower of Perseus and the Wall of the Milesians; for in the time of Psammitichus (who lived in the time of Cyaxares the Mede) the Milesians, with thirty ships, put in at the Bolbitine mouth, and then, disembarking, fortified with a wall the above-mentioned settlement; but in time they sailed up into the Saïtic Nome, defeated the city Inaros in a naval fight, and founded Naucratis, not far above Schedia. After the Wall of the Milesians, as one proceeds towards the Sebennytic mouth, one comes to two lakes, one of which, Buticê, has its name from the city Butus, and also to the Sebennytic city, and to Saïs, the metropolis of the lower country, in which Athena is worshipped; and in her temple lies the tomb of Psammitichus. In the neighbourhood of Butus is also an Hermupolis, which is situated on an island; and in Butus there is an oracle of Leto.
In the interior above the Sebennytic and Phatnitic mouths lies Xoïs, both an island and a city, in the Sebennytic Nome. Here, also, are an Hermupolis and a Lycupolis, and Mendes, at which place they worship Pan and, among animals, a he-goat; and, as Pindar says, the he‑goats have intercourse with women there: "Mendes, along the crag of the sea, farthermost horn of the Nile, where the goat-mounting he-goats have intercourse with women." Near Mendes lie also a Diospolis and the lakes in its neighbourhood and Leontopolis; and then, at a greater distance, the city Busiris in the Busirite Nome, and Cynospolis. According to Eratosthenes, the expulsion of foreigners is a custom common to all barbarians, and yet the Aegyptians are condemned for this fault because of the myths which have been circulated about Busiris in connection with the Busirite Nome, since the later writers wish falsely to malign the inhospitality of this place, although, by heavens, no king or tyrant named Busiris ever existed; and, he says, the poet's words are also constantly cited — "to go to Aegypt, long and painful journey" — the want of harbours contributing very much to this opinion, as also the fact that even the harbour which Aegypt did have, the one at Pharos, gave no access, but was guarded by shepherds who were pirates and who attacked those who tried to bring ships to anchor there; and the Carthaginians likewise, he adds, used to drown in the sea any foreigners who sailed past their country to Sardo or to the Pillars, and it is for this reason that most of the stories told about the west are disbelieved; and also the Persians, he says, would treacherously guide the ambassadors over roundabout roads and through difficult regions.
Bordering on this Nome is the Athribite Nome and the city Athribis, and also the Prosopite Nome, in which is a City of Aphroditê. Above the Mendesian and Tanitic mouths lie a large lake and the Mendesian and Leontopolite Nomes and a City of Aphroditê and the Pharbetite Nome; and then one comes to the tanitic mouth, which some call Saïtic, and to the Tanite Nome, and to Tanis, a large city therein.
Between the Tanitic and Pelusiac mouths lie lakes, and large and continuous marshes which contain many villages. Pelusium itself also has marshes lying all round it, which by some are called Barathra, and muddy ponds; its settlement lies at a distance of more than twenty stadia from the sea, the wall has a circuit of twenty stadia, and it has its name for the pelos and the muddy ponds. Here, too, Aegypt is difficult to enter, I mean from the eastern regions about Phoenicia and Judaea, and from the Arabia of the Nabataeans, which is next to Aegypt; these are the regions which the road to Aegypt traverses. The country between the Nile and the Arabian Gulf is Arabia, and at its extremity is situated Pelusium; but the whole of it is desert, and impassable for an army. The isthmus between Pelusium and the recess of the gulf at Heroönpolis is one thousand stadia, but, according to Poseidonius, less than one thousand five hundred; and in addition to its being waterless and sandy, it contains a multitude of reptiles, the sand-burrowers.
From Schedia, as one sails towards Memphis, there are, on the right, a very large number of villages, extending as far as Lake Mareia, among which is the Village of Chabrias, as it is called; and, on the river, one comes to an Hermupolis, and then to Gynaeconpolis and the Gynaecopolite Nome, and, next in order, to Momemphis and the Momemphite Nome; but in the interval there are several canals which empty into Lake Mareotis. The Momemphitae honour Aphroditê; and a sacred cow is kept there, as is Apis in Memphis and Mneuïs in Heliupolis. Now these animals are regarded as gods, but those in the other places (for in many either a bull or cow is kept) — those others, I say, are not regarded as gods, though they are held sacred.
Above Momemphis are two nitre-beds, which contain very large quantities of nitre, and the Nitriote Nome. Here Sarapis is held in honour; and they are the only people in Aegypt who sacrifice a sheep. Near by, and in this Nome, is a city Menelaüs; and on the left, in the Delta, lies Naucratis, which is on the river, whereas Saïs lies at a distance of two schoeni from the river. A little above Saïs is the asylum of Osiris, in which the body of Osiris is said to lie; but many lay claim to this, and particularly the inhabitants of the Philae which is situated above Syenê and Elephantinê; for they tell the mythical story, namely, that Isis placed coffins of Osiris beneath the earth in several places (but only one of them, and that unknown to all, contained the body of Osiris), and that she did this because she wished to hide the body from Typhon, fearing that he might find it and cast it out of its tomb.
Now this is the full description of the country from Alexandria to the vertex of the Delta; and, according to Artemidorus, the voyage up the river is twenty-eight schoeni, that is, eight hundred and forty stadia, reckoning the schoenus as thirty stadia. When I made the voyage, however, they used different measures at different times when they gave the distances, so that even forty stadia, or still more, was the accepted measure of the schoenus, according to the place. That the measure of the schoenus among the Aegyptians in unstable is made clear by Artemidorus himself in his next statement; for from Memphis to Thebaïs each schoenus, he says, is one hundred and twenty stadia, and from Thebaïs to Syenê sixty, and, as one sails up from Pelusium to the same vertex of the Delta, the distance, he says, is twenty-five schoeni, that is, seven hundred and fifty stadia, using the same measure. The first canal, as one proceeds from Pelusium, he says, is the one which fills the Marsh-lakes, as they are called, which are two in number and lie on the left of the great river above Pelusium in Arabia; and he also speaks of other lakes and canals in the same regions outside the Delta. There is also the Sethroïte Nome by the second lake, although he counts this Nome too as one of the ten1in the Delta; and two other canals meet in the same lakes. |
|
|
|
|
17 Africa. 3 110 1:32 
|
17 - 1 Egypt and Ethiopia 
1 Since, in my description of Arabia, I have also included the gulfs which pinch it and make it a peninsula, I mean the Persian and Arabian Gulfs, and at the same time have gone the rounds of certain parts both of Aegypt and of Aethiopia, I mean the countries of the Troglodytes and the peoples situated in order thereafter as far as the Cinnamon-bearing country, I must now set forth the remaining parts that are continuous with these tribes, that is, the parts in the neighbourhood of the Nile; and after this I shall traverse Libya, which is the last remaining subject of my whole geography. And here too I must first set forth the declarations of Eratosthenes.
2 Now according to him the Nile is nine hundred or a thousand stadia distant towards the west from the Arabian Gulf, and is similar in shape to the letter N written reversed; for after flowing, he says, from Meroê towards the north about two thousand seven hundred stadia, it turns back towards the south and the winter sunset about three thousand seven hundred stadia, and after almost reaching the same parallel as that of the region of Meroê and projecting far into Libya and making the second turn, flows towards the north five thousand three hundred stadia to the great cataract, turning aside slightly towards the east, and then one thousand two hundred stadia to the smaller cataract at Syenê, and then five thousand three hundred more to the sea. Two rivers empty into it, which flow from some lakes on the east and enclose Meroê, a rather large island. One of these rivers, which flows on the eastern side of the island, is called Astaboras and the other is called Astapus, though some call it Astasobas and say that another river, which flows from some lakes in the south, is the Astapus and that this river forms almost all the straight part of the body of the Nile, and that it is filled by the summer rains. Above the confluence of the Astaboras and the Nile, he says, at a distance of seven hundred stadia, lies Meroê, a city bearing the same name as the island; and there is another island above Meroê which is held by the Aegyptian fugitives who revolted in the time of Psammitichus, and are called "Sembritae," meaning "foreigners." They are ruled by a queen, but they are subject to the kings of Meroê. The lower parts of the country on either side of Meroê, along the Nile towards the Red Sea, are inhabited by Megabari and Blemmyes, who are subject to the Aethiopians and border on the Aegyptians, and, along the sea, by Troglodytes (the Troglodytes opposite Meroê are a ten or twelve days' journey distant from the Nile), but the parts on the left side of the course of the Nile, in Libya, are inhabited by Nubae, a large tribe, who, beginning at Meroê, extend as far as the bends of the river, and are not subject to the Aethiopians but are divided into several separate kingdoms. The extent of Aegypt along the sea from the Pelusiac to the Canobic mouth is one thousand three hundred stadia. This, then, is what Eratosthenes says.
3 But it is necessary to speak at greater length, and first of the parts about Aegypt, in order to proceed from those that are better known to those that come in order thereafter; for the Nile effects certain common results in this country and in that which is continuous with it and lies above it, I mean the country of the Aethiopians, in that it waters them at the time of its rise and also leaves also those parts of them habitable which have been covered during the overflows, and in that it merely passes through all the higher parts that are at a greater altitude than its current, leaving them uninhabited and desert on both sides because of the same lack of water. However, the Nile does not pass through the whole of Aethiopia, nor alone, nor in a straight line, but it alone passes through Aegypt, through the whole of it and in a straight line, beginning from the little cataract above Syenê and Elephantinê, which are the boundaries of Aegypt and Aethiopia, to its outlets on the sea-coast. And p9indeed the Aethiopians lead for the most part a nomadic and resourceless life, on account of the barrenness of the country and of the unseasonableness of its climate and of its remoteness from us, whereas with the Aegyptians the contrary is the case in all these respects; for from the outset they have led a civic and cultivated life and have been settled in well-known regions, so that their organisations are a matter of comment. And they are commended in that they are thought to have used worthily the good fortune of their country, having divided it well and having taken good care of it; for when they had appointed a king they divided the people into three classes, and they called one class soldiers, another farmers, and another priests; and the last class had the care of things sacred and the other two of things relating to man; and some had charge of the affairs of war, and others of all the affairs of peace, both tilling soil and following trades, from which sources the revenues were gathered for the king. The priests devoted themselves both to philosophy and to astronomy; and they were companions of the king. The country was first divided into Nomes, the Thebaïs containing ten, the country in the Delta ten, and the country between them sixteen (according to some, the number of the Nomes all told was the same as that of the halls in the Labyrinth, but the number of these is less than thirty); and again the Nomes were divided into other sections, for most of them were divided into toparchies, and these also into other sections; and the smaller portions were the arourae. There was need of this accurate and minute division on account of the continuous confusion of the boundaries caused by the Nile at the time of its increases, since the Nile takes away and adds soil, and changes conformations of lands, and in general hides from view the signs by which one's own land is distinguished from that of another. Of necessity, therefore, the lands must be re-measured again and again. And here it was, they say, that the science of geometry originated, just as accounting and arithmetic originated with the Phoenicians, because of their commerce. Like the people as a whole, the people in each Nome were also divided into three parts, since the land had been divided into three equal parts. The activity of people in connection with the river goes so far as to conquer nature through diligence. For by nature the land produces more fruit than do other lands, and still more when watered; but diligence has oftentimes, when nature has failed, availed to bring about the watering of as much land even at the time of the smaller rises of the river as at the greater rises, that is, through the means of canals and embankments. At any rate, in the times before Petronius the crop was the largest and the rise the highest when the Nile would rise to fourteen cubits, and when it would rise to only eight a famine would ensue; but in the time of his reign over the country, and when the Nilometer registered only twelve cubits, the crop was the largest, and once, when it registered only eight cubits, no one felt hunger. Such is the organisation of Aegypt; but let me now describe the things that come next in order.
4 The Nile flows from the Aethiopian boundaries towards the north in a straight line to the district called "Delta," and then, being "split at the head," as Plato says, the Nile makes this place as it were the vertex of a triangle, the sides of the triangle being formed by the streams that split in either direction and extend to the sea — the one on the right to the sea at Pelusium and the other on the left to the sea at Canobus and the neighbouring Heracleium, as it is called, — and the base by the coast-line between Pelusium and the Heracleium. An island, therefore, has been formed by the sea and the two streams of the river; and it is called Delta on account of the similarity of its shape; and the district at the vertex has been given the same name because it is the beginning of the above-mentioned figure; and the village there is also called Delta. Now these are two mouths of the Nile, of which one is called Pelusiac and the other Canobic or Heracleiotic; but between these there are five other outlets, those at least that are worth mentioning, and several that are smaller; for, beginning with the first parts of the Delta, many branches of the river have been split off throughout the whole island and have formed many streams and islands, so that the whole Delta has become navigable — canals on canals having been cut, which are navigated with such ease that some people even use earthenware ferry-boats. Now the island as a whole is as much as three thousand stadia in perimeter; and they also call it, together with the opposite river-lands of the Delta, Lower Egypt; but at the rising of the Nile the whole country is under water and becomes a lake, except the settlements; and these are situated on natural hills or on artificial mounds, and contain cities of considerable size and villages, which, when viewed from afar, resemble islands. The water stays more than forty days in summer and then goes down gradually just as it rose; and in sixty days the plain is completely bared and begins to dry out; and the sooner the drying takes place, the sooner the ploughing and the sowing; and the drying takes place sooner in those parts where the heat is greater. The parts above the Delta are also watered in the same way, except that the river flows in a straight course about four thousand stadia through only one channel, except where some island intervenes, of which the most noteworthy is that which comprises the Heracleiotic Nome, or except where the river is diverted to a greater extent than usual by a canal into a large lake or a territory which it can water, as, for instance, in the case of the canal which waters the Arsinoïte Nome and Lake Moeris and of those which spread over Lake Mareotis. In short, Aegypt consists of only the river-land, I mean the last stretch of river-land on either side of the Nile, which, beginning at the boundaries of Aethiopia and extending to the vertex of the Delta, scarcely anywhere occupies a continuous habitable space as broad as three hundred stadia. Accordingly, when it is dried, it resembles lengthwise a girdle-band, the greater diversions of the river being excepted. This shape of the river-land of which I am speaking, as also of the country, is caused by the mountains on either side, which extend from the region of Syenê down to the Aegyptian Sea; for in proportion as these mountains lie together or at a distance from one another, in that proportion the river is contracted or widened, and gives to the lands that are habitable their different shapes. But the country beyond the mountains is for a great distance uninhabited.
5 Now the ancients depended mostly on conjecture, but the men of later times, having become eyewitnesses, perceived that the Nile was filled by summer rains, when Upper Aethiopia was flooded, and particularly in the region of its farthermost mountains, and that when the rains ceased the inundation gradually ceased. This fact was particularly clear to those who navigated the Arabian Gulf as far as the Cinnamon-bearing country, and to those who were sent out to hunt elephants or upon any other business which may have prompted the Ptolemaic kings of Aegypt to despatch men thither. For these kings were concerned with things of this kind; and especially the Ptolemy surnamed Philadelphus, since he was of an inquiring disposition, and on account of the infirmity of his body was always searching for novel pastimes and enjoyments. But the kings of old were not at all concerned with such things, although they proved themselves congenial to learning, both they and the priests, with whom they spent the greater part of their lives; and therefore we may well be surprised, not only on this account, but also by the fact that Sesostris traversed the whole of Aethiopia as far as the Cinnamon-bearing country, and that memorials of his expedition, pillars and inscriptions, are to be seen even to this day. Further, when Cambyses took possession of Aegypt, he advanced with the Aegyptians even as far as Meroê; and indeed this name was given by him to both the island and the city, it is said, because his sister Meroê — some say his wife — died there. The name, at any rate, he bestowed upon the place in honour of the woman. It is surprising, therefore, that the men of that time, having such knowledge to begin with, did not possess a perfectly clear knowledge of the rains, especially since the priests rather meticulously record in their sacred books, and thus store away, all facts that reveal any curious information; for they should have investigated, for they made any investigations at all, the question, which even to this day is still being investigated, I mean why in the world rains fall in summer but not in winter, and in the southernmost parts but not in Thebaïs and the country round Syenê; but the fact that the rising of the river results from rains should not have been investigated, nor yet should this matter have needed such witnesses as Poseidonius mentions; for instance, he says that it was Callisthenes who states that the summer rains are the cause of the risings, though Callisthenes took the assertion from Aristotle, and Aristotle from Thrasyalces the Thasian (one of the early physicists), and Thrasyalces from someone else, and he from Homer, who calls the Nile "heaven-fed": "And back again to the land of Aegyptus, heaven-fed river."
But I dismiss this subject, since it has been discussed by many writers, of whom it will suffice to report only the two who in my time have written the book about the Nile, I mean Eudorus and Ariston the Peripatetic philosopher; for except in the matter of arrangement everything found in the two writers is the same as regards both style and treatment. I, at any rate, being in want of copies with which to make a comparison, compared the one work with the other; but which of the two men it was who appropriated to himself the other's work might be discovered at Ammon's temple! Eudorus accused Ariston; the style, however, is more like that of Ariston.
Now the early writers gave the name Aegypt to only the part of the country that was inhabited and watered by the Nile, beginning at the region of Syenê and extending to the sea; but the later writers down to the present time have added on the eastern side approximately all the parts between the Arabian Gulf and the Nile (the Aethiopians do not use the Red Sea at all), and on the western side the parts extending as far as the oases, and on the sea-coast the parts extending from the Canobic mouth to Catabathmus and the domain of the Cyrenaeans. For the kings after Ptolemy became so powerful that they took possession of Cyrenaea itself and even united Cypros with Aegypt. The Romans, who succeeded the Ptolemies, separated their three dominions and have kept Aegypt within its former limits. The Aegyptians call "oases" the inhabited districts which are surrounded by large deserts, like islands in the open sea. There is many an oasis in Libya, and three of them lie close to Aegypt and are classed as subject to it. This, then, is my general, or summary, account of Aegypt, and I shall now discuss the separate parts and the excellent attributes of the country.
6 Since Alexandria and its neighbourhood constitute the largest and most important part of this subject, I shall begin with them. The sea-coast, then, from Pelusium, as one sails towards the west, as far as the Canobic mouth, is about one thousand three hundred stadia — the "base" of the Delta, as I have called it; and thence to the island Pharos, one hundred and fifty stadia more. Pharos is an oblong isle, is very close to the mainland, and forms with it a harbour with two mouths; the shore of the mainland forms a bay, since it thrusts two promontories into the open sea, and between these is situated the island, which closes the bay, for it lies lengthwise parallel to the shore. Of the extremities of Pharos, the eastern one lies closer to the mainland and to the promontory opposite it (the promontory called Lochias), and thus makes the harbour narrow at the mouth; and in addition to the narrowness of the intervening passage there are also rocks, some under the water, and others projecting out of it, which at all hours roughen the waves that strike them from the open sea. And likewise the extremity of the isle is a rock, which is washed all round by the sea and has upon it a tower that is admirably constructed of white marble with many stories and bears the same name as the island. This was an offering made by Sostratus of Cnidus, a friend of the kings, for the safety of mariners, as the inscription says: for since the coast was harbourless and low on either side, and also had reefs and shallows, those who were sailing from the open sea thither needed some lofty and conspicuous sign to enable them to direct their course aright to the entrance of the harbour. And the western mouth is also not easy to enter, although it does not require so much caution as the other. And it likewise forms a second harbour, that of Eunostus, as it is called, which lies in front of the closed harbour which was dug by the hand of man. For the harbour which affords the entrance on the side of the above-mentioned tower of Pharos is the Great Harbour, whereas these two lie continuous with that harbour in their innermost recess, being separated from it only by the embankment called the Heptastadium. The embankment forms a bridge extending from the mainland to the western portion of the island, and leaves open only two passages into the harbour of Eunostus, which are bridged over. However, this work formed not only a bridge to the island but also an aqueduct, at least when Pharos was inhabited. But in these present times it has been laid waste by the deified Caesar in his war against the Alexandrians, since it had sided with the kings. A few seamen, however, live near the tower. As for the Great Harbour, in addition to its being beautifully enclosed both by the embankment and by nature, it is not only so deep close to the shore that the largest ship can be moored at the steps, but also is cut up into several harbours. Now the earlier kings of the p29Aegyptians, being content with what they had and not wanting foreign imports at all, and being prejudiced against all who sailed the seas, and particularly against the Greeks (for owing to scarcity of land of their own the Greeks were ravagers and coveters of that of others), set a guard over this region and ordered it to keep away any who should approach; and they gave them as a place of abode Rhacotis, as it is called, which is now that part of the city of the Alexandrians which lies above the ship-houses, but was at that time a village; and they gave over the parts round about the village to herdsmen, who likewise were able to prevent the approach of outsiders. But when Alexander visited the place and saw the advantages of the site, he resolved to fortify the city on the harbour. Writers record, as a sign of the good fortune that has since attended the city, an incident which occurred at the time of tracing the lines of the foundation: When the architects were marking the lines of the enclosure with chalk, the supply of chalk gave out; and when the king arrived, his stewards furnished a part of the barley-meal which had been prepared for the workmen, and by means of this the streets also, to a larger number than before, were laid out. This occurrence, then, they are said to have interpreted as a good omen.
7 The advantages of the city's site are various; for, first, the place is washed by two seas, on the north by the Aegyptian Sea, as it is called, and on the south by Lake Mareia, also called Mareotis. This is filled by many canals from the Nile, both from above and on the sides, and through these canals the imports are much larger than those from the sea, so that the harbour on the lake was in fact richer than that on the sea; and here the exports from Alexandria also are larger than the imports; and anyone might judge, if he were at either Alexandria or Dicaearchia and saw the merchant vessels both at their arrival and at their departure, how much heavier or lighter they sailed thither or therefrom. And in addition to the great value of the things brought down from both directions, both into the harbour on the sea and into that on the lake, the salubrity of the air is also worthy of remark. And this likewise results from the fact that the land is washed by water on both sides and because of the timeliness of the Nile's risings; for the other cities that are situated on lakes have heavy and stifling air in the heats of summer, because the lakes then become marshy along their edges because of the evaporation caused by the sun's rays, and, accordingly, when so much filth-laden moisture rises, the air inhaled is noisome and starts pestilential diseases, whereas at Alexandria, at the beginning of summer, the Nile, being full, fills the lake also, and leaves no marshy matter to corrupt the rising vapours. At that time, also, the Etesian winds blow from the north and from a vast sea, so that the Alexandrians pass their time most pleasantly in summer.
8 The shape of the area of the city is like a chlamys; the long sides of it are those that are washed by the two waters, having a diameter of about thirty stadia, and the short sides are the isthmuses, each being seven or eight stadia wide and pinched in on one side by the sea and on the other by the lake. The city as a whole is intersected by streets practicable for horse-riding and chariot-driving, and by two that are very broad, extending to more than a plethrum in breadth, which cut one another into two sections and at right angles. And the city contains most beautiful public precincts and also the royal palaces, which constitute one-fourth or even one-third of the whole circuit of the city; for just as each of the kings, from love of splendour, was wont to add some adornment to the public monuments, so also he would invest himself at his own expense with a residence, in addition to those already built, so that now, to quote the words of the poet, "there is building upon building." All, however, are connected with one another and the harbour, even those that lie outside the harbour. The Museum is also a part of the royal palaces; it has a public walk, an Exedra with seats, and a large house, in which is the common mess-hall of the men of learning who share the Museum. This group of men not only hold property in common, but also have a priest in charge of the Museum, who formerly was appointed by the kings, but is now appointed by Caesar. The Sema also, as it is called, is a part of the royal palaces. This was the enclosure which contained the burial-places of the kings and that of Alexander; for Ptolemy, the son of Lagus, forestalled Perdiccas by taking the body away from him when he was bringing it down from Babylon and was turning aside towards Aegypt, moved by greed and a desire to make that country his own. Furthermore, Perdiccas lost his life, having been slain by his soldiers at the time when Ptolemy attacked him and hemmed him up in a desert island. So Perdiccas was killed, having been transfixed by his soldiers' sarissae when they attacked him; but the kings who were with him, both Aridaeus and the children of Alexander, and also Rhoxanê, Alexander's wife, departed for Macedonia; and the body of Alexander was carried off by Ptolemy and given sepulture in Alexandria, where it still now lies — not, however, in the same sarcophagus as before, for the present one is made of glass, whereas the one wherein Ptolemy laid it was made of gold. The latter was plundered by the Ptolemy nicknamed "Cocces" and "Pareisactus," who came over from Syria but was immediately expelled, so that his plunder proved unprofitable to him.
9 In the Great Harbour at the entrance, on the right hand, are the island and the tower Pharos, and on the other hand are the reefs and also the promontory Lochias, with a royal palace upon it; and on sailing into the harbour one comes, on the left, to the inner royal palaces, which are continuous with those on Lochias and have groves and numerous lodges painted in various colours. Below these lies the harbour that was dug by the hand of man and is hidden from view, the private property of the kings, as also Antirrhodos, an isle lying off the artificial harbour, which has both a royal palace and a small harbour. They so called it as being a rival of Rhodes. Above the artificial harbour lies the theatre; then the Poseidium — an elbow, as it were, projecting from the Emporium, as it is called, and containing a temple of Poseidon. To this elbow of land Antony added a mole projecting still farther, into the middle of a harbour, and on the extremity of it built a royal lodge which he called Timonium. This was his last act, when, forsaken by his friends, he sailed away to Alexandria after his misfortune at Actium, having chosen to live the life of a Timon the end of his days, which he intended to spend in solitude from all those friends. Then one comes to the Caesarium and the Emporium and the warehouses; and after these to the ship-houses, which extend as far as the Heptastadium. So much for the Great Harbour and its surroundings.
Next, after the Heptastadium, one comes to the Harbour of Eunostus, and, above this, to the artificial harbour, which is also called Cibotus; it too has ship-houses. Farther in there is a navigable p41canal, which extends to Lake Mareotis. Now outside the canal there is still left only a small part of the city; and then one comes to the suburb Necropolis, in which are many gardens and groves and halting-places fitted up for the embalming of corpses, and, inside the canal, both to the Sarapium and to other sacred precincts of ancient times, which are now almost abandoned on account of the construction of the new buildings at Nicopolis; for instance, there are an amphitheatre and a stadium at Nicopolis, and the quinquennial games are celebrated there; but the ancient buildings have fallen into neglect. In short, the city is full of public and sacred structures; but the most beautiful is the Gymnasium, which has porticoes more than a stadium in length. And in the middle are both the court of justice and the groves. Here, too, is the Paneium, a "height," as it were, which was made by the hand of man; it has the shape of a fir-cone, resembles a rocky hill, and is ascended by a spiral road; and from the summit one can see the whole of the city lying below it on all sides. The broad street that runs lengthwise extends from Necropolis past the Gymnasium to the Canobic Gate; and then one comes to the Hippodrome, as it is called, and to the other (streets?) that lie parallel, extending as far as the Canobic canal. Having passed through the Hippodrome, one comes to Nicopolis, which has a settlement on the sea no smaller than a city. It is thirty stadia distant from Alexandria. Augustus Caesar honoured this place because it was here that he conquered in battle those who came out against him with Antony; and when he had taken the city at the first onset, he forced Antony to put himself to death and Cleopatra to come into his power alive; but a little later she too put herself to death secretly, while in prison, by the bite of an asp or (for two accounts are given) by applying a poisonous ointment; and the result was that the empire of the sons of Lagus, which had endured for many years, was dissolved.
For Ptolemy the son of Lagus succeeded Alexander; and he in turn was succeeded by Philadelphius, and he by Euergetes, and then he by Philopator the son of Agathocleia, and then he by Epiphanes, and then he by Philometor, a son always succeeding a father; but Philometor was succeeded by a brother, the second Euergetes, who is also called Physcon, and he by the Ptolemy nicknamed Lathurus, and he by the Auletes of our own time, who was the father of Cleopatra. Now all at kings after the third Ptolemy, being corrupted by luxurious living, have administered the affairs of government badly, but worst of all the fourth, seventh, and the last, Auletes, who, apart from his general licentiousness, practised the accompaniment of choruses with the flute, and upon this he prided himself so much that he would not hesitate to celebrate contests in the royal palace, and at these contests would come forward to vie with the opposing contestants. He, however, was banished by the Alexandrians; and since he had three daughters, of whom one, the eldest, was legitimate, they proclaimed her queen; but his two sons, who were infants, were completely excluded from service at the time. When she had been established on the throne, they sent after a husband for her from Syria, a certain Cybiosactes, who had pretended that he belonged to the family of the Syrian kings. Now the queen had this man strangled to death within a few days, being unable to bear his coarseness and vulgarity; but in his place came a man who likewise had pretended that he was a son of Mithridates Eupator — I mean Archelaüs, who was son of the Archelaüs who carried on war against Sulla and afterwards was honoured by the Romans, and was grandfather of the man who was last to reign as king over the Cappadocians in our time, and was priest of Comana in Pontus. At that time he had been tarrying with Gabinius, in the hope of joining with him on an expedition against the Parthians, but without the knowledge of Gabinius he was brought by certain agents to the queen and proclaimed king. In the meantime Pompeius Magnus, having received Auletes, who had arrived at Rome, recommended him to the Senate and effected, not only his restoration, but also the death of most of the ambassadors, one hundred in number, who had undertaken the embassy against him, and among these was Dion the academic philosopher, who had been made chief ambassador. Accordingly, on being restored by Gabinius, Ptolemy slew both Archelaüs and his own daughter. But before he had added much time to his reign, he died of disease, leaving behind two sons and also two daughters, the eldest daughter being Cleopatra. Now the Alexandrians proclaimed as sovereigns both the elder of the boys and Cleopatra; but the associates of the boy caused an uprising and banished Cleopatra, and she set sail with her sister to Syria. In the meantime Pompeius Magnus had come in flight from Palaepharsalus to Pelusium and Mt. Casius. Now Pompey was treacherously slain by the king's party, but when Caesar arrived he put the lad to death, and, having summoned Cleopatra from exile, established her as queen of Aegypt; and he appointed her remaining brother to reign as king with her, although he was exceedingly young. After the death of Caesar and the battle of Philippi, Antony crossed over to Asia and held Cleopatra in such extraordinary honour that he chose her as wife and had children by her; and he undertook the battle at Actium with her and fled with her; and after this Augustus Caesar pursued them, destroyed both, and put an end to Aegypt's being ruled with drunken violence.
Egypt is now a Province; and it not only pays considerable tribute, but also is governed by prudent men — the praefects who are sent there from time to time. Now he who is sent has the rank of the king; and subordinate to him is the administrator of justice, who has supreme authority over most of the law-suits; and another is the official called Idiologus, who inquires into all properties that are without owners and that ought to fall to Caesar; and these are attended by freedmen of Caesar, as also by stewards, who are entrusted with affairs of more or less importance. There are also three legions of soldiers, one of which is stationed in the city and the others in the country; and apart from these there are nine Roman cohorts, three in the city, three on the borders of Aethiopia in Syenê, as a guard for that region, and three in the rest of the country. And there are also three bodies of cavalry, which likewise are assigned to the various critical points. Of the native officials in the city, one is the Interpreter, who is clad in purple, has hereditary prerogatives, and has charge of the interests of the city; and another the Recorder; and another the Chief Judge; and the fourth the Night Commander. Now these officers existed also in the time of the kings, but, since the kings were carrying on a bad government, the prosperity of the cities was also vanishing on account of the prevailing lawlessness. At any rate, Polybius, who had visited the city, is disgusted with the state of things then existing; and he says that three classes inhabited the city: first, the Aegyptian or native stock of people, who were quick-tempered and not inclined to strife; and, secondly, the mercenary class, who were severe and numerous and intractable (for by an ancient custom they would maintain foreign men-at‑arms, who had been trained to rule rather than to be ruled, on account of the worthlessness of the kings); and, third, the tribe of the Alexandrians, who also were not distinctly inclined to civil life, and for the same reasons, but still they were better than those others, for even though they were a mixed people, still they were Greeks by origin and mindful of the customs common to the Greeks. But after this mass of people had also been blotted out, chiefly by Euergetes Physcon, in whose time Polybius went to Alexandria (for, being opposed by factions, Physcon more often sent the masses against the soldiers and thus caused their destruction) — such being the state of affairs in the city, Polybius says, in very truth there remained for one, in the words of the poet, merely "to go to Aegypt, a long and painful journey."
Such, then, if not worse, was the state of affairs under the later kings also; but the Romans have, to the best of their ability, I might say, set most things right, having organised the city as I have said, and having appointed throughout the country officials called Epistrategi and Nomarchs and Ethnarchs, thought worthy to superintend affairs of no great importance. Among the happy advantages of the city, the greatest is the fact that this is the only place in all Aegypt which is by nature well situated with reference to both things — both to commerce by sea, on account of the good harbours, and to commerce by land, because the river easily conveys and brings together everything into a place so situated — the greatest emporium in the inhabited world.
Now one might call these the excellent attributes of the city; and as for the revenues of Aegypt, Cicero tells about them in a certain speech, saying that a tribute of twelve thousand five hundred talents was paid annually to Auletes, the father of Cleopatra. If, then, the man who administered the kingdom in the worst and most careless way obtained so large a revenue, what should one think of the present revenues, which are managed with so much diligence, and when the commerce with the Indians and the Troglodytes has been increased to so great an extent? In earlier times, at least, not so many as twenty vessels would dare to traverse the Arabian Gulf far enough to get a peep outside the straits, but at the present time even large fleets are despatched as far as India and the extremities of Aethiopia, from which the most valuable cargoes are brought to Aegypt, and thence sent forth again to the other regions; so that double duties are collected, on both imports and exports; and on goods that cost heavily the duty is also heavy. And in fact the country has monopolies also; for Alexandria alone is not only the receptacle of goods of this kind, for the most part, but also the source of supply to the outside world. And, further, one can perceive more clearly these natural advantages if one travels round the country, visiting first of all the part of the coast which begins at Catabathmus — for Aegypt extends as far as that place, though the country next thereafter belongs to the Cyrenaeans and to the neighbouring barbarians, the Marmaridae.
Now the run from Catabathmus to Paraetonium, if one sails in a straight course, is nine hundred stadia. It is a city and large harbour of about forty stadia. Some call the city Paraetonium, but others Ammonia. In the interval, one comes to the village of the Aegyptians, to the promontory Aenesisphyra, and to the Tyndareian Rocks, which latter are four small islands with a harbour; then next to Drepanum, a promontory, and to Aenesippeia, an island with a harbour, and to Apis, a village, from which the distance to Paraetonium is one hundred stadia, and to the temple of Ammon, a five days' journey. The distance from Paraetonium to Alexandria is approximately one thousand three hundred stadia; and in the interval one comes first to a promontory of white earth, Leucê Actê, as it is called, and then to Phoenicus, a harbour, and to Pnigeus, a village, and then of Pedonia, an island with a harbour, and then to Antiphrae, which is at only a little distance from the sea. The whole of this country is without good wine, since the wine-jars receive more sea-water than wine; and this they call "Libyan" wine, which, as also beer, is used by most of the tribe of Alexandrians; but Antiphrae is ridiculed most. Then one comes to the harbour Derrhis, so called because of the black rock near by, which resembles a "derrhis"; and the neighbouring place is also called Zephyrium. Then to another harbour, Leucaspis and several others; and then to Cynos-Sema; and then to Taposeiris, not on the sea, which holds a great public festival. (There is also another Taposeiris on the other side of the city and quite far from it.) And near it there is a rocky place on the sea where likewise crowds of people in the prime of life assemble during every season of the year. And then one comes to Plinthinê and to the village of Nicias, and to Cherronesus, a stronghold, where we are now near Alexandria and Necropolis, a distance of seventy stadia. Lake Mareia, which extends even as far as this, has a breadth of more than one hundred and fifty stadia and a length of less than three hundred. It contains eight islands; and all the shores round it are well inhabited; and the vintages in this region are so good that the Mareotic wine is racked off with a view to ageing it.
The byblus was in the Aegyptian marshes and lakes, as also the Aegyptian cyamus, from which comes the ciborium; you have stalks approximately equal in height, about ten feet. But whereas the byblus is a bare stock with a tuft on top, the cyamus produces leaves and flowers in many parts, and also a fruit like our cyamus, differing only in size and taste. Accordingly, the bean-fields afford a pleasing sight, and also enjoyment to those who wish to hold feasts therein. They hold feasts in cabin-boats, in which they enter the thick of the cyami and the shade of the leaves; for the leaves are so very large that they are used both from drinking-cups and for bowls, for these even have a kind of concavity suited to this purpose; and in fact Alexandria is full of these in the work-shops, where they are used as vessels and the farms have also this as one source of their revenues — I mean the revenue from the leaves. Such, then, is the cyamus. As for the byblus, it does not grow in large quantities here (for it is not cultivated), but it grows in large quantities in the lower parts of the Delta, one kind p61being inferior, and the other superior, that is, the Hieratica. And here, too, certain of those who wished to enhance the revenues adopted the shrewd practice of the Judaeans, which the latter had invented in the case of the palm tree (particularly the caryotic palm) and the balsam tree; for they do not allow the byblus to grow in many places, and because of the scarcity they set a higher price on it and thus increase the revenues, though they injure the common use of the plant.
On the right of the Canobic Gate, as one goes out, one comes to the canal which is connected with the lake and leads to Canobus; and it is by this canal that one sails, not only to Schedia, that is, to the great river, but also to Canobus, though first to Eleusis. Eleusis is a settlement near both Alexandria and Necropolis, is situated on the Canobic canal itself, and has lodging-places and commanding views for those who wish to engage in revelry, both men and women, and is a beginning, as it were, of the "Canobic" life and the shamelessness there current. On proceeding a slight distance from Eleusis, and on the right, one comes to the canal which leads up the Schedia. Schedia is four schoeni distant from Alexandria; it is a settlement of the city, and contains the station of the cabin-boats on which the praefects sail to Upper Aegypt. And at Schedia is also the station for paying duty on the goods brought down from above it and brought up from below it; and for this purpose, also, a schedia has been laid across the river, from which the place has its name. After the canal which leads to Schedia, one's next voyage, to Canobus, is parallel to that part of the coast-line which extends from Pharos to the Canobic mouth; for a narrow ribbon-like strip of land extends between the sea and the canal, and on this, after Nicopolis, lies the Little Taposeiris, as also the Zephyrium, a promontory which contains a shrine of Aphroditê Arsinoê. In ancient times, it is said, there was also a city called Thonis here, which was named after the king who received Menelaüs and Helen with hospitality. At any rate, the poet speaks of Helen's drugs as follows: "goodly drugs which Polydamna, the wife of Thon, had given her."
Canobus is a city situated at a distance of one hundred and twenty stadia from Alexandria, if one goes on foot, and was named after Canobus, the pilot of Menelaüs, who died there. It contains the temple of Sarapis, which is honoured with great reverence and effects such cures that even the most reputable men believe in it and sleep in it — themselves on their own behalf or others for them. Some writers go on to record the cures, and others the virtues of the oracles there. But to balance all this is the crowd of revellers who go down from Alexandria by the canal to the public festivals; for every day and every night is crowded with people on the boats who play the flute and dance without restraint and with extreme licentiousness, both men and women, and also with the people of Canobus itself, who have resorts situated close to the canal and adapted to relaxation and merry-making of this kind.
After Canobus one comes to the Heracleium, when contains a temple of Heracles; and then to the Canobic mouth and the beginning of the Delta. The parts on the right of the Canobic canal are the Menelaïte Nome, so called from the brother of the first Ptolemy — not, by heaven, from the hero, as some writers say, among whom is also Artemidorus. After the Canobic mouth one comes to the Bolbitine mouth, and then to the Sebennytic, and to the Phatnitic, which is third in size as compared with the first two, which form the boundaries of the Delta; for not far from the vertex of the Delta the Phatnitic splits, sending a branch into the interior of the Delta. Lying close to the Phatnitic mouth is the Mendesian; and then one comes to the Tanitic, and, last of all, to the Pelusiac. There are also others in among these, pseudo-mouths as it were, which are rather insignificant. Their mouths indeed afford entrance to boats, but are adapted, not to large boats, but to tenders only, because the mouths are shallow and marshy. It is chiefly, however, the Canobic mouth that they used as an emporium, since the harbours at Alexandria were kept closed, as I have said before. After the Bolbitine mouth one comes to a low and sandy promontory which projects rather far into the sea; it is called Agnu-Ceras. And then to the Watch-tower of Perseus and the Wall of the Milesians; for in the time of Psammitichus (who lived in the time of Cyaxares the Mede) the Milesians, with thirty ships, put in at the Bolbitine mouth, and then, disembarking, fortified with a wall the above-mentioned settlement; but in time they sailed up into the Saïtic Nome, defeated the city Inaros in a naval fight, and founded Naucratis, not far above Schedia. After the Wall of the Milesians, as one proceeds towards the Sebennytic mouth, one comes to two lakes, one of which, Buticê, has its name from the city Butus, and also to the Sebennytic city, and to Saïs, the metropolis of the lower country, in which Athena is worshipped; and in her temple lies the tomb of Psammitichus. In the neighbourhood of Butus is also an Hermupolis, which is situated on an island; and in Butus there is an oracle of Leto.
In the interior above the Sebennytic and Phatnitic mouths lies Xoïs, both an island and a city, in the Sebennytic Nome. Here, also, are an Hermupolis and a Lycupolis, and Mendes, at which place they worship Pan and, among animals, a he-goat; and, as Pindar says, the he‑goats have intercourse with women there: "Mendes, along the crag of the sea, farthermost horn of the Nile, where the goat-mounting he-goats have intercourse with women." Near Mendes lie also a Diospolis and the lakes in its neighbourhood and Leontopolis; and then, at a greater distance, the city Busiris in the Busirite Nome, and Cynospolis. According to Eratosthenes, the expulsion of foreigners is a custom common to all barbarians, and yet the Aegyptians are condemned for this fault because of the myths which have been circulated about Busiris in connection with the Busirite Nome, since the later writers wish falsely to malign the inhospitality of this place, although, by heavens, no king or tyrant named Busiris ever existed; and, he says, the poet's words are also constantly cited — "to go to Aegypt, long and painful journey" — the want of harbours contributing very much to this opinion, as also the fact that even the harbour which Aegypt did have, the one at Pharos, gave no access, but was guarded by shepherds who were pirates and who attacked those who tried to bring ships to anchor there; and the Carthaginians likewise, he adds, used to drown in the sea any foreigners who sailed past their country to Sardo or to the Pillars, and it is for this reason that most of the stories told about the west are disbelieved; and also the Persians, he says, would treacherously guide the ambassadors over roundabout roads and through difficult regions.
Bordering on this Nome is the Athribite Nome and the city Athribis, and also the Prosopite Nome, in which is a City of Aphroditê. Above the Mendesian and Tanitic mouths lie a large lake and the Mendesian and Leontopolite Nomes and a City of Aphroditê and the Pharbetite Nome; and then one comes to the tanitic mouth, which some call Saïtic, and to the Tanite Nome, and to Tanis, a large city therein.
Between the Tanitic and Pelusiac mouths lie lakes, and large and continuous marshes which contain many villages. Pelusium itself also has marshes lying all round it, which by some are called Barathra, and muddy ponds; its settlement lies at a distance of more than twenty stadia from the sea, the wall has a circuit of twenty stadia, and it has its name for the pelos and the muddy ponds. Here, too, Aegypt is difficult to enter, I mean from the eastern regions about Phoenicia and Judaea, and from the Arabia of the Nabataeans, which is next to Aegypt; these are the regions which the road to Aegypt traverses. The country between the Nile and the Arabian Gulf is Arabia, and at its extremity is situated Pelusium; but the whole of it is desert, and impassable for an army. The isthmus between Pelusium and the recess of the gulf at Heroönpolis is one thousand stadia, but, according to Poseidonius, less than one thousand five hundred; and in addition to its being waterless and sandy, it contains a multitude of reptiles, the sand-burrowers.
From Schedia, as one sails towards Memphis, there are, on the right, a very large number of villages, extending as far as Lake Mareia, among which is the Village of Chabrias, as it is called; and, on the river, one comes to an Hermupolis, and then to Gynaeconpolis and the Gynaecopolite Nome, and, next in order, to Momemphis and the Momemphite Nome; but in the interval there are several canals which empty into Lake Mareotis. The Momemphitae honour Aphroditê; and a sacred cow is kept there, as is Apis in Memphis and Mneuïs in Heliupolis. Now these animals are regarded as gods, but those in the other places (for in many either a bull or cow is kept) — those others, I say, are not regarded as gods, though they are held sacred.
Above Momemphis are two nitre-beds, which contain very large quantities of nitre, and the Nitriote Nome. Here Sarapis is held in honour; and they are the only people in Aegypt who sacrifice a sheep. Near by, and in this Nome, is a city Menelaüs; and on the left, in the Delta, lies Naucratis, which is on the river, whereas Saïs lies at a distance of two schoeni from the river. A little above Saïs is the asylum of Osiris, in which the body of Osiris is said to lie; but many lay claim to this, and particularly the inhabitants of the Philae which is situated above Syenê and Elephantinê; for they tell the mythical story, namely, that Isis placed coffins of Osiris beneath the earth in several places (but only one of them, and that unknown to all, contained the body of Osiris), and that she did this because she wished to hide the body from Typhon, fearing that he might find it and cast it out of its tomb.
Now this is the full description of the country from Alexandria to the vertex of the Delta; and, according to Artemidorus, the voyage up the river is twenty-eight schoeni, 804 that is, eight hundred and forty stadia, reckoning the schoenus as thirty stadia. When I made the voyage, however, they used different measures at different times when they gave the distances, so that even forty stadia, or still more, was the accepted measure of the schoenus, according to the place. That the measure of the schoenus among the Aegyptians in unstable is made clear by Artemidorus himself in his next statement; for from Memphis to Thebaïs each schoenus, he says, is one hundred and twenty stadia, and from Thebaïs to Syenê sixty, and, as one sails up from Pelusium to the same vertex of the Delta, the distance, he says, is twenty-five schoeni, that is, seven hundred and fifty stadia, using the same measure. The first canal, as one proceeds from Pelusium, he says, is the one which fills the Marsh-lakes, as they are called, which are two in number and lie on the left of the great river above Pelusium in Arabia; and he also speaks of other lakes and canals in the same regions outside the Delta. There is also the Sethroïte Nome by the second lake, although he counts this Nome too as one of the ten in the Delta; and two other canals meet in the same lakes.
There is another canal which empties into the Red Sea and the Arabian Gulf near the city Arsinoê, a city which some call Cleopatris. It flows also through the Bitter Lakes, as they are called, which were indeed bitter in earlier times, but when the above-mentioned canal was cut they underwent a change because of the mixing with the river, and now are well supplied with fish and full also of aquatic birds. The canal was first cut by Sesostris before the Trojan War — though some say by the son of Psammitichus, who only began the work and then died — and later by Dareius the First, who succeeded to the next work done upon it. But he, too, having been persuaded by a false notion, abandoned the work when it was already near completion; for he was persuaded that the Red Sea was higher than Aegypt, and that if the intervening isthmus were cut all the way through, Aegypt would be inundated by the sea. The Ptolemaïc hands, however, cut through it and made the strait a closed passage, so when they wished they could sail out without hindrance into the outer sea and sail in again. But I have already discussed the levels of the bodies of water in my first commentaries.
Near Arsinoê one comes also to Heroönpolis and Cleopatris, in the recess of the Arabian Gulf towards Aegypt, and to harbours and settlements, and near there, to several canals and lakes. Here, too, is the Phagroriopolite Nome and the city Phagrioropolis. The canal which empties into the Red Sea begins at Phacussa, a village, to which the Village of Philae is contiguous; the canal has a breadth of one hundred cubits and a depth sufficient for very large merchant-vessels; and these places are near the vertex of the Delta.
Here are both the city Bubastus and the Bubastite Nome; and above it is the Heliopolite Nome. In this Nome is Heliupolis, which is situated upon a noteworthy mound; it contains the temple of Helios, and the ox Mneuïs, which is kept in a kind of sanctuary and is regarded among the inhabitants as god, as is Apis in Memphis. In front of the mound are lakes, which receive the overflow from the neighbouring canal. The city is now entirely deserted; it contains the ancient temple constructed in the Aegyptian manner, which affords many evidences of the madness and sacrilege of Cambyses, who partly by fire and partly by iron sought to outrage the temples, mutilating them and burning them on every side, just as he did with the obelisks. Two of these, which were not completely spoiled, were brought to Rome, but others are either still there or at Thebes, the present Diospolis — some still standing, thoroughly eaten by the fire, and others lying on the ground.
The plan of the construction of the temples is as follows: at the entrance into the sacred precinct there is a floor paved with stones, with a breadth of about a plethrum, or less, and a length either three or four times as great, or in some cases more; and this is called the dromus, as Callimachus states: "This is the dromus, sacred to Anubis." Throughout its whole length are stone sphinxes placed in order on each of its two sides, at a distance from one another of twenty cubits or a little more, so that one row of the sphinxes is on the right and one row on the left. And after the sphinxes one comes to a large propylum, and then, as one proceeds, another, then another; but there is no prescribed number either of propyla or of sphinxes, and they are different in different temples, as are also the lengths and the breadths of the dromi. After the propylaea one comes to the naos, which has a large and noteworthy pronaos, and to a sanctuary of commensurate size, though it has no statue, or rather no statue of human form, but only of some irrational animal. On either side of the pronaos project the wings, as they are called. These are two walls equal in height to the naos, which are at first distant from one another a little more than the breadth of the foundation of the naos, and then, as one proceeds onward, follow converging lines as far as fifty or sixty cubits; and these walls have figure of large images cut in low relief, like the Tyrrhenian images and the very old works of art among the Greeks. There is also a kind of hall with numerous columns (as at Memphis, for example), which is constructed in the barbaric manner; for, except for the fact that the columns are large and numerous and form many rows, the hall has nothing pleasing or picturesque, but is rather a display of vain toil.
In Heliupolis I also saw large houses in which the priests lived; for it is said that this place in particular was in ancient times a settlement of priests who studied philosophy and astronomy; but both this organisation and its pursuits have now disappeared. At Heliupolis, in fact, no one was pointed out to me as presiding over such pursuits, but only those who performed the sacrifices and explained to strangers what pertained to the sacred rites. When Aelius Gallus the praefect sailed up into Aegypt, he was accompanied by a certain man from Alexandria, Chaeremon by name, who pretended to some knowledge of this kind, but was generally ridiculed as a boaster and ignoramus. However, at Heliupolis the houses of the priests and schools of Plato and Eudoxus were pointed out to us; for Eudoxus went up to that place with Plato, and they both passed thirteen years with the priests, as is stated by some writers; for since these priests excelled in their knowledge of the heavenly bodies, albeit secretive and slow to impart it, Plato and Eudoxus prevailed of them in time and by courting their favour to let them learn some of the principles of their doctrines; but the barbarians concealed most things. However, these men did teach them the fractions of the day and night which, running over and above the three hundred and sixty five days, fill out the time of the true year. But at that time the true year was unknown among the Greeks, as also many other things, until the later astrologers learned from the men who had translated into Greek the records of the priests; and even to this day they learn their teachings, and likewise those of the Chaldaeans.
From Heliupolis, then, one comes to the Nile above the Delta. Of this, the parts on right, as one sails up, are called Libya, as also the parts round Alexandria and Lake Mareotis, whereas those on the left are called Arabia. Now Heliupolis is in Arabia, but the city Cercesura, which lies near the observatories of Eudoxus, is in Libya; a kind of watch-tower is to be seen in front of Heliupolis, as also in front of Cnidus, with reference to which Eudoxus would note down his observations of certain movements of the heavenly bodies. Here the Nome is the Letopolite. And, having sailed farther up the river, one comes to Babylon, a stronghold, where some Babylonians had withdrawn in revolt and then successfully negotiated for permission from the kings to build a settlement; but now it is an encampment of one of the three legions that guard Aegypt. There is a ridge extending from the encampment even as far as the Nile, on which the water is conducted up from the river by wheels and screws; and one hundred and fifty prisoners are employed in the work; and from here one can clearly see the pyramids1on the far side of the river at Memphis, and they are near to it.
Memphis itself, the royal residence of the Aegyptians, is also near Babylon; for the distance to it from the Delta is only three schoeni. It contains temples, one of which is that of Apis, who is the same as Osiris; it is here that the bull Apis is kept in a kind of sanctuary, being regarded, as I have said, as god; his forehead and certain other small parts of his body are marked with white, but the other parts are black; and it is by these marks that they always choose the bull suitable for the succession, when the one that holds the honour has died. In front of the sanctuary is situated a court, in which there is another sanctuary belonging to the bull's mother. Into this court they set Apis loose at a certain hour, particularly that he may be shown to foreigners; for although people can see him through the window in the sanctuary, they wish to see him outside also; but when he has finished a short bout of skipping in the court they take him back again to his familiar stall.
There is here, then, not only the temple of Apis, which lies near the Hephaesteium, but also the Hephaesteium itself, which is a costly structure both in the size of its naos and in all other respects. In front, in the dromus, stands also a colossus made of one stone; and it is the custom to hold bull-fights in this dromus, and certain men breed these bulls for the purpose, like horse-breeders; for the bulls are set loose and join in combat, and the one that is regarded as victor gets a prize. And at Memphis there is also a temple of Aphroditê, who is considered to be a Greek goddess, though some say that it is a temple of Selenê.
There is also a Sarapium at Memphis, in a place so very sandy that dunes of sand are heaped up by the winds; and by these some of the sphinxes which I saw were buried even to the head and others were only half-visible; from which one might guess the danger if a sand-storm should fall upon a man travelling on foot towards the temple. The city is both large and populous, ranks second after Alexandria, and consists of mixed races of people, like those who have settled together at Alexandria. There are lakes situated in front of the city and the palaces, which latter, though now in ruins and deserted, are situated on a height and extend down to the ground of the city below; and adjoining the city are a grove and a lake.
On proceeding forty stadia from the city, one comes to a kind of mountain-brow; on it are numerous pyramids, the tombs of kings, of which three are noteworthy; and two of these are even numbered among the Seven Wonders of the World, for they are a stadium in height, are quadrangular in shape, and their height is a little greater than the length of each of the sides; and one of them is only a little larger than the other. High up, approximately midway between the sides, it has a movable stone, and when this is raised up there is a sloping passage to the vault. Now these pyramids are near one another and on the same level; but farther on, at a greater height of the hill, is the third, which is much smaller than the two, though constructed at much greater expense; for from the foundations almost to the middle it is made of black stone, the stone from which mortars are made, being brought from a great distance, for it is brought from the mountains of Aethiopia; and because of its being hard and difficult to work into shape it rendered the undertaking very expensive. It is called "Tomb of the Courtesan," having been built by her lovers — the courtesan whom Sappho the Melic poetess calls Doricha, the beloved of Sappho's brother Charaxus, who was engaged in transporting Lesbian wine to Naucratis for sale, but others give her the name Rhodopis. They tell the fabulous story that, when she was bathing, an eagle snatched one of her sandals from her maid and carried it to Memphis; and while the king was administering justice in the open air, the eagle, when it arrived above his head, flung the sandal into his lap; and the king, stirred both by the beautiful shape of the sandal and by the strangeness of the occurrence, sent men in all directions into the country in quest of the woman who wore the sandal; and when she was found in the city of Naucratis, she was brought up to Memphis, became the wife of the king, and when she died was honoured with the above-mentioned tomb.
One of the marvellous things I saw at the pyramids should not be omitted: there are heaps of stone-chips lying in front of the pyramids; and among these are found chips that are like lentils in both form and size; and under some of the heaps lie winnowings, as it were, as of half-peeled grains. They say that what was left of the food of the workmen has petrified; and this is not improbable. Indeed, in my home-country, in a plain, there is a long hill which is full of lentil-shaped pebbles of porous stone; and the pebbles both of the seas and of the rivers present about the same puzzling question; but while these latter find an explanation in the motion caused by the current of water, the speculation in that other case is more puzzling. It has been stated elsewhere that in the neighbourhood of the quarry of the stones from which the pyramids are built, which is in sight of the pyramids, on the far side of the river in Arabia, there is a very rocky mountain which is called "Trojan," and that there are caves at the foot of it, and a village near both these and the river which is called Troy, being an ancient settlement of the captive Trojans who accompanied Menelaüs but stayed there.
After Memphis one comes to a city Acanthus, likewise situated in Libya, and to the temple of Osiris and the grove of the Thebaïc acantha, from which the gum is obtained. Then to the Aphroditopolite Nome, and to the city of like name in Arabia, where is kept a white cow which is sacred. Then to the Heracleote Nome, on a large island, where, on the right, is the canal which leads into Libya to the Arsenoïte Nome, so that the canal has two mouths, a part of the island intervening between the two. This Nome is the most noteworthy of all in respect to its appearance, its fertility, and its material development, for it alone is planted with olive trees that are large and full-grown and bear fine fruit, and it would also produce good olive oil if the olives were carefully gathered. But since they neglect this matter, although they make much oil, it has a bad smell (the rest of Aegypt has no olive trees, except the gardens near Alexandria, which are sufficient for supplying olives, but furnish no oil). And it produces wine in no small quantity, as well as grain, pulse, and the other seed-plants in very great varieties. It also contains the wonderful lake called the Lake of Moeris, which is an open sea in size and like a sea in colour; and its shores, also, resemble those of a sea, so that one may make the same supposition about this region as about that of Ammon (in fact, Ammon and the Heracleote Nome are not very far distant from one another or from Paraetonium), that, just as from the numerous evidences one may surmise that that temple was in earlier times situated on the sea, so likewise these districts were in earlier times on the sea. And Lower Aegypt and the parts extending as far as Lake Sirbonis were sea — this sea being confluent, perhaps, with the Red Sea in the neighbourhood of Heroönpolis and the Aelanites Gulf.
I have already discussed this subject at greater length in the First Commentary of my Geography, but now also I must comment briefly on the work of Nature and at the same time upon that of Providence, since they contribute to one result. The work of Nature is this, that all things converge to one thing, the centre of the whole, and form a sphere around this; and the densest and most central thing is the earth, and the thing that is less so and next in order after it is the water; and that each of the two is a sphere, the former solid, the latter hollow, having the earth inside of it. And the work of Providence is this, that being likewise a broiderer, as it were, and artificer of countless works, it has willed, among its first works, to beget living beings, both gods and men, on whose account everything else has been formed. Now to the gods Providence assigned the heavens and to men the earth, which are the extremities of the two parts of the universe; and the two extremities of the sphere are the central part and the outermost part. But since water surrounds the earth, and man is not an aquatic animal, but a land animal that needs air and requires much light, Providence has made numerous elevations and hollows on the earth, so that the whole, or the most, of the water is received in the hollows, hiding the earth beneath it, and the earth projects in the elevations, hiding the water beneath itself, except so much of the latter as is useful for the human race, as also for the animals and plants round it. But since all things are continually in motion and undergo great changes (for it is not possible otherwise for things of this kind and number and size in the universe to be regulated), we must take it for granted, first, that the earth is not always so constant that it is always of this or that size, adding nothing to itself nor subtracting anything, and, secondly, that the water is not, and, thirdly, that neither of the two keeps the same fixed place, especially since the reciprocal change of one into the other is most natural and very near at hand; and also that much of the earth changes into water, and many of the waters become dry land in the same manner as on the earth, where also so many variations take place; for one kind of earth crumbles easily and others are solid, or rocky, or contain ore, and so with the rest. And the case is the same with the properties of liquids: one water is salty, another sweet and potable, and others contain drugs, salutary or deadly, or are hot or cold. Why, then, is it marvellous if some parts of the earth which are at present inhabited were covered with sea in earlier times, and if what are now seas were inhabited in earlier times? Just as fountains of earlier times have given out and others have sprung forth, and rivers and lakes, so also mountains and plains have changed one into another. But I have discussed this subject at length before, and now let this suffice.
Be this as it may, the Lake of Moeris, on account of its size and its depth, is sufficient to bear the flood-tides at the risings of the Nile and not overflow into the inhabited and planted parts, and then, in the retirement of the river, to return the excess water to the river by the same canal at each of its two mouths and, both itself and the canal, to keep back an amount remaining that will be useful for irrigation. While these conditions are the work of nature, yet locks have been placed at both mouths of the canal, by which the engineers regulate both the inflow and the outflow of the water. In addition to the things mentioned, this Nome has the Labyrinth. Near the first entrance to the canal, and on proceeding thence about thirty or forty stadia, one comes to a flat, trapezium-shaped place, which has a village, and also a great palace composed of many palaces — as many in number as there were Nomes in earlier times; for this is the number of courts, surrounded by colonnades, continuous with one another, all in a single row and along one wall, the structure being as it were a long wall with the courts in front of it; and the roads leading into them are exactly opposite the wall. In front of the entrances are crypts, as it were, which are long and numerous and have winding passages communicating with one another, so that no stranger can find his way either into any court or out of it without a guide. But the marvellous thing is that the roof of each of the chambers consists of a single stone, and that the breadths of the crypts are likewise roofed with single slabs of surpassing size, with no intermixture anywhere of timber or of any other material. And, on ascending to the roof, which is at no great height, one can see a plain of stone, consisting of stones of that great size; and thence, descending out of the courts again, one can see that they lie in a row and are each supported by twenty-seven monolithic pillars; and their walls, also, are composed of stones that are no smaller in size. At the end of this building, which occupies more than a stadium, is the tomb, a quadrangular pyramid, which has sides about four plethra in width and a height equal thereto. Imandes is the name of the man buried there. It is said that this number of courts was built because it was the custom for all the Nomes to assemble there in accordance with their rank, together with their own priests and priestesses, for the sake of sacrifice and of offering gifts to the gods and of administering justice in matters of the greatest importance. And each of the Nomes was conducted to the court appointed to it.
Sailing along shore for a distance of one hundred stadia, one comes to the city Arsinoê, which in earlier times was called Crocodeilonpolis; for the people in this Nome hold in very great honour the crocodile, and there is a sacred one there which is kept and fed by itself in a lake, and is tame to the priests. It is called Suchus; and it is fed on grain and pieces of meat and on wine, which are always being fed to it by the foreigners who go to see it. At any rate, our host, one of the officials, who was introducing us into the mysteries there, went with us to the lake, carrying from the dinner a kind of cooky and some roasted meat and a pitcher of wine mixed with honey. We found the animal lying on the edge of the lake; and when the priests went up to it, some of them opened its mouth and another put in the cake, and again the meat, and then poured down the honey mixture. The animal then leaped into the lake and rushed across to the far side; but when another foreigner arrived, likewise carrying an offering of first-fruits, the priests took it, went around the lake in a run, took hold of the animal, and in the same manner fed it what had been brought.
After the Arsinoïte and Heracleotic Nomes, one comes to a City of Heracles, where the people hold in honour the ichneumon,a the very opposite of the practice of the Arsinoïtae; for whereas the latter hold the crocodile in honour — and on this account both their canal and the Lake of Moeris are full of crocodiles, for the people revere them and abstain from harming them — the former hold in honour the ichneumons, which are the deadliest enemies of the crocodile, as also of the asp; for they destroy, not only the eggs of the asps, but also the asps themselves, having armed themselves with a breastplate of mud; for they first roll themselves in mud, make it dry in the sun, and then, seizing the asps by either the head or the tail, drag them down into the river and kill them; and as for the crocodiles, the ichneumons lie in wait for them, and when the crocodiles are basking in the sun with their mouths open the ichneumons throw themselves into their open jaws, eat through their entrails and bellies, and emerge from their dead bodies.
One comes next to the Cynopolite Nome, and to Cynonpolis, where Anubis is held in honour where a form of worship and sacred feeding has been organised for all dogs. On the far side of the river lie the city Oxyrynchusº and a nome bearing the same name. They hold in honour the oxyrynchus and have a temple sacred to Oxyrynchus, though the other Aegyptians in common also hold in honour the oxyrynchus. In fact, certain animals are worshipped by all Aegyptians in common, as, for example, three land animals, bull and dog and cat, and two birds, hawk and ibis, and two aquatics, scale-fish and oxyrynchus, but there are other animals which are honoured by separate groups independently of the rest, as, for example, a sheep by the Saïtae and also by the Thebans; a latus, a fish of the Nile, by the Latopolitae; a lycus by the Lycopolitae; a cynocephalus by the Hermopolitae; a cebus by the Babylonians who live near Memphis (the cebus has a face like a satyr, is between a dog and a bear in other respects, and is bred in Aethiopia); an eagle by the Thebans; a lion by the Leontopolitae; a female and male goat by the Mendesians; a shrew-mouse by the Athribitae, and other animals by other peoples; but the reasons which they give for such worship are not in agreement.
One comes next to the Hermopolitic garrison, a kind of toll-station for goods brought down from the Thebaïs; here begins the reckoning of schoeni at sixty stadia, extending as far as Syenê and Elephantinê; and then to the Thebaïc garrison and the canal that leads to Tanis; and then to Lycopolis and to Aphroditopolis and to Panopolis, an old settlement of linen-workers and stone-workers.
Then one comes to the city of Ptolemaïs, which is the largest of the cities in the Thebaïs, is no smaller than Memphis, and has also a form of government modelled on that of the Greeks. Above this city lies Abydus, where is the Memnonium, a royal building, which is a remarkable structure built of solid stone, and of the same workmanship as that which I ascribed to the Labyrinth, though not multiplex; and also a fountain which lies at a great depth, so that one descends to it down vaulted galleries made of monoliths of surpassing size and workmanship. There is a canal leading to the place from the great river; and in the neighbourhood of the canal is a grove of Aegyptian acantha, sacred to Apollo. Abydus appears once to have been a great city, second only to Thebes, but it is now only a small settlement. But if, as they say, Memnon is called Ismandes by the Aegyptians, the Labyrinth might also be a Memnonium and a work of the same man who built both the Memnonia in Abydus and those in Thebes; for it is said that there are also some Memnonia in Thebes. Opposite Abydus is the first of the above-mentioned three oases in Libya; it is a seven days' journey distant from Abydus through a desert; and it is a settlement which abounds in water and in wine, and is sufficiently supplied with other things. The second oasis is that in the neighbourhood of the Lake of Moeris; and the third is that in the neighbourhood of the oracle in Ammon; and these, also, are noteworthy settlements.
Now that I have already said much about Ammon, I wish to add only this: Among the ancients both divination in general and oracles were held in greater honour, but now great neglect of them prevails, since the Romans are satisfied with the oracles of Sibylla, and with the Tyrrhenian prophecies obtained by means of the entrails of animals, flight of birds, and omens from the sky; and on this account, also, the oracle at Ammon has been almost abandoned, though it was held in honour in earlier times; and this fact is most clearly shown by those who have recorded the deeds of Alexander, since, although they add numerous forms of mere flattery, yet they do indicate some things that are worthy of belief. At any rate, Callisthenes says that Alexander conceived a very great ambition to go inland to the oracle, since he had heard that Perseus, as also Heracles, had done so in earlier times; and that he started from Paraetonium, although the south winds had set in, and forced his way; and that when he lost his way because of the thick dust, he was saved by rainfalls and by the guidance of two crows. But this last assertion is flattery and so are the next: that the priest permitted the king alone to pass into the temple in his usual dress, but the rest changed their clothes; that all heard the oracles from outside except Alexander, but he in; that the oracular responses were not, as at Delphi and among the Branchidae, given in words, but mostly by nods and tokens, as in Homer, "Cronion spoke and nodded assent with his dark brows" — the prophet having assumed the rôle of Zeus; that, however, the fellow expressly told the king that he, Alexander, was the son of Zeus. And to this statement Callisthenes dramatically adds that, although the oracle of Apollo among the Branchidae had ceased to speak from the time the temple had been robbed by the Branchidae, who sided with the Persians in the time of Xerxes, and although the spring also had ceased to flow, yet at Alexander's arrival the spring began to flow again and that many oracles were carried by the Milesian ambassadors to Memphis concerning Alexander's descent from Zeus, his future victory in the neighbourhood of Arbela, the death of Dareius, and the revolutionary attempts in Lacedaemon. And he says that the Erythraean Athenaïs also gave out an utterance concerning Alexander's high descent; for, he adds, this woman was like the ancient Erythraean Sibylla. Such, then, are the accounts of the historians.
At Abydus they hold in honour Osiris; and in the temple of Osiris neither singer nor flute-player nor harp-player is permitted to begin the rites in honour of the god, as is the custom in the case of the other gods. After Abydus one comes to the Little Diospolis, and to the city tentyra, where the people, as compared with the other Aegyptians, hold in particular dishonour the crocodile and deem it the most hateful of all animals. For although the others know the malice of the animal and how destructive it is to the human race, still they revere it and abstain from harming it, whereas the Tentyritae track them and destroy them in every way. Some say that, just as there is a kind of natural antipathy between the Psylli near Cyrenaea and reptiles, so there is between the Tentyritae and crocodiles, so that they suffer no injury from them, but even dive in the river without fear and cross over, though no others are bold enough to do so. When the crocodiles were brought to Rome for exhibition, they were attended by the Tentyritae; and when a reservoir and a kind of stage above one of the sides had been made for them, so that they could go out of the water and have a basking-place in the sun, these men at one time, stepping into the water all together, would drag them in a net to the basking-place, so that they could be seen by the spectators, and at another would pull them down again into the reservoir. They worship Aphrodite; and back of her shrine is a temple of Isis. And then one comes to the Typhonia, as they are called, and to the canal that leads to Coptus, a city common to the Aegyptians and the Arabians.
Thence one crosses an isthmus, which extends to the Red Sea, near a city Berenicê. The city has no harbour, but on account of the favourable lay of the isthmus has convenient landing-places. It is said that Philadelphus was the first person, by means of an army, to cut this road, which is without water, and to build stations, as though for the travels of merchants on camels, and that he did this because the Red Sea was hard to navigate, particularly for those who set sail from its innermost recess. So the utility of his plan was shown by experience to be great, and now all the Indian merchandise, as well as the Arabian and such of the Aethiopian as is brought down by the Arabian Gulf, is carried to Coptus, which is the emporium for such cargoes. Not far from Berenicê lies Myus Hormus, a city containing the naval station for sailors; and not far distant from Coptus lies Apollonospolis, as it is called, so that on either side there are two cities which form the boundaries of the isthmus. But now it is Coptus and Myus Hormus that have high repute; and people frequent these places. Now in earlier times the camel-merchants travelled only by night, looking to the stars for guidance, and, like the mariners, also carried water with them when they travelled; but now they have constructed watering-places, having dug down to a great depth, and, although rain-water is scarce, still they have made cisterns for it. The journey takes six or seven days. On this isthmus are also the mines of smaragdus, where the Arabians dig deep tunnels, I might call them, and of other precious stones.
After Apollonospolis one comes to Thebes (now called Diospolis), "Thebes of the hundred gates, whence sally forth two hundred men through each with horses and chariots." So Homer; and he speaks also of its wealth, "even all the revenue of Aegyptian Thebes, where lies in treasure-houses the greatest wealth." And others also say things of this kind, making this city the metropolis of Aegypt. Even now traces of its magnitude are pointed out, extending as they do for a distance of eighty stadia in length; and there are several temples, but most of these, too, were mutilated by Cambyses; and now it is only a collection of villages, a part of it being in Arabia, where was the city, and a part on the far side of the river, where was the Memnonium. Here are two colossi, which are near one another and are each made of a single stone; one of them is preserved, but the upper parts of the other, from the seat up, fell when an earthquake took place, so it is said. It is believed that once each day a noise, as of a slight blow, emanates from the part of the latter that remains on the throne and its base; and I too, when I was present at the places with Aelius Gallus and his crowd of associates, both friends and soldiers, heard the noise at about the first hour, but whether it came from the base or from the colossus, or whether the noise was made on purpose by one of the men who were standing all round and near to the base, I am unable positively to assert; for on account of the uncertainty of the cause I am induced to believe anything rather than that the sound issued from stones thus fixed. Above the Memnonium, in caves, are tombs of kings, which are stone-hewn, are about forty in number, are marvellously constructed, and are a spectacle worth seeing. And among the tombs, on some obelisks, are inscriptions which show the wealth of the kings at that time, and also their dominion, as having extended as far as the Scythians and the Bactrians and the Indians and the present Ionia, and the amount of tributes they received, and the size of army they had, about one million men. The priests there are said to have been, for the most part, astronomers and philosophers; and it is due to these priests also that people reckon the days, not by the moon, but by the sun, adding to the twelve months of thirty days each five days each year; and, for the filling out of the whole year, since a fraction of the day runs over and above, they form a period of time from enough whole days, or whole years, to make the fractions that run over and above, when added together, amount to a day. They attribute to Hermes all wisdom of this particular kind; but to Zeus, whom they hold highest in honour, they dedicate a maiden of greatest beauty and most illustrious family (such maidens are called "pallades" by the Greeks); and she prostitutes herself, and cohabits with whatever men she wishes until the natural cleansing of her body takes place; and after her cleansing she is given in marriage to a man; but before she is married, after the time of her prostitution, a rite of mourning is celebrated for her.
After Thebes, one comes to a city of Hermonthis, where both Apollo and Zeus are worshipped; and there, too, a bull is kept. And then to a City of Crocodiles, which holds in honour that animal. And then to a City of Aphroditê, and, after this, to Latopolis, which holds in honour Athena and the latus; and then to a City of Eileithuia and a temple; and on the far side of the river lies a City of Hawks, which holds the hawk in honour; and then to Apollonospolis, which also carries on war against the crocodiles.c
As for Syenê and Elephantinê, the former is a city on the borders of Aethiopia and Aegypt, and the latter is an island in the Nile, being situated in front of Syenê at a distance of half a stadium, and a city therein which has a temple of Cnuphis and, like Memphis, a nilometer. The nilometer is a well on the bank of the Nile constructed with close-fitting stones, in which are marks showing the greatest, least, and mean rises of the Nile; for the water in the well rises and lowersº with the river. Accordingly, there are marks on the wall of the well, measures of the complete rises and of the others. So when watchers inspect these, they give out word to the rest of the people, so that they may know; for long beforehand they know from such signs and the days what the future rise will be, and reveal it beforehand. This is useful, not only to the farmers with regard to the water-distribution, embankments, canals, and other things of this kind, but also to the praefects, with regard to the revenues; for the greater rises indicate that the revenues also will be greater. But in Syenê is also the well that marks the summer tropic, for the reason that this region lies under the tropic circle and causes the gnomons to cast no shadow at midday; for if from our region, I mean that of Greece, we proceed towards the south, it is at Syenê that the sun first gets over our heads and causes the gnomons to cast no shadow at midday; and necessarily, when the sun gets over our heads, it also casts its rays into wells as far as the water, even if they are very deep; for we ourselves stand perpendicular to the earth and wells are dug perpendicular to the surface. And here are stationed three cohorts as a guard.
A little above Elephantinê is the little cataract, on which the boatmen exhibit a kind of spectacle for the praefects; for the cataract is at the middle of the river, and is a brow of rock, as it were, which is flat on top, so that it receives the river, but ends in a precipice, down which the water dashes; whereas on either side towards the land there is a stream which generally can even be navigated up-stream. Accordingly, the boatmen, having first sailed up-stream here, drift down to the cataract, are thrust along with the boat over the precipice, and escape unharmed, boat and all. A little above the cataract lies Philae, a common settlement of Aethiopians and Aegyptians, which is built like Elephantinê and is equal to it in size; and it has Aegyptian temples. Here, also, a bird is held in honour, which they call a hawk, though to me it appeared to be in no respect like the hawks in our country and in Aegypt, but was both greater in size and far different in the varied colouring of its plumage. They said that it was an Aethiopian bird, and that another was brought from Aethiopian bird, and that another was brought from Aethiopia whenever the one at hand died, or before. And in fact the bird shown to us at the time mentioned was nearly dead because disease.
We went to Philae from Syenê by wagon through an exceedingly level plain — a distance all told of about one hundred stadia. Along the whole road on either side one could see in many places a stone like our Hermae; it was huge, round, quite smooth, nearly sphere-shaped, and consisted of the black, hard stone from which mortars are made — a smaller stone lying on a larger, and on that stone again another. Sometimes, however, it was only a single stone; and the largest was in diameter no less than twelve feet, though one and all were larger than half this measure. We crossed to the island on a pacton. The pacton is a small boat constructed of withes, so that it resembles woven-work; and though standing in water or seated on small boards, we crossed easily, being afraid without cause, for there is no danger unless the ferry-boat is over-laden.
Throughout the whole of Aegypt the palm tree is not of a good species; and in the region of the Delta and Alexandria it produces fruit that is not good to eat; but the palm tree in the Thebaïs is better than any of the rest. Now it is a thing worth marvelling at, that a country which is in the same latitude as Judaea and borders on it, I mean the country round the delta and Alexandria, differs so much, since Judaea, in addition to another palm, produces also the caryotic, which is somewhat better than the Babylonian. There are two kinds in the Thebaïs as well as in Judaea, both the caryotic and the other; and the Thebaïc date is harder, but more agreeable to the taste. There is also an island which is particularly productive of the best date, yielding a very large revenue for the praefects; for it used to be a royal possession, and no private individual shared in it, but it now belongs to the praefects.
Both Herodotus and others talks much nonsense, adding to their account marvellous tales, to give it, as it were, a kind of tune or rhythm or relish; as, for example, the assertion that the sources of the Nile are in the neighbourhood of the islands near Syenê and Elephantinê (of which there are several), and that at this place its channel has a bottomless depth. The Nile has very many islands scattered along its course, of which some are wholly covered at its risings and others only partly; but the exceedingly high parts of the latter are irrigated by means of screws.
Now Aegypt was generally inclined to peace from the outset, because of the self-sufficiency of the country and of the difficulty of invasion by outsiders, being protected on the north by a harbourless coast and by the Aegyptian Sea, and on the east and west by the desert mountains of Libya and Arabia, as I have said; and the remaining parts, those towards the south, are inhabited by Troglodytes, Blemmyes, Nubae, and Megabari, those Aethiopians who live about Syenê. These are nomads, and not numerous, or warlike either, though they were thought to be so by the ancients, because often, like brigands, they would attack defenceless persons. As for those Aethiopians who extend towards the south and Meroê, they are not numerous either, nor do they collect in one mass, inasmuch as they inhabitant a long, narrow, and winding stretch of river-land, such as I have described before; neither are they well equipped either for warfare or for any other kind of life. And now, too, the whole of the country is similarly disposed to peace. And the following is a sign of the fact: the country is sufficiently guarded by the Romans with only three cohorts, and even these are not complete; and when the Aethiopians dared to make an attack upon them, they imperilled their own country. The remaining Roman forces in Aegypt are hardly as large as these, nor have the Romans used them collectively even once; for neither are the Aegyptians themselves warriors, although they are very numerous, nor are the surrounding tribes. Cornelius Gallus, the first man appointed praefect of the country by Caesar, attacked Heroönpolis, which had revolted, and took it with only a few soldiers, and in only a short time broke up a sedition which had taken place in the Thebaïs on account of the tributes. And at a later time Petronius, when all that countless multitude of Alexandrians rushed to attack him with a throwing of stones, held out against them with merely his own body-guard, and after killing some of them put a stop to the rest. And I have already stated how Aelius Gallus, when he invaded Arabia with a part of the guard stationed in Aegypt, discovered that the people were unwarlike; indeed, if Syllaeus had not betrayed him, he would even have subdued the whole of Arabia Felix.
5But the Aethiopians, emboldened by the fact that a part of the Roman force in Aegypt had been drawn away with aelius Gallus when he was carrying on war against the Arabians, attacked the Thebaïs and the garrison of the three cohorts at Syenê, and by an unexpected onset took Syenê and Elephantinê and Philae, and enslaved the inhabitants, and also pulled down the statues of Caesar. But Petronius, setting out with less than ten thousand infantry and eight hundred cavalry against thirty thousand men, first forced them to flee back to Pselchis, an Aethiopian city, and sent ambassadors to demand what they had taken, as also to ask the reasons why they had begun war; and when they said that they had been wronged by the Nomarchs, he replied that these were not rulers of the country, but Caesar; and when they had requested three days for deliberation, but did nothing they should have done, he made an attack and forced them to come forth to battle; and he quickly turned them to flight, since they were badly marshalled and badly armed; for they had large oblong shields, and those too made of raw ox-hide, and as weapons some had only axes, others pikes, and others swords. Now some were driven together into the city, others fled into the desert, and others found refuge on a neighbouring island, having waded into the channel, for on account of the current the crocodiles were not numerous there. Among these fugitive were the generals of Queen Candacê, who was ruler of the Aethiopians in my time — a masculine sort of woman, and blind in one eye. These, one and all, he captured alive, having sailed after them in both rafts and ships, and he sent them forthwith down to Alexandria; and he also attacked Pselchis and captured it; and if the multitude of those who fell in the battle be added to the number of the captives, those who escaped must have been altogether few in number. From Pselchis he went to Premnis, a fortified city, after passing through the sand-dunes, where the army of Cambyses was overwhelmed when a wind-storm struck them; and having made an attack, he took the fortress at the first onset. After this he set out for Napata. This was the royal residence of Candacê; and her son was there, and she herself was residing at a place near by. But though she sent ambassadors to treat for friendship and offered to give back the captives and the statues brought from Syenê, Petronius attacked and captured Nabata too, from which her son had fled, and rased it to the ground; and having enslaved its inhabitants, he turned back again with the booty, having decided that the regions farther on would be hard to traverse. But he fortified Premnis better, threw in a garrison and food for four hundred men for two years, and set out for Alexandria. As for the captives, he sold some of them as booty, and sent one thousand to Caesar, who had recently returned from Cantabria; and the others died of diseases. Meantime Candacê marched against the garrison with many thousands of men, but Petronius set out to its assistance and arrived at the fortress first; and when he had made the place thoroughly secure by sundry devices, ambassadors came, but he bade them go to Caesar; and when they asserted that they did not know who Caesar was or where they should have to go to find him, he gave them escorts; and they went to Samos, since Caesar was there and intended to proceed to Syria from there, after despatching Tiberius to Armenia. And when the ambassadors had obtained everything they pled for, he even remitted the tributes which he had imposed. |
|
|
|
|
17 - 2 Ethiopia and Egypt, conclusion 
1 In the earlier parts of my work I have already said many things about the Aethiopian tribes, so that the description of their country may be said to be included with that of Aegypt. In general, the extremities of the inhabited world, which lies alongside the part of the earth that is not temperate and habitable, because of heat or cold, must needs be defective and inferior to the temperate part; and this is clear from the modes of life of the inhabitants and from their lack of human necessities. They indeed live a hard life, go almost naked, and are nomads; and their domestic animals — sheep, goats, and cattle — are small; and their dogs are small though rough and pugnacious. And perhaps it is from the natural smallness of the people that men have conceived of Pygmies and fabricated them; for no man worthy of belief professes to have seen them.
2 The Aethiopians live on millet and barley, from which they also make a drink; but instead of olive-oil they have butter and tallow. Neither do they have fruit trees, except a few date-palms in the royal gardens. But some use grass as food, as also tender twigs, lotus, and reed-roots; and they use meats, blood, milk, and cheese. They reverence as gods their kings, who generally stay shut up at home. Their greatest royal seat is Meroê, a city bearing the same name as the island. The island is said to be like an oblong shield in shape. Its size has perhaps been exaggerated: about three thousand stadia in length and one thousand in breadth. The island has both numerous mountains and large thickets; it is inhabited partly by nomads, partly by hunters, and partly by farmers; and it has mines of copper, iron, gold, and different kinds of precious stones. It is bounded on the Libyan side by large sand-dunes, and on the Arabian side by continuous precipices, and above, on the south, by the confluence of the three rivers — the Astaboras, and the Astapus and the Astasobas and on the north by the next course of the Nile, which extends to Aegypt along the aforesaid windings of the river. In the cities the dwellings are made of split pieces of palm-wood woven together, or of brick. And they have quarried salt, as do the Arabians. And, among the plants, the palm, the persea, the ebony, and the ceratia are found in abundance. And they have, not only elephants to hunt, but also lions and leopards. They also have serpents, the elephant-fighters, as also many other wild animals; for the animals flee for refuge from the hotter and more arid regions to those that are watery and marshy.
3 Above Meroê lies Psebo, a large lake containing an island that is rather well settled. And since the Libyans hold the land on the western side of the Nile and the Aethiopians that on the opposite side, it comes to pass that they take turns in dominating the islands and the river-land, one of the two being driven out and yielding place to those who have proved stronger. The Aethiopians also use bows, which are four cubits long, are made of wood, and are hardened by fire; and they arm the women also, most of whom have a copper ring through the lip; and they wear sheep-skins, since they have no wool, their sheep having hair like that of goats; and some go naked, or wear round their loins small sheep-skins or girdles of well-woven hair. They regard as god the immortal being, whom they consider the cause of all things, and also the mortal being, who is without name and not to be identified. But in general they regard their benefactors and royal personages as gods: of these the kings as the common saviours and guardians of all, and special individuals as in a special sense gods to those who have received benefactions from them. Among those who live near the torrid zone, some are considered atheists, since it is said that they hate even the sun, and revile it when they behold it rising, on the ground that it burns them and carries on war with them, and flee for refuge from it into the marshes. The inhabitants of Meroê worship Heracles, Pan, and Isis, in addition to some other, barbaric, god. As for the dead, some cast them into the river, others enclose them in glass and keep them at home; but some bury them around the temples in coffins made of clay; and they exact fulfilment of oaths sworn over the dead, and consider them the most sacred of all things. They appoint as kings those who excel in beauty, or in superiority in cattle-breeding, or in courage, or in wealth. In Meroê the highest rank was in ancient times held by the priests, who indeed would give orders even to the king, sometimes ordering him through a messenger to die, and would appoint another in his stead; but later one of the kings broke up the custom by marching with armed men against the temple where the golden shrine is and slaughtering all the priests. The following is also an Aethiopian custom: whenever any one of the kings is maimed in any part of his body in any way whatever, his closest associates suffer the same thing, and they even die with him; and hence these men guard the king most carefully. This will suffice on the subject of the Aethiopians.
4 But to my account of things Aegyptian I must add an enumeration of the things that are peculiar to that country, as, for example, the Aegyptian cyamus, as it is called, from which ciborium is derived, and the byblus, for the byblus is found only here and among the Indians; and the persea is found only here and among the Aethiopians — a large tree with large, sweet fruit; and the sycaminus that products the fruit called sycomorus, for it resembles a sycum, though it is not prized for its taste; and the corsium is also found here — a relish somewhat like pepper, but slightly larger. As for fish in the Nile, they are indeed many in number and different in kind, with a special indigenous character, but the best known are the oxyrynchus and the lepidotus, latus, alabes, coracinus, choerus, and phagrorius, also called phagrus, and, besides, the silurus, citharus, thrissa, cestreus, lychnus, physa, and bos; and, among shell-creatures, there are large conchliae which emit a sound like a croak. As for indigenous animals, Aegypt has also the ichneumon and the Aegyptian asp, which latter has a peculiarity as compared with the asp of other countries; but it is of two kinds, one only a span long, which causes a quicker death, and the other nearly a fathom, as is stated by Nicander, who wrote the Theriaca. Among the birds are found the ibis and the Aegyptian hierax, which latter is tame, like the cat, as compared with those elsewhere; and also nycticorax is here of a peculiar species, for in our country it has the size of an eagle and a harsh caw, but in Aegypt the size of a jackdaw and a different caw. The ibis, however, is the tamest bird; it is like a stork in shape and size, but it is of two kinds in colour, one kind like the stork and the other black all over. Every cross-road in Alexandria is full of them; and though they are useful in one way, they are not useful in another. The bird is useful because it singles out every animal and the refuse in the meat-shops and bakeries, but not useful because it eats everything, is unclean, but can only with difficulty be kept away from things that are clean and do not admit of any defilement.
5 The statement of Herodotus is also true, that it is an Aegyptian custom to knead mud with their hands, but suet for bread-making with their feet. Further, kakeis is a peculiar kind of bread with checks the bowels; and kiki is a kind of fruit sown in the fields, from which oil is pressed, which is used not only in lamps by almost all the people in the country, but also for anointing the body by the poorer classes and those who do the heavier labour, both men and women; and further, the koïkina are Aegyptian textures made of some plant, and are like those made of rush or of the date-palm. And beer is prepared in a peculiar way among the Aegyptians; it is a drink common the many peoples, but the ways of preparing it in the different countries are different. One of the customs most zealously observed among the Aegyptians is this, that they rear every child that is born, and circumcise the males, and excise the females, as is also customary among the Jews, who also Aegyptians in origin, as I have already stated in my account of them. Aristobulus says that on account of the crocodiles no fish swim up into the Nile from the sea except the cestreus and the thrissa and the dolphin — the dolphin, because it is stronger than the crocodile, and the cestreus, because it is escorted by the choeri along the bank, in accordance with some natural affinity; and that the crocodiles keep away from the choeri, since the latter are round and have spines on the head which offer danger to the beasts. Now cestreus, he says, runs up the river in spring when it is carrying its spawn, but for the purpose of spawning comes down in schools before the setting of the Pleiad, at which time they are captured, being caught in schools by the fenced enclosures. And some such cause might be conjectured also in the case of the thrissa. So much for Aegypt. |
|
|
|
|
17 - 3 Libya (North Africa) 
1 Next let me describe Libya, which is the only part left for the completion of my Geography as a whole. Now I have said much about this country before, but I must now comment also on other matters in so far as they may be timely, adding what has not been said before. Now the writers who have divided the inhabited world according to continents have divided it unequally, for the threefold division indicates a division into three equal parts; but Libya lacks so much of being a third part of the inhabited world that even if it were combined with Europe it would seem not to be equal to Asia. Perhaps it is even smaller than Europe; and in power it is much inferior, for the greater part of the interior and of its ocean-coast is desert, and it is dotted with settlements that are small, scattered, and mostly nomadic; and in addition to its deserts, its being a nursery of wild beasts drives out people even from land that could be inhabited; and it overlaps a considerable part of the torrid zone. However, the whole of the coast opposite to us, I mean that between the Nile and the Pillars, and particularly the part which was subject to the Carthaginians, is settled and prosperous; but here too some parts here and there are destitute of water, as, for example, in the regions about the Syrtes, the Marmaridae, and Catabathmus.
Libya has the shape of a right-angled triangle, conceived of as drawn on a plane surface, having as base the coast opposite us, from Aegypt and the Nile to Maurusia and the Pillars, and as the side perpendicular to this that which is formed by the Nile as far as Aethiopia and by me produced to the ocean, and as the side subtending the right angle the whole of the coast between the Aethiopians and the Maurusians. Now as for the part at the very vertex of the above-mentioned foregoing, which begins approximately with the torrid zone, I speak only from conjecture, because it is inaccessible, although in a previous part of my work I have said thus much, that, as one goes southward from Alexandria to Meroê, the royal seat of the Aethiopians, the distance is about ten thousand stadia, and from there in a straight line to the boundaries between the torrid zone and the inhabited world three thousand more. At any rate, the same should be put down as the maximum breadth of Libya, I mean thirteen or fourteen thousand stadia, and a little less than double that sum as the length. This, then, is my account of Libya as a whole, but I must describe it in detail, beginning with its western, or more famous, parts.
2 Here dwell a people whom the Greeks call Maurusians, and the Romans and the natives Mauri — a large and prosperous Libyan tribe, who live on the side of the strait opposite Iberia. Here also is the strait which is at the Pillars of Heracles, concerning which I have often spoken. On proceeding outside the strait at the Pillars, with Libya on the left, one comes to a mountain which the Greeks call Atlas and the barbarians Dyris. From this mountain projects a farthermost spur, as it were, towards the west of Maurusia — the Coteis, as it is called; and near by is a small town above the sea which the barbarians call Tinx, though Artemidorus has given it the name Lynx and Eratosthenes Lixus. It is situated across the strait opposite Gadeira at a distance of eight hundred stadia, which is about the distance of each of the two places from the strait at the Pillars. To the south of Lixus and the Coteis lies a gulf called the Emporicus Gulf, which contains settlements of Phoenician merchants. Now the whole of the coast continuous with this gulf is indented by gulfs, but one should exclude from consideration the gulfs and the projections of land, in accordance with the triangular figure which I have suggested, and conceive rather of the continent as increasing in extent in the direction of the south and east. The mountain, which extends through the middle of Maurusia from the Coteis to the Syrtes, is inhabited, both itself and other mountains that run parallel with Maurusia, at first by the Maurusians but deep in the interior by the largest of the Libyan tribes, who are called Gaetulians.
3 The historians, beginning with The Circumnavigation of Ophelas, have added numerous other fabrications in regard to the outside coast of Libya; and these I have already mentioned somewhere before, but I am again speaking of them, asking pardon for introducing marvellous stories, if perchance I shall be forced to digress into a thing of that sort, since I am unwilling wholly to pass them over in silence and in a way to cripple my history. Now they say that the Emporicus Gulf has a cave which at the full tides admits the sea inside it for a distance of even seven stadia, and that in front of this gulf there is a low, level place containing an altar of Heracles, which, they say, is never inundated by the tide — and it is this that I regard as one of their fabrications. And nearly as bad as this is the statement that on the gulfs which come next after the Emporicus Gulf there were ancient settlements of Tyrians, now deserted — no fewer than three hundred cities, which were destroyed by the Pharusians and the Nigritae; and these people, they say, are at a distance of a thirty day's journey from Lynx.
4 However, it is agreed by all that Maurusia is a fertile country, except a small desert part, and is supplied with both lakes and rivers. It is surpassing in the size and in the number of its trees, and is also productive of everything; at any rate, this is the country which supplies the Romans with the tables that are made of one single piece of wood, very large and most variegated. The rivers are said to contain crocodiles, as also other kinds of animals similar to those in the Nile. Some think that even the sources of the Nile are near the extremities of Maurusia. And they say that in a certain river are found leeches seven cubits long, with gills pierced through with holes, through which they breathe. They also say of this country that it produces a vine so thick that it can hardly be encircled by the arms of two men, and that it yields clusters of about one cubit; and that every herb grows high, and every vegetable, as, for example, arum and dracontium; and the stalks of the staphylini and the hippomarathi and the scolymi grow twelve cubits high and four palms thick. And for serpents, also, and elephants and gazelles and bubali and similar animals, as also for lions and leopards, the country is a nurse in every way. It also produces ferrets equal in size to cats, and like them, except that their noses project further; and also a very great number of apes, concerning which Poseidonius states that, when he was sailing from Gadeira to Italy, he was carried close to the Libyan coast and saw on a low-lying shore a forest full of these animals, some in the trees and others on the ground, and some having young and suckling them; that he fell to laughing, however, when he saw some with heavy udders, some with bald heads, and others ruptured or displaying other disabilities of that kind.
5 Above Maurusia, on the outside sea, lies the country of the western Aethiopians, as they are called, a country for the most part poorly settled. Here too, according to Iphicrates, are found camelopards, elephants, and the rhizeis, as they are called, which are like bulls in their form, but like elephants in their manner of living and their size and their courage in fighting. And he speaks of serpents so large that even grass grows upon the backs; and says that the lions attack the young of the elephants, but, after they have drawn blood, flee when the mothers approach, and that the mothers, when they see their young stained with the blood, kill them, and that the lions return to the victims and eat them. And he says that Bogus, the king of the Maurusians, when he went up against the western Aethiopians, sent down to his wife as gifts reeds like those of India, of which each joint held eight choenices, and also asparagus of similar size.
6 As one sails into the inner sea from Lynx, one comes to the city Zelis and to Tinx; and then to the Monuments of the Seven Brothers and to the mountain that lies above them, Abilê by name, which abounds in wild animals and large trees. The length of the strait at the Pillars is said to be one hundred and twenty stadia, and the minimum breadth, measured at Elephas, sixty. On sailing into the sea, one comes next to several cities and rivers — to the Molochath River, which forms the boundary between the lands of the Maurusians and the Masaesylians. Near the river lies a large promontory, and also Metagonium, a waterless and barren place; and I might almost say that the mountain which begins at the Coteis extends as far as this; and its length from the Coteis to the boundaries of the Masaesylians is five thousand stadia. Metagonium is about opposite New Carthage, on the other side of the sea, but Timosthenes wrongly says that it is opposite Massalia. The passage across from New Carthage to Metagonium is three thousand stadia, and the coasting-voyage to Massalia is over six thousand.
7 Although the most of the country inhabited by the Maurusians is so fertile, yet even to this time most of the people persist in living a nomadic life. But nevertheless they beautify their appearance by braiding their hair, growing beards, wearing golden ornaments, and also by cleaning their teeth and paring their nails. And only rarely can you see them touch one another in walking, for fear that the adornment of their hair may not remain intact. Their horsemen any mostly with a javelin, using bridles made of rush, and riding bareback; but they also carry daggers. The foot-soldiers hold before them as shields the skins of elephants, and clothe themselves with the skins of lions, leopards, and bears, and sleep in them. I might almost say that these people, and the Masaesylians, who live next after them, and the Libyans in general, dress alike and are similar in all other respects, using horses that are small but swift, and so ready to obey that they are governed with a small rod. The horses wear collars made of wood or of hair, to which the rein is fastened, though some follow even without being led, like dogs. These people have small shields made of raw-hide, small spears with broad heads, wear ungirded tunics with wide borders, and, as I have said, use skins as mantles and shields. The Pharusians and Nigretes who live above these people near the western Aethiopians also use bows, like the Aethiopians; and they also use scythe-bearing chariots. The Pharusians mingle only rarely even with the Maurusians when passing through the desert since they carry skins of water fastened beneath the bellies of their horses. Sometimes, however, they come even to Cirta, passing through certain marshy regions and over lakes. Some of them are said to live like Troglodytes, digging homes in the earth. And it is said that here too the summer rains are prevalent, but that in winter there is a drought, and that some of the barbarians in this part of the world use also the skins of snakes and fish both as wraps and as bed-covers. And the Maurusians are said by some to be the Indians who came thither with Heracles. Now a little before my time the kings of the house of Bogus and of Bocchus, who were friends of the Romans, possessed the country, but when these died Juba succeeded to the throne, Augustus Caesar having given him this in addition to his father's empire. He was the son of the Juba who with Scipio waged war against the deified Caesar. Now Juba died lately, but his son Ptolemy, whose mother was the daughter of Antony and Cleopatra, has succeeded to the throne.
Artemidorus disputes the view of Eratosthenes because the latter calls a certain city in the neighbourhood of western extremities of Maurusia "Lixus" instead of Lynx; and because he calls "Phoenician" a very great number of rased cities of which no trace is to be seen; and because, after calling the air among the western Aethiopians "salty," he says that the air is thick and misty in the hours both of early morning and of evening. For, argues Artemidorus, how can these things be in a region that is arid and torrid? But he himself gives a much worse account of the same region, for he tells a story of certain migrants, Lotophagi, who roam the waterless country and feed on lotus, a kind of plant and root, from eating which they have no need of drink; and that they extend as far as the region above Cyenê; but that those in that region also drink milk and eat meat, although they are in the same latitude. And Gabinius also, the Roman historian, does not abstain from telling marvellous stories of Maurusia; for example, he tells a story of a tomb of Antaeus near Lynx, and a skeleton sixty feet in length, which, he says, Sertorius exposed to view, and then covered again with earth. And he tells fabulous stories about the elephants; for example, he says that whereas the other animals flee from fire, the elephants carry on war with it and defend themselves against it, because it destroys the timber, and that they engage in battle with human beings, sending out scouts before them, and that when they see them fleeing, they flee too, and that when they receive wounds, as suppliants they hold out branches of a tree or an herb or dust.
9 After the land of the Maurusians, one comes to that of the Masaesylians, which takes its beginning at the Molochath River and ends at the promontory which is called Tretum, the boundary between the lands of the Masaesylians and the Masylians. The distance from Metagonium to Tretum is six thousand stadia, though some say less. The coast has several cities and rivers and is a goodly territory, but it is sufficient to mention only those of renown. At a distance of one thousand stadia from the above-mentioned boundaries is Siga, which was the royal residence of Sophax, though it is now in ruins. After Sophax the country was possessed by Masanasses, and then by Micipsas, and then by his successors, and in my time by Juba, the father of the Juba who recently died. Zama, his royal residence, has also been laid in ruins by the Romans. After Siga, and at a distance of six hundred stadia, one comes to Theon Limen; and then to the other, insignificant, places. Now the parts deep in the interior are indeed mountainous and desert (sometimes they are interspersed with habitations and these parts are held by the Gaetulians), even as far as the Syrtes, but the parts there near the sea consist of fertile plains, many cities, rivers, and lakes.
I do not know whether Poseidonius tells the truth when he says that Libya is intersected by rivers "only few and small"; for merely the rivers mentioned by Artemidorus, those between Lynx and Carthage, are by him called "both many and large." This statement can be made more truthfully in regard to the interior of the country; and he himself states the cause of this, saying that "no rain falls in the northern parts," as is also said to be the case in Aethiopia, and therefore pestilences often ensue because of droughts, and the lakes are filled with mud, and the locust is prevalent. And he further says that "the eastern regions are moist, for the sun passes quickly when it is rising, whereas the western regions are arid, for there it turns back." For regions are called moist and arid, partly in proportion to abundance or scarcity of waters, and partly in proportion to that of the sun's rays; but Poseidonius means to speak only of the effects of the sun's rays; and these effects are by all writers defined by latitude, north or south; and indeed both the eastern and western regions, when spoken of which reference to the habitations of man, vary according to each several habitation and the change in their horizons, so that it is also impossible to make a general assertion in regard to places whose number passes all comprehension that the eastern are moist and the western arid; but since such statements are made with reference to the inhabited world as a whole and to such extremities of it as India and Iberia, perhaps he could make such a statement. What plausibility, however, can there be in his explanation of the cause? For in the revolution of the sun, which is continuous and unintermitting, what "turning back" could there be? And further, the speed of the sun's transit is everywhere equal. Besides, it is contrary to the evidence to call the extremities of Iberia or Maurusia, I mean the extremities on the west, the most arid places in the world, for they not only have a temperate atmosphere but also are well supplied with numerous waters. But if the "turning back" of the sun is interpreted in this way, that there it is last above the inhabited world, wherein does this contribute to aridity? For there, as well as in the other places of the inhabited world that are in the same latitude, the sun leaves an equal interval of night, and comes back again and warms the earth.
Somewhere here there are also copper mines and a spring of asphalt; and writers speak also of a multitude of scorpions, both winged and wingless, which in size are heptaspondylic, and likewise of tarantulas which are exceptional both in size and in number; and lizards which are said to be two cubits long. Now on the mountain-side are said to be found the "Lychnite" and Carthaginian stones, as they are called, and, in the plains, oyster-shells and mussel-shells in great quantities, like those mentioned by me in my description of Ammon. And there is also a tree called melilotus, from which they prepare a wine. And some of the people have land that produces two crops of grain, reaping two harvests, one in spring and the other in summer; and the stalk is five cubits in height, has the thickness of the little finger, and yields a crop ‑fold. In the spring they do not even sow seed, but harrow the ground lightly with bundles of paliuri, and are satisfied with the seed-grain that has fallen out of the ear at the time of the harvest; for this products a perfect summer crop. On account of the number of wild animals they work with legging on and also clothe the rest of their bodies with skins. And when they lie down to sleep, they smear the feet of their beds with garlic and tie a bunch of paliuri around them, on account of the scorpions.a
On this coast was a city named Iol, which Juba, the father of Ptolemy, rebuilt, changing its name to Caesareia; it has a harbour, and also, in front of the harbour, a small island. Between Caesareia and Tretum is a large harbour called Salda, which is now a boundary between the territories subject to Juba and the Romans; for the divisions of the country have been made in various ways, inasmuch as its occupants have been several in number and the Romans have dealt with them in different ways at different times, treating some as friends and others as enemies, the result being that different parts were taken away from, or presented to, different peoples, but not in the same way. The country towards Maurusia not only produced more revenue but was also more powerful, whereas that towards Carthage and the Masylians was both more flourishing and better built up, although it had been put in a bad plight, first, on account of the Carthaginian Wars, and then on account of the war against Jugurtha; for he took by siege Adarbal, a friend of the Romans, at Itycê and slew him, and thus filled all Libya with war; and then wars on wars broke out, and, last of all, the war that broke out between the deified Caesar and Scipio, in which even Juba was killed; and with the leaders the cities were wiped out too, I mean Tisiäus, Vaga, and Thala, as also Capsa, the treasure-hold of Jugurtha, and Zama, and Zincha, and those cities near which the deified Caesar defeated Scipio, first winning a victory over him near Ruspinum, and then near Uzita, and then near Thapsus and the lake near by, and the other cities. And near by also are Zella and Acholla, free cities. And Caesar captured at the first onset the island Cercinna, and Thena, a town on the coast. Of all these, some were utterly wiped out and the others left half-destroyed; but Phara was burned by Scipio's cavalry.
Now after Tretum one comes to the land of the Masylians, and to the land of the Carthaginians, which is similar thereto. Cirta, the royal residence of Masanasses and his successors, is in the interior; it is very strongly fortified and has been beautifully built up in every way, particularly by Micipsas, who not only settled a colony of Greeks in it, but also made it so great that it could send forth ten thousand cavalry and twice as many infantry. Cirta, then, is here, and so are the two Hippos, one near Itycê and the other farther away, rather towards Tretum; and both are royal residences. Itycê was second only to Carthage in size and importance, and when Carthage was destroyed, that city served the Romans as a metropolis, and as a base of operations for their activities in Libya. It is situated in the same gulf as Carthage, near one of the two promontories which form the gulf, of which the one near Itycê is called Apollonium and the other Hermaea; and the two cities are in sight of one another. Near Itycê flows the Bagradas River. The distance from Tretum to Carthage is two thousand five hundred stadia. But neither this distance nor that to the Syrtes is generally agreed upon.
Carthage, also, is situated on a kind of peninsula, which comprises a circuit of three hundred and sixty stadia; and this circuit has a wall; and sixty stadia of the length of this circuit are occupied by the neck itself, which extendº from sea to sea; and this, a spacious place, is where the Carthaginians had their elephant-stalls. Near the middle of the city was the acropolis, which they called Byrsa; it was a fairly steep height and inhabited on all sides, and at the top it had a temple of Asclepius, which, at the time of the capture of the city, the wife of Asdrubal burnt along with herself. Below the acropolis lie the harbours, as also Cothon, a circular isle surrounded by a strait, which latter has ship-houses all round on either side.
Carthage was founded by Dido, who brought a host of people from Tyre. The colonisation proved to be so fortunate an enterprise for the Phoenicians, both this at Carthage and that which extended as far as Iberia — I mean the part of Iberia outside the Pillars as well as the rest of it — that even to this day the best part of continental Europe and also the adjacent islands are occupied by Phoenicians; and they also gained possession of all that part of Libya which men can live in without living a nomadic life. From this dominion they not only raised their city to be a rival of Rome, but also waged three great wars against the Romans. Their power might become clearly evident from the last war, in which they were defeated by Scipio Aemilianus and their city was utterly wiped out. For when they began the wage this war they had three hundred cities in Libya and seven hundred thousand people in their city; and when they were being besieged and were forced to resort to surrender, they gave up two hundred thousand full suits of armour and three thousand catapults, on the assumption that they would not be engaged in war again; but when they resolved to renew the war, they suddenly organised the manufacture of arms, and each day produced one hundred and forty finished shields, three hundred swords, five hundred spears, and one thousand missiles for the catapults; and the women-servants furnished their hair for the catapults. Furthermore, although from fifty years back they had possessed only twelve ships, in accordance with the treaty made at the second war, they then, although they had already fled together for refuge into the Byrsa, built one hundred and twenty decked ships in two months; and since the mouth of the Cothon was being guarded, they dug another mouth through and their fleet sallied forth unexpectedly; for old timber had been stored away in readiness, and a large number of skilled workmen, maintained at public expense, had been lying in wait for this occasion. But though Carthage was so resourceful, still it was captured and rased to the ground. As for the country, the Romans proclaimed one part of it a Province, I mean the part which had been subject to the Carthaginians, and appointed as sovereign of the other part Masanasses, as also his descendants, the house of Micipsas; for Masanasses was held in very high respect among the Romans because of his valour and friendship; and indeed it was he who transformed the Nomads into citizens and farmers, and taught them to be soldiers instead of brigands. For a peculiar thing had happened in the case of these people, although they lived in a country blest by nature, except for the fact that it abounded in wild animals, they would forbear to destroy these and thus work the land in security, and would turn against one another, abandoning the land to the wild animals. In this way it came to pass that they kept leading a wandering and migratory life, no less so than peoples who are driven by poverty and by wretched soil or climate to resort to this kind of life; so that the Masaesylians have obtained this as their special designation, for they are called nomades. Such people of necessity must lead a frugal life, being more often root-eaters than meat-eaters, and using milk and cheese for food. Be that as it may, Carthage for a long time remained desolate, about the same length of time as Corinth, but it was restored again at about the same time as Corinth by the deified Caesar, who sent thither as colonists such Romans as preferred to go there and some soldiers; and now it is as prosperous a city as any other in Libya.
Opposite the middle of the mouth of the Carthaginian Gulf is Corsura, an island. Across the arm of the sea, opposite this region, is that part of Sicily wherein lies Lilybaeum, at a distance of about one thousand five hundred stadia; for the distance from Lilybaeum to Carthage is said to be as great as this. Not far distant from Corsura, nor yet from Sicily, are Aegimuros and other islands. The voyage from Carthage across to the nearest point of the opposite mainland is sixty stadia, from which the journey inland to Nepheris is one hundred and twenty stadia — a city fortified by nature and built upon a rock. But on the same gulf as that on which Carthage is situated lies a city Tynis, as also hot springs and stone-quarries; and then one comes to the rugged promontory Hermaea, and to a city on it bearing the same name; and then to Neapolis; and then to a promontory Taphitis, and to a hill on it, which, from the resemblance, is called Aspis; this is the hill that Agathocles, the tyrant of Sicily, colonised at the time when he sailed against the Carthaginians. But these cities were demolished by the Romans at the same time as Carthage. At a distance of four hundred stadia from Taphitis lies an island Cossurus, opposite the Selinus River in Sicily, and a city bearing the same name, which is one hundred and fifty stadia in circuit and is about six hundred stadia distant from Sicily; and there is also an island Melithê and the island Cossurus. Then one comes to a city Adrymes, there was also a naval arsenal; and then to the Taricheiae, as they are called, which are numerous small islands lying close together; and then to a city Thapsus; and after this to Lopadussa, an island in the open sea; and then to a promontory of Ammon Balithon, near which is a place for watching for the tunny-fish; and then to a city Thena, which lies near the beginning of the Little Syrtis. In the interval lie numerous small towns not worth mentioning. Near the beginning of the Syrtis lies a long island, Cercinna, which is rather large and contains a city of the same name; and there is another smaller island, Cercinnitis.
Continuous with these is the Little Syrtis, which is also called the Syrtis of the Lotus-eaters. The circuit of this gulf is one thousand six hundred stadia, and the breadth of the mouth six hundred; and at each of the two promontories which form its mouth are islands close to the mainland — the Cercinna above-mentioned and Meninx, which are about equal in size. Meninx is regarded as the land of the Lotus-eaters mentioned by Homer; and certain tokens of this are pointed out — both an altar of Odysseus and the fruit itself; for the tree which is called the lotus abounds in the island, and its fruit is delightful. There are several towns on Meninx, and one of them bears the same name as the island. On the coast of the Syrtis itself are several small towns. In the recess of the gulf is a very large emporium, which has a river that empties into the gulf; and the effects of the flow and ebb of the tides extend thus far, at which times the neighbouring inhabitants rush forth on the run to catch the fish.
After the Syrtis, one comes to Zuchis, a lake with a circuit of four hundred stadia; it has a narrow entrance, and near it is a city bearing the same name which contains dye-factories and all kinds of fish-salting establishments; and then to another lake, which is much smaller; and after this to a city Abrotonum and to several others; and contiguous to these is Neapolis, which is also called Leptis; and from here the passage across to the Epizephyrian Locrians is three thousand six hundred stadia. Next in order one comes to a river; and afterwards to a kind of cross-wall which the Carthaginians built, wishing to bridge over some gorges which extend up into the interior. There are also some harbourless regions here, although the rest of the coast has harbours. Then one comes to a lofty, wooded promontory, which forms the beginning of the Great Syrtis and is called Cephalae; and the distance to this promontory from Carthage is a little more than five thousand stadia.
Above the coast-line which extends from Carthage to Cephalae and to the land of Masaesylians lies the land of the Libo-Phoenicians, which extends to the mountainous country of the Gaetulians, where Libya begins. The land above the Gaetulians is that of the Garamantes, which lies parallel to the former and is the land whence the Carthaginian stones are brought. The Garamantes are said to be distant from the Aethiopians who live on the ocean a nine or ten days' journey, and from Ammon fifteen. Between the Gaetulians and our seaboard there are not only many plains, but also many mountains, large lakes, and rivers, some of which sink beneath the earth and become invisible. The inhabitants are very simple in their modes of life and in their dress; but the men have many wives and many children, and in other respects are like the nomadic Arabians; and both horses and cattle have longer necks than those of other countries. Horse-breeding is followed with such exceptional interest by the kings that the number of colts every year amounts to one hundred thousand. The sheep are brought up on milk and meats, particularly in the regions near Aethiopia. Such is my account of the interior.
The Great Syrtis has a circuit of about three thousand and nine hundred and thirty stadia, and a diameter, to the inmost recess, of one thousand five hundred stadia, and also a breadth at the mouth of about one thousand five hundred. The difficulty with both this Syrtis and the Little Syrtis is that in many places their deep waters contain shallows, and the result is, at the ebb and the flow of the tides, that sailors sometimes fall into the shallows and stick there, and that the safe escape of a boat is rare. On this account sailors keep at a distance when voyaging along the coast, taking precautions not to be caught off their guard and driven by winds into these gulfs. However, the disposition of man to take risks causes him to try anything in the world, and particularly voyages along coasts. Now as one sails into the Great Syrtis, on the right, after Cephalae is passed, one comes to a lake about three hundred stadia in length and seventy in breadth, which empties into the gulf and contains both small islands and a mooring place in front of its mouth. After the harbour one comes to a place called Aspis, and to the finest harbour in the Syrtis. Continuous with this is the Euphrantas Tower, the boundary between the former country of the Carthaginians and the Cyrenaean country as it was under Ptolemy; and then one comes to another place, called Charax, which the Carthaginians used as an emporium, taking wine thither and in exchange receiving loads of silphium-juice and silphium from merchants who brought them clandestinely from Cyrenê; and then to the Altars of the Philaeni; and after these to Automala, a stronghold which has a garrison and is situated at the inmost recess of the whole gulf. The parallel of latitude through this gulf is a little more to the south than that through Alexandria, one thousand stadia, and than that through Carthage, less than two thousand stadia; but it would coincide with the parallel which passes through the Heroönpolis situated on the recess of the Arabian Gulf and through the interior of the countries of the Masaesylians and the Maurusians. The remainder of the coast from here on to the city Berenicê is one thousand five hundred stadia in length. Lying inland above this stretch of coast, and extending even as far as the Altars of the Philaeni, is the country of the Nasamones, as they are called, a Libyan tribe. In the intervening distance there are only a few harbours; and the watering-places are scarce. There is, however, a promontory called Pseudo-penias, on which Berenicê is situated, near a certain lake, Tritonias, in which the principal things are an isle and on it a temple of Aphroditê. In this region are also the harbour of the Hesperides and the river Lathon which empties into it. Farther inside than Berenicê lies the small promontory called Boreium, which with Cephalae forms the mouth of the Syrtis. Berenicê lies opposite the promontories of the Peloponnesus, opposite Ichthys, as it is called, and also opposite Zacynthos, the distance across being three thousand six hundred stadia. Setting out from this city Marcus Cato travelled round the Syrtis by land in thirty days, leading an army of more than ten thousand men, having separated them into divisions on account of the scarcity of watering-places and he travelled on foot in deep sand and scorching heat. After Berenicê one comes to a city Taucheira, which is also called Arsinoê; and then to a city formerly called Barcê, but now Ptolemaïs; and then to a promontory Phycus, which is low-lying and projects farthest towards the north as compared with the rest of the Libyan coast; it lies opposite Taenarum in Laconia, the distance across being two thousand and eight hundred stadia; and there is also a small town which bears the same name as the promontory. Not far distant from Phycus is the naval station of the Cyrenaeans, Apollonia, about one hundred and seventy stadia from Phycus, one thousand from Berenicê, and eighty from Cyrenê, a large city situated in a trapezium-shaped plain, as it looked to me from the sea.
Cyrenê was founded by colonists from Thera, a Laconian island, which in ancient times was called Callistê, as Callimachus says: "Callistê was its first name, but its later name was Thera, mother of my fatherland, famed for its good horses." The naval station of the Cyrenaeans lies opposite the western promontory of Crete, Criumetopon, the distance across being two thousand stadia. The voyage is made with Leuconotus. Cyrenê is said to have been founded by Battus; and Callimachus asserts that Battus was his ancestor. Cyrenê grew strong because of the fertility of its territory, for it is excellent for the breeding of horses and produces beautiful fruit, and it had many men who were noteworthy and who were able to defend its liberty in a noteworthy manner and to resist strongly the barbarians who lived above them. Now in ancient times the city was independent; and then the Macedonians, who had taken possession of Aegypt, grew in power and attacked the Cyrenaeans, under the leadership of Thibron and his associates, who had slain Harpalus; and having been ruled by kings for some time the city came under the power of the Romans and is now joined with Crete into one Province. But Apollonia, Barcê, Taucheira, Berenicê, and the other towns near by, are dependencies of Cyrenê.
Bordering on Cyrenaea is the country which produces silphium and the Cyrenaean juice, which latter is produced by the silphium through the extraction of its juice. But it came near giving out when the barbarians invaded the country because of some grudge and destroyed the roots of the plant. The inhabitants are nomads. The Cyrenaeans who became famous were Aristippus the Socratic philosopher, who also laid the foundations of the Cyrenaïc philosophy; and his daughter, Aretê by name, who succeeded him as head of the school; and again her son Aristippus, Aretê's successor, who was called Mêtrodidactus; and Anniceris, who is reputed to have revised the doctrines of the Cyrenaïc sect and to have introduced in place of it those of the Annicerian sect. Callimachus, also, was a Cyrenaean, and Eratosthenes, both of whom were held in honour by the Aegyptian kings, the former being a poet and at the same time a zealous student of letters, and the latter being superior, not only in these respects, but also in philosophy, and in mathematics, if ever a man was. Furthermore, Carneades, who by common agreement was the best of the Academic philosophers, and also Apollonius Cronus, were from Cyrenê, the latter being the teacher of Diodorus the Dialectician, who also was given the appellation "Cronus," certain persons having transferred the epithet of the teacher to the pupil. After Apollonia one comes to the remainder of the coast of the Cyrenaeans, which extends as far as Catabathmus, a distance of two thousand two hundred stadia; the coasting-voyage is not at all easy, for there are but few harbours, mooring-places, settlements, and watering-places. Among the places along the coast that are best known are Naustathmus and Zephyrium, which has anchorage, and a second Zephyrium, and a promontory Cherronesus, which has a harbour. This promontory lies opposite Cyclus in Crete; and the distance across is one thousand five hundred stadia if one has a south-west wind; and then one comes to a kind of temple of Heracles, and, above it, to a village called Paliurus; and then one comes to a harbour, Menelaüs, and to Ardanis, which is a low-lying promontory with a mooring-place; and then to a large harbour, opposite which lies the Cherronesus in Crete, the interval between the two places being about two thousand stadia; indeed, I might almost say that Crete as a whole, being narrow and long, lies opposite, and parallel, to this coast. After the large harbour one comes to another harbour, which is called Plynus, and above it lies Tetrapyrgia; but the place is called Catabathmus; and Cyrenaea extends thus far. The remaining part of the coast, extending to Paraetonium and thence to Alexandria, I have already mentioned in my account of Egypt.
The country lying deep in the interior above the Syrtis and Cyrenaea, a barren and arid region, is occupied by the Libyans: first by the Nasamones, and then by the Psyllians and certain Gaetulians, and then by the Garamantes, and, still more towards the east, by the Marmaridae, who border to a greater extent on Cyrenaea and extend as far as Ammon. Now it is said that persons going on foot from the recess of the Great Syrtis, from about the neighbourhood of Automala, approximately in the direction of winter sunrise, arrive at Augilab on the fourth day. This region resembles Ammon, being productive of palm-trees and also well supplied with water. It lies above Cyrenaea to the south, and for a distance of one hundred stadia produces trees, but for another hundred the land is only sown, although, on account of its aridity, the land does not grow rice. Above this region is the country which produces silphium; and then one comes to the uninhabited country and to that of the Garamantes. The country which produces silphium is narrow, long, and somewhat arid, extending in length, as one goes approximately towards the east, about one thousand stadia, and in breadth three hundred or a little more, at least that part which is known; for we may conjecture that all lands lying in unbroken succession on the same parallel of latitude are similar as regards both climate and plants, but since several deserts intervene, we do not know all these regions. Similarly, the regions above Ammon and the oases as far as Aethiopia are likewise unknown. Neither can we tell the boundaries either of Aethiopia or of Libya, nor yet accurately even those of the country next to Aegypt, much less of that which borders on the Ocean.
This, then, is the lay of the different parts of our inhabited world; but since the Romans occupy the best and the best known portions of it, having surpassed all former rulers of whom we have record, it is worth while, even though briefly, to add the following account of them. Now I have already stated that, setting out with only one city, Rome, the Romans acquired the whole of Italy through warfare and statesmanlike rulership, and that, after Italy, by exercising the same superior qualities, they also acquired the regions round about Italy. And of the continents, being three in number, they hold almost the whole of Europe, except that part of it which lies outside the Ister River and the parts along the ocean which lie between the Rhenus and the Tanaïs Rivers. Of Libya, the whole of the coast on Our Sea is subject to them; and the rest of the country is uninhabited or else inhabited only in a wretched or nomadic fashion. In like manner, of Asia also, the whole of the coast on our Sea is subject to them, unless one takes into account the regions of the Achaei and the Zygi and the Heniochi, who live a piratical and nomadic life in narrow and sterile districts; and of the interior and the country deep inland, one part is held by the Romans themselves and another by the Parthians and the barbarians beyond them; and on the east and north live Indians and Bactrians and Scythians, and then Arabians and Aethiopians; the some further portion is constantly being taken from these peoples and added to the possessions of the Romans. Of this whole country that is subject to the Romans, some parts are indeed ruled by kings, but the Romans retain others themselves, calling them Provinces, and send to them praefects and collectors of tribute. But there are also some free cities, of which some came over to the Romans at the outset as friends, whereas others were set free by the Romans themselves as a mark of honour. There are also some potentates and phylarchs and priests subject to them. Now these live in accordance with certain ancestral laws.
But the Provinces have been divided in different ways at different times, though at the present time they are as Augustus Caesar arranged them; for when his native land committed to him the foremost place of authority and he became established as lord for life of war and peace, he divided the whole of his empire into two parts, and assigned one portion to himself and the other to the Roman people; to himself, all parts that had need of a military guard (that is, the part that was barbarian and in the neighbourhood of tribes not yet subdued, or lands that were sterile and difficult to bring under cultivation, so that, being unprovided with everything else, but well provided with strongholds, they would try to throw off the bridle and refuse obedience), and to the Roman people all the rest, in so far as it was peaceable and easy to rule without arms; and he divided each of the two portions into several Provinces, of which some are called "Provinces of Caesar" and the others "Provinces of the People." And to "Provinces of Caesar" Caesar sends legati and procurators, dividing the countries in different ways at different times and administering them as the occasion requires, whereas to the "Provinces of the People" the people send praetors or proconsuls, and these Provinces also are brought under different divisions whenever expediency requires. But at the outset Caesar organised the Provinces of the People by creating, first, two consular provinces; I mean ( Libya, in so far as it was subject to the Romans, except the part which was formerly subject to Juba and is now subject to Ptolemy his son, and ( the part of Asia that lies this side the Halys River and the Taurus, except the countries of the Galatians and of the tribes which had been subject to Amyntas, and also of Bithynia and the Propontis; and, secondly, ten praetorial provinces, first, in Europe and the islands near it, I mean ( Iberia Ulterior, as it is called, in the neighbourhood of the Baetis and Anas Rivers, ( Narbonitis in Celtica, ( Sardo together with Cyrnus, ( Sicily, (5 and Macedonia and, in Illyria, the country next to Epeirus, Achaea as far as Thessaly and Aetolia and Acarnania and certain Epeirotic tribes which border on Macedonia, Crete along with Cyrenaea, Cypros, and Bithynia along with the Propontis and certain parts of the Pontus. But the rest of the Provinces are held by Caesar; and to some of these he sends as curators men of consular rank, to others men of praetorian rank, and to others men of the rank of knights. Kings, also, and potentates and decarchies are now, and always have been, in Caesar's portion.  |
|
|
|
|
|
|